The observation of a conductivity threshold on the electrorheological effect of p-phenylenediamine oxidized with p-benzoquinone

Abstract

p-Phenylenediamine was oxidized with p-benzoquinone in the presence of 0.1–5 M methanesulfonic acid (MSA) solutions. The resulting methanesulfonate salts of 2,5-(di-p-phenylenediamine)-1,4-benzoquinone are semiconducting and the particles were further suspended in silicone oil in a weight ratio of 1 : 9 in order to create novel electrorheological fluids. Conductivity measurements using the two-point method along with dielectric spectroscopy were carried out in order to investigate their electrical and dielectric properties, including their silicone-oil suspensions. The higher the concentration of MSA was present during the synthesis, the higher the conductivity was observed. Nevertheless, a certain threshold of the ER effect has been found and a further significant increase in conductivity causes only a slight ER effect enhancement. At an electric field strength of 1.5 kV mm⁻¹, the observed yield stresses read at the low shear rate values were 11.5 Pa, 20.3 Pa, 24.5 Pa, and 28.2 Pa for particles with conductivities 1.5 × 10⁻¹², 8.5 × 10⁻¹¹, 1.0 × 10⁻⁸, and 1.5 × 10⁻⁷ S cm⁻¹, respectively. From dielectric spectra, it was observed that the conductivity of the particles determines the relaxation times of their silicone-oil suspensions.

---

1. Introduction

Electrorheological (ER) fluids are known as liquids whose rheological properties can be controlled by means of an external electric field. Generally, dry-based ER fluids are suspensions consisting of electrically polarizable particles dispersed in a non-conducting liquid medium. In the absence of electric field, particles are randomly distributed within ER fluids; however, the application of electric field leads to a creation of electric field-induced chain-like structures along the electric field strength direction spanning a gap between the electrodes due to dipole–dipole interactions.^1–3 This formation of internal structures is fast and reversible,⁴ and leads to a steep increase in the viscosity⁵ of ER fluids. This phenomenon is called the ER effect.

It was proposed that the main factors responsible for the ER effect of ER fluids are the optimal conductivity of dispersed particles and the high dielectric relaxation strength of the ER fluids.^3,6,7 The role of conductivity is major mainly in the presence of a DC electric field and at low frequencies of an AC electric field.⁸ Conductivity of the particles also determines the response time of ER fluids to an applied electric field.⁹ It has been demonstrated that the local electric field, E_L, between two aligned polar particles is much higher than the overall applied electric field, E.^10,11 For a strong E_L (E_L ≫ E) leading to the formation of stiff chain-like structures, the ratio ε_p/ε_lm, where ε_p represents the relative permittivity of dispersed particles and ε_lm is the relative permittivity of a liquid medium, is crucial. Thus, a high mismatch between the dielectric constants of a dispersed phase and a liquid medium is required for high ER effects. Introducing of polar groups into the particles can then lead to high ER effects due to their increased polarizability.^11,12 The other important factors influencing the ER effect are the size and morphology of the dispersed particles.¹³ It has been shown that ER fluids based on polypyrrole nanofibers¹⁴ or polyaniline nanofibers¹⁵ exhibit a higher ER effect than ER fluids based on their globular analogues with similar conductivities. Also the higher aspect ratio of the fibers contributes to higher ER effects.¹⁴ In general, in the case of the particles with plate-like or fibrous morphology, these exhibit higher ER response also due to the higher interparticle friction.⁷ On the other hand, Cheng et al. in their work have shown that in the case of dielectric particles the smaller particle-based ER fluid exhibited higher ER effects probably due to an increased content of polar molecules together with their increased surface area.¹⁶

Various ER fluids have been introduced so far, where a continuous phase was mainly represented by mineral or silicone oils, owing to their low relative permittivity. As a dispersed phase, both organic and inorganic electrically polarizable particles have been used. The latter are represented by clays, various titanium oxides,^17,18 silica particles,¹⁹etc. Organic particles are primarily represented by various carbon materials^20–23 and conducting polymers such as polyaniline,^24–26 polypyrrole,^27,28 and their derivatives.²⁹ Polyphenylenediamine, a derivative of polyaniline, can form three isomers, i.e. poly(ortho-, meta-, and para-phenylenediamine). All of them have been used in ER fluids as a dispersed phase, and the para isomer has exhibited the highest ER effect among them due to its highest conductivity.²⁹ Conductivity of these materials is provided by the presence of a conjugated system containing sp² hybridized carbon atoms possessing delocalized electrons. The movement of these electrons is even enhanced by a doping process. While the conductivity of deprotonated conducting polymers is low (approximately 10⁻¹²–10⁻⁹ S cm⁻¹),^29,30 by doping process it increases even over units of S cm⁻¹.³¹ This controllable conductivity makes these materials favorable for use in ER fluids. However, oligomers of conducting polymers prepared in the presence of p-benzoquinone forming trimers do not contain the conjugated system. Thus, the conductivity of oligomers can be then understood as a result of an inter-molecular charge transport,^32,33 where the delocalized electrons are responsible for the hole transport and hydrogen bonding interactions influencing the electron transport.³⁴ The doping process is then crucial for the conductivity of such oligomers.

Aniline oligomers have been recently introduced in electrorheology exhibiting high ER effects³⁵ that can be even increased by their carbonization in an inert atmosphere.²² Their ER effects increase with the amount of polar groups presented in the structure of aniline oligomers. Therefore, this study deals with the synthesis of analogous “trimers” obtained by the oxidation of p-phenylenediamine (pPDA) with p-benzoquinone in the solutions of methanesulfonic acid (MSA) along with their utilization as a dispersed phase in novel ER fluids. It is known that high concentrations of MSA presented during the synthesis should provide particles with high conductivity and polarizability³⁶ suitable for their use in electrorheology.

2. Experimental

2.1. Preparation of solids

pPDA (0.2 M, Sigma-Aldrich) was oxidized with p-benzoquinone (0.5 M, Sigma-Aldrich) in MSA (Sigma-Aldrich) aqueous solutions of various concentrations of MSA (0.1–5 M).³⁶ Both reactants were dissolved separately in MSA solutions, the solutions were mixed, and left at room temperature for 24 h. The solids were then isolated by filtration, rinsed with corresponding acid solution, then with ethanol, dried in the air at room temperature, and then over the silica gel in a desiccator. For more detailed characterization of the particles the reader is referred to ref. 36.

2.2. Characterization of the particles

Morphology and dimensions of the particles were observed using scanning electron microscopy (SEM; Vega II LMU, Tescan, Czech Republic). Conductivity of the particles was measured by the two-point method at ambient temperature using an electrometer (Keithley 6517B, USA). For the measurement of conductivity the particles were pressed into pellets of diameter 13 mm. Thermal stability of the prepared particles was studied using thermogravimetric analysis (TGA; TA Q500, TA Instruments, USA). Thermogravimetic measurements were carried out in a nitrogen atmosphere at a heating rate of 10 °C min⁻¹ in the temperature range 25–900 °C. In the case of SEM images and the ER fluid preparation, the particles were firstly ground using a ball mill Lab Wizz 320 (Laarmann, The Netherlands), and further sieved on a sieve with a mesh diameter of 45 μm. The particles were subsequently dried in a vacuum oven at 60 °C for 24 h and stored in a desiccator for further analyses.

2.3. Preparation of ER fluids

Each batch of the dry particles was mixed separately with silicone oil (Fluid 200, Dow Corning, UK, viscosity η_c = 108 mPa s, density ρ_c ≈ 0.965 g cm⁻³) in a mass ratio of 1 : 9 in order to create ER fluids of particle concentration 10 wt%. Before each measurement, the prepared ER fluids were manually stirred with a glass stick and sonicated for 1 min to ensure homogenous distribution of the particles within the suspension.

2.4. Rheological measurements

Rheological parameters of the ER fluids in the absence and in the presence of electric field were investigated using a rotational rheometer Bohlin Gemini (Malvern Instruments, UK) with a parallel-plate geometry (a gap of 0.5 mm and a diameter of 40 mm). Experiments were carried out at 25 °C, and electric field strengths of 0.5–3 kV mm⁻¹ were supplied by a DC high voltage supplier TREK 668B (TREK, USA). The rheological measurements were performed in both the steady shear and oscillatory mode at shear rates 0.1–200 s⁻¹ and at the frequencies 0.1–10 Hz, respectively. To ensure that the measurements in a frequency sweep mode are carried out in a linear viscoelastic region, the amplitude sweep mode experiment at the fixed frequency 1 Hz was firstly carried out. Before each measurement in the presence of electric field, the electric field was applied for 1 min prior the shearing in order to provide sufficient time for the creation of oriented chain-like structures. After each measurement, the ER fluids were sheared for 60 s at a constant shear rate of 50 s⁻¹ to destroy the residual structures.

2.5. Dielectric measurements

Dielectric spectra of the prepared ER fluids were studied using a Broadband Dielectric Impedance Analyzer Concept 40 (Novocontrol, Germany) in the frequency range 0.1–10⁷ Hz. The dielectric parameters were obtained by application of the Havriliak–Negami model (eqn (1)) to the obtained data.³⁷

In eqn (1), ε* stays for complex permittivity, ε₀′ and ε_∞′ for their real part at “static” and “infinite” frequency, respectively. Their algebraic difference, Δε, represents the dielectric relaxation strength, and a parameter ω represents angular frequency. The relaxation time is expressed as τ_rel. Parameters a and b describe a width and skewness of the relaxation time distribution, respectively.³⁷

3. Results and discussion

3.1. Particle characterization

It has been demonstrated,³⁶ that the oxidation of p-PDA with p-benzoquinone produced a “trimer”, 2,5(di-p-phenylenediamine)-1,4-benzoquinone (DPB; Fig. 1 (1)). p-Benzoquinone is thus not a mere oxidant, as it is included in the final structure of oligomers.^33,38,39 When the reaction is carried out in the solutions of MSA the corresponding methanesulfonate salts are produced (Fig. 1 (2)). The degree of incorporation of MSA counter-ions into the salts depends obviously on the concentration of MSA in the reaction mixtures. Such salts are semiconducting, as discussed below.

Fig. 1 p-Phenylenediamine is oxidized with p-benzoquinone to 2,5(di-p-phenylenediamine)-1,4-benzoquinone (1). After the “keto–enol” rearrangement, the resulting imine nitrogen atoms may become protonated with (methanesulfonate) acid (HA) to corresponding salt (2).

Morphology of the DPB particles is not affected by the concentration of MSA during their synthesis (Fig. 2). These particles possess irregular shape and create agglomerates (Fig. 2a–c), whose sizes increase with higher MSA concentration (Fig. 2d–f). The higher amount of MSA introduced in the DPB oligomer trimers increases their polarity and also provides oxygen atoms that can form hydrogen bonds with hydrogens from the trimers leading to a creation of agglomerates. Thus, with increasing of MSA concentration, the size of the particles increases.

Fig. 2 SEM images of DPB trimers prepared in the presence of 0.1 M (a), 0.2 M (b), 0.5 M (c), 1 M (d), 2 M (e), and 5 M (f) MSA.

Thermal decomposition of DPB salts can be divided into three main steps. The first step between 25 and 100 °C represents the loss of adsorbed humidity. The amount of adsorbed water increases with increasing concentration of MSA present during the synthesis of DPB (Fig. 3a). While for particles prepared at low concentrations of MSA the loss was 4–6%, for the particles prepared in the presence of 2 M and 5 M MSA the losses were 9.2 and 14.3%, respectively. The higher amount of MSA salts incorporated into DPB increases their polar character; thus, they then adsorb more humidity. The second step was found at approximately 100–260 °C. This can be associated with decomposition of p-PDA⁴⁰ or, more likely, with the release of MSA constituting the DPB salt. The further losses up to ∼370 °C can be among others ascribed mainly to leaving of sulfur dioxide.⁴¹ This trend considerably increased with the increasing concentration of MSA presented during the synthesis (Fig. 3b) due to higher amount of MSA salts linked to DPB. The decomposition at higher temperatures represents the transformation of DPB into a nitrogen-enriched carbonaceous structure involving probable leaving of carbon monoxide, carbon dioxide, aromatic amines and organic groups containing oxygen (p-benzoquinone).⁴¹

Fig. 3 TGA (a) and DTGA (b) curves of DPB prepared at various concentrations of MSA. Atmosphere: N₂; heating rate: 10 °C min⁻¹.

The low conductivity of DPB salts prepared at low concentration of the MSA (Table 1) can be explained by neutralization of the MSA with the monomer pPDA.³³ The steep increase in conductivity of about three orders of magnitude between the particles prepared in the presence of 0.2 M and 0.5 M MSA resembles a certain percolation threshold. With a further increase in concentration of MSA, the conductivity increased up to the ≈10⁻⁴ S cm⁻¹ (Table 1). The MSA serves as a dopant; thus, the higher concentration of MSA leads to higher conductivity of DPB obtained also due to the formation of a higher amount of hydrogen bonds.³⁴

Table 1 Conductivity of DPB prepared at various molar concentrations of MSA

[MSA] (mol L^−1)	Conductivity, σ, (S cm^−1)
0.1	1.5 × 10^−12
0.2	8.5 × 10^−11
0.5	1.0 × 10^−8
1	1.4 × 10^−7
2	5.8 × 10^−5
5	3.4 × 10^−4

---

3.2. Electrorheological behavior

The ER fluids based on DPB prepared in the presence of 2 M and 5 M MSA caused a short-circuit of the measuring apparatus due to too high conductivity of these particles (the limit for passing current was 5 mA). Therefore, properties of these ER fluids are no longer discussed. The conductivity of DPB prepared in the presence of 0.5 M and 1 M MSA enabled the measurements of their ER fluids only at the electric field strengths up to 1.5 kV mm⁻¹.

The prepared ER fluids exhibited Newtonian behavior in the absence of external electric field, which is expressed as a linear increase in shear stress with the slope = 1 (Fig. 4a–c). Only the ER fluid based on pPDA particles prepared in 1 M MSA showed slightly pseudoplastic fluid character (Fig. 4d). After the application of an external electric field, the ER fluids started to behave as Bingham fluids. The ER effect of the prepared ER fluids increased with the increasing concentration of MSA presented during the synthesis, thus, with the higher conductivity of the particles the higher ER effect was observed for their ER fluid, which fits well with the theory that the stiffness of the induced chain-like structures is mainly directed by the conductivity of the particles in the presence of a DC electric field.⁸ The higher conductivity of the particles leads to higher electrostatic interactions between them. Such chain-like structures can then withstand higher hydrodynamic forces before the flow begins. The increasing size of the particles could also positively contribute to higher ER effects of ER fluids based on particles prepared in a higher amount of MSA concentrations.^42,43

Fig. 4 The double-logarithmic plot of the shear stress, τ, on the shear rate, [small gamma, Greek, dot above], for the ER fluids based on DPB prepared in the presence of 0.1 M (a), 0.2 M (b), 0.5 M (c), and 1 M (d) MSA at various electric field strengths.

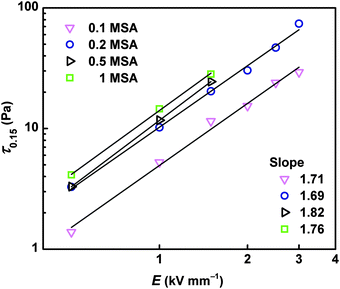
The double-logarithmic plot of the yield stress of the ER fluids on the electric field strength conforms the power law trend

τ_y = q × E^α (2)

where τ_y represents a yield stress, q and E stand for rigidity of the system and electric field strength, respectively, and an exponent α is the slope of the exponential equation.³⁵ Since it is complicated to exactly determine a yield stress, the values of shear stress at a very low shear rate of 0.15 s⁻¹, τ_0.15, were used for this evaluation. For well-developed internal structures within the ER fluids upon an application of an external electric field, the values of exponent α should be within 1.5–2. The slope of an exponent for all prepared ER fluids is within this border and the power law fits very well the τ value dependence on E (Fig. 5). In addition, it is evident that with an increasing amount of MSA presented during the synthesis (increasing conductivity) the ER effect increases. A further increase in the conductivity of the particles would probably lead to higher ER effects, however, also to higher current density passing through the ER fluid, which was represented by the short-circuits in a measuring device for the more conducting particle-based ER fluids.

Fig. 5 The double-logarithmic plot of shear stress values obtained at a shear rate of 0.15 s⁻¹, τ_0.15, vs. electric field strength, E, for the prepared ER fluids. The lines represent the exponential fit and their slope values involved in the graph.

Nevertheless, from the dependence of the yield stress on the MSA concentration, it can be seen that the increment in the ER effect is not exactly proportional to the increment in conductivity of the particles. While a certain threshold in the conductivity of DPB salts was observed between the concentrations 0.2 and 0.5 MSA, the sort of threshold in the ER effect can be observed between 0.1 and 0.2 MSA concentrations (Fig. 6). In other words, although the DPB prepared at 0.5 MSA solution possesses conductivity of about 3 orders magnitude higher than those prepared at 0.2 MSA, the change in the ER effect of ER fluids based on 0.2 and 0.5 MSA particles is not so significant, as between ER fluids of 0.1 and 0.2 MSA-based particles, where the conductivity difference was only one order of magnitude (Fig. 6, inset). This indicates that a certain threshold of formation of the particles exists, under which a further increment of conductivity does not provide a proportional increase in the ER effect.

Fig. 6 The plot of shear stress values obtained at a shear rate of 0.15 s⁻¹vs. concentration of MSA presented during the synthesis of DPB for their 10 wt% ER fluids. The inset depicts shear stress values obtained at a shear rate of 0.15 s⁻¹, τ_0.15, vs. conductivity of the suspended particles.

Behavior closer to the real applications is described by dynamic loadings of the prepared ER fluids presented by frequency sweep measurements with a fixed strain inside the linear viscoelastic region giving information about viscoelastic behavior of prepared ER fluids. The prepared ER fluids based on DPB behave like liquid materials, which is represented by the values of the viscous modulus higher than the storage modulus (G′′ > G′) (Fig. 7a). However, after the application of an electric field, the ER fluids underwent a transition from liquid-like to a solid-like state leading to a steep increase in both moduli; nevertheless, the increase in the storage modulus is much more significant and starts to dominate over the viscous modulus (G′′ ≪ G′). First things first, the ER fluids based on DPB prepared in 1 M, 0.5 M, 0.2 M, and 0.1 M MSA solution exhibit the highest ER effect (the storage modulus) in oscillatory measurements at an electric field strength of 1.5 kV mm⁻¹ (Fig. 7b). These findings correlate well with the steady shear measurements, the conductivity of the particles, and also with dielectric properties of the prepared ER fluids. Thus, the higher conductivity and dielectric relaxation strength of the particles lead to stiffer created chain-like structures induced by an electric field.

Fig. 7 The double-logarithmic plot of the storage, G′ (solid symbols), and viscous, G′′ (open symbols), moduli vs. the angular frequency, ω, for ER fluids based on DPB prepared in the presence of various MSA solutions in the absence (a) and in the presence of an electric field strength of 1.5 kV mm⁻¹ (b).

3.3. Impedance spectroscopy

Values of dielectric relaxation strengths of 0.1 M and 0.2 M MSA-based ER fluids are almost the same (Table 2); however, the relaxation process of the latter ER fluid occurs at higher frequencies than the former one, which is represented by its faster relaxation time (Fig. 8a). The faster relaxation time positively contributes to the higher ER effect. The conductivity of DPB salts dramatically increased at concentration 0.5 MSA (Table 1). Dielectric spectra of their ER fluids are then distorted at low frequencies probably due to the electrode polarization, which is observed in conducting suspensions at low frequencies. In an alternating electric field, the free ions start to migrate to electrodes,⁴⁴ which leads to development of ionic double layers on the electrodes implying a huge polarization of the double layer. Nevertheless, the relaxation times of the ER fluids and their polarizability can be read from undistorted data (Fig. 8b). Although, the polarizability is higher for the ER fluids based on DPB prepared in 0.5 MSA, the faster relaxation time is observed for the ER fluids based on DPB prepared in 1 MSA, corresponding to the higher conductivity of the latter particles. With increasing concentration of MSA presented during the synthesis of DPB, the higher polarizability and faster relaxation times are observed, which is in accordance with findings in the dielectric spectra of aniline oligomers by Mrlik et al.³⁵

Table 2 Dielectric parameters of prepared ER fluids obtained from the Havriliak–Negami model

Parameter	Concentration of MSA
	0.1 M	0.2 M	0.5 M	1 M
ε 0′	4.86	4.89	6.55	6.14
ε ∞′	3.02	3.04	3.00	3.00
Δε	1.84	1.85	3.55	3.14
τ rel [s]	1.80	1.34 × 10^−1	5.01 × 10^−2	7.54 × 10^−3
a	0.80	0.67	0.89	0.39
b	0.62	0.96	0.42	0.99

---

Fig. 8 Real, ε′, (solid symbols) and imaginary, ε′′, (open symbols) parts of complex permittivity for the ER fluids based on DPB prepared in the presence of 0.1 M and 0.2 M MSA (a), and 0.5 M and 1 M MSA (b). The full lines represent the Havriliak–Negami model fits. The dashed lines represent original data indicating the electrode polarization that were excluded from fitting.

4. Conclusions

Oxidation of p-phenylenediamine with p-benzoquinone in the presence of methanesulfonic acid leads to the formation of “trimers”, 2,5(di-p-phenylenediamine)-1,4-benzoquinone methanesulfonate salts. Their conductivity increases with concentration of methanesulfonic acid present during the synthesis. The difference of about three orders of magnitude between conductivity of particles prepared in 0.2 M and 0.5 M methanesulfonic acid represents a certain percolation threshold, which prompts that the conductivity of trimer salts is directed by inter-molecular charge transport. Electrorheological fluids based on the suspension of these salts in silicone oil exhibited a considerable electrorheological effect directed by conductivity and polarizability of the particles. The higher the conductivity the higher and more stable electrorheological effect was observed. On the other hand, a certain threshold at which a further increase of conductivity only slightly contributes to the ER effect was found.

Acknowledgements

The author T. P. would like to thank the Internal Grant Agency of Tomas Bata University (IGA/CPS/2015/007) for financial support. This work was supported by the Ministry of Education, Youth and Sports of the Czech Republic – Program NPU I (LO1504). The support of the Czech Science Foundation (P205/12/0911) is also gratefully acknowledged.

References

1. H. S. Chae, W. L. Zhang, S. H. Piao and H. J. Choi, Appl. Clay Sci., 2015, 107, 165–172.
2. D. S. Jang and H. J. Choi, Colloids Surf., A, 2015, 469, 20–28.
3. Y. Z. Dong, J. B. Yin and X. P. Zhao, J. Mater. Chem. A, 2014, 2, 9812–9819.
4. M. Sedlacik, M. Mrlik, Z. Kozakova, V. Pavlinek and I. Kuritka, Colloid Polym. Sci., 2013, 291, 1105–1111.
5. M. Mrlik, V. Pavlinek, Q. L. Cheng and P. Saha, Int. J. Mod. Phys. B, 2012, 26, 1250007.
6. T. Hao, Adv. Colloid Interface Sci., 2002, 97, 1–35.
7. J. B. Yin, X. X. Wang, R. T. Chang and X. P. Zhao, Soft Matter, 2012, 8, 294–297.
8. L. C. Davis, J. Appl. Phys., 1992, 72, 1334–1340.
9. T. Hao, J. Colloid Interface Sci., 1998, 206, 240–246.
10. L. C. Davis, J. Appl. Phys., 1997, 81, 1985–1991.
11. R. Shen, X. Z. Wang, Y. Lu, D. Wang, G. Sun, Z. X. Cao and K. Q. Lu, Adv. Mater., 2009, 21, 4631–4635.
12. T. Plachy, M. Mrlik, Z. Kozakova, P. Suly, M. Sedlacik, V. Pavlinek and I. Kuritka, ACS Appl. Mater. Interfaces, 2015, 7, 3725–3731.
13. A. Lengalova, V. Pavlinek, P. Saha, O. Quadrat and J. Stejskal, Colloids Surf., A, 2003, 227, 1–8.
14. X. A. Xia, J. B. Yin, P. F. Qiang and X. P. Zhao, Polymer, 2011, 52, 786–792.
15. J. B. Yin, X. P. Zhao, X. Xia, L. Q. Xiang and Y. P. Qiao, Polymer, 2008, 49, 4413–4419.
16. Y. C. Cheng, J. J. Guo, X. H. Liu, A. H. Sun, G. J. Xu and P. Cui, J. Mater. Chem., 2011, 21, 5051–5056.
17. Y. He, Q. L. Cheng, V. Pavlinek, C. Z. Li and P. Saha, J. Ind. Eng. Chem., 2009, 15, 550–554.
18. W. Q. Jiang, C. X. Jiang, X. L. Gong and Z. Zhang, J. Sol-Gel Sci. Technol., 2009, 52, 8–14.
19. Q. L. Cheng, V. Pavlinek, Y. He, A. Lengalova, C. Z. Li and P. Saha, Colloids Surf., A, 2008, 318, 169–174.
20. B. Sim, W. L. Zhang and H. J. Choi, Mater. Chem. Phys., 2015, 153, 443–449.
21. W. L. Zhang and H. J. Choi, Soft Matter, 2014, 10, 6601–6608.
22. T. Plachy, M. Sedlacik, V. Pavlinek, M. Trchová, Z. Morávková and J. Stejskal, Chem. Eng. J., 2014, 256, 398–406.
23. J. Y. Hong, E. Lee and J. Jang, J. Mater. Chem. A, 2013, 1, 117–121.
24. H. J. Choi, T. W. Kim, M. S. Cho, S. G. Kim and M. S. Jhon, Eur. Polym. J., 1997, 33, 699–703.
25. M. Stenicka, V. Pavlinek, P. Saha, N. V. Blinova, J. Stejskal and O. Quadrat, Colloid Polym. Sci., 2011, 289, 409–414.
26. Y. D. Liu, F. F. Fang and H. J. Choi, Mater. Lett., 2010, 64, 154–156.
27. J. W. Goodwin, G. M. Markham and B. Vincent, J. Phys. Chem. B, 1997, 101, 1961–1967.
28. Y. D. Kim and I. C. Song, J. Mater. Sci., 2002, 37, 5051–5055.
29. J. Trlica, P. Saha, O. Quadrat and J. Stejskal, Physica A, 2000, 283, 337–348.
30. M. Stenicka, V. Pavlinek, P. Saha, N. V. Blinova, J. Stejskal and O. Quadrat, Colloid Polym. Sci., 2009, 287, 403–412.
31. T. Abdiryim, R. Jamal and I. Nurulla, J. Appl. Polym. Sci., 2007, 105, 576–584.
32. M. Mrlik, R. Moucka, M. Ilcikova, P. Bober, N. Kazantseva, Z. Spitalsky, M. Trchova and J. Stejskal, Synth. Met., 2014, 192, 37–42.
33. J. Stejskal, P. Bober, M. Trchová, J. Horský, J. Pilař and Z. Walterová, Synth. Met., 2014, 192, 66–73.
34. L. Liu, G. C. Yang, X. D. Tang, Y. Geng, Y. Wu and Z. M. Su, J. Mol. Graphics, 2014, 51, 79–85.
35. M. Mrlik, M. Sedlacik, V. Pavlinek, P. Bober, M. Trchová, J. Stejskal and P. Saha, Colloid Polym. Sci., 2013, 291, 2079–2086.
36. J. Stejskal, M. Trchová, Z. Morávková, P. Bober, M. Bláha, J. Pfleger, P. Magdziarz, J. Prokeš, M. Havlicek, N. Sariciftci, A. Sperlich, V. Dyakonov and Z. Zujovic, J. Solid State Electrochem., 2015 DOI:10.1007/s10008-015-2838-3.
37. S. Havriliak and S. Negami, Polymer, 1967, 8, 161–210.
38. C. H. B. Silva, D. C. Ferreira, V. R. L. Constantino and M. L. A. Temperini, J. Raman Spectrosc., 2011, 42, 1653–1659.
39. S. R. Surwade, V. Dua, N. Manohar, S. K. Manohar, E. Beck and J. P. Ferraris, Synth. Met., 2009, 159, 445–455.
40. I. M. Khan and A. Ahmad, J. Mol. Struct., 2010, 975, 381–388.
41. Z. Morávková, M. Trchová, E. Tomšík, A. Zhigunov and J. Stejskal, J. Phys. Chem. C, 2013, 117, 2289–2299.
42. A. Kawai, K. Uchida and F. Ikazaki, Int. J. Mod. Phys. B, 2002, 16, 2548–2554.
43. Y. G. Ko, U. S. Choi and Y. J. Chun, J. Colloid Interface Sci., 2009, 335, 183–188.
44. P. Ben Ishai, M. S. Talary, A. Caduff, E. Levy and Y. Feldman, Meas. Sci. Technol., 2013, 24, 102001.

---