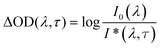Antimony sulfide as a light absorber in highly ordered, coaxial nanocylindrical arrays: preparation and integration into a photovoltaic device

Abstract

We demonstrate the preparation of functional ‘extremely thin absorber’ solar cells consisting of massively parallel arrays of nanocylindrical, coaxial n-TiO₂/i-Sb₂S₃/p-CuSCN junctions. Anodic alumina is used as an inert template that provides ordered pores of 80 nm diameter and 1–50 μm length. Atomic layer deposition (ALD) then coats pores of up to 20 μm with thin layers of the electron conductor and the intrinsic light absorber. The crystallization of the initially amorphous Sb₂S₃ upon annealing is strongly promoted by an underlying crystalline TiO₂ layer. After the remaining pore volume is filled with the hole conductor by solution evaporation, the resulting coaxial p-i-n junctions display stable diode and photodiode electrical characteristics. A recombination timescale of 40 ms is extracted from impedance spectroscopy in open circuit conditions, whereas transient absorption spectroscopy indicates that holes are extracted from Sb₂S₃ with a lifetime of 1 ns.

---

Introduction

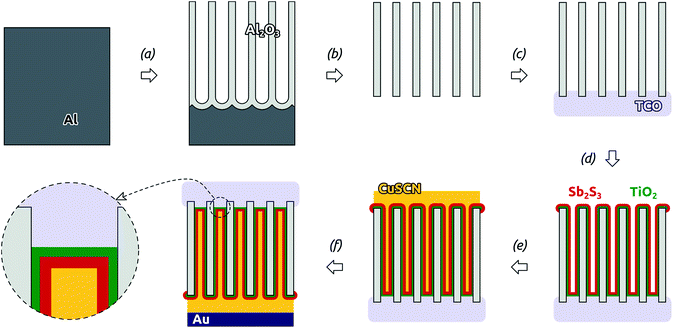
Nanostructured ‘third-generation’ types of solar cells are meant to replace the costly materials of planar cells (needed for the extreme efficiency of either light absorption or charge transport) with inexpensive ones by exploiting the geometric parameters smartly.^1–4 However, these systems have not reached the efficiencies of the planar cells yet. Part of the difficulty in the optimization of these cells resides in the lack of control over the structure of the interface, typically based on a colloidal oxide layer.^5,6 A direct investigation of the device physics via systematic variation of well-defined individual geometric parameters would be possible in a semiconductor junction organized in parallel cylindrical nanostructures of tunable length and diameter.¹⁵ This paper demonstrates the preparation of such a coaxial nanocylindrical solar cell, the principle of which is illustrated in Scheme 1.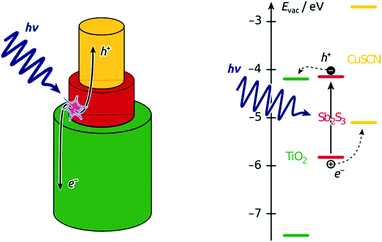

Scheme 1 Function principle of the coaxial nanocylindrical solar cell. Left, schematic view of the geometry of one individual coaxial p-i-n junction amongst the large numbers of parallel cylinders constituting the solar cell device. Right, band diagram of the semiconductors involved.^7–14

We focus on the so-called extremely thin absorber (ETA) cell, also described as a solid dye-sensitized cell (sDSSC). In ETA cells, a very thin intrinsic layer of strongly absorbing, inorganic solid (typically a II–VI or V₂–VI₃ semiconductor, such as CdSe, In₂S₃ or Sb₂S₃) is combined with solid electron and hole conductors, such as n-TiO₂ and p-CuSCN, respectively.^16,17 We propose a general preparative strategy based on coating the ordered, cylindrical nanopores of ‘anodic’ alumina (used as the template) with consecutive layers of the functional materials. To this goal, we use atomic layer deposition (ALD) as the crucial method that enables the experimentalist to coat thin layers on porous substrates with the following properties: (a) homogeneous deposition along the length of deep pores; (b) accurate tuning of the thickness deposited between 1 and 20 nm approximately; (c) high quality of the material, in particular accurate stoichiometry and absence of unwanted oxide.^18–21 We have previously demonstrated that ALD is applicable to the deposition of Sb₂S₃ as the light absorber of ETA cells based on colloidal TiO₂ crystals.²² We now have characterized the ALD of Sb₂S₃ in pores, investigated the necessary post-deposition treatment, and quantified some of the photovoltaic parameters of the functional device based on the nanocylindrical geometry. Our results establish a versatile preparative strategy towards the elusive ‘nanorod’ or ‘interdigitated’ solar cell.

Results and discussion

ALD-based Sb₂S₃ nanotube preparation: structure and tunability

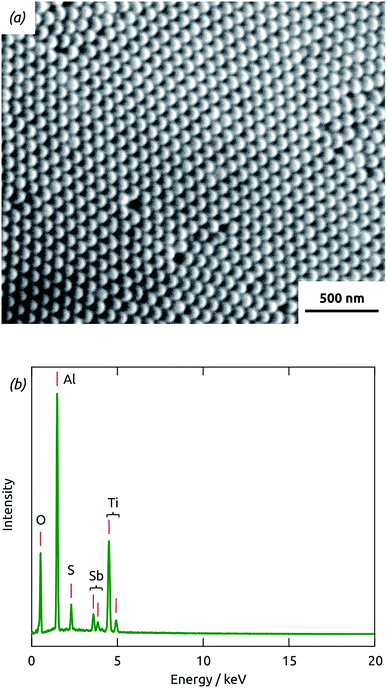
The overall preparative procedure foreseen for our ordered arrays of nanocylindrical, coaxial p-i-n junctions as ETA solar cells is presented in Scheme 2. The preparation bases on mostly published individual steps. The two-step anodization of Al in oxalic acid provides an inert matrix the pores of which are ordered with a period of 105 nm (±10%) and pore diameter (after pore widening) 80 nm (±10%).^1,23 We note that with these parameters, only 47% of the sample's total volume is taken up by the matrix. The remaining can be filled with the functional materials. This is performed by atomic layer deposition (ALD)¹⁸ and evaporative infiltration.² The thin film technique ALD possesses the unique ability of coating complex substrates conformally, especially highly porous ones.²⁴ In particular, it has been exploited for n-TiO₂ layers in similar geometries in the context of dye-sensitized solar cells already.²⁵ The Sb₂S₃ ALD procedure^26,27 delivers a material of high quality (purity and stoichiometry) applicable to photovoltaic applications,^22,28 which can even grow epitaxially near room temperature given an appropriate substrate.²⁹ However, its capability to coat deep pores has not been investigated to date. Therefore, we will start with an extensive characterization of the Sb₂S₃ layers.

Scheme 2 Preparation of ‘extremely thin absorber’ (ETA) solar cells in ordered arrays of coaxial, nanocylindrical p-i-n junctions: (a) two-step anodization of Al, (b) wet chemical removal of the Al substrate (Cu²⁺) and the Al₂O₃ barrier layer, pore widening (H⁺), (c) RF sputter coating of the transparent conducting oxide (TCO), (d) ALD of TiO₂ and Sb₂S₃, (e) evaporative infiltration of CuSCN, (f) Au DC sputter coating.

With long durations of the exposure and purge within each ALD cycle (exposure 50 s, purge 60 s) performed at 120 °C in our home-built hot-wall reactor, the ALD reaction²⁶ between Sb(NMe₂)₃ and H₂S delivers reproducible Sb₂S₃ coatings in cylindrical, straight pores of 80 nm diameter and 30 μm length. Fig. 1(a) displays a scanning electron micrograph (SEM) of a sample in which pores closed at one extremity with the barrier layer of oxide were coated with TiO₂ and Sb₂S₃ consecutively, after which the barrier layer was removed in acid. On the side of the sample which used to be closed by the barrier layer (the deepest point of the pores for ALD precursor diffusion), the hemispherical closed extremities of the acid-resistant TiO₂ tubes visibly protrude out of the matrix. The energy-dispersive X-ray spectrum (EDX) taken on the same sample area, presented in Fig. 1(b) and quantified in Table 1, exhibits exclusively the elements expected for Al₂O₃, TiO₂ and Sb₂S₃. Most importantly, the elements constituting Sb₂S₃ are detected by EDX in significant amounts, even though the method only probes the uppermost micron of the sample. This demonstrates the penetration of Sb₂S₃ ALD into the 30 μm long pores. Additionally, the 2 : 3 stoichiometric ratio of the compound is reflected in the EDX intensities obtained for Sb and S, within uncertainty. Note that the elemental EDX composition discussed here is representative of other positions of the sample, including its cross-section and its front side.

Fig. 1 (a) Scanning electron micrograph of the backside of a sample coated with TiO₂ and Sb₂S₃ ALD after the barrier layer of alumina closing the pore extremities was removed. (b) Energy-dispersive X-ray (EDX) spectrum recorded on the area displayed in (a), together with the corresponding element labels.

Table 1 EDX analysis of an anodic alumina membrane coated with TiO₂ and Sb₂S₃, recorded on the backside of the sample

Element	Line	Atomic composition
O	Kα	67.3%
Al	Kα	20.2%
S	Kα	1.9%
Ti	Kα	9.2%
Sb	Lα	1.4%

---

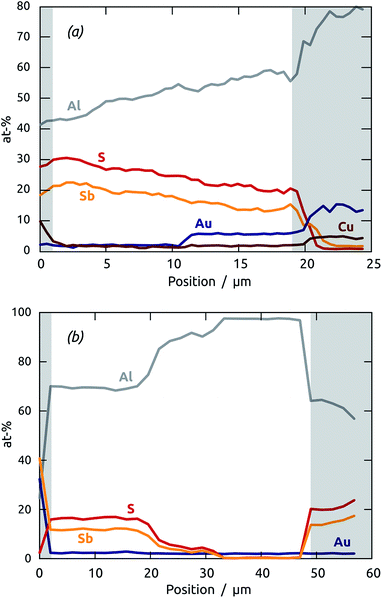
The maximal ALD deposition depth achievable in our cylindrical pores can be determined by EDX profiles along the depth axis of thick matrices. Fig. 2 displays results obtained with two membranes of 20 μm (a) and 50 μm (b), respectively. Note that for this study, care was taken to leave the barrier layer of oxide closing one pore extremity intact, so that penetration of ALD precursor gases into the pores is unidirectional. In both cases, the pore opening is presented on the left-hand side of the graph (near distance zero). The short pores are obviously coated completely with an Sb₂S₃ layer of homogeneous composition, whereby a slight but significant downwards trend of the Sb₂S₃ amount is observable from the pore opening to the extremity (about 30% over 20 μm). Such a variation, albeit undesirable, is within the range tolerable for applications. It certainly represents a large improvement over solution-based deposition methods (‘chemical bath deposition’ or CBD), traditionally used for ETA cells.^30–32 The sample with the longer pores demonstrates the limit reachable by our ALD method (with the conditions used in this study). The first 20 μm of the pores are coated essentially homogeneously, whereas the Sb₂S₃ amount (corresponding to the thickness of the deposited layer) drops to zero between the thicknesses 20 μm and 35 μm. Thus, our ALD method is limited to straight pores of aspect ratio 1 : 250 if conformal coatings are essential, and can be applied up to aspect ratio 1 : 370 or so if a strong thickness variation can be tolerated for the application. It should be possible to increase the deposition depth further by increasing the precursor dosage (via exposure duration and/or precursor bottle temperature), and possibly by varying the reaction chamber temperature, as well.

Fig. 2 Energy-dispersive X-ray spectroscopic profiles of samples prepared by Sb₂S₃ ALD in porous alumina templates, observed in cross-section. The samples have overall thicknesses of (a) approx. 20 μm and (b) approx. 50 μm. Gray, Al; red, S; orange, Sb; blue, Au; brown, Cu. The elements C and O are not accounted for in the percentage values. The data points corresponding to analyses outside the confines of the sample (where percentages are not meaningful) are grayed out for clarity. A 5 nm Au layer was sputtered for investigation for better conductivity, and the Cu signal is an artefact originating from the sample holder.

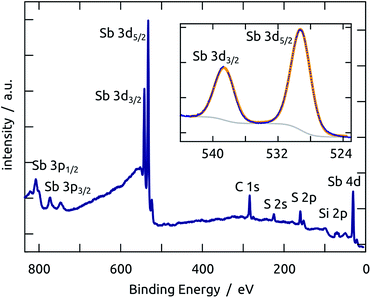
X-ray photoelectron spectroscopy performed on a planar Sb₂S₃/SiO₂/Si sample demonstrates that not only the bulk of the material deposited is stoichiometric and free of oxide, but also its surface. The spectrum presented in Fig. 3 is dominated by the prominent Sb 3d peaks in the region 520–540 eV.³³ The other elements found are S (as expected) and C (due to the usual surface contamination). Silicon is practically absent, which demonstrates that the Sb₂S₃ layer is continuous and closed. The 1s peak of oxygen would be found near 528 eV, which would overlap with the Sb 3d signal. However, the experimental data can be perfectly fitted with only the Sb doublet (the spin–orbit splitting is 9.6 eV and the maxima are located at 529.6 and 539.2 eV respectively, consistent with previous studies),^34–36 without any O contribution, as shown in the inset of Fig. 3.

Fig. 3 XPS spectrum recorded on an Sb₂S₃ layer grown on a Si/SiO₂ wafer. The inset shows the high-resolution Sb 3d region: experimental data are drawn in deep blue, the Shirley background in gray and the calculated fit (with two Gaussian peaks) in orange.

Annealing the initially amorphous Sb₂S₃ layers deposited by ALD not only causes crystallization, it may also affect the morphology of the films. Fig. 4 compares transmission electron micrographs of Sb₂S₃ films grown on flat Si(100) wafers covered by a 200 nm thick thermal SiO₂ layer (a) before and (b) after an annealing post-treatment carried out at 315 °C for 5 hours in Ar atmosphere. As grown, the Sb₂S₃ solid film is a smooth and continuous layer exhibiting a thickness of about 20 nm after 500 ALD cycles. Upon annealing, the film dewets and contracts to large crystallites of 50 to 200 nm diameter on the SiO₂ layer. This phenomenon shows the potentially significant mobility of the solid at elevated temperature,^29,37 as well as its poor adhesion to certain oxidic surfaces.³⁸

Fig. 4 TEM micrographs showing the cross-section of an Sb₂S₃ layer deposited on thermal silicon oxide, (a) as grown and (b) after subsequent annealing at 315 °C. Both micrographs are presented at the same scale.

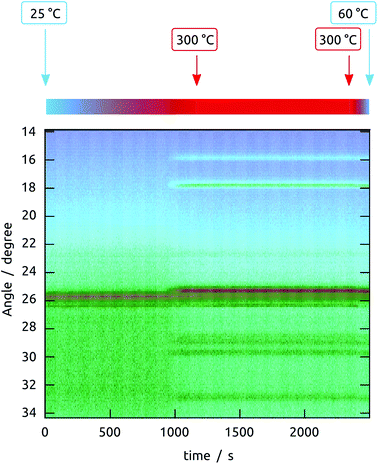
However, the planar Si/SiO₂ substrate, although convenient for TEM investigation, is not representative of our photovoltaic samples, in which the Sb₂S₃ layer not only experiences a different underlying oxide, but also a certain geometric confinement. Realistic data were collected on nanoporous samples by in situ XRD monitoring during annealing. Fig. 5 summarizes all data collected on a nanoporous sample in which amorphous Sb₂S₃ was coated onto crystalline TiO₂, and evidences that crystallization starts slightly below 300 °C already. It is also found to be highly dependent on the exact geometry, chemical identity, and crystal structure of the surface. To characterize these effects, the behavior of various Sb₂S₃ layer thicknesses on three different substrates are compared in Fig. 6: (1) Sb₂S₃ on bare (amorphous) anodic alumina pores, (2) Sb₂S₃ on pores preliminarily coated by amorphous TiO₂ (by ALD), and finally, (3) Sb₂S₃ on pores preliminarily coated by TiO₂ and crystallized at 400 °C.

Fig. 5 Full dataset obtained by in situ XRD monitoring of a sample upon annealing to 300 °C. The temperature is ramped up linearly from 25 °C to 300 °C, then maintained at 300 °C and finally cooled as sketched above the graph. The sample was prepared by anodization (pore diameter 80 nm, length >100 μm), followed by ALD of TiO₂ (20 nm), crystallization of TiO₂ (400 °C, 4 h), and finally ALD of Sb₂S₃ (10 nm). Color code: the X-ray signal intensity increases from blue to green to brown. The constant signal observed near 26° present from the very start is due to the initially crystalline TiO₂.

Fig. 6 Contrasting crystallization behaviors of Sb₂S₃ layers of various thicknesses and on various substrates upon annealing to 300 °C in situ. Left, five different thicknesses in anodized alumina matrix. Right, three different thicknesses in the same matrix preliminarily coated with TiO₂ (ALD, 20 nm); the solid lines represent samples the TiO₂ layer of which was crystallized by annealing before the Sb₂S₃ ALD, the thin dotted lines refer to samples in which this annealing was not performed before Sb₂S₃ ALD. Reference spectra are provided for Sb₂S₃ in green,³⁹ and for anatase TiO₂ in purple.⁴⁰

On the amorphous anodic alumina matrix, thin Sb₂S₃ layers (5 nm) do not crystallize at 300 °C (note that this is not due to the low absolute signal intensity, as we have demonstrated separately). Not only does crystallization occur only with at least 9 nm Sb₂S₃, but the crystallization behavior of thicker layers changes with thickness drastically. As long as the layer are thin with respect to the pore diameter (100 nm in this case), the low-index peaks (002), (201) and (103) appear in roughly powder intensity ratios. When the pore is completely filled with Sb₂S₃ (sample with nominal 59 nm thickness), crystallization takes place in a strongly preferred orientation, namely with the c axis parallel to the pore long axis. The situation is different altogether on amorphous TiO₂. Here, no significant crystallization is evident. The case of crystalline TiO₂ as the underlying surface yields yet another completely new picture. Indeed, all thicknesses of Sb₂S₃ crystallize on it with random orientation, as shown by the peak intensities, which follow the powder pattern over the full 2θ scale. This piece of information is encouraging for the final solar cell devices, as it allows one to expect not only a high crystal quality of the ‘extremely thin’ absorber layer, but also indicates a good interfacial contact between the individual semiconductors.

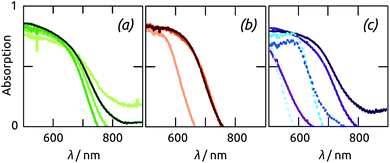
The capability of our methods to generate sample series in which one geometric parameter (either cylinder length L or wall thickness d) is varied systematically whereas the others are kept constant, and the value of this experimental possibility, is exemplified by the optical properties shown in Fig. 7. We note that the cylinder outer diameter D can also be experimentally varied, however at one given period of the order in the pore array, one expects a monotonous improvement of all performance parameters with D. In this paper, we therefore use a value of D close to the experimentally reachable maximum. All samples absorb essentially all photons more energetic than 500 nm, and transmit essentially all photons beyond 800 nm. That the experimental spectra rarely reach exactly A = 1 and A = 0 in these spectral regions is a common artifact of diffuse absorbance spectra, obtained by subtracting diffuse transmittance and diffuse reflectance from unity, due to ambiguities in referencing. Thus, the significant differences between the various samples are found in the band gap region, where A transitions form unity to zero.

Fig. 7 Optical properties (diffuse absorption A obtained from diffuse transmission and diffuse reflection) of nanotubular Sb₂S₃ samples with various geometric parameters (length L and tube wall thickness d). (a) Variation of L at constant d = 9.5(±0.5) nm: L = 10/20/30/50 μm (±10%), from light green to dark green. (b) Variation of d at constant L = 30(±3) μm: d = 6/10/13(±0.5) nm, from orange to brown. (c) Effect of annealing at constant L = 35(±3) μm: the wall thicknesses d = 6/10/15(±0.5) nm are represented in increasingly dark shades of dashed blue before annealing and of solid purple after it.

The absorption range of Sb₂S₃ samples grown with the same ALD deposition in pores of different lengths increases with L, as expected (Fig. 7(a)). However, no further improvement is obtained beyond L = 30 μm, which corresponds to the limitation in ALD penetration depth described above. Light absorption is also increased by d (Fig. 7(b)). However, for the rather long samples studied here, increases beyond 10 nm do not result in any measurable gain. The structural changes occurring upon annealing (documented above) are also apparent in the optical properties of the samples (Fig. 7(c)). The absorption band edge shifts by almost 100 nm (from somewhat beyond 650 nm to almost 750 nm) for the sufficiently thick Sb₂S₃ layers, which crystallize efficiently. In contrast to this, the variation is minute for the 5 nm thick sample, due to its unsuccessful or incomplete crystallization demonstrated by XRD.

Physical characterization of films, junctions, and functional solar cells

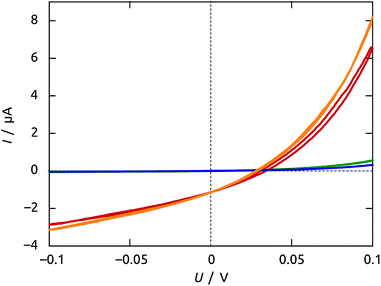
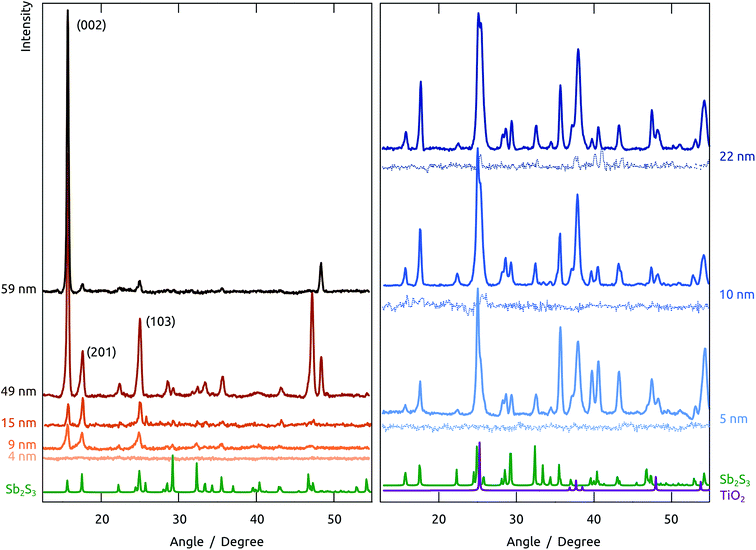
Once a sample is prepared through all steps of Scheme 1, a functional solar cell is obtained, as demonstrated by the I–V curves of Fig. 8 in the dark and under irradiation (1 sun). The curves measured following preparation immediately are not completely stable: the samples must be first stabilized by passing moderate current for a couple of hours before the properties are quantitatively reproducible.

Fig. 8 Electrical current–voltage curves recorded at 1 mV s⁻¹ on a sample of 0.126 cm² area with L = 30 μm, d(TiO₂) = d(Sb₂S₃) = 11 nm: blue and red, dark and irradiated curves recorded on a freshly prepared sample; green and orange, dark and irradiated curves recorded after several hours of electrical measurements. Solar spectrum AM1.5 irradiation was performed under 1 sun.

A slightly hysteretic behavior is often observed on the I–V curves, as in Fig. 8. The timescales associated with it are characterized by time-resolved measurements of open-circuit potential and short-circuit current, shown in Fig. 9. The U_OC and I_SC buildups upon exposure to solar light are essentially instantaneous (<100 ms), indicating that our materials have few traps that can be occupied by photogenerated carriers. The U_OC(t) decay obtained after turning off the irradiation is monoexponential and characterized by a lifetime of 117(±2) ms. This corresponds to a recombination lifetime of the photogenerated charge carriers in our experimental conditions, and is in line with values reported for photovoltaic systems based on TiO₂ nanocrystals of colloidal origin.^41–43 In addition to this, both U_OC and I_SC also decay from their respective value obtained immediately after turn-on, with contrasting lifetimes on the order of tens of seconds (for U_OC) and hundreds of milliseconds (for I_SC). This behavior has been described as an effective ‘negative capacitance’ and observed in this type of solar cell in numerous cases.⁴⁴

Fig. 9 Time-dependent behavior of (a) open-circuit potential and (b) short-circuit current upon turning full-spectrum irradiation at 1 sun on (white) and off (gray).

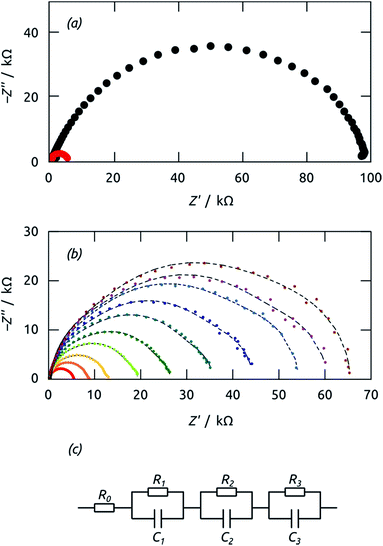
Further insight into the phenomena limiting the performance of our system, and more reliable values of the time constants involved, are provided by impedance spectroscopy. Fig. 10(a) shows data recorded at +0.1 V bias in the dark and under irradiation. The overall real resistance, evident as the abscissa of the lowest-frequency points (on the right-hand side), is reduced by over an order of magnitude upon irradiation, as should be the case. The evolution of the Nyquist plots from +0.1 V to −0.1 V under irradiation is shown in Fig. 10(b). The shape of all curves can be described as a significantly depressed semicircle. Consequently, an equivalent circuit model featuring three RC elements in series (in addition to the series resistance, Fig. 10(c)) must be used to deliver adequate fits (thin dashed black curves) to the experimental data.

Fig. 10 (a) Nyquist plots of impedance spectroscopy data recorded on a cell (area 0.126 cm²) in the dark (black) and under 1 sun irradiation (red) at +0.1 V. (b) Nyquist plots of the same cell recorded under 1 sun at various voltages from −0.1 V (brown datapoints) to +0.1 V (red datapoints). The dashed lines are curves calculated from a fit. (c) Equivalent circuit model used for fitting the data.

The characteristic time constants obtained in short circuit conditions are τ₁ = 13 ms, τ₂ = 40 ms, and τ₃ = 6 ms. The short constants are not accessible in the U_OC(t) and I_SC(t) experiments of Fig. 9, but we note that τ₂ coincides with the decay time constants observed in the real-time curves rather well. The attribution of τ₂ to recombination is corroborated by the very large capacitance value of C₂ = 56 μF cm⁻² (at 0 V), which is larger than C₁ and C₃ by factors larger than 50 and 20, respectively. Indeed, this large value must be expected based on the large specific surface area of our elongated nanocylindrical p-i-n junction. The corresponding resistance is R₂ = 750 Ω cm² (still at 0 V), which is comparable to values reported for a colloidal TiO₂/Sb₂S₃/CuSCN system.⁴⁵ We attribute the resistance R₁ to the p-CuSCN phase based on its very limited, linear variation with applied potential (Fig. 11): the values are larger than those reported in the colloidal system,⁴¹ consistent with the longer transport paths to the electrode in our system (30 μm, as compared to ≤3 μm in the colloidal case). Finally, the remaining resistance R₃ = 2.6 kΩ cm² must be associated with transport in the n-TiO₂ phase. The large value is likely related to the geometry (long TiO₂ tubes with thin walls), and seems to be the major factor limiting the performance of our novel system.

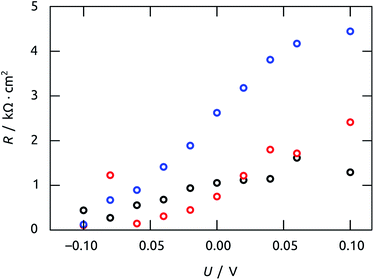Fig. 11 Values of resistances R obtained by impedance spectroscopy vs. applied potential U. The values were calculated from the model of Fig. 10(c) to fit the Nyquist plots in Fig. 10(b). Color code: R₁, black; R₂, red; R₃, blue.

Insight into exciton dynamics and charge transfer processes, which occur on much faster timescales, is obtained by femtosecond transient absorption spectroscopy of a crystalline, planar Sb₂S₃ film deposited on ITO, as a transparent layer able to accept both electrons and holes (since its Fermi energy lies higher than its conduction band edge).^46,47 It has been established that holes, instead of electrons, limit the overall kinetics of charge separation in the materials system studied here, as the transport of localized holes within Sb₂S₃ and their subsequent transfer into another phase are slow.^48,49 When excited with ultrashort (i.e. 150 fs) pump pulses at 665 nm and probed with temporally delayed, white-light continuum probe pulses, the sample gives rise to two salient features (Fig. 12). A photoinduced bleach due to exciton formation appears within 1 ps near 460 nm, whereas a transient absorption centered around 600 nm emerges later and can be attributed to the localized trapping of valence-band holes (likely at interfaces).⁴⁸

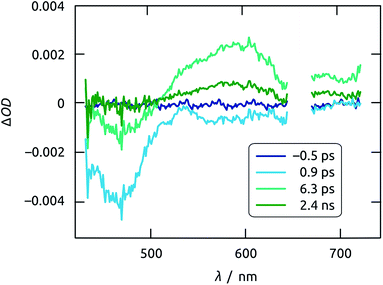Fig. 12 Time evolution of the transient absorption spectra of Sb₂S₃ film on ITO excited using 665 nm pump pulses. Note that the spectrum recorded at negative time is a perfect blank.

The bleach at 460 nm recovers with monoexponential kinetics characterized by τ_b = 2 ps. This value is identical (within uncertainty) to the characteristic rise time of the transient absorption of trapped holes, recorded at 620 nm (Fig. 13(a)). Thus, either the photogenerated hole is captured very quickly and localized, or the exciton recombines nonradiatively on a somewhat slower time scale. The trapped holes disappear on a much slower timescale, with a decay time of τ_a = 1 ns (in addition to a minor component on the order of 10 ps), as shown in Fig. 13(b). The physical process taking place on the 1 ns timescale is unveiled by comparison with a Sb₂S₃ film sample grown directly on glass, that is, in which holes cannot be injected into a second semiconductor. In this reference sample, the transient absorption signal (recorded at 590 nm) also appears concurrently with the decay of the bleach, but remains constant at a non-zero, positive value on the nanosecond scale. That this trapped state is long-lived on glass but decays with τ_a = 1 ns on ITO assigns it as being due to hole injection into ITO. The timescale found in this system for hole injection coincides with that determined previously in a TiO₂/Sb₂S₃/CuSCN cell in which Sb₂S₃ particles were generated by chemical bath deposition.⁴⁸

Fig. 13 Dynamics of Sb₂S₃ thin film samples. (a) Ultrafast decay of the exciton bleach (460 nm, green) and subsequent appearance of a transient absorption due to trapped holes (620 nm, blue) in Sb₂S₃/ITO. (b) Slow decay of the trapped holes in the Sb₂S₃/ITO system (620 nm, blue), compared to the non-decaying signal recorded for Sb₂S₃/glass (590 nm, brown).

This confirms the capability of our ALD-grown light absorber to carry out its function in ETA cells. Therefore, we can conclude that physical insight to be gained in the future from our model system featuring the well-defined nanocylindrical geometry will be applicable to understanding ETA systems generated by colloidal methods, as well.

Experimental

Materials

Oxalic acid, phosphoric acid, copper(II) chloride dihydrate, chromium(VI) oxide, ethanol, hydrochloric acid, perchloric acid, and argon were purchased from commercial suppliers and used as received. The ALD precursor tris(dimethylamido)antimony(III) was from Sigma Aldrich, H₂S from Air Liquide (3% H₂S in N₂), and Ti(OⁱPr)₄ from Alfa Aesar. The p-semiconductor CuSCN was obtained from Strem Chemical, ⁱPr₂S from Alfa Aesar and LiSCN from Sigma Aldrich. The aluminum (99.999%) for anodization was purchased from Goodfellow. Boron-doped [100] CZ silicon wafers with 200 nm thermal oxide were ordered from Silicon Materials. Water was purified immediately before use in a Millipore Direct-Q system. The sputter targets (ITO and Au) were obtained from Stanford Advanced Materials.

Sample preparation

Anodization. To prepare the cylindrical nanostructured membrane, a two-step anodization (electrochemical oxidation of aluminum in a protic solution) is carried out under 40 V in oxalic acid at 7 °C according to the standard procedure:⁵⁰ after the first anodization, the disordered porous aluminum oxide layer obtained is removed in chromic acid, then the ordered porous layer is obtained by a second anodization in the same conditions. The length of the pores is defined by the duration of this second anodization. The aluminum substrate was removed on a circular sample section of 4 mm diameter (as defined with a polyamide Kapton® mask) and the barrier oxide layer opened in warm phosphoric acid, whereby the pores were widened simultaneously. An ITO layer of 800 nm thickness was subsequently RF-sputtered onto the reverse side of the membrane in a coater model CRC 622 by Torr International, Inc.

ALD layers. Atomic layer deposition was carried out in a home-built hot-wall reactor equipped with DP-series pneumatic valves from Swagelok and with an MV10C pump from Vacuubrand. TiO₂ was deposited with Ti(OⁱPr)₄ and water. The reactor temperature was 120 °C. The Ti(OⁱPr)₄ precursor was kept at 90 °C. Ti(OⁱPr)₄ was pulsed into the reactor for 2 s and then held for 50 s before evacuating the chamber and purging for 60 s. The H₂O was kept at 40 °C and pulsed into the reactor for 0.5 s, then held for 50 s before opening the pump valve and purging for 60 s. The deposited TiO₂ was then annealed aerobically in an oven model L3/11/P330 from Nabertherm. The temperature was raised to 400 °C over 14 h, maintained at 400 °C for 4 h, then the samples were cooled down to room temperature over 14 h. After this, Sb₂S₃ was deposited using Sb(NMe₂)₃ and H₂S.^26,51 The reactor temperature was 120 °C. The Sb(NMe₂)₃ reservoir was kept at 40 °C. Sb(NMe₂)₃ was pulsed into the reactor for 1.5 s and then held for 50 s before evacuating the chamber and purging for 60 s. H₂S was pulsed into the reactor for 0.2 s (from a line held at 200 mbar gauge pressure) and then held for 50 s before purging for 60 s. A final Sb₂S₃ annealing was carried out in a glovebox under argon on a hotplate. The temperature was raised to 315 °C over 5 h, maintained constant for 30 min and then cooled down to room temperature over 5 h.

Characterization methods

Spectroscopic ellipsometry data were collected from 400 to 1000 nm under a 70° incidence angle with an instrument model EL X-02 P Spec from DRE Dr Riss Ellipsometerbau GmbH. Fits were performed using the database of material files provided with the instrument or the optical spectra published for amorphous Sb₂S₃.²⁶

Diffuse optical absorption spectroscopy was measured using a DH-2000-L light source, an HR4000 spectrometer, and an ISP-50-8-R integrating sphere from OceanOptics. For each sample, a diffuse transmission spectrum was recorded with respect to a blank taken without sample, and then a diffuse reflectance spectrum was recorded with respect to a blank taken on a reflective standard (anodic alumina membrane with underlying aluminum substrate). The diffuse absorption (A) spectra displayed in the article were obtained by subtracting the transmitted and reflected/scattered intensities (T and R, respectively) from the incident intensity, A = 1 − T − R.

Scanning electron micrographs were taken on a Jeol JSM 6400 equipped with a LaB₆ cathode and with an EDX system based on an SDD detector. Transmission electron microscopy (TEM) of ion-milled thin sample sections was performed on a Jeol 3010 equipped with a LaB₆ cathode.

The electrochemistry data were collected with a CompactStat potentiostat from Ivium Technologies and the impedance spectroscopy fits were performed between 17 782.8 Hz and 1 Hz by the instrument's software. A solar simulator from Newport Model 69907 with a 150 W Xe lamp was used as the light source and the light intensity was calibrated to AM1.5 with a reference Si solar cell.

The chemical surface composition analysis was performed by X-ray photoelectron spectroscopy (XPS) using a Mg Kα (1253.6 eV) source from a commercial HA 150 VSW spectrometer, on a planar sample prepared by depositing approximately 20 nm of Sb₂S₃ onto a Si wafer. The energy scale was calibrated on the C 1s peak. Spectrum fitting was performed with the XPS Peak 4.1 software, whereby a Shirley background was used. An identical sample was investigated by TEM after preparation of a microtome lamella.

Annealing of the Sb₂S₃ layers with in situ X-ray diffraction (XRD) monitoring was performed in an experimental stainless steel heating chamber, mounted in a dedicated Bruker D8 Discover. Cu K-alpha radiation (λ = 0.15406 nm) was used as the X-ray source, while a linear Vantec detector monitored the crystallinity of the thin films. The samples were heated in a helium atmosphere to 300 °C at a rate of 0.25 °C s⁻¹, after which the temperature was kept constant for 30 min. The diffraction pattern was captured over a 2θ range of 20° in 4 s intervals.

Femtosecond transient absorption spectroscopy experiments were conducted on planar samples (8.5 nm Sb₂S₃ on glass and 30 nm Sb₂S₃ on ITO/glass) with a Clark MXR CPA 2101 laser system in conjunction with an Ultrafast TAPPS HELIOS detection system, consisting primarily of a glass fiber based spectrometer. Output pulses at 387 nm and 665 nm with a 150 fs pulse and a 1 kHz repetition rate were used as pump pulses. They were obtained by amplifying and frequency-doubling the 775 nm seeding pulses of the Er³⁺-doped glass fiber oscillator in a regenerative chirped-pulse titanium-sapphire amplifier and with either a frequency-doubling BBO crystal or a nonlinear optical parametric amplifier (NOPA). All samples were pumped at excitation energy densities per pulse between 100 and 300 μJ cm⁻². A fraction of the fundamental was simultaneously passed through a sapphire plate (16 mm) to generate a fs white-light continuum between 400 and 1650 nm. Transient absorption spectra were taken at delay times between −2 ps and +1 ns. They were recorded between 450 and 730 nm in the magic-angle configuration of the polarization vectors of pump and probe pulse. The chirp of this spectral range was approximately 350 fs. No photochemical degradation was observed after each experiment, as the subsequently recorded absorption spectra of the samples showed. The transient absorption spectra were obtained as temporal evolution of the spectral changes in the optical density (ΔOD) of the sample. Therefore a chopper wheel provided the blocking of every other pump pulse so that the probe pulse was alternately transmitted through a pump-pulse excited and a ground-state sample. The intensity of the transmitted probe pulse after the pump pulse excited sample, I*(λ, τ), and that without pump pulse excitation, I₀(λ) were measured as function of the delay time τ. The ΔOD values were determined as

For I₀(λ) > I*(λ, τ) the ΔOD signal attains positive values and is assigned to absorption transitions of excited species, the so-called photoinduced absorption (PIA), whereas negative values of ΔOD result from I₀(λ) < I*(λ, τ) and are ascribed to photoinduced bleaching (PIB) of the ground state population density. Single-wavelength kinetic traces were fitted with exponentials or biexponentials after deconvolution of the apparatus time response function.

Conclusions

An ALD-based method for generating parallel arrays of elongated, cylindrical p-CuSCN/i-Sb₂S₃/n-TiO₂ coaxial heterojunctions is established and yields functional ETA solar cells. The cylinders are arranged hexagonally with a 105 nm pitch, they have a fixed outer diameter of 80 nm and a length L tunable up to a maximal 30 μm. The hole conductor and light absorber layers thicknesses d can be set accurately between 0 and 20 nm approximately. The crystallization behavior and optical properties of Sb₂S₃ depend strongly on the geometric parameters L and d(Sb₂S₃), as well as on the identity of the underlying surface. The transfer of photogenerated holes out of the light-absorbing layer occurs on the timescale of 1 ns, as is the case in similar materials systems prepared with colloidal methods. In the sample geometry presented in this paper, characteristic lifetimes associated with transport and recombination are on the millisecond timescale. Recombination of charge carriers at the large interface areas is the likely cause of the low power conversion efficiency recorded here. Thus, reducing the charge carrier transport distances by shortening the cylinder length L will likely improve the device performance.

This piece of work provides the long-sought preparative scheme towards ordered nanorod solar cells. Our scheme is quite practical experimentally and highly general. Members of the photovoltaics community can now apply it to the generation of series of samples in which each geometric parameter (rod diameter and length, individual layer thicknesses) is varied systematically. They can also replace each of the three materials with alternatives, given that many n-type oxides are accessible by ALD, as well as several intrinsic semiconductor compounds of the heavier chalcogens featuring large extinction coefficients.

Acknowledgements

Our work was supported by the DFG Excellence Cluster ‘Engineering of Advanced Materials’ and by the Centre de Coopération Universitaire Franco-Bavarois/Französisch-Bayrisches Hochschulzentrum (CCUFB/FBHZ). The in situ XRD measurements were supported by Flanders (FWO), UGENT-GOA-01G01513 and IWT-SBO. The fs TA measurements were supported by the Deutsche Forschungsgemeinschaft (graduate school 1161/2). We thank M. Künzel (FAU) for his support with optical absorption measurements, as well as D. Chaudanson, S. Nitsche and J.-Y. Hoarau (CINaM) for TEM observations and XPS measurements.

References

1. K. M. Coakley and M. D. McGehee, Chem. Mater., 2004, 16, 4533.
2. G. Dennler and N. S. Sariciftci, Proc. IEEE, 2005, 93, 1429.
3. A. Hagfeldt and M. Grätzel, Acc. Chem. Res., 2000, 33, 269.
4. M. Grätzel, Chem. Lett., 2005, 34, 8.
5. C. Groves, O. G. Reid and D. S. Ginger, Acc. Chem. Res., 2010, 43, 612.
6. R. A. Marsh, C. R. McNeill, A. Abrusci, A. R. Campbell and R. H. Friend, Nano Lett., 2008, 8, 1393.
7. N. Tigau, V. Ciupina, G. I. Rusu, G. Prodan and E. Vasile, Rom. J. Phys., 2005, 50, 859.
8. P. Pattanasattayavong, N. Yaacobi-Gross, K. Zhao, G. O. Ngongang Ndjawa, J. Li, F. Yan, B. C. O'Regan, A. Amassian and T. D. Anthopoulos, Adv. Mater., 2013, 25, 1504.
9. B. C. O'Regan and F. Lenzmann, J. Phys. Chem. B, 2004, 108, 4342.
10. Y. Xu and M. A. A. Schoonen, Am. Mineral., 2000, 85, 543.
11. W. H. Strehlow and E. L. Cook, J. Phys. Chem. Ref. Data, 1973, 2, 163.
12. M. Grätzel and F. P. Rotzinger, Chem. Phys. Lett., 1985, 118, 474.
13. K. Hara, H. Sugihara, L. P. Singh, A. Islam, R. Katoh, M. Yanagida, K. Sayama, S. Murata and H. Arakawa, J. Photochem. Photobiol., A, 2001, 145, 117.
14. C. A. Melendres, T. J. O'Leary and J. Solis, Electrochim. Acta, 1991, 36, 505.
15. B. M. Kayes, H. A. Atwater and N. S. Lewis, J. Appl. Phys., 2005, 97, 114302.
16. K. Tennakone, G. R. R. A. Kumara, I. R. M. Kottegoda, V. P. S. Perera and G. M. L. P. Aponsu, J. Phys. D: Appl. Phys., 1998, 31, 2326.
17. I. Kaiser, K. Ernst, C.-H. Fischer, R. Könenkamp, C. Rost, I. Sieber and M. C. Lux-Steiner, Sol. Energy Mater. Sol. Cells, 2001, 67, 89.
18. R. L. Puurunen, J. Appl. Phys., 2005, 97, 121301.
19. J. Bachmann, J. Jing, M. Knez, S. Barth, H. Shen, S. Mathur, U. Gösele and K. Nielsch, J. Am. Chem. Soc., 2007, 129, 9554.
20. J. Bachmann, R. Zierold, Y. T. Chong, R. Hauert, C. Sturm, R. Schmidt-Grund, B. Rheinlnder, M. Grundmann, U. Gösele and K. Nielsch, Angew. Chem., Int. Ed., 2008, 47, 6177.
21. Y. T. Chong, D. Görlitz, S. Martens, M. Y. E. Yau, S. Allende, J. Bachmann and K. Nielsch, Adv. Mater., 2010, 22, 2435.
22. H. Wedemeyer, J. Michels, R. Chmielowski, S. Bourdais, T. Muto, M. Sugiura, G. Dennler and J. Bachmann, Energy Environ. Sci., 2013, 6, 67.
23. O. Jessensky, F. Müller and U. Gösele, Appl. Phys. Lett., 1998, 72, 1173.
24. J. Bachmann, Beilstein J. Nanotechnol., 2014, 5, 245.
25. A. B. F. Martinson, M. S. Góes, F. Fabregat-Santiago, J. Bisquert, M. J. Pellin and J. T. Hupp, J. Phys. Chem. A, 2009, 113, 4015.
26. R. B. Yang, J. Bachmann, M. Reiche, J. W. Gerlach, U. Gösele and K. Nielsch, Chem. Mater., 2009, 21, 2586.
27. R. B. Yang, J. Bachmann, E. Pippel, A. Berger, J. Woltersdorf, U. Gösele and K. Nielsch, Adv. Mater., 2009, 21, 3170.
28. D. H. Kim, S. J. Lee, M. S. Park, J. K. Kang, J. H. Heo, S. H. Im and S. J. Sung, Nanoscale, 2014, 6, 14549.
29. R. B. Yang, N. Zakharov, O. Moutanabbir, K. Scheerschmidt, L. M. Wu, U. Gösele, J. Bachmann and K. Nielsch, J. Am. Chem. Soc., 2010, 132, 7592.
30. D. S. Boyle, P. O'Brien, D. J. Otway and O. Robbe, J. Mater. Chem., 1999, 9, 725.
31. P. P. Hankare, V. M. Bhuse, K. M. Garadkar, S. D. Delekar and I. S. Mulla, Semicond. Sci. Technol., 2004, 19, 70.
32. P. O'Brien and J. McAleese, J. Mater. Chem., 1998, 8, 2309.
33. V. P. Zakaznova-Herzog, S. L. Harmer, H. W. Nesbitt, G. M. Bancroft, R. Flemming and A. R. Pratt, Surf. Sci., 2006, 600, 348.
34. C. M. Park, Y. Hwa, N. E. Sung and H. J. Sohn, J. Mater. Chem., 2010, 20, 1097.
35. http://srdata.nist.gov/xps/ .
36. Handbook of X-ray photoelectron spectroscopy, ed. C. D. Wagner, W. M. Riggs, L. E. Davis, J. F. Moulder and G. E. Muilenberg, Perkin-Elmer Corporation, Physical Electronics Division, 1979.
37. C. V. Thompson, Annu. Rev. Mater. Res., 2012, 42, 399.
38. P. R. Gadkari, A. P. Warrant, R. M. Todi, R. V. Petrova and K. R. Coffey, J. Vac. Sci. Technol., A, 2005, 23, 1152.
39. ICSD_171568.
40. ICSD_9853.
41. Z.-S. Wang, M. Yanagida, K. Sayama and H. Sugihara, Chem. Mater., 2006, 18, 2912.
42. K. Zhu, N. R. Neale, A. Miedaner and A. J. Frank, Nano Lett., 2007, 7, 69.
43. M. Quintana, T. Edvinsson, A. Hagfeldt and G. Boschloo, J. Phys. Chem. C, 2007, 111, 1035.
44. I. Mora-Sero, J. Bisquert, F. Fabregat-Santiago, G. Garcia-Belmonte, G. Zoppi, K. Durose, Y. Proskuryakov, I. Oja, A. Belaidi, T. Dittrich, R. Tena-Zaera, A. Katty, C. Levy-Clément, V. Barrioz and S. J. C. Irvine, Nano Lett., 2006, 6, 640.
45. P. P. Boix, G. Larramona, A. Jacob, B. Delatouche, I. Mora-Seró and J. Bisquert, J. Phys. Chem. C, 2012, 116, 1579.
46. O. Malik and F. J. De la Hidalga-W, Physical and Technological Aspects of Solar Cells Based on Metal Oxide-Silicon Contacts with Induced Surface Inversion Layer, 2013, ch. 5, p. 124.
47. O. Malik, V. Grimalsky and J. De la Hidalga-W, J. Non-Cryst. Solids, 2006, 352, 1461.
48. J. A. Christians, D. T. Leighton and P. V. Kamat, Energy Environ. Sci., 2014, 7, 1148.
49. J. A. Christians and P. V. Kamat, ACS Nano, 2013, 7, 7967.
50. T. Grünzel, Y. J. Lee, K. Kuepper and J. Bachmann, Beilstein J. Nanotechnol., 2013, 4, 655.
51. Caution! Hydrogen sulfide is a highly toxic gas and should be used only in an appropriate environment, safety precautions include a fume hood, an alarm sensor, corrosion-resistant parts, and an exhaust H₂S remover, we use Sulfatreat Select HP granules from MI Swaco on the exhaust line and a four-stage, eight-cylinder teflon-coated membrane pump MV10C from Vacuubrand.

---