Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Buckling of paramagnetic chains in soft gels†
Shilin
Huang
a,
Giorgio
Pessot
b,
Peet
Cremer
b,
Rudolf
Weeber
c,
Christian
Holm
c,
Johannes
Nowak
d,
Stefan
Odenbach
d,
Andreas M.
Menzel
b and
Günter K.
Auernhammer
*a
aMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: auhammer@mpip-mainz.mpg.de; Fax: +49 6131 379 100; Tel: +49 6131 379 113
bInstitut für Theoretische Physik II: Weiche Materie, Heinrich-Heine-Universität Düsseldorf, 40225 Düsseldorf, Germany
cInstitute for Computational Physics, Universität Stuttgart, 70569 Stuttgart, Germany
dChair of Magnetofluiddynamics, Measuring and Automation Technology, Institute of Fluid Mechanics, Technische Universität Dresden, 01069 Dresden, Germany
First published on 8th October 2015
Abstract
We study the magneto-elastic coupling behavior of paramagnetic chains in soft polymer gels exposed to external magnetic fields. To this end, a laser scanning confocal microscope is used to observe the morphology of the paramagnetic chains together with the deformation field of the surrounding gel network. The paramagnetic chains in soft polymer gels show rich morphological shape changes under oblique magnetic fields, in particular a pronounced buckling deformation. The details of the resulting morphological shapes depend on the length of the chain, the strength of the external magnetic field, and the modulus of the gel. Based on the observation that the magnetic chains are strongly coupled to the surrounding polymer network, a simplified model is developed to describe their buckling behavior. A coarse-grained molecular dynamics simulation model featuring an increased matrix stiffness on the surfaces of the particles leads to morphologies in agreement with the experimentally observed buckling effects.
1 Introduction
Magneto-responsive hybrid gels (MRGs) have been attracting great attention due to their tunable elasticity, swelling properties and shape that can be remotely controlled by a magnetic field. They have potential applications as soft actuators, artificial muscles, as well as sensors1–3 and can serve as model systems to study the heat transfer in hyperthermal cancer treatment.4 Compared to other stimuli-responsive gels, MRGs have the advantage of fast response, controlled mechanical properties and reversible deformabilities.5–7 A typical MRG consists of a chemically cross-linked polymer network, swollen in a good solvent, and embedded magnetic particles.5,8 The size of the magnetic particles can range from ∼10 nm to several μm.7The origin of the magneto-responsive behavior of MRGs is the magnetic interaction between the magnetic filler particles as well as their interaction with external magnetic fields.9,10 In a uniform magnetic field, paramagnetic particles can be polarized and act as approximate magnetic dipoles. Depending on their mutual azimuthal configuration, the dipolar interactions can be either attractive or repulsive. In a liquid carrier, the dipolar interaction drives the magnetic particles to form chains and columns11–14 aligning in the direction of the magnetic field. However, in a polymer gel, the particles cannot change their position freely. Instead, relative displacements of the particles, induced e.g. by changes in the magnetic interactions, lead to opposing deformations of the polymer network. As a result, the magnetic interactions can induce changes in the modulus of the gel.7,15 This magneto-elastic effect is well known to be related to the spatial distribution of the magnetic particles.16–21 For example, the modulus of anisotropic materials that contain aligned chain-like aggregates of magnetic filler particles15,22–24 can be significantly enhanced when an external magnetic field is applied along the chain direction.7 The anisotropic arrangement of particles also dominates the anisotropic magnetostriction effects.25–27
Different theoretical routes have been pursued to investigate the magneto-elastic effects of MRGs: macroscopic continuum mechanics approaches,28,29 mesoscopic modeling,16–19 and more microscopic approaches30–32 that resolve individual polymer chains. Theoretical routes to connect and unify these different levels of description have recently been proposed.33–35 The authors of ref. 34 show how the interplay between the mesoscopic particle distribution and the macroscopic shape of the sample affects the magneto-elastic effect. In addition to these factors, recent experiments and computer simulations also point out that a direct coupling between the magnetic particles and attached polymer chains can play another important role.1,30,31,36–39
An experimental model system showing a well-defined particle distribution and a measurable magneto-elastic effect can help to understand the magneto-elastic behavior of MRGs at different length scales. Projected into a two-dimensional plane, the distribution of magnetic particles in thin diluted MRGs can be detected using optical microscopy or light scattering methods.15,40 By combining these techniques with magnetic or mechanical devices, it is possible to observe the particle rearrangement when the MRG sample is exposed to a magnetic field or mechanical stimuli.15,41 For three-dimensional (3D) characterization, X-ray micro-tomography has been used.23 Here we introduce another 3D imaging technique – laser scanning confocal microscopy (LSCM). Compared to normal optical microscopy, LSCM is able to observe 3D structures and it has a better resolution.42 Compared to X-ray micro-tomography, LSCM is faster in obtaining a 3D image and easier to combine with other techniques for real-time investigation.43,44
We use LSCM to study the magneto-elastic effects of paramagnetic chains in soft gels. As a result, we find that the paramagnetic chains in soft gels (elastic modulus <2 Pa) under an oblique magnetic field show rich morphologies. Depending on the length of the chain, modulus of the gel and strength of an external magnetic field, the chains can rotate, bend, and buckle. The deformation field in the polymer network around the deformed paramagnetic chains can also be tracked. The result confirms that the chains are strongly coupled to the polymer network. A simplified model is developed to understand the magnetically induced buckling behavior of the paramagnetic chains in soft gels. In addition to serving as a model experimental system for studying the magneto-elastic effect of MRGs, our approach may also provide a new microrheological technique to probe the mechanical property of a soft gel.45 Furthermore, our results may be interesting to biological scientists who study how magnetosome chains interact with the surrounding cytoskeletal network in magnetotactic bacteria.46
2 Materials and methods
The elastic network was obtained by hydrosilation of a difunctional vinyl-terminated polydimethylsiloxane (vinyl-terminated PDMS, DMS-V25, Gelest Inc.) prepolymer with a SiH-containing cross-linker (PDMS, HMS-151, Gelest Inc.). Platinum(0)-1,3-divinyl-1,1,3,3-tetramethyldisiloxane complex (Alfa Aesar) was used as a catalyst. A low-molecular-weight trimethylsiloxy-terminated PDMS (770 g mol−1, Alfa Aesar GmbH & Co. KG, in the following “PDMS 770”) served as a solvent that carried the polymer network and the paramagnetic particles. The paramagnetic particles were purchased from microParticles GmbH. They were labeled with fluorophores (visible in LSCM). The materials consist of porous polystyrene spheres. Within the pores, nanoparticulate iron oxide was distributed rendering the particles superparamagnetic. To prevent iron oxide leaching, the particles had a polymeric sealing that also held the fluorophores. The particles had a diameter of 1.48 ± 0.13 μm (ESI,† Fig. S1a). We measured the magnetization curve (ESI,† Fig. S1b) of the paramagnetic particles by a vibrating sample magnetometer (VSM, Lake Shore 7407). We found about 20% deviations in the magnetic properties of the magnetic particles (e.g., magnetic moment, see ESI,† Fig. S2). In order to observe the deformation field in the polymer network, we used fluorescently labeled silica particles as tracers. They had a diameter of 830 ± 50 nm and the surface was modified with N,N-dimethyl-N-octadel-3-amino-propyltrimethoxysilylchloride.After drying under vacuum at room temperature overnight, the paramagnetic particles were dispersed into PDMS 770. In some samples, tracer particles (3 wt%) were also dispersed into PDMS 770 in this step. The prepolymer mixture was prepared with 9.1 wt% vinyl-terminated PDMS and 90.9 wt% SiH-containing cross-linker. The prepolymer mixture (2.86 wt%) was dissolved in PDMS 770, which contained the paramagnetic particles. Finally, by adding PDMS 770, which carried the catalyst, the concentration of the prepolymer mixture in the sol solution was carefully adjusted in the range from 2.74 wt% to 2.78 wt%. This concentration range guaranteed the formation of soft gels with an elastic modulus lower than 10 Pa (see ESI,† Fig. S3). In the sol solution, the catalyst concentration was 0.17 wt%, and the concentration of magnetic particles was 0.09 wt%. The sol solution was agitated at 2500 rpm with a Reax Control (Heidolph, Schwabach, Germany) for 2 min for homogenization, followed by ultrasonication (2 min, Transsonic 460/H, Elma) to disperse the magnetic particles. Then the sol solution was introduced into a thin sample cell (∼160 μm thick and ∼1 cm wide) by capillary forces. The sample cells consisted of two No. 1 standard coverslips, separated by ∼160 μm spacers. After sealing with two-component glue, the cells that contained the sol were exposed to a 100.8 ± 0.5 mT magnetic field. The paramagnetic particles aligned into chains along the direction of the applied magnetic field while the prepolymer was crosslinking. A visible reaction of the prepolymer occurred within 10 min, and the rheological measurements showed that it took about 40 min to form a gel. Due to the low concentration of magnetic particles, the magnetic chains in the gel were well separated (>30 μm). The length of the chains varied from a single particle up to about 170 particles. We stored the samples at ambient temperature for at least two weeks before testing. The modulus of the gels in the sample cells was characterized using microrheological techniques (see ESI,† Fig. S4).47
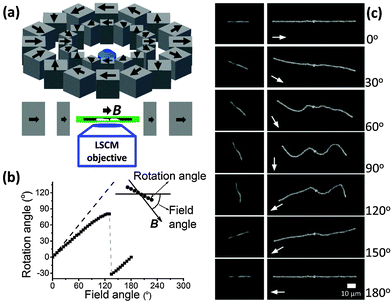
A home-built LSCM setup was used to observe the chain structure in the gel.43,44 We were able to analyze a sample of thickness of about 150 μm. A homogeneous magnetic field was attained by building Halbach magnetic arrays near the sample stage of the LSCM.48 A 32-magnet array (Fig. 1a) was used to change the field direction while keeping the field strength constant (216.4 ± 1.1 mT, see ESI,† Fig. S5). Another 4-magnet Halbach array (see ESI,† Fig. S6) was used to change the field strength (up to 100.8 ± 0.5 mT). The magnetic field was measured by a Lake Shore Model 425 Gaussmeter with a transverse probe.
To study the deformation of the PDMS gel around the magnetic chain, the magnetic field strength was increased from 0 mT to 60.2 ± 0.3 mT in 8 steps (∼30 min per step). 3D images of the sample with randomly distributed tracer particles were recorded in every step. One isolated magnetic chain was chosen for further analysis. Thus, from the 3D images we extracted a time series of 2D images that focused on this magnetic chain. From these 2D images, the trajectories of the embedded tracer particles were determined using the particle tracker plug-in developed on ImageJ software.49 The corresponding displacements of the tracers were deduced from the trajectories. Naturally, the tracer particles were stochastically distributed over the sample. We divided the images into a grid of small rectangles (7.0 × 5.5 μm2, containing, on average ∼3.5 tracer particles) and determined the average displacement in each cell.
3 Results
In the absence of a magnetic field, the paramagnetic chains in a soft gel kept the aligned morphologies (ESI,† Section S1, Movie S1). When a magnetic field (216.4 ± 1.1 mT) was applied in the direction parallel to the chains (Fig. 1c, images for 0°), the paramagnetic chains still aligned with the original chain direction (horizontal). We changed the direction of the magnetic field step-by-step (5° steps) in the clockwise direction (∼1 min between steps, quasi-static). We also define the orientation of the magnetic field B as the angle included between the magnetic field and the initial chain direction (see Fig. 1b). The left images of Fig. 1c show a short chain with 15 particles in a gel of elastic modulus G′ of 0.25 ± 0.06 Pa. The chain rotated to follow the magnetic field. However, the rotation angle of the chain was smaller than the orientation angle of the magnetic field (Fig. 1b). This difference increased until the orientation of B reached 135°, where the chain flipped backward and had a negative angle. The chain again became parallel to the field when the orientation of B increased to 180°. The morphology of the chain was the same at orientations of the magnetic field of 0° and 180° because of the superparamagnetic nature of the particles. Note that the chain was not straight at the intermediate angles (e.g., images for 60°, 90° and 120°). Instead it bended.The images on the right-hand side of Fig. 1c show a longer chain with 59 particles in the same gel. When the orientation of B was 30°, the chain rotated and bended, with its two ends tending to point in the direction of the magnetic field. When the orientation of B was 60°, the chain wrinkled and started to buckle. A sinusoidal-shape buckling morphology was observed when the magnetic field was perpendicular to the original chain (orientation of the magnetic field of 90°, see ESI,† Section S1, Movie S2). When the orientation of B increased from 90° to 120°, the left part of the chain flipped downward in order to follow the magnetic field. The right part flipped upward when the orientation of B increased from 120° to 150°. Finally, when the field direction was again parallel to the original chain direction (orientation of the magnetic field of 180°), the chain became straight. The same rotation/buckling morphologies as in Fig. 1c could be observed when increasing the orientation of B from 180° to 360°.
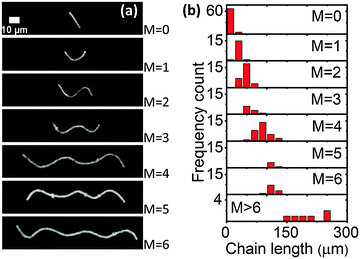
We also directly applied a perpendicular magnetic field to the paramagnetic chains in the soft gels. The paramagnetic chains showed different buckling morphologies (Fig. 2a) depending on the chain length. Fig. 2b gives frequency counts of the different morphologies in the same sample (G′ = 0.25 ± 0.06 Pa) under a magnetic field of 100.8 ± 0.5 mT. In total 180 chains were observed. Longer chains tended to buckle with a higher number of half waves. Moreover, the distributions overlapped, implying that paramagnetic chains of identical length could have different morphologies under the perpendicular magnetic field.
These buckling morphologies are reminiscent of the buckling of paramagnetic chains in a liquid medium under a perpendicular magnetic field.50,51 The most stable morphology in the latter system was a straight chain aligning along the magnetic field direction. However, in our system this morphology was not observed. Even the short chains showed a rotation angle smaller than the orientation of the magnetic field (e.g., Fig. 1b). The major difference between our experiments and ref. 50 and 51 was the nature of the surrounding medium. In our system, the polymer network around the paramagnetic chains impeded the rotation of the chains into the magnetic field direction (a more detailed discussion will be given below).
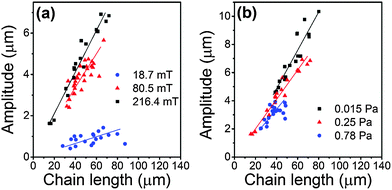
We used ImageJ software (NIH52) to extract the skeletons of the chains that have 2 half waves (S-shaped). The amplitude of deflection or deformation of different chains was quantified by the square root of the mean square displacement, i.e. amplitude = (〈y2〉 − 〈y〉2)1/2, where y measures the particle displacement along the field direction. The results are shown in Fig. 3. The amplitude increased with increasing chain length. At the same chain length, the amplitude tends to increase with increasing magnetic field strength (Fig. 3a; an example is also given in Fig. 4a) or with decreasing gel modulus (Fig. 3b).
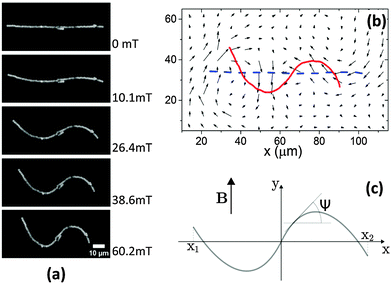
The modulus dependence of the amplitude demonstrated that the polymer network around the paramagnetic chains impeded the chain deformations. Therefore, the deformation field within the polymer network plays an important role to understand the buckling of the chains. We thus added tracer particles into the gel matrix, and used their trajectories to record the deformation field around the paramagnetic chains. As shown in Fig. 4a, a linear paramagnetic chain buckled and formed an S shape in a perpendicular magnetic field. The amplitude increased with increasing field strength, while the contour length of the chain remained constant. The chain extension decreased along the original chain direction (horizontal direction) and increased along the perpendicular direction. Simultaneously, the polymer network around the chain followed the deformation (Fig. 4b) of the paramagnetic chain, both in the transverse and longitudinal directions. This confirmed that the paramagnetic chain is strongly coupled to the polymer network. Within our experimental resolution, the chain seemed to have a rigid non-slip contact to the surrounding network.
4 Modeling
We now turn to a qualitative description of the situation in the framework of a reduced minimal model. Theoretically capturing in its full breadth the problem of displacing rigid magnetic inclusions in an elastic matrix is a task of high complexity and enormous computational effort.53 We do not pursue this route in the following. Instead, we reduce our characterization to a phenomenological description in terms of the shape of the magnetic chain only. This is possible if the dominant modes of deformation of the surrounding matrix are reflected by the deformational modes of the magnetic chain.Below, we assume that the chain is composed of identical spherical particles. In its undeformed state, the straight chain is located on the x-axis of our coordinate frame. The contour line of the deformed chain running through the particle centers is parameterized as y(x), see Fig. 4c.
4.1 Magnetic energy
First, concerning the magnetic energy along the chain, we assume dipolar magnetic interactions between the particles. In the perpendicular geometry (Fig. 4c), the external magnetic field approximately aligns all dipoles along the y-axis. For simplicity, we only include nearest-neighbor magnetic interactions. In an infinite straight chain, this would result in an error given by a factor of ζ(3) ≈ 1.2, where ζ is the Riemann zeta function.33,54,55 Within our qualitative approach this represents a tolerable error. Replacing the magnetic interaction energy between the discrete magnetic particles by a continuous line integral and shifting the path of integration from the contour line of the chain to the x-axis, we obtain the magnetic interaction energy (see ESI,† Section S3.1)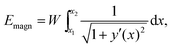 | (1) |
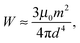 | (2) |
4.2 Elastic bending energy
Next, we need to include terms that provide a measure for the magnitude of the elastic deformation energy. To estimate the importance of different modes of the elastic matrix deformation, we analyze the experimentally determined displacement field around the distorted chain shown in Fig. 4b. For this purpose, we model the continuous matrix by a discretized spring network.19,56 Network nodes are set at the positions where the displacement field was tracked experimentally. The nodes are then connected by elastic springs. After that, we determine the normal modes of deformation of this network.56 Finally, we can decompose the experimentally observed deformation field in Fig. 4b into these normal modes. Occupation numbers ϕn give the contribution of the nth mode to the overall deformation.The four most occupied modes are shown in Fig. 5. We find a major contribution of “oscillatory” modes, i.e. alternating up and down displacements along the central horizontal axis. Such oscillatory displacements of the matrix are connected to corresponding oscillatory displacements of the chain, see Fig. 4b. A bending term of the form (see ESI,† Section S3.2)
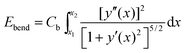 | (3) |
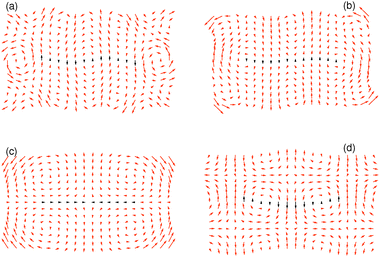 | ||
| Fig. 5 The four most occupied normal modes of the deformation field in Fig. 4b after projection to an elastic spring network, ordered by decreasing magnitude of contribution to the overall deformation. The normal modes (a), (b) and (d) are of an “oscillatory” type, whereas mode (c) represents a longitudinal contraction. Corresponding relative weights of the modes are ϕ(a)2 = 0.095, ϕ(b)2 = 0.057, ϕ(c)2 = 0.055, and ϕ(d)2 = 0.051, where we normalized the sum of the weights over all modes to unity. For better visualization, the overall amplitudes are rescaled as against the actual weights. The matrix region in close vicinity of the chain is indicated by black arrows. | ||
4.3 Elastic displacement energy
The bending term does not energetically penalize rotations of a straight chain, see Fig. 2a for M = 0. Yet, such rotations cost energy. Boundaries of the block of material are fixed, therefore any displacement of an inclusion induces a distortion of the surrounding gel matrix. We model this effect by a contribution (see ESI,† Section S3.3)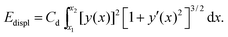 | (4) |
Moreover, in Fig. 5c the third dominating mode of the matrix deformation corresponds to a contraction along the chain direction and an expansion perpendicular to it. We conjecture that this should be the dominating mode in the deformational far-field, yet this hypothesis needs further investigation. It is induced by chain deflections in y-direction, which imply a matrix contraction in x-direction (experimentally we observe that the chain length is conserved under deformations and that the individual magnetic particles remain in close contact). We simultaneously use Edispl to represent the energetic contribution of this type of underlying matrix deformation.
4.4 Energetic evaluation
We now consider the resulting phenomenological model energy Etot = Emagn + Ebend + Edispl. A standard procedure would consist of minimizing Etot with respect to the functional form of y(x). Corresponding calculations and results are listed in the ESI,† Section S3.4. There are, however, severe limitations to this route in the present case. In contrast to several previous approaches in different contexts,57–61 our magnetic chains are of finite length and show significant displacements at their end points, see Fig. 2. Detailed knowledge of the boundary conditions of the deflection y(x) and its derivatives at the end points of the chain would be necessary to determine the chain shape. Indeed the solutions become very sensitive to additional conditions (see ESI,† Section S3.4). In our case, the necessary additional boundary conditions depend on the interaction with the matrix. They are not accessible in the present reduced framework.Therefore, we proceed in a different way. We use as an input for our calculations the experimental observations. The experimentally found chain shapes can to good approximation be represented by a polynomial form
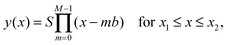 | (5) |
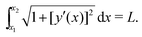 | (6) |
Next, we insert eqn (5) into the above expressions for the energy and minimize with respect to S, x1, and x2 for a given M, with the constraint of constant length L, see eqn (6). The minimization was performed using Wolfram Mathematica minimization routines.62 Parameter values of the coefficients Cb and Cd are found by matching the resulting shapes to the corresponding experimental profiles (chain deformations for G′ = 0.25 Pa and magnetic field B = 100.8 mT as in Fig. 2a, M = 2, are used for this purpose). We obtain Cb ≈ 0.01Wb2 and Cd ≈ 2W/b2.
To illustrate how the energetic contributions vary under increasing preset deformation, we plot in Fig. 6 the energies for increasing S for two fixed combinations of M and L. The total energy Etot shows a global minimum in both panels, which we always observed for symmetric chain deformations. As expected, with increasing S the magnetic energy decreases, whereas the deformation energies increase.
 | ||
| Fig. 6 Contributions to the total energy as a function of the amount S of deformation and minimized with respect to x1 and x2 for a chain of the shape given by eqn (5). Here we show the cases (a) M = 2, L = 3b and (b) M = 4, L = 4.5b. The total energy Etot has a global minimum as a function of S, which corresponds to the most stable chain shape. We always observed the global minimum for symmetric shapes. | ||
Next, we determine the minimal total energy as a function of chain length L for different numbers of half-oscillations M, see Fig. 7. With increasing chain length L the shapes that minimize the energy show an increasing number of half-waves M in good agreement with the experimental data in Fig. 2b.
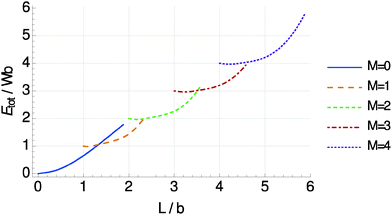 | ||
| Fig. 7 Energies Etot of chain deformations of the shape given by eqn (5), minimized with respect to S, x1, and x2, as a function of chain length L and number of half-oscillations M. Each curve describes a shape of M half-waves with a minimum total length of (M − 1)b. The resulting curves show crossing points from where the total energy for an increasing L is lowered by bending one extra time (jumping to a higher M) rather than conserving the same shape. | ||
Moreover, we quantify the amplitude of the chain deflection or deformation by
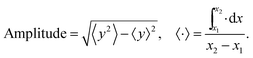 | (7) |
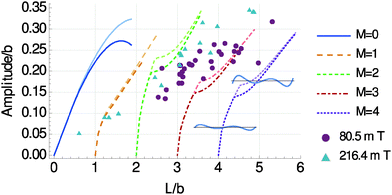 | ||
| Fig. 8 Resulting deflection amplitudes of the chain deformation, calculated according to eqn (7). Darker curves represent the model parameters optimized with respect to the experimental shapes for a magnetic field intensity B = 100.8 mT. Brighter curves were obtained by increasing the magnetic energy scale W by a factor ∼1.42, which corresponds to an increased magnetic field intensity of B ∼ 216 mT (see ESI,† Fig. S1b), comparable with the triangular experimental data points. Both, model curves and included experimental data points, demonstrate that moderate variations of the magnetic field intensities only slightly affect the observed deflection and deformation amplitudes. The value of b necessary to perform the analysis was determined from the M = 2 experimental data as b = 12.6 μm. For M ≥ 2 “kinks” appear in the curves, which arise from a change in the type of solution as illustrated by the insets: for each M ≥ 2 curve, left of the kink the chain deformation shows nodes at the end points of the chain, i.e. y(x1) ≃ y(x2) ≃ 0 (lower left inset); right from the kink, these outer nodes are shifted to the inside of the chain (upper right inset). As seen from Fig. 7, the solutions left of the kinks are not energetically preferred. | ||
Together, although the curves for M = 2 in Fig. 8 slightly overshoot the data points, Fig. 7 and 8 are in good agreement with the experimental results. The amplitude of deflection and deformation is not observed to unboundedly increase with chain length L in the experiments. Likewise, our model predicts that longer chains prefer to bend one extra time (switching to higher-M shape) rather than to show too large deflection amplitudes.
5 Coarse-grained molecular dynamics simulation
We also studied the buckling of the chain using two-dimensional coarse-grained molecular dynamics simulations by means of the ESPResSo software.63,64 A simple model was developed that allowed us to analyze the influence of particular interactions and material properties on the buckling effect. Here, we focus on the elasticity of the polymer matrix in the immediate vicinity of the magnetic particles.By choosing the coarse-grained scale for our model, we ignore any chemical details but rather describe the system in terms of the magnetic particles as well as small pieces of polymer gel. As the buckling effect appears to be two-dimensional, and as the ground states for systems of dipolar particles have also been found to be two-dimensional,55 we use this dimensionality for our simulations. We study a chain of 100 magnetic particles with a significant amount of surrounding elastic matrix.
As in the analytical approach, the gel matrix is modeled by a network of springs. Here, however, we use a regular hexagonal mesh as a basis. To mimic the non-linear elastic behavior of polymers, we use a finitely extensible non-linear elastic spring potential (FENE-potential65) for the springs along the edges of the mesh. As a simple implementation of the finite compressibility, we introduce FENE-like angular potentials on the angles at the mesh points, with a divergence at 0° and 180° (see ESI,† Section S4.2). The magnetic particles are modeled as rigid spheres interacting by a truncated, purely repulsive Lennard-Jones potential, the so-called Weeks-Chandler-Andersen potential (see ESI,† Section S4.1).66 Their magnetic moment is assumed to be determined purely by the external magnetic field and to be constant throughout the simulation, i.e. we assume that the external field is significantly stronger than the field created by the particles. The magnetic moments are taken parallel to the external field and with a magnitude given by the experimentally observed magnetization curve. The coupling between the particles and the mesh is introduced in such a way, that under the volume occupied by a particle, the mesh does not deform, but rigidly follows the translational and rotational motion of the particle (see ESI,† Section S4.3). A local shear strain on the matrix can rotate a magnetic particle, but not its magnetic moment.
An important point is the elasticity of the polymer matrix in the immediate vicinity of the magnetic particles and, in particular, between two magnetic particles. We study two situations here, the first one including a stiffer region in the immediate vicinity of the particles, the second one without such a stiffer layer and directly jumping to the bulk elasticity. The stiffer layer, if imposed, is created using a spring constant larger by three orders of magnitude on those springs which originate from mesh sites within the particle volumes (see ESI,† Section S4.3). The angular potentials are unchanged.
A comparison between the cases with and without a stiffer layer of gel around the magnetic particles can be seen in Fig. 9. The images show a small part of the resulting configuration of magnetic particles and the surrounding mesh for a field applied perpendicular to the initial chain direction. Thus the magnetic moments of the particles are oriented perpendicular to the undistorted chain direction. This results in an energetically unfavorable parallel side-by-side configuration for the dipole moments. The energy can be reduced either by increasing the distance between the dipoles along the initial chain direction, or by moving dipoles perpendicularly to the initial chain direction so that they approach the energetically most favorable head-to-tail configuration. If the matrix is made stiffer immediately around the particles, and thus the contour length of the chain cannot change significantly, the re-positioning towards the head-to-tail configuration causes the buckling effect observed in the experiments (Fig. 9). When one assumes the matrix immediately around the magnetic particles to be as soft as in the bulk of the material, neighboring particles can move apart and the chain breaks up into individual particles or small columns perpendicular to the original chain direction. Additionally, a layer of increased stiffness also introduces a bending rigidity of the chain. In Fig. 10, the full chain and the surrounding matrix is shown for an external field of magnitude 216 mT, which from the experimental magnetization measurements corresponds to a magnetic moment of about 4.5 × 10−14 A m2 (see ESI,† Fig. S1b). Due to the different dimensionalities, the elastic modulus of the surrounding matrix could not be directly matched to the experimental system.
Actually, the amplitude of the chain oscillation increases when the external field is higher and induces larger dipole moments in the particles. This increases the tendency of the magnetic moments to approach the head-to-tail configuration, which in turn leads to a stronger deformation of the matrix. We note that the relative amplitude of the buckling along the chain is similar in the simulations (Fig. 9) and experiments (Fig. 2). The matrix surrounding the chain follows the chain oscillation with an amplitude that decreases over distance from the chain. Deviations may be expected from the deformational far-field in the experimental system due to the different dimensionalities of the systems.
In the ESI† (Fig. S7) we show an experimental evidence for the existence of a stiff polymer layer around the magnetic particles. The sample was prepared at a concentration of prepolymer mixture well below the percolation threshold, i.e., some cross-linking of the polymer took place in the sample but no macroscopic gel was formed. When this cross-linking was done under an applied magnetic field, the particle chains stayed intact even after removal of the magnetic field (Fig. S7a, ESI†). Hairpin or “S”-shape morphologies were observed when these chains were exposed to a magnetic field (Fig. S7b, ESI†), indicating that they have a bending rigidity.50,51 Our interpretation of this behavior is that a stiff gel layer connects the particles and stabilizes the particle chains, even though no bulk gel is formed. As the magnetic particles have a good affinity for PDMS (e.g., the magnetic particles can be easily dispersed into PDMS), we conjecture that there is an adsorbed layer of polymer (i.e., PDMS prepolymer or cross-linker) on the surface of the magnetic particles.67 Therefore, the gel layer on the particles is denser and thus stiffer than in the bulk. Further study of the stiff polymer layer and its effect on the buckling behavior is under way.
Moreover, in Fig. S8 (ESI†) we show that the buckling behavior of the magnetic chains can still be observed in the gel when we increase the elastic modulus to 170 Pa (for this purpose, carbonyl iron particles are used as magnetic filler particles). Our studies on that stiffer sample provide further evidence that the interaction between the magnetic particles and the polymer matrix in their close vicinity can play an important role in the magneto-elastic response of soft MRGs.
6 Conclusions
We have shown that paramagnetic chains in a soft polymer gel can buckle in a perpendicular magnetic field. The buckling morphology depends on the length of the chain, the strength of the magnetic field and the modulus of the gel. Longer chains form buckling structures with a higher number of half waves. Higher strengths of the magnetic field and a lower modulus of the gel matrix can lead to higher deformation amplitudes. The deformation field in the surrounding gel matrix confirms that the embedding polymer network is strongly coupled to the paramagnetic chain. A minimal magneto-elastic coupling model is developed to describe the morphological behavior of the paramagnetic chains in the soft gel under a perpendicular magnetic field. It shows that the chains deform in order to decrease the magnetic energy. This is hindered by the simultaneous deformation of the gel matrix, which costs elastic energy. Additionally, we have introduced a coarse-grained molecular dynamics simulation model, which covers both, the magnetic particles and the surrounding polymer mesh. In this model, the buckling of the chains can only be observed when the surface layer around the particles is assumed to be stiffer than the bulk of the gel. This prevents the chains from breaking up into columns oriented perpendicular to the initial chain direction or into isolated particles. These findings support the picture that the embedded magnetic chains themselves feature a certain bending rigidity, possibly due to the existence of a stiff polymer layer on the particle surfaces.Since the magneto-elastic effect demonstrated and analyzed in this paper is pronounced, reversible, and controllable, it may be useful for designing micro-devices, e.g. micro-valves and pumps for microfluidic control.68 As the morphologies of the buckling paramagnetic chains are correlated with the modulus of the gel matrix, we may use them as mechanical probes for soft gels (similarly to active microrheology techniques).45 Moreover, our study may help to understand the physical interactions between the magnetic chains and the surrounding cytoskeleton network in magnetotactic bacteria.46 In our future study we will focus on how the interfacial coupling between the magnetic particles and the polymer network influences the local magneto-elastic coupling effect.
Acknowledgements
The authors acknowledge support by the Deutsche Forschungsgemeinschaft (DFG) through the SPP 1681 (SH and GKA acknowledge the project AU321/3-1; GP, PC and AMM acknowledge the project LO418/16-1; RW and CH acknowledge the project HO 1108/23-1; JN and SO acknowledge the project OD18/21). RW and CH acknowledge funding through the cluster of excellence EXC 310, SimTech at the University of Stuttgart. We thank Dr Peter Blümler for inspiring discussions on designing the Halbach magnetic arrays.References
- P. Ilg, Soft Matter, 2013, 9, 3465–3468 RSC.
- R. L. Snyder, V. Q. Nguyen and R. V. Ramanujan, Smart Mater. Struct., 2010, 19, 055017 CrossRef.
- K. Zimmermann, V. A. Naletova, I. Zeidis, V. Böhm and E. Kolev, J. Phys.: Condens. Matter, 2006, 18, S2973–S2983 CrossRef CAS.
- R. Hergt, S. Dutz, R. Müller and M. Zeisberger, J. Phys.: Condens. Matter, 2006, 18, S2919–S2934 CrossRef CAS.
- D. Szabó, G. Szeghy and M. Zrínyi, Macromolecules, 1998, 31, 6541–6548 CrossRef.
- S. S. Abramchuk, D. A. Grishin, E. Y. Kramarenko, G. V. Stepanov and A. R. Khokhlov, Polym. Sci., Ser. A, 2006, 48, 138–145 CrossRef.
- G. Filipcsei, I. Csetneki, A. Szilágyi and M. Zrínyi, Adv. Polym. Sci., 2007, 206, 137–189 CrossRef CAS.
- D. Collin, G. K. Auernhammer, O. Gavat, P. Martinoty and H. R. Brand, Macromol. Rapid Commun., 2003, 24, 737–741 CrossRef CAS.
- J. Faraudo, J. S. Andreu and J. Camacho, Soft Matter, 2013, 9, 6654–6664 RSC.
- D. J. Griffiths, Introduction to Electrodynamics, Prentice-Hall, Upper Saddle River, NJ, 3rd edn, 1999, p. 282 Search PubMed.
- S. H. L. Klapp and M. Schoen, J. Chem. Phys., 2002, 117, 8050–8062 CrossRef CAS.
- S. H. L. Klapp, J. Phys.: Condens. Matter, 2005, 17, R525–R550 CrossRef CAS.
- G. P. Gajula, M. T. Neves-Petersen and S. B. Petersen, Appl. Phys. Lett., 2010, 97, 103103 CrossRef.
- J. de Vicente, D. J. Klingenberg and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 3701–3710 RSC.
- G. K. Auernhammer, D. Collin and P. Martinoty, J. Chem. Phys., 2006, 124, 204907 CrossRef PubMed.
- D. S. Wood and P. J. Camp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 011402 CrossRef PubMed.
- D. Ivaneyko, V. Toshchevikov, M. Saphiannikova and G. Heinrich, Condens. Matter Phys., 2012, 15, 33601 CrossRef.
- Y. Han, W. Hong and L. E. Faidley, Int. J. Solids Struct., 2013, 50, 2281–2288 CrossRef CAS.
- G. Pessot, P. Cremer, D. Y. Borin, S. Odenbach, H. Löwen and A. M. Menzel, J. Chem. Phys., 2014, 141, 124904 CrossRef PubMed.
- A. M. Menzel, Phys. Rep., 2015, 554, 1–46 CrossRef CAS.
- O. V. Stolbov, Y. L. Raikher and M. Balasoiu, Soft Matter, 2011, 7, 8484–8487 RSC.
- G. Filipcsei, I. Csetneki, A. Szilágyi and M. Zrínyi, Magnetic Field-Responsive Smart Polymer Composites, Springer, Berlin, Heidelberg, 2007, vol. 206, pp. 137–189 Search PubMed.
- D. Günther, D. Y. Borin, S. Günther and S. Odenbach, Smart Mater. Struct., 2012, 21, 015005 CrossRef.
- T. Borbáth, S. Günther, D. Y. Borin, T. Gundermann and S. Odenbach, Smart Mater. Struct., 2012, 21, 105018 CrossRef.
- X. C. Guan, X. F. Dong and J. P. Ou, J. Magn. Magn. Mater., 2008, 320, 158–163 CrossRef CAS.
- K. Danas, S. V. Kankanala and N. Triantafyllidis, J. Mech. Phys. Solids, 2012, 60, 120–138 CrossRef CAS.
- A. Y. Zubarev, Soft Matter, 2013, 9, 4985–4992 RSC.
- E. Jarkova, H. Pleiner, H. W. Müller and H. R. Brand, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 041706 CrossRef CAS PubMed.
- S. Bohlius, H. R. Brand and H. Pleiner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 061411 CrossRef CAS PubMed.
- R. Weeber, S. Kantorovich and C. Holm, Soft Matter, 2012, 8, 9923–9932 RSC.
- R. Weeber, S. Kantorovich and C. Holm, J. Magn. Magn. Mater., 2015, 383, 262 CrossRef CAS.
- A. V. Ryzhkov, P. V. Melenev, C. Holm and Y. L. Raikher, J. Magn. Magn. Mater., 2015, 383, 277 CrossRef CAS.
- A. M. Menzel, J. Chem. Phys., 2014, 141, 194907 CrossRef PubMed.
- D. Ivaneyko, V. Toshchevikov, M. Saphiannikova and G. Heinrich, Soft Matter, 2014, 10, 2213–2225 RSC.
- G. Pessot, R. Weeber, C. Holm, H. Löwen and A. M. Menzel, J. Phys.: Condens. Matter, 2015, 27, 325105 CrossRef PubMed.
- L. Roeder, M. Reckenthäler, L. Belkoura, S. Roitsch, R. Strey and A. M. Schmidt, Macromolecules, 2014, 47, 7200–7207 CrossRef CAS.
- N. Frickel, R. Messing, T. Gelbrich and A. M. Schmidt, Langmuir, 2009, 26, 2839–2846 CrossRef PubMed.
- N. Frickel, R. Messing and A. M. Schmidt, J. Mater. Chem., 2011, 21, 8466–8474 RSC.
- R. Messing, N. Frickel, L. Belkoura, R. Strey, H. Rahn, S. Odenbach and A. M. Schmidt, Macromolecules, 2011, 44, 2990–2999 CrossRef CAS.
- I. Csetneki, G. Filipcsei and M. Zrínyi, Macromolecules, 2006, 39, 1939–1942 CrossRef CAS.
- H. N. An, J. Groenewold, S. J. Picken and E. Mendes, Soft Matter, 2014, 10, 997–1005 RSC.
- M. Minsky, Scanning, 1988, 10, 128–138 CrossRef.
- M. Roth, M. Franzmann, M. D'Acunzi, M. Kreiter and G. K. Auernhammer, 2011, arXiv preprint, arXiv:1106.3623.
- M. Roth, C. Schilde, P. Lellig, A. Kwade and G. K. Auernhammer, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 124 CrossRef PubMed.
- C. Wilhelm, Phys. Rev. Lett., 2008, 101, 028101 CrossRef PubMed.
- A. Körnig, J. Dong, M. Bennet, M. Widdrat, J. Andert, F. D. Müller, D. Schüler, S. Klumpp and D. Faivre, Nano Lett., 2014, 14, 4653–4659 CrossRef PubMed.
- T. G. Mason, T. Gisler, K. Kroy, E. Frey and D. A. Weitz, J. Rheol., 2000, 44, 917–928 CrossRef CAS.
- H. Raich and P. Blümler, Concepts Magn. Reson., Part B, 2004, 23, 16–25 CrossRef.
- I. F. Sbalzarini and P. Koumoutsakos, J. Struct. Biol., 2005, 151, 182–195 CrossRef CAS PubMed.
- C. Goubault, P. Jop, M. Fermigier, J. Baudry, E. Bertrand and J. Bibette, Phys. Rev. Lett., 2003, 91, 260802 CrossRef CAS PubMed.
- V. P. Shcherbakov and M. Winklhofer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 061803 CrossRef PubMed.
- http://imagej.nih.gov/ij/ .
- C. Spieler, M. Kästner, J. Goldmann, J. Brummund and V. Ulbricht, Acta Mech., 2013, 224, 2453–2469 CrossRef.
- M. A. Annunziata, A. M. Menzel and H. Löwen, J. Chem. Phys., 2013, 138, 204906 CrossRef PubMed.
- T. Prokopieva, V. Danilov, S. Kantorovich and C. Holm, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031404 CrossRef PubMed.
- M. Tarama, P. Cremer, D. Y. Borin, S. Odenbach, H. Löwen and A. M. Menzel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 042311 CrossRef PubMed.
- I. Gelfand and S. Fomin, Calculus of variations, Prentice-Hall Inc., Englewood Cliffs, NJ, 1963 Search PubMed.
- G. W. Hunt, M. Wadee and N. Shiacolas, J. Appl. Mech., 1993, 60, 1033–1038 CrossRef.
- B. Audoly, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011605 CrossRef CAS PubMed.
- H. Diamant and T. A. Witten, 2010, arXiv preprint arXiv:1009.2487.
- H. Diamant and T. A. Witten, Phys. Rev. Lett., 2011, 107, 164302 CrossRef PubMed.
- Wolfram Research, Mathematica 10.0, 2014 Search PubMed.
- H. J. Limbach, A. Arnold, B. A. Mann and C. Holm, Comput. Phys. Commun., 2006, 174, 704–727 CrossRef CAS.
- A. Arnold, O. Lenz, S. Kesselheim, R. Weeber, F. Fahrenberger, D. Röhm, P. Košovan and C. Holm, Meshfree Methods for Partial Differential Equations VI, 2013, pp. 1–23 Search PubMed.
- H. R. Warner, Ind. Eng. Chem. Fundam., 1972, 11, 379–387 CAS.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237 CrossRef CAS.
- L. Cohen-Tannoudji, E. Bertrand, L. Bressy, C. Goubault, J. Baudry, J. Klein, J.-F. Joanny and J. Bibette, Phys. Rev. Lett., 2005, 94, 038301 CrossRef PubMed.
- E. K. Fleischmann, H. L. Liang, N. Kapernaum, F. Giesselmann, J. Lagerwall and R. Zentel, Nat. Commun., 2012, 3, 1178 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm01814e |
| This journal is © The Royal Society of Chemistry 2016 |