Open Access Article
Open Access ArticleA theory for the phase behavior of mixtures of active particles†
Sho C.
Takatori
and
John F.
Brady
*
Division of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, CA 91125 USA. E-mail: Takatori@caltech.edu
First published on 1st September 2015
Abstract
Systems at equilibrium like molecular or colloidal suspensions have a well-defined thermal energy kBT that quantifies the particles' kinetic energy and gauges how “hot” or “cold” the system is. For systems far from equilibrium, such as active matter, it is unclear whether the concept of a “temperature” exists and whether self-propelled entities are capable of thermally equilibrating like passive Brownian suspensions. Here we develop a simple mechanical theory to study the phase behavior and “temperature” of a mixture of self-propelled particles. A mixture of active swimmers and passive Brownian particles is an ideal system for discovery of the temperature of active matter and the quantities that get shared upon particle collisions. We derive an explicit equation of state for the active/passive mixture to compute a phase diagram and to generalize thermodynamic concepts like the chemical potential and free energy for a mixture of nonequilibrium species. We find that different stability criteria predict in general different phase boundaries, facilitating considerations in simulations and experiments about which ensemble of variables are held fixed and varied.
1 Introduction
Active matter systems like colonies of bacteria and self-propelled synthetic microswimmers are a rich area of study for soft matter. The fundamental and seemingly elementary ability of self-propulsion allows active systems to free themselves from classical thermodynamic constraints and to control their own motion and the surrounding environment. Their inherently nonequilibrium properties engender intriguing behavior such as spontaneous self-assembly and pattern formation,1,2 making active matter a fascinating but challenging system to study.Recently a new “swim pressure” concept was introduced—namely, all active entities exert a unique mechanical pressure owing to their self-motion.3,4 This perspective was applied5 to predict the self-assembly of a suspension of active particles into regions of dense and dilute phases observed in both experiments and simulations.6–10 The usefulness of the mechanical pressure to illuminate active matter's physical principles begs the question: what is the temperature of active matter? Do active swimmers “thermally equilibrate” with their surroundings? Although it is clear that the mechanical pressure can be quantified and is valid out of equilibrium, it is uncertain whether the notion of a temperature exists and can be explained in basic physical quantities.
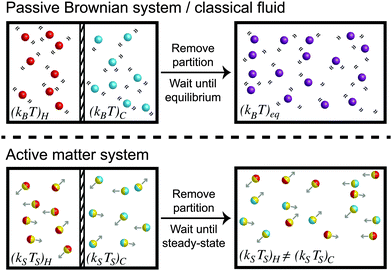
To understand the temperature of active matter, we shall first discuss a simple experiment involving passive Brownian suspensions (i.e., no self-propulsion) which can be rigorously related to conventional thermodynamic quantities like the temperature and free energy. Suppose we have a purely Brownian suspension with thermal energy (kBT)H that is separated by a thermally-insulated partition from another Brownian system with a different temperature (kBT)C, as shown in Fig. 1. The partition is suddenly removed and the particles at different temperatures are allowed to mix. The “hot” and “cold” particles undergo many collisions, share their kinetic energy with each other, and eventually equilibrate to a common temperature (kBT)eq.
Now suppose we do the same mixing experiment with self-propelled swimmers at two different activity levels. For simplicity we consider self-propelled spheres of radii a that translate with an intrinsic swim speed U0, reorient with a reorientation time τR, and experience a hydrodynamic drag factor ζ from the surrounding continuous Newtonian fluid. Their motion can be described as a random-walk process for times t > τR with a diffusivity Dswim = U02τR/2 in two dimensions (2D). Their characteristic “energy scale” is not the thermal energy kBT = ζD0 where D0 is the Stokes–Einstein–Sutherland translational diffusivity, but comes from their self-propulsive activity, defined as ksTs ≡ ζDswim = ζU02τR/2 (see later section for a more detailed treatment).
A system of “hot” active swimmers with (ksTs)H is initially separated from “cold” swimmers with (ksTs)C as shown in Fig. 1. When the partition is removed, the swimmers with different activity levels spontaneously mix and undergo collisions with each other. When a swimmer collides into another swimmer, it displaces the body by its size a until they move completely clear of each others' trajectories. After the collision, each swimmer then continues its motion with the same activity it had initially—there is no sharing of kinetic activity (ksTs) upon collisions. This implies that the swimmers' activity scale ksTs ≡ ζU02τR/2 does not get shared via collisions and thus does not “equilibrate” like the temperature of a classical fluid kBT. This simple experiment already reveals the richness and challenge to understand the “temperature” of nonequilibrium active systems.
A simple multicomponent mixture of self-propelled particles with two different activities is an ideal system to discover and study this problem in greater detail. Previous studies have provided various interpretations of the temperature in a nonequilibrium active matter system.11–13 We discuss a new perspective by developing a mechanical pressure theory for predicting the phase behavior of a mixture of active swimmers over the entire phase space of the system. Our theory applies in general to a multicomponent suspension with swimmers of different activities, but perhaps the most straightforward mixture is that of active self-propelled particles and passive Brownian particles in a single solvent. In this mixture we must treat active swimmers and passive particles as independent species, because their compositions vary in space due to the phase-separating behavior of active suspensions. This is true in general for multicomponent systems—in a simple polymeric solution of polyethylene in benzene, the polyethylene molecules do not all have the same number of segments or molecular weight, and thus generally need to be treated as different components. Experiments also often use mixed solvents in which the solvent composition inside a polymer coil (or gel) is in general different from the outer regions, as certain solvent species preferentially remain inside (or outside) the polymer coil.14
We consider a simple mixture of spherical active and passive Brownian particles with equal size a; the passive particles translate by Brownian motion but are otherwise inactive (see Appendix A for the equations of motion). We do not include the effects of hydrodynamic interactions, and there is no polar order of the swimmers or any large-scale collective motion (e.g., bioconvection). We find that many new insights about the temperature of active matter can be obtained from this simple system.
In the next section we further extend the mixing example discussed above (Fig. 1) by analyzing the effects of adding a small concentration of passive Brownian particles into an active system. We analyze the quantities that “equilibrate” in an active system by studying the collisions between a swimmer and a passive particle. In Section 3 we develop a simple mechanical theory by identifying the different contributions that make up the total active pressure of the mixture. Since active matter is an inherently nonequilibrium system, we do not rely upon the thermodynamic free energy or chemical potential to predict the phase behavior of the system. Unlike these thermodynamic quantities, the mechanical stress (or pressure) is defined out of equilibrium and can be used to analyze mechanical instability of active matter. We then take our equation of state to compute what would be the nonequilibrium analogs of the free energy and chemical potential. Lastly, we analyze different stability criteria, facilitating discussion about the variables that may be held fixed and varied in experiments and computer simulations.
2 Do active particles “thermally” equilibrate?
From the mixing process in Fig. 1 we learned that the characteristic activity scale of the swimmers do not equilibrate (i.e., (ksTs)H ≠ (ksTs)C) unlike the thermal energy kBT of passive Brownian particles. To gain further insight into the quantities that get shared in an active system, suppose now that we have a dilute concentration of passive bath particles in a sea of active swimmers. The motion and behavior of passive bath particles are influenced markedly by the swimmers' reorientation Péclet number PeR ≡ a/(U0τR), a ratio of the swimmer size a to its run length U0τR.Swimmers with run lengths small compared to their size (PeR ≫ 1) reorient rapidly and take small swim steps behaving as Brownian walkers. When a swimmer takes a step and collides into a bath particle, the passive particle gets a displacement of order the swimmer's step size 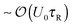 . After many such collisions, the change in the translational diffusivity of the passive bath particle is (Dbath − D0) ∼ U0(U0τR)ϕa, where D0 = kBT/ζ is the Stokes–Einstein–Sutherland diffusivity of an isolated bath particle and ϕa is the area (or volume in 3D) fraction of the swimmers. In this limit active swimmers repeatedly displace the bath particle by their run length U0τR, which allows the bath particle to sense the activity or ‘temperature’ of the swimmers via collisions. In other words, the bath particle behaves as a ‘thermometer’ of the active suspension,12 where the collisional displacements it receives from the swimmer can be used to infer the swimmers' characteristic ‘energy scale’ ksTs = ζU02τR/2. This activity scale is analogous to the thermal energy kBT, the kinetic activity of passive Brownian particles, which can also be probed by analyzing the collisions between two passive particles. In this sense a suspension of swimmers with small run lengths U0τR < a behaves similarly to a purely Brownian suspension with an effective ‘temperature’ ksTs. For active Brownian particles, this contribution is in addition to the thermal kBT that gets shared as usual as a result of translational Brownian motion. However, one would not be able to distinguish between the two contributions because the dynamics of swimmers with PeR ≫ 1 is equivalent to that of passive Brownian particles. If we placed active swimmers that behave identically to passive Brownian particles behind an osmotic barrier, we would not be able to distinguish one from the other. In this sense a Brownian particle can be interpreted as a “swimmer” having an extreme value of the reorientation Péclet number PeBR → ∞.
. After many such collisions, the change in the translational diffusivity of the passive bath particle is (Dbath − D0) ∼ U0(U0τR)ϕa, where D0 = kBT/ζ is the Stokes–Einstein–Sutherland diffusivity of an isolated bath particle and ϕa is the area (or volume in 3D) fraction of the swimmers. In this limit active swimmers repeatedly displace the bath particle by their run length U0τR, which allows the bath particle to sense the activity or ‘temperature’ of the swimmers via collisions. In other words, the bath particle behaves as a ‘thermometer’ of the active suspension,12 where the collisional displacements it receives from the swimmer can be used to infer the swimmers' characteristic ‘energy scale’ ksTs = ζU02τR/2. This activity scale is analogous to the thermal energy kBT, the kinetic activity of passive Brownian particles, which can also be probed by analyzing the collisions between two passive particles. In this sense a suspension of swimmers with small run lengths U0τR < a behaves similarly to a purely Brownian suspension with an effective ‘temperature’ ksTs. For active Brownian particles, this contribution is in addition to the thermal kBT that gets shared as usual as a result of translational Brownian motion. However, one would not be able to distinguish between the two contributions because the dynamics of swimmers with PeR ≫ 1 is equivalent to that of passive Brownian particles. If we placed active swimmers that behave identically to passive Brownian particles behind an osmotic barrier, we would not be able to distinguish one from the other. In this sense a Brownian particle can be interpreted as a “swimmer” having an extreme value of the reorientation Péclet number PeBR → ∞.
The swim activity ksTs can also be understood by comparing the statistical correlation of the self-propulsive swim force, Fswim ≡ ζU0 = ζU0q where q is the unit orientation vector specifying the swimmer's direction of self-propulsion, to that of the Brownian force, FB. The swim force correlation 〈Fswim(t)Fswim(t′)〉 = (ζU0)2〈q(t)q(t′)〉 = (ζU0)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(t − t′)/τR) turns into a delta-function correlation 〈Fswim(t)Fswim(t′)〉 ∼ (ζU0)2τRδ(t − t′) as τR → 0.15 Recall that as τR → 0 the active swimmers behave as random Brownian walkers, which have the white noise statistics
exp(−(t − t′)/τR) turns into a delta-function correlation 〈Fswim(t)Fswim(t′)〉 ∼ (ζU0)2τRδ(t − t′) as τR → 0.15 Recall that as τR → 0 the active swimmers behave as random Brownian walkers, which have the white noise statistics 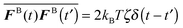 where the overline indicates an average over the solvent fluctuations. A comparison of these two correlations again suggests that the swimmers' kinetic activity can be interpreted by ksTs ≡ ζU02τR/2.
where the overline indicates an average over the solvent fluctuations. A comparison of these two correlations again suggests that the swimmers' kinetic activity can be interpreted by ksTs ≡ ζU02τR/2.
For swimmers with run lengths large compared to their size, (PeR ≪ 1), we observe a different behavior. Colliding into a bath particle, the swimmer continues to push the bath particle until it moves completely clear of the swimmer's trajectory. The bath particles receive a displacement of 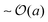 upon colliding with a swimmer, not the run length U0τR. Therefore the length scale associated with collisions is the swimmer size a, and the change in the long-time diffusivity of the bath particles (Dbath − D0) ∼ U0aϕa. Unlike the limit of PeR ≫ 1 discussed above, here the bath particles cannot probe the activity or ‘temperature’ of the swimmers because it only receives a displacement of its size a, even though the swimmers actually diffuse with their swim diffusivity Dswim ∼ U02τR. The ratio of the two diffusivities (Dbath − D0)/Dswim ∼ U0aϕa/(U02τR) = ϕaPeR, suggesting that the reorientation Péclet number PeR ≡ a/(U0τR) is the quantity that gets shared between the swimmers via collisions for small PeR.5 This implies that the swimmers' energy scale ksTs = ζU02τR/2 does not get shared in the collisions and thus does not represent the ‘temperature’ in the classical sense.
upon colliding with a swimmer, not the run length U0τR. Therefore the length scale associated with collisions is the swimmer size a, and the change in the long-time diffusivity of the bath particles (Dbath − D0) ∼ U0aϕa. Unlike the limit of PeR ≫ 1 discussed above, here the bath particles cannot probe the activity or ‘temperature’ of the swimmers because it only receives a displacement of its size a, even though the swimmers actually diffuse with their swim diffusivity Dswim ∼ U02τR. The ratio of the two diffusivities (Dbath − D0)/Dswim ∼ U0aϕa/(U02τR) = ϕaPeR, suggesting that the reorientation Péclet number PeR ≡ a/(U0τR) is the quantity that gets shared between the swimmers via collisions for small PeR.5 This implies that the swimmers' energy scale ksTs = ζU02τR/2 does not get shared in the collisions and thus does not represent the ‘temperature’ in the classical sense.
The bath particles' entirely different behavior for large and small PeR reveals the richness and challenge to understanding the ‘temperature’ of nonequilibrium active systems. This marked change in the quantity that gets shared in active systems is due to the capability of swimmers to have run lengths U0τR that can be small or large compared to their size a. This is a key fundamental difference between the swimmers' activity ksTs and the thermal energy kBT. In a classical molecular fluid, kBT is always the quantity that equilibrates because the displacements of a passive Brownian particle are small compared to its size a (or any other length scale), i.e. PeBR ≡ a/(UBτB) → ∞ where UB = D0/a is the characteristic speed of a Brownian step and τB is its momentum relaxation timescale.
Moreover, the swimmers must continuously collide with the passive particle to impart information about their kinetic activity, ksTs—even after many collisions, the passive particle only possesses kBT units of thermal energy once all collisions stop. This is in stark contrast with a molecular or kinetic fluid particle that is able to completely transmit its kinetic activity to another particle upon collisions. If a molecular fluid particle with initially zero activity is placed inside a container full of fluid particles with energy kBT, the inactive particle would collide repeatedly and eventually attain the thermal energy kBT. Furthermore, it will keep its kBT activity even when the other particles are removed. In contrast, a passive particle would cease to move (aside from its translational Brownian motion) if active swimmers are removed because of the damping due to the solvent. In this sense the temperature of an active nonequilibrium fluid is not well defined, as each swimmer has its own unique intrinsic kinetic activity that does not get shared and equilibrated.5
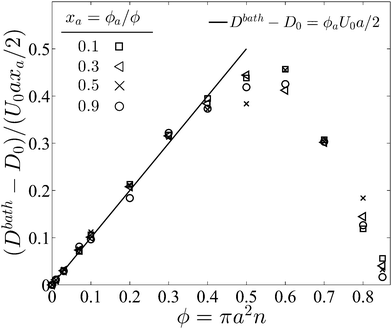
In pursuant of the discussion above we conducted Brownian dynamics (BD) simulations (see Appendix) and computed the long-time self diffusivity 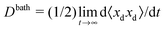 , where xd is the position of the passive bath particles. As shown in Fig. 2, for small PeR we indeed find that Dbath = D0 + U0aϕa/2 fits the data for all ϕ ≲ 0.4. At higher ϕ the passive particles are trapped into clusters by the swimmers and Dbath decays to 0. Fig. 2 suggests that the parameter PeR gets shared upon swimmer collisions and not the scale ksTs.
, where xd is the position of the passive bath particles. As shown in Fig. 2, for small PeR we indeed find that Dbath = D0 + U0aϕa/2 fits the data for all ϕ ≲ 0.4. At higher ϕ the passive particles are trapped into clusters by the swimmers and Dbath decays to 0. Fig. 2 suggests that the parameter PeR gets shared upon swimmer collisions and not the scale ksTs.
Finally, an important concept here is that the departure induced by a swimmer is the same whether it collides into a passive particle or into another active swimmer. In both cases the displacement due to the collision is the swimmer size a (for small PeR), and this is the key idea underlying the mechanical theory which we explain below.
3 Mechanical theory
Our theory applies in general to a mixture of active swimmers with different activity levels, but here we focus on a mixture of active swimmers and passive particles. Since a passive particle behaves equivalently to an “active” particle with a very small reorientation time and step size, this system corresponds to the limiting case of a mixture of one group of swimmers with a finite, nonzero PeR and another group of “swimmers” with PeR → ∞. The general case is a mixture of active swimmers with two different, finite PeaR and PedR. However, the active and passive limit is interesting from an experimental perspective because a mixture of passive and active particles is easy to make. Mixtures of swimmers with different, finite PeR are difficult to analyze because of the inherent variations in activity in living organisms and in synthetic self-propelled particles due to fabrication defects.We are now in a position to derive a simple mechanical pressure theory to predict the phase behavior of a mixture of active and passive particles. The total active pressure of the mixture is given by
| Πact = Πswim + ΠPa + ΠPd + nkBT, | (1) |
In general Πact is a function of (ϕ, xa, PeR, ksTs, kBT), where ϕ is the total area fraction (ϕ = ϕa + ϕd), ϕa and ϕd are the area fractions of the active and passive particles, respectively, xa = ϕa/ϕ is the active swimmer composition, the reorientation Péclet number PeR ≡ a/(U0τR) is the ratio of swimmer size a to its run length U0τR, ksTs ≡ ζU02τR/2 is the swimmers' characteristic ‘energy scale’ as discussed earlier, and kBT is the thermal energy. We can also express the active pressure using the area fractions of the active and passive particles, Πact(ϕa, ϕd, PeR, ksTs, kBT). To reduce the number of parameters, we take equal size active and passive particles aa = ad = a and assume that swimmer reorientation is thermally induced so that the translational and reorientational diffusivities are related via the Stokes–Einstein–Sutherland expressions: (D0/a2)/τR = 4/3. Thus the ratio of the thermal energy to the swim activity is kBT/(ksTs) = 8PeR2/3. This is not a requirement; one can also vary a swim Péclet number, Pes ≡ U0a/D0 in addition to the reorientation Péclet number PeR ≡ a/(U0τR).
We now explain the independent pressure contributions in detail below. The theory is presented for 2D, but it is straightforward to generalize to 3D.
3.1 Swim pressure of active swimmers, Πswim
The swim pressure is defined as the first moment of the swim force Πswim = −na〈x·Fswim〉/2 (in 2D), where na is the number density of swimmers and the angle brackets denote an average.3 It is permissible for computing the stress to interpret the self-propulsion of an active swimmer as arising from a swim force, Fswim ≡ ζU0,‡ where U0 = U0q; U0 is the swimming speed and q is the unit orientation vector defining the swimmer's direction of self-propulsion. Physically, Fswim represents the force required to prevent an active swimmer from moving, for example by optical tweezers. The origin of the swim pressure stems from the notion that confined self-propelled bodies exert a pressure on the container boundaries as they collide into the surrounding walls. The same notion applies to molecular gases that collide into the container walls to exert a pressure or to colloidal solutes that collide into a semipermeable membrane to exert an osmotic pressure. The swim pressure is the “osmotic” pressure of active particles.A dilute system of purely active swimmers exerts an ‘ideal-gas’ swim pressure given by Πswim = naζU02τR/2 = naksTs in 2D.3 The swim pressure is a single-particle self contribution in which the relevant length scale (i.e. moment arm) is the swimmers' run length U0τR. As discussed earlier the ratio of the swimmer size a to the run length U0τR is the reorientation Péclet number PeR ≡ a/(U0τR), and this parameter impacts the phase behavior of active systems.5 For large PeR the swimmers take small swim steps and behave as Brownian walkers, exerting the swim pressure Πswim = naζU02τR/2 = naksTs for all concentrations.
For small PeR the swimmers have large run lengths and undergo many collisions with passive particles and other swimmers in a time τR. The average distance traveled by a swimmer between reorientation events is reduced and the same is true for the swim pressure. Extending the results for a purely active system,5 we take (for small PeR)
| Πswim = naksTs(1 − ϕ − 0.2ϕ2), | (2) |
Fig. 3 confirms that all data from BD simulations collapse onto eqn (2). To better understand eqn (2), we can analyze the limits for large and small concentrations of active swimmers relative to passive particles. Expanding the swim pressure for small ϕd/ϕa = (1 − xa)/xa, we find
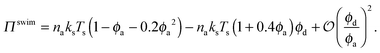 | (3) |
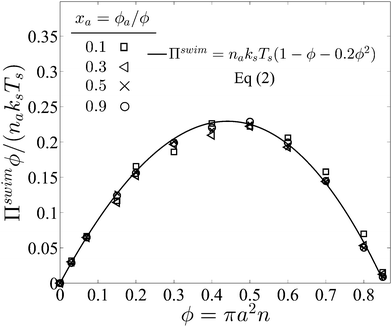 | ||
| Fig. 3 Swim pressure exerted by active swimmers in a mixture as a function of the total area fraction ϕ = ϕa + ϕd for different values of active composition xa = ϕa/ϕ and fixed PeR ≡ a/(U0τR) = 0.1. Subscripts “a” and “d” refer to active and passive particles, respectively. The solid curve is the mechanical theory eqn (2) and the symbols are BD simulations. The swimmer activity ksTs ≡ ζU02τR/2. | ||
In the other limit of small concentration of active swimmers relative to passive particles (i.e., small ϕa/ϕd = xa/(1 − xa)), we find
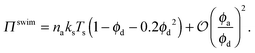 | (4) |
3.2 Interparticle (collisional) pressure
In addition to the swim pressure, which is a single-particle contribution to the mechanical pressure, there is also an interparticle (or collisional) pressure arising from interactions between the particles. Since two bodies are required for an interaction (or collision for a hard-sphere potential) and the relevant length scale is the particle size a, the interparticle pressure scales as ΠP ∼ n2ζU0a3 ∼ nksTsPeRϕ, fundamentally different from the swim pressure. Furthermore, the interparticle pressure monotonically increases with concentration for a repulsive potential and helps stabilize a system. The competition between the destabilizing effect of the swim pressure and the stabilizing effect of the interparticle (or collisional) pressure controls the phase behavior of active systems. For clarity we split the interparticle pressure into two contributions—collisions induced by active swimmers and passive particles separately.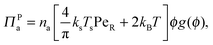 | (5) |
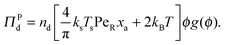 | (6) |
Fig. 4 graphs the sum of the collisional pressures of the contributions from both active and passive particles as a function of the total area fraction. We see a dependence on the composition of active swimmers xa especially at high area coverage. We assume that swimmer reorientation is thermally induced so that the translational and reorientational diffusivities are related via the Stokes–Einstein–Sutherland expressions, (D0/a2)/τR = 4/3, and the ratio of the thermal energy to the swim activity is kBT/(ksTs) = 8PeR2/3.
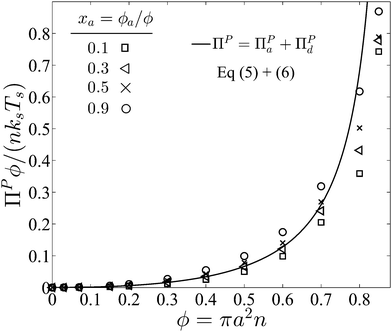 | ||
| Fig. 4 Collisional pressure exerted by active and passive particles ΠP = ΠPa + ΠPd for fixed PeR ≡ a/(U0τR) = 0.1 as a function of the total area fraction ϕ = ϕa + ϕd and different values of active composition xa = ϕa/ϕ. The solid curve is the mechanical theory eqn (5) and (6) for xa = 0.3, and the symbols are BD simulations. We take the swimmer reorientation to be thermally induced so that kBT/(ksTs) = 8PeR2/3. | ||
4 Phase behavior
Experiments and computer simulations have shown that a suspension of purely active particles may self-assemble into regions of dense and dilute phases, resembling an equilibrium liquid–gas coexistence.6–10 The source of this phase separation is that swimmers collide and obstruct each others' movement, causing large clusters to form at sufficiently high concentrations.13 Now, if this active system also contained passive Brownian particles, recent computer simulations20 and experiments21 have shown that the composition of passive particles inside the dense cluster phase is generally larger than that in the dilute phase, as they tend to stay inside the cluster once they are pushed into one by an active swimmer. In contrast, the active swimmers prefer to swim freely in the dilute phase because their activity allows them to escape the dense clusters.Theory and simulations have produced phase diagrams for a suspension of purely active swimmers,5,8,15,22–24 but a mixture of active and passive particles is yet to be thoroughly analyzed. Recently Stenhammar et al.20 conducted Brownian dynamics simulations of a mixture of active and passive Brownian particles and used a kinetic model to locate the phase boundaries. The kinetic model based upon Redner et al.8 accurately predicts many regions of phase space, but due to the theory's inherent assumptions the lower spinodal boundary is not well characterized.
Our theory is based upon the new ‘swim pressure’ perspective which accurately predicts the phase behavior of a system of active swimmers.3–5 Others have subsequently used the swim pressure to study phase-separating active systems.25,26 We now have eqn (1), an equation of state that allows us to predict the phase behavior of the active/passive mixture.
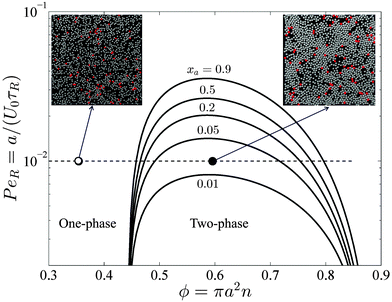
Interpreting the total density derivative of the active pressure as a global mechanical instability, (∂Πact/∂ϕ)xa,Ts,PeR = 0, we can identify the regions of stability in the phase diagram. This is a purely mechanical definition of the spinodal and does not rely upon thermodynamic arguments. As shown by the red curve in Fig. 5, our prediction agrees well with Stenhammar et al.'s20 simulation data. Here the spinodal and the simulation data correspond to a global dense/dilute-phase separation based upon fluctuations in the total particle—active plus passive—density. This is different from the phase separation that may occur locally within each phase, as commonly seen in immiscible polymer mixtures. There are no adjustable parameters in the comparison.
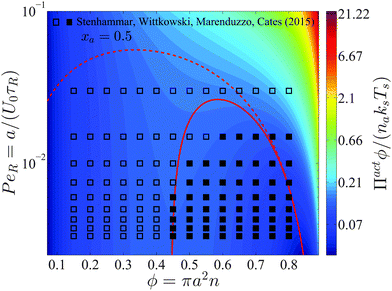 | ||
| Fig. 5 Phase diagram in the PeR − ϕ plane in 2D for a fixed active swimmer composition xa = 0.5. The colorbar shows the active pressure scaled with the swim activity ksTs = ζU02τR/2. The open and filled symbols are simulation data of Stenhammar et al.20 with a homogeneous and phased-separated state, respectively. The solid and dashed red curves are the spinodals delineating the regions of stability based upon fluctuations in the total particle density and the thermodynamic definition, respectively. | ||
Compared to a purely active swimmer system, onset of phase transition occurs at lower PeR when passive particles are present. For xa = ϕa/ϕ = 0.5 shown in Fig. 5, phase transition is possible for PeR ≲ 0.025, compared to PeR ≲ 0.04 for a purely active system xa = 1. Therefore, given a fixed total area fraction the presence of passive particles makes it more difficult for phase separation to occur, which may be an important consideration in the design of experiments of active systems.
In Section 2 we discussed that the reorientation Péclet number PeR is the quantity that gets shared upon collisions between swimmers for PeR ≪ 1. Using the swimmer activity ksTs ≡ ζU02τR/2, we can rewrite PeR ≡ a/(U0τR) = ζU0a/(2ksTs), which is interpreted as the interactive energy of the swimmer (ζU0)a to its swim activity scale ksTs. In Fig. 5 phase separation becomes possible for small PeR, or large ksTs. In contrast, phase transition in a classical thermodynamic system is usually driven by attractive enthalpic interactions and becomes possible for small kBT (low temperatures). If ksTs is interpreted as the “temperature” of active matter, Fig. 5 suggests that mixtures of active and passive particles may exhibit a lower critical solution temperature (LCST) transition,27 commonly seen in thermosensitive polymer systems.28 The LCST phase transition is dominated by entropy—as PeR decreases (ksTs increases), the run length of the swimmer increases, and the particle becomes effectively larger in size and has less space available for entropic mixing.5 However, because PeR is the quantity that gets shared upon collisions for PeR ≪ 1 (and not the activity ksTs), the activity ksTs does not play the same role as the thermal energy scale kBT in LCST phase transitions of polymer mixtures. This further verifies that the “temperature” of active matter is an elusive quantity that does not have a direct mapping to the temperature of an equilibrium system.
5 Limits of active pressure
Recent experiments by Kümmel et al.21 analyzed the phase behavior of a mixture of passive particles with a small concentration of active swimmers (ϕa ≈ 0.01). They observed swimmers gathering and compressing the passive particles into clusters. By varying the concentration of passive particles, they observed a phase separation of the mixture even at very small active swimmer concentrations.Our BD simulations agree qualitatively with the experiments.21 The active swimmers create tunnels in the sea of passive particles, which open a path for other trailing swimmers to move through. This leads to the formation of large clusters composed of purely passive particles and individual swimmers moving in the dilute phase, as shown in simulation images in Fig. 6. Based upon our mechanical theory, there is an equality between the Brownian collisional pressure of the dense passive clusters and the swim pressure of the dilute active swimmers compressing the crystals. A video of the BD simulation is available in the ESI.†
To model these observations, it is instructive to analyze the limits of the active pressure for large and small concentrations of active swimmers relative to passive particles. Since the mechanical pressure exerted by a system of purely active swimmers and purely Brownian particles are known, we can interrogate the effect of adding a small amount of passive or active particles into the suspension. This may be particularly useful for further experimental pursuits of active/passive mixtures.
In the limit of small active swimmer concentration relative to passive particles, the active pressure is
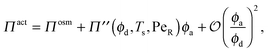 | (7) |
| Πosm = ndkBT(1 + 2ϕdg(ϕd)), | (8) |
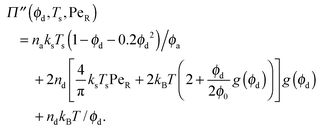 | (9) |
In the other limit of large active swimmer concentration relative to passive particles, we expect phase behavior similar to those observed in purely active suspensions.5 The passive particles can act as nucleation sites for cluster formation, which may spark an earlier onset of phase separation. The active pressure has the form
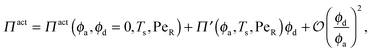 | (10) |
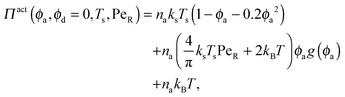 | (11) |
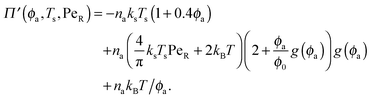 | (12) |
6 ‘Thermodynamic’ quantities
Thermodynamic quantities like the chemical potential and free energy are defined only for equilibrium systems. However, standard macroscopic mechanical balances can be applied to define quantities that are nonequilibrium analogs for active systems.3,5 Here we extend the derivation of the nonequilibrium free energy and chemical potential to mixtures of active and passive particles, and interpret these quantities as a natural extension for nonequilibrium systems.The virtual work done by an external mechanical force (i.e., stress) due to an infinitesimal change in the system volume δV is given by δW = −ΠδV where Π is the applied mechanical pressure. One can interpret this virtual work as the change in Helmholtz free energy of the system due to an applied mechanical stress, as is commonly done in elasticity theory.29 Upon carefully imposing incompressibility of the solvent, one can relate the nonequilibrium free energy to the mechanical pressure of a multicomponent mixture as14
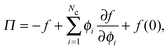 | (13) |
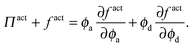 | (14) |
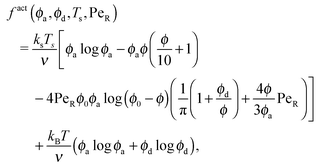 | (15) |
As done previously for a purely active system,3 we can derive the nonequilibrium chemical potential for multicomponent mixtures using purely mechanical arguments (see Appendix C). For a mixture of active and passive particles, it is given by
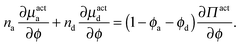 | (16) |
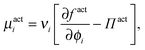 | (17) |
From the thermodynamics of mixtures, the stability criterion using the free energy is given by det(∂2f/∂ϕi∂ϕj) = 0.14 For our system this reduces to
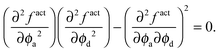 | (18) |
The dashed curve in Fig. 5 is the spinodal curve using eqn (18) for a fixed active swimmer fraction xa = 0.5. This spinodal boundary does not agree with the simulation data of Stenhammar et al.,20 as eqn (18) predicts a different phase boundary than those observed in a simulation. The simulations reflect a global dilute/dense phase separation based upon fluctuations in the total particle (both active and passive) density. In contrast, eqn (18) interrogates the stability of the free energy due to fluctuations in the active particle concentration while keeping the passive particle concentration fixed, and vice versa.
This facilitates an important consideration in both experiments and simulations about which variables are held fixed and varied. Depending on the ensemble of variables that are held fixed (active swimmer density, composition, etc.), the theory predicts in general different phase boundaries. To produce a phase diagram in a simulation, one typically fixes the overall swimmer composition xa and swimmer PeR, and varies the total area fraction ϕ or vice versa. This corresponds to a global dense/dilute-phase separation based upon fluctuations in the total particle density, which is well described by the mechanical instability criterion (∂Πact/∂ϕ)xa,Ts,PeR = 0, as shown by the red solid curve in Fig. 5.
In the experiments of Kümmel et al.,21 the active swimmer area fraction (ϕa = 0.01) and Péclet number 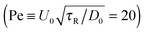 were held fixed, and the passive particle area fraction (ϕd) was varied. The ensemble of variables that we fix and vary must therefore be considered when we predict of the phase behavior of active mixtures. It is likely that one can conduct an experiment or simulation where the phase behavior agrees with the thermodynamic spinodal det(∂2f/∂ϕi∂ϕj) = 0 (red dashed curve in Fig. 5). There remains much more to the phase portrait than the existing studies and our mechanical theory have revealed.
were held fixed, and the passive particle area fraction (ϕd) was varied. The ensemble of variables that we fix and vary must therefore be considered when we predict of the phase behavior of active mixtures. It is likely that one can conduct an experiment or simulation where the phase behavior agrees with the thermodynamic spinodal det(∂2f/∂ϕi∂ϕj) = 0 (red dashed curve in Fig. 5). There remains much more to the phase portrait than the existing studies and our mechanical theory have revealed.
7 Conclusions
We developed a simple mechanical theory to address an important question in active matter: do active particles thermally equilibrate, and if so, what is the quantity that gets shared upon collisions? We found that the swimmers' activity ksTs ≡ ζU02τR/2 does not have the same properties of the thermal energy kBT. The swimmers' capability to have run lengths U0τR small or large compared to their size a (and other length scales in the problem) distinguishes them from passive Brownian particles whose step size is smaller than any other length scale in the system.We discovered that for PeR ≡ a/(U0τR)≪ 1 the quantity that gets shared upon collisions is PeR, not the scale ksTs. This was seen in the simple mixing experiment in Fig. 1 and from analyzing the motion of a passive particle as a probe to measure the kinetic activity of the swimmers (ksTs). The notion of the swimmers' energy ksTs and/or PeR being shared via collisions is an interesting concept that may facilitate further theoretical and experimental studies.
Another fundamental difference between an active system and a classical fluid was found by observing the motion of a passive particle in a sea of active swimmers. Even after undergoing many collisions with swimmers, the passive bath particle ceases to move (aside from its translational Brownian motion) if the swimmers are removed because of the damping by the solvent. In contrast, a passive bath particle placed inside a classical molecular or colloidal solution keeps its kBT activity even when the other particles are removed. Because the swimmers must continuously collide into the passive bath particle to impart information about their kinetic activity, there is no “thermal equilibration” that takes place in an active suspension.
To understand the temperature and phase behavior of active matter, we studied a mixture of active and passive Brownian particles. Our theory applies more generally to a mixture of active systems with different activities. In fact, we showed that a passive Brownian particle behaves equivalently to a “swimmer” with PeR → ∞, so the active/passive mixture corresponds to a limiting case of a mixture of active systems with different activities. A swimmer that takes small steps and reorients rapidly is indistinguishable from a purely Brownian particle if it is placed behind an osmotic barrier. For a mixture of active particles with different, finite PeR, we would simply write the swim and collisional pressures for each individual species Pe(1)R, Pe(2)R, etc. The total active pressure of the system is a sum of the contributions from all species, as in eqn (1).
By understanding the dependence of the active swimmer composition xa and the total area fraction ϕ in each of the active pressure contributions, we obtained an explicit equation of state for the active/passive mixture. The key principle in deriving the equation of state was that a swimmer imparts the same displacement whether it collides into another swimmer or a passive particle. We found that the swim pressure decreases with increasing area fraction and is the destabilizing term that leads to a phase separation in active systems. In contrast, the interparticle (collisional) pressure increases monotonically with the area fraction and helps to stabilize the suspension from phase separation. The competition between these two effects is determined by the reorientation Péclet number, PeR ≡ a/(U0τR). The spinodal specifies the regions in the phase diagram where these two opposing effects cancel precisely, and these regions were identified in the PeR − ϕ space for our mixture.
We corroborated our theory with recent simulations20 and experiments21 of active/passive mixtures. Our simple model may be a useful tool for predicting phase behavior in both experiments and simulations, as many regions of phase space are difficult to explore because of experimental and computational challenges of covering the parameter space.
We found that different stability conditions give rise to different phase boundaries, facilitating considerations in simulations about which variables are held fixed and varied. The derivative of our active pressure with respect to the total area fraction predicts accurately the global dense/dilute phase transitions observed in simulations. To predict the local phase separation within the dense or dilute phase (as in immiscible polymer mixtures), a different stability criterion is required. Finally, we extended the mechanical theory to determine the nonequilibrium chemical potential and free energy for a mixture of active and passive species.
Extension of our theory to 3D and for different particle size ratios is straightforward. In 3D the characteristic activity scale becomes ksTs ≡ ζU02τR/6 instead of ζU02τR/2 due to the extra degree of freedom. For a mixture of particles with different sizes a and b, the pair-distribution function adjusts to different collision pairs gaa(ϕ), gad(ϕ), etc because now the particle–particle separation at contact is different. For a polydispersed active system, the large clusters are no longer crystalline and are less stable than those in a monodisperse system. Therefore the two-phase region in Fig. 5 shrinks and shifts to smaller PeR.
In our model we neglected hydrodynamic interactions between the particles, which may contribute additional terms such as the “hydrodynamic stresslet”30 to the active pressure. We also did not consider the effects of polar order and alignment of the swimmers, which are not necessary for phase-separating systems.
Appendix
A. Micromechanical equations of motion
The active particle dynamics are governed by the N-particle Langevin equation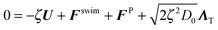 | (A1) |
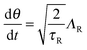 | (A2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, sin
θ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), FP is the interparticle force between the particles to enforce no overlap, ΛT and ΛR are unit random normal deviates, τR is the orientation time of the swimmer, and D0 is the Stokes–Einstein–Sutherland translational diffusivity. The passive Brownian particles are governed by the same equation but without the self-propulsive force:
θ), FP is the interparticle force between the particles to enforce no overlap, ΛT and ΛR are unit random normal deviates, τR is the orientation time of the swimmer, and D0 is the Stokes–Einstein–Sutherland translational diffusivity. The passive Brownian particles are governed by the same equation but without the self-propulsive force: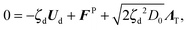 | (A3) |
B. Limits of active free energy
To gain further insight into the free energy, we analyze the limits of fact for our mixture system for large and small concentrations of active swimmers relative to passive particles. Expanding the active free energy for small ε = ϕd/ϕa = (1 − xa)/xa, we find in the limit of large active concentration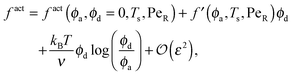 | (B1) |
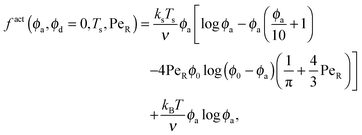 | (B2) |
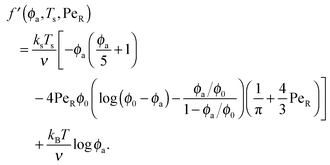 | (B3) |
Expanding the swim pressure for small ε′ = ϕa/ϕd = xa/(1 − xa), we find in the limit of small active concentration
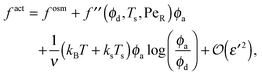 | (B4) |
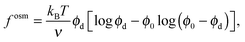 | (B5) |
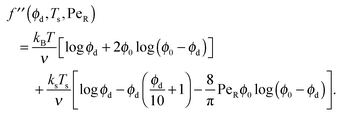 | (B6) |
C. Mechanical derivation of the chemical potential for multicomponent systems
The number density of an Nc-component system§ satisfies the conservation equation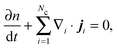 | (C1) |
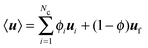 , and ui and uf are the number averaged velocity of swimmer species i and fluid at a continuum point, respectively. The total volume (or area) fraction of the particles is
, and ui and uf are the number averaged velocity of swimmer species i and fluid at a continuum point, respectively. The total volume (or area) fraction of the particles is 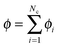 . Incompressibility requires the suspension-average velocity (particles plus the fluid) to satisfy ∇·〈u〉 = 0.
. Incompressibility requires the suspension-average velocity (particles plus the fluid) to satisfy ∇·〈u〉 = 0.
We apply an averaged macroscopic mechanical momentum balance to obtain an expression for jreli. Following the standard Irving–Kirkwood approach, we obtain
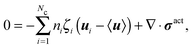 | (C2) |
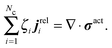 | (C3) |
We can use our mechanical derivation to define a nonequilibrium chemical potential by analogy to the quantity whose gradient would drive a flux:
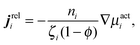 | (C4) |
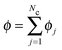 . This definition is analogous to that of a thermodynamic system where the relative flux is driven by gradients in the thermodynamic chemical potential. Substituting eqn (C4) into eqn (C3) and using the definition Πact ≡ −tr
. This definition is analogous to that of a thermodynamic system where the relative flux is driven by gradients in the thermodynamic chemical potential. Substituting eqn (C4) into eqn (C3) and using the definition Πact ≡ −tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σact/2, we arrive at
σact/2, we arrive at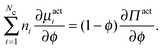 | (C5) |
This relationship between the chemical potential and pressure is equivalent for a system of passive Brownian particles and active swimmers with small τR. We thus interpret μact as a natural definition and extension of the chemical potential for nonequilibrium systems.
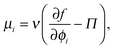 | (C6) |
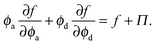 | (C7) |
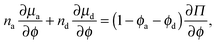 | (C8) |
Therefore the mechanical derivations of the stress, momentum balance, and flux are in full agreement with thermodynamics.
Acknowledgements
SCT is supported by the Gates Millennium Scholars fellowship and the National Science Foundation Graduate Research Fellowship under Grant No. DGE-1144469. This work is also supported by NSF Grant CBET 1437570.References
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- J. Toner, Y. Tu and S. Ramaswamy, Ann. Phys., 2005, 318, 170–244 CAS.
- S. C. Takatori, W. Yan and J. F. Brady, Phys. Rev. Lett., 2014, 113, 028103 CrossRef CAS.
- X. Yang, M. L. Manning and M. C. Marchetti, Soft Matter, 2014, 10, 6477–6484 RSC.
- S. C. Takatori and J. F. Brady, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 032117 CrossRef CAS.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940 CrossRef CAS PubMed.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef.
- J. Bialké, H. Löwen and T. Speck, Europhys. Lett., 2013, 103, 30008 CrossRef.
- J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2013, 111, 145702 CrossRef.
- X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2000, 84, 3017–3020 CrossRef CAS.
- D. Loi, S. Mossa and L. F. Cugliandolo, Soft Matter, 2011, 7, 10193–10209 RSC.
- M. E. Cates and J. Tailleur, Europhys. Lett., 2013, 101, 20010 CrossRef CAS.
- M. Doi, Soft Matter Physics, Oxford University Press, Oxford, United Kingdom, 2013 Search PubMed.
- Y. Fily, S. Henkes and M. C. Marchetti, Soft Matter, 2014, 10, 2132–2140 RSC.
- S. C. Takatori and J. F. Brady, Soft Matter, 2014, 10, 9433–9445 RSC.
- W. Yan and J. F. Brady, Soft Matter, 2015, 11, 6235–6244 RSC.
- W. Russel, D. Saville and W. Schowalter, Colloidal Dispersions, Cambridge University Press, 1992 Search PubMed.
- J. F. Brady, J. Chem. Phys., 1993, 98, 3335–3341 CrossRef CAS PubMed.
- J. Stenhammar, R. Wittkowski, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2015, 114, 018301 CrossRef.
- F. Kümmel, P. Shabestari, C. Lozano, G. Volpe and C. Bechinger, Soft Matter, 2015, 11, 6187–6191 RSC.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489–1499 RSC.
- T. Speck, J. Bialké, A. M. Menzel and H. Löwen, Phys. Rev. Lett., 2014, 112, 218304 CrossRef.
- A. Wysocki, R. G. Winkler and G. Gompper, Europhys. Lett., 2014, 105, 48004 CrossRef.
- A. P. Solon, J. Stenhammar, R. Wittkowski, M. Kardar, Y. Kafri, M. E. Cates and J. Tailleur, Phys. Rev. Lett., 2015, 114, 198301 CrossRef.
- R. G. Winkler, A. Wysocki and G. Gompper, Soft Matter, 2015, 11, 6680–6691 RSC.
- R. B. Griffiths and J. C. Wheeler, Phys. Rev. A: At., Mol., Opt. Phys., 1970, 2, 1047–1064 CrossRef.
- P. I. Freeman and J. S. Rowlinson, Polymer, 1960, 1, 20–26 CrossRef CAS.
- L. Landau and E. Lifshitz, Theory of Elasticity, Butterworth-Heinemann, 3rd edn, 1986, vol. 7 Search PubMed.
- D. Saintillan and M. J. Shelley, Phys. Fluids, 2008, 20, 123304 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm01792k |
| ‡ This however does not imply that the intrinsic swimming mechanism generates a long-range (1/r) Stokes velocity field as does an external force.16,17 |
| § There are Nc + 1 total components, including the solvent. |
| This journal is © The Royal Society of Chemistry 2015 |