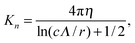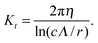DOI:
10.1039/C5SM01678A
(Paper)
Soft Matter, 2015,
11, 7867-7876
Modelling the mechanics and hydrodynamics of swimming E. coli
Received
8th July 2015
, Accepted 5th August 2015
First published on 5th August 2015
Abstract
The swimming properties of an E. coli-type model bacterium are investigated by mesoscale hydrodynamic simulations, combining molecular dynamics simulations of the bacterium with the multiparticle particle collision dynamics method for the embedding fluid. The bacterium is composed of a spherocylindrical body with attached helical flagella, built up from discrete particles for an efficient coupling with the fluid. We measure the hydrodynamic friction coefficients of the bacterium and find quantitative agreement with experimental results of swimming E. coli. The flow field of the bacterium shows a force-dipole-like pattern in the swimming plane and two vortices perpendicular to its swimming direction arising from counterrotation of the cell body and the flagella. By comparison with the flow field of a force dipole and rotlet dipole, we extract the force-dipole and rotlet-dipole strengths for the bacterium and find that counterrotation of the cell body and the flagella is essential for describing the near-field hydrodynamics of the bacterium.
1 Introduction
The bacterium E. coli is an example of a widely-studied class of motile microorganisms that exploit multiple helical flagella for locomotion.1 Each flagellum is propelled by a reversible rotary motor anchored in the cell's membrane.1–3 When all the motors rotate in the same direction, the flagella form a bundle and the bacterium swims forward; the so-called ‘run’ phase. It is interrupted by short periods of ‘tumble’ events, where the reversal of the motor-rotation direction of some flagella causes the associated flagella to leave the bundle, thereby inducing erratic rotation of the cell body.1,4–8 When the reversed motors switch back to their initial rotation direction, the bundle is reformed and the bacterium swims in a new direction. The alternating runs and tumbles allow the bacterium to efficiently execute a biased random walk toward favorable environments such as food-concentrated regions by adjusting run and tumble durations to the environmental conditions.
Numerous experimental, theoretical, and simulation studies have been performed to unravel the physical aspects of bacteria locomotion.9 These comprise aspects of the bacteria flagella such as their polymorphic transformations4,5,10–14 and bundle formation.15–20 Moreover, bacterial propulsion properties have been investigated,16,20–23 their run-and-tumble dynamics,16,24 as well as the influence of hydrodynamic interactions on their motion adjacent to surface.25–35 In addition, the effects of external flows on the dynamical behaviors of bacteria suspension have been addressed36–38 along with their rheological properties.39–41
The complexity of the bundling and swimming processes, especially near-field hydrodynamics, poses substantial challenges for an analytical description of bacteria locomotion. Here, mesoscale hydrodynamic simulations are particularly valuable to gain insight into the microscopic aspects of swimming, because they are able to bridge the large length- and time-scale differences between the bacterium and fluid degrees of freedom.42,43 The multiparticle collision dynamics (MPC) method42–44 has proven to be very valuable for the studies of active systems.9,34,45–53 Specifically, MPC has successfully been applied to elucidate synchronization between the flagella beating of nearby swimming sperm,54 as well as bundling of helical flagella of bacteria.18,19
Valuable theoretical insight into the swimming behavior of bacteria is achieved by very simplified models. An ellipsoidal or spherical body is often combined with either a single effective flagellum attached at one pole,13,35,55 or with several flagella attached in a more or less random manner.20,24,34 Thereby, hydrodynamic interactions are typically taken into account by a hydrodynamic tensor,20,24,35,55e.g., the Oseen or Rotne–Prager tensor.56 Such an approach is useful for a moderate number of hydrodynamically interacting units, typically a single or very few flagella. In contrast, studies of large systems and collective phenomena involving multi-flagellated cells require a different approach. We suggest to exploit the MPC method to account for fluid hydrodynamics. Moreover, a model for E. coli-type bacteria that can reproduce experimental results and allows for quantitative predictions of their swimming properties is desirable; here, only a few modelling studies are available so far.20,24,34
In this article, we present a bacterium model which closely resembles the geometry, flagellar elastic properties, and rotary motor torque of E. coli. By MPC simulations, we show that this model quantitatively reproduces the experimentally measured properties of E. coli for both the hydrodynamic friction and the relation between the bacterial swimming speed and flagellar rotation frequency. We find that the flow field near the model bacterium is rather complex with two spiral vortices arising from counterrotation of the cell body and flagella. At larger distances, the flow field displays a dipole pattern comparable to that of swimming E. coli. We perform a detailed analysis of the flow by comparison with the force-dipole and rotlet-dipole approximations, which enables us to access the force-dipole and rotlet-dipole strengths, which are essential quantities for the description of bacterial swimming.
The rest of the manuscript is structured as follows. Section 2 outlines the bacterium model and the MPC method for the fluid. Simulation results are presented in Section 3, and Section 4 summaries our findings. Further technical details for the flagellum modelling are presented in Appendix A, and the analysis of the flow field for periodic systems in Appendix B, respectively.
2 Simulation model and method
2.1 Bacterium model
The bacterium consists of a body and flagellar filaments, as shown in Fig. 1, which are composed of point-like particles of mass M = 10m. The cell body is represented by a spherocylinder of diameter d = 9a and length lb = 25a, composed of 51 circular sections of particles with a spacing of 0.5a, see Fig. 2(a). Here, m and a are mass and length units related to the MPC fluid, as described in Section 2.2. Both pole sections consist of a single particle only. In each of the other 49 sections, 60 particles are uniformly distributed along circles on the spherocylinder surface. To maintain the shape of the body, nearest- and next-nearest-neighboring pairs of particles are bonded by a harmonic potential| | 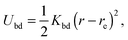 | (1) |
where r and re are the distance between the pair and the preferred value, respectively. Moreover, two particles separated by 10, 20, and 30 particles along each of the 49 circular sections are additionally connected via the potential (1) in order to obtain stable circles. The two pole particles are only bonded to their 60 nearest neighbors. The bond strength Kbd = 104kBT/a2 is chosen for all bonds, whereas the preferred length re of each bond is determined by the geometry. Here, kB is the Boltzmann constant and T the temperature.
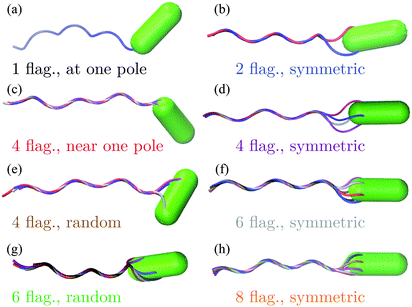 |
| | Fig. 1 Model of E. coli. Bacteria differ in the number of flagella and arrangement of flagella on the cell body. In a ‘symmetric’ arrangement, the first contour particle of each flagellum is uniformly distributed along a circle on the body. In a ‘random’ arrangement, the first contour particle is randomly located on the body. | |
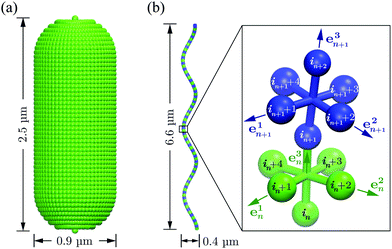 |
| | Fig. 2 (a) Model of the spherocylindrical cell body of diameter d = 0.9 μm and length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b = 2.5 μm. It is composed of 51 circular sections of particles, which are connected by the bond potential of eqn (1). (b) The flagellum, a three-turn left-handed helix of radius R = 0.2 μm, pitch Λ = 2.2 μm and contour length Lc = 7.6 μm (corresponding to the parallel length L∥ = 6.6 μm), consists of 76 consecutive segments. b = 2.5 μm. It is composed of 51 circular sections of particles, which are connected by the bond potential of eqn (1). (b) The flagellum, a three-turn left-handed helix of radius R = 0.2 μm, pitch Λ = 2.2 μm and contour length Lc = 7.6 μm (corresponding to the parallel length L∥ = 6.6 μm), consists of 76 consecutive segments. | |
A flagellum is described by the helical wormlike chain model,13,57 with an adaptation suitable for the combination with MPC. As shown in Fig. 2(b), a helical flagellum consists of N = 76 segments with a total of 381 particles. In each segment, six particles are arranged in an octahedron of edge length 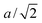 , forming 12 bonds along the edges and three along the diagonals. The preferred bond lengths are
, forming 12 bonds along the edges and three along the diagonals. The preferred bond lengths are 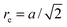 for edges and re = a for diagonals. The octahedron construction allows for a straightforward description of the intrinsic twist of the flagellum and a coupling of the twist to the forces exerted by the MPC fluid.
for edges and re = a for diagonals. The octahedron construction allows for a straightforward description of the intrinsic twist of the flagellum and a coupling of the twist to the forces exerted by the MPC fluid.
The bonds b3n = rin+1 − rin with n = 1,…,N specify the contour of the flagellum, and, together with b1n = rin+1 − rin+3 and b2n = rin+2 − rin+4, define orthonormal triads {e1n,e2n,e3n}, where eαn = bαn/|bαn| with α ∈ {1,2,3}. Here, the rin denote the positions of the backbone particles, and the rin+k (k = 1, 2, 3, 4) the positions of the particles in the plane with the normal e3n.
To characterize the local elastic deformation of a flagellum, the triad {e1n,e2n,e3n} is transported to {e1n+1,e2n+1,e3n+1} along the chain. This process is performed in two steps: (i) the rotation of {e1n,e2n,e3n} around e3n by a twist angle φn, and (ii) the rotation of the twisted triad {ẽ1n,ẽ2n,ẽ3n} by a bending angle ϑn around the normal nn = (e3n × e3n+1)/|e3n × e3n+1| to the plane defined by the contour bonds b3n and b3n+1. The elastic deformation energy is then
| | 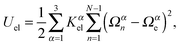 | (2) |
where
K1el =
K2el is the bending strength,
K3el the twist strength, and
Ωn =
Ω1ne1n +
Ω2ne2n +
Ω3ne3n =
ϑnnn +
φne3n the strain vector. We choose
K1el =
K2el =
K3el = 5 × 10
4kBT, corresponding to a bending stiffness of 2 × 10
−23 N m
2 for flagellar filaments within the experimental range of about 10
−24–10
−21 N m
2. The parameters
Ωαe in
eqn (2) define the equilibrium geometry of the model flagellum and are chosen to recover the shape of an
E. coli flagellum in the normal state,
i.e., a three-turn left-handed helix of radius 0.2 μm and pitch 2.2 μm.
16 See the Appendix A for details.
A flagellum is attached to the cell body by choosing a body particle as its first contour particle (i1, see Fig. 2(b) for the notation). The rotation of the flagellum is induced by a motor torque T decomposed into a force couple F and − F acting on particles i1 + 2 and i1 + 4 (T = b21 × F with F antiparallel to b11), or equivalently i1 + 1 and i1 + 3 (T = b11 × F with F parallel to b21). Hence, there is no net force on the bacterium. We consider |T| ≤ 1000 kBT ≃ 4100 pN nm, smaller than the stall torque of approximately 4500 pN nm of the flagellar motor.58 An opposite torque −T is applied to the body to ensure that the bacterium is torque-free. We do not explicitly model the hook that connects a flagellum and the body, in contrast to the model of ref. 20, but incorporate the physical features of the hook: (i) transmitting the motor torque to the flagellum for rotation, and (ii) provide the flagellum the freedom to adopt any orientation relative to the body. To prevent a flagellum from crossing the cell body or another flagellum, we use the repulsive Lennard-Jones potential
| | 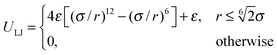 | (3) |
with
ε =
kBT to capture excluded-volume interactions. For flagellum-body repulsion,
r is the distance between a flagellar contour particle and a body particle, and
σ = 0.5
a is equal to the section spacing of the body. For flagellum–flagellum repulsion,
r is the closest distance between contour bonds of two flagella, and
σ = 0.25
a is set by the filament diameter around 25 nm.
16
The dynamics of the bacterium is determined by the forces resulting from the potentials in eqn (1)–(3) and the forces for generating the torques T and −T, and by the momentum exchange with the MPC fluid via the collision rule described by eqn (5) below.
2.2 Fluid model: multiparticle collision dynamics
The MPC fluid is modeled by a collection of point-like particles of mass m. Their dynamics proceeds by alternating streaming and collision steps. In the streaming step, the fluid particles move ballistically and the position ri of particle i with its velocity vi is updated according to| | | ri(t + Δt) = ri(t) + vi(t)Δt, | (4) |
where Δt is the time interval between collisions. In the collision step, all particles are sorted into cubic cells of length a and the velocity vi of particle i in cell c is renewed via the collision rule59| | 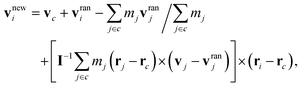 | (5) |
where vc and rc are the center-of-mass velocity and position of the particles in c, mj the mass of particle j in c, vranj a random velocity sampled from the Maxwell–Boltzmann distribution, and I the moment-of-inertia tensor of all particles in c. The collision rule (i) conserves both linear and angular momentum in each cubic cell, (ii) includes thermal fluctuations of the fluid, and (iii) maintains a constant temperature. To satisfy Galilean invariance, a random shift of the collision-cell grid is performed before each collision step.60
2.3 Parameters
The length a of a collision cell, the mass m of a MPC particle, and the thermal energy kBT define the length, mass, and energy units in our simulations. Other units are easily derived, e.g., density ρ0 = a−3, velocity 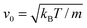 , time
, time 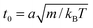 , and shear viscosity
, and shear viscosity 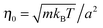 .
.
The simulations are performed in cubic boxes of length up to L = 250a with periodic boundary conditions. The largest system contains more than 1.5 × 108 fluid particles. We choose the collision time step Δt = 0.05t0 and the fluid density ρ = 10ρ0, leading to the fluid viscosity η = 7.15η0 and the Schmidt number Sc = 20, for which the fluid exhibits liquid-like dynamics.61 Newton's equations of motion for the bacterium model are integrated with the time step δt = Δt/25 using the velocity-Verlet algorithm. The Reynolds number Re = dρv/η is within the range 0.01–0.2 for the simulated bacteria with body diameter d = 9a and swimming speed v = 0.00075–0.0125v0.
Matching the geometry of our model bacteria to E. coli with a body of length of 2.5 μm and diameter 0.9 μm16 leads to the physical length a ≃ 0.1 μm of a collision cell. The thermal energy is kBT ≃ 4.1 pN nm at T = 300 K. A comparison with the viscosity of water of approximately 9 × 10−4 N s m−2 with η = 7.15η0 of the MPC fluid gives the physical time scale t0 ≃ 30 μs.
3 Results and discussion
3.1 Hydrodynamic friction coefficients of the bacterium
3.1.1 Flagellum.
The flagellar hydrodynamic coefficients relate the force ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) and torque
and torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) exerted by the fluid on the flagellar bundle to its translational velocity v and rotation frequency ω (angular velocity −ω by right-hand rule) via
exerted by the fluid on the flagellar bundle to its translational velocity v and rotation frequency ω (angular velocity −ω by right-hand rule) via| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = −γtfv + γcf(−ω), = −γtfv + γcf(−ω), | (6) |
| | ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = +γcfv − γrf(−ω), = +γcfv − γrf(−ω), | (7) |
where γtf and γrf are the translational and rotational friction coefficients about the helical axis, and γcf is the rotation-translation coupling coefficient. These coefficients, known as elements of the propulsion matrix,62 are essential quantities of bacterial swimming. We determine these coefficients by simulating a translating non-rotating (ω = 0, v ≠ 0) flagellum and a rotating non-translating (v = 0, ω ≠ 0) flagellum in the absence of the cell body. In the first case, the flagellum is pulled by a force ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pull along its helical axis, say x-axis, and y-, z-positions of each of its contour particles are trapped by harmonic potentials. This yields a confining torque
pull along its helical axis, say x-axis, and y-, z-positions of each of its contour particles are trapped by harmonic potentials. This yields a confining torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) conf that prevents the rotation by counteracting the torque in eqn (7). In the second case, a flagellum is rotated by a motor torque, and harmonic potentials are applied on its contour particles that prevent its translation, but allow for the rotation about the helical axis, causing a net axial torque
conf that prevents the rotation by counteracting the torque in eqn (7). In the second case, a flagellum is rotated by a motor torque, and harmonic potentials are applied on its contour particles that prevent its translation, but allow for the rotation about the helical axis, causing a net axial torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) rot and a confining force
rot and a confining force ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) conf opposite to the force in eqn (6). The two measurements lead to γtf =
conf opposite to the force in eqn (6). The two measurements lead to γtf = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pull/v, γcf = −
pull/v, γcf = −![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) conf/v, γrf = −
conf/v, γrf = −![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) rot/ω, and γcf =
rot/ω, and γcf = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) conf/ω. In the latter measurement, two no-slip walls63,64 orthogonal to the flagellum are included to ensure that the flagellar speed v vanishes with respect to the background fluid at rest. Without such no-slip walls, the translational speed of the flagellum is still v relative to the fluid velocity at the boundaries since the rotating flagellum is constantly pumping fluid backwards. From the results shown in Fig. 3, we obtain γtf/(m/t0) = 1028 ± 2,
conf/ω. In the latter measurement, two no-slip walls63,64 orthogonal to the flagellum are included to ensure that the flagellar speed v vanishes with respect to the background fluid at rest. Without such no-slip walls, the translational speed of the flagellum is still v relative to the fluid velocity at the boundaries since the rotating flagellum is constantly pumping fluid backwards. From the results shown in Fig. 3, we obtain γtf/(m/t0) = 1028 ± 2, 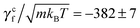 , γrf/(kBTt0) = 11
, γrf/(kBTt0) = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 051 ± 89, and
051 ± 89, and 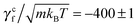 . The two estimates of γcf agree within 5%, confirming the consistency of our measurements.
. The two estimates of γcf agree within 5%, confirming the consistency of our measurements.
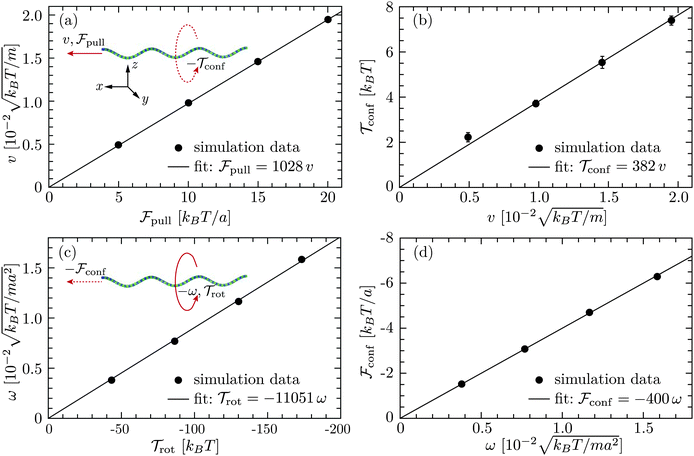 |
| | Fig. 3 Results for a single flagellum from simulations in cubic boxes of length L = 12 μm: (a) translational speed v versus axial force ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pull and (b) confining torque pull and (b) confining torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) confversus v for a translating nonrotating flagellum; (c) rotation frequency ω versus axial torque confversus v for a translating nonrotating flagellum; (c) rotation frequency ω versus axial torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) rot and (d) confining force rot and (d) confining force ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) confversus ω for a rotating nontranslating flagellum. The red solid arrows indicate the direction of translation or rotation caused by confversus ω for a rotating nontranslating flagellum. The red solid arrows indicate the direction of translation or rotation caused by ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pull or pull or ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) rot, whereas the red dashed arrows imply the direction of rotation or translation which would have arisen from the rotation-translation coupling, but are prevented by rot, whereas the red dashed arrows imply the direction of rotation or translation which would have arisen from the rotation-translation coupling, but are prevented by ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) conf or conf or ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) conf from the harmonic potentials on the flagellum. conf from the harmonic potentials on the flagellum. | |
3.1.2 Cell body.
In a similar way, we measure the translational and rotational friction coefficients γtb and γrb of the cell body by considering the body under an axial force ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pull or torque
pull or torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) rot. We obtain γtb =
rot. We obtain γtb = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pull/v = (1118 ± 5)m/t0 and γrb =
pull/v = (1118 ± 5)m/t0 and γrb = ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) rot/ω = (52
rot/ω = (52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 435 ± 236) kBTt0 from simulations with box size L = 12 μm. These values are consistent with the theoretical values γtb/(m/t0) = 1023 and γrb/(kBTt0) = 46
435 ± 236) kBTt0 from simulations with box size L = 12 μm. These values are consistent with the theoretical values γtb/(m/t0) = 1023 and γrb/(kBTt0) = 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 618 for a solid spherocylinder of the same size.65,66 The quantitative agreement confirms that the applied particle-based mesoscale hydrodynamics model can well capture the no-slip boundary conditions on the bacterium surface, as already demonstrated for hard sphere colloids in ref. 67.
618 for a solid spherocylinder of the same size.65,66 The quantitative agreement confirms that the applied particle-based mesoscale hydrodynamics model can well capture the no-slip boundary conditions on the bacterium surface, as already demonstrated for hard sphere colloids in ref. 67.
3.2 Comparison with experimental results and resistive-force theory
Table 1 summarizes the hydrodynamic coefficients of the bacterium body and a flagellum. The values measured for the system sizes L = 8 and 12 μm differ by at most 10%, implying that the periodic boundaries in the simulations have a rather small effect. The experimental values in Table 1 are from measurements of swimming E. coli21 with an average body length of 3.0 ± 0.8 μm, close to 2.5 μm in our model. The flagellar properties determined from experiments are for a bundle with, on average, 3–4 flagella, rather than for a single flagellum. In addition, the cell body is found to wobble around the swimming axis. Given these caveats, the hydrodynamic properties of our model flagellum and cell body are in good agreement with experimental results for E. coli.
Table 1 Comparison of hydrodynamic properties for the model bacterium with experimental results of E. coli.21γt and γr are the translational and rotational friction coefficients, and γc is the rotation-translation coupling coefficient. The subscripts ‘b’ and ‘f’ refer to body and flagellum, respectively. All the coefficients are rescaled by the absolute values of γtb, which are 1281 and 1118 m/t0 from simulations in cubic boxes of lengths L = 8 and 12 μm, and γtb = 1.4 × 10−2 pN s μm−1 from experiments
| |
Model |
Exp. |
|
L = 8 μm |
L = 12 μm |
|
γ
rb/γtb [μm2] |
0.41 |
0.47 |
0.30 |
|
γ
tf/γtb |
0.84 |
0.88 |
1.1 |
|
γ
rf/γtb [μm2] |
0.087 |
0.099 |
0.050 |
|
γ
cf/γtb [μm] |
−0.032 |
−0.036 |
−0.056 |
Table 2 compares the friction coefficients with results obtained by resistive-force theory (RFT).21,22,25,68 We use the theoretical expressions derived in ref. 68; the terms for the respective friction coefficients are summarized in Appendix C. In order to avoid ambiguities by different expressions for the factors Kn and Kt of eqn (21) and (22), as presented in ref. 21, 25 and 68, we discuss ratios of the various friction coefficients only. For the theoretical results, we use the pitch angle ζ = π/6, the pitch length Λ = 2.2 μm, and the hydrodynamic radius r = 0.1 μm of the flagellum string (cf. Appendix C). The ratio γcf/γtf is in close agreement for the various approaches. However, ratios for the simulation model including γrf are about twice larger than the prediction of RFT or even three times compared to those determined from experimental results. As far as the comparison with RFT is concerned, the agreement is reasonable, considering the fact that the simulation model uses a discrete representation of the helix, and the ambiguities in the various parameters of the analytical approach. Here, a more thorough comparison between theory and simulation, and between the various theoretical approaches would be desirable. In experiments, the helical bundle seems to yield a much smaller rotational fiction coefficient. To which extent this friction coefficient is affected by the nature of the bundle and the above mentioned wobbling dynamics needs to be studied further.
Table 2 Comparison of the friction coefficients of a flagellum with estimates by resistive-force theory (RFT)68 and experimental results of E. coli.21 The theoretical expressions derived by resistive-force theory are presented in Appendix C. For the current model, only results for the box size L = 12 μm are presented
| |
Model |
RFT |
Exp. |
| |γcf/γtf| [μm] |
0.04 |
0.04 |
0.05 |
|
γ
rf/γtf [μm2] |
0.1 |
0.05 |
0.05 |
| |γrf/γcf| [μm] |
2.7 |
1.3 |
0.9 |
3.3 Swimming speed and flagellar rotation frequency
In Fig. 4(a), the bacterial swimming speed v is displayed as a function of the rotation frequency ω of the flagellar bundle for our model bacteria of Fig. 1, which differ in the number of flagella and the arrangement of flagella on the cell body, ranging from one to eight flagella with symmetric and random arrangements of the anchoring points. The rotation frequency of the flagellar bundle is ω = 2π/τ, where τ is the average time for the helical bundle to complete one revolution. The data points in Fig. 4(a) are obtained from extensive MPC simulations, where each bacterium travels a distance larger than its own length of about 10 μm. The solid line in Fig. 4 is a least-square fit to all data points through the origin, yielding v/ωR = 0.07, comparable to the experimental ratio v/ωR = 0.14,16 where R = 0.2 μm is the helix radius of the E. coli flagellum. The scatter of the data points around the linear relation may arise from the fact that individual bacteria exhibit different wobbling amplitudes of the body.
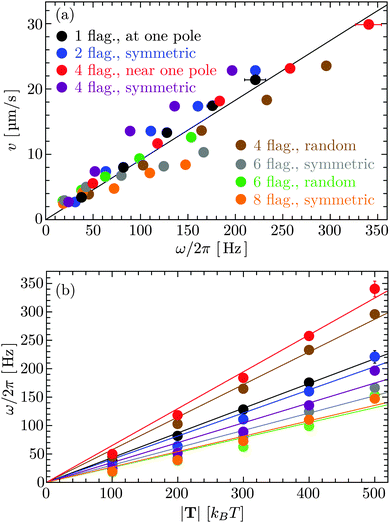 |
| | Fig. 4 (a) Bacterial swimming speeds v as function of the rotation frequency ω of the flagellar bundle and (b) rotation frequency ω as function of the flagellar motor torque |T| for the model bacteria shown in Fig. 1. The solid line in (a) is a least-square fit to all data points. The solid lines in (b) are least-square fits to the data points in the same color. | |
The ratio of swimming speed v to flagellar rotation frequency ω can be understood from the hydrodynamic properties of the bacterium. The force in eqn (6) is balanced by the translational friction force −γtbv exerted by the fluid on the cell body, which gives
| | 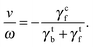 | (8) |
We obtain
v/
ωR ≃ 0.1 and 0.13 using the model and experimental values in
Table 1, respectively. These ratios are close to
v/
ωR = 0.07 from the fitted line in
Fig. 4(a) and the experimental ratio
v/
ωR = 0.14. The agreement emphasizes the importance of hydrodynamic coefficients for a quantitative understanding of bacterial swimming.
Fig. 4(b) shows that the rotation frequency of a bundle formed by four flagella near one pole of the cell body (red points) is larger than that of a single flagellum (black points) at the same motor torque, e.g., ω/2π = 340 Hz versus 223 Hz at |T| = 500 kBT. This result is consistent with the experimental observation16 that a flagellar bundle rotates faster than a single flagellum. The enhanced rotation as a result of the hydrodynamic coupling between the flagella has also been found in simulations of helical bundles,18 where one of the ends of the helices is fixed in space. We note, however, that such hydrodynamic enhancement can be outweighed by the flagellum-body friction, depending on the connection of flagellar filaments to the body. As shown in Fig. 4(b), the bundle of four flagella with a ‘symmetric’ arrangement on the body (purple points, Fig. 1(d)), rotates slower than both a single flagellum (black points, Fig. 1(a)) and the bundle of four flagella near one pole of the body (red points, Fig. 1(c)) at the same motor torque |T| ≤ 400 kBT. In E. coli, each flagellum is attached to the body via a flexible hook of approximately 50 nm length,69 much shorter than the flagellar helix radius of 0.2 μm. The rotating flagella that form a bundle spanning over the body are very likely to collide with the body, contributing to the flagellum-body friction. With the single-flagellum rotational friction coefficient γrf = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 051 kBTt0, the torque rotating the bundle of four flagella with ω/2π = 196 Hz (ω = 0.037/t0, see the purple point at |T| = 500 kBT) is γrfω ≃ 409 kBT, only about one-fifth of the total motor torque 2000 kBT, indicating a significant flagellum–flagellum and flagellum-body friction.
051 kBTt0, the torque rotating the bundle of four flagella with ω/2π = 196 Hz (ω = 0.037/t0, see the purple point at |T| = 500 kBT) is γrfω ≃ 409 kBT, only about one-fifth of the total motor torque 2000 kBT, indicating a significant flagellum–flagellum and flagellum-body friction.
3.4 Flow field
Fig. 5 shows the time-averaged flow field created by a model bacterium of approximately 8 μm length in a periodic cubic simulation box of length L = 25 μm. Each of the four flagella is turned by a motor torque |T| = 1000 kBT, leading to a bundle with rotation frequency ω = 0.074/t0. The bacterial swimming speed is v ≃ 0.0125v0 and the propulsion force fp = γtbv ≃ 0.57 pN consistent with the experimental values of about 0.4–0.6 pN.21,29 Harmonic potentials are applied to y- and z-positions of the center-of-mass of the body and flagellar bundle such that the swimming axis is parallel to the x-axis. The flow field in the swimming plane, shown in Fig. 5(a), is computed by averaging the velocities of the fluid particles cylindrically symmetrically around the swimming axis. The flow fields in Fig. 5(c)–(g) are obtained as time average of the fluid-particle velocities in the planes perpendicular to the swimming axis at the different locations indicated by the white vertical lines in Fig. 5(a).
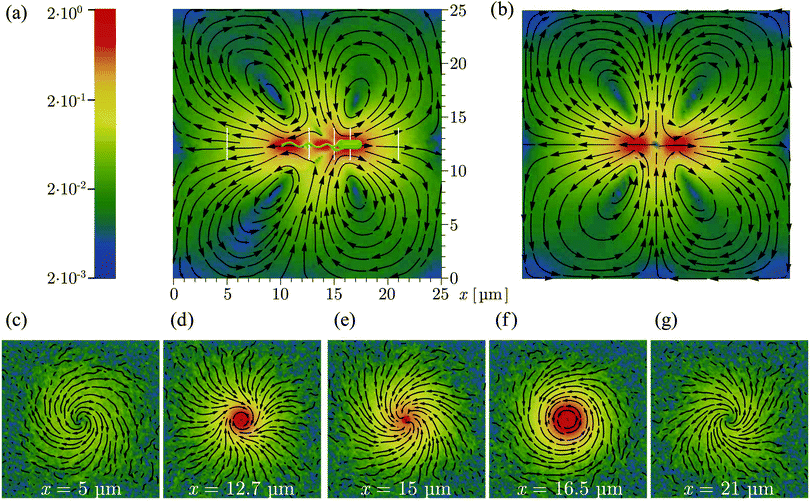 |
| | Fig. 5 Time-averaged flow field generated by a single swimming bacterium as obtained from simulations: (a) flow field in the swimming plane (b) the theoretical flow pattern for a finite-distance force dipole as illustrated in Fig. 6(a) as superposition of two Stokeslets within the same periodic box as for our simulations. (c–g) Flow fields in planes perpendicular to the swimming plane at positions indicated by the white vertical lines in (a). The streamlines indicate the flow direction, and the logarithmic color scheme indicates the magnitude of the flow speed scaled by the bacterial swimming velocity. | |
The flow pattern not too close to the bacterium approximately resembles that of swimming E. coli determined from experiments (see Fig. 1A in ref. 29). Closer to the bacterium, the flow field exhibits specific features reflecting the bacterium's detailed structure. In particular, the flow field reveals a front-back asymmetry, since the cell body and flagellar bundle are physically different units. Along the cell axis, we find low fluid velocities in front of the cell, behind the cell body as well as in the middle and behind the flagellar bundle. The flow velocity is high along the whole cell body, at the flagellar bundle somewhat behind the cell body, and toward the end of the bundle. The streamlines are closed in Fig. 5(a) as a consequence of the applied periodic boundary conditions, which implies differences in the far field compared to experimental observations. The effect of the boundary conditions is confirmed by the theoretical flow field for a finite-distance force dipole with the same boundary condition in Fig. 5(b).
The flow patterns in the planes perpendicular to the swimming axis illustrate the interplay between the rotating flagellar bundle and counterrotating cell body. As shown in Fig. 5(c) and (g), the flow field exhibits two spiral vortices associated with the rotation of the cell body and flagellar bundle, respectively. In Fig. 5(d), the fluid follows the clockwise rotation of the flagellar bundle in the central region, and tends to rotate counterclockwise in the outer region, implying a strong influence of the cell body. In Fig. 5(f), the fluid rotates counterclockwise as the body and there is no significant effect from the flagellar rotation.
The flow field of the discrete-particle bacterium model of ref. 20, with a triangular-prism body and three flagella, each composed of 15 beads, involves an infinite fluid domain, because hydrodynamic interactions are captured by the Rotne–Prager hydrodynamic tensor. Consistent with this study, we find spiral and helical flows (Fig. 5(c)–(g)). However, there are also distinct differences, namely (i) three vortices are predicted in Fig. 5 of ref. 20, and (ii) fluid flows toward the flagellar bundle from behind (Fig. 4 and 7) rather than away from the cell as in Fig. 5. It is not a prior evident where these differences come from. A reason could be the more detailed modelling of the cylindrical cell body and the flagella in our approach. Furthermore, in agreement with our studies, the experimentally determined flow field presented in ref. 29 shows no indication of a forward flow at the end of the flagellar bundle.
We analyse next, how well the flow field can be reproduced by a simplified description in terms of a force-dipole and rotlet-dipole model. Fig. 6(a) displays the fluid velocity along the swimming axis both in front of the body and behind the flagellar bundle. The theoretical result for the force dipole, with the force fp ≃ 0.57 pN and the length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) d = 3.84 μm (see Appendix B), agrees quite well with the simulation data for distance r/
d = 3.84 μm (see Appendix B), agrees quite well with the simulation data for distance r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b > 1, i.e., more than one body length away from the cell. The flow for r/
b > 1, i.e., more than one body length away from the cell. The flow for r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b > 3 decays much faster than r−2 due to the periodic boundary conditions. In this regime, the flow field is consistent with the result for the finite-distance force dipole of two Stokeslets with periodic boundary conditions (cf. Appendix B). In the range 0.8 < r/
b > 3 decays much faster than r−2 due to the periodic boundary conditions. In this regime, the flow field is consistent with the result for the finite-distance force dipole of two Stokeslets with periodic boundary conditions (cf. Appendix B). In the range 0.8 < r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b < 1.8, vfluid decreases approximately as r−3, a dependence previously observed in ref. 20. Already for r/
b < 1.8, vfluid decreases approximately as r−3, a dependence previously observed in ref. 20. Already for r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b ≳ 2, our flow field agrees well with that of the finite-distance force dipole. Hence, up to r/
b ≳ 2, our flow field agrees well with that of the finite-distance force dipole. Hence, up to r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b ≲ 3−4 the flow field is hardly affected by the boundary conditions. The asymptotic force-dipole dependence vfluid ∼ r−2 is only reached for distances r/
b ≲ 3−4 the flow field is hardly affected by the boundary conditions. The asymptotic force-dipole dependence vfluid ∼ r−2 is only reached for distances r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b>5. Fig. 6(b) displays the flow field in planes perpendicular to the swimming axis through the center of mass of the body or flagellar bundle, respectively. The simulation results for r/
b>5. Fig. 6(b) displays the flow field in planes perpendicular to the swimming axis through the center of mass of the body or flagellar bundle, respectively. The simulation results for r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b ≳ 1 are well described by a superposition of a force dipole with force fp ≃ 0.57 pN and a rotlet dipole with the torque N ≃ 80 kBT, one-tenth of the torque rotating the flagellar bundle γrfω ≃ 800 kBT. The rotlet-dipole contribution dominates at r/
b ≳ 1 are well described by a superposition of a force dipole with force fp ≃ 0.57 pN and a rotlet dipole with the torque N ≃ 80 kBT, one-tenth of the torque rotating the flagellar bundle γrfω ≃ 800 kBT. The rotlet-dipole contribution dominates at r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b < 2, whereas the force-dipole contribution dominates at larger distances. This suggests that the counterrotation of cell body and flagella needs to be taken into account for an appropriate description of near-field hydrodynamics of bacteria. Our result provide the first measurement of the rotlet-dipole strength, which is important for a quantitative description of near-surface swimming behaviors of bacteria.34,70 It would be interesting to compare our predictions with future experimentally determined rotlet-dipole strengths for flagellated bacteria.
b < 2, whereas the force-dipole contribution dominates at larger distances. This suggests that the counterrotation of cell body and flagella needs to be taken into account for an appropriate description of near-field hydrodynamics of bacteria. Our result provide the first measurement of the rotlet-dipole strength, which is important for a quantitative description of near-surface swimming behaviors of bacteria.34,70 It would be interesting to compare our predictions with future experimentally determined rotlet-dipole strengths for flagellated bacteria.
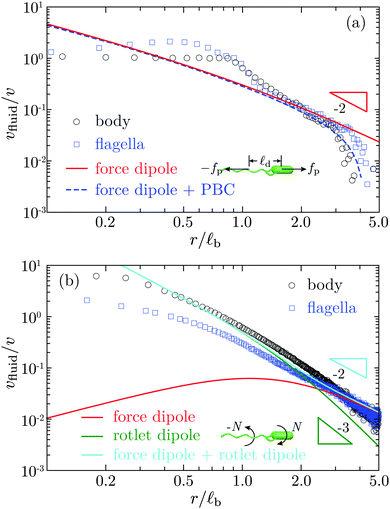 |
| | Fig. 6 The fluid velocity vfluid as a function of distance r to the center of mass of the body or flagellar bundle (a) along the swimming axis, and (b) in the planes perpendicular to the swimming axis through the body or flagellar center of mass, respectively. v is the swimming speed and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b the body length. In (a), the solid line is the theoretical result for a force dipole of strength fp b the body length. In (a), the solid line is the theoretical result for a force dipole of strength fp![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) d, where fp ≃ 0.57 pN is the bacterial propulsion force and d, where fp ≃ 0.57 pN is the bacterial propulsion force and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) d = 3.84 μm the center-of-mass separation between the body and flagellar bundle. The dashed line is for the force dipole with the same periodic boundary conditions (PBC) as in simulations. In (b), the red and green solid lines represent the results for the force dipole as in (a) and the rotlet dipole with torque N≃80 kBT, one-tenth of the torque rotating the flagellar bundle γrfω ≃ 800 kBT. The cyan solid line is the superposition of the force dipole and rotlet dipole. d = 3.84 μm the center-of-mass separation between the body and flagellar bundle. The dashed line is for the force dipole with the same periodic boundary conditions (PBC) as in simulations. In (b), the red and green solid lines represent the results for the force dipole as in (a) and the rotlet dipole with torque N≃80 kBT, one-tenth of the torque rotating the flagellar bundle γrfω ≃ 800 kBT. The cyan solid line is the superposition of the force dipole and rotlet dipole. | |
4 Conclusions
We have developed a coarse-grained model for an E. coli-type bacterium and investigated its swimming behavior by mesoscale hydrodynamics simulations. The suggested implementation of octahedron-type segments to construct a model flagellum of helical structure with bending and torsion elastic energy is particularly suitable in combination with a particle-based fluid, because it provides a simple means to capture the twist by the fluid on a flagellum. The hydrodynamic friction coefficients of the model bacterium and the relation between its swimming speed and flagellar rotation frequency both quantitatively agree with experimental results for E. coli. The flow field created by the model bacterium exhibits a rather complex pattern adjacent to the bacterium, with and a two-vortex structure due to the counterrotation of the cell body and flagellar bundle. From comparison to theoretical predictions for force dipole and rotlet dipole, we find the simplified dipole model can well describe the flow more than one cell-body length away from the bacterium, and the rotation of the body and flagella makes a dominant contribution to the near-field flow. We provide the first measurement of the rotlet-dipole strength, an essential quantity for modeling bacterial motion near surfaces.
The simulations show that our model is very well suited for theoretical studies of swimming bacteria. By adjusting the geometric parameters, one expects to achieve a similar quantitative description for other bacteria such as Bacillus subtilis, Saolmonella typhimurium, Rhodobacter spheroides, and Rhizobium lupini.
Naturally, further aspects of swimming bacteria can be investigated by our approach. By modifications of the elastic deformation energy in eqn (2) to account for flagellar polymorphic transformations13,14 and by implementing reversal of the flagellar motor torque T, the full run-and-tumble motion can be addressed. Since boundaries and external flow are easily implemented in the MPC method, our simulation approach opens an avenue for detailed studies of confinement effects51 and non-equilibrium aspects in bacteria locomotion.
Appendix
A Flagellum model
We estimate the bending and twist strength Kαel of our discrete flagellum by mapping the elastic energy in eqn (2) to a continuous form. We identify the directions e3n of the bond vectors b3n as local tangent vectors on the filament. Then, the discrete measure of the local curvature κ = |e3n+1 − e3n|/a = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϑn/2)/a turns into κ ≈ ϑn/a for small bending angles ϑn and the local torsion becomes τ = −|nn+1 − nn|/a = − 2
sin(ϑn/2)/a turns into κ ≈ ϑn/a for small bending angles ϑn and the local torsion becomes τ = −|nn+1 − nn|/a = − 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ψn/2)/a ≈ −ψn/a for small torsional angles ψn between the normal vectors nn and nn+1, where nn = (e3n × e3n+1)/|e3n × e3n+1|. At small ϑn, ψn ≈ φn since the deformation mainly originates from twist. In eqn (2), the components of the strain vector are
sin(ψn/2)/a ≈ −ψn/a for small torsional angles ψn between the normal vectors nn and nn+1, where nn = (e3n × e3n+1)/|e3n × e3n+1|. At small ϑn, ψn ≈ φn since the deformation mainly originates from twist. In eqn (2), the components of the strain vector are| | 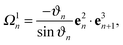 | (9) |
| | 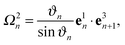 | (10) |
Using e3n+1 = sinϑn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕne1n + sin
ϕne1n + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑn
ϑn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕne2n + cos
ϕne2n + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑne3n, where ϕn is the azimuthal angle of e3n+1 in the plane defined by e1n and e2n, expansion of eqn (2) yields
ϑne3n, where ϕn is the azimuthal angle of e3n+1 in the plane defined by e1n and e2n, expansion of eqn (2) yields| | 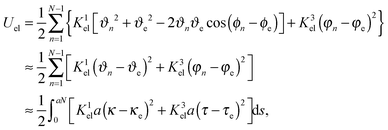 | (12) |
with the Ωαn of the linearized expressions of eqn (9)–(11) and for small deviations of ϕn from its equilibrium value ϕe. The integral over the flagellar contour describes the continuous elastic energy.57
The experimental values for the bending stiffness of bacterial flagella range from about 10−24 to 10−21 N m2.16,71,72 For S. typhimurium, K1ela is estimated as 2–4 × 10−24 N m2 from quasi-elastic light scattering in ref. 71, consistent with the value 3.5 × 10−24 N m2 measured from pulling experiments in ref. 16. In ref. 72, a Young's modulus of about 10−11 N m−2 has been determined for S. typhimurium and E. coli from electron micrographs, which yields the approximate bending stiffness 10−21 N m2 given a filament radius of 10 nm. The twist or torsional stiffness has been generally assumed to be of the same order of magnitude as the bending stiffness. Our choice K1el = K2el = K3el = 5 × 104kBT, with the physical length scale a ≈ 0.1 μm, corresponds to a bending stiffness of K1ela ≃ 2 × 10−23 N m2 well within the experimental range.
In order to determine the equilibrium parameters Ωαe in eqn (2), we consider a flagellum in the normal state—a three-turn left-handed helix of radius 0.2 μm and pitch 2.2 μm. The bending angle between subsequent discrete bond vectors is then ϑe = arccos(e3n·e3n+1) = 0.125 for the bond length a = 0.1 μm. We choose e1n in each segment such that it coincides with nn after the twist with angle φe, i.e., ẽ1n = nn. ẽ1n is thus invariant in bending from e3n to e3n+1 around nn by the angle ϑe, hence, e1n+1 = ẽ1n = e3n × e3n+1/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑe. Then, φe = − arccos(e1n·e1n+1) = −0.217. From eqn (9)–(11), we obtain Ω1e = 0.122, Ω2e = −0.027, and Ω3e = −0.217, which are the values used in our simulations.
ϑe. Then, φe = − arccos(e1n·e1n+1) = −0.217. From eqn (9)–(11), we obtain Ω1e = 0.122, Ω2e = −0.027, and Ω3e = −0.217, which are the values used in our simulations.
B Force-dipole flow field for periodic boundary conditions
We consider the flow generated by a force dipole as illustrated by the cartoon in Fig. 6(a). The two point forces f1 = (−fp,0,0) and f2 = (fp,0,0) are located at r1 = (−![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) d/2,0,0) and r2 = (
d/2,0,0) and r2 = (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) d/2,0,0), respectively. The fluid velocity at position r is given by
d/2,0,0), respectively. The fluid velocity at position r is given by| | | u(r) = G(r − r1)·f1 + G(r − r2)·f2, | (13) |
with the Oseen tensor| | 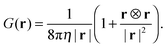 | (14) |
To calculate the flow of the force dipole in a cubic box of length L with periodic boundaries, one can start with the Oseen tensor in k-space| | 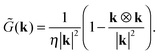 | (15) |
The k-space fluid velocity is then| | ũ(k) = ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (k) (k)![[f with combining tilde]](https://www.rsc.org/images/entities/b_char_0066_0303.gif) 1(k) + 1(k) + ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (k) (k)![[f with combining tilde]](https://www.rsc.org/images/entities/b_char_0066_0303.gif) 2(k), 2(k), | (16) |
with the Fourier-transformed point force 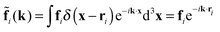 , i = 1, 2. Inverse Fourier transformation for the periodic system yields the flow field
, i = 1, 2. Inverse Fourier transformation for the periodic system yields the flow field| | 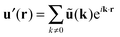 | (17) |
with the three components of k assuming multiples of 2π/L.
C Resistive-force theory for helix
Expressions for the friction coefficients of eqn (6) and (7) for a helix have been presented in ref. 21, 22, 25 and 68. The original expressions of ref. 68 are| | 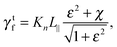 | (18) |
| | 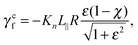 | (19) |
| | 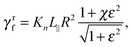 | (20) |
with χ = Kt/Kn, ε = tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ, where ζ is the pitch angle, and
ζ, where ζ is the pitch angle, and| | 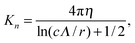 | (21) |
| | 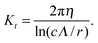 | (22) |
Here, Λ is the pitch, r the (hydrodynamic) radius of the flagella filament, and c = 0.18 a constant.68 For χ = 1/2, which corresponds to the ratio of the viscous coefficients of an infinitely long rod, and c = 2, the eqn (18)–(22) reduce to the definitions in ref. 25. The viscous coefficients of ref. 21 are somewhat different, specifically the expression for Kt.
Acknowledgements
We thank Adam Wysocki and Anoop Varghese for helpful discussions. Financial support by the VW Foundation (VolkswagenStiftung) within the program Computer Simulation of Molecular and Cellular Biosystems as well as Complex Soft Matter of the initiative New Conceptual Approaches to Modeling and Simulation of Complex Systems is gratefully acknowledged.
References
-
H. C. Berg, E. Coli in Motion, Springer, 2004 Search PubMed.
- C. Brennen and H. Winet, Annu. Rev. Fluid Mech., 1977, 9, 339 CrossRef.
- H. C. Berg, Annu. Rev. Biochem., 2003, 72, 19 CrossRef CAS PubMed.
- R. M. Macnab, Proc. Natl. Acad. Sci. U. S. A., 1977, 74, 221 CrossRef CAS.
- L. Turner, W. S. Ryu and H. C. Berg, J. Bacteriol., 2000, 182, 2793–2801 CrossRef CAS PubMed.
- B. Scharf, J. Bacteriol., 2002, 184, 5979 CrossRef CAS PubMed.
- N. C. Darnton and H. C. Berg, Biophys. J., 2007, 92, 2230–2236 CrossRef CAS PubMed.
- D. B. Kearns, Nat. Rev. Microbiol., 2010, 8, 634–644 CrossRef CAS PubMed.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- C. R. Calladine, Nature, 1975, 255, 121 CrossRef CAS PubMed.
- H. Wada and R. R. Netz, EPL, 2008, 82, 28001 CrossRef.
- C. R. Calladine, B. F. Luisi and J. V. Pratap, J. Mol. Biol., 2013, 425, 914 CrossRef CAS PubMed.
- R. Vogel and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 33, 259–271 CrossRef CAS PubMed.
- R. Vogel and H. Stark, Phys. Rev. Lett., 2013, 110, 158104 CrossRef PubMed.
- M. Reichert and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 17, 493 CrossRef CAS PubMed.
- N. C. Darnton, L. Turner, S. Rojevsky and H. C. Berg, J. Bacteriol., 2007, 189, 1756–1764 CrossRef CAS PubMed.
- P. J. A. Janssen and M. D. Graham, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011910 CrossRef CAS PubMed.
- S. Y. Reigh, R. G. Winkler and G. Gompper, Soft Matter, 2012, 8, 4363–4372 RSC.
- S. Y. Reigh, R. G. Winkler and G. Gompper, PLoS One, 2013, 8, e70868 CrossRef CAS PubMed.
- N. Watari and R. G. Larson, Biophys. J., 2010, 98, 12–17 CrossRef CAS PubMed.
- S. Chattopadhyay, R. Moldovan, C. Yeung and X. L. Wu, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13712–13717 CrossRef CAS PubMed.
- B. Rodenborn, C.-H. Chen, H. L. Swinney, B. Liu and H. P. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E338 CrossRef CAS PubMed.
- H. Flores, E. Lobaton, S. Méndez-Diez, S. Tlupova and R. Cortez, Bull. Math. Biol., 2005, 67, 137 CrossRef CAS PubMed.
- M. Kong, Y. Wu, G. Li and R. G. Larson, Soft Matter, 2015, 11, 1572–1581 RSC.
- E. Lauga, W. R. DiLuzio, G. M. Whitesides and H. A. Stone, Biophys. J., 2006, 90, 400–412 CrossRef CAS PubMed.
- G. Li, L.-K. Tam and J. X. Tang, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18355–18359 CrossRef CAS PubMed.
- H. Shum, E. A. Gaffney and D. J. Smith, Proc. R. Soc. A, 2010, 466, 1725 CrossRef.
- R. Di Leonardo, D. Dell'Arciprete, L. Angelani and V. Iebba, Phys. Rev. Lett., 2011, 106, 038101 CrossRef CAS PubMed.
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940–10945 CrossRef CAS PubMed.
- S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105 CrossRef.
- L. Lemelle, J.-F. Palierne, E. Chatre, C. Vaillant and C. Place, Soft Matter, 2013, 9, 9759–9762 RSC.
- M. Molaei, M. Barry, R. Stocker and J. Sheng, Phys. Rev. Lett., 2014, 113, 068103 CrossRef PubMed.
- J. Elgeti and G. Gompper, EPL, 2015, 109, 58003 CrossRef.
- J. Hu, A. Wysocki, R. G. Winkler and G. Gompper, Sci. Rep., 2015, 5, 9586 CrossRef PubMed.
- H. Shum and E. A. Gaffney, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 033012 CrossRef PubMed.
- Marcos, H. C. Fu, T. R. Powers and R. Stocker, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4780–4785 CrossRef CAS PubMed.
- R. Rusconi, J. S. Guasto and R. Stocker, Nat. Phys., 2014, 10, 212 Search PubMed.
- M. Tournus, A. Kirshtein, L. V. Berlyand and I. S. Aranson, J. R. Soc., Interface, 2014, 12, 20140904 CrossRef PubMed.
- S. Rafaï, L. Jibuti and P. Peyla, Phys. Rev. Lett., 2010, 104, 098102 CrossRef PubMed.
- T. Kaya and H. Koser, Biophys. J., 2012, 102, 1514 CrossRef CAS PubMed.
- R. Karmakar, R. Gulvady, M. S. Tirumkudulu and K. V. Venkatesh, Phys. Fluids, 2014, 26, 071905 CrossRef.
- R. Kapral, Adv. Chem. Phys., 2008, 140, 89–146 CrossRef CAS.
- G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, Adv. Polym. Sci., 2009, 221, 1–87 CAS.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
- G. Rückner and R. Kapral, Phys. Rev. Lett., 2007, 98, 150603 CrossRef PubMed.
- I. O. Götze and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041921 CrossRef PubMed.
- M. Yang and M. Ripoll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061401 CrossRef PubMed.
- R. Kapral, Adv. Chem. Phys., 2008, 140, 89 CrossRef CAS.
- J. Elgeti and G. Gompper, EPL, 2009, 85, 38002 CrossRef.
- D. J. Earl, C. M. Pooley, J. F. Ryder, I. Bredberg and J. M. Yeomans, J. Chem. Phys., 2007, 126, 064703 CrossRef PubMed.
- J. Elgeti, U. B. Kaupp and G. Gompper, Biophys. J., 2010, 99, 1018 CrossRef CAS PubMed.
- J. Elgeti and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4470 CrossRef CAS PubMed.
- M. Theers and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 023012 CrossRef PubMed.
- Y. Yang, J. Elgeti and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 061903 CrossRef PubMed.
- R. Vogel and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 1 CrossRef PubMed.
-
J. K. G. Dhont, An Introduction to Dynamics of Colloids, Elsevier, Amsterdam, 1996 Search PubMed.
-
H. Yamakawa, Helical Wormlike Chains in Polymer Solutions, Springer-Verlag, Berlin Heidelberg, 1997 Search PubMed.
- R. M. Berry and H. C. Berg, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 14433–14437 CrossRef CAS.
- H. Noguchi, N. Kikuchi and G. Gompper, EPL, 2007, 78, 10005 CrossRef.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 020201 CrossRef CAS PubMed.
- M. Ripoll, K. Mussawisade, R. G. Winkler and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 016701 CrossRef CAS PubMed.
- E. M. Purcell, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 11307–11311 CrossRef CAS.
- A. Lamura, G. Gompper, T. Ihle and D. M. Kroll, EPL, 2001, 56, 319 CrossRef CAS.
- J. K. Whitmer and E. Luijten, J. Phys.: Condens. Matter, 2010, 22, 104106 CrossRef PubMed.
- T. Norisuye, M. Motowoka and H. Fujita, Macromolecules, 1979, 12, 320–323 CrossRef CAS.
- T. Yoshizaki and H. Yamakawa, J. Chem. Phys., 1980, 72, 57–69 CrossRef CAS.
- S. Poblete, A. Wysocki, G. Gompper and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 033314 CrossRef PubMed.
- J. Lighthill, SIAM Rev., 1976, 161 CrossRef.
- I. Kawagishi, M. Homma, A. W. Williams and R. M. Macnab, J. Bacteriol., 1996, 178, 2954 CrossRef CAS PubMed.
- D. Lopez and E. Lauga, Phys. Fluids, 2014, 26, 071902 CrossRef.
- S. Fujime, M. Maruyama and S. Asakura, J. Mol. Biol., 1972, 68, 347–359 CrossRef CAS PubMed.
- S. Trachtenberg and I. Hammel, J. Struct. Biol., 1992, 109, 18–27 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article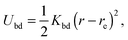

![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b = 2.5 μm. It is composed of 51 circular sections of particles, which are connected by the bond potential of eqn (1). (b) The flagellum, a three-turn left-handed helix of radius R = 0.2 μm, pitch Λ = 2.2 μm and contour length Lc = 7.6 μm (corresponding to the parallel length L∥ = 6.6 μm), consists of 76 consecutive segments.
b = 2.5 μm. It is composed of 51 circular sections of particles, which are connected by the bond potential of eqn (1). (b) The flagellum, a three-turn left-handed helix of radius R = 0.2 μm, pitch Λ = 2.2 μm and contour length Lc = 7.6 μm (corresponding to the parallel length L∥ = 6.6 μm), consists of 76 consecutive segments.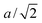 , forming 12 bonds along the edges and three along the diagonals. The preferred bond lengths are
, forming 12 bonds along the edges and three along the diagonals. The preferred bond lengths are 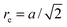 for edges and re = a for diagonals. The octahedron construction allows for a straightforward description of the intrinsic twist of the flagellum and a coupling of the twist to the forces exerted by the MPC fluid.
for edges and re = a for diagonals. The octahedron construction allows for a straightforward description of the intrinsic twist of the flagellum and a coupling of the twist to the forces exerted by the MPC fluid.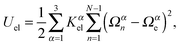
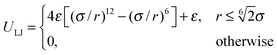
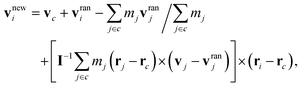
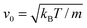 , time
, time 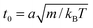 , and shear viscosity
, and shear viscosity 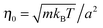 .
.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) and torque
and torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) exerted by the fluid on the flagellar bundle to its translational velocity v and rotation frequency ω (angular velocity −ω by right-hand rule) via
exerted by the fluid on the flagellar bundle to its translational velocity v and rotation frequency ω (angular velocity −ω by right-hand rule) via![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = −γtfv + γcf(−ω),
= −γtfv + γcf(−ω),![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = +γcfv − γrf(−ω),
= +γcfv − γrf(−ω),![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pull along its helical axis, say x-axis, and y-, z-positions of each of its contour particles are trapped by harmonic potentials. This yields a confining torque
pull along its helical axis, say x-axis, and y-, z-positions of each of its contour particles are trapped by harmonic potentials. This yields a confining torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) conf that prevents the rotation by counteracting the torque in eqn (7). In the second case, a flagellum is rotated by a motor torque, and harmonic potentials are applied on its contour particles that prevent its translation, but allow for the rotation about the helical axis, causing a net axial torque
conf that prevents the rotation by counteracting the torque in eqn (7). In the second case, a flagellum is rotated by a motor torque, and harmonic potentials are applied on its contour particles that prevent its translation, but allow for the rotation about the helical axis, causing a net axial torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) rot and a confining force
rot and a confining force ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) conf opposite to the force in eqn (6). The two measurements lead to γtf =
conf opposite to the force in eqn (6). The two measurements lead to γtf = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pull/v, γcf = −
pull/v, γcf = −![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) conf/v, γrf = −
conf/v, γrf = −![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) rot/ω, and γcf =
rot/ω, and γcf = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) conf/ω. In the latter measurement, two no-slip walls63,64 orthogonal to the flagellum are included to ensure that the flagellar speed v vanishes with respect to the background fluid at rest. Without such no-slip walls, the translational speed of the flagellum is still v relative to the fluid velocity at the boundaries since the rotating flagellum is constantly pumping fluid backwards. From the results shown in Fig. 3, we obtain γtf/(m/t0) = 1028 ± 2,
conf/ω. In the latter measurement, two no-slip walls63,64 orthogonal to the flagellum are included to ensure that the flagellar speed v vanishes with respect to the background fluid at rest. Without such no-slip walls, the translational speed of the flagellum is still v relative to the fluid velocity at the boundaries since the rotating flagellum is constantly pumping fluid backwards. From the results shown in Fig. 3, we obtain γtf/(m/t0) = 1028 ± 2, 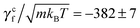 , γrf/(kBTt0) = 11
, γrf/(kBTt0) = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 051 ± 89, and
051 ± 89, and 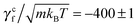 . The two estimates of γcf agree within 5%, confirming the consistency of our measurements.
. The two estimates of γcf agree within 5%, confirming the consistency of our measurements.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pull or torque
pull or torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) rot. We obtain γtb =
rot. We obtain γtb = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pull/v = (1118 ± 5)m/t0 and γrb =
pull/v = (1118 ± 5)m/t0 and γrb = ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) rot/ω = (52
rot/ω = (52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 435 ± 236) kBTt0 from simulations with box size L = 12 μm. These values are consistent with the theoretical values γtb/(m/t0) = 1023 and γrb/(kBTt0) = 46
435 ± 236) kBTt0 from simulations with box size L = 12 μm. These values are consistent with the theoretical values γtb/(m/t0) = 1023 and γrb/(kBTt0) = 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 618 for a solid spherocylinder of the same size.65,66 The quantitative agreement confirms that the applied particle-based mesoscale hydrodynamics model can well capture the no-slip boundary conditions on the bacterium surface, as already demonstrated for hard sphere colloids in ref. 67.
618 for a solid spherocylinder of the same size.65,66 The quantitative agreement confirms that the applied particle-based mesoscale hydrodynamics model can well capture the no-slip boundary conditions on the bacterium surface, as already demonstrated for hard sphere colloids in ref. 67.

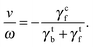
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 051 kBTt0, the torque rotating the bundle of four flagella with ω/2π = 196 Hz (ω = 0.037/t0, see the purple point at |T| = 500 kBT) is γrfω ≃ 409 kBT, only about one-fifth of the total motor torque 2000 kBT, indicating a significant flagellum–flagellum and flagellum-body friction.
051 kBTt0, the torque rotating the bundle of four flagella with ω/2π = 196 Hz (ω = 0.037/t0, see the purple point at |T| = 500 kBT) is γrfω ≃ 409 kBT, only about one-fifth of the total motor torque 2000 kBT, indicating a significant flagellum–flagellum and flagellum-body friction.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) d = 3.84 μm (see Appendix B), agrees quite well with the simulation data for distance r/
d = 3.84 μm (see Appendix B), agrees quite well with the simulation data for distance r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b > 1, i.e., more than one body length away from the cell. The flow for r/
b > 1, i.e., more than one body length away from the cell. The flow for r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b > 3 decays much faster than r−2 due to the periodic boundary conditions. In this regime, the flow field is consistent with the result for the finite-distance force dipole of two Stokeslets with periodic boundary conditions (cf. Appendix B). In the range 0.8 < r/
b > 3 decays much faster than r−2 due to the periodic boundary conditions. In this regime, the flow field is consistent with the result for the finite-distance force dipole of two Stokeslets with periodic boundary conditions (cf. Appendix B). In the range 0.8 < r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b < 1.8, vfluid decreases approximately as r−3, a dependence previously observed in ref. 20. Already for r/
b < 1.8, vfluid decreases approximately as r−3, a dependence previously observed in ref. 20. Already for r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b ≳ 2, our flow field agrees well with that of the finite-distance force dipole. Hence, up to r/
b ≳ 2, our flow field agrees well with that of the finite-distance force dipole. Hence, up to r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b ≲ 3−4 the flow field is hardly affected by the boundary conditions. The asymptotic force-dipole dependence vfluid ∼ r−2 is only reached for distances r/
b ≲ 3−4 the flow field is hardly affected by the boundary conditions. The asymptotic force-dipole dependence vfluid ∼ r−2 is only reached for distances r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b>5. Fig. 6(b) displays the flow field in planes perpendicular to the swimming axis through the center of mass of the body or flagellar bundle, respectively. The simulation results for r/
b>5. Fig. 6(b) displays the flow field in planes perpendicular to the swimming axis through the center of mass of the body or flagellar bundle, respectively. The simulation results for r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b ≳ 1 are well described by a superposition of a force dipole with force fp ≃ 0.57 pN and a rotlet dipole with the torque N ≃ 80 kBT, one-tenth of the torque rotating the flagellar bundle γrfω ≃ 800 kBT. The rotlet-dipole contribution dominates at r/
b ≳ 1 are well described by a superposition of a force dipole with force fp ≃ 0.57 pN and a rotlet dipole with the torque N ≃ 80 kBT, one-tenth of the torque rotating the flagellar bundle γrfω ≃ 800 kBT. The rotlet-dipole contribution dominates at r/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b < 2, whereas the force-dipole contribution dominates at larger distances. This suggests that the counterrotation of cell body and flagella needs to be taken into account for an appropriate description of near-field hydrodynamics of bacteria. Our result provide the first measurement of the rotlet-dipole strength, which is important for a quantitative description of near-surface swimming behaviors of bacteria.34,70 It would be interesting to compare our predictions with future experimentally determined rotlet-dipole strengths for flagellated bacteria.
b < 2, whereas the force-dipole contribution dominates at larger distances. This suggests that the counterrotation of cell body and flagella needs to be taken into account for an appropriate description of near-field hydrodynamics of bacteria. Our result provide the first measurement of the rotlet-dipole strength, which is important for a quantitative description of near-surface swimming behaviors of bacteria.34,70 It would be interesting to compare our predictions with future experimentally determined rotlet-dipole strengths for flagellated bacteria.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϑn/2)/a turns into κ ≈ ϑn/a for small bending angles ϑn and the local torsion becomes τ = −|nn+1 − nn|/a = − 2
sin(ϑn/2)/a turns into κ ≈ ϑn/a for small bending angles ϑn and the local torsion becomes τ = −|nn+1 − nn|/a = − 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ψn/2)/a ≈ −ψn/a for small torsional angles ψn between the normal vectors nn and nn+1, where nn = (e3n × e3n+1)/|e3n × e3n+1|. At small ϑn, ψn ≈ φn since the deformation mainly originates from twist. In eqn (2), the components of the strain vector are
sin(ψn/2)/a ≈ −ψn/a for small torsional angles ψn between the normal vectors nn and nn+1, where nn = (e3n × e3n+1)/|e3n × e3n+1|. At small ϑn, ψn ≈ φn since the deformation mainly originates from twist. In eqn (2), the components of the strain vector are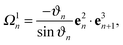
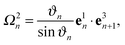
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕne1n + sin
ϕne1n + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑn
ϑn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕne2n + cos
ϕne2n + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑne3n, where ϕn is the azimuthal angle of e3n+1 in the plane defined by e1n and e2n, expansion of eqn (2) yields
ϑne3n, where ϕn is the azimuthal angle of e3n+1 in the plane defined by e1n and e2n, expansion of eqn (2) yields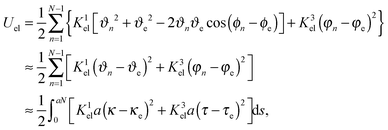
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑe. Then, φe = − arccos(e1n·e1n+1) = −0.217. From eqn (9)–(11), we obtain Ω1e = 0.122, Ω2e = −0.027, and Ω3e = −0.217, which are the values used in our simulations.
ϑe. Then, φe = − arccos(e1n·e1n+1) = −0.217. From eqn (9)–(11), we obtain Ω1e = 0.122, Ω2e = −0.027, and Ω3e = −0.217, which are the values used in our simulations.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) d/2,0,0) and r2 = (
d/2,0,0) and r2 = (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) d/2,0,0), respectively. The fluid velocity at position r is given by
d/2,0,0), respectively. The fluid velocity at position r is given by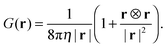
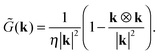
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (k)
(k)![[f with combining tilde]](https://www.rsc.org/images/entities/b_char_0066_0303.gif) 1(k) +
1(k) + ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (k)
(k)![[f with combining tilde]](https://www.rsc.org/images/entities/b_char_0066_0303.gif) 2(k),
2(k),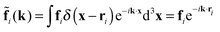 , i = 1, 2. Inverse Fourier transformation for the periodic system yields the flow field
, i = 1, 2. Inverse Fourier transformation for the periodic system yields the flow field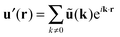
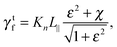
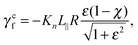
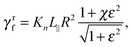
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ, where ζ is the pitch angle, and
ζ, where ζ is the pitch angle, and