Open Access Article
Open Access ArticleLung surfactants and different contributions to thin film stability†
Eline
Hermans‡
a,
M.
Saad Bhamla‡
 b,
Peter
Kao
c,
Gerald G.
Fuller
*b and
Jan
Vermant
*d
b,
Peter
Kao
c,
Gerald G.
Fuller
*b and
Jan
Vermant
*d
aDepartment of Chemical Engineering, KU Leuven, Belgium
bDepartment of Chemical Engineering, Stanford University, USA. E-mail: ggf@stanford.edu
cDepartment of Pulmonary and Critical Care Medicine, Stanford University, USA
dDepartment of Materials, ETH Zürich, Vladimir Prelog Weg 5, CH 8093-Zürich, Switzerland. E-mail: jan.vermant@mat.ethz.ch
First published on 13th August 2015
Abstract
The surfactant lining the walls of the alveoli in the lungs increases pulmonary compliance and prevents collapse of the lung at the end of expiration. In premature born infants, surfactant deficiency causes problems, and lung surfactant replacements are instilled to facilitate breathing. These pulmonary surfactants, which form complex structured fluid–fluid interfaces, need to spread with great efficiency and once in the alveolus they have to form a thin stable film. In the present work, we investigate the mechanisms affecting the stability of surfactant-laden thin films during spreading, using drainage flows from a hemispherical dome. Three commercial lung surfactant replacements Survanta, Curosurf and Infasurf, along with the phospholipid dipalmitoylphosphatidylcholine (DPPC), are used. The surface of the dome can be covered with human alveolar epithelial cells and experiments are conducted at the physiological temperature. Drainage is slowed down due to the presence of all the different lung surfactant replacements and therefore the thin films show enhanced stability. However, a scaling analysis combined with visualization experiments demonstrates that different mechanisms are involved. For Curosurf and Infasurf, Marangoni stresses are essential to impart stability and interfacial shear rheology does not play a role, in agreement with what is observed for simple surfactants. Survanta, which was historically the first natural surfactant used, is rheologically active. For DPPC the dilatational properties play a role. Understanding these different modes of stabilization for natural surfactants can benefit the design of effective synthetic surfactant replacements for treating infant and adult respiratory disorders.
1 Introduction
Lung surfactant synthesised by alveolar type II cells is a complex mixture of proteins and lipids. It is present as a thin film lining the alveolar surface of the lung with an essential function of lowering the surface tension and the energy for breathing. It also prevents alveolar collapse.1–4 In addition to the thermodynamic properties, the transport properties are of vital importance. The lung surfactant flows up the terminal airways and reduces the formation of liquid plugs that can obstruct terminal airways at end-expiration.5–7 Further up the bronchial tree, the intermixing of lung surfactant with airway mucus may improve fluidity and clearance of mucus by cilia on the bronchial epithelium. Taken together, flows of lung surfactant up the airway tree support clearance of inhaled particulates and pathogens from the alveoli and distal airways, contributing to overall respiratory health.8 In the neonatal respiratory distress syndrome (NRDS), where naturally occurring surfactant is insufficient, artificial surfactant replacements can be introduced by endotracheal intubation. In this case, both the spreading flow of the surfactants during instillation and the consequent formation of thin stable films are of prime importance.Natural lung surfactant consists of 80 wt% phospholipids, predominantly dipalmitoylphosphatidylcholine (DPPC), 5 to 10% neutral lipids (mainly cholesterol), and 5 to 10% (surfactant associated) proteins.9,10 The most common clinically used replacements are natural, animal derived surfactants. They are either extracted from minced cow lung with the addition of DPPC, palmitic acid and tripalmitin (Beractant, trade name Survanta), extracted from calf lung lavage fluid (Calfactant, trade name Infasurf) or from material obtained from minced pig lung (Poractant, trade name Curosurf). Synthetic surfactants are often based on DPPC.
The complexity of composition is required for different reasons. For example, clinical lung surfactants need to adsorb faster than pure phospholipids. Still, to reach an equilibrium surface tension under physiological conditions, a time scale of minutes is typically required.11 Past work has focussed on understanding of the low level of surface tension in relation to composition. Lung surfactants (and the clinical replacements) adsorb till the surface tension of the air–water interface decreases from 72 to about ∼30 mN m−1,12 or in terms of the surface pressure it increases to 40 mN m−1. Though the different clinical surfactants have similar isotherms, AFM studies of deposited layers show fairly different topological features, including multilayer structures or “reservoirs” of fluid phase that are formed beneath the surface.13–15 These structures are most pronounced in Survanta, and less so in Curosurf or Infasurf.15 The collapse and respreading of monolayers into multilayers or aggregates have been hypothesised as being essential in the development of the characteristic surface tension area loops associated with pulmonary surfactant at high concentrations.16,17
In consideration of the stability of the thin surfactant films, several fluid mechanical processes are apparent. For example the proper functioning of the clinical lung surfactant replacements demands an efficient spreading, followed by the formation of stable thin films that resist rapid thinning and de-wetting. The role of the interfacial viscosity,13 or more generally interfacial rheology, has been suggested to be of great importance, in addition to the adsorption/desorption dynamics. However, the data on the rheological properties of lung surfactant systems have been reported to vary greatly.18 Two approaches have been used to investigate the dynamical response of these substances. One approach is to study specific combinations of known elements of the lung surfactant. Hermans and Vermant studied the interfacial shear rheology of DPPC under physiologically relevant conditions.19 Alonso et al. combined DPPC with surfactant protein C (SP-C), and found that this combination led to a highly viscoelastic interface.20 Zasadzinsky and coworkers systematically added cholesterol to DPPC and found that it dramatically reduced the interfacial shear viscosity.21–23 In the second approach, which is followed here, clinically approved natural lung surfactant replacements are utilized to mimic in vitro lung surfactant as closely as possible. One of the clinical surfactants, Survanta®, has been shown to possess a very high surface viscosity.20 However, it has been reported that other commercially available products differ strongly in their interfacial rheologies.18
This paper examines the role of lung surfactants during drainage flows from a hemispherical dome that is quickly raised through the interface and assesses their ability in maintaining stable thin liquid films, under conditions related to fast interfacial deformations. The present work is distinguished from earlier work in two ways. First, there is a comparative rheological characterisation of three clinically most used natural surfactants (Survanta®, Curosurf®, and Infasurf®) as well as DPPC monolayers. Second, we perform a drainage analysis of the same substances, under conditions where adsorption dynamics are not playing a role. A scaling analysis is performed to investigate and separate the mechanisms affecting the stability of surfactant-laden thin films during spreading. Further refinements to replicate the alveolar environment include the lining of the dome surface with alveolar epithelial cells.
2 Theoretical background
2.1 Different possible contributions to the surface stress
When the interface is deformed, different stresses can arise at the interface, as schematically depicted in Fig. 1. The surface stress is defined as| σ = σαβ(Γ)I + σe | (1) |
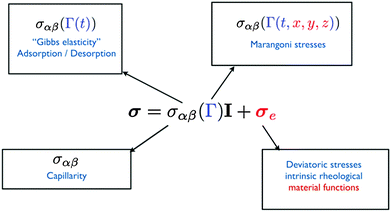 | ||
| Fig. 1 Potential contributions to the surface stress tensor σ when an interface is deformed and dilated. | ||
2.2 Drainage flow
In Fig. 2, a schematic representation of the experimental geometry is shown. As the film thickness h(θ,t) is much smaller than the radius of the dome (R), variations of film thickness across the hemisphere are being neglected. We will also show that for the experimental conditions used here, the dome is elevated sufficiently high for capillary effects to be neglected. The flow hence occurs due to drainage from the hemisphere under the action of gravity. As a result, the mathematical problem can be analysed using the lubrication approximation, which reduces the problem to a flat, two-dimensional geometry with a cartesian coordinate system (y, θ). The dominant driving force for flow is due to hydrostatic pressure, Ph = ρghe, where he is the height at which the apex of the dome has been elevated (see Fig. 3, vide infra). This pressure must exceed the capillary pressure, Pc = 2σαβ/R. The ratio of these two pressures is the Bond number, Bo = Ph/Pc = Rhe/2λ2, where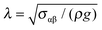 is the capillary length. As demonstrated below our experiments are operated under conditions where Bo ≫ 1.
is the capillary length. As demonstrated below our experiments are operated under conditions where Bo ≫ 1.
The evolution of the film thickness in time is fully determined by the velocity profile in the film. In the lubrication limit, the Navier–Stokes equation reduces to eqn (2):
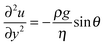 | (2) |
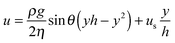 | (3) |
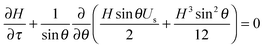 | (4) |
2.3 Detailed interfacial stress balance
The interfacial stress balance determines the value of Us and consists of contributions originating from the surfactant's interfacial rheological characteristics (in both shear and dilation) and Marangoni stresses due to surface tension gradients. Assuming that the interface is Newtonian and neglecting interfacial viscoelasticity, we adopt the commonly used Boussinesq–Scriven model for the interface.24 Thus, characterising the following parameters for the interface, surface dilatational viscosity, κs, and surface shear viscosity, ηs, we can write the tangential interfacial stress balance as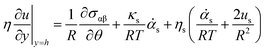 | (5) |
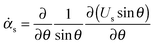 is related to the rate of change of interfacial area.
is related to the rate of change of interfacial area.
The first term on the right, the surface tension gradient 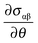 , can be rewritten as
, can be rewritten as 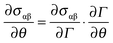 . The first term measures the rate of change of surface tension with surface concentration, Γ, and the second term corresponds to the gradient of the surfactant concentration across the surface in the θ-direction. For the observed velocities (>0.3 mm s−1), and as the phospholipids are larger sized molecules than surfactants for which Ds is well known,25 the surface Peclet number, Pes = h0us/Ds, can be estimated to be ≫1, and the surfactant transport will be convection dominated. Thus, we can re-write eqn (5) as the tangential stress balance in dimensionless terms as
. The first term measures the rate of change of surface tension with surface concentration, Γ, and the second term corresponds to the gradient of the surfactant concentration across the surface in the θ-direction. For the observed velocities (>0.3 mm s−1), and as the phospholipids are larger sized molecules than surfactants for which Ds is well known,25 the surface Peclet number, Pes = h0us/Ds, can be estimated to be ≫1, and the surfactant transport will be convection dominated. Thus, we can re-write eqn (5) as the tangential stress balance in dimensionless terms as
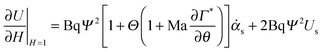 | (6) |
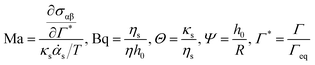 | (7) |
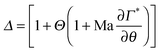 | (8) |
Analytical solutions to eqn (4) and (6) have been previously obtained in two limits for the time dependence of the film thickness at the apex of the dome (θ = 0) by Bhamla et al.26 The first of these limits is the case of a surfactant free draining liquid layer, where Bq = 0, while the second limit corresponds to an extremely viscous interface, where Bq → ∞. In both cases, the form of the solution is
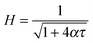 | (9) |
3 Materials and methods
3.1 Lung surfactant replacements
Three commercial lung surfactant replacements are compared: Curosurf (Chiesi, Italy), Survanta (AbbVie, USA) and Infasurf (ONY Inc., USA). These are, respectively, porcine, bovine and bovine calf surfactants containing 76, 28 and 35 mg phospholipids (PL) per ml (see ESI,† Table S1). Survanta is obtained from minced bovine lung tissue, extracted and precipitated and supplemented with synthetic DPPC, palmitic acid and tripalmitin.27 Curosurf comes from minced porcine lung tissue. It is depleted of cholesterol during manufacture.28 Infasurf is prepared from lung lavage of newborn calves and contains all of the hydrophobic components, including cholesterol.18 All three were diluted in a phosphate buffered saline (PBS) solution (pH 7.4; Gibco) to identical concentrations of 0.8 mg PL ml−1. The concentration was chosen based on the dependence of surface tension on concentration as shown in the ESI,† Fig. S1, where the surface tension of the lung surfactant mixture as measured with a Wilhelmy plate is approximately constant from a concentration of 0.4 mg PL ml−1 onwards. The clinical lung surfactant replacements were allowed to come to adsorption equilibrium at a temperature of 37 °C, so surface tensions were in the range of 25–30 mN m−1 before the start of the drainage experiments. Temperature was maintained at 37 °C, except in the visualisation experiments, which had to be performed at room temperature.DPPC was procured from Avanti Polar Lipids Inc. (Alabaster, AL) in 25 mg ml−1 glass vials. Stock solutions of 1 mg ml−1 in chloroform (Sigma-Aldrich, St. Louis, MO) were created and stored in a freezer until required. DPPC was spread at the interface using chloroform as a spreading solvent and was then compressed to a surface pressure of 20 mN m−1 before starting any experiment. This particular surface pressure was chosen as to give it the same order of magnitude of surface viscosity as Curosurf and Infasurf (see further).
3.2 Interfacial rheology
The double wall ring (DWR) geometry accessory combined with a sensitive magnetic bearing stress rheometer (Discovery HR-3, TA Instruments, USA) and magnetic needle interfacial shear rheometer (ISR) was used to characterise the interfacial rheology of the lung surfactant replacements and the DPPC.29–31 Only Survanta had sufficiently high viscosities and elasticities to be measured with the DWR, and the other systems were outside of the sensitivity limits and necessitated the use of the ISR. In all cases, the results were corrected for subphase drag as described in the literature.29–32The three lung surfactant replacements were used from their stock solutions as described above and dispersed into the rheometer trough. Following natural adsorption of a monolayer from the bulk fluid and attainment of an equilibrium surface pressure of 47 mN m−1, the interfacial rheology was measured. Infasurf and Curosurf interfacial rheologies were obtainable only at room temperature whereas Survanta, being much more viscoelastic, could be studied at 37 °C.
DPPC was spread at the air–water interface in a Langmuir trough by touching microdrops of lipid stock solution (1 mg ml−1) using a clean Hamilton syringe. We used deionized-distilled water as the subphase from a Milli-Q filtering system (EMD Millipore, Billerica, MA) with a resistivity of 18.2 MΩ cm and a surface tension of 72 mN m−1. The surface pressure was monitored using a platinum Wilhelmy plate connected to a surface pressure sensor (KSV NIMA Ltd., Helsinki, Finland). The volume of DPPC spread was 35 μl, and the spreading pressure was less than 0.5 mN m−1. After chloroform was allowed to evaporate for 30 min, the interface was compressed using symmetric Teflon barriers at a speed of 10 mm min−1 till a surface pressure of 20 mN m−1 was achieved, in order to compare with earlier drainage experiments.26 The rheology measurements were performed at a strain amplitude of 1%, which is in the linear viscoelastic regime for this material.19
3.3 Drainage apparatus
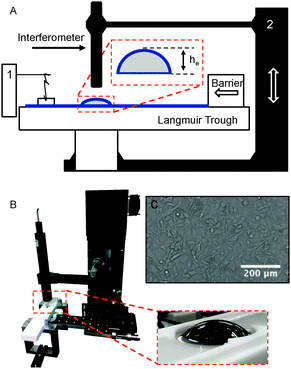
To characterise the effect of different substances on film mobility, the drainage of thin films is observed using a modification of the device used previously for the study of tear film lipids.26,33 A picture and schematic of the instrument are shown in Fig. 3. The device consists of a hemi-spherical glass dome (Newport KPX579) with a (curvature) radius of 19.97 mm mounted on a pedestal that is initially submerged below the air–solution interface. In the case of DPPC, the dome is submerged below an air–liquid interface on which DPPC is spread and then compressed to a known surface pressure. For the lung surfactants barrier compression is not required and experiments are commenced once adsorption to the interface has achieved equilibrium. In both cases, after reaching the desired surface pressure, the dome is elevated using a motorised stage through the interface allowing it to capture a thin liquid film. The thickness of this film is monitored with a high speed white light interferometer (F70, Filmetrics, USA) combined with a halogen light (Fiber-Lite PL-800). A temperature control unit was added to the setup to maintain a temperature of 37 °C during the experiments. Electrical heating elements (Omega) are connected to solid aluminum blocks which are pressed into voids at the bottom of the trough. The thin Teflon bottom in contact with the metal blocks together with a thermocouple feedback system allows for an accurate temperature setting (±1 °C) inside the trough.During the experiments the following protocol was followed. The dome is initially submerged in the trough and positioned approximately 130 μm below the fluid surface. Subsequently, the geometry is raised quickly at a speed of 10 mm s−1 and the evolution of the film thickness in time is captured by the interferometer at 4 points per second. To compare the drainage results for the different systems and test conditions, the first 4 seconds of height versus time data were fitted with eqn (9) to obtain a characteristic value of the fitting parameter α for every dataset. Drainage of the lung surfactant replacements was investigated for three different conditions: on a clean dome at 23 and 37 °C to observe the effect of temperature and additionally on a dome covered with cells at 37 °C. The effect of elevation of the dome has been investigated, as will be discussed below. An elevation of the dome by 2.5 mm was used in most experiments, and is in the regime where gravitational stress dominates the capillary stress.
3.4 Visualisation of Marangoni stress-induced flows
Past work by Joye et al.34 has shown that film drainage and stability are influenced by both Marangoni stress-induced flows and interfacial rheology. In their work a Scheludko cell was used to reveal the presence of interfacial flow phenomena during drainage. In the present work, we examine drainage flows associated with bubbles approaching an air–solution interface in the presence of the surfactants employed in this study. To visualise the Marangoni flows, the setup was slightly modified. A spherical air bubble (1.1 mm, dia) was now elevated toward the air–fluid interface. The use of an air bubble instead of a glass dome has the advantage of providing a better index of refraction contrast. The air bubble is generated at the tip of a glass capillary (Drummond Micropipette, Fisher Scientific Inc., MA, USA). The bubble is elevated at a speed of 0.5 mm s−1 by a vertical distance of 2 mm. This ensures that only a fraction of the bubble cap interacts with the air–fluid interface. This thin curved film (<1 μm) under white light illumination (420–780 nm) results in colour interference patterns that are captured using a colour CCD camera. These experiments were carried out at room temperature.3.5 Culture of A549 lung epithelial cells
To mimic the alveolar surface, adenocarcinomic human alveolar basal epithelial cells (A549) were purchased from ATCC. They were cultured according to the ATCC guidelines in a F-12K (Kaighn's modification) growth medium (Gibco) enriched with 10% fetal bovine serum (BFS, Gibco) and 1% Pen Strep (penicillin, streptomycin; Gibco). Four days before the drainage experiment, cells were transferred from a full Petri dish to the glass dome. Two-thirds of the cells were deposited in a sterile cup (50 ml) containing the glass lens on an aluminum pedestal and growth medium. A549 cells are adherent and form a monolayer on top of the geometry (Fig. 3C); no pre-coating was applied to the surface. The remaining one-third of the cells were transferred to a Petri dish as a control for contamination and growth rate. Experiments were performed with domes at a surface coverage of >95%. After two days the growth medium was refreshed.Prior to drainage experiments, the cell covered geometries were rinsed gently but extensively using a PBS buffer to avoid surface active material from the growth medium to affect results. After 30 minutes the buffer was removed from the trough and replaced by the lung surfactant mixture. Experiments were carried out within one hour to limit cell death.
4 Experimental results and discussion
4.1 Drainage experiments: introductory remarks
During the drainage experiments, the evolution of the film thickness was monitored in time using an interferometer. A typicalresult of the height as a function of time for Survanta and Curosurf (at equal bulk lipid concentration 0.8 mg PL ml−1) and after reaching the equilibrium surface pressure of 47 mN m−1 is given in Fig. 4. The typical time scale of the experiment is only a few seconds. This time scale was observed to be an order of magnitude smaller than the time scale of adsorption/deposition dynamics, which is on a time scale of minutes.11 This was confirmed by observations using a Langmuir trough for an area change of 10% (not shown here).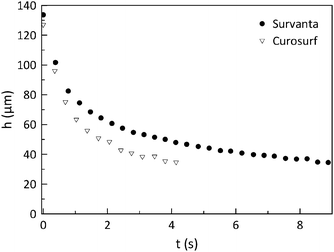 | ||
| Fig. 4 Typical results of the drainage experiments. The height as a function of time (t) for Survanta and Curosurf at 37 °C. | ||
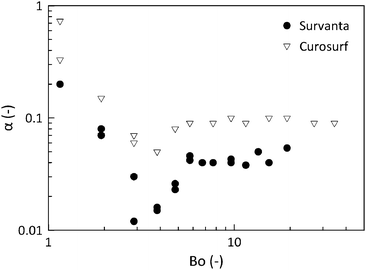
As indicated in Fig. 1, capillary forces can play a role in drainage and stability. However, the importance of these forces can be diminished by elevating the dome to heights larger than the capillary length of the liquid. The drainage rate was measured for different values of he and, as such, different magnitudes of the hydrostatic pressure. In Fig. 5, the parameter α, which captures the drainage speed, is plotted versus Bo = PH/PC, the ratio of the hydrostatic pressure versus capillary pressure. For small he or small PH/PC, the drainage is fast and α is even larger than the value for the free draining limit of 1/3. After a local minimum, for values of PH/PC > 10, a constant value is obtained for all of the surfactants. This independence also suggests that the initial dilatational deformation that accompanies the deformation of the circle into a hemispherical cap does not have a significant effect on the subsequent drainage and that the initial condition is reproducible.
In the following, we report only experiments at a step height (he) of 2.5 mm, where PH/PC > 10 and from this section it can be concluded that for the experimental conditions used, neither capillarity nor adsorption dynamics will play a major role. For an elevation height of he = 2.5 mm and the geometry used, the initial local change in area is 6.8%. We will now investigate if either the rheological response of the interface or Marangoni stresses, or both, determine the drainage rate and hence govern film stability.
4.2 Drainage experiments: experimental results
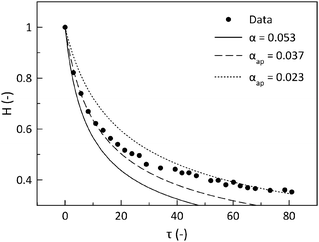
Fig. 6A showing the results from the interferometry measurements displays how the normalized height (H = h/h0) evolves as a function of dimensionless time (τ), scaled by the gravitational time. The drainage results in Fig. 6A are fit to eqn (9) using only α as the fitting parameter. A comparison of α values for all three lung surfactant systems and DPPC is summarized in Fig. 6B. Also shown are α values for these systems at three different conditions: 25 °C and 37 °C on uncoated surfaces and on a cell-coated surface at 37 °C. The standard deviations for all experiments are calculated from 5 trials or more.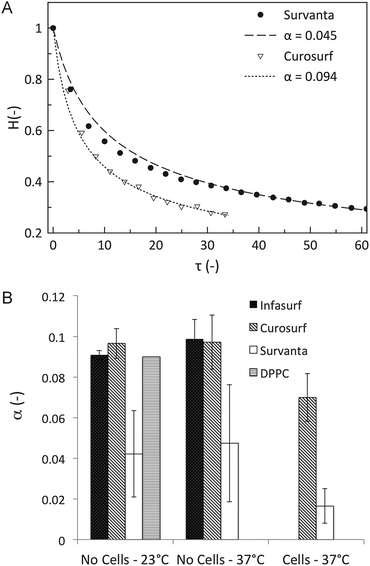 | ||
| Fig. 6 Results of the drainage experiments. (A) The normalized height (H) as a function of rescaled time (τ) for Survanta and Curosurf at 37 °C. The fit of eqn (9) is shown as a dashed line and is used to obtain the fitting parameter α. (B) The value for the fitting parameter α for all lung surfactant replacements in the three studied conditions: at 23 °C without cells and at 37 °C with and without cells. The error bars correspond to the stochastic error of minimum 5 experiments. | ||
For uncoated surfaces at both temperatures, Infasurf and Curosurf films drain at a similar rate, α ∼ 0.1, which is the value expected for an immobile interface. Survanta films drain significantly slower than the lower limit of the hydrodynamical analysis, by as much as 50% (α ∼ 0.05). The presence of an alveolar epithelial cell monolayer has a striking influence in slowing film drainage. Only results for Curosurf and Survanta are shown here with α ∼ 0.07 and α ∼ 0.02, respectively. The different contributions to this reduction in drainage speed will now be investigated and quantified.
4.3 Interfacial shear rheology: Bq
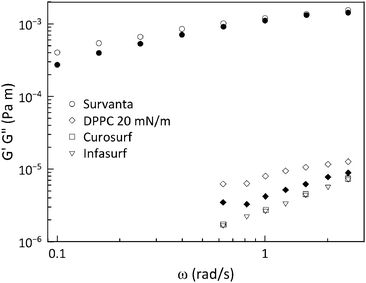
To evaluate the effect of the surface rheology, experiments were first performed in shear flow. Linear viscoelastic surface moduli were measured for all four systems and are shown in Fig. 7. Only Survanta films possess strong interfacial viscoelasticity with surface shear moduli, Gs′ and Gs′′ ∼ 10−4 Pa m. This unusually high viscoelasticity for Survanta is probably due to the presence of palmitic acid and DPPC, as these two components can co-crystallize easily, rendering enhancement of solid phase domains and the possible presence of aggregates protruding in the subphase.13 Curosurf and Infasurf exhibit interfacial moduli that are two orders of magnitude smaller for both systems and no elastic modulus could reliably be measured. Consequently, the Boussinesq numbers obtained for Curosurf and Infasurf were found to be ∼20, making these substances difficult to measure using the ISR.32 DPPC shows dominantly viscous interfacial shear rheological properties, with the loss modulus Gs′′ ∼ 10−5 Pa m being slightly larger than that of Curosurf and Infasurf. We desire to map our measured α values against the Boussinesq numbers that are appropriate for each experiment. From eqn (9), evaluation of this number requires the interfacial viscosity and for this purpose, we use the modulus of the complex viscosity defined as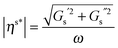 where the moduli are retrieved from Fig. 7 and ω is the lowest accessible frequency.
where the moduli are retrieved from Fig. 7 and ω is the lowest accessible frequency.
The theoretical analysis developed in Sections 2.2 and 2.3 can be used to numerically determine the parameter α as a function of the parameter Δ defined in eqn (8). This is shown in Fig. 8 along with the data acquired for the lung surfactants and DPPC. There are two sets of experimental data in this plot, one setting Θ to zero, and a second set, where the dilatational and Marangoni numbers are adjusted according to a procedure discussed in the following section. The predictions of the model have alpha undergo a sharp transition from 1/3 (a stress-free interface) to 1/12 (a no-slip interface) as BqΨ2Δ transitions between 0.1 and 1. When only the interfacial shear viscosity of the substances is considered, as was done in previous studies,19–23,26,33 the theory is unable to capture the experimentally observed response. This discrepancy is resolved by introducing the combined contributions of dilatational rheology and Marangoni stresses.
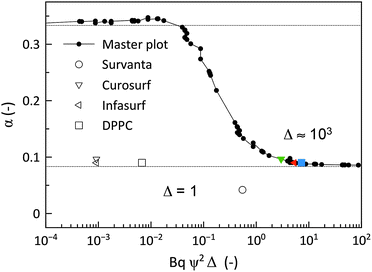 | ||
| Fig. 8 Mapping of the experimental values of α for Curosurf (down-pointing open triangle, down-pointing green triangle), Infasurf (left-pointing open triangle, left-pointing red triangle) and DPPC (open square, blue square) onto the numerical solutions of the drainage rate versus BqΨ2Δ from solving eqn (4) and (6) (black circles). Taking only interfacial shear viscosity (Δ = 1, open symbols) does not map the results, and a value of Δ ≥ 1000 is required to map the results (coloured symbols) suggesting important contributions of dilatational viscosity or Marangoni stress. | ||
4.4 Dilatational and Marangoni effects: Θ and Ma
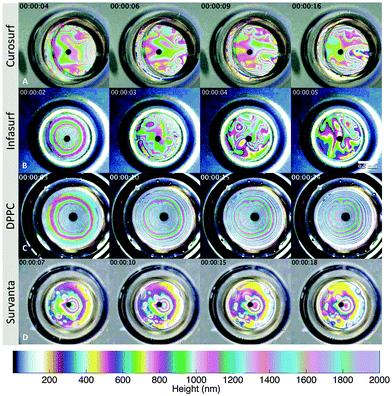
It is evident from Fig. 8 that interfacial shear viscosity alone (Δ = 1) cannot describe the measured drainage phenomena. However, by shifting the data laterally, we can estimate the value of the parameter Δ that is necessary to bring the theory into alignment with experiments. This translation has been performed in Fig. 8, where it was determined that a value on the order of Δ = 103 is required. Specifically, the Δ values for Curosurf, Infasurf, and DPPC are 3.2 × 103, 5.7 × 103, and 1.1 × 103, respectively. This shifting is not applicable to the drainage data collected for the Survanta system due to its very high interfacial viscoelasticity, as discussed in the following section. It is evident, however, that the other three surfactants stabilise thin films and reduce drainage rates through a combination of dilatational rheology and Marangoni stresses.The relative importance of interfacial dilatational rheology and Marangoni stresses in drainage dynamics can be assessed directly through visualisation of the thickness variations on thin, draining films. For this purpose, the elevating glass dome was replaced by an elevating air bubble to enhance the refractive index contrast, creating very strong interference fringes using a colour interferometer. Analogous to the drainage experiments, the bubble is elevated to the air–fluid interface, capturing a thin liquid film that drains back into the surrounding excess reservoir. Under illumination with a white LED light source, these thin films exhibit thin-film color interference, which can be clearly seen in the attached ESI,† videos. A compilation of time-lapse images for all the four surfactant systems is shown in Fig. 9. Using a combination of experiment and theoretical analysis, Joye et al.34 classify the drainage patterns as symmetric and asymmetric. The latter is a typical signature of surface tension driven Marangoni stresses at the interface, caused by dilatation of the air–fluid interface and re-distribution of surfactant molecules at the air–fluid interface. However, Joye et al.34 show that these Marangoni instabilities can be quenched by the presence of dilatational and surface shear viscosities, and surface elasticity, in which case stable and symmetric drainage patterns are typically observed.
The Curosurf and Infasurf films indeed exhibit asymmetric drainage with moderate and highly chaotic surface motions, respectively. These patterns suggest a dominant role of Marangoni stresses in slowing drainage for these films. The low surface shear viscosities point to a very weak structuring at the interface and what is observed is consistent with low molecular weight surfactants. The experiments for DPPC at 20 mN m−1 show symmetric patterns without any interfacial turbulence over the time span of 20 s, after which the films burst. This symmetric drainage can be qualitatively understood as having its origin in the small but finite viscoelasticity of this lipid, in agreement with the observations of Joye et al.34 and the occurrence of significant dilatational stresses which quench potential Marangoni stresses. Also shown in Fig. 9 are the time-lapsed interferometric patterns associated with the drainage of Survanta. As in the case of DPPC, this surfactant arrests Marangoni convection due to its large surface viscoelasticity. The drainage behaviour of Survanta is further discussed in the next section.
4.5 Survanta and surface viscoelasticity
The drainage and film stability dynamics of Survanta were observed to be qualitatively different compared to the other surfactants. The observed drainage rate is slower than the lower theoretical limit of 1/12 predicted for an immobile, no-slip interface. As this lower limit corresponds to the state of a zero surface velocity, a further reduced drainage rate might indicate a negative surface velocity towards the apex of the geometry. Only surface tension gradients (Marangoni stress) in the direction of the apex or a mechanical surface elasticity is capable of producing such a recoil effect. It should be noted that in a previously published study with highly viscoelastic meibomian lipids, values of α < 1/12 were obtained,26 but as yet it is unclear how the surface elasticity couples to the subphase flows. In the visualisation experiments shown in Fig. 9, the Survanta film was observed to be very inhomogeneous, and remained essentially motionless over the lifetime of the film (18 s). This behaviour is characteristic of surfaces exhibiting surface gelation resulting in interfacial elasticity.35 Thus, the drainage pattern for Survanta and its highly viscoelastic interface (Fig. 7) are in good agreement, but it is not clear how the drainage velocity falls below the immobile limit. Possibly the presence of multilayers in the subphase should also be considered, which could indeed lower the velocity. These aggregate structures are most pronounced in adsorbed Survanta, and less so in Curosurf or Infasurf.13,155 Effect of attached cells on drainage rates
The presence of epithelial cells attached to the glass dome had a significant effect on the drainage rate in comparison to similar experiments on a bare, smooth geometry. In contrast to a smooth geometry, the alveolar epithelial cells induce a microscopic roughness, which slows down the drainage of the fluid film. In the literature, many methods are available to describe the flow of a liquid on top of a rough surface, ranging from flow on a porous layer36,37 to a surface with distinct obstacles,38 but the analysis goes beyond the scope of the present work. The result of the surface roughness is that the data can no longer be fitted by a single value of α and only an average value can be obtained. Fig. 10 shows that the drainage rate, expressed by the fitting parameter α, decreases in time. This effect will be more pronounced for systems with a low interfacial viscosity in comparison to a high interfacial viscosity.6 Physiological implications
In the present work, both DPPC and clinically approved natural lung surfactant replacements were subjected to a step dilation flow to investigate at least one aspect of thin film stability. The drainage experiments showed that the dominating physical phenomena determining the overall drainage rate differ. For Survanta and DPPC the interfacial rheological properties play an important, if not dominating, role, whereas for Curosurf and Infasurf they are too weak, resulting in a flow pattern dominated by the local Marangoni gradients.The studied natural lung surfactant replacements are mainly used for the treatment of the neonatal respiratory distress syndrome (NRDS) in which a liquid bolus is instilled into a baby's lung. The surfactant spreads throughout the lung in a very short time aided by mechanical ventilation and presumably Marangoni flow.39 This is only possible if the physical properties of the surfactant interface allow fast spreading. Clinical trials comparing the efficiency of the surfactant replacements Curosurf, Infasurf and Survanta also reveal clinical differences.40,41 Of course, several factors will contribute to the overall clinical efficacy. What has been shown here is that they all stabilise thin films, but we observe a high surface viscoelasticity for Survanta. This can be expected to lead to a slower spreading and a different mechanism of stabilising the interface (at least initially). Curosurf and Infasurf are expected to spread better throughout the lung. In the light of designing synthetic lung surfactants, the results of this study suggest that the presence of surface viscoelasticity should be minimised in order to allow Marangoni flows to distribute the lung surfactant more efficiently, while maintaining stability against rapid drainage.
7 Conclusion
We have shown that the presence of lung surfactant replacement layers and DPPC monolayers at the air–fluid interface is able to enhance the stability of thin films. Three possible physical mechanisms were identified: the interfacial shear rheological properties of the interface, the dilatational rheological properties and the presence of Marangoni stresses due to surface tension gradients. Characterisation of the interfacial shear moduli in combination with a mathematical model describing the drainage experiment revealed that the interfacial shear viscosity is not dominant in any of the systems studied. We also showed the relative levels of surface mobility of the surfactants during drainage. These images revealed the importance of Marangoni stresses for the two low viscous surfactants, Curosurf and Infasurf. In the case of DPPC and Survanta, the local film mobility was much smaller, indicating a relatively strong contribution of the dilatational properties for DPPC and shear surface elasticity in the case of Survanta. More broadly, a fundamental understanding of the different stabilisation mechanisms of natural lung surfactants may give clues for engineering synthetic replacements for treatment of the respiratory distress syndrome.Acknowledgements
The authors would like to thank FWO Vlaanderen for PhD Fellowship to E.H. Chiesi Farmaceutici is gratefully acknowledged for providing Curosurf and AbbVie for providing Survanta. We would like to thank Benoit Scheid (ULB, Belgium) for fruitful discussions and Y. Strakovsky (Stanford University) for contributions to the design of graphics and schematics. Finally, we would like to thank Joannes Vermant, Chew Chai and Marco A. Àlvarez-Valenzuela for their help with the Marangoni bubble experiments, and Javier Tajuelo for discussions on the ISR.References
- R. E. Pattle, Properties, function and origin of the alveolar lining layer, Nature, 1955, 175, 1125–1126 CrossRef CAS PubMed.
- R. E. Pattle, Surface lining of lung alveoli, Phys. Rev., 1965, 45, 48–79 CAS.
- E. S. Brown, R. P. Johnson and J. A. Clements, Pulmonary surface tension, J. Appl. Physiol., 1958, 14, 717–720 Search PubMed.
- J. A. Clements, R. F. Hustead, R. P. Johnson and I. Gribetz, Pulmonary surface tension and alveolar stability, J. Appl. Physiol., 1961, 16, 444–450 CAS.
- D. Halpern, H. Fujioka, S. Takayama and J. B. Grotberg, Liquid and surfactant delivery into pulmonary airways, Respir. Physiol. Neurobiol., 2008, 163, 222–231 CrossRef CAS PubMed.
- K. Koch, et al. Surface tension gradient driven spreading on aqueous mucin solutions: a possible route to enhanced pulmonary drug delivery, Mol. Pharmaceutics, 2011, 8, 387–394 CrossRef CAS PubMed.
- R. Levy, D. B. Hill, M. G. Forest and J. B. Grotberg, Pulmonary Fluid Flow Challenges for Experimental and Mathematical Modeling, Integr. Comp. Biol., 2014, 54, 985–1000 CrossRef PubMed.
- A. Podgorski and L. Gradon, Dynamics of pulmonary surfactant system its role in alveolar cleansing, Ann. Occup. Hyg., 1990, 34, 137–147 CrossRef CAS.
- J. Goerke and J. A. Clements, Pulmonary surfactant: an engineering marvel, In: Proc. Ann. Int. Conf. – IEEE Eng., Med. Biol., 1999, 1, 355 Search PubMed.
- J. Perez-Gil and T. E. Weaver, Pulmonary Surfactant Pathophysiology: Current Models and Open Questions, Physiology, 2010, 25, 132–141 CrossRef CAS PubMed.
- R. H. Notter, J. N. Finkelstein and R. D. Taubold, Comparative adsorption of natural lung surfactant, extracted phospholipids, and artifical phospholipids mixtures to the air water interface, Chem. Phys. Lipids, 1983, 33, 67–80 CrossRef CAS.
- S. Schurch, J. Goerke and J. A. Clemnets, Direct determination of volume-dependence and time-dependence of alveolar surface-tension in excised lungs, Proc. Natl. Acad. Sci. U. S. A., 1978, 75, 3417–3421 CrossRef CAS.
- C. Alonso, T. Alig, J. Yoon, F. Bringezu, H. Warriner and J. Zasadzinski, More than a monolayer: relating lung surfactant structure and mechanics to composition, Biophys. J., 2004, 87, 4188–4202 CrossRef CAS PubMed.
- H. Bachofen, et al. Structures of pulmonary surfactant films adsorbed to an air–liquid interface in vitro, Biochim. Biophys. Acta, Biomembr., 2005, 1720, 59–72 CrossRef CAS PubMed.
- H. Zhang, Q. Fan, Y. E. Wang, C. R. Neal and Y. Y. Zuo, Comparative study of clinical pulmonary surfactants using atomic force microscopy, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 1832–1842 CrossRef CAS PubMed.
- S. R. Schürch, H. Qanbar, H. Bachofen and F. Possmayer, The surface associated surfactant reservoir in the alveolar lining, Biol. Neonate, 1995, 67, 61–67 CrossRef PubMed.
- A. Von Nahmen, M. Schenk, M. Sieber and M. Amrein, The structure of a model pulmonary surfactant as revealed by scanning force microscopy, Biophys. J., 1997, 72, 463–469 CrossRef CAS.
- M. Rudiger, A. Tolle, W. Meier and B. Rustow, Naturally derived commercial surfactants differ in composition of surfactant lipids and in surface viscosity, Am. J. Physiol., 2005, 288, L379–L383 Search PubMed.
- E. Hermans and J. Vermant, Interfacial shear rheology of DPPC under physiologically relevant conditions, Soft Matter, 2014, 10, 175–186 RSC.
- C. Alonso, A. Waring and J. A. Zasadzinski, Keeping lung surfactant where it belongs: protein regulation of two-dimensional viscosity, Biophys. J., 2005, 89, 266–273 CrossRef CAS PubMed.
- K. Kim, S. Q. Choi, Z. A. Zell, T. M. Squires and J. A. Zasadzinski, Effect of cholesterol nanodomains on monolayer morphology and dynamics, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3054–3060 CrossRef PubMed.
- K. Kim, S. Q. Choi, J. A. Zasadzinski and T. M. Squires, Interfacial microrheology of DPPC monolayers at the air–water interface, Soft Matter, 2011, 7, 7782–7789 RSC.
- S. Q. Choi, et al. Influence of molecular coherence on surface viscosity, Langmuir, 2014, 30, 8829–8838 CrossRef CAS PubMed.
- L. E. Scriven, Dynamics of a fluid interface, equation of motion of newtonian surface fluids, Chem. Eng. Sci., 1960, 12, 98–108 CrossRef CAS.
- D. C. Clark, et al. Surface diffusion in sodium dodecyl sulfate-stabilized thin liquid films, J. Colloid Interface Sci., 1990, 138, 195–206 CrossRef CAS.
- M. S. Bhamla, C. E. Giacomin, C. Balemans and G. G. Fuller, Influence of interfacial rheology on drainage from curved surfaces, Soft Matter, 2014, 10, 6197–6206 RSC.
- R. H. Notter, Z. Wang, E. A. Egan and B. A. Holm, Component-specific surface and physiological activity in bovine-derived lung surfactants, Chem. Phys. Lipids, 2002, 114, 21–34 CrossRef CAS.
- O. Blanco and J. Perez-Gil, Biochemical and pharmacological differences between preparations of exogenous natural surfactant used to treat respiratory distress syndrome: role of the different components in an efficient pulmonary surfactant, Eur. J. Pharmacol., 2007, 568, 1Đ15 CrossRef PubMed.
- S. Vandebril, A. Franck, G. G. Fuller, P. Moldenaers and J. Vermant, A double wall-ring geometry for interfacial shear rheometry, Rheol. Acta, 2010, 49, 131–144 CrossRef CAS.
- C. F. Brooks, G. G. Fuller, C. W. Curtis and C. W. Robertson, An interfacial stress rheometer to study rheological transitions in monolayers at the air–water interface, Langmuir, 1999, 15, 2450–2459 CrossRef CAS.
- S. Reynaert, C. F. Brooks, P. Moldenaers, J. Vermant and G. G. Fuller, Analysis of the magnetic rod interfacial stress rheometer, J. Rheol., 2008, 52, 261–285 CrossRef CAS.
- T. Verwijlen, P. Moldenaers, H. A. Stone and J. Vermant, Study of the flow field in the magnetic rod interfacial stress rheometer, Langmuir, 2011, 27, 9345–9358 CrossRef CAS PubMed.
- M. S. Bhamla, C. Balemans and G. G. Fuller, Dewetting and deposition of thin films with insoluble surfactants from curved silicone hydrogel substrates, J. Colloid Interface Sci., 2015, 449, 428–435 CrossRef CAS PubMed.
- J. L. Joye, G. J. Hirasaki and C. A. Miller, Asymmetric drainage in foam films, Langmuir, 1994, 10, 3174–3179 CrossRef CAS.
- C. Monteux, et al. Adsorption of oppositely charged polyelectrolyte/surfactant complexes at the air/water interface: formation of interfacial gels, Langmuir, 2004, 20, 57–63 CrossRef CAS.
- G. S. Beavers and D. D. Joseph, Boundary conditions at a naturally permeable wall, J. Fluid Mech., 1967, 30, 197–207 CrossRef.
- C. Carotenuto and M. Minale, Shear flow over a porous layer: velocity in the real proximity of the interface via rheological tests, Phys. Fluids, 2011, 23, 063101 CrossRef PubMed.
- J. Seiwert, M. Maleki, C. Clanet and D. Quéré, Drainage of a rough surface, EPL, 2011, 94, 16002 CrossRef.
- K. J. Cassidy, et al. A rat lung model of instilled liquid transport in the pulmonary airways, J. Appl. Phys., 2001, 90, 1955–1967 CrossRef CAS PubMed.
- C. A. Malloy, P. Nicoski and J. K. Muraskas, A randomized trial comparing beractant and poractant treatment in neonatal respiratory distress syndrome, Acta Paediatr., 2007, 94, 779–784 CrossRef PubMed.
- R. Ramanathan, et al. A randomized, multicenter masked comparison trial of Poractant alfa (Curosurf) versus Beractant (Survanta) in the treatment of respiratory distress syndrome in preterm infants, Am. J. Perinat., 2004, 21, 109–119 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm01603g |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2015 |