 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fluctuations in flows near jamming†
Erik
Woldhuis
a,
Vijayakumar
Chikkadi
bcd,
Merlijn S.
van Deen
d,
Peter
Schall
b and
Martin
van Hecke
*de
aInstituut-Lorentz, Universiteit Leiden, Postbus 9506, 2300 RA Leiden, The Netherlands
bInstitute of Physics, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
cLaboratoire de Physique, Ecole Normale Supérieure de Lyon, Université de Lyon, CNRS, 46, Allée d' Italie, 69007 Lyon, France
dHuygens-Kamerlingh Onnes Lab, Universiteit Leiden, Postbus 9504, 2300 RA Leiden, The Netherlands. E-mail: mvHecke@physics.leidenuniv.nl
eFOM Institute AMOLF, Science Park 104, 1098 XG Amsterdam, The Netherlands
First published on 30th July 2015
Abstract
Bubbles, droplets or particles in flowing complex media such as foams, emulsions or suspensions follow highly complex paths, with the relative motion of the constituents setting the energy dissipation rate. What is their dynamics, and how is this connected to the global rheology? To address these questions, we probe the statistics and spatio-temporal organization of the local particle motion and energy dissipation in a model for sheared disordered materials. We find that the fluctuations in the local dissipation vary from nearly Gaussian and homogeneous at low densities and fast flows, to strongly intermittent for large densities and slow flows. The higher order moments of the relative particle velocities reveal strong evidence for a qualitative difference between two distinct regimes which are nevertheless connected by a smooth crossover. In the critical regime, the higher order moments are related by novel multiscaling relations. In the plastic regime the relations between these moments take on a different form, with higher moments diverging rapidly when the flow rate vanishes. As these velocity differences govern the energy dissipation, we can distinguish two qualitatively different types of flow: an intermediate density, critical regime related to jamming, and a large density, plastic regime.
1 Introduction
Flowing complex media exhibit both highly nontrivial macroscopic rheology and spatiotemporally heterogeneous microscopic fluctuations,1 and understanding, linking and predicting the micro and macro behavior remains a formidable challenge.2–6 In this paper we will focus on the microscopic fluctuations and micro-macro link for a model which describes the wide class of complex yield-stress fluids that consist of discrete constituents which interact through short range interactions, such as foams, emulsions, granular media, (colloidal) suspensions and Lennard–Jones glasses.7,8At sufficiently low density, such disordered materials lose their yield stress and are unjammed. The rheology for dilute systems is Newtonian, and the particle motions lack complex features.2 At sufficiently high density, such materials are jammed—they have a finite yield stress, and their rheology is then necessarily non-Newtonian.2,3 For slow, dense flows, a phenomenological elasto-plastic scenario has emerged, where the central role is played by localized, plastic events, called shear transformation zones, T1 events or Eshelby inclusions.9–13 During flow, episodes of elastic loading of the system are punctuated by these plastic events which lower the shear stresses, so that the rate and magnitude of the stress drops together with the rate of elastic loading govern the steady state. Many models have been developed that capture this phenomenology.9,14,15 In particular the collective organization and buildup of correlations, where one event triggers the next, leading potentially to the formation of large scale avalanches, have received much attention.16
In between these two extremes, i.e., with densities closer to the jamming transition, the phenomenological scenario is far less clear. For static packings, the jamming transition has a critical nature as evidenced by power law scaling of response quantities and diverging time and length scales.17,18 How this static critical point influence the dynamics is far from understood. Just above jamming, the system has a low yield stress and the material becomes exceedingly fragile.19–24 The elastic shear modulus vanishes, the elastic response becomes strongly non affine, and the strain scale for which an elastic description is valid vanishes.17,18 Nevertheless, these systems are sufficiently crowded that particle motion must be strongly correlated. The question of the nature and role of fluctuations and plastic events in flows of disordered media close to jamming is wide open—at the very least their very weak elastic response suggests that episodes of elastic loading will be short lived, if they even can be distinguished. The crucial question is whether, close to jamming, we find the same type of physics—elastic loading punctuated by localized plastic events—as far away from jamming.
Here we address this question for one of the simplest models for the flow of disordered media, the Durian bubble model.8 In this over-damped, athermal model, originally developed for the flow of foams or emulsions, particle interactions combine harmonic repulsion—as in many models for jamming17—with viscous like dissipation.2,3 In the version of this model used here, the dissipative forces are linear in the relative motion Δv of two particles in contact. The two crucial control parameters are the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and packing fraction ϕ, and by varying these we can probe two qualitatively different flow regimes. For moderate densities, the static yield stress is low, and the flow dynamics is complex and presumably governed by the proximity of the (static) critical jamming point, whereas for large densities, the static yield stress is large and deformations take the form of well-delineated elastic loading and plastic relaxation events known as elasto-plastic flows.
and packing fraction ϕ, and by varying these we can probe two qualitatively different flow regimes. For moderate densities, the static yield stress is low, and the flow dynamics is complex and presumably governed by the proximity of the (static) critical jamming point, whereas for large densities, the static yield stress is large and deformations take the form of well-delineated elastic loading and plastic relaxation events known as elasto-plastic flows.
To make progress, we note that the microscopic particle motion and macroscopic rheology remain intimately connected: in steady flows, the energy supplied to the system must be balanced by dissipation.25 The power input is set by the product of shear stress σ and strain rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . The dissipation rate is governed locally by interactions between the constituents. In particular, for the bubble model the energy dissipation rate is given by the sum of Δv2 over contacts.3,25 Hence, power balance takes the form
. The dissipation rate is governed locally by interactions between the constituents. In particular, for the bubble model the energy dissipation rate is given by the sum of Δv2 over contacts.3,25 Hence, power balance takes the form  —we will determine the exact relation below. The crucial point is that this powerful and precise connection has strong implications for the magnitude of the local fluctuations: in particular this underlies the finding that in many weakly jammed media the local fluctuations decay sub-linearly with flow rate, such that the relative fluctuations diverge for slow flows.25,26
—we will determine the exact relation below. The crucial point is that this powerful and precise connection has strong implications for the magnitude of the local fluctuations: in particular this underlies the finding that in many weakly jammed media the local fluctuations decay sub-linearly with flow rate, such that the relative fluctuations diverge for slow flows.25,26
Powerful as this link is, it only predicts the 2nd moment of the distribution P(Δv), and most aspects of the microscopic fluctuations in flows near jamming are completely open. Is P(Δv) essentially Gaussian or do their probability distribution functions exhibit additional structure? Are these fluctuations intermittent in time and/or localized in space? What are the systematic variations with strain rate and density?
Here we address these questions and characterize the dissipative fluctuations, focusing on the higher moments of Δv which directly characterize deviations from Gaussianity, and also probe spatiotemporal heterogeneities. We first show that the probability distribution P(Δv) varies from near Gaussian in the critical regime to near power law in the yield stress regime. Similarly, the spatiotemporal distributions vary from essentially homogeneous near jamming to strongly heterogeneous in the yield stress regime. Second, we find that the nontrivial 4th and 6th moments of Δv can be related to the 2nd moment via nontrivial scaling relations which are reminiscent of multiscaling in turbulence. Crucially, these scaling relations take on a different form in the intermediate density, jamming and large density, yield stress regimes, which suggest an objective criterion to separate these two. As the velocity differences govern the energy dissipation, this qualitative difference in their statistics points to an important difference in the nature of energy dissipation. The broad picture that emerges is that we can both distinguish and connect two qualitatively different regimes: the yield stress regime that exhibits the well know elasto-plastic phenomenology seen in many other systems, and the near jamming regime with qualitatively different and new features.
2 Numerical model
We perform simulations on Durian's bubble model in 2D, for systems of N = 1024 particles in a 50/50 mixture of disks of diameter 1 and 1.4. The contact force fij between particles i and j is only nonzero when the particles are in contact, when it is the sum of a repulsive linear elastic force feij and a linearly viscous damping force fvij, where:feij = −k![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ijδij, ijδij, | (1) |
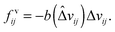 | (2) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij is the unit vector pointing from the center of particle i to j, δij is their overlap, Δvij is their relative velocity, and k and b are the elastic and viscous constants.
ij is the unit vector pointing from the center of particle i to j, δij is their overlap, Δvij is their relative velocity, and k and b are the elastic and viscous constants.
The particles are massless so that their motion is overdamped and the contact forces remain in balance. The velocities are then determined by solving a matrix equation at each time step.3 Simulations become much faster for the well studied ‘mean field’ variant of the bubble model, where the dissipative forces are calculated with respect to a mean flow.27 However this model is less realistic and leads to anomalous results for the fluctuations and their spatial correlations.2,3,28
The shear stress σ is calculated from the contact forces via the Born–Huang formula:29
 | (3) |
We perform numerical simulations at constant strain rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) between 10−5 and 3 × 10−3, and for our system we previously estimated that ϕc ≈ 0.8423.3 We focuss on excess packing fractions Δϕ := ϕ − ϕc from 10−4 to 0.16 but also show some results for runs below jamming. All runs have a duration of 20/
between 10−5 and 3 × 10−3, and for our system we previously estimated that ϕc ≈ 0.8423.3 We focuss on excess packing fractions Δϕ := ϕ − ϕc from 10−4 to 0.16 but also show some results for runs below jamming. All runs have a duration of 20/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) so that the total strain is 20, and σ and Δv are sampled each 0.67 percent of strain; transients are less then 1.5 units of strain and are excluded from the averaging.
so that the total strain is 20, and σ and Δv are sampled each 0.67 percent of strain; transients are less then 1.5 units of strain and are excluded from the averaging.
3 Power balance and phenomenology
The power supplied to the system by driving it must be dissipated by the relative motion of the particles. As the injected power is the product of strain rate and stress, and the dissipated power is set by the local particle motion, power balance sets up a powerful relation between the macroscopic rheology and microscopic fluctuations that we explore here.The time averaged power injected into the system is
Pin = V![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 〈σ〉t, 〈σ〉t, | (4) |
 | (5) |
 | ||
Fig. 1 (a) Scatter plot of Pin := V![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 〈σ〉 vs. Pout := Nc 〈Δv2〉. Straight lines indicate equality, red (light) symbols denote high density and blue (dark) symbols denote low density. The inset shows that in our simulations Pin and Pout never differ more than a few percent. (b) The simplified version of the power balance equation, used in ref. 3, ignores the variation of the contact number and the contribution of the viscous stress. When we fix the contact number at four, we find that this simplified version works well for scaling, and that R := (2N〈Δv2〉)/(V 〈σ〉 vs. Pout := Nc 〈Δv2〉. Straight lines indicate equality, red (light) symbols denote high density and blue (dark) symbols denote low density. The inset shows that in our simulations Pin and Pout never differ more than a few percent. (b) The simplified version of the power balance equation, used in ref. 3, ignores the variation of the contact number and the contribution of the viscous stress. When we fix the contact number at four, we find that this simplified version works well for scaling, and that R := (2N〈Δv2〉)/(V![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 〈σe〉) is within a factor two of unity. 〈σe〉) is within a factor two of unity. | ||
In our simulations, 〈Δv2〉xt varies over several orders of magnitude whereas the contact number z only varies between 3.5 and 6. Moreover, the elastic stresses σe remain much larger than the viscous stresses σv. Hence, the simplified scaling σe![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ 〈Δv2〉, which was used in earlier work to describe the scaling behavior of the rheology of this model near jamming,3 captures the dominant trend well as shown in Fig. 1b.
∼ 〈Δv2〉, which was used in earlier work to describe the scaling behavior of the rheology of this model near jamming,3 captures the dominant trend well as shown in Fig. 1b.
3.1 Trends with Δϕ and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/h3_i_char_e0a2.gif)
Power balance has important consequences for the nature of the velocity fluctuations. Defining the relative velocity  , the power balance equation can be written as
, the power balance equation can be written as | (6) |
Previous results for the stress as function of density and flow rate distinguish (at least) three qualitatively different regimes: the regime below jamming (Δϕ < 0), the critical regime near jamming (Δϕ ≈ 0) and the yield stress regime above jamming (Δϕ > 0).2,3 Using these results we can now understand the following trends in  : (i) below jamming, the rheology becomes Newtonian (σ ∼
: (i) below jamming, the rheology becomes Newtonian (σ ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) so that from eqn (6) it follows that the relative fluctuations
) so that from eqn (6) it follows that the relative fluctuations  are essentially independent of the flow rate. (ii) In the critical regime, the material is shear thinning: the stress scales as
are essentially independent of the flow rate. (ii) In the critical regime, the material is shear thinning: the stress scales as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) β, with different groups2,3,6 reporting different values of β between 0.2 and 0.5. For any β < 1, power balance implies that
β, with different groups2,3,6 reporting different values of β between 0.2 and 0.5. For any β < 1, power balance implies that  diverges as
diverges as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) β−1 when
β−1 when ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0. (iii) In the yield stress regime, the stress reaches a finite yield stress when
→ 0. (iii) In the yield stress regime, the stress reaches a finite yield stress when ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0, and
→ 0, and  diverges as
diverges as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1.
−1.
The divergence of the relative velocity fluctuations in the critical and yield stress regimes implies a breakdown of the quasistatic limit. For a meaningful quasistatic limit to exist, characteristics of the particle positions as function of strain should not depend on strain rate, and Δv and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) have to scale similarly, but as discussed above, power balance forbids this near and above jamming. Similar divergencies have been observed in experiments on flowing two dimensional foams,26 and we note that for other models (such as the “mean field” versions of the bubble model8), similar arguments also imply the breakdown of the quasi-static limit.2,25
have to scale similarly, but as discussed above, power balance forbids this near and above jamming. Similar divergencies have been observed in experiments on flowing two dimensional foams,26 and we note that for other models (such as the “mean field” versions of the bubble model8), similar arguments also imply the breakdown of the quasi-static limit.2,25
4 Non-Gaussianity and heterogeneity
Power balance does not dictate the detailed statistics of Δv, nor its spatial or temporal homogeneity. For amorphous, plastic flow, one expects the energy dissipation to be heterogeneous in space and time, with concomitant non-Gaussian behavior of Δv. Near jamming, plastic rearrangements have been shown to be related to quasi-localized modes30,31 which suggest a heterogeneous picture; on the other hand, many quantities such as the connectivity near jamming remain fairly homogeneous.3,32–34 Here we show that near jamming Δv is Gaussian and homogeneous in space and time, whereas for larger densities, progressively stronger deviations from Gaussian statistics and concurrent spatiotemporal heterogeneity is observed. As the velocity differences govern the energy dissipation, this qualitative difference in their statistics points to an important difference between the nature of energy dissipation: near jamming, this energy is homogeneously dissipated, whereas far above jamming the energy dissipation becomes increasingly localized. As we will discuss at the end of the paper, this suggests two distinct flow phenomenologies.In Fig. 2 we show the distribution of the normalized velocity differences,  , for a range of densities and strain rates. The variations in the shape of this distribution with Δϕ and
, for a range of densities and strain rates. The variations in the shape of this distribution with Δϕ and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) immediately show that the second moment of Δv is not sufficient to fully characterize the velocity fluctuations. In the critical regime, i.e., for low Δϕ and large
immediately show that the second moment of Δv is not sufficient to fully characterize the velocity fluctuations. In the critical regime, i.e., for low Δϕ and large ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , these distributions are narrower than an exponential distribution and approach Gaussians (Fig. 2). In contrast, in the yield stress regime, i.e., for large Δϕ and low
, these distributions are narrower than an exponential distribution and approach Gaussians (Fig. 2). In contrast, in the yield stress regime, i.e., for large Δϕ and low ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , the tails of P(|Δv|) become significantly fatter than exponentials—in the most extreme case (Δϕ = 10−1,
, the tails of P(|Δv|) become significantly fatter than exponentials—in the most extreme case (Δϕ = 10−1, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 10−5) the tail may tend to a power law, although our range of data is insufficient to establish this with certainty. Be that as it may, the distributions clearly indicate a change from homogeneous to heterogeneous velocity distributions when Δϕ is increased and
= 10−5) the tail may tend to a power law, although our range of data is insufficient to establish this with certainty. Be that as it may, the distributions clearly indicate a change from homogeneous to heterogeneous velocity distributions when Δϕ is increased and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is decreased.
is decreased.
To get insight into the temporal and spatial structure of the velocity differences we have studied two quantities. To elucidate the temporal heterogeneity of the energy dissipation, we calculate the ratio of instantaneous to mean energy dissipation:
| D := 〈Δv2〉x/〈Δv2〉xt, | (7) |
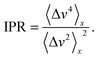 | (8) |
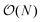 when Δv is concentrated on a single contact.
when Δv is concentrated on a single contact.
As illustrated in Fig. 3, in the critical regime, both the energy dissipation and IPR are fairly constant in time, with both D and the IPR being of order one indicating both spatial and temporal homogeneity. In contrast, in the yield stress regime, the energy dissipation rate varies over many orders of magnitude. In episodes when D ≪ 1, little energy is dissipated, which means that all the work done on the system is stored as elastic energy; when D ≫ 1, this stored energy is released. Concomittant with this increase in temporal heterogeneity, the IPR values become larger. Hence, in the yield stress regime, the energy dissipation occurs in bursts that are localized in both space and time.
 | ||
Fig. 3 The strain dependencies of the normalized energy dissipation Dp := 〈Δv2〉x/〈Δv2〉xt and of the inverse participation ratio IPR := 〈Δv4〉x/〈Δv2〉x2 exhibit systematic trends with Δϕ and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . . | ||
In Fig. 4 we illustrate the underlying spatiotemporal intermittent behavior by showing snapshots of the normalized velocity differences per particle
| Dp := 〈Δv2〉p/〈Δv2〉xt. | (9) |
 , the sum runs over all contacts of a single particle i with number of contacts zi, and 〈Dp〉x = D. In Fig. 4, left column, we show representative examples of the essentially homogenous case that we encounter for low density and large flow rates (
, the sum runs over all contacts of a single particle i with number of contacts zi, and 〈Dp〉x = D. In Fig. 4, left column, we show representative examples of the essentially homogenous case that we encounter for low density and large flow rates (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 10−3 and Δϕ = 10−3). For this particular snapshot we selected a local minimum and maximum of the IPR, but for these flow parameters the IPR does not vary much with time. Moreover, the spatial fluctuations are short ranged and lack any distinct features, and essentially appear like random noise. In contrast, in Fig. 4, right column, we show Dp for large density and slow flows (
= 10−3 and Δϕ = 10−3). For this particular snapshot we selected a local minimum and maximum of the IPR, but for these flow parameters the IPR does not vary much with time. Moreover, the spatial fluctuations are short ranged and lack any distinct features, and essentially appear like random noise. In contrast, in Fig. 4, right column, we show Dp for large density and slow flows (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 10−5 and Δϕ = 10−1). Here, the IPR varies significantly, and we show both snapshots where the IPR is in a local minimum and in a local maximum. For the low IPR snapshot, the amount of dissipation is very low, and the material is therefore in an elastic loading episode; for the large IPR snapshot, the dissipation is strongly localized around a core where Dp reaches almost 200, i.e. more that two orders of magnitude larger than the mean Dp which is of order one. Around this highly active “core”, we can observe a quadrupolar structure familiar for dense flows. This type of intermittency is familiar for slow, dense flows, but the striking observation is that signatures of such localized events essentially disappear near jamming. In the ESI,† we provide four movies, showing Dp and the evolution of D and the IPR, at Δϕ = 10−3 and 10−1 and
= 10−5 and Δϕ = 10−1). Here, the IPR varies significantly, and we show both snapshots where the IPR is in a local minimum and in a local maximum. For the low IPR snapshot, the amount of dissipation is very low, and the material is therefore in an elastic loading episode; for the large IPR snapshot, the dissipation is strongly localized around a core where Dp reaches almost 200, i.e. more that two orders of magnitude larger than the mean Dp which is of order one. Around this highly active “core”, we can observe a quadrupolar structure familiar for dense flows. This type of intermittency is familiar for slow, dense flows, but the striking observation is that signatures of such localized events essentially disappear near jamming. In the ESI,† we provide four movies, showing Dp and the evolution of D and the IPR, at Δϕ = 10−3 and 10−1 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 10−5 and 10−3, that illustrate the trends with density and strain rate in more detail.
= 10−5 and 10−3, that illustrate the trends with density and strain rate in more detail.
5 Scaling of higher order moments of Δv
Can we capture the qualitative changes in the statistics between the Gaussian, critical regime and the intermittent yield stress regime? Here we show how the aforementioned spatial and temporal heterogeneity manifests in the higher moments of Δv, which we show to exhibit nontrivial scaling relations that allow us to quantify the statistics of Δv in detail. These scaling relations between the higher moments are reminiscent of multiscaling in turbulence.35,36 Moreover, these scaling relations allow us to distinguish two distinct scaling regimes, which suggest objective criteria to separate the critical/jamming and yield stress/plastic phenomenology.We will focus on even moments of the velocity differences 〈Δv2n〉 as these are scalar,37 and restrict ourselves to n = 1, 2 and 3.38 The second moment of Δv is equal to the second moment of what we call the dissipation rate  , and the 4th and 6th and standardized moments of
, and the 4th and 6th and standardized moments of  can be written as 〈Γ4〉/〈Γ2〉2 and 〈Γ6〉/〈Γ2〉3, where all averages are over both space and time. To probe deviations from Gaussianity, we recall that when Γ2 is normal distributed, Γ4/〈Γ2〉2 equals 3 and Γ6/〈Γ2〉3 equals 15.
can be written as 〈Γ4〉/〈Γ2〉2 and 〈Γ6〉/〈Γ2〉3, where all averages are over both space and time. To probe deviations from Gaussianity, we recall that when Γ2 is normal distributed, Γ4/〈Γ2〉2 equals 3 and Γ6/〈Γ2〉3 equals 15.
As shown in Fig. 5a, where we plot the 4th standardized moment of Γ as function of 〈Γ2〉, we approach the Gaussian limit in the critical regime where 〈Γ2〉 is small. However, the 4th standardized moment of Γ reaches values exceeding 100 for large 〈Γ2〉, which corresponds to strongly non-Gaussian behavior as observed in Fig. 2. We note that the data does not collapse when plotted simply as function of 〈Γ2〉 (in particular data at a single, fixed strain rate, does not follow the overall trend). Inspired by the success of scaling approaches near jamming,2–4,32,39,40 we attempt to rescale all our data by introducing a standard scaling function of the form
〈Γ4〉 = 〈Γ2〉α4F4(Δϕβ4/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) ) | (10) |
As shown in Fig. 5b, we find good data collapse for α4 = 2.36 ± 0.05 and β4 = 1.3 ± 0.1. Crucially, the scaling function F4 reveals the existence of two distinct scaling regimes depending on the magnitude of Δϕβ4/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) —in both, F4 takes a particularly simple form, with F4(x) → cnst for x < 10 and
—in both, F4 takes a particularly simple form, with F4(x) → cnst for x < 10 and 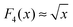 for x > 100.
for x > 100.
The situation for the 6th standardized moment is analogous to that of the 4th. As shown in Fig. 5c, we approach the Gaussian limit for small 〈Γ2〉, but strongly deviate from Gaussian behavior, reaching values of 〈Γ6〉/〈Γ2〉3 of order 105 for larger 〈Γ2〉. Using the scaling form
〈Γ6〉 = 〈Γ2〉α6F6(Δϕβ6/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) ) | (11) |
We note that β4 and β6 are not particularly sensitive to the precise choice of ϕc: when we adjust ϕc by up to ±10−3, i.e., far beyond our estimate of its error bar, our estimates for βi are not significantly affected; moreover, our estimates for αi are essentially independent of the choice of ϕc. We have run exploratory simulations in smaller systems (N = 64) to see whether the crossovers in F4 and F6 are due to finite size effects, but have found no indications for this.
Finally, to see if the scaling regimes expressed in eqn (10) and (11) extend below jamming, we have also analyzed data for Δϕ < 0. As shown in the insets of Fig. 5, the data for 4th and 6th moment of 〈Γ〉 for small |Δϕ| scale as 〈Γ4〉 = 〈Γ2〉α4 and 〈Γ6〉 = 〈Γ2〉α6 as long as Δϕ is not too negative. Some deviations for the 6th moments for relatively large ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) can be seen in the plateau region—whether these are physical, or due to numerical artefacts (the code was developed for Δϕ > 0) we cannot determine. Nevertheless we believe that the plateau region extends into the Δϕ < 0 regime—when crossing the Δϕ = 0 boundary at finite flow rate, nothing dramatic occurs in the nature of the fluctuations, consistent with the analysis of a robust powerlaw elastic correlation length across Δϕ = 0 shown recently.13
can be seen in the plateau region—whether these are physical, or due to numerical artefacts (the code was developed for Δϕ > 0) we cannot determine. Nevertheless we believe that the plateau region extends into the Δϕ < 0 regime—when crossing the Δϕ = 0 boundary at finite flow rate, nothing dramatic occurs in the nature of the fluctuations, consistent with the analysis of a robust powerlaw elastic correlation length across Δϕ = 0 shown recently.13
6 Conclusion and outlook
We have probed the statistics, spatial and temporal organization of the local energy dissipation in a model for sheared disordered materials, and observe strong variations with the control parameters Δϕ and![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . Broadly speaking, for low densities and/or fast flows, the fluctuations become nearly Gaussian, and spatial and temporal fluctuations are small. The rheology in this regime is that of a powerlaw fluid, and may be amenable to simple, mean-field modeling.2,3 In contrast, for large densities and/or slow flows, the fluctuation distributions become very wide, and strongly heterogeneous in space and time. This broad trend is intuitive: for large densities, the material can be deformed elastically over a substantial range, and the dynamics is a mix of elastic loading and plastic, dissipative events, whereas for low densities near jamming, the elastic range vanishes and the dynamics becomes more homogeneous.
. Broadly speaking, for low densities and/or fast flows, the fluctuations become nearly Gaussian, and spatial and temporal fluctuations are small. The rheology in this regime is that of a powerlaw fluid, and may be amenable to simple, mean-field modeling.2,3 In contrast, for large densities and/or slow flows, the fluctuation distributions become very wide, and strongly heterogeneous in space and time. This broad trend is intuitive: for large densities, the material can be deformed elastically over a substantial range, and the dynamics is a mix of elastic loading and plastic, dissipative events, whereas for low densities near jamming, the elastic range vanishes and the dynamics becomes more homogeneous.
Surprisingly, our results for the scaling of the fluctuations (eqn (10) and (11)) show that, in addition to these overall trends, we can clearly distinguish two qualitatively different regimes, which we now refer to as a critical and a plastic regime. As shown in Fig. 6, where we sketch a schematic state diagram, these regimes are connected via a smooth crossover, governed by the ratio Δϕβ/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (pink, dashed line). The distinction between these regimes and the form of this crossover follows from the crossovers observed for both 〈Γ4〉 and 〈Γ6〉. Even though our best estimates for the exponents β4 and β6 are slightly different, they are equal to within error bars, and we suggest that both scaling relations eqn (10) and (11) point to the same crossover, with β ≈ 1. We further suggest that the crossover between the plastic and critical regimes is related to rheological crossovers observed previously.2,3
(pink, dashed line). The distinction between these regimes and the form of this crossover follows from the crossovers observed for both 〈Γ4〉 and 〈Γ6〉. Even though our best estimates for the exponents β4 and β6 are slightly different, they are equal to within error bars, and we suggest that both scaling relations eqn (10) and (11) point to the same crossover, with β ≈ 1. We further suggest that the crossover between the plastic and critical regimes is related to rheological crossovers observed previously.2,3
We now briefly summarize the phenomenology in the critical and plastic regimes, and discuss the relation to quasistatic flows as well as to the quasistatic jamming point.
Critical regime
In the critical regime, eqn (10) and (11) reduce to a simple form, reminiscent of multiscaling of higher moments of the velocity differences observed in turbulence:| 〈Γ4〉 = 〈Γ2〉α4, | (12) |
| 〈Γ6〉 = 〈Γ2〉α6. | (13) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and small |Δϕ|, where Γ is small, this predicts that the fluctuations approach a Gaussian, consistent with what is shown in Fig. 2, and as shown in Fig. 3 and 4, the temporal and spatial fluctuations become small here. However, the fluctuations become increasingly non-Gaussian when one approaches the jamming point from the critical regime. As discussed above (see Fig. 1), the combination of powerlaw rheology and power balance dictates that the 2nd moment of the relative velocity fluctuation distributions 〈Γ2〉 diverges when
and small |Δϕ|, where Γ is small, this predicts that the fluctuations approach a Gaussian, consistent with what is shown in Fig. 2, and as shown in Fig. 3 and 4, the temporal and spatial fluctuations become small here. However, the fluctuations become increasingly non-Gaussian when one approaches the jamming point from the critical regime. As discussed above (see Fig. 1), the combination of powerlaw rheology and power balance dictates that the 2nd moment of the relative velocity fluctuation distributions 〈Γ2〉 diverges when ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0. In that case, eqn (12) and (13) imply that the fluctuations become strongly non-Gaussian, although the ratio 〈Γ4〉/〈Γ2〉α4 remains finite and fixed.
→ 0. In that case, eqn (12) and (13) imply that the fluctuations become strongly non-Gaussian, although the ratio 〈Γ4〉/〈Γ2〉α4 remains finite and fixed.
Plastic regime
In the plastic regime, the (simple) expressions of and F6(x) ∼ x (see eqn (10) and (11)), indicate a very rapid growth of the non-Gaussian behavior when
and F6(x) ∼ x (see eqn (10) and (11)), indicate a very rapid growth of the non-Gaussian behavior when ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0: the ratio between, e.g., 〈Γ〉 and 〈Γ2〉α4, diverges, in stark contrast to what happens in the critical regime. This divergence is consistent with the avalanche-like phenomenology observed in strongly jammed quasistatic or very slow flows, that have been studied extensively.11,16,43 Such flows proceed by a sequence of plastic events localized in space and time, which are referred to as shear transformation zones, T1 events or Eshelby events, with concomitant sharp drops in the stress just after such a plastic event.
→ 0: the ratio between, e.g., 〈Γ〉 and 〈Γ2〉α4, diverges, in stark contrast to what happens in the critical regime. This divergence is consistent with the avalanche-like phenomenology observed in strongly jammed quasistatic or very slow flows, that have been studied extensively.11,16,43 Such flows proceed by a sequence of plastic events localized in space and time, which are referred to as shear transformation zones, T1 events or Eshelby events, with concomitant sharp drops in the stress just after such a plastic event.
Outlook
We close by putting our results in a wider context. Earlier work on a probe particle pushed through a packing at densities below, near and above jamming, evidenced multiscaling of the particles fluctuations.41 At present it is an open question if and how these and our observations are related. Fluctuations of flowing matter have also received widespread interest in the context of dynamical heterogeneities42—how to relate those observations to ours is an important open question. Our results are obtained for a simple viscous model where the dissipative forces scale as Δv. In more realistic systems, dissipation can take a more complex form such as ∝Δvξ, where ξ ≈ 2/3 in foams,5 and ξ tends to zero in frictional systems. As long as ξ remains positive, the power balance suggest a divergence in the limit of vanishing strain rates, and it would be interesting to see what types of multi scaling this yields. Intriguingly, the frictional case is marginal as far as power balance is concerned, and it is an open question whether a similar divergence of the strength of the relative fluctuations arises then.Finally we briefly discuss the role of the static jamming point at Δϕ → 0, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0. Even though this point appears to organize much of the rheology and fluctuations of disordered media, we note here that the nature of the crossover between the critical and plastic regime in both the present and prior studies strongly indicate that the approach to the point depends on the order of limits. For example, quasistatic simulations performed at the jamming density35,43 require a very careful analysis. More generally, the relation between the purely quasistatic, linear response phenomenology near jamming,17 and the rheology near jamming needs clarification. For example, for flows near jamming, power-balance dictates that at fixed
→ 0. Even though this point appears to organize much of the rheology and fluctuations of disordered media, we note here that the nature of the crossover between the critical and plastic regime in both the present and prior studies strongly indicate that the approach to the point depends on the order of limits. For example, quasistatic simulations performed at the jamming density35,43 require a very careful analysis. More generally, the relation between the purely quasistatic, linear response phenomenology near jamming,17 and the rheology near jamming needs clarification. For example, for flows near jamming, power-balance dictates that at fixed ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) the fluctuations grow in magnitude when Δϕ is increased. In the case of elastic deformations near jamming, various measures of randomness and non-affinity diverge when decreasing the density towards the jamming density.17,18 These completely opposite trends highlight that the relation between elastic and viscous quantities is highly intricate near jamming.
the fluctuations grow in magnitude when Δϕ is increased. In the case of elastic deformations near jamming, various measures of randomness and non-affinity diverge when decreasing the density towards the jamming density.17,18 These completely opposite trends highlight that the relation between elastic and viscous quantities is highly intricate near jamming.
Acknowledgements
EW and VC acknowledge support from FOM and MvD, PS and MvH support from NWO via VICI grants. This work is part of the research programme of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organisation for Scientific Research (NWO).References
- P. Schall and M. van Hecke, Annu. Rev. Fluid Mech., 2010, 42, 67 CrossRef.
- P. Olsson and S. Teitel, Phys. Rev. Lett., 2007, 99, 178001 CrossRef PubMed; P. Olsson and S. Teitel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 030302 CrossRef; P. Olsson and S. Teitel, Phys. Rev. Lett., 2012, 109, 108001 CrossRef PubMed; D. Vagberg, P. Olsson and S. Teitel, Phys. Rev. Lett., 2014, 112, 208303 CrossRef; D. Vagberg, P. Olsson and S. Teitel, Phys. Rev. Lett., 2014, 113, 148002 CrossRef PubMed.
- B. P. Tighe, E. Woldhuis, J. C. Remmers, W. van Saarloos and M. van Hecke, Phys. Rev. Lett., 2010, 105, 088303 CrossRef PubMed.
- B. P. Tighe, Phys. Rev. Lett., 2011, 107, 158303 CrossRef PubMed; B. P. Tighe, Phys. Rev. Lett., 2012, 109, 168303 CrossRef PubMed.
- G. Katgert, M. E. Möbius and M. van Hecke, Phys. Rev. Lett., 2008, 101, 058301 CrossRef PubMed; G. Katgert, A. Latka, M. E. Möbius and M. van Hecke, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 066318 CrossRef.
- T. Hatano, M. Otsuki and S. I. Sasa, J. Phys. Soc. Jpn., 2007, 76, 023001 CrossRef; T. Hatano, J. Phys. Soc. Jpn., 2008, 77, 123002 CrossRef; T. Hatano, Prog. Theor. Phys. Suppl., 2010, 184, 143 CrossRef.
- G. Katgert, B. P. Tighe and M. van Hecke, Soft Matter, 2013, 9, 9739 RSC.
- D. J. Durian, Phys. Rev. Lett., 1995, 75, 4780 CrossRef CAS PubMed; D. J. Durian, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 1739 CrossRef.
- M. L. Falk and J. S. Langer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 7192 CrossRef CAS.
- M. Dennin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 041406 CrossRef CAS; M. Durand and H. A. Stone, Phys. Rev. Lett., 2006, 97, 226101 CrossRef PubMed; A. L. Biance, S. Cohen-Addad and R. Höhler, Soft Matter, 2009, 5, 4672 RSC; A. S. Argon, Acta Meter., 1979, 27, 47 CrossRef.
- P. Schall, D. A. Weitz and F. Spaepen, Science, 2007, 318, 1895 CrossRef CAS PubMed.
- J. D. Eshelby, Proc. R. Soc. A, 1959, 252, 561 CrossRef.
- V. Chikkadi, E. Woldhuis, M. van Hecke and P. Schall, 2015, arXiv:1507.04893.
- P. Sollich, F. Lequeux, P. Hebraud and M. E. Cates, Phys. Rev. Lett., 1997, 78, 2020 CrossRef CAS.
- L. Bocquet, A. Colin and A. Ajdari, Phys. Rev. Lett., 2009, 103, 036001 CrossRef PubMed.
- C. E. Maloney and A. Lemaitre, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 016118 CrossRef CAS; A. Lemaitre and C. Caroli, Phys. Rev. Lett., 2009, 103, 065501 CrossRef PubMed; E. Lerner and I. Procaccia, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 066109 CrossRef; H. G. E. Hentschel, S. Karmakar, E. Lerner and I. Procaccia, Phys. Rev. Lett., 2010, 104, 025501 CrossRef PubMed; V. Chikkadi, G. Wegdam, D. Bonn, B. Nienhuis and P. Schall, Phys. Rev. Lett., 2011, 107, 198303 CrossRef PubMed.
- C. S. O'Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011306 CrossRef CAS; M. Wyart, L. E. Silbert, S. R. Nagel and T. A. Witten, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 051306 CrossRef; M. Wyart, Ann. Phys., 2005, 30, 1 Search PubMed; M. Wyart, S. R. Nagel and T. A. Witten, Europhys. Lett., 2005, 72, 486 CrossRef; L. E. Silbert, A. J. Liu and S. R. Nagel, Phys. Rev. Lett., 2005, 95, 098301 CrossRef PubMed; M. van Hecke, J. Phys.: Condens. Matter, 2010, 22, 033101 CrossRef PubMed.
- W. G. Ellenbroek, E. Somfai, M. van Hecke and W. van Saarloos, Phys. Rev. Lett., 2006, 97, 258001 CrossRef PubMed; W. G. Ellenbroek, Z. Zeravcic, W. van Saarloos and M. van Hecke, EPL, 2009, 87, 34004 CrossRef; W. G. Ellenbroek, M. van Hecke and W. van Saarloos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061307 CrossRef.
- N. Xu, V. Vitelli, A. J. Liu and S. R. Nagel, EPL, 2010, 90, 56001 CrossRef.
- M. L. Manning and A. J. Liu, Phys. Rev. Lett., 2011, 107, 108302 CrossRef CAS PubMed.
- C. F. Schreck, T. Bertrand, C. S. O'Hern and M. D. O'Hern, Phys. Rev. Lett., 2011, 107, 078301 CrossRef PubMed.
- L. R. Gomez, A. M. Turner, M. van Hecke and V. Vitelli, Phys. Rev. Lett., 2012, 108, 058001 CrossRef PubMed.
- S. van den Wildenberg, R. van Loo and M. van Hecke, Phys. Rev. Lett., 2013, 111, 218003 CrossRef PubMed.
- M. S. van Deen, J. Simon, Z. Zeravcic, S. Dagois-Bohy, B. P. Tighe and M. van Hecke, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, R020202 CrossRef.
- I. K. Ono, S. Tewari, S. A. Langer and A. J. Liu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 061503 CrossRef.
- M. E. Möbius, G. Katgert and M. van Hecke, EPL, 2010, 90, 44003 CrossRef.
- The method of dissipation described above is not the simplest imaginable. A simpler method was introduced as an approximation by Durian in his original model8 and has since been used often2. This simpler method of dissipation is called ‘Mean Field dissipation’ and has dissipation take place not when contacting bubbles move relative to each other, as in eqn (1), but when bubbles move relative to the overall flow field:
where v(xi, yi) is the value of the overall flow field at the position of particle i. While this approximation was introduced mainly for its computational benefits, it has a clear physical interpretation: viscous drag with the background fluid. Still, in actual foam systems dissipation takes place mostly between bubbles and not between bubbles and the fluid.7.Fvi = −b(vi − v(xi, yi)), (14) - P. Olsson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 040301 CrossRef; P. Olsson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 031303 CrossRef.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon, Oxford, 1988 Search PubMed.
- N. Xu, V. Vitelli, A. J. Liu and S. R. Nagel, EPL, 2010, 90, 56001 CrossRef.
- M. L. Manning and A. J. Liu, Phys. Rev. Lett., 2011, 107, 108302 CrossRef CAS PubMed.
- M. Wyart, H. Liang, A. Kabla and L. Mahadevan, Phys. Rev. Lett., 2008, 101, 215501 CrossRef CAS PubMed.
- S. Henkes, K. Shundyak, W. van Saarloos and M. van Hecke, Soft Matter, 2010, 6, 2935 RSC.
- W. G. Ellenbroek, V. F. Hagh, A. Kumar, M. F. Thorpe and M. van Hecke, Phys. Rev. Lett., 2015, 114, 135501 CrossRef PubMed.
- F. Radjai and S. Roux, Phys. Rev. Lett., 2002, 89, 064302 CrossRef PubMed.
- K. R. Sreenivasan, Annu. Rev. Fluid Mech., 1991, 23, 539 CrossRef.
- We have checked that the first moment behaves as expected: the first moment of Δv|| := Δv·
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) equals zero, consistent with the particles not coming apart or together on average. Moreover, the first moment of Δv⊥, the component of Δv perpendicular to
equals zero, consistent with the particles not coming apart or together on average. Moreover, the first moment of Δv⊥, the component of Δv perpendicular to ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) , equals
, equals ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , thus respecting the globally applied strain rate. Higher order odd moments of Δv become increasingly complicated due to their non-scalar character.
, thus respecting the globally applied strain rate. Higher order odd moments of Δv become increasingly complicated due to their non-scalar character. - The 8th and higher moments of Δv are difficult to extract reliably from our datasets.
- S. Dagois-Bohy, B. P. Tighe, J. Simon, S. Henkes and M. van Hecke, Phys. Rev. Lett., 2012, 109, 095703 CrossRef PubMed.
- C. P. Goodrich, S. Dagois-Bohy, B. P. Tighe, M. van Hecke, A. J. Liu and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022138 CrossRef.
- J. A. Drocco, M. B. Hastings, C. J. Olson Reichhardt and C. Reichhardt, Phys. Rev. Lett., 2005, 95, 088001 CrossRef CAS PubMed; C. J. Olson Reichhardt and C. Reichhardt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 051306 CrossRef.
- F. Lechenault, O. Dauchot, G. Biroli and J. P. Bouchaud, EPL, 2008, 83, 46002 CrossRef; F. Lechenault, O. Dauchot, G. Biroli and J. P. Bouchaud, EPL, 2008, 83, 46003 CrossRef; C. Heussinger, L. Berthier and J. L. Barrat, EPL, 2010, 90, 20005 CrossRef.
- C. Heussinger and J. L. Barrat, Phys. Rev. Lett., 2009, 102, 218303 CrossRef PubMed.
Footnote |
† Electronic supplementary information (ESI) available: We provide four movies, showing time traces of the mean energy dissipation D and the IPR, as well as the time evolution of the the dissipation per particle Dp, as in Fig. 4. This data is taken for Δϕ = 10−3 and 10−1 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 10−5 and 10−3. These movies illustrate the trends with density and strain rate in detail. Each frame corresponds to a strain step, which means the = 10−5 and 10−3. These movies illustrate the trends with density and strain rate in detail. Each frame corresponds to a strain step, which means the ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 10−5 video is 100× sped up compared that with = 10−5 video is 100× sped up compared that with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 10−3. See DOI: 10.1039/c5sm01592h = 10−3. See DOI: 10.1039/c5sm01592h |
| This journal is © The Royal Society of Chemistry 2015 |




