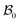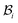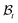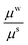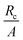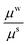DOI:
10.1039/C5SM01135C
(Paper)
Soft Matter, 2015,
11, 6499-6508
Interfacial growth during closure of a cutaneous wound: stress generation and wrinkle formation
Received
11th May 2015
, Accepted 6th July 2015
First published on 6th July 2015
Abstract
A biomechanical growth model for the proliferation stage of cutaneous wound healing is developed emphasizing the emergence of stress and wrinkled skin during the healing process. The healing is assumed to be primarily driven by growth at the wound edge (i.e. the interface between the wound and the skin) leading to incompatible growth strains. A closed form solution of the boundary value problem is obtained using a Varga hyperelastic membrane model for both the skin and the wound. The nature of the solution is explored for various parametric values of the skin tension, healing rate, edge incompatibility, wrinkled region radius, and wound stiffness. The obtained results for the stress field, wrinkling, and rate of healing are qualitatively in good agreement with the existing experimental observations.
1 Introduction
Cutaneous wound healing is vital for restoring the integrity of damaged skin tissues.31 The healing process is influenced by both growth factors (cytokines)36 and mechanical stimuli (stresses/strains)2,10,46 while undergoing four major stages: hemostasis, inflammation, proliferation, and remodeling.33 During hemostasis, blood coagulates to form a fibrin clot which controls the loss of blood and body fluids, avoids exposure of the wound to the outer environment, and also acts as a provisional matrix for various cell migration processes. In the inflammatory stage, various white blood cells permeate into the wound to assist its cleansing from debris and unwanted bacteria. The macrophages formed in this stage help in the secretion of various growth factors required for wound repair. During the proliferation stage, the wound begins to resurface by means of reepithelialization (restoration of epidermis), collagen deposition (restoration of dermis), and restoration of vascular networks (angiogenesis). Additionally, the fibroblasts, which are otherwise responsible for the synthesis of collagen, elastin, and extracellular matrix (ECM), transform into myofibroblasts under mechanical influence so as to facilitate wound contraction. The final stage of healing is remodelling, which brings about structural changes (cellular and tissue level rearrangements) in the scar tissue after a complete closure of the wound; this is essential to improve the mechanical properties of the scar.21
“Fundamental to our understanding of wound-healing biology is knowledge of the signals that trigger relatively sedentary cell linages at the wound margin to proliferate, to become invasive, and then to lay down new matrices in the wound gap”.28 The central role played by the wound edge during wound healing is taken as the basis of the model proposed in the present work. Our consideration is motivated by several experimental observations as summarised below. The wound edge is a site for active secretion of growth factors.28 Both epithelial and non-epithelial cells therein have been observed to produce a large number of cytokines so as to assist in the formation of actin filaments which allows cell migration over the provisional matrix.36 The proliferation of epithelial cells is encouraged by the absence of healthy cells adjacent to the wound edge.36 Furthermore, it is observed that a narrow ring of fibroblasts is accumulated under the wound margin, which is responsible for closure of the wounds.18 The migrating fibroblasts at the margin exert sufficient force for wound contraction, thereby transforming fibroblasts into myofibroblasts and consequently increasing the resistance to migration.16 The experiments have also noted an increase in mitotic activity during epidermal migration in the 1 mm thick band near the newly formed epidermis with a maximal increase at the wound edge, where it is fifteen times higher than the normal epidermis.31
Several continuum mechanics based models of wound healing incorporating skin elasticity have been proposed in the literature; for a comprehensive review see chapters 9 and 10 in ref. 31. Most of these follow Tranquillo and Murray42 in formulating the healing problem within a mechanochemical framework consisting of reaction-diffusion equations for fibroblasts, myofibroblasts, and growth factors, mass balance equations for ECM density evolution, and force balance equations for ECM displacements. While these models have made significant progress in understanding the nature of chemical kinetics associated with the wound healing process, they assume elastic strains to be infinitesimal and ignore the role of wound edge in the growth process. Moreover, they are single compartment models, wherein only the wound domain has been considered while ignoring the effect of the healthy skin adjacent to the wound (an exception is the two-compartment model of Murphy et al.30). The assumption on elastic strains is inappropriate due to the nature of skin elasticity; it results in unphysical stress magnitudes as well as prevents the possibility of instabilities such as wrinkling in the skin. More recently, Wu and Amar45 have proposed a mechanistic model of growth which incorporates the nonlinear elasticity of skin and the proliferating wound. Restricting both growth and proliferation to an annular region of the wound in the neighborhood of healthy skin, but allowing for anisotropic growth, they have used this model to primarily investigate interfacial instability leading to the loss of circularity of wound edge under various material and geometric parameters.
Our model is fundamentally based on the theory of biomechanical growth where growth is regarded as the irreversible addition of mass which may or may not result in a change in form.8,9,14,25 The mechanistic effect of growth is represented by a growth distortion tensor, whose incompatibility is related to the emergence of residual stress fields34,37 (the notion of incompatibility is explained in Section 2.1). This naturally leads to a kinematics involving multiplicative decomposition of deformation gradients,34 analogous to formulations of elastoplasticity and thermoelasticity.27 However, unlike the models of bulk growth, we propose a framework where mass addition, as well as incompatibility in growth distortion, is restricted to sharp interfaces within the solid.19 A similar interfacial growth model, but one which neglects incompatibility at the interface, has been proposed by Ciarletta and co-authors.6 On the other hand, the incompatibility of growth distortion has been incorporated in some recent models of bulk growth, see e.g.ref. 29 and 45, mainly towards explaining emergence of interfacial instabilities. We introduce our growth model by developing a novel formulation of the wound healing phenomenon where wound and skin, both considered to be two-dimensional hyperelastic membranes (with wound having lower stiffness), are treated as different domains separated by a sharp interface. Our framework is suitable for deep partial thickness injuries,35 which normally heal with fibroplasia and contraction ending up with scar formation. We restrict our attention to the proliferation stage alone, ignoring retraction of the wound immediately after the injury as well as remodelling. We also ignore skin anisotropy and any interaction with substrates; these can be included in a straightforward manner in our model. An important aspect of our work is to predict wrinkling of skin in the vicinity of the wound margin and relate it to the nature of interfacial growth. The formation of wrinkles during wound healing has been observed experimentally,5,26 but it has not been accounted for in any of the available models of wound healing. Wrinkle formation in unwounded skin has however been studied extensively, see e.g.ref. 5, 7 and 11. In this paper, we have used the tension field theory, following Pipkin and Steigmann,32,39,40 to model wrinkles in nonlinear elastic skin membranes.
The interfacial growth model for cutaneous wound healing is formulated in Section 2. In doing so we depart from the established growth models by considering mass addition and deformation incompatibility at a non-material interface in the body. The model is kept simple enough to derive analytical solutions, which we discuss in detail in Section 2.5; a comparison with relevant experimental data is also given therein. Finally, in Section 4 we conclude our study.
2 A model for cutaneous wound closure
The wound healing problem that we are concerned with involves growth of the healthy skin and annihilation of the wound driven by a mass source at the wound edge. For analytical convenience, we consider the wound to be a thin circular disc surrounded by skin (in the form of an annular circular disc) such that the thickness h (possibly nonuniform) of the arrangement is much smaller than the wound radius. Both wound and skin are assumed to behave as Varga hyperelastic membranes with nonlinear responses (see Section 2.3 for details). The wound-skin configuration at a certain time instant t is shown as  in Fig. 1, where a denotes the wound radius and b the outer radius of the skin. We also consider an axisymmetric traction distribution over the skin edge and assume the skin region surrounding the wound to be large enough such that the traction forces at the boundary are obtainable from the internal stress values in the unwounded skin. We assume body forces and inertia to be negligible. The deformation is assumed to be axisymmetric so that the wound-skin arrangement remains in the form of a circular disc as skin grows radially towards the wound center. In this section, we provide details of our model and use it to obtain closed form solutions for the stress field and wrinkling instability in the skin region during healing.
in Fig. 1, where a denotes the wound radius and b the outer radius of the skin. We also consider an axisymmetric traction distribution over the skin edge and assume the skin region surrounding the wound to be large enough such that the traction forces at the boundary are obtainable from the internal stress values in the unwounded skin. We assume body forces and inertia to be negligible. The deformation is assumed to be axisymmetric so that the wound-skin arrangement remains in the form of a circular disc as skin grows radially towards the wound center. In this section, we provide details of our model and use it to obtain closed form solutions for the stress field and wrinkling instability in the skin region during healing.
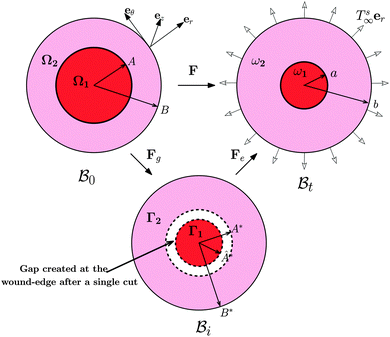 |
| | Fig. 1 Kinematics of growth during wound closure. Here, 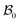 is the reference configuration with Ω1 (wound) and Ω2 (skin), is the reference configuration with Ω1 (wound) and Ω2 (skin), 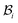 is the intermediate grown configuration with Γ1 (wound) and Γ2 (skin), and is the intermediate grown configuration with Γ1 (wound) and Γ2 (skin), and 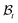 is the current configuration with ω1 (wound) and ω2 (skin). is the current configuration with ω1 (wound) and ω2 (skin). | |
2.1 Kinematics
The deformation of the wound and the skin is measured with respect to a fixed reference configuration 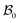 , taken to be the initial state of the wounded domain, see Fig. 1. In this configuration, the wound and the skin regions are of radius A and B, respectively. For a contracting wound we require a < A. The thickness H of the disc in
, taken to be the initial state of the wounded domain, see Fig. 1. In this configuration, the wound and the skin regions are of radius A and B, respectively. For a contracting wound we require a < A. The thickness H of the disc in 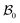 is assumed to be uniform such that H ≪ A. The thickness h of the deformed disc in
is assumed to be uniform such that H ≪ A. The thickness h of the deformed disc in 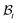 is taken to be a function of only the radial distance. The wound-skin arrangement has residual stresses, whose nature can be determined by unloading the body to a zero stress state. Presently, we assume that in order to unload the body
is taken to be a function of only the radial distance. The wound-skin arrangement has residual stresses, whose nature can be determined by unloading the body to a zero stress state. Presently, we assume that in order to unload the body 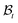 we will have to cut it along the wound edge, in addition to removing the traction force at the skin edge. Such a consideration is to emphasize the role of the wound edge in driving the closure of the wound. As we shall see, growth at the wound edge leads to a residually stressed state in the body which provides the driving force for wound healing. We call the stress-free configuration as the intermediate relaxed configuration and denote it as
we will have to cut it along the wound edge, in addition to removing the traction force at the skin edge. Such a consideration is to emphasize the role of the wound edge in driving the closure of the wound. As we shall see, growth at the wound edge leads to a residually stressed state in the body which provides the driving force for wound healing. We call the stress-free configuration as the intermediate relaxed configuration and denote it as 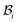 , see Fig. 1. As expected the wound edge and the internal edge of the skin are no longer coincident in
, see Fig. 1. As expected the wound edge and the internal edge of the skin are no longer coincident in 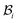 , but are separated by an axisymmetric gap (the axisymmetry of the gap is an additional assumption on the nature of the growth, see the following paragraph). The wound in
, but are separated by an axisymmetric gap (the axisymmetry of the gap is an additional assumption on the nature of the growth, see the following paragraph). The wound in 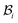 has a radius Â*. The annular skin region in
has a radius Â*. The annular skin region in 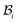 is of inner and outer radius A* and B*, respectively.
is of inner and outer radius A* and B*, respectively.
The current and the reference configuration are related by a continuous bijective map which transforms position vector 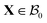 , given in terms of polar coordinates as X = Rer(Θ) + Zez (with 0 ≤ R ≤ B, 0 ≤ Θ ≤ 2π, and −H/2 ≤ Z ≤ H/2), to
, given in terms of polar coordinates as X = Rer(Θ) + Zez (with 0 ≤ R ≤ B, 0 ≤ Θ ≤ 2π, and −H/2 ≤ Z ≤ H/2), to 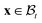 where x = rer(θ) + zez (with 0 ≤ r ≤ b, 0 ≤ θ ≤ 2π, and −h/2 ≤ z ≤ h/2) such that r = r(R), θ = Θ, and z = (h(R)/H)Z (we do not restrict h to be continuous at R = A). Here er, eθ and ez are unit basis vectors along radial, circumferential, and axial directions, respectively of the polar coordinate system. The deformation gradient F := ∂Xx is then given by
where x = rer(θ) + zez (with 0 ≤ r ≤ b, 0 ≤ θ ≤ 2π, and −h/2 ≤ z ≤ h/2) such that r = r(R), θ = Θ, and z = (h(R)/H)Z (we do not restrict h to be continuous at R = A). Here er, eθ and ez are unit basis vectors along radial, circumferential, and axial directions, respectively of the polar coordinate system. The deformation gradient F := ∂Xx is then given by
| | 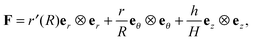 | (2.1) |
where ∂
X denotes the partial derivative with respect to
X and the superscript prime is used to denote the derivative with respect to
R. The tensor product
a ⊗
b between two vectors
a and
b is defined such that for any third vector
c, (
a ⊗
b)
c = (
b·
c)
a, where
b·
c denotes the Euclidean dot product between vectors
b and
c. On the other hand, position vector
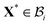
is related to
X by a piecewise continuous map such that
X* =
R*
er(
Θ*) +
Z*
ez, where
R* =
R*(
R),
Θ* =
Θ, and
Z* =
Z. This characterises the nature of growth kinematics in our model. We will assume a piecewise linear form for
R* given by
k1R if 0 ≤
R ≤
A and
k2R if
A ≤
R ≤
B, where
k1 and
k2 are constants (we will discuss more about them in the following). The growth distortion tensor
Fg := ∂
XX* therefore is of the form
| | | Fg = ka(er ⊗ er + eθ ⊗ eθ) + ez ⊗ ez, | (2.2) |
where
ka should be replaced by
k1 and
k2 for 0 ≤
R ≤
A and
A ≤
R ≤
B, respectively; it is clear that growth distortion is isotropic in the plane. The elastic distortion tensor
Fe := ∂
X*x satisfies the multiplicative decomposition
F =
FeFg,
34 and hence is given by
| | 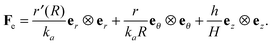 | (2.3) |
We assume elastic deformation to be incompressible,
i.e. det
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe
Fe = 1; hence det
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F
F = det
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fg
Fg, which yields
| | 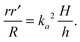 | (2.4) |
This equation cannot be solved until we determine
h(
R) using equilibrium equations, as discussed below.
The distortions F, Fe, and Fg are compatible away from the wound edge since they can all be written as a gradient of a certain (position) vector field. On the other hand, we call the distortion, say F, to be compatible on the wound edge if (F+ − F−)eθ = 0, where F+ is the limiting value of F at the wound edge as it is approached from the skin side, and F− as it is approached from the wound side (this notation has also been used in subsequent sections). For a general discussion on compatibility, both in the bulk and at a singular interface, see ref. 19 and 20. It is clear from (2.1) that F indeed satisfies this condition and is hence compatible at the wound edge. However, (Fg+ − Fg−)eθ = (k2 − k1)eθ and consequently the growth distortion is incompatible unless k1 = k2. This incompatibility manifests itself geometrically as a gap in the form of a annular region (between wound and skin) in  ; in fact we require k2 > k1, otherwise the two domains will penetrate into each other in
; in fact we require k2 > k1, otherwise the two domains will penetrate into each other in  . The elastic deformation overcomes this radial incompatibility so as to make the total deformation compatible. As a result internal forces are generated at the wound edge. The biological origin of such forces is due to the presence of fibroblasts, myofibroblasts, and keratinocytes in the vicinity of the wound edge and their interaction with the surrounding cells in the skin.26 These internal forces supplement external forces (due to skin tension and body movement) in driving the wound to its closure.2 The preceding arguments provide physical basis for the introduction of incompatibility at the wound edge, here represented by non-vanishing of (k1 − k2). The parameters ka can of course be constitutively related to the biochemical processes governing the healing process; we discuss this briefly in the following subsection, but otherwise ignore the details in the present work. We note that unlike most of the existing theories of volumetric growth, where both growth and elastic distortions are incompatible in the domain, the incompatibility is restricted here to the interface at the wound edge, cf.ref. 29 and 45.
. The elastic deformation overcomes this radial incompatibility so as to make the total deformation compatible. As a result internal forces are generated at the wound edge. The biological origin of such forces is due to the presence of fibroblasts, myofibroblasts, and keratinocytes in the vicinity of the wound edge and their interaction with the surrounding cells in the skin.26 These internal forces supplement external forces (due to skin tension and body movement) in driving the wound to its closure.2 The preceding arguments provide physical basis for the introduction of incompatibility at the wound edge, here represented by non-vanishing of (k1 − k2). The parameters ka can of course be constitutively related to the biochemical processes governing the healing process; we discuss this briefly in the following subsection, but otherwise ignore the details in the present work. We note that unlike most of the existing theories of volumetric growth, where both growth and elastic distortions are incompatible in the domain, the incompatibility is restricted here to the interface at the wound edge, cf.ref. 29 and 45.
2.2 Mass balance
Consider an arbitrary part ω (with thickness h) of  such that it intersects the wound edge on a surface s. Allowing for a mass source (represented by a density π per unit area) at the interface, the statement of balance of mass for ω is given by
such that it intersects the wound edge on a surface s. Allowing for a mass source (represented by a density π per unit area) at the interface, the statement of balance of mass for ω is given by| | 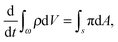 | (2.5) |
where ρ is the mass density per unit volume of the current configuration and dV and dA represent the infinitesimal volume and the area in 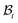 . In writing the above relation we have ignored the presence of any excess mass density at the interface as well as neglected any sources/sinks of mass in the bulk domain away from the interface. The mass source π can be attributed to the proliferation of various cells and growth factors at the wound edge. The global mass balance equation is equivalent to the following local relations:
. In writing the above relation we have ignored the presence of any excess mass density at the interface as well as neglected any sources/sinks of mass in the bulk domain away from the interface. The mass source π can be attributed to the proliferation of various cells and growth factors at the wound edge. The global mass balance equation is equivalent to the following local relations:| | 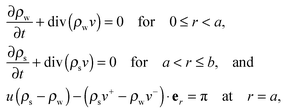 | (2.6) |
where ρw and ρs are mass densities of the wound and the surrounding skin in the current configuration, u is the normal velocity of the wound edge in 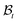 , and v is the particle velocity; div stands for the divergence operator. According to the last of these equations, a mass source can be present at the interface only when there is a non-trivial difference in the reference densities of the neighboring domains and the interface is not stationary in the reference configuration; the latter requires the wound edge to be a non-material interface. The mass balance at the wound edge can be used to derive a relationship between ka, u, ρ0 and π. Towards this end, let ρ0w and ρ0s be mass densities of the wound and surrounding skin with respect to
, and v is the particle velocity; div stands for the divergence operator. According to the last of these equations, a mass source can be present at the interface only when there is a non-trivial difference in the reference densities of the neighboring domains and the interface is not stationary in the reference configuration; the latter requires the wound edge to be a non-material interface. The mass balance at the wound edge can be used to derive a relationship between ka, u, ρ0 and π. Towards this end, let ρ0w and ρ0s be mass densities of the wound and surrounding skin with respect to 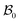 . We have ρ = ρ0
. We have ρ = ρ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) det
det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fg owing to incompressible elastic deformation. We assume a quasi-static evolution, where particle velocities have much small magnitudes than the wound edge velocity, so as to reduce (2.6)3 to
Fg owing to incompressible elastic deformation. We assume a quasi-static evolution, where particle velocities have much small magnitudes than the wound edge velocity, so as to reduce (2.6)3 to| | | u(k22ρ0s − k12ρ0w) = π. | (2.7) |
This equation relates growth distortions to the mass addition and the evolution of the wound edge. It is clear that mass addition is possible even at a compatible interface but with discontinuous density.
2.3 Equilibrium relations and constitutive assumptions
For quasi-static deformations with no body force, and recalling the symmetry in the problem, we have only one non-trivial equilibrium condition for stress, i.e.24| | 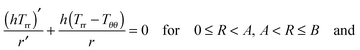 | (2.8) |
| | | (h+Trr+ − h−Trr−) = 0 at R = A, | (2.9) |
where Trr(R), etc. are components of the Cauchy stress with respect to the cylindrical coordinate system.
Skin is an anisotropic viscoelastic material exhibiting non-linear stress–strain response.13 However, the viscoelasticity of skin can be neglected for the time scales involved in wound healing.22 Moreover, since the dermis is much softer than the epidermis, skin easily slides over the substrate, allowing us to model it as an elastic membrane.5 For analytical simplicity we assume the membrane to behave like an incompressible Varga hyperelastic material whose strain energy density is given as
| | | W(λ1, λ2, λ3) = 2μ(λ1 + λ2 + λ3 − 3), | (2.10) |
where
μ is a material constant and
λi are principle stretches associated with elastic distortion. Elastic incompressibility requires
λ3 = 1/(
λ1λ2), hence we introduce
| | 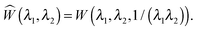 | (2.11) |
For the wound a similar model can be assumed with a different material parameter. We assume wound to be less stiffer than skin since it has inferior properties. The granulating surface of the wound acts as a single contractile body, hence wound can be considered as a solid domain.
3 We note that ignoring the viscoelasticity of the wound is a strong assumption and it would be important to extend the present formulation to include this physical property and study its effect on stress generation and wrinkling.
The non-trivial components of the Cauchy stress for hyperelastic response are given by24
| | 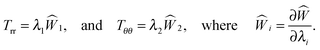 | (2.12) |
For the Varga material
| | 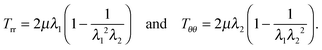 | (2.13) |
Substituting these in equilibrium
eqn (2.8), while recalling from
(2.3) that
λ1 =
r′/
ka,
λ2 =
r/(
Rka), and
λ3 =
h/
H, we get
| | | r′′rR + (r′)2R − r′r = 0 for 0 ≤ R < A and A < R ≤ B. | (2.14) |
2.4 Unwrinkled solution
Eqn (2.14) can be solved separately in the skin and the wound region to get| | 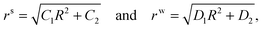 | (2.15) |
respectively. Here, and in what follows below, we use superscripts ‘s’ and ‘w’ to differentiate between skin side and wound side variables. Substituting these in (2.4) we can immediately see that h(R) is a piecewise constant, i.e. hw = k12H/D1 and hs = k22H/C1.
The solution will be completed using the following boundary and interfacial conditions: (i) Tsrr(B) = Ts∞(>0), where Ts∞ is the magnitude of the far field stress in the skin (obtained from unwounded skin), (ii) rw(0) = 0 (therefore cavitation is not allowed), (iii) rs(A) = rw(A), and (iv) stress equilibrium at the wound edge given by (2.9). The first condition will be considered assuming B → ∞. In this limit 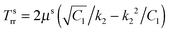 which is to be equated to Ts∞ to solve for C1/k22. It should be noted that, for Ts∞ > 0, the cubic equation has only one real root as can be checked by calculating the discriminant; moreover, we should necessarily have C1 > k22. The second condition implies D2 = 0, reducing (2.15)2 to
which is to be equated to Ts∞ to solve for C1/k22. It should be noted that, for Ts∞ > 0, the cubic equation has only one real root as can be checked by calculating the discriminant; moreover, we should necessarily have C1 > k22. The second condition implies D2 = 0, reducing (2.15)2 to 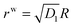 . With this we readily obtain
. With this we readily obtain 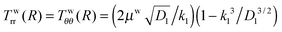 ; the wound region therefore is in a constant hydrostatic stress state. The stresses are tensile if and only if D1 > k12. It is useful to interpret D1 in terms of the current position of the wound edge (given by a) which is usually available from the experimental data (see for instance4). The velocity of healing or the rate of contraction is known to decrease with time.4 This motivates us to take a = Aζd−1, where ζ is the healing constant (ζ < 1 for healing) and d is the number of days (d > 1 assuming that there will be no proliferation of wound during the first day). We get
; the wound region therefore is in a constant hydrostatic stress state. The stresses are tensile if and only if D1 > k12. It is useful to interpret D1 in terms of the current position of the wound edge (given by a) which is usually available from the experimental data (see for instance4). The velocity of healing or the rate of contraction is known to decrease with time.4 This motivates us to take a = Aζd−1, where ζ is the healing constant (ζ < 1 for healing) and d is the number of days (d > 1 assuming that there will be no proliferation of wound during the first day). We get 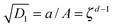 . The continuity of the deformation at the wound edge (third condition) is used to determine C2 in terms of C1 and D1 as C2 = (D1 − C1)A2. If we fix the value of parameters μs, μw, ζ, d, and k2, then the fourth condition simplifies to a fourth order equation which can be solved for k1; the selected value of k1 should satisfy k1 < k2 and D1 > k12. Knowing reference densities, this will also determine the rate of mass addition π in (2.7), where u can be inferred from D1. On the other hand, if we fix π, then we have to keep both k1 and k2 as unknown variables, to be solved using the fourth boundary condition and (2.7) while being restricted by various inequalities as discussed above.
. The continuity of the deformation at the wound edge (third condition) is used to determine C2 in terms of C1 and D1 as C2 = (D1 − C1)A2. If we fix the value of parameters μs, μw, ζ, d, and k2, then the fourth condition simplifies to a fourth order equation which can be solved for k1; the selected value of k1 should satisfy k1 < k2 and D1 > k12. Knowing reference densities, this will also determine the rate of mass addition π in (2.7), where u can be inferred from D1. On the other hand, if we fix π, then we have to keep both k1 and k2 as unknown variables, to be solved using the fourth boundary condition and (2.7) while being restricted by various inequalities as discussed above.
2.5 Wrinkled solution using tension field theory
It is well known that elastic membranes remain stable only for non-negative stress fields.38 The emergence of compressive stresses can be accommodated by buckling of the membrane in the form of infinitesimal wrinkles. As the wound heals the wrinkles are expected to appear only in the circumferential direction.5,12 The radial stresses accordingly should remain positive throughout. In the wound region, the radial and the hoop stresses are both equal and hence no wrinkling is predicted. The positivity of stresses in the wound is guaranteed as long as D1 > k12; this inequality is used as a restriction on the admissible values for k1 assuming that D1 is known from experimental data of wound contraction (see the discussion above). In the skin region we have 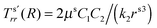 and
and 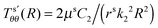 . We have already seen that, for far field radial stress in the skin to be positive, C1 > k22. Observations of wrinkling during healing reveal that it is restricted to a finite region in the skin adjacent to the wound edge. Therefore, the hoop stress should increase as we go from the wound edge towards healthier skin. This requires C2 < 0 which is equivalent to D1 < C1. The wrinkled region has Tsθθ < 0. To find the size of this region (denoted by radius Rc) we can use Tsθθ = 0 which in the present case yields a nonlinear equation
. We have already seen that, for far field radial stress in the skin to be positive, C1 > k22. Observations of wrinkling during healing reveal that it is restricted to a finite region in the skin adjacent to the wound edge. Therefore, the hoop stress should increase as we go from the wound edge towards healthier skin. This requires C2 < 0 which is equivalent to D1 < C1. The wrinkled region has Tsθθ < 0. To find the size of this region (denoted by radius Rc) we can use Tsθθ = 0 which in the present case yields a nonlinear equation| | 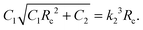 | (2.16) |
The limiting condition which ensures no wrinkling can be obtained by substituting Rc ≤ A in the above equation to get 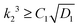 .
.
The solution in the preceding subsection assumes non-negative stress in the whole domain. In the presence of wrinkling the domain will be divided into three regions: wound (0 ≤ R ≤ A), wrinkled regions (A ≤ R ≤ Rc), and skin (Rc ≤ R ≤ B). The solution (2.15) remains valid in the wound and the skin region. To solve the boundary value problem in the wrinkled region we will use the tension field theory as proposed by Pipkin and Steigmann32,39,40 (see also ref. 24). For an annular region to lower its circumference below what would be in simple (radial) tension, compressive hoop stress would be required. The tension field theory instead postulates that the reduction of circumference is accomplished by wrinkling while keeping hoop stress to a vanishing value throughout the wrinkled region. The fine scale nature of the wrinkled pattern remains unresolved in this theory; in order to do so one would need to incorporate bending into membrane energetics.41 The essential features of the tension field theory emerge as a consequence of a relaxed strain energy density.32 Towards this end we first solve Tθθ = 0 from (2.13)2 to obtain λ2 in terms of λ1; we get 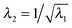 , the ‘natural width’ of the membrane.32 The relaxed strain energy density for the incompressible Varga material is obtained by substituting this expression in place of λ2 in (2.10):
, the ‘natural width’ of the membrane.32 The relaxed strain energy density for the incompressible Varga material is obtained by substituting this expression in place of λ2 in (2.10):
| | 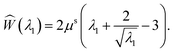 | (2.17) |
In the wrinkled region,
i.e. A ≤
R ≤
Rc,
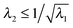
and
Tθθ = 0. Using the latter in
(2.8) reduces the stress equilibrium relation to
| | 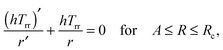 | (2.18) |
which immediately implies that
rhTrr is constant. The radial stress
Trr can be written in terms of the relaxed energy density as
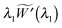
. With
r =
λ2Rk2,
h =
λ3H, and
λ1λ2λ3 = 1, the stress equilibrium implies that
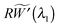
or, equivalently,
R(1 −
λ1−3/2) is a constant in the wrinkled region. The use of
λ1 =
r′/
k2 and subsequent integration yields
| | 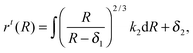 | (2.19) |
where
δ1 and
δ2 are constants; the superscript
t is used to identify the variables in the tension field (wrinkled) region. The solution is completed using the following boundary and interfacial conditions: (i)
Tsrr(
B) =
Ts∞(>0), (ii)
rw(0) = 0, (iii)
rt(
A) =
rw(
A), (iv)
rs(
Rc) =
rt(
Rc), and (v) (
htTtrr −
hwTwrr) = 0 at
R =
A, and (vi) (
hsTsrr −
htTtrr) = 0 at
R =
Rc. As before, the first condition is used to solve for
C1/
k22 and the second one implies
D2 = 0. Also, we can continue to interpret
D1 in terms of the wound healing rate. Then, fixing the value of parameters
μs,
μw,
ζ,
d, and
k2, we can use the rest of the conditions, in conjunction with
(2.16), to find
C2,
δ1,
δ2,
Rc, and
k1.
3 Discussion
Before venturing into a detailed parametric study we illustrate the nature of the solution for a typical choice of constants. We consider μs = 6.5 kPa, μw = 0.7μs, ζ = 0.95, k2 = 1.1, and Ts∞ = 1 kPa. The value for μs is taken from the available experimental results13 while μw is chosen so as to ensure that wound is less stiffer than the skin. We have taken d = 2 to investigate the nature of healing after the first day. The value of healing constant ζ is motivated from the wound healing data given in ref. 4 for a 36 year old patient with a wound on the left iliac region. We converted the area of the wound, available from the study, into an equivalent circular wound and subsequently determined the radius. The decrease in normalized current wound radius r/A versus time is shown in Fig. 2. The value of k2, which essentially provides the skin growth deformation, has been taken in the range of 1 to 1.3. A large value of k2 would signify a large opening at the wound edge after making an incision and vice-versa. Even though no experimental data is available for k2, we solve our problem with data which does not create large openings. The considered skin tension value of 1 kPa is lower than the reported literature range of about 5.4 kPa to 90 kPa.10,13 We are restricted to work with lower values of skin tension because we would otherwise get imaginary values for the constant D1 inside the wound. This restriction is an outcome of the simple hyperelastic model chosen for analytical convenience. The stresses in the skin region are plotted against the normalized radius R/A shown in Fig. 3. The critical wrinkle radius can be read as Rc = 1.424A. We have here illustrated a case of wrinkle formation which is inline with the literature.5,12
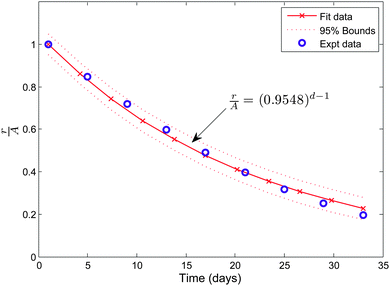 |
| | Fig. 2 The healing data for an open wound for patient no. 217 taken from ref. 4. | |
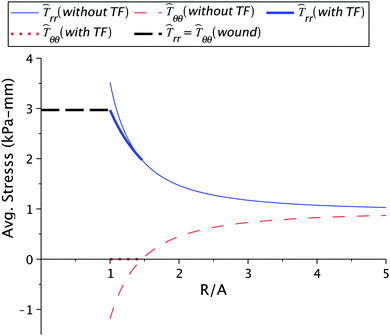 |
| | Fig. 3 Stress values in the skin region calculated for μs = 6.5 kPa, μw = 0.7μs, ζ = 0.95, Ts∞ = 1 kPa, and k2 = 1.1. Here, and in subsequent figures, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rr = hTrr and rr = hTrr and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) θθ = hTθθ. ‘TF’ stands for the tension field. θθ = hTθθ. ‘TF’ stands for the tension field. | |
We will now investigate how stress generation and wrinkling are affected by varying skin tension, healing constants, incompatibility at the wound edge, the radius of the wrinkled region, and wound stiffness. In several of these studies we will fix the wrinkle radius and instead calculate the healing constant as a part of the solution. Fixing the wrinkle radius simulates the condition of the constrained boundary for instance during vacuum or adhesive bandage assisted healing. The variation of the wrinkle radius in this paper is considered in the range of 1 to 3. This range is inspired from the experimental results obtained in ref. 5 and 12.
3.1 Effect of skin tension
The effect of the skin tension on the solution is given in Fig. 4 and 5, and in Tables 1(a) and 2(a). With a fixed healing constant, the wrinkle radius increases with decrease in the far field skin tension. This result is in agreement with earlier analytical studies23 and experiments.5,12,15 For higher tension smaller wrinkled regions will appear, in addition to higher stresses. This would also help the fibroblasts to transform into myofibroblasts, which furthers the contraction process.2,10,16 Hence, wounds under large tensile forces show less apoptosis and promote fibrosis and fibroplasia leading to hypertrophic scars.1,2,10,44 The evidence of abnormal scars appearing at mobile sites such as chest, shoulder muscles, abdomen and scapula, where the skin is frequently stretched due to respiration, upper limb movements, seating, and standing motions are some illustrations. Immobile sites like the scalp and the anterior low leg do not show such scars.2,43,44 The results in Table 1(a) show that the stresses in the wound and the skin region decrease with decreasing skin tension; this is of course related to the incompatibility k2 − k1 generated at the edge. The loss of tension during healing results in wound atrophy due to the disappearance of alpha-SMA (smooth muscle actin) and myofibroblasts from the wound site.2,17 In another parametric study, we keep the wrinkle radius constant and vary the skin tension as shown in Fig. 5 and Table 2(a). In this case, the healing constant increased (slower healing) with loss in skin tension, and higher stresses in the wound and the surrounding skin appear as a result of higher skin tension. For normal wound healing an optimized tension is required to limit the spreading of scar and formation of wrinkles.5
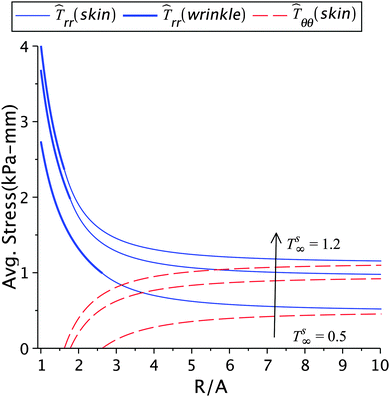 |
| | Fig. 4 The radial and circumferential stresses plotted for Ts∞ = 1.2 kPa, 1 kPa, and 0.5 kPa, with μs = 6.5 kPa, μw = 0.7μs, k2 = 1.2, and ζ = 0.95. | |
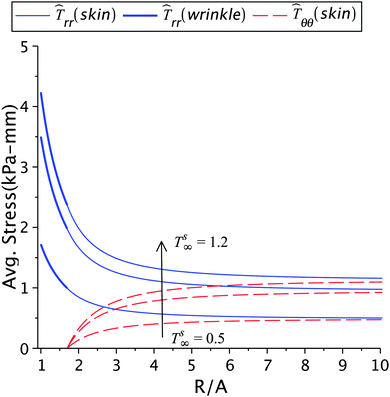 |
| | Fig. 5 The radial and circumferential stresses plotted for Ts∞ = 1.2 kPa, 1 kPa, and 0.5 kPa, with μs = 6.5 kPa, μw = 0.7μs, k2 = 1.2, and Rc = 1.7A. | |
Table 1 Effect of various parameters on wrinkling, stresses, and incompatibility when healing constant (ζ), k2, μs, μw, and Ts∞ are known. The stress ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rr(A) would be both the radial and hoop stress inside the wound
rr(A) would be both the radial and hoop stress inside the wound
| Parameter variation |
Parameter values |
R
c/A |
k
1
|
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rr
[kPa mm] (R = Rc)
rr
[kPa mm] (R = Rc) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rr
[kPa mm] (R = A)
rr
[kPa mm] (R = A) |
| (a) ζ = 0.95, k2 = 1.2, μs = 6.5 kPa, μw = 0.7μs |
|
T
s∞ (kPa) |
1.2 |
1.623 |
0.7 |
2.365 |
4.018 |
| 1 |
1.78 |
0.746 |
1.976 |
3.685 |
| 0.5 |
2.63 |
0.824 |
0.994 |
2.739 |
|
|
| (b) k2 = 1.2, μs = 6.5 kPa, μw = 0.7μs, Ts∞ = 1 kPa |
|
ζ
|
0.9 |
1.948 |
0.6533 |
|
4.08 |
| 0.95 |
1.78 |
0.7460 |
1.976 |
3.685 |
| 0.99 |
1.637 |
0.811 |
|
3.359 |
|
|
| (c) ζ = 0.95, μw = 0.7μs, μs = 6.5 kPa, Ts∞ = 1 kPa |
|
k
2
|
1.05065 |
1.258 |
0.8377 |
|
2.522 |
| 1.10065 |
1.463 |
0.8086 |
1.976 |
2.969 |
| 1.20065 |
1.78 |
0.7456 |
|
3.685 |
|
|
| (d) ζ = 0.95, k2 = 1.2, μs = 6.5 kPa, Ts∞ = 1 kPa |
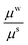
|
0.7 |
|
0.746 |
|
|
| 0.75 |
1.78 |
0.7708 |
1.976 |
3.685 |
| 0.9 |
|
0.8158 |
|
|
Table 2 Effect of various parameters on healing constant, stresses, and incompatibility when wrinkle radius (Rc/A), k2, μs, μw, and Ts∞ are known. The stress ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rr(A) would be both the radial and hoop stress inside the wound
rr(A) would be both the radial and hoop stress inside the wound
| Parameter variation |
Parameter values |
Healing const. (ζ) |
k
1
|
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rr
[kPa mm] (R = Rc)
rr
[kPa mm] (R = Rc) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rr
[kPa mm] (R = A)
rr
[kPa mm] (R = A) |
| (a) Rc/A = 1.7, k2 = 1.2, μs = 6.5 kPa, μw = 0.7μs |
|
T
s∞ (kPa) |
1.2 |
0.9238 |
0.63075 |
2.365 |
4.235 |
| 1 |
0.9726 |
0.7831 |
1.976 |
3.502 |
| 0.5 |
1.0894 |
1.0095 |
0.994 |
1.722 |
|
|
| (b) k2 = 1.2, μs = 6.5 kPa, μw = 0.7μs, Ts∞ = 1 kPa |
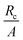
|
1.5 |
1.026 |
0.867 |
|
3.052 |
| 1.7 |
0.973 |
0.783 |
1.976 |
3.502 |
| 2 |
0.884 |
0.614 |
|
4.202 |
|
|
| (c) Rc/A = 1.7, μs = 6.5 kPa, μw = 0.7μs, Ts∞ = 1 kPa |
|
k
2
|
1.1 |
0.8915 |
0.7179 |
|
|
| 1.2 |
0.9726 |
0.7831 |
1.976 |
3.502 |
| 1.3 |
1.0536 |
0.8484 |
|
|
|
|
| (d) Rc/A = 1.7, k2 = 1.2, μs = 6.5 kPa, Ts∞ = 1 kPa |
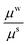
|
0.7 |
|
0.7831 |
|
|
| 0.75 |
0.9726 |
0.8044 |
1.976 |
3.502 |
| 0.9 |
|
0.8448 |
|
|
3.2 Effect of healing constant
The effect of varying healing constant on the solution is shown in Fig. 6 and Table 1(b). Higher rates of contraction can be achieved through artificial means such as vacuum assisted closure, adhesive tapes, bandages, skin grafts, scaffolds seeded with stem cells, dampening the wound, and maintaining proper hygiene.2–3,10 From our results we observe that lower values of the healing constant (faster healing) lead to higher stresses and larger wrinkled regions. This is in qualitative agreement with the available experimental results.5,12,15 The lower values also lead to greater incompatibilities at the wound edge. A large incompatibility is related to high contractile forces being generated near the wound edge, as highlighted in the previous section. It should be noted that artificial wound control methods have to appropriately balance the skin tension and the natural healing rate. The formation of scars strongly depends on the contraction during healing,46 which in turn is related to the cellular densities inside the wound. These densities should decrease during the progression of wound healing to avoid the formation of an ugly scar.
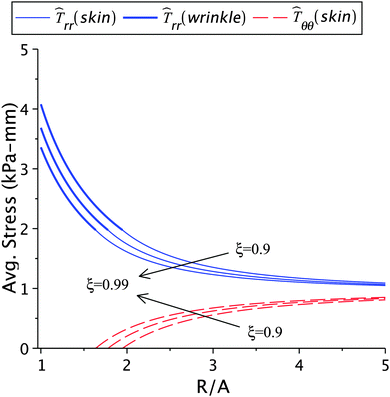 |
| | Fig. 6 The radial and circumferential stresses plotted for ζ = 0.99, 0.95, and 0.9; here μs = 6.5 kPa, μw = 0.7μs, Ts∞ = 1 kPa, and k2 = 1.2. | |
3.3 The role of incompatibility in the wound edge
The variation of incompatibility, i.e. k2 − k1, controls the generation of internal stresses at the wound edge. A balance between the external and internal stresses is maintained for natural healing leading to normal scars.2 The incompatibility also has a direct influence on the contraction rate. The effect of the skin growth factor k2 on healing and other parameters is shown in Fig. 7 and in Tables 1(c) and 2(c). For a fixed healing constant, an increase in k2 results in higher radial stress, lower hoop stress, and larger wrinkled regions. It also results in a lower value of k1 but a higher value of k2 − k1. Note that smaller values of k1 indicate large contraction, hence higher cellular densities with increased activities. On the other hand, when the wrinkle radius is kept constant, the effect of lowering k2 value (as reported in Table 2(c)) has an adverse effect on healing. It can be noticed that k2 − k1 does not change appreciably in this case. The constrained wrinkling increases the value of k1 when k2 is increased, which means that the cellular activities in the wound are balanced out by the extracellular activities in the skin; as a result excessive internal stresses are not generated. The skin tension away from the wound remains constant in this case, implying that healing cannot be accelerated with constant external forces.
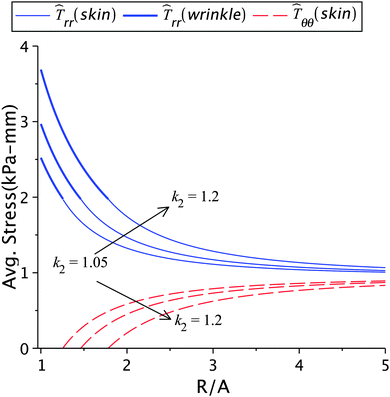 |
| | Fig. 7 The radial and circumferential stresses plotted for k2 = 1.01, 1.05, 1.1, and 1.2, with μs = 6.5 kPa, μw = 0.7μs, Ts∞ = 1 kPa, and ζ = 0.95. | |
3.4 Effect of the radius of the wrinkled region
The dependence of the solution on the size of the wrinkled region is presented in Fig. 8 and Table 2(b). An increased wrinkle radius decreases the healing constant but increases the stress and incompatibility at the wound edge. It is clear that the size of the wrinkled region has a strong effect on wound healing, especially on the quality of scars formed after healing.12 For instance, when the large wrinkling radius is associated with small values of stress (as in Table 1(a)), the scar may no longer remain hypertrophic and can turn ugly.12 However, when it is associated with high stress values (as shown in Table 2(b)) then the scar is hypertrophic. Sometimes keloids can be larger than the initial wound, which can be considered as the after-effect of the large wrinkling radius associated with high stresses.3
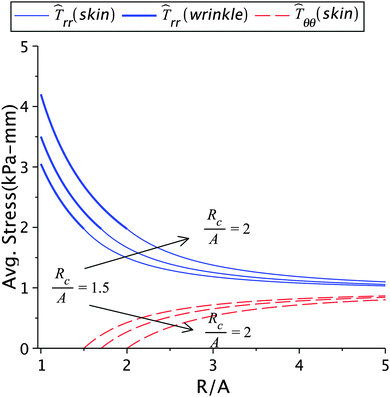 |
| | Fig. 8 The radial and circumferential stresses plotted for Rc = 1.5A, 1.7A, and 2A; Here μs = 6.5 kPa, μw = 0.7μs, k2 = 1.2, and Ts∞ = 1 kPa. | |
3.5 Effect of wound stiffness
The effect of wound stiffness on wound healing is shown in Tables 1(d) and 2(d). In both the cases, a change in wound stiffness value does not bring any change in the average stresses generated in the skin (the mid-plane stress values do change). In fact, as is clear from the governing equations, an increase in μw is accommodated by an increase in k1 for fixed values of μs, Ts∞, k2, and ζ (or Rc). This is expected since incompatibility should decrease with improved wound properties. The decreased incompatibility also decreases the (mid-plane) stress in the wound, making it favourable for scar control. Therefore, methods which improve wound properties, such as grafting, autologous seeding, stem cells, etc., have a positive effect on healing and scars.
4 Concluding remarks
We have proposed a continuum mechanics based biomechanical growth model for cutaneous wound closure after an injury locally alters the stress state of the skin. The formation of scars is an outcome of such an altered stress state in the skin after healing. Our approach differs from the existing wound healing literature in the way we have incorporated mass addition and incompatibility at the wound edge, and their relation with the stress field generated and wrinkle formation in the wound and the adjoining skin area. The results of our model are in excellent qualitative agreement with the available experimental data. However, as noted in the previous section, the model works only for far field skin tension values which are significantly below actual values. This is due to the simplistic Varga hyperelastic model chosen from obtaining exact solutions. Numerical solutions with a more realistic Ogden hyperelastic model or including viscoelastic effects may allow us to use realistic tension values in the unwounded skin.
For the known properties of the skin, our model can be used for an a priori estimation of stresses developed during wound closure at various stages of healing. It has been shown that the stresses generated depend directly on the extent of healing. Therefore, cases of abnormal or rapid healing can be identified easily by altering various parameters based on the microscopic events. In particular, the stress states can be used to indicate the severity of the scar formed and a better wound treatment plan can be evolved to prevent cases of hypertrophic scars and keloids. Our simplistic model can be enriched in many ways to deal with realistic healing situations. For example, the microscopic equations for cell activity in the two compartment models can be used to evolve skin growth factors k1 and k2. These factors can be related constitutively to various chemical (biochemical) and biological processes occurring during the healing process. On the other hand, we can modify the membrane model to include some bending energy, which can then be used to resolve finer features of the wrinkled skin.41
References
- S. Aarabi, K. A. Bhatt, Y. Shi, J. Paterno, E. I. Chang, S. A. Loh, J. W. Holmes, M. T. Longaker, H. yee and G. C. Gurtener, Mechanical load initiates hypertrophic scar formation through decreased cellular apoptosis, FASEB J., 2007, 21, 3250–3261 CrossRef CAS PubMed.
- R. Agha, R. Ogawa, G. Pietramaggiori and D. P. Orgill, A review of the role of mechanical forces in cutaneous wound healing, J. Surg. Res., 2011, 171, 700–708 CrossRef PubMed.
- G. Broughton and R. J. Rohrich, Wounds and scars, Selected Readings in Plastic Surgery, 2005, 10, 1–54 Search PubMed.
- A. Carrel and A. Hartmann, Cicatrization of wounds I. The relation between the size of a wound and the rate of its cicatrization, J. Exp. Med., 1916, 24, 429–450 CrossRef CAS.
- E. Cerda, Mechanics of scars, J. Biomech., 2005, 38, 1598–1603 CrossRef CAS PubMed.
- P. Ciarletta, L. Preziosi and G. A. Maugin, Mechanobiology of interfacial growth, J. Mech. Phys. Solids, 2013, 61, 852–872 CrossRef PubMed.
- D. A. Danielson, Wrinkling of the human skin, J. Biomech., 1977, 10, 201–204 CrossRef CAS.
-
M. Epstein, The Elements Of Continuum Biomechanics, Wiley, 2012 Search PubMed.
- M. Epstein and G. A. Maugin, Theromechanics of volumetric growth in uniform bodies, Int. J. Plast., 2000, 16, 951–978 CrossRef.
- N. D. Evans, R. O. C. Oreffo, E. Healy, P. J. Thurner and Y. H. Man, Epithelial mechanobiology, skin wound healing and stem cell niche, J. Mech. Behav. Biomed. Mater., 2013, 28, 397–409 CrossRef PubMed.
- C. Flynn and B. A. O. McCormack, Finite element modelling of forearm skin wrinkling, Skin Res. Technol., 2008, 14, 261–269 CrossRef PubMed.
- C. Flynn and B. A. O. McCormack, A simplified model of scar contraction, J. Biomech., 2008, 41, 1582–1589 CrossRef PubMed.
- C. Flynn, A. Taberner and P. Neilsen, Modeling the mechanical response of in vivo human skin under rich set of deformations, Ann. Biomed. Eng., 2011, 39, 1935–1946 CrossRef PubMed.
- K. Garikipati, E. M. Arruda, K. Grosh, H. Narayanan and S. Calve, A continuum treatment of growth in biological tissue: The coupling of mass transport and mechanics, J. Mech. Phys. Solids, 2004, 52, 1595–1625 CrossRef PubMed.
- J. C. Geminard, R. Bernal and F. Melo, Wrinkle formations in axi-symmetrically stretched membranes, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 15, 117–126 CrossRef CAS PubMed.
- F. Grinnel, Fibroblasts, myofibroblasts and wound contraction, J. Cell Biol., 1994, 124, 401–404 CrossRef.
- F. Grinnel, M. Zhu, M. A. Carlson and J. M. Abrams, Release of mechanical tension triggers apoptosis of human fibroblasts in a model of regressing granulation tissue, Exp. Cell Res., 1999, 248, 608–619 CrossRef PubMed.
- J. Gross, W. Farinelli, P. Sadow, R. Anderson and R. Bruns, On the mechanisms of skin wound “contraction”: a granulation tissue “knockout” with a normal phenotype, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 5982–5986 CrossRef CAS.
- A. Gupta and D. J. Steigmann, Plastic flow in solids with interfaces, Math. Models Methods Appl. Sci., 2012, 35, 1799–1824 CrossRef PubMed.
- A. Gupta, D. J. Steigmann and J. Stölken, On the evolution of plasticity and incompatibility, Math. Mech. Solids, 2007, 12, 583–610 CrossRef PubMed.
-
G. C. Gurtner, Wound healing: Normal and abnormal, in Grabb and Smith's Plastic Surgery, ed. C. H. Throne, Lippincott Williams and Wilkins, 2007, pp. 15–22 Search PubMed.
-
C. L. Hall, Modeling of some biological materials using continuum mechanics, PhD thesis, Queensland University of Technology, Australia, 2008 Search PubMed.
-
D. M. Haughton, Elastic membranes, in Non-linear Elasticity: Theory and Applications, ed. Y. B. Fu and R. W. Ogden, Cambridge University Press, 2001, pp. 233–267 Search PubMed.
- D. M. Haughton and B. A. McKay, Wrinkling of annular discs subjected to radial displacements, Int. J. Eng. Sci., 1995, 33, 335–350 CrossRef.
- S. M. Klisch, T. J. V. Dyke and A. Hoger, A theory of volumetric growth for compressible elastic biological materials, Math. Mech. Solids, 2001, 6, 551–575 CrossRef PubMed.
- B. Li and J. H.-C. Wang, Fibroblasts and myofibroblasts in wound healing: Force generation and measurement, J. Tissue Viability, 2011, 20, 108–120 CrossRef PubMed.
- V. A. Lubarda, Constitutive theories based on the multiplicative decomposition of deformation gradient: thermoelasticity, elastoplasticity and biomechanics, Appl. Mech. Rev., 2004, 57, 95–108 CrossRef.
- P. Martin, Wound healing – aiming for perfect skin regeneration, Science, 1997, 276, 75–81 CrossRef CAS.
- D. E. Moulton and A. Goriely, Circumferential buckling instability of a growing cylindrical tube, J. Mech. Phys. Solids, 2011, 59, 525–537 CrossRef PubMed.
- K. E. Murphy, C. L. Hall, S. W. McCue and D. L. S. McElwain, A two-compartment mechanochemical model of the roles of transforming growth factor β and tissue tension in dermal wound healing, J. Theor. Biol., 2011, 272, 145–159 CrossRef CAS PubMed.
-
J. D. Murray, Mathematical Biology II: Spatial Models and Biomedical Applications, Springer-Verlag, New York, 2003 Search PubMed.
- A. C. Pipkin, The relaxed energy density for isotropic elastic membranes, J. Inst. Math. Its Appl., 1986, 36, 85–99 CrossRef PubMed.
- J. M. Reinke and H. Sorg, Wound repair and regeneration, Eur. Surg. Res., 2012, 49, 35–43 CrossRef CAS PubMed.
- E. K. Rodriguez, A. Hoger and A. D. Mcculloch, Stress-dependent finite growth in soft elastic tissues, J. Biomech., 1994, 21, 455–467 CrossRef.
- R. V. Shevchenko, S. L. James and S. E. James, A review of tissue-engineered skin bioconstructs available for skin reconstruction, J. R. Soc., Interface, 2010, 7, 229–258 CrossRef CAS PubMed.
- A. J. Singer and R. A. F. Clark, Cutaneous wound healing, N. Engl. J. Med., 1999, 341, 738–746 CrossRef CAS PubMed.
- R. Skalak, S. Zargaryan, S. Jain, R. K. Netti and A. Hoger, Compatibility and the genesis of residual stress during volumetric growth, J. Math. Biol., 1996, 34, 889–914 CrossRef CAS.
- D. J. Steigmann, Proof of a conjecture in elastic membrane theory, J. Appl. Mech., 1986, 53, 955–956 CrossRef.
- D. J. Steigmann, Tension-field theory, Proc. R. Soc. London, Ser. A, 1990, 429, 141–173 CrossRef.
- D. J. Steigmann and A. C. Pipkin, Finite deformations of wrinkle membranes, Q. J. Mech. Appl. Math., 1989, 42, 427–440 CrossRef.
- M. Taylor, K. Bertoldi and D. J. Steigmann, Spatial resolution of wrinkle patterns in thin elastic sheets at finite strain, J. Mech. Phys. Solids, 2014, 62, 163–180 CrossRef PubMed.
- R. T. Tranquillo and J. D. Murray, Continuum model of fibroblast-driven wound contraction: inflammation-mediation, J. Theor. Biol., 1992, 158, 135–172 CrossRef CAS.
- V. W. Wong, S. Akaishi, T. Longaker and G. C. Gurtner, Pushing back: Wound mechanotransduction in repair and regeneration, J. Invest. Dermatol., 2011, 131, 2186–2196 CrossRef CAS PubMed.
- V. W. Wong, K. Levi, S. Akaishi, G. Schultz and R. H. Dauskardt, Scar zones: region-specific differences in skin tension may determine incisional scar formation, Plast. Reconstr. Surg., 2012, 129, 1272–1276 CrossRef CAS PubMed.
- M. Wu and M. B. Amar, Growth and remodelling for profound circular wounds in skin, Biomech. Model. Mechanobiol., 2015, 14, 357–370 CrossRef PubMed.
- L. Yang, T. M. Witten and R. M. Pidaparti, A biomechanical model of wound contraction and scar formation, J. Theor. Biol., 2013, 332, 228–248 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article in Fig. 1, where a denotes the wound radius and b the outer radius of the skin. We also consider an axisymmetric traction distribution over the skin edge and assume the skin region surrounding the wound to be large enough such that the traction forces at the boundary are obtainable from the internal stress values in the unwounded skin. We assume body forces and inertia to be negligible. The deformation is assumed to be axisymmetric so that the wound-skin arrangement remains in the form of a circular disc as skin grows radially towards the wound center. In this section, we provide details of our model and use it to obtain closed form solutions for the stress field and wrinkling instability in the skin region during healing.
in Fig. 1, where a denotes the wound radius and b the outer radius of the skin. We also consider an axisymmetric traction distribution over the skin edge and assume the skin region surrounding the wound to be large enough such that the traction forces at the boundary are obtainable from the internal stress values in the unwounded skin. We assume body forces and inertia to be negligible. The deformation is assumed to be axisymmetric so that the wound-skin arrangement remains in the form of a circular disc as skin grows radially towards the wound center. In this section, we provide details of our model and use it to obtain closed form solutions for the stress field and wrinkling instability in the skin region during healing.
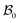 , taken to be the initial state of the wounded domain, see Fig. 1. In this configuration, the wound and the skin regions are of radius A and B, respectively. For a contracting wound we require a < A. The thickness H of the disc in
, taken to be the initial state of the wounded domain, see Fig. 1. In this configuration, the wound and the skin regions are of radius A and B, respectively. For a contracting wound we require a < A. The thickness H of the disc in 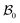 is assumed to be uniform such that H ≪ A. The thickness h of the deformed disc in
is assumed to be uniform such that H ≪ A. The thickness h of the deformed disc in 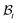 is taken to be a function of only the radial distance. The wound-skin arrangement has residual stresses, whose nature can be determined by unloading the body to a zero stress state. Presently, we assume that in order to unload the body
is taken to be a function of only the radial distance. The wound-skin arrangement has residual stresses, whose nature can be determined by unloading the body to a zero stress state. Presently, we assume that in order to unload the body 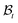 we will have to cut it along the wound edge, in addition to removing the traction force at the skin edge. Such a consideration is to emphasize the role of the wound edge in driving the closure of the wound. As we shall see, growth at the wound edge leads to a residually stressed state in the body which provides the driving force for wound healing. We call the stress-free configuration as the intermediate relaxed configuration and denote it as
we will have to cut it along the wound edge, in addition to removing the traction force at the skin edge. Such a consideration is to emphasize the role of the wound edge in driving the closure of the wound. As we shall see, growth at the wound edge leads to a residually stressed state in the body which provides the driving force for wound healing. We call the stress-free configuration as the intermediate relaxed configuration and denote it as 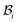 , see Fig. 1. As expected the wound edge and the internal edge of the skin are no longer coincident in
, see Fig. 1. As expected the wound edge and the internal edge of the skin are no longer coincident in 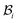 , but are separated by an axisymmetric gap (the axisymmetry of the gap is an additional assumption on the nature of the growth, see the following paragraph). The wound in
, but are separated by an axisymmetric gap (the axisymmetry of the gap is an additional assumption on the nature of the growth, see the following paragraph). The wound in 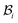 has a radius Â*. The annular skin region in
has a radius Â*. The annular skin region in 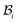 is of inner and outer radius A* and B*, respectively.
is of inner and outer radius A* and B*, respectively.
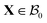 , given in terms of polar coordinates as X = Rer(Θ) + Zez (with 0 ≤ R ≤ B, 0 ≤ Θ ≤ 2π, and −H/2 ≤ Z ≤ H/2), to
, given in terms of polar coordinates as X = Rer(Θ) + Zez (with 0 ≤ R ≤ B, 0 ≤ Θ ≤ 2π, and −H/2 ≤ Z ≤ H/2), to 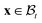 where x = rer(θ) + zez (with 0 ≤ r ≤ b, 0 ≤ θ ≤ 2π, and −h/2 ≤ z ≤ h/2) such that r = r(R), θ = Θ, and z = (h(R)/H)Z (we do not restrict h to be continuous at R = A). Here er, eθ and ez are unit basis vectors along radial, circumferential, and axial directions, respectively of the polar coordinate system. The deformation gradient F := ∂Xx is then given by
where x = rer(θ) + zez (with 0 ≤ r ≤ b, 0 ≤ θ ≤ 2π, and −h/2 ≤ z ≤ h/2) such that r = r(R), θ = Θ, and z = (h(R)/H)Z (we do not restrict h to be continuous at R = A). Here er, eθ and ez are unit basis vectors along radial, circumferential, and axial directions, respectively of the polar coordinate system. The deformation gradient F := ∂Xx is then given by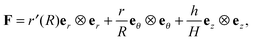
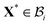 is related to X by a piecewise continuous map such that X* = R*er(Θ*) + Z*ez, where R* = R*(R), Θ* = Θ, and Z* = Z. This characterises the nature of growth kinematics in our model. We will assume a piecewise linear form for R* given by k1R if 0 ≤ R ≤ A and k2R if A ≤ R ≤ B, where k1 and k2 are constants (we will discuss more about them in the following). The growth distortion tensor Fg := ∂XX* therefore is of the form
is related to X by a piecewise continuous map such that X* = R*er(Θ*) + Z*ez, where R* = R*(R), Θ* = Θ, and Z* = Z. This characterises the nature of growth kinematics in our model. We will assume a piecewise linear form for R* given by k1R if 0 ≤ R ≤ A and k2R if A ≤ R ≤ B, where k1 and k2 are constants (we will discuss more about them in the following). The growth distortion tensor Fg := ∂XX* therefore is of the form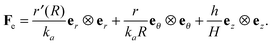
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe = 1; hence det
Fe = 1; hence det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F = det
F = det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fg, which yields
Fg, which yields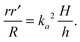
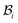 ; in fact we require k2 > k1, otherwise the two domains will penetrate into each other in
; in fact we require k2 > k1, otherwise the two domains will penetrate into each other in 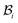 . The elastic deformation overcomes this radial incompatibility so as to make the total deformation compatible. As a result internal forces are generated at the wound edge. The biological origin of such forces is due to the presence of fibroblasts, myofibroblasts, and keratinocytes in the vicinity of the wound edge and their interaction with the surrounding cells in the skin.26 These internal forces supplement external forces (due to skin tension and body movement) in driving the wound to its closure.2 The preceding arguments provide physical basis for the introduction of incompatibility at the wound edge, here represented by non-vanishing of (k1 − k2). The parameters ka can of course be constitutively related to the biochemical processes governing the healing process; we discuss this briefly in the following subsection, but otherwise ignore the details in the present work. We note that unlike most of the existing theories of volumetric growth, where both growth and elastic distortions are incompatible in the domain, the incompatibility is restricted here to the interface at the wound edge, cf.ref. 29 and 45.
. The elastic deformation overcomes this radial incompatibility so as to make the total deformation compatible. As a result internal forces are generated at the wound edge. The biological origin of such forces is due to the presence of fibroblasts, myofibroblasts, and keratinocytes in the vicinity of the wound edge and their interaction with the surrounding cells in the skin.26 These internal forces supplement external forces (due to skin tension and body movement) in driving the wound to its closure.2 The preceding arguments provide physical basis for the introduction of incompatibility at the wound edge, here represented by non-vanishing of (k1 − k2). The parameters ka can of course be constitutively related to the biochemical processes governing the healing process; we discuss this briefly in the following subsection, but otherwise ignore the details in the present work. We note that unlike most of the existing theories of volumetric growth, where both growth and elastic distortions are incompatible in the domain, the incompatibility is restricted here to the interface at the wound edge, cf.ref. 29 and 45.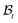 such that it intersects the wound edge on a surface s. Allowing for a mass source (represented by a density π per unit area) at the interface, the statement of balance of mass for ω is given by
such that it intersects the wound edge on a surface s. Allowing for a mass source (represented by a density π per unit area) at the interface, the statement of balance of mass for ω is given by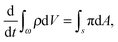
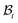 . In writing the above relation we have ignored the presence of any excess mass density at the interface as well as neglected any sources/sinks of mass in the bulk domain away from the interface. The mass source π can be attributed to the proliferation of various cells and growth factors at the wound edge. The global mass balance equation is equivalent to the following local relations:
. In writing the above relation we have ignored the presence of any excess mass density at the interface as well as neglected any sources/sinks of mass in the bulk domain away from the interface. The mass source π can be attributed to the proliferation of various cells and growth factors at the wound edge. The global mass balance equation is equivalent to the following local relations: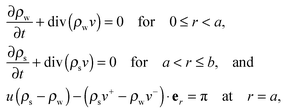
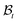 , and v is the particle velocity; div stands for the divergence operator. According to the last of these equations, a mass source can be present at the interface only when there is a non-trivial difference in the reference densities of the neighboring domains and the interface is not stationary in the reference configuration; the latter requires the wound edge to be a non-material interface. The mass balance at the wound edge can be used to derive a relationship between ka, u, ρ0 and π. Towards this end, let ρ0w and ρ0s be mass densities of the wound and surrounding skin with respect to
, and v is the particle velocity; div stands for the divergence operator. According to the last of these equations, a mass source can be present at the interface only when there is a non-trivial difference in the reference densities of the neighboring domains and the interface is not stationary in the reference configuration; the latter requires the wound edge to be a non-material interface. The mass balance at the wound edge can be used to derive a relationship between ka, u, ρ0 and π. Towards this end, let ρ0w and ρ0s be mass densities of the wound and surrounding skin with respect to 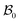 . We have ρ = ρ0
. We have ρ = ρ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) det
det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fg owing to incompressible elastic deformation. We assume a quasi-static evolution, where particle velocities have much small magnitudes than the wound edge velocity, so as to reduce (2.6)3 to
Fg owing to incompressible elastic deformation. We assume a quasi-static evolution, where particle velocities have much small magnitudes than the wound edge velocity, so as to reduce (2.6)3 to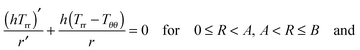
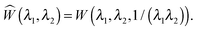
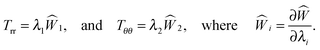
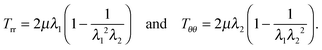
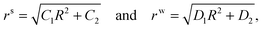
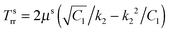 which is to be equated to Ts∞ to solve for C1/k22. It should be noted that, for Ts∞ > 0, the cubic equation has only one real root as can be checked by calculating the discriminant; moreover, we should necessarily have C1 > k22. The second condition implies D2 = 0, reducing (2.15)2 to
which is to be equated to Ts∞ to solve for C1/k22. It should be noted that, for Ts∞ > 0, the cubic equation has only one real root as can be checked by calculating the discriminant; moreover, we should necessarily have C1 > k22. The second condition implies D2 = 0, reducing (2.15)2 to 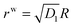 . With this we readily obtain
. With this we readily obtain 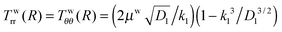 ; the wound region therefore is in a constant hydrostatic stress state. The stresses are tensile if and only if D1 > k12. It is useful to interpret D1 in terms of the current position of the wound edge (given by a) which is usually available from the experimental data (see for instance4). The velocity of healing or the rate of contraction is known to decrease with time.4 This motivates us to take a = Aζd−1, where ζ is the healing constant (ζ < 1 for healing) and d is the number of days (d > 1 assuming that there will be no proliferation of wound during the first day). We get
; the wound region therefore is in a constant hydrostatic stress state. The stresses are tensile if and only if D1 > k12. It is useful to interpret D1 in terms of the current position of the wound edge (given by a) which is usually available from the experimental data (see for instance4). The velocity of healing or the rate of contraction is known to decrease with time.4 This motivates us to take a = Aζd−1, where ζ is the healing constant (ζ < 1 for healing) and d is the number of days (d > 1 assuming that there will be no proliferation of wound during the first day). We get 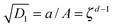 . The continuity of the deformation at the wound edge (third condition) is used to determine C2 in terms of C1 and D1 as C2 = (D1 − C1)A2. If we fix the value of parameters μs, μw, ζ, d, and k2, then the fourth condition simplifies to a fourth order equation which can be solved for k1; the selected value of k1 should satisfy k1 < k2 and D1 > k12. Knowing reference densities, this will also determine the rate of mass addition π in (2.7), where u can be inferred from D1. On the other hand, if we fix π, then we have to keep both k1 and k2 as unknown variables, to be solved using the fourth boundary condition and (2.7) while being restricted by various inequalities as discussed above.
. The continuity of the deformation at the wound edge (third condition) is used to determine C2 in terms of C1 and D1 as C2 = (D1 − C1)A2. If we fix the value of parameters μs, μw, ζ, d, and k2, then the fourth condition simplifies to a fourth order equation which can be solved for k1; the selected value of k1 should satisfy k1 < k2 and D1 > k12. Knowing reference densities, this will also determine the rate of mass addition π in (2.7), where u can be inferred from D1. On the other hand, if we fix π, then we have to keep both k1 and k2 as unknown variables, to be solved using the fourth boundary condition and (2.7) while being restricted by various inequalities as discussed above.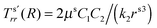 and
and 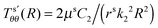 . We have already seen that, for far field radial stress in the skin to be positive, C1 > k22. Observations of wrinkling during healing reveal that it is restricted to a finite region in the skin adjacent to the wound edge. Therefore, the hoop stress should increase as we go from the wound edge towards healthier skin. This requires C2 < 0 which is equivalent to D1 < C1. The wrinkled region has Tsθθ < 0. To find the size of this region (denoted by radius Rc) we can use Tsθθ = 0 which in the present case yields a nonlinear equation
. We have already seen that, for far field radial stress in the skin to be positive, C1 > k22. Observations of wrinkling during healing reveal that it is restricted to a finite region in the skin adjacent to the wound edge. Therefore, the hoop stress should increase as we go from the wound edge towards healthier skin. This requires C2 < 0 which is equivalent to D1 < C1. The wrinkled region has Tsθθ < 0. To find the size of this region (denoted by radius Rc) we can use Tsθθ = 0 which in the present case yields a nonlinear equation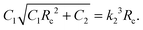
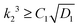 .
.
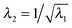 , the ‘natural width’ of the membrane.32 The relaxed strain energy density for the incompressible Varga material is obtained by substituting this expression in place of λ2 in (2.10):
, the ‘natural width’ of the membrane.32 The relaxed strain energy density for the incompressible Varga material is obtained by substituting this expression in place of λ2 in (2.10):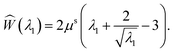
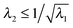 and Tθθ = 0. Using the latter in (2.8) reduces the stress equilibrium relation to
and Tθθ = 0. Using the latter in (2.8) reduces the stress equilibrium relation to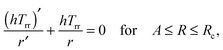
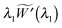 . With r = λ2Rk2, h = λ3H, and λ1λ2λ3 = 1, the stress equilibrium implies that
. With r = λ2Rk2, h = λ3H, and λ1λ2λ3 = 1, the stress equilibrium implies that 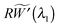 or, equivalently, R(1 − λ1−3/2) is a constant in the wrinkled region. The use of λ1 = r′/k2 and subsequent integration yields
or, equivalently, R(1 − λ1−3/2) is a constant in the wrinkled region. The use of λ1 = r′/k2 and subsequent integration yields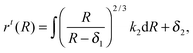



![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rr(A) would be both the radial and hoop stress inside the wound
rr(A) would be both the radial and hoop stress inside the wound
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) rr(A) would be both the radial and hoop stress inside the wound
rr(A) would be both the radial and hoop stress inside the wound