DOI:
10.1039/C5SM01133G
(Opinion)
Soft Matter, 2015,
11, 5792-5798
Linear microrheology with optical tweezers of living cells ‘is not an option’!
Received
11th May 2015
, Accepted 8th June 2015
First published on 8th June 2015
Abstract
Optical tweezers have been successfully adopted as exceptionally sensitive transducers for microrheology studies of complex fluids. Despite the general trend, in this article I explain why a similar approach should not be adopted for microrheology studies of living cells. This conclusion is acheived on the basis of statistical mechanics principles that indicate the unsuitability of optical tweezers for such purpose.
Introduction
It is thanks to the pioneering studies of Ashkin and co-workers1–3 that optical tweezers (OTs) have become an invaluable tool for a myriad of applications throughout the natural sciences,4–9 revolutionising the field of micro-sensing.10–12 Their success relies on the inherent property that a highly focused laser beam has to trap (in three dimensions) micron-sized dielectric objects suspended in a fluid. In particular, OTs have been adopted as exceptionally sensitive transducers (i.e., able to resolve pN forces and nm displacements, with temporal resolution down to a few μs) to study a multitude of biological processes, such as measuring the compliance of bacterial tails,13 the forces exerted by a single motor protein,14 the mechanical properties of human red blood cells15 and those of individual biological molecules,16–18 normally inaccessible by conventional methods.
Accessing the time-dependent trajectory of a micron-sized sphere, to high spatial and temporal resolution, is one of the basic principles underpinning microrheology techniques.19,20 Microrheology is a branch of rheology (the study of flow of matter), but it works on micron length scales and with micro-litre sample volumes. Therefore, microrheology techniques are revealed to be very useful tools for all those rheological studies where rare or precious materials are employed, e.g. in biophysical studies.21–25 Moreover, microrheology measurements can be performed in situ in an environment that cannot be reached by a conventional rheology experiment, for instance inside a living cell.26,27 The most popular microrheology techniques are: video particle tracking microrheology,28 diffusing wave spectroscopy,29,30 atomic force microscopy,31 magnetic tweezers21,32 and optical tweezers.33–39 These are classified as either ‘active’ or ‘passive’ techniques, depending on whether the particle displacement is induced by an external force field or generated by the thermal fluctuations of the fluid molecules surrounding the probe particle, respectively. For a good overview and understanding of the historical roots of the most common microrheology techniques, the reader can refer to ref. 20 and 40–42.
In general, microrheology techniques are aimed at relating the time-dependent tracers' trajectories to the linear viscoelastic (LVE) properties of the fluid in which they are dispersed. In the particular case of OTs, methods for performing microrheology measurements of complex fluids have been presented36,37,43 and validated43–45 against conventional bulk rheology methods. However, when similar approaches are considered for rheological studies of living cells, there exist some issues related to the ‘time-scales’ involved during the measurements, which preclude the determination of the viscoelastic properties of such systems. This conclusion is explained in this article on the basis of simple statistical mechanics principles.
Theoretical background
Linear rheology
The linear viscoelastic properties of a generic material can be expressed in terms of its shear complex modulus G*(ω) = G′(ω) + iG′′(ω), which is a complex number whose real and imaginary parts provide information on the elastic and the viscous nature of the material under investigation.46 These are commonly indicated as the storage (G′(ω)) and the loss (G′′(ω)) moduli, respectively. The conventional method of measuring the LVE properties of a material is based on the imposition of an oscillatory shear stress σ(ω,t) = σ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) (where σ0 is the amplitude of the stress function) and the measurement of the resulting oscillatory shear strain, which would be in a form like γ(ω,t) = γ0(ω)
sin(ωt) (where σ0 is the amplitude of the stress function) and the measurement of the resulting oscillatory shear strain, which would be in a form like γ(ω,t) = γ0(ω)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt − φ(ω)), where γ0(ω) and φ(ω) are the frequency-dependent strain amplitude and the phase shift between the stress and the strain, respectively. The relationship between the shear complex modulus and the two experimental functions describing the stress and the strain is:46
sin(ωt − φ(ω)), where γ0(ω) and φ(ω) are the frequency-dependent strain amplitude and the phase shift between the stress and the strain, respectively. The relationship between the shear complex modulus and the two experimental functions describing the stress and the strain is:46| | 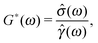 | (1) |
where ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (ω) and
(ω) and ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) (ω) are the Fourier transforms of σ(ω,t) and γ(ω,t), respectively. Note that, eqn (1) is of general validity; i.e., it applies to any temporal forms of the stress and the strain. In the particular case of sinusoidal functions eqn (1) is rewritten as:
(ω) are the Fourier transforms of σ(ω,t) and γ(ω,t), respectively. Note that, eqn (1) is of general validity; i.e., it applies to any temporal forms of the stress and the strain. In the particular case of sinusoidal functions eqn (1) is rewritten as:| | 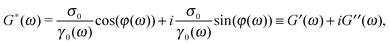 | (2) |
which provides the expressions of the moduli as a function of both the frequency-dependent functions γ0(ω) and φ(ω). Note that, G*(ω) is a time invariant.46
Fig. 1 shows the typical behaviour of the moduli as a function of the frequency for both (left) a generic viscoelastic fluid and (right) a generic complex solid. Over the past century, the frequency behaviour of the viscoelastic moduli has been correlated, both theoretically and experimentally,46–49 to the material's topological structure at different length scales, i.e., from the bulk sample at relatively low frequencies down to atomic length scales for frequencies of the order of THz, hence the importance of their knowledge.
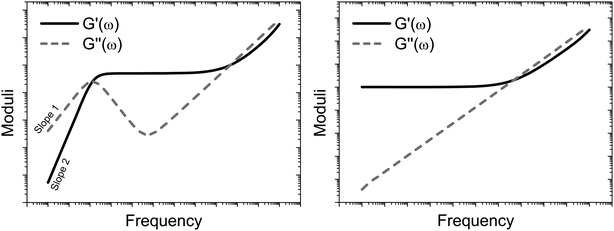 |
| | Fig. 1 Schematic representations of the frequency dependent moduli for a generic viscoelastic fluid (left) and a generic complex solid (right). Both the graphs have double logarithmic scales. | |
Passive microrheology with OTs
As described in ref. 43 in the case of a stationary trap, the statistical mechanics analysis of the thermal fluctuations of an optically trapped micron-sized spherical particle (see Fig. 2), suspended in a generic fluid at thermal equilibrium, has the potential of revealing both (i) the trap stiffness κ and (ii) the frequency-dependent viscoelastic properties of the suspending fluid. The analytical procedure for evaluating G*(ω) from the trajectory ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t) of an optically trapped micro-sphere involves the solution of a generalised Langevin equation in the form of:
(t) of an optically trapped micro-sphere involves the solution of a generalised Langevin equation in the form of:| | 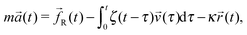 | (3) |
where m is the mass of the particle, ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) (t) is its acceleration,
(t) is its acceleration, ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) (t) is its velocity and
(t) is its velocity and ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) R(t) is the usual Gaussian white noise term, modelling stochastic thermal forces acting on the particle. The integral term, which incorporates a generalised time-dependent memory function ζ(t), represents viscous damping by the fluid. The last term on the right side of eqn (3) is the restoring force exerted by the OT (
R(t) is the usual Gaussian white noise term, modelling stochastic thermal forces acting on the particle. The integral term, which incorporates a generalised time-dependent memory function ζ(t), represents viscous damping by the fluid. The last term on the right side of eqn (3) is the restoring force exerted by the OT (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) OT = −κ
OT = −κ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t)) on the particle, when the confining field E(
(t)) on the particle, when the confining field E(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) generated by the OT is assumed to be harmonic:
) generated by the OT is assumed to be harmonic: 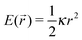 . Following the assumption made by Mason and Weitz in their seminal work that established the field of microrheology19 (i.e., that the Laplace-transformed bulk viscosity of the fluid
. Following the assumption made by Mason and Weitz in their seminal work that established the field of microrheology19 (i.e., that the Laplace-transformed bulk viscosity of the fluid ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) (s) is proportional to the microscopic memory function
(s) is proportional to the microscopic memory function ![[small zeta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e126.gif) (s) = 6πa
(s) = 6πa![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) (s), where a is the bead radius), eqn (3) can be solved for G*(ω) in terms of either of the following two time-averaged functions of the particle trajectory, i.e. the Normalised Mean-Square Displacement (NMSD):36
(s), where a is the bead radius), eqn (3) can be solved for G*(ω) in terms of either of the following two time-averaged functions of the particle trajectory, i.e. the Normalised Mean-Square Displacement (NMSD):36| | 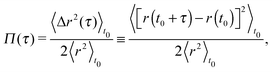 | (4) |
or the Normalised Position Autocorrelation Function (NPAF):37| | 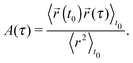 | (5) |
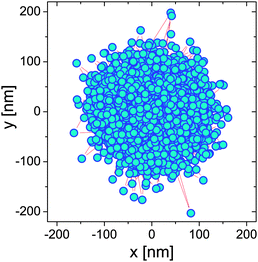 |
| | Fig. 2 The 2D trajectory of an optically trapped bead of 2.5 μm radius suspended in water over a period of 22 min. | |
Eqn (4) and (5) are, by time-translation invariance, only functions of the time interval (lag-time) τ = (t − t0). Moreover, the brackets 〈⋯〉t0 denote an average over all initial times t0. The term 〈r2〉t0 is the time-independent variance of the vector describing the particle's displacement from the trap center, the origin of ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t). Fig. 3 shows the temporal behaviour of both the above functions in the case of an optically trapped microsphere suspended in a Newtonian fluid (i.e., water).
(t). Fig. 3 shows the temporal behaviour of both the above functions in the case of an optically trapped microsphere suspended in a Newtonian fluid (i.e., water).
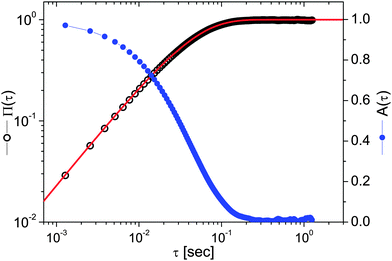 |
| | Fig. 3 The NMSD (left axis) and the NPAF (right axis) vs. lag-time τ evaluated from the particle trajectory shown in Fig. 2. The red line is the theoretical prediction described by eqn (13). | |
From eqn (3), the fluid's shear complex modulus can be expressed as:
| | 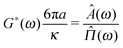 | (6) |
where
![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif)
(
ω) and
Â(
ω) are the Fourier transforms of
Π(
τ) and
A(
τ), respectively. Notably, these two functions are simply related to each other both in the time- and in the frequency-domain:
Π(
τ) +
A(
τ) = 1 and
iω![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif)
(
ω) +
iωÂ(
ω) = 1, respectively. Note that,
eqn (6) is valid as long as the particle inertia (
i.e.,
mω2) is negligible, which, in the case of micron sized particles (with
m ≈ 10
−15), is a reasonable assumption for frequency values
ω ≲ MHz.
Active microrheology with OTs
Active microrheology with OTs is commonly performed via oscillatory measurements like the conventional bulk rheology method described by eqn (1) and (2). However, in the case of microrheology with OTs of complex fluids, the expression of G*(ω) must be obtained via the solution of a generalised Langevin equation similar to eqn (3), but now with an extra term accounting for a non-stationary trap:| | 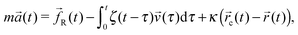 | (7) |
where all the terms are the same as in eqn (3) plus ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) c(t) that is the position vector describing the driven motion of the optical trap center. Eqn (7) can be solved for G*(ω) in terms of the particle position
c(t) that is the position vector describing the driven motion of the optical trap center. Eqn (7) can be solved for G*(ω) in terms of the particle position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t) and the resulting expression is:
(t) and the resulting expression is:| | 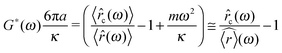 | (8) |
where ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) c(ω) and
c(ω) and ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (ω) are the Fourier transforms of
(ω) are the Fourier transforms of ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) c(t) and
c(t) and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t), respectively. The brackets 〈⋯〉 denote the average over several independent measurements. For the last equality it has been considered that: (i) 〈
(t), respectively. The brackets 〈⋯〉 denote the average over several independent measurements. For the last equality it has been considered that: (i) 〈![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) c(ω)〉 ≡
c(ω)〉 ≡ ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) c(ω), the latter being the driving component, thus reproducible over several independent measurements, (ii)
c(ω), the latter being the driving component, thus reproducible over several independent measurements, (ii) 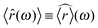 because of linearity of the involved operators, and (iii) the particle inertia is negligible. Note that, eqn (8) is of general validity, whatever the temporal form of
because of linearity of the involved operators, and (iii) the particle inertia is negligible. Note that, eqn (8) is of general validity, whatever the temporal form of ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) c(t).
c(t).
In the simplest case when the optical trap is periodically oscillating with a driving frequency β, i.e. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) c(t) = ‖rc‖sin(βt), the particle displacement will assume a temporal form like
c(t) = ‖rc‖sin(βt), the particle displacement will assume a temporal form like ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t) = ‖r‖sin(βt − φ(β)); where ‖rc‖ and ‖r‖ are the amplitudes of the sinusoidal functions
(t) = ‖r‖sin(βt − φ(β)); where ‖rc‖ and ‖r‖ are the amplitudes of the sinusoidal functions ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) c(t) and
c(t) and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t), respectively. In this case, eqn (8) simplifies:
(t), respectively. In this case, eqn (8) simplifies:
| | 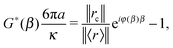 | (9) |
from which the viscoelastic moduli assume the following expressions:
| | 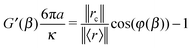 | (10) |
| | 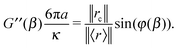 | (11) |
The above equations are similar to those obtained previously,
38 but here they have been derived rigorously from
eqn (7)viaeqn (8), which is of general validity. Moreover, it is important to highlight that, experimentally, in order to obtain an accurate value of the fluid's viscoelastic moduli (
i.e. of both the phase shift
φ(
β) and the amplitude ‖〈
r〉‖), for each explored frequency
β, several cycles must be measured to average out the thermal fluctuations that disrupt the particle trajectory. Therefore, in order to measure
G*(
ω) over a wide frequency spectrum (
e.g., from 0.01 Hz to kHz), a total measurement duration
Tm of the order of hours would be required.
An alternative and less time-consuming method than the oscillatory measurements has been presented by Preece et al.37 They introduced a hybrid self-consistent procedure for measuring the LVE properties of materials across the widest frequency range achievable using optical tweezers, by combining both passive and active OT operating modes. In particular, their procedure consists of two steps: (I) measuring the thermal fluctuations of a trapped bead for a sufficiently long time; (II) measuring the transient displacement of a bead flipping between two optical traps (spaced at fixed distance D0 ≤ 0.8a, to ensure the linearity of the optical trap50) that alternately switch on/off at a sufficiently low frequency. The analysis of the first step (I) provides: (a) the traps stiffness (κi, i = 1, 2)—note that this has the added advantage of making the method self-calibrated—and (b) the high frequency viscoelastic properties of the material, to high accuracy (by means of eqn (6)). The second step (II) has the potential to provide information about the material's viscoelastic properties over a very wide frequency range, which is only limited (at the top end) by the acquisition rate of the bead position and (at the bottom end) by the duration (P) of the on/off state of the two traps. The procedure consists of analysing the bead's transient displacements as it moves between two traps with separation D0 that swaps their on/off state at times t = t0 + nP, as shown in Fig. 4. They defined the normalised mean position of the particle as D(t) = |〈![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t)〉|/D0 (see Fig. 5), where the brackets 〈⋯〉 denote the average over several independent measurements, but not over absolute time, since time-translation invariance is broken by periodic switching. The full viscoelastic spectrum of the fluid is resolved by combining the results obtained from steps (I) and (II).
(t)〉|/D0 (see Fig. 5), where the brackets 〈⋯〉 denote the average over several independent measurements, but not over absolute time, since time-translation invariance is broken by periodic switching. The full viscoelastic spectrum of the fluid is resolved by combining the results obtained from steps (I) and (II).
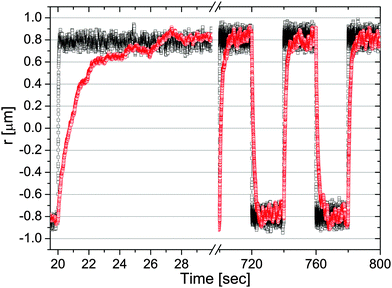 |
| | Fig. 4 The trajectory of a 5 μm diameter bead flipping between two optical traps κ1 (bottom) and κ2 (top) repeatedly switching after a duration P = 20 s. The bead is suspended in (squares) water (with κ1 = 2.7 and κ2 = 2.5 μN m−1) and (circles) a water-based solution of PAM at concentrations of 1% w/w (with κ1 = 2.1 and κ2 = 2.2 μN m−1). Image taken from ref. 37. | |
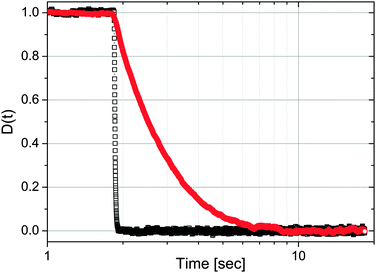 |
| | Fig. 5 The normalised mean position of all step-down data shown in Fig. 4; i.e., when simultaneously trap 2 (top) switches off and trap 1 (bottom) switches on. Image taken from ref. 37. | |
In the simple case of two identical optical traps (κ1 ≡ κ2) and particle inertia being negligible, the expression of the fluid's complex modulus is:
| | 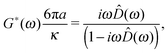 | (12) |
where
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif)
(
ω) is the Fourier transform of
D(
t), with
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
(
t) being the particle position from the active trap.
Discussion
The need for long measurements in microrheology
Most of the microrheology techniques are based on the statistical mechanics analysis of particle trajectories. Therefore, in order to obtain an accurate evaluation of the fluids' LVE properties, measurements are required to be statistically valid or, in other words, they need to be averaged over a sufficient number of independent readings, which in microrheology translates in long measurements of duration Tm. This, indeed, is an essential requirement that is very often overlooked and that may compromise the quality of the results and their validity, especially when measurements are performed in living organisms, as explained in this article.
In the case of passive microrheology, the execution of long measurements is an imperative requisite to obtain an accurate estimation of the aimed time-averaged functions, such as Π(τ) or A(τ). In order to quantify the uncertainty in the valuation of such functions (measured over a finite set of data) with respect to their expected values, in Fig. 643 are shown the simulation results of the MSD versus lag-time for a freely diffusing particles evaluated over 104 simulated trajectories, each of them comprising 106 random steps, drawn from a uniform distribution of unit width. The resulting MSD satisfies the expected scaling law; i.e. MSD ∝ τ. Moreover, it has been shown that, for each trajectory, the percentage deviation of the MSD(τ) from its expected value grows with lag-time as a power law close to τ1/2.
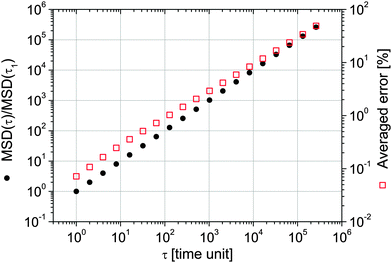 |
| | Fig. 6 (left axis) The MSD vs. lag-time of 104 simulated trajectories of freely diffusing particles; each trajectory is made up of 106 data points (i.e. steps). (right axis) The averaged percentage deviation of the MSD from its expected value. Image taken from ref. 43. | |
From Fig. 6, it is possible to infer that, within a single trajectory of 106 steps the error in the measured MSD, for a lag-time of τ = 106 time units is typically as large as 100%. Unfortunately, this is particularly true for measurements performed with OT setups equipped with a quadrant photodiode (QPD), which allows high speed (∼MHz) detection of the probe particle position, but fills very quickly the personal computer's memory buffer register allowing only a few seconds of measurement duration (Tm ∼ 1 s). Whereas, in the case of OT setups equipped with a charge-coupled device (CCD) camera for the particle's position detection, the acquisition rates (AR) are of the order of kHz. Therefore, for a measurement duration of Tm ≃ 22 min (i.e., 106 data points acquired at AR ≃ 800 Hz), the error in estimating MSD at τ = 1 s is typically of the order of a few percents. This is confirmed by the results shown in the inset of Fig. 7, where the normalised mean square displacement of an optically trapped bead suspended in water is compared with the theoretical prediction43 derived in the case when the suspending fluid is Newtonian:
where
λ =
κ/6π
aη and
η is the fluid viscosity.
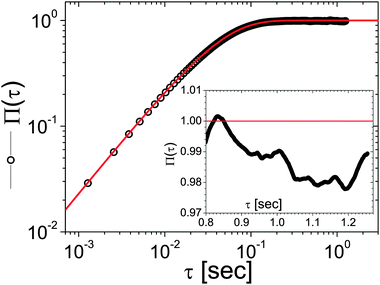 |
| | Fig. 7 Comparison between the Π(τ) (circles) and its prediction (continuous line), viaeqn (13), for an optically trapped 4.74 μm diameter silica bead suspended in water, with κ = 0.93 μN m−1 and η = 0.896 mPa s. The NMSD has been obtained from the analysis of 106 data points representing the particle trajectory, acquired at AR ≃ 800 Hz. The inset highlights the behaviour of Π(τ) within a small time-window taken at lag-time τ ≃ 1 s. | |
A possible solution to the experimental issue of performing passive microrheology measurements using a QPD equipped with OTs would imply a non-constant acquisition rate. For example, this could be achieved by performing a two speed measurement: i.e., during the first second, data could be acquired at 1 MHz with lag-times evaluated up to τ = 10−3 s and then the AR could be dropped to a kHz for the remaining ≃17 min. So that, the average error of the measured NMSD would remain below a few percents up to τ = 1 s and the total number of acquired data points would be 2 × 106.
In the case of active microrheology, long measurements are also essential to achieve a high signal to noise ratio; where the ‘noise’ is the thermally driven particle fluctuation, which in this case is an undesired presence that debases the (active) signal. Therefore, whether the fluids' LVE properties are evaluated by means of a frequency sweep oscillatory measurement (viaeqn (9)) or by a more efficient hybrid method37 (viaeqn (6) and (12)), measurements need to be averaged over several repetitions (or cycles). This brings the total measurement duration Tm to be at least of the order of a few tens of minutes.
Microrheology with OTs of gels
One of the key challenges in the field of microrheology is the choice of the probe size. This is because, in order to retrieve the material's bulk rheology properties the particle diameter (d = 2a) must be bigger than the characteristic length scale of the system under investigation. For example, in the case of a polymer gel, the particle diameter must be bigger than the average mesh size (ξ) of the polymer network; so that, for d > ξ, the particle would not be able to diffuse through the polymer network and its fluctuations would have the potential of revealing the gel's LVE properties (in a similar way to conventional bulk rheology measurements, where the used tools are much bigger than ξ). Whereas, for d < ξ, the particle is not trapped by the polymer network and the analysis of its trajectory (whether it is optically trapped or not) would provide information on the hydrodynamic coupling between the gel network and the probe particle, but not on the gel's LVE properties.
Moreover, if the first condition is fulfilled (i.e., d > ξ), then one could argue that there is no need of OTs for constraining the particle diffusion, as the gel would work as a trap itself. Nevertheless, it is important to highlight that, even when the particle is trapped by the gel, OT setups equipped with a quadrant photodiode could turn to be very useful for high frequency detection of the particle position, as long as the OT laser is not constraining the particle displacement. This condition can be simply achieved by tuning the laser power so that the trap stiffness is lower than the gel's low-frequency elastic modulus G0′:
| | 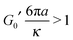 | (14) |
In this case,
eqn (6) and (12) are no longer applicable and the well known generalised Stokes–Einstein equation must be used:
| | 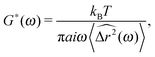 | (15) |
where
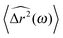
is the Fourier transform of the particle mean square displacement 〈Δ
r2(
τ)〉
t0.
Therefore, although optical tweezing is not necessary for linear microrheology measurements of gels, the use of a laser combined with a QPD as a high frequency particle position detector could turn to be advantageous if the right choice of the acquisition rate is made.
Microrheology with OTs of living cells
In the case of microrheology measurements performed in living cells or more in general in living organisms (e.g., parasites), things get more complicated, because their mechanical properties are not time-invariant; at least not at all the time-scales. In particular, it has been shown27,51,52 that the presence of “athermal” fluctuations within a living cell, due to the existence of active processes (e.g., actin-myosin interactions53) that dissipate energy not just by simple friction, drives the system out of thermodynamic equilibrium. Indeed, their existence should not be neglected as they may substantially alter the viscoelastic response of the system (mostly at low frequencies), with the risk of gathering deceptive information. Unfortunately, the evaluation of the error carried by such negligence is not trivial as different organisms may present different ways of dissipating energy at different time scales; hence the non-uniqueness of the error estimation. Moreover, athermal fluctuations can occur anywhere within a cell and their effects can be felt throughout the cytoplasm, from the plasma membrane to the nucleus. They usually occur at rates that may vary not only from different kinds of cells, but also within the same cell line, and are expected27,51–53 to occur within a range of frequencies spanning from 10−2 Hz to 102 Hz.
From a microrheology point of view, one could consider the fastest rate (Γorg) of all the biological process occurring within the cell as the lower frequency limit for the applicability of the fluctuation–dissipation theorem,54 which is the underpinning principle of the field of microrheology,19 linking the particle motion to the viscoelastic nature of the suspending medium.
It follows that, microrheology of living cells can still be performed if the right assumptions on the time-scales involved during the measurement are made; i.e., on the Deborah number.55 This is defined as the ratio between the characteristic relaxation time of the system under study and the time taken to observe such a system:
| |  | (16) |
Therefore, for each living organism, one could assume the existence of a characteristic time (
τorg =
Γorg−1) such that, for measurements having duration
Tm shorter than
τorg (
i.e., De ≳ 1), the living system can be seen as a complex material (either a fluid or solid) with ‘
time-invariant’ viscoelastic properties; whereas, for observations lasting longer than
τorg (
i.e., De ≲ 1), the living organism has time to self-reorganise and to move out of thermodynamic equilibrium. However, notwithstanding that for De ≳ 1 microrheology measurements of a living system are possible, in the case of OTs the following consideration excludes them from being considered for such purpose. Specifically, whether the living organism is assumed to behave as a viscoelastic fluid or a complex solid, microrheology with OTs requires sufficiently long measurements, of the order of tens of minutes, for an accurate evaluation of the relevant time-averaged functions (
e.g.,
Π(
τ),
A(
τ),
D(
t) or the MSD). This would very likely result in De ≲ 1 for the majority of the living organisms, with the subsequent loss of the pseudo-equilibrium assumption because of the initiation of athermal fluctuations within the system. Thus the inappropriateness of OTs for measuring the linear viscoelastic properties of living cells.
Conclusions
Optical tweezers have been successfully adopted as exceptionally sensitive transducers for microrheology studies of viscoelastic fluids at thermodynamic equilibrium. However, despite the general trend, a similar approach cannot be adopted for microrheology studies of living cells. This is because the time-scales required by optical tweezers to perform microrheology measurements are much longer than the characteristic time-scales of the biological processes occurring within cells. This results in a violation of the fluctuation–dissipation theorem, which links the particle motion to the linear viscoelastic properties of the suspending medium. Therefore, based on simple rheological concepts, it has been shown that microrheology with optical tweezers of living cells ‘is not an option’!
Acknowledgements
I thank Thomas Waigh, Nancy Forde, Mike Evans, Steven Neale, Michael Lee, Jonathan Cooper and Miles Padgett for helpful conversations. I acknowledge support via personal research fellowships from the Royal Academy of Engineering/EPSRC (10216/101).
References
- A. Ashkin, Phys. Rev. Lett., 1970, 24, 156–159 CrossRef CAS.
- A. Ashkin and J. M. Dziedzic, Appl. Phys. Lett., 1971, 19, 283–285 CrossRef.
- A. Ashkin, J. M. Dziedzic, J. E. Bjorkholm and S. Chu, Opt. Lett., 1986, 11, 288–290 CrossRef CAS PubMed.
- K. Svoboda and S. Block, Annu. Rev. Biophys. Biomol. Struct., 1994, 23, 247–285 CrossRef CAS PubMed.
- L. Novotny, R. Bian and X. Xie, Phys. Rev. Lett., 1997, 79, 645–648 CrossRef CAS.
- J. E. Curtis, B. A. Koss and D. G. Grier, Opt. Commun., 2002, 207, 169–175 CrossRef CAS.
- J. E. Molloy and M. J. Padgett, Contemp. Phys., 2002, 43, 241–258 CrossRef CAS.
- D. Grier, Nature, 2003, 424, 810–816 CrossRef CAS PubMed.
- J. R. Moffitt, Y. R. Chemla, S. B. Smith and C. Bustamante, Annu. Rev. Biochem., 2008, 77, 205–228 CrossRef CAS PubMed.
- R. W. Bowman and M. J. Padgett, Rep. Prog. Phys., 2013, 76, 026401 CrossRef PubMed.
- D. Phillips, J. Grieve, S. Olof, S. Kocher, R. Bowman, M. Padgett, M. Miles and D. Carberry, Nanotechnology, 2011, 22, 285503 CrossRef CAS PubMed.
- D. B. Phillips, S. Simpson, J. Grieve, R. Bowman, G. Gibson, M. Padgett, J. Rarity, S. Hanna, M. Miles and D. Carberry, Europhys. Lett., 2012, 99, 58004 CrossRef.
- S. Block, D. Blair and H. Berg, Nature, 1989, 338, 514–518 CrossRef CAS PubMed.
- J. Finer, R. Simmons and J. Spudich, Nature, 1994, 368, 113–119 CrossRef CAS PubMed.
- Y.-Z. Yoon, J. Kotar, G. Yoon and P. Cicuta, Phys. Biol., 2008, 5, 036007 CrossRef PubMed.
- A. Ashkin and J. M. Dziedzic, Science, 1987, 235, 1517–1520 CAS.
- L. Tskhovrebova, J. Trinick, J. Sleep and R. Simmons, Nature, 1997, 387, 308–312 CrossRef CAS PubMed.
- A. Mehta, M. Rief, J. Spudich, D. Smith and R. Simmons, Science, 1999, 283, 1689–1695 CrossRef CAS PubMed.
- T. Mason and D. Weitz, Phys. Rev. Lett., 1995, 74, 1250–1253 CrossRef CAS PubMed.
- T. M. Squires and T. G. Mason, Annu. Rev. Fluid Mech., 2010, 42, 413–438 CrossRef.
- M. Tassieri, T. Waigh, J. Trinick, A. Aggeli and R. Evans, J. Rheol., 2010, 54, 117–131 CrossRef CAS.
- M. Tassieri, R. Evans, L. Barbu-Tudoran, J. Trinick and T. Waigh, Biophys. J., 2008, 94, 2170–2178 CrossRef CAS PubMed.
- M. Tassieri, R. Evans, L. Barbu-Tudoran, G. N. Khaname, J. Trinick and T. A. Waigh, Phys. Rev. Lett., 2008, 101, 198301 CrossRef PubMed.
- F. Watts, L. E. Tan, C. G. Wilson, J. M. Girkin, M. Tassieri and A. J. Wright, J. Opt., 2014, 16, 015301 CrossRef.
- E. J. Robertson, G. Najjuka, M. A. Rolfes, A. Akampurira, N. Jain, J. Anantharanjit, M. von Hohenberg, M. Tassieri, A. Carlsson, D. B. Meya, T. S. Harrison, B. C. Fries, D. R. Boulware and T. Bicanic, J. Infect. Dis., 2014, 209, 74–82 CrossRef CAS PubMed.
- P. Kollmannsberger and B. Fabry, Annu. Rev. Mater. Res., 2011, 41, 75–97 CrossRef CAS.
- A. W. Harrison, D. A. Kenwright, T. A. Waigh, P. G. Woodman and V. J. Allan, Phys. Biol., 2013, 10, 036002 CrossRef PubMed.
- S. Kuo, J. Gelles, E. Steuer and M. Sheetz, J. Cell Sci., 1991,(suppl.), 135–138 CrossRef CAS.
- D. Pine, D. Weitz, P. Chaikin and E. Herbolzheimer, Phys. Rev. Lett., 1988, 60, 1134–1137 CrossRef CAS PubMed.
- D. Weitz, J. Zhu, D. Durian, H. Gang and D. Pine, Phys. Scr., 1993, T49B, 610–621 CrossRef CAS.
- T. Okajima and H. Tokumoto, Nihon Reoroji Gakkaishi, 2008, 36, 81–86 CrossRef CAS.
- A. Bausch, W. Moller and E. Sackmann, Biophys. J., 1999, 76, 573–579 CrossRef CAS PubMed.
- R. Brau, J. Ferrer, H. Lee, C. Castro, B. Tam, P. Tarsa, P. Matsudaira, M. Boyce, R. Kamm and M. Lang, J. Opt. A: Pure Appl. Opt., 2007, 9, S103–S112 CrossRef CAS.
- M. Fischer and K. Berg-Sorensen, J. Opt. A: Pure Appl. Opt., 2007, 9, S239–S250 CrossRef.
- M. Atakhorrami, J. I. Sulkowska, K. M. Addas, G. H. Koenderink, J. X. Tang, A. J. Levine, F. C. MacKintosh and C. F. Schmidt, Phys. Rev. E, 2006, 73, 061501 CrossRef CAS.
- M. Tassieri, G. M. Gibson, R. Evans, A. M. Yao, R. Warren, M. J. Padgett and J. M. Cooper, Phys. Rev. E, 2010, 81, 026308 CrossRef.
- D. Preece, R. Warren, R. Evans, G. M. Gibson, M. J. Padgett, J. M. Cooper and M. Tassieri, J. Opt., 2011, 13, 044022 CrossRef.
- M. Valentine, L. Dewalt and H. OuYang, J. Phys.: Condens. Matter, 1996, 8, 9477–9482 CrossRef CAS.
- L. Starrs and P. Bartlett, J. Phys.: Condens. Matter, 2003, 15, S251–S256 CrossRef CAS.
- T. Waigh, Rep. Prog. Phys., 2005, 68, 685–742 CrossRef.
- C. J. Pipe and G. H. McKinley, Mech. Res. Commun., 2009, 36, 110–120 CrossRef.
- P. Cicuta and A. M. Donald, Soft Matter, 2007, 3, 1449–1455 RSC.
- M. Tassieri, R. Evans, R. L. Warren, N. J. Bailey and J. M. Cooper, New J. Phys., 2012, 14, 115032 CrossRef.
- A. Pommella, V. Preziosi, S. Caserta, J. M. Cooper, S. Guido and M. Tassieri, Langmuir, 2013, 29, 9224–9230 CrossRef CAS PubMed.
- M. Tassieri, F. Del Giudice, E. J. Robertson, N. Jain, B. Fries, R. Wilson, A. Glidle, F. Greco, P. A. Netti and P. L. Maffettone,
et al.
, Sci. Rep., 2015, 5, 8831 CrossRef CAS PubMed.
-
J. D. Ferry, Viscoelastic properties of polymers, Wiley, 3rd edn, 1980 Search PubMed.
-
C. W. Macosko and R. G. Larson, Rheology: principles, measurements, and applications, VCH, New York, 1994 Search PubMed.
-
M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, 2003 Search PubMed.
- T. McLeish, Adv. Phys., 2002, 51, 1379–1527 CrossRef CAS.
- A. Ashkin, Biophys. J., 1992, 61, 569–582 CrossRef CAS PubMed.
- D. Mizuno, C. Tardin, C. F. Schmidt and F. C. MacKintosh, Science, 2007, 315, 370–373 CrossRef CAS PubMed.
- T. Toyota, D. A. Head, C. F. Schmidt and D. Mizuno, Soft Matter, 2011, 7, 3234–3239 RSC.
-
B. Alberts, A. Johnson, J. Lewis, D. Morgan, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, 6th edn, 2015, pp. 1–1342 Search PubMed.
-
L. D. Landau, E. M. Lifshitz and L. P. Pitaevski, Statistical physics, Pergamon Press, Oxford, New York, 3d rev. and enl. ed edn, 1980 Search PubMed.
- M. Reiner, Phys. Today, 1964, 17, 62 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) (where σ0 is the amplitude of the stress function) and the measurement of the resulting oscillatory shear strain, which would be in a form like γ(ω,t) = γ0(ω)
sin(ωt) (where σ0 is the amplitude of the stress function) and the measurement of the resulting oscillatory shear strain, which would be in a form like γ(ω,t) = γ0(ω)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt − φ(ω)), where γ0(ω) and φ(ω) are the frequency-dependent strain amplitude and the phase shift between the stress and the strain, respectively. The relationship between the shear complex modulus and the two experimental functions describing the stress and the strain is:46
sin(ωt − φ(ω)), where γ0(ω) and φ(ω) are the frequency-dependent strain amplitude and the phase shift between the stress and the strain, respectively. The relationship between the shear complex modulus and the two experimental functions describing the stress and the strain is:46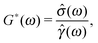
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (ω) and
(ω) and ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) (ω) are the Fourier transforms of σ(ω,t) and γ(ω,t), respectively. Note that, eqn (1) is of general validity; i.e., it applies to any temporal forms of the stress and the strain. In the particular case of sinusoidal functions eqn (1) is rewritten as:
(ω) are the Fourier transforms of σ(ω,t) and γ(ω,t), respectively. Note that, eqn (1) is of general validity; i.e., it applies to any temporal forms of the stress and the strain. In the particular case of sinusoidal functions eqn (1) is rewritten as: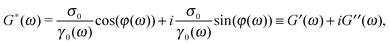

![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t) of an optically trapped micro-sphere involves the solution of a generalised Langevin equation in the form of:
(t) of an optically trapped micro-sphere involves the solution of a generalised Langevin equation in the form of: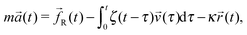
![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) (t) is its acceleration,
(t) is its acceleration, ![[small nu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0ea.gif) (t) is its velocity and
(t) is its velocity and ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) R(t) is the usual Gaussian white noise term, modelling stochastic thermal forces acting on the particle. The integral term, which incorporates a generalised time-dependent memory function ζ(t), represents viscous damping by the fluid. The last term on the right side of eqn (3) is the restoring force exerted by the OT (
R(t) is the usual Gaussian white noise term, modelling stochastic thermal forces acting on the particle. The integral term, which incorporates a generalised time-dependent memory function ζ(t), represents viscous damping by the fluid. The last term on the right side of eqn (3) is the restoring force exerted by the OT (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) OT = −κ
OT = −κ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t)) on the particle, when the confining field E(
(t)) on the particle, when the confining field E(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) generated by the OT is assumed to be harmonic:
) generated by the OT is assumed to be harmonic: 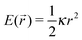 . Following the assumption made by Mason and Weitz in their seminal work that established the field of microrheology19 (i.e., that the Laplace-transformed bulk viscosity of the fluid
. Following the assumption made by Mason and Weitz in their seminal work that established the field of microrheology19 (i.e., that the Laplace-transformed bulk viscosity of the fluid ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) (s) is proportional to the microscopic memory function
(s) is proportional to the microscopic memory function ![[small zeta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e126.gif) (s) = 6πa
(s) = 6πa![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) (s), where a is the bead radius), eqn (3) can be solved for G*(ω) in terms of either of the following two time-averaged functions of the particle trajectory, i.e. the Normalised Mean-Square Displacement (NMSD):36
(s), where a is the bead radius), eqn (3) can be solved for G*(ω) in terms of either of the following two time-averaged functions of the particle trajectory, i.e. the Normalised Mean-Square Displacement (NMSD):36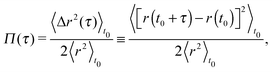
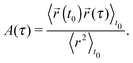

![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t). Fig. 3 shows the temporal behaviour of both the above functions in the case of an optically trapped microsphere suspended in a Newtonian fluid (i.e., water).
(t). Fig. 3 shows the temporal behaviour of both the above functions in the case of an optically trapped microsphere suspended in a Newtonian fluid (i.e., water).
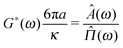
![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) (ω) and Â(ω) are the Fourier transforms of Π(τ) and A(τ), respectively. Notably, these two functions are simply related to each other both in the time- and in the frequency-domain: Π(τ) + A(τ) = 1 and iω
(ω) and Â(ω) are the Fourier transforms of Π(τ) and A(τ), respectively. Notably, these two functions are simply related to each other both in the time- and in the frequency-domain: Π(τ) + A(τ) = 1 and iω![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) (ω) + iωÂ(ω) = 1, respectively. Note that, eqn (6) is valid as long as the particle inertia (i.e., mω2) is negligible, which, in the case of micron sized particles (with m ≈ 10−15), is a reasonable assumption for frequency values ω ≲ MHz.
(ω) + iωÂ(ω) = 1, respectively. Note that, eqn (6) is valid as long as the particle inertia (i.e., mω2) is negligible, which, in the case of micron sized particles (with m ≈ 10−15), is a reasonable assumption for frequency values ω ≲ MHz.
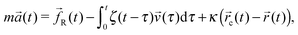
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) c(t) that is the position vector describing the driven motion of the optical trap center. Eqn (7) can be solved for G*(ω) in terms of the particle position
c(t) that is the position vector describing the driven motion of the optical trap center. Eqn (7) can be solved for G*(ω) in terms of the particle position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t) and the resulting expression is:
(t) and the resulting expression is: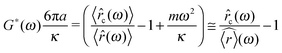
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) c(ω) and
c(ω) and ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) (ω) are the Fourier transforms of
(ω) are the Fourier transforms of ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) c(t) and
c(t) and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t), respectively. The brackets 〈⋯〉 denote the average over several independent measurements. For the last equality it has been considered that: (i) 〈
(t), respectively. The brackets 〈⋯〉 denote the average over several independent measurements. For the last equality it has been considered that: (i) 〈![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) c(ω)〉 ≡
c(ω)〉 ≡ ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) c(ω), the latter being the driving component, thus reproducible over several independent measurements, (ii)
c(ω), the latter being the driving component, thus reproducible over several independent measurements, (ii) 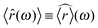 because of linearity of the involved operators, and (iii) the particle inertia is negligible. Note that, eqn (8) is of general validity, whatever the temporal form of
because of linearity of the involved operators, and (iii) the particle inertia is negligible. Note that, eqn (8) is of general validity, whatever the temporal form of ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) c(t).
c(t).
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) c(t) = ‖rc‖sin(βt), the particle displacement will assume a temporal form like
c(t) = ‖rc‖sin(βt), the particle displacement will assume a temporal form like ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t) = ‖r‖sin(βt − φ(β)); where ‖rc‖ and ‖r‖ are the amplitudes of the sinusoidal functions
(t) = ‖r‖sin(βt − φ(β)); where ‖rc‖ and ‖r‖ are the amplitudes of the sinusoidal functions ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) c(t) and
c(t) and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t), respectively. In this case, eqn (8) simplifies:
(t), respectively. In this case, eqn (8) simplifies: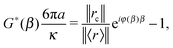
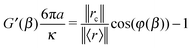
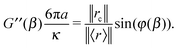
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t)〉|/D0 (see Fig. 5), where the brackets 〈⋯〉 denote the average over several independent measurements, but not over absolute time, since time-translation invariance is broken by periodic switching. The full viscoelastic spectrum of the fluid is resolved by combining the results obtained from steps (I) and (II).
(t)〉|/D0 (see Fig. 5), where the brackets 〈⋯〉 denote the average over several independent measurements, but not over absolute time, since time-translation invariance is broken by periodic switching. The full viscoelastic spectrum of the fluid is resolved by combining the results obtained from steps (I) and (II).

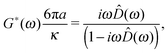
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) (ω) is the Fourier transform of D(t), with
(ω) is the Fourier transform of D(t), with ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t) being the particle position from the active trap.
(t) being the particle position from the active trap.


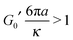
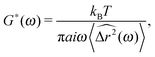
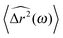 is the Fourier transform of the particle mean square displacement 〈Δr2(τ)〉t0.
is the Fourier transform of the particle mean square displacement 〈Δr2(τ)〉t0.

