Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bending elasticity of vesicle membranes studied by Monte Carlo simulations of vesicle thermal shape fluctuations
Samo
Penič
a,
Aleš
Iglič
b,
Isak
Bivas
c and
Miha
Fošnarič
*b
aLaboratory of Bioelectromagnetics, Faculty of Electrical Engineering, University of Ljubljana, Tržaška 25, 1000 Ljubljana, Slovenia
bLaboratory of Biophysics, Faculty of Electrical Engineering, University of Ljubljana, Tržaška 25, 1000 Ljubljana, Slovenia. E-mail: miha.fosnaric@fe.uni-lj.si; Fax: +386 1 4264 630; Tel: +386 1 4768 826
cInstitute of Solid State Physics, Bulgarian Academy of Sciences, 72 Tzarigradsko chaussee blvd., Sofia 1784, Bulgaria
First published on 20th April 2015
Abstract
The membrane bending stiffness of nearly spherical lipid vesicles can be deduced from the analysis of their thermal shape fluctuations. The theoretical basis of this analysis [Milner and Safran, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 4371–4379] uses the mean field approximation. In this work we apply Monte Carlo simulations and estimate the error in the determination of the bending stiffness due to the approximations applied in the theory. It is less than 10%. The method presented in this work can also be used to determine the changes of the bending stiffness of biological membranes due to their chemical and/or structural modifications.
1 Introduction
Biomembranes are one of the main building blocks of living matter. Due to their important role in biological systems, there is a large interest in their structure and functioning principles.A widely accepted description of the biomembrane structure is given by the model of Singer and Nicolson1 representing the biomembrane as a lipid bilayer embedded with integral proteins. One of the factors determining the functioning of biomembranes are their mechanical properties, which play an important role in defining intermembrane interactions, membrane fusion, the motion of cells in flow, etc. The mechanical properties of biomembranes are determined to a great extent by the mechanical properties of their lipid bilayers. The lipid bilayer can be considered as a simplified model of the biomembrane and theoretical and experimental investigations of the mechanical properties of lipid bilayers are continuously rising.2–5
In most cases the thickness of the lipid bilayer is much smaller than the typical dimension of the studied object (cell, vesicle, etc.) and the bilayer can be considered as a two-dimensional structure. The macroscopic mechanical properties of such membranes are determined by their stretching, bending, and shear moduli.6 In this paper we consider a special case of membranes with zero shear modulus, corresponding to a two-dimensional liquid. We assume that during the characteristic observation time, i.e. during the measurement, the number of amphiphilic molecules in each of the two monolayers comprising the bilayer does not change and that the volume enclosed by the membrane remains constant. This permits us to consider the studied object as an equilibrium structure. Note, however, that we do not impose a restriction for the membrane to be tensionless.
One of the most commonly used experimental methods for determining the bending stiffness of lipid membranes is the analysis of the thermal shape fluctuations of a nearly spherical lipid vesicle.7–15 The theoretical basis of this analysis was proposed by Milner and Safran16 by considering the fluctuating vesicle as an ensemble of non-interacting harmonic oscillators. The time mean squares of the amplitudes of these oscillators depend on several factors, including the lateral stretching of the membrane that induces a lateral membrane tension. When such time and position dependent membrane tension is taken into account, the Hamiltonian of the fluctuating vesicle is not a function of an ensemble of independent oscillators. In order to obtain that, a mean field approximation is used, where the fluctuations of the membrane tension are neglected and the fluctuating tension is replaced with its mean value. A question arises, whether this approximation provides adequate results. Recently, an essay on this topic was done by Bivas and Tonchev,17 who used the Bogolyubov inequalities and the method of the approximating Hamiltonian.18 Necessary conditions assuring the validity of the Milner and Safran theory were found. One of these conditions is the high enough value of the mean lateral tension of the vesicle membrane.
One of the aims of the presented work is the verification of the results of the Milner and Safran theory by means of Monte Carlo simulations of the shape fluctuations of a nearly spherical lipid vesicle. The results of the simulations are considered as experimental data whose accuracy increases with the increase in the length of the simulation. The obtained results show that the determination of the bending stiffness is possible using the theory of Milner and Safran with acceptable precision.
The analysis of simulations presented in this work can serve as a tool to quantitatively measure the changes of the bending stiffness of biological membranes due to the chemical and/or structural modifications of lipid bilayers. This can be, for example, the change of the composition of lipid molecules in the bilayer (multicomponent lipid bilayers), the insertion of inclusions (like peptides and other proteins) in the bilayer,19 or the polymer coating of the vesicle (like PEGylated20,21 and polyelectrolyte-grafted22,23 vesicles).
2 The model
2.1 Bending energy
We consider thermal fluctuations of a lipid vesicle in thermodynamic equilibrium. The membrane of the vesicle is a fluid lipid bilayer. For the bending energy Wb of the membrane we use the standard Helfrich expression6 for a tensionless membrane with a zero spontaneous curvature and a fixed topology (the contribution of the Gaussian curvature to the bending energy does not depend on the fluctuations): | (1) |
The lipid bilayer is on a timescale of thermal fluctuations impermeable for water molecules and due to the low compressibility of water we can assume the vesicle's volume to be constant during thermal fluctuations.
With thermal fluctuations some lateral stretching of the membrane occurs on the scale of phospholipid molecules, however, the energy required to significantly change the area of the membrane greatly exceeds the thermal energy kT (product of the Boltzmann constant and the absolute temperature), therefore we can assume that the overall area A of the membrane remains almost constant during thermal fluctuations (ΔA ≪ A).
2.2 Randomly triangulated surface
The membrane of the vesicle is described by a set of N vertices linked with bonds of flexible length d to form a closed, randomly triangulated, self-avoiding network.24–26 Lengths of the bonds can vary between their minimal value dmin and maximal value dmax. All vertices experience a hard-core repulsive potential at their mutual distances dmin.In our simulations the initial state of triangulation is a pentagonal dipyramid with all the edges divided into equilateral bonds so that the network is composed of 3(N − 2) bonds forming 2(N − 2) triangles. The system is initially thermalized – evolved into the nearly spherical equilibrium state using the Metropolis–Hastings algorithm (as described below).
The thermal fluctuations of the vesicle membrane are simulated by employing the Monte Carlo method, where Monte Carlo steps are vertex moves, assuring shape fluctuations, and bond flips, assuring lateral fluidity within the membrane. The vertex move includes a random displacement of the vertex within a sphere with radius s positioned at the center of the vertex. In this work we choose dmax/dmin = 1.7 and s/dmin = 0.15, resulting in a self-avoiding nearly spherical network with approximately one-half of vertex moves accepted. The bond flip involves four vertices of the two neighboring triangles. The bond shared by the neighboring triangles is cut and reestablished between the other two, previously unconnected, vertices.
The microstates of the vesicle are sampled according to the Metropolis–Hastings algorithm. To obtain the canonical ensemble representing the system in a thermodynamical equilibrium, each individual Monte Carlo step (vertex move or bond flip) is accepted with probability min[1,exp(−ΔE/kT)], where ΔE is the energy change due to the vertex move or bond flip.
Some discussion was done in the past on choosing an appropriate discretization of the bending energy on a triangulated surface (for example, see Section 2 in Gompper and Kroll, 1996,25 eqn (70) in Gompper and Kroll, 2004,24 or Ramakrishnan et al., 201126). In this work we used for the discretization of the bending energy (eqn (1)) the relation27,28
 | (2) |
 | (3) |
The volume of the vesicle is kept constant at the given value V0 by the constraint |V − V0| < εV, where εV must be small enough to fulfill the condition εV ≪ V0, but still not so small to completely suppress the out-of-plane shape fluctuations of the membrane. The choice of εV depends on the discretization and is in our work taken to be the volume of the tetrahedron consisting of equilateral triangles with areas A0/Nt, where A0 is the area of the spherical vesicle with volume V0 and Nt the number of triangles in the triangulated surface:
 | (4) |
2.3 Obtaining elastic properties through spectral analysis of thermal fluctuations
Using the theory of Milner and Safran16 the bending stiffness Kc of the membrane can be measured from the spectral analysis of thermal fluctuations of our randomly triangulated surface of the nearly spherical vesicle. Note that the bending stiffness κ is an input parameter in our simulations and that we used a different symbol (Kc) for the bending stiffness obtained from the spectral analysis of thermal fluctuations. From now on, to distinguish the two values κ and Kc, we name them the input bending stiffness and the measured bending stiffness, respectively.Let us consider our triangulated nearly spherical vesicle with volume V0 and let R0 be the radius of a sphere with the same volume. The length of the radial vector Ri(t) = R(ϑi,φi,t) from the origin to the vertex i at time t is then defined as
| R(ϑi,φi,t) = R0[1 + r(ϑi,φi,t)], | (5) |
Relative displacements r(ϑi,φi,t) are decomposed into a series with respect to the spherical harmonics Yml(ϑi,φi):
 | (6) |
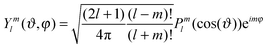 | (7) |
The complex coefficients uml(t) can then be calculated using the relation
 | (8) |
 | (9) |
The mean squared amplitudes of spherical harmonics 〈|uml|2〉 are calculated by averaging the |uml(t)|2 values over an ensemble of microstates of the vesicle in the thermal equilibrium. Using the expression of Milner and Safran,16
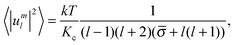 | (10) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) of the membrane can be obtained.
of the membrane can be obtained.
Note that eqn (10) were deduced for vesicles the membranes of which are lipid bilayers with a zero spontaneous curvature as well as for emulsion droplets the membranes of which are monolayers consisting of amphiphilic molecules with a zero spontaneous curvature.16 In the case of lipid bilayers Kc is the bending stiffness at free flip-flop15 (for the definition of bending elasticity at blocked and free flip-flop, see Helfrich6). If the stretching of the membrane of the emulsion droplet is high enough, then the sufficient condition for the validity of eqn (10) will be fulfilled.17 The same is valid for the stretched enough vesicle membrane.
Since the rhs of eqn (10) do not depend on the order of spherical harmonics m, the mean squared amplitudes of spherical harmonics obtained from simulations are first averaged over m and then the obtained values 〈|ul|2〉 are used on the lhs of eqn (10):
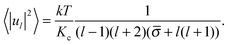 | (11) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) of the membrane together with their standard errors, the 〈|ul|2〉 from simulations are fitted with the formula of Milner and Safran (eqn (11)) using an inverse squared variance weighted nonlinear fit.
of the membrane together with their standard errors, the 〈|ul|2〉 from simulations are fitted with the formula of Milner and Safran (eqn (11)) using an inverse squared variance weighted nonlinear fit.
3 Results and discussion
For each set of parameters the system is initially thermalized into a nearly spherical vesicle and then the volume is fixed. The squared amplitudes of spherical harmonics |uml|2 are obtained from Monte Carlo simulations as described in Section 2.To obtain the ensemble of microstates that are statistically independent, the autocorrelations of squared amplitudes f(|uml|2,τ) are calculated with the autocorrelation function
 | (12) |
Fig. 1 shows the autocorrelation functions of the few lowest relevant modes for a system with N = 1127 vertices and input bending stiffness κ = 20kT. It can be seen that the longest decay times are for |um2|2i.e. the decay time decreases with the increasing degree of the spherical harmonics l, as expected. Let us denote the largest decay time of all the relevant modes for a given system with N vertices as τN (in Fig. 1 we have τ1127 ≈ 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). The largest decay time τN decreases with the increasing input bending stiffness κ, while it increases with the number of vertices N in the triangulated network.
000). The largest decay time τN decreases with the increasing input bending stiffness κ, while it increases with the number of vertices N in the triangulated network.
The decay time τN is important for our spectral analysis since it can be used to estimate the “time” interval between two microstates that can be regarded as statistically uncorrelated. The ensemble of statistically uncorrelated states is needed for the estimation of the standard errors together with the means of squared amplitudes of spherical harmonics. Those standard errors of 〈|uml|2〉 have to be taken into account in the fitting procedure in eqn (11), to obtain relevant values of the bending stiffness Kc and the dimensionless mean lateral tension ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) of the membrane. In this work the interval between two consecutive microstates in an ensemble of statistically uncorrelated states, i.e. between two consecutive “measurements”, was always larger than three times the largest decay time τN. In Fig. 1, for example, the x-axis spans the “time” interval between consecutive measurements for a system with N = 1127 and κ = 20kT.
of the membrane. In this work the interval between two consecutive microstates in an ensemble of statistically uncorrelated states, i.e. between two consecutive “measurements”, was always larger than three times the largest decay time τN. In Fig. 1, for example, the x-axis spans the “time” interval between consecutive measurements for a system with N = 1127 and κ = 20kT.
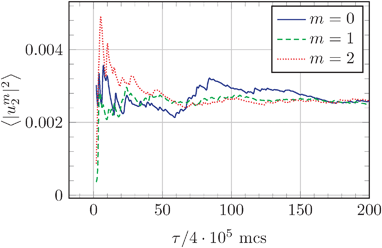
When squared amplitudes |uml|2 are averaged over the ensemble of microstates, the obtained 〈|uml|2〉 with the same order m converge towards the same value, as shown in Fig. 2 for |um2|2. This is in accordance with the theory of Milner and Safran (rhs of eqn (10) are independent of m). Also Fig. 3 shows that the mean squared amplitudes obtained from simulations are independent of m. Note that our previously reported31 inability to observe this independence of 〈|uml|2〉 on m was a result of numerical errors.
The measured bending stiffness Kc and the dimensionless mean lateral tension ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) are obtained from the mean squared amplitudes as described in Section 2.3. The result of a fitting procedure for Kc is shown in Fig. 4 as a function of the maximal degree l of spherical harmonics used in the fitting of 〈|ul|2〉 in eqn (11) (eqn for all values from l = 2 up to the maximal degree l are taken into account).
are obtained from the mean squared amplitudes as described in Section 2.3. The result of a fitting procedure for Kc is shown in Fig. 4 as a function of the maximal degree l of spherical harmonics used in the fitting of 〈|ul|2〉 in eqn (11) (eqn for all values from l = 2 up to the maximal degree l are taken into account).
The measured bending stiffness Kc is shown in Fig. 5 as a function of the number of vertices N of the triangulated surface. As expected, the difference between the measured bending stiffness Kc and the input bending stiffness κ = 20kT decreases as we increase the number of vertices in the triangulation (i.e. as we increase the resolution of the discretization).
Fig. 5 also shows the obtained values of the dimensionless mean lateral tension ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) for the same sets of measurements. Let us note that the measured Kc should not depend on the value of
for the same sets of measurements. Let us note that the measured Kc should not depend on the value of ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) . The mean lateral tension in the membrane depends on the value of the fixed volume of the vesicle, i.e. how much the vesicle is “swollen”. This is somewhat arbitrarily chosen by picking a random microstate in the thermodynamical equilibrium when fixing the volume and starting the measuring procedure for Kc and
. The mean lateral tension in the membrane depends on the value of the fixed volume of the vesicle, i.e. how much the vesicle is “swollen”. This is somewhat arbitrarily chosen by picking a random microstate in the thermodynamical equilibrium when fixing the volume and starting the measuring procedure for Kc and ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) . As expected, the exact choice of the equilibrium microstate used when fixing the volume, i.e. the value of
. As expected, the exact choice of the equilibrium microstate used when fixing the volume, i.e. the value of ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) , does not observably influence the measured Kc.
, does not observably influence the measured Kc.
Fig. 6 shows the relative difference between the measured and the input bending stiffness, Kc/κ − 1, for different values of the input bending stiffness κ. It can be seen that increasing the input bending stiffness decreases the mismatch between the input and the measured bending stiffness. Note that, as already reported above, the correlation times of squared amplitudes decrease with the increasing bending stiffness of the membrane.
 | ||
| Fig. 6 Relative difference between the measured and the input bending stiffness as a function of the input bending stiffness for the membrane triangulated with N = 1447 vertices. | ||
A group of methods for the investigation of lipid–water systems exists, the results of which are explained by the fluctuations of the membranes of these systems. These are the different kinds of scattering: neutron,32,33 laser light,34etc. Zilman and Granek,32,33 investigating the neutron scattering in the lamellar lipid–water phase, used periodic boundary conditions and developed the out-of-plane fluctuations of the layers in the Fourier series. The periodic boundary conditions resemble monodisperse vesicular suspensions, with their repeating distance being the analog of the radius of the vesicle. The authors determined the decay rate of different fluctuation modes from their experimental data. Due to the absence of real timescale in our Monte Carlo simulations, we cannot determine the true values of these decay rates from simulations and a direct comparison with the experimental results cannot be made. As already noted in Section 2.2, real timescale could be introduced in our simulations through the lateral diffusion of vertices on the randomly triangulated surface, which is beyond the scope of this work.
Brocca, et al.34 have investigated the shape fluctuations of large unilamellar lipid vesicles using laser light scattering. The analysis of their experimental results permits the simultaneous deduction of the time mean squares 〈|uml(t)|2〉 (see eqn (10)) of the amplitudes uml(t) and the decay rate of these amplitudes. According to the theory of Milner and Safran16 a relation between these two quantities exists, however the results obtained by Brocca, et al.34 do not satisfy it. This discrepancy could be explained by the fact that in the systems studied by Brocca, et al.34 the requirements, assuring the validity of the theory of Milner and Safran are not fulfilled: the thickness of the membrane needs to be much less than the radius of the vesicle; the viscosity of the liquid environment inside and outside the vesicle needs to be constant; etc. It must be noted that these authors used the theory of Milner and Safran that does not take into account the dissipation of the energy due to the friction between the monolayers of the bilayer, which yields a double-exponential decay of each fluctuation mode15 instead of the mono-exponential one in the theory of Milner and Safran.16 The results of our Monte Carlo simulations cannot be used for the explanation of the discrepancy found by Brocca, et al.34 As in the case when the data of Zilman and Granek32,33 were considered, the reason is the fact that our data from the simulations do not permit the determination of the true decay rate of the fluctuation modes.
4 Conclusion
The analysis of thermally induced shape fluctuations of a nearly spherical giant lipid vesicle is one of the commonly used methods to determine the bending stiffness of the vesicle's membrane. The theoretical basis of this analysis, proposed by Milner and Safran,16 uses the mean field approximation. In the present work, the error of the determination of the bending stiffness due to the approximations used in the theory was estimated.Monte Carlo simulations of the fluctuating nearly spherical vesicle have been performed using a randomly triangulated surface. The results for the time mean squares of the amplitudes of the fluctuations, obtained from the simulations, can be determined with an arbitrarily high precision, depending only on the length of the simulation. One of the parameters in the simulations is the input value of the bending stiffness. The obtained time mean squares of the amplitudes of the fluctuations can be considered as experimental values, which can be used for the determination of the output value of the bending stiffness by means of the theory of Milner and Safran. The theory would be “exact” if the output value of the bending stiffness would have been equal to the input one. Our results show that the difference between the two values of the bending stiffness decreases with the increase of the resolution of the triangulated network and can be well below 10%.
Therefore, we can conclude that the theory of Milner and Safran can be successfully used in the determination of the bending stiffness of the membrane of a nearly spherical lipid vesicle. According to our results, the errors due to the approximations adopted in the theory are less than 10%.
In conclusion, the analysis presented in this work can be a useful tool to predict the change of the bending stiffness of biological membranes due to their chemical modification. Altering the properties of the triangulated surface and/or introducing other membrane-interacting objects in the simulations, and then measure the change of the bending stiffness, offers many useful applications. Multicomponent lipid bilayers, membranes decorated with inclusions like peptides, polymer coated vesicles like PEGylated and polyelectrolyte-grafted vesicles, just to name a few.
Acknowledgements
The authors wish to acknowledge the Slovenian Research Agency grants (Grant No. P2-0232). MF thanks Sylvio May and Dan Kroll for stimulating discussions.References
- S. J. Singer and G. L. Nicolson, Science, 1972, 175, 720–731 CAS.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS PubMed.
- S. A. Safran, Adv. Phys., 1999, 48, 395–448 CrossRef CAS PubMed.
- J. F. Nagle, Faraday Discuss., 2013, 161, 11–29 RSC.
- R. Dimova, Adv. Colloid Interface Sci., 2014, 208, 225–234 CrossRef CAS PubMed.
- W. Helfrich, Z. Naturforsch., 1973, 28, 693–703 CAS.
- M. Schneider, J. Jenkins and W. Webb, J. Phys., 1984, 45, 1457–1472 CAS.
- H. Engelhardt, H. Duwe and E. Sackmann, J. Phys. Lett., 1985, 46, 395–400 CrossRef CAS.
- I. Bivas, P. Hanusse, P. Bothorel, J. Lalanne and O. Aguerre-Chariol, J. Phys., 1987, 48, 855–867 Search PubMed.
- J. Faucon, M. D. Mitov, P. Méléard, I. Bivas and P. Bothorel, J. Phys., 1989, 50, 2389–2414 Search PubMed.
- T. Pott and P. Méléard, Europhys. Lett., 2002, 59, 87 CrossRef CAS.
- J. Pécréaux, H.-G. Döbereiner, J. Prost, J.-F. Joanny and P. Bassereau, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 13, 277–290 CrossRef PubMed.
- R. Rodríguez-García, L. R. Arriaga, M. Mell, L. H. Moleiro, I. López-Montero and F. Monroy, Phys. Rev. Lett., 2009, 102, 128101 CrossRef.
- R. S. Gracià, N. Bezlyepkina, R. L. Knorr, R. Lipowsky and R. Dimova, Soft Matter, 2010, 6, 1472–1482 RSC.
- I. Bivas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 061911 CrossRef.
- S. T. Milner and S. A. Safran, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 4371–4379 CrossRef CAS.
- I. Bivas and N. S. Tonchev, J. Phys.: Conf. Ser., 2014, 558, 012020 CrossRef.
- J. G. Brankov, D. M. Danchev and N. S. Tonchev, Theory of Critical Phenomena in Finite-Size Systems: Scaling and Quantum Effects, Series in Modern Condensed Matter Physics, World Scientific, Singapore, 2000, ch. 2, vol. 9 Search PubMed.
- V. Kralj-Iglič, V. Heinrich, S. Svetina and B. Žekš, Eur. Phys. J. B, 1999, 10, 5–8 CrossRef.
- M. Wang and M. Thanou, Pharmacol. Res., 2010, 62, 90–99 CrossRef CAS PubMed.
- D. Needham and D. H. Kim, Colloids Surf., B, 2000, 18, 183–195 CrossRef CAS.
- F. Quemeneur, M. Rinaudo, G. Maret and B. Pépin-Donat, Soft Matter, 2010, 6, 4471–4481 RSC.
- S. Sennato, D. Truzzolillo and F. Bordi, Soft Matter, 2012, 8, 9384–9395 RSC.
- G. Gompper and D. M. Kroll, Statistical Mechanics of Membranes and Surfaces, World Scientific, Singapore, 2004, pp. 359–426 Search PubMed.
- G. Gompper and D. M. Kroll, J. Phys. I, 1996, 6, 1305–1320 CrossRef.
- N. Ramakrishnan, P. B. S. Kumar and J. H. Ipsen, Macromol. Theory Simul., 2011, 20, 446–450 CrossRef CAS PubMed.
- C. Itzykson, Proceedings of the GIFT Seminar, Jaca 85, World scientific, Singapore, 1986, pp. 130–188 Search PubMed.
- D. Espriu, Phys. Lett. B, 1987, 194, 271–276 CrossRef CAS.
- H. Noguchi and G. Gompper, Phys. Rev. Lett., 2004, 93, 258102 CrossRef.
- H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011901 CrossRef.
- M. Fošnarič, S. Penič, A. Iglič and I. Bivas, Advances in Planar Lipid Bilayers and Liposomes, Academic Press, 2013, vol. 17, pp. 331–357 Search PubMed.
- A. G. Zilman and R. Granek, Phys. Rev. Lett., 1996, 77, 4788 CrossRef CAS.
- A. G. Zilman and R. Granek, Chem. Phys., 2002, 284, 195–204 CrossRef CAS.
- P. Brocca, L. Cantù, M. Corti, E. Del Favero and S. Motta, Langmuir, 2004, 20, 2141–2148 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |