 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanical response of adherent giant liposomes to indentation with a conical AFM-tip
Edith
Schäfer
,
Marian
Vache
,
Torben-Tobias
Kliesch
and
Andreas
Janshoff
*
Department of Chemistry, University of Goettingen, Goettingen, Germany. E-mail: ajansho@gwdg.de
First published on 28th April 2015
Abstract
Indentation of giant liposomes with a conical indenter is described by means of a tension-based membrane model. We found that nonlinear membrane theory neglecting the impact of bending sufficiently describes the mechanical response of liposomes to indentation as measured by atomic force microscopy. Giant vesicles are gently adsorbed on glassy surfaces via avidin–biotin linkages and indented centrally using an atomic force microscope equipped with conventional sharp tips mounted on top of an inverted microscope. Force indentation curves display a nonlinear response that allows to extract pre-stress of the bilayer T0 and the area compressibility modulus KA by computing the contour of the vesicle at a given force. The values for KA of fluid membranes correspond well to what is known from micropipet suction experiments and inferred from membrane undulation monitoring. Assembly of actin shells inside the liposome considerably stiffens the vesicles resulting in significantly larger area compressibility modules. The analysis can be easily extended to different indenter geometries with rotational symmetry.
1 Introduction
Cell mechanics plays a pivotal role in many biological processes such as exo- and endo-cytosis, tether formation, cell adhesion, growth, and migration. The cell's mechanical response to external deformation originates mainly from the plasma membrane firmly attached to the contractile cortical cytoskeleton, which is composed of cross-linked actin filaments as well as motor proteins such as myosin II.1–7 It is therefore of great interest to understand how cells respond to forces and how these forces are transduced into biochemical signals to generate a biological response.1–3In order to better understand the intricate nature of active shells surrounding living cells, model membranes were frequently employed to reduce complexity, while still mimicking the essential physical properties of the plasma membrane connected to the cytoskeleton.8,9 Among the different model membranes, giant unilamellar vesicles (GUVs) are often employed for bottom-up strategies to mimic and investigate the mechanical properties of cells.10,11 In this context, mechanical properties of lipid bilayers were inferred from micropipet suction experiments,12–14 flicker spectroscopy15–17 and atomic force microscopy.18 Depending on the used method different aspects of membrane mechanics were accessible such as area compressibility modules and lysis tension form micropipet suction, bending rigidity from flicker spectroscopy or Young's modules and breakthrough forces obtained from indentation experiments. In the context of mimicking eukaryotic cells it is also desirable to assemble an actin-based cortex at the inner leaflet of a giant liposome. Sackmann and coworkers pioneered in forming thin actin shells inside giant lioposomes. Monitoring membrane undulations allowed them to assess bending and area compressiblity modules of the composite shell.15 Apart from the early work of Sackmann, vesicles have successfully been coated with an actin cortex by gentle hydration,19 electroformation,15 inkjet electroformation,20,21 the inverted emulsion method22,23 and hydration of lipids spread on an agarose hydrogel.24 Besides passive actin networks also contractile actomyosin cortices were successfully reconstituted in cell-sized vesicles.25
Generally, membrane mechanics compiles contributions from pre-stress, area dilatation and bending elasticity. It is safe to assume that vesicles can be described as fluid-filled capsules with a thin wall and low water permeability. Therefore, stretching of the bilayer dominates at larger strains, while pre-stress and bending prevail only at small deformations. This is due to the small bending modules of lipid bilayer on the order of only few kBT, while the area compressibility modulus is on the order of 0.1 N m−1. Interestingly, however, in current literature different ways exist to describe the mechanical properties of liposomes often depending on the experimental technique that is used to assess the mechanical parameters. While researchers using atomic force microscopes to indent sessile liposomes frequently rely on contact mechanics such as the generic Hertz model to describe the deformation,26,27 micropipet suction experiments and parallel plate compression of giant liposomes are generally interpreted in terms of thin plate or shell theory in conjunction with Young–Laplace's equation.18,28 The Hertz or Sneddon approaches, which are often the model of choice to describe cellular mechanics in the context of AFM experiments, assume that the capsules behave like a solid, homogeneous continuum and therefore provide a single parameter to describe the mechanics of the material, the Young's modulus.29,30 Although this is a convenient way to analyse the deformation at low strain its underlying assumptions are clearly unfulfilled in the context of membranes due to the shell-like structure of liposomes and cells. Especially at larger strain conventional contact mechanics models fail to match the experimental data sufficiently well. Cells with a thick cortex might, however, be successfully be described by models borrowed from contact mechanics if the penetration depth is kept low.
However, also more realistic models exist describing, for instance, point load forces exerted on surface bound capsules or parallel plate compression.28,31–33 The corresponding theoretical models employ shell mechanics showing that bending governs the mechanical response at low strain smaller than the thickness of the shell, while at larger strain nonlinear contributions from area dilatation of the shell rule especially if the enclosed volume is conserved. If the enclosed volume is variable bending at larger strain adopts a square root dependence.31 The treatment of these problems is often very involved since it is necessary to compute the exact shape of the liposome during indentation, which can be difficult due to the contact of the fluid membrane with the indenter. Therefore, limiting cases such as point-load forces or parallel plate compression are usually considered.28,32,33
In atomic force microscopy experiments, however, two main indenter geometries dominate, spheres and tips with conical or pyramidal shape. The latter ones are the most frequently used ones since this geometry is also employed to image the specimen by scanning the surface in conventional atomic force microscopy experiments. It is therefore desirable to find a solution that describes the indentation of a spherical liposome with conical indenter in the context of a tension-based model capturing the essential physics of lipid bilayers enclosing a fixed volume.
Here, we present a straightforward numerical scheme that allows to assess the exact shape of liposomes and the force response upon indentation by solving the Young–Laplace equation. We neglect bending contributions to the elastic response and assume homogeneous tension and constant volume. Membrane theory is used to describe the contour of the liposome as a function of indention depth allowing us to generate a fitting function to access both tension (pre-stress) T0 and area compressibility modulus KA from experimental force indentation curves. We could largely reproduce KA values of GUVs composed of fluid lipids such as DOPC obtained from micropipet suction experiments and found that the presence of an actin shell stiffens the composite membrane shell considerably. The work is based on an earlier study using parallel plates to compress the liposomes.28 This is, however, an experimentally less convenient way to assess the mechanical properties of liposomes. For one reason, it is difficult to realize exact parallel plate conditions due to the inherent tilt of the cantilever necessary for monitoring cantilever deflection by laser reflection. Secondly, it is difficult to combine optical microscopy with AFM experiments due to tilt compensation an impossible to image a sample with a tipless cantilever.
2 Theoretical analysis
Fig. 1 illustrates the envisioned geometry of a spherical liposome subject to indentation with a conical indenter. The shape of the deformed vesicle should be axisymmetric and the initial radius of the spherical vesicle prior to compression is Rv. The contact region with the flat substrate extends from s0 → s1. The free contour ranges from s1 → s4 with largest radius R0 at s2 and largest height z at s3. The contour is parametrised by the angle β between the surface normal and the z-direction.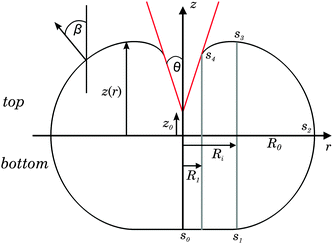 | ||
| Fig. 1 Schematic illustration and parametrisation of a liposome subject to indentation with a conical indenter (red). | ||
The following treatment is partly based on the work of Yoneda,38 Evans and Skalak,39 Bando et al.33,40 and Sen et al.41 The goal is to compute force indentation curves from the deformed shape. Central assumptions are negligible bending stiffness, uniform tension and constant volume.
2.1 Contour of the vesicle
The shape of the indented liposome can be computed under the assumption that tension is uniform, the enclosed volume fixed and pressure across the membrane conserved. In general, pressure relates to tension T according to Young–Laplace's law: | (1) |
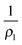 and
and  denote the principal curvatures at each point of the contour. Considering a small line element ds of the meridian at an arbitrary point O(r,z) on the contour, in which dr is the projection of ds on the r-axis (dr = ds
denote the principal curvatures at each point of the contour. Considering a small line element ds of the meridian at an arbitrary point O(r,z) on the contour, in which dr is the projection of ds on the r-axis (dr = ds![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β), we find that r = ρ2
β), we find that r = ρ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β and ds = ρ1dβ. Eliminating ds leads to
β and ds = ρ1dβ. Eliminating ds leads to | (2) |
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β. Small angles allow for
β. Small angles allow for  . Therefore, eqn (1) can be written as
. Therefore, eqn (1) can be written as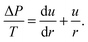 | (4) |
Since  is constant we can integrate eqn (4) to obtain
is constant we can integrate eqn (4) to obtain
 | (5) |
 | (6) |
| β = 0 at r = Ri. | (7) |
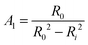 | (8) |
 | (9) |
In region 2 (s2 → s3) the free contour is created from the boundary conditions:41,42
 | (10) |
| β = 0 at r(s3). | (11) |
Hence,
 | (12) |
 | (13) |
Since the contour is continuous at R0 we find that r(s3) = Ri and therefore A1 = A2 and B1 = B2. A3 and B3 for region 3 corresponding to s3 → s4 up to the contact with the indenter with a half opening angle of θ are obtained from the following boundary conditions:
| β = 0 at r = Ri | (14) |
 | (15) |
 | (16) |
 | (17) |
Continuity of solutions for eqn (5) in s3 requires
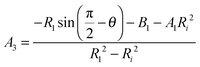 | (18) |
 | (19) |
Once the radii R0, Ri, and R1 are found, the free contour can be readily obtained from the following identity:
 | (20) |
Integrating eqn (20) numerically in the corresponding regions (s1 → s2 using u1(r), s2 → s3 using u2(r) = u1(r), and s3 → s4 using u3(r)) results in the free contour z(r) of the vesicle subject to indentation. The remaining contour is defined by the boundaries, a flat substrate at the bottom and the conical indenter at the top.
The goal is now to find expressions for R0, R1, and Ri as a function of the distance between the tip of the indenter an the flat base plate at the bottom. Three conditions apply to an indented liposome, essentially allowing to compute the corresponding force-indentation curve (f(δ)). These force-indentation curves depend only on two mechanical parameters of the membrane, pre-stress T0 and area compressibility modulus KA. Fitting of these parameters to the experimental data permits to estimate tension and area compressibility of giant liposomes. The following section describes the three conditions, which are needed to compute the free contour, i.e. to find a set of parameter R0, R1, and Ri at a given force.
2.2 Constraints and force balances
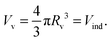 | (21) |
This is the first condition to solve the free contour. For computing the volume of the indented liposome we divide it into a top and bottom solid of revolution (see Fig. 1) leading to Vind = Vtopind + Vbottomind. Using the method of washers, we can numerically compute the volume of the top part Vtopind from the following sum:
 | (22) |
 . The volume of the bottom part of the compressed liposome Vbottomind is:
. The volume of the bottom part of the compressed liposome Vbottomind is: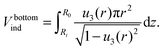 | (23) |
The following section provides the two additional conditions that are required to calculate all three parameters R0, R1, and Ri of the full contour at any given force.
 . KA is the area compressibility modulus, ΔA = Aind − Av the difference between the actual area Aind and the initial area prior to compression Av. T0 is the membrane tension or pre-stress. The force balance of the top part in the z-direction is:41
. KA is the area compressibility modulus, ΔA = Aind − Av the difference between the actual area Aind and the initial area prior to compression Av. T0 is the membrane tension or pre-stress. The force balance of the top part in the z-direction is:41 | (24) |
 | (25) |
The next task will be to find an expression for the actual surface area Aind of the liposome as a function of indentation depth δ.
2.3 Actual surface area Aind of the vesicle
In order to account for the in-plane stretching of the membrane during indentation the actual area needs to be calculated as a function of indentation depth. The area Av prior to indentation is 4πRv2. The actual area Aind is divided again into the top Atop and bottom part Abot of the liposome according to Fig. 1: | (26) |
 | (27) |
2.4 Indentation depth
The indentation depth in the center at r = 0 is readily obtained from the contour, i.e. from integrating eqn (20) in two regions of the free contour: | (28) |
The contour in region s1 → s3 gives rise to the first integral, while the contour along the path s3 → s4 produces the second integral of eqn (28).
2.5 Procedure to compute shape and force response
The shape of the indented liposome and the corresponding force indentation curves are now obtained from the following procedure:40(1) A value for the force f is assigned.
(2) Potential values for the radii R1, Ri, and R0 are guessed.
(3) The contour is calculated by numerically solving the system of eqn (21), (24) and (25) for the three parameters R1, Ri, and R0 to provide u1 = u2 and u3.
(4) The corresponding indentation depth δ is calculated from eqn (28).
(5) The force value is changed by a given increment using the previous set of radii (R1, Ri, and R0) as new starting values. The scheme is continued with item (3).
In essence, the three unknown parameters R1, Ri, and R0 are obtained for a given force by solving the system of nonlinear equations comprising force balances (eqn (24) and (25)) and volume constraint (eqn (21)). Once the three parameters are estimated using a minimization procedure such as the trust-region-dogleg or Levenberg–Marquardt algorithm the corresponding indentation depth can be calculated. Afterwards the force is changed by a small increment and the procedure repeated. The numerical procedure is more stable if starting with the highest load force.
2.6 Bending
The deformation of a liposome formed by a fluid lipid bilayer can be either an in-plane stretching and shear or an out-of-plane bending. Biological membranes are characterized by a low resistance to bending and shearing so that stretching is avoided and vesicles deform either in pure bending or in-plane shear. Generally, in spherical shells stretching cannot be avoided. Especially in biological systems the capsules are filled with liquid and display only a limited permeability of the shell material. The incompressibility of the fluid inside the capsule requires volume conservation at all times during deformations. As a consequence, conservation of the volume enclosed by the capsule inevitably leads to in-plane stretching of the shell. Stretching of the shell is by far more energy costly than bending also mirrored in the elastic constants that are many orders of magnitude apart (KA ≈ 0.1 N m−1vs. κ ≈ 10−19 N m). Therefore, bending has been neglected in our analysis as an appreciable energy contribution since the volume constraint forces the membrane to laterally dilate in order to maintain its enclosed volume upon indentation. Here, we ignore the fact that at the tip of the conical indenter at r = 0 curvature becomes infinite. In reality the tip has a finite curvature around 20–60 nm (MLCT cantilever). Stretching energy Estr relates to bending energy Ebend for point load forces roughly as .31 The bilayer is extremely thin d ≈ 5 nm and the radius of the liposome on the order of several micrometers. Therefore, bending only plays a role at the tip of the cantilever where the curvature is large. Since the tip of the cone is entirely wrapped with a bilayer, which occurs already at low indentation depth (few nm), the energy contribution due to bending decreases with increasing indentation depth since the cone widens. Hence, bending is not the reason for the observed force indentation curves showing a nonlinear increase of force with penetration depth. Generally, since the bilayer is very thin, the bending module is rather small κ ≈ 10−19 J so that at large indentation (δ ≫ d) the nonlinear stretching term dominates as long as the volume constraint holds. Moreover, it has been shown that ‘leaky’ capsules indented by a point load force display a square root dependence on indentation depth (F ∝ δ1/2), while stretching usually obeys a cubic dependency on indention (F ∝ δ3) as found also in our experiments (vide infra).44 Local bending might play a role at very low strain, in the order of the thickness of the bilayer, but pre-stress in the bilayer originating from adhesion generates a capsule stiffness (≈0.1 N m−1) orders of magnitude larger than those predicted by Reissner theory (≈10−5 N m−1) assuming pure bending due to a point load force.31
.31 The bilayer is extremely thin d ≈ 5 nm and the radius of the liposome on the order of several micrometers. Therefore, bending only plays a role at the tip of the cantilever where the curvature is large. Since the tip of the cone is entirely wrapped with a bilayer, which occurs already at low indentation depth (few nm), the energy contribution due to bending decreases with increasing indentation depth since the cone widens. Hence, bending is not the reason for the observed force indentation curves showing a nonlinear increase of force with penetration depth. Generally, since the bilayer is very thin, the bending module is rather small κ ≈ 10−19 J so that at large indentation (δ ≫ d) the nonlinear stretching term dominates as long as the volume constraint holds. Moreover, it has been shown that ‘leaky’ capsules indented by a point load force display a square root dependence on indentation depth (F ∝ δ1/2), while stretching usually obeys a cubic dependency on indention (F ∝ δ3) as found also in our experiments (vide infra).44 Local bending might play a role at very low strain, in the order of the thickness of the bilayer, but pre-stress in the bilayer originating from adhesion generates a capsule stiffness (≈0.1 N m−1) orders of magnitude larger than those predicted by Reissner theory (≈10−5 N m−1) assuming pure bending due to a point load force.31
3 Results and discussion
Fig. 2 shows simulated force indentation curves and contour plots of a liposome subject to indention with a conical indenter as a function of different parameter sets. The influence of the area compressiblilty modulus KA on the force response of a liposome is shown in Fig. 2A, while the impact of pre-stress T0 is displayed in Fig. 2B. Clearly a rise in KA results in a steeper slope at large strain, while increasing the pre-stress T0 leads to stiffening at low indentation depth. Fig. 2C shows how the two radii Ri and R1 increase with indention depth. While Ri rapidly grows at low indention depth, R1 follows a linear trend as one would expect for wetting of a cone with an unstressed membrane.In Fig. 2D and F we show the influence of indenter geometry on the expected force indention curves. A flat or blunt indenter does not need to penetrate as deep as a sharp, needle-like indenter to achieve the same force response from the liposome. A blunt indenter, however, forces the liposome into a more pancake-like geometry producing larger radii R0, Ri and R1, while sharper indenters reach deep inside the vesicle. Fig. 2E illustrates the shape of the liposome at different pre-set forces. It becomes clear that both flattening of the shell and deeper penetration takes place. Notably, rupture of membranes consisting of two phospholipid leaflet occurs at an area dilatation 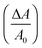 of merely 2–5% corresponding roughly to the shape shown in Fig. 2E for the largest indentation depth.
of merely 2–5% corresponding roughly to the shape shown in Fig. 2E for the largest indentation depth.
The experimental setup used for indentation experiments is illustrated in Fig. 3A. We used a conventional atomic force microscope with square-based pyramidal tips (MLCT) mounted on an inverted optical microscope. Tip height was 2.5–8 μm, tip radius in between 20–60 nm and the nominal spring constant of the cantilver was 0.03 N m−1. We modeled the pyramidal tip with a cone assumed a half opening angle of 18°. Immobilization of vesicles is achieved as previously described and detailed in the experimental section (Fig. 3B). In brief, small amounts of biotinylated phospholipids are used to link the liposome gently to the surface functionalized with avidin and passivated with casein to prevent spreading of the GUVs. Fig. 3C and D show bright field and confocal images of an adhered vesicles demonstrating that only a small contact zone is formed with the glassy substrate. In Fig. 3C also the cantilever is visible and the tip (arrow) is placed over the center of the liposome prior to indentation experiment. Fig. 3D shows z-stacks of the sessile liposome recorded with a confocal microscope (Olympus FluoView, FV1000) placed under the AFM prior to indentation and at 2 nN load force (overlay). Indentation or compression experiments do not show a pronounced hysteresis, which confirms our most important assumption that the volume does not change during indentation. Recently, we showed that giant liposomes can be continuously compressed without loosing volume.28Fig. 4 shows in sparse data representation (one marker every 70 data points) a typical force indentation curve (grey dots) of a giant liposome. The red continuous line represents a fit (Simplex algorithm followed by Levenberg–Marquardt) according to our tension model providing an area compressibility modulus of about KA = 0.026 ± 0.001 N m−1 and a relatively high tension of T0 = 0.76 ± 0.006 mN m−1. The mean area compressibility modulus from 7 independent measurements was KA = 0.04 ± 0.02 N m−1.
The area compressibility modulus KA of membranes determines the amount of elastic energy required to laterally stretch or compress a lipid bilayer. It is an intrinsic property of the lipid bilayer and is related to the surface tension γ of the interface between the aqueous phase and the aliphatic chains of the phospholipids (KA ≈ 4γ). The bending modulus of the bilayer κ can also be inferred from the area compressibility modulus through the thickness d of the bilayer (KA ≈ κd−2). Albeit the bending modulus of the bilayer is extremely small on the order of few kBT, the associated area compressibility modulus suggests a laterally almost inextensible material. The pre-stress in the sessile liposome can be largely attributed to adhesion and the associated area dilatation.23,28,45,46 Since the liposomes change their shape from a sphere in solution to a truncated sphere upon adhesion, their surface area increases in order to keep the enclosed volume constant. This increase in surface area essentially generates a finite membrane tension  , the largest contribution to the pre-stress T0.
, the largest contribution to the pre-stress T0.
Generally, a number of error sources need to be considered when extracting mechanical parameters from force indentation experiments. Central indentation is mandatory otherwise the vesicle has space to ‘escape’ the load exerted by the AFM cantilever. This leads to systematical lower KA values. Moreover, adhesion forces of the vesicle need to be as low as possible to ensure that the central assumptions in Section 2 are not violated. Since we could not obtain conical tips with a spherical base attached to soft cantilevers for our experiments the use of cones with a squared base also slightly changes the outcome compared to those with a circular base. Indentation depth is limited by the tip height (2.5–8 μm) and the lysis tension of the bilayer (≈10 mN m−1). Blunter tips allow to exert larger forces.
We also investigated what happens if the shell of the liposome is reinforced with an inner layer of actin. The procedure has previously been characterized in detail.28 In general, the additional actin shell forms a composite with the outermost membrane and by this might contribute to a stiffening of the structure. Depending on the thickness of the shell and the coupling to the bilayer this is detectable by force compression experiments.28
Fig. 5 shows typical force indentation experiments with two vesicles, one without actin (circles) and one with a clearly visible actin shell (squares). The plots show force f as a function of the dimensionless indentation δ/Rv to account for the two different radii of the two vesicles and thereby illustrate the substantial stiffening due to the presence of actin in a single graph.
 | ||
| Fig. 5 (A) Typical experimental force indentation curve of GUVs with an actin shell (filled squares) subject to fitting of the tension-based model (green line) resulting in T0 = 0.53 ± 0.02 mN m−1 and KA = 0.434 ± 0.008 N m−1. For comparison, the force indentation curve shown in Fig. 4 corresponding to a GUV in the absence of actin is displayed. Fixed parameters for modeling the actin-filled GUV: Rv = 10.25 μm; θ = 18°. (B) CLSM image of a GUV with an actin shell (green dye: Alexa Fluor 488 actin). (C) Scheme illustrating the envisioned actin shell assembled inside the vesicle. | ||
The red and green lines are fits according to the tension model. The area compressibility modulus increases by a factor of ten from 0.04 N m−1 to 0.4 N m−1 due to the presence of the actin shell. On average the effect is less pronounced (KA = 0.34 ± 0.3 N m−1 from n = 7 independent measurements) since many liposomes that possess an actin cortex do not show an altered elastic response compared to liposomes in the absence of actin. This is probably due to variations in the thickness of the artificial cortex. We attribute the increase in KA mainly to an increase in shell thickness d (KA ≈ EYd). The shell is, however, a composite consisting of a thin incompressible layer attached to network that is less resistible to lateral dilatation. Therefore, the actin shell only stiffens the capsule if its sufficiently thick.15 Additionally, the area compressibility modulus of the membrane itself might be strongly increased due to electrostatic interactions leading to cross-linking of phospholipids at the interface between the filaments and the inner leaflet. These cross-links would lead to a larger apparent KA and thereby explain the observed stiffening.
4 Conclusions
We describe how indentation experiments of giant liposomes carried out with a conventional atomic force microscope can be described in the framework of membrane theory. The absence of volume changes during indentation forces the liposomes to increase their surface area and thereby produce considerable restoring forces. If compared with force indentation experiments carried out on living epithelial cells, giant liposomes display a larger pre-stress and also higher area compressibility modulus because membrane reservoirs to buffer tension and to create excess area are missing in artificial systems. It is therefore conceivable that the actomysin cortex of cells serves as a scaffold for the plasma membrane to allow for excess membrane area which can readily be sacrificed if needed for compensating large tension as it happens if the cells change their morphology during migration or division but also if they experience osmotic stress.5 Experimentals
5.1 Materials
1,2-Dioleoyl-sn-glycero-3-phospho-choline (DOPC), 1,2-dioleoyl-sn-glycero-3-phospho-ethanolamine (DOPE), 1,2-dioleoyl-sn-glycero-3-phospho-ethanolamine-N-(cap biotinyl) (DOPE-biotin) were purchased from Avanti Polar Lipids (Alabaster, USA), the ionophore A23187 was obtained from Sigma-Aldrich (Steinheim, Germany). Membranes were labeled (0.5 mol%) with sulforhodamine-1,2-dihexanoyl-sn-glycero-3-phospho-ethanolamine (TR-DHPE, Life Technology, Carlsbad, USA). Rabbit skeletal muscle actin (>95% pure) was obtained from Cytoskeleton (Denver, USA) and labeled rabbit skeletal muscle Alexa Fluor488 actin from Life Technology. Tris(hydroxymethyl) aminomethane hydrochloride (Tris-HCl), magnesium chloride (MgCl2), adenosine triphosphate (ATP), dithiothreitol (DTT) were purchased from Sigma-Aldrich, sucrose from ACROS Organics (Geel, Belgium) and D-glucose from Carl Roth (Karlsruhe, Germany). For surface functionalization avidin from Sigma-Aldrich and casein from Merck Millipore (Darmstadt, Germany) were used. Water used for preparation of buffers was filtered by a Millipore system (Milli-Q System from Millipore, Molsheim, France; resistance >18 MΩ cm−1).5.2 Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5)) were deposited on indium tin oxide (ITO) slides and spread uniformly on an area of 12 × 12 mm2. Afterwards, residual solvent was removed using vacuum for at least 3 h at 55 °C. Subsequently, two ITO slides covered with lipid films and a 1 mm thick square silicon spacer between the slides were assembled to form a sealed chamber. The chamber was filled with 300 μl of buffer consisting of Tris-HCl (2 mM), MgCl2 (0.5 mM), ATP (0.2 mM), DTT (0.25 mM), and sucrose (50 mM) (pH 7.5). For actin containing vesicles 5–7 μM actin monomers and 0.5–1 μM Alexa Fluor 488 actin were added additionally. The chamber was connected to a waveform generator set to 70 Hz with a peak-to-peak voltage of ∼2.4 V applied for 3 h at room temperature (fluid membranes) or 55 °C (gel phase membranes), respectively. Eventually, GUVs were transferred to a plastic vial and can be stored at 4 °C for 2 days.
0.5)) were deposited on indium tin oxide (ITO) slides and spread uniformly on an area of 12 × 12 mm2. Afterwards, residual solvent was removed using vacuum for at least 3 h at 55 °C. Subsequently, two ITO slides covered with lipid films and a 1 mm thick square silicon spacer between the slides were assembled to form a sealed chamber. The chamber was filled with 300 μl of buffer consisting of Tris-HCl (2 mM), MgCl2 (0.5 mM), ATP (0.2 mM), DTT (0.25 mM), and sucrose (50 mM) (pH 7.5). For actin containing vesicles 5–7 μM actin monomers and 0.5–1 μM Alexa Fluor 488 actin were added additionally. The chamber was connected to a waveform generator set to 70 Hz with a peak-to-peak voltage of ∼2.4 V applied for 3 h at room temperature (fluid membranes) or 55 °C (gel phase membranes), respectively. Eventually, GUVs were transferred to a plastic vial and can be stored at 4 °C for 2 days.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, v/v) solution heated to 75 °C for 20 min resulting in formation of a thin SiO2 layer. The hydrophilic surface was first incubated in an avidin solution (1 μM) for 30 min followed by deposition of casein (100 μM, wafer incubated for 30 min) in order to ensure full protein coverage of the surface. Afterwards, the sample was washed with G-buffer (Tris HCl: 2 mM, MgCl2: 0.5 mM, glucose: 50 mM, pH 7.5) and 40 μl vesicle solution was added. After approximately 10 min, the Mg2+ ion concentration was increased at least to 2 mM to achieve a better fixation of the vesicles on the surface and to initiate actin polymerization.15
5, v/v) solution heated to 75 °C for 20 min resulting in formation of a thin SiO2 layer. The hydrophilic surface was first incubated in an avidin solution (1 μM) for 30 min followed by deposition of casein (100 μM, wafer incubated for 30 min) in order to ensure full protein coverage of the surface. Afterwards, the sample was washed with G-buffer (Tris HCl: 2 mM, MgCl2: 0.5 mM, glucose: 50 mM, pH 7.5) and 40 μl vesicle solution was added. After approximately 10 min, the Mg2+ ion concentration was increased at least to 2 mM to achieve a better fixation of the vesicles on the surface and to initiate actin polymerization.15
Acknowledgements
We gratefully acknowledge financial support through SFB 803 (B08).References
- D. A. Fletcher and R. D. Mullins, Cell mechanics and the cytoskeleton, Nature, 2010, 463, 485–492 CrossRef CAS PubMed.
- B. D. Hoffman and J. C. Crocker, Cell mechanics: dissecting the physical responses of cells to force, Annu. Rev. Biomed. Eng., 2009, 11, 259–288 CrossRef CAS PubMed.
- P. A. Janmey and C. A. McCulloch, Cell mechanics: integrating cell responses to mechanical stimuli, Annu. Rev. Biomed. Eng., 2007, 9, 1–34 CrossRef CAS PubMed.
- T. D. Pollard and G. G. Borisy, Cellular motility driven by assembly and disassembly of actin filaments, Cell, 2003, 112, 453–465 CrossRef CAS.
- T. D. Pollard and J. A. Cooper, Actin, a central player in cell shape and movement, Science, 2009, 326, 1208–1212 CrossRef CAS PubMed.
- J. Stricker, T. Falzone and M. L. Gardel, Mechanics of the F-actin cytoskeleton, J. Biomech., 2010, 43, 9–14 CrossRef PubMed.
- A. Pietuch, B. R. Brückner and A. Janshoff, Membrane tension and homeostasis of epithelial cells through surface area regulation in response to osmotic stress, Biochim. Biophys. Acta, Mol. Cell Res., 2013, 1833, 712–722 CrossRef CAS PubMed.
- S. F. Fenz and K. Sengupta, Giant vesicles as cell models, Integr. Biol., 2012, 4, 982–995 RSC.
- E. Evans and W. Rawicz, Elasticity of fuzzy biomembranes, Phys. Rev. Lett., 1997, 79, 2379–2382 CrossRef CAS.
- D. L. Richmond, E. M. Schmid, S. Martens, J. C. Stachowiak, N. Liska and D. A. Fletcher, Forming giant vesicles with controlled membrane composition, asymmetry, and contents, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 9431–9436 CrossRef CAS PubMed.
- S. Pautot, B. J. Frisken and D. A. Weitz, Engineering asymmetric vesicles, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10718–10721 CrossRef CAS PubMed.
- D. Needham and R. S. Nunn, Elastic deformation and failure of lipid bilayer membranes containing cholesterol, Biophys. J., 1990, 58, 997–1009 CrossRef CAS.
- D. Needham and E. Evans, Structure and mechanical properties of giant lipid (DMPC) vesicle bilayers from 20 °C below to 10 °C above the liquid crystal-crystalline phase transition at 24 °C, Biochemistry, 1988, 27, 8261–8269 CrossRef CAS.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Effect of chain length and unsaturation on elasticity of lipid bilayers, Biophys. J., 2000, 79, 328–339 CrossRef CAS.
- (a) W. Häckl, M. Bärmann and E. Sackmann, Shape changes of self-assembled actin bilayer composite membranes, Phys. Rev. Lett., 1998, 80, 1786–1789 CrossRef; (b) L. Limozin and E. Sackmann, Polymorphism of cross-linked actin networks in giant vesicles, Phys. Rev. Lett., 2002, 89, 168103 CrossRef; (c) L. Limozin, M. Bärmann and E. Sackmann, On the organization of self-assembled actin networks in giant vesicles, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 10, 319–330 CrossRef CAS PubMed.
- C. Esposito, A. Tian, S. Melamed, C. Johnson, S.-Y. Tee and T. Baumgart, Flicker Spectroscopy of Thermal Lipid Bilayer Domain Boundary Fluctuations, Biophys. J., 2007, 93, 3169–3181 CrossRef CAS PubMed.
- J. Pécréaux, H.-G. Doebereiner, J. Prost, J.-F. Joanny and P. Bassereau, Refined contour analysis of giant unilamellar vesicles, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 13, 277–290 CrossRef PubMed.
- S. Dieluweit, A. Csiszár, W. Rubner, J. Fleischhauer, S. Houben and R. Merkel, Mechanical properties of bare and protein-coated giant unilamellar phospholipid vesicles, A comparative study of micropipet aspiration and atomic force microscopy, Langmuir, 2010, 26, 11041–11049 CrossRef CAS PubMed.
- M. Honda, K. Takiguchi, S. Ishikawa and H. Hotani, Morphogenesis of liposomes encapsulating actin depends on the type of actin-crosslinking, J. Mol. Biol., 1999, 287, 293–300 CrossRef CAS PubMed.
- J. C. Stachowiak, D. L. Richmond, T. H. Li, F. Brochard-Wyart and D. A. Fletcher, Inkjet formation of unilamellar lipid vesicles for cell-like encapsulation, Lab Chip, 2009, 9, 2003–2009 RSC.
- J. C. Stachowiak, D. L. Richmond, T. H. Li, A. P. Liu, S. H. Parekh and D. A. Fletcher, Unilamellar vesicle formation and encapsulation by microfluidic jetting, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 4697–4702 CrossRef CAS PubMed.
- L. L. Pontani, J. van der Gucht, G. Salbreux, J. Heuvingh, J. F. Joanny and C. Sykes, Reconstitution of an actin cortex inside a liposome, Biophys. J., 2009, 96, 192–198 CrossRef CAS PubMed.
- M. Murrell, L. L. Pontani, K. Guevorkian, D. Cuvelier, P. Nassoy and C. Sykes, Spreading dynamics of biomimetic actin cortices, Biophys. J., 2011, 100, 1400–1409 CrossRef CAS PubMed.
- F. C. Tsai, B. Stuhrmann and G. H. Koenderink, Encapsulation of active cytoskeletal protein networks in cell-sized liposomes, Langmuir, 2011, 27, 10061–10071 CrossRef CAS PubMed.
- K. Carvalho, F.-C. Tsaid, E. Lees, R. Voituriez, G. H. Koenderink and C. Sykes, Cell-sized liposomes reveal how actomyosin cortical tension drives shape change, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 16456–16461 CrossRef CAS PubMed.
- H. Brochu and P. Vermette, Young's moduli of surface-bound liposomes by atomic force micropscopy force measurements, Langmuir, 2008, 24, 2009–2014 CrossRef CAS PubMed.
- X. Liang, G. Mao and K. Y. S. Ng, Mechanical properties and stability measurement of cholesterol-containing liposome on mica by atomic force microscopy, Adv. Colloid Interface Sci., 2004, 278, 53–62 CrossRef CAS PubMed.
- E. Schaefer, T.-T. Kliesch and A. Janshoff, Mechanical Properties of Giant Liposomes Compressed between Two Parallel Plates: Impact of Artificial Actin Shells, Langmuir, 2013, 29, 10463–10474 CrossRef PubMed.
- H. R. Hertz, On contact between elastic bodies [Ueber die Beruehrung fester elastischer koerper], J. Reine Angew. Math., 1882, 94, 156–171 Search PubMed.
- I. N. Sneddon, The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile, Int. J. Eng. Sci., 1965, 3, 47–57 CrossRef.
- A. Fery and R. Weinkamer, Mechanical properties of micro- and nanocapsules: single-capsule measurements, Polymer, 2007, 48, 7221–7235 CrossRef CAS PubMed.
- D. Vella, A. Ajdari, A. Vaziri and A. Boudaoud, The indentation of pressurized elastic shells: from polymeric capsules to yeast cells, J. R. Soc., Interface, 2012, 68, 448–455 CrossRef PubMed.
- K. Bando, K. Ohba and Y. Oiso, Deformation analysis of microcapsules compressed by two rigid parallel plates, Biorheology, 2013, 27, 18–25 CrossRef PubMed.
- L. A. Bagatolli, T. Parasassi and E. Gratton, Giant phospholipid vesicles: comparison among the whole lipid sample characteristics using different preparation methods: a two photon fluorescence microscopy study, Chem. Phys. Lipids, 2000, 105, 135–147 CrossRef CAS.
- (a) D. S. Dimitrov and M. I. Angelova, Lipid swelling and liposome formation on solid surfaces in external electric fields, Prog. Colloid Polym. Sci., 1987, 73, 48–56 CAS; (b) M. Kocun, T. D. Lazzara, C. Steinem and A. Janshoff, Preparation of Solvent-Free, Pore-Spanning Lipid Bilayers: Modeling the Low Tension of Plasma Membranes, Langmuir, 2011, 27, 7672–7680 CrossRef CAS PubMed.
- J. L. Hutter and J. Bechhoefer, Calibration of atomic-force microscope tips, Rev. Sci. Instrum., 1993, 64, 1868–1873 CrossRef CAS PubMed.
- H. J. Butt and M. Jaschke, Calculation of thermal noise in atomic force microscopy, Nanotechnology, 1995, 6, 1–7 CrossRef.
- M. Yoneda, Tension at the surface of sea-urchin egg: a critical examination of Cole's experiment, J. Exp. Biol., 1964, 41, 893–906 CAS.
- E. Evans and R. Skalak, Mechanics and Thermodynamics of Biomembranes, CRC Press Inc., 1980 Search PubMed.
- K. Bando and Y. Oiso, Indentation analysis of microcapsule with initial stretch, J. Biomech. Sci. Eng., 2013, 8, 268–277 CrossRef PubMed.
- S. Sen, S. Subramanian and D. E. Discher, Indentation and Adhesive Probing of a Cell Membrane with AFM: Theoretical Model and Experiments, Biophys. J., 2005, 89, 3203–3213 CrossRef CAS PubMed.
- A. Pietuch, B. R. Brueckner, T. Fine, I. Mey and A. Janshoff, Elastic properties of cells in the context of confluent cell monolayers: impact of tension and surface area regulation, Soft Matter, 2013, 9, 11490–11502 RSC.
- E. Boroske, M. Elwenspoek and W. Helfrich, Osmotic shrinkage of giant egg-lecithin vesicles, Biophys. J., 1981, 34, 95–109 CrossRef CAS.
- C. I. Zoldesi, I. L. Ivanovska, V. Quilliet, G. J. L. Wuite and A. Imhof, Elastic properties of hollow colloidal particles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 051401 CrossRef CAS.
- U. S. Schwarz and S. A. Safran, Physics of adherent cells, Rev. Mod. Phys., 2013, 85, 1327–1381 CrossRef CAS.
- U. Seifert, Configurations of fluid membranes and vesicles, Adv. Phys., 1997, 46, 13–137 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |



