 Open Access Article
Open Access ArticleSelf-assembly of active attractive spheres†
Vasileios
Prymidis
 *,
Harmen
Sielcken
and
Laura
Filion
*,
Harmen
Sielcken
and
Laura
Filion
Soft Condensed Matter, Debye Institute for Nanomaterials Science, Utrecht University, Princetonplein 5, 3584 CC Utrecht, The Netherlands. E-mail: v.prymidis@uu.nl
First published on 27th March 2015
Abstract
We study the self-assembly of a system of self-propelled, Lennard-Jones particles using Brownian dynamics simulations. We examine the state diagrams of the system for different rotational diffusion coefficients of the self-propelled motion of the particles. For fast rotational diffusion, the state diagram exhibits a strong similarity to that of the equilibrium Lennard-Jones fluid. As we decrease the rotational diffusion coefficient, the state diagram is slowly transformed. Specifically, the liquid–gas coexistence region is gradually replaced by a highly dynamic percolating network state. We find significant local alignment of the particles in the percolating network state despite the absence of aligning interactions, and propose a simple mechanism to justify the formation of this novel state.
I. Introduction
In recent years a significant amount of research has been focused on active matter systems, whose individual units are able to convert internal energy or energy from the local environment into their own motion (see ref. 1–4 for recent reviews). This focus was boosted by important experimental advances in the synthesis of artificial swimmers and walkers on the colloidal and granular scale,5–14 and the possible link between the behaviour of these man-made systems and the collective motion of living organisms (for example swimming cells or bacteria).15,16 Active systems show a plethora of exotic phenomena such as giant density fluctuations,9,17 vortex formation,11,18 and swarming.11 Moreover, they may play an important role in useful future applications such as targeted cargo delivery and novel types of materials.19–21However, even though experimentalists gain increasingly better control over the realization of active systems, the physics community lacks a fundamental understanding of the laws that govern their collective behavior. Thus, it comes as no surprise that a substantial amount of research is devoted to seemingly simple theoretical models of active particles, with the Viscek model being possibly the most studied one.22,23 Another much studied example, more related to the colloidal world, is the system of self-propelled, hard or purely repulsive disks.24 Computer simulations and continuum models have established that this active fluid phase-separates into a dense and a dilute region for sufficiently fast swimming velocities.24–28 Even though the phase-separation of self-propelled disks can partially be linked with the clustering of particles reported in many experiments,13,29,30 there has not yet been a satisfying explanation for the latter phenomenon, as the interactions between the colloids are more complex than simple steric interactions.31
A simple step towards complexity is the addition of attractive interactions between the particles, which was shown to also lead to clustering of particles. Specifically, Palacci et al. showed in a numerical study that phoretic attraction between self-propelled hard disks gives qualitative agreement between the clustering properties of their model and their experiments.13 A more elaborate numerical study on the interplay between attraction and self-propulsion was done by Redner et al.32 The authors studied a two-dimensional ensemble of self-propelled particles that interact via Lennard-Jones interactions. By varying the strength of the attraction and the swimming velocity of the particles, they showed that the self-propulsion can have two opposing effects for a given strength of attraction – for slow swimmers it can break aggregations caused by the attractive force, while it can induce aggregation for fast enough swimmers. For intermediate swimming velocities, the steady state of the system was identified as a homogeneous fluid phase. A first study of a similar model in three dimensions has been done by Mognetti et al.33 The focus of this work was mainly on the clustering properties of the system – as the strength of attraction is increased, the system passes from a homogeneous state to a clustered state caused by the attractive interactions. A state of rotating clusters has also been reported in ref. 34 for active attractive dumbbells.
However, the transition from homogeneity to clustering in active attractive systems has not yet been clearly linked with the known phase behaviour of the corresponding equilibrium systems. Moreover, structural properties of the clustered state have not been examined and compared to the well-studied gas–liquid phase separation.
In the present work we study a three-dimensional model of self-propelled Brownian particles that interact via a Lennard-Jones potential. The choice of the potential qualitatively accounts for the steric repulsion and the short range attraction that are present in many colloidal systems. By tuning the rotational diffusion rate of the particles, we are able to continuously move the system from the regime of fast rotational diffusion, where strong similarities with the equilibrium behavior are expected,35 to small values of the diffusion rate where non-equilibrium features arise. Thus, we are able to construct a series of state diagrams that evolve from a diagram similar to the well-established Lennard-Jones phase diagram to diagrams with novel properties.
Moreover, we find that the interplay between attraction and self-propulsive motion in three dimensions gives rise to a highly dynamic, percolating network. As we will show in this paper, this percolating network has many similarities to living clusters, observed in ref. 33. It is, however, a system spanning structure. This new state is accompanied by an unexpected result – the emergence of local alignment of the axes of self-propulsion of the particles despite the absence of an aligning mechanism.
In Section II we describe the model, the dynamics implemented for our simulations and the analysis methods used in the subsequent parts of the article. In Section IIIA we present the state diagrams of the system, and in IIIB we focus on properties of the percolating network state. Lastly, we compare our work with the results of ref. 33 in Section IIIC and give a short discussion of our results in Section IV.
II. Methods
A. Model
In this paper we examine the behaviour of self-propelled, attractive particles immersed in a solvent. We consider a three-dimensional system, consisting of spherical particles (colloids) in a periodic cubic box of length L. The position of the center of mass of the ith particle at time t is given by the vector![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t). To each particle i, we associate a three-dimensional unit vector
i(t). To each particle i, we associate a three-dimensional unit vector ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) i(t) that identifies the direction in which the self-propelling force propels the particle at a given time. The particles interact with each other via a Lennard-Jones potential
i(t) that identifies the direction in which the self-propelling force propels the particle at a given time. The particles interact with each other via a Lennard-Jones potential | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j −
j − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i|, ε is the strength of the interaction and
i|, ε is the strength of the interaction and  is the inverse temperature of the system, with kB the Boltzmann constant and T the temperature.
is the inverse temperature of the system, with kB the Boltzmann constant and T the temperature.
B. Dynamics
We do not model the solvent explicitly, but rather only include it implicitly. We use two distinct expressions to describe the translational motion of the individual colloidal particles inside the solvent, namely the underdamped and overdamped Langevin equations. The underdamped Langevin equation is given by | (2) |
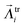 is a unit-variance random vector, with mean value and variation
is a unit-variance random vector, with mean value and variation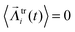 | (3) |
 | (4) |
![[Doublestruck I]](https://www.rsc.org/images/entities/i_char_e16c.gif) 3 is the unit matrix in three dimensions. The forces that appear on the right-hand side of eqn (2) are, from left to right, the force due to particle interactions, the drag force, the self-propelling force and a stochastic force. The drag and stochastic forces account for the constant collisions between the colloidal particles and the molecules of the solvent.
3 is the unit matrix in three dimensions. The forces that appear on the right-hand side of eqn (2) are, from left to right, the force due to particle interactions, the drag force, the self-propelling force and a stochastic force. The drag and stochastic forces account for the constant collisions between the colloidal particles and the molecules of the solvent.
In the regime of low Reynolds numbers (typical of a colloidal system) one can neglect the inertial term, and thus the translational motion of each particle follows from the overdamped Langevin equation
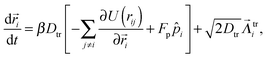 | (5) |
The axis of self-propulsion is subject to rotational diffusion and in our simulations its motion always obeys the overdamped rotational Langevin equation
 | (6) |
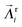 satisfies relations analogous to eqn (3) and (4). For spherical particles in the low-Reynolds number regime, the translational and rotational diffusion coefficients are linked via the Stokes–Einstein relation Dr = 3Dtr/σ2. Nevertheless, the rotational diffusion coefficient is considered as an independent parameter in our study, similar to previous theoretical work.35–37 The reason for this extra degree of freedom is that individual particles in experimental active systems, such as bacterial colonies,15 are often subject to athermal rotational diffusion.
satisfies relations analogous to eqn (3) and (4). For spherical particles in the low-Reynolds number regime, the translational and rotational diffusion coefficients are linked via the Stokes–Einstein relation Dr = 3Dtr/σ2. Nevertheless, the rotational diffusion coefficient is considered as an independent parameter in our study, similar to previous theoretical work.35–37 The reason for this extra degree of freedom is that individual particles in experimental active systems, such as bacterial colonies,15 are often subject to athermal rotational diffusion.
In order to implement the aforementioned equations of motion eqn (5) and (6) we used the Euler–Maruyama integration scheme.38 To implement the underdamped Langevin eqn (2), we employed the integration scheme proposed by Grønbech-Jensen and Farago.39 We have verified that simulations in the overdamped regime give indistinguishable results with ones in the highly viscous underdamped regime. A time step of dt = 3 × 10−5τ was used for the numeric integration of the equations of motion and the simulations ran for at least 106τ, so that we get sufficient statistics for the system.
The behavior of the system was probed as the following dimensionless parameters were systematically varied: the strength of the Lennard-Jones potential ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = βε, the magnitude of the propulsion force
= βε, the magnitude of the propulsion force ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) = βFpσ, the rotational diffusion coefficient Drτ and the density of the system
= βFpσ, the rotational diffusion coefficient Drτ and the density of the system  . In the case of the underdamped system, we also varied the (dimensionless) damping coefficient
. In the case of the underdamped system, we also varied the (dimensionless) damping coefficient ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = βmγσ2/τ. Following ref. 33, we quantified the ratio between the strength of attraction and the magnitude of self-propulsion by the aggregation propensity
= βmγσ2/τ. Following ref. 33, we quantified the ratio between the strength of attraction and the magnitude of self-propulsion by the aggregation propensity
 | (7) |
C. Steady state and initial configurations
Due to the self-propelling force there is constant energy input in the system. Nevertheless, by following the evolution of the total potential energy of the system with time, we observed that after a short transient period there was no energy drift. After this period the potential energy of the system fluctuated around a mean value. We identified this regime of quasi-constant energy with the steady state of the system. For our measurements we considered configurations from the steady state only. Furthermore, for each point in the parameter space, a minimum of two simulations was performed, starting from two different initial configurations: one where the particles were on a cubic lattice that spanned the entire system, and one where all the particles were part of a dense liquid slab. These two initial conditions were chosen in order to study any possible effect the starting configuration could have on the steady state of the system. We found that after the transient period, the average potential energy in both simulations converged to the same value, which indicates that the system indeed relaxed at the same state and we can safely identify the regime of quasi-constant potential energy with the steady state. For a limited number of simulations we also looked at the time evolution of the degree of clustering and the local density histograms, both of which are described in detail later in this paper, and we found that in the regime of quasi-constant energy these structural functions were also only subject to fluctuations and there were no major changes. Once again the results obtained for different initial configurations coincided. All the above ensure that potential energy is a reasonable indicator of when the system reaches the steady state.For sets of parameters where the system is close to crystallization, the system was additionally initialized from a gaseous state that contains a large (face-centered-cubic) crystalline cluster. The cluster contained approximately 25% of the system's particles. We observed high crystallization and melting barriers in many cases, which caused difficulties in identifying the true state of the system, as the simulations would have to run for a very long time. We found that these difficulties were enhanced by finite size effects. Nevertheless, the results obtained for the parameter space points presented in this article have been thoroughly verified.
D. Analysis methods
We used a Voronoi construction to construct local density histograms of the system.40 By calculating the volume of the Voronoi cells we were able to estimate the local density of particles. Furthermore, the identification of surface particles was performed by means of the cone algorithm.41In order to distinguish the percolating network state from the bulk gas–liquid coexistence region we used the following criterion. First, we considered two particles as clustered when their center of mass distance was less than 1.2σ. Note that in our system, the first minimum in the radial distribution function is typically between 1.3σ and 1.6σ. We chose 1.2σ as the cutoff distance in order to both be consistent with that used in ref. 33 and ensure that we did not overestimate the amount of connectedness in our system.
Second, we calculated the probability of having a cluster percolating simultaneously in all three dimensions in the system. To determine whether a cluster percolates in a given direction we duplicated the system in that direction, doubling the number of particles. If the number of particles in the cluster doubled as well, then the cluster percolated. When the probability of percolation was found higher than a certain threshold that was density-dependent, we identified the system as being in the percolating cluster state. This threshold was used for the necessary distinction between strong fluctuations of the liquid phase that can temporarily percolate in three dimensions and the percolating network structure. The probability threshold was set at 35%, 90% and 95% for total densities ρσ3 = 0.191, 0.382 and 0.445 accordingly. However, for a total density higher than ρσ3 = 0.5 this criterion failed as the liquid cluster always percolated.
III. Results
A. State diagrams
Passive Lennard-Jones particles have been extensively studied and their phase behaviour is well-characterized (see e.g.ref. 42). At high temperatures, Lennard-Jones systems exhibit a single first-order phase transition from a fluid to a face-centered-cubic crystal as the density of the system is increased. Upon lowering the temperature, a critical temperature is reached where a second phase transition appears separating the fluid phase into gas and liquid phases. At even lower temperatures a triple point appears below which the liquid phase disappears and only the gas and crystal remain.When the passive particles are replaced by active particles by introducing self-propulsion, deviations from the equilibrium behaviour are expected. To explore these deviations, we study the behaviour of the system as a function of the rotational diffusion coefficient Drτ while keeping the self-propulsion force and temperature fixed. Note that in the limit of fast rotational diffusion, Drτ → ∞, the persistence length of the particles goes to zero and the active force acts effectively as translational diffusion.35 As a result, we expect the behaviour in this limit to coincide with the behaviour in the equilibrium (passive) system, but with a modified interaction strength. However, as Drτ is decreased, the non-equilibrium effects should become more evident.
In this section we use overdamped Brownian dynamics simulations to explore the behaviour of systems with Drτ between 0.3 and 30 and densities ρσ3 between 0.191 and 0.764. In all cases, the magnitude of the self-propelling force is fixed at ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) = 50.
= 50.
For all values of Drτ we consider, we find that the system forms a homogeneous fluid for a sufficiently low value of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (see Fig. 1(a)). As the strength of the attraction is increased, the particles tend to aggregate. The structure of the aggregate depends strongly on the rotational diffusion coefficient. For a high rotational diffusion coefficient, the aggregated phase appears as the liquid in a classical liquid–gas phase separation, namely, the liquid phase is organized such that the surface of the cluster is minimal (Fig. 1(b)). However, for slower rotational diffusion, the aggregated phase is much less compact as shown in Fig. 1(c), and frequently spans the entire system or forms “living” clusters as described in ref. 33.
(see Fig. 1(a)). As the strength of the attraction is increased, the particles tend to aggregate. The structure of the aggregate depends strongly on the rotational diffusion coefficient. For a high rotational diffusion coefficient, the aggregated phase appears as the liquid in a classical liquid–gas phase separation, namely, the liquid phase is organized such that the surface of the cluster is minimal (Fig. 1(b)). However, for slower rotational diffusion, the aggregated phase is much less compact as shown in Fig. 1(c), and frequently spans the entire system or forms “living” clusters as described in ref. 33.
In order to better quantify the aggregation of particles, we obtained density histograms for the systems we examined. We found that in most cases the density histograms transitioned from a unimodal to a bimodal curve as the strength of attraction is increased, a transition that indicates passing from a homogeneous state into a coexistence state. Examples of such histograms are presented in Fig. 2. We subsequently used the local maxima of the density histograms, which we identified as the local densities of the coexisting phases ρl, to construct the state diagram of the system for different rotational diffusion coefficients, see Fig. 3. Note that in Fig. 2 some of the peaks in the gas phase are very low compared to the peaks of the liquid phase, indicating that only a small fraction of our system consisted of gas particles. We identified as fluid the state where only a single peak is visible in the local density histogram. States which exhibited two peaks but showed no signs of global phase separation were identified as percolating network states, and states which exhibited a clear phase separation were marked are either gas–liquid or gas–crystal, depending on whether the high density phase is crystalline. Note that we have not probed the exact positions of the critical or triple points in any of the diagrams presented in Fig. 3. Additionally, the boundaries presented in black dashed lines are simply approximate state boundaries.
As shown in Fig. 3(a), for a rotational diffusion coefficient Drτ = 30 (ten times larger than the value dictated by the Stokes–Einstein relation), the behaviour of the system is very similar to the phase diagram seen for passive systems. The system transitions with increasing attractive strength ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) from a homogeneous fluid state to a gas–liquid coexistence state and eventually to a gas–crystal coexistence state. Moreover, the binodal envelope is similar to that of the equilibrium system, in the sense that the value of attraction alone dictates the densities of the two coexisting phases. The low-density curves do not fall exactly on top of each other for high values of attraction due to surface effects that are discussed at the end of this section.
from a homogeneous fluid state to a gas–liquid coexistence state and eventually to a gas–crystal coexistence state. Moreover, the binodal envelope is similar to that of the equilibrium system, in the sense that the value of attraction alone dictates the densities of the two coexisting phases. The low-density curves do not fall exactly on top of each other for high values of attraction due to surface effects that are discussed at the end of this section.
Decreasing the rotational diffusion to Drτ = 9 (Fig. 3(b)) results in the emergence of a new state, which we refer to as a percolating network. This new state consists of a dynamic network of clustered particles coexisting with a gas phase and in static images resembles an equilibrium system which has undergone spinodal decomposition (see the ESI† Movie S1). However, in contrast to such a state, the percolating network we observe is clearly not kinetically trapped (see the ESI† Movie S2). From Fig. 3(b) we see that the system now transitions with increasing strength of attraction from a homogeneous fluid state to a percolating network and then to a gas–liquid coexistence state.
Setting the rotational diffusion coefficient equal to the value dictated by the Stokes–Einstein relation, namely Drτ = 3, results in the state diagram shown in Fig. 3(c). Here, we find that the region where the percolating network state occurs is increased at the expense of the gas–liquid coexistence region. Additionally, in the percolating network region, attraction does not solely dictate the densities of the coexisting states anymore. In contrast, the peaks in the local density histograms also depend on the total density of the system. We note that this non-collapse was validated for various system sizes as described below.
For very low rotational diffusion (Drτ = 0.3), the state diagram continues to evolve (Fig. 3(d)). The percolating network has now completely replaced the gas–liquid region – according to our simulations, the system transitions directly from the percolating network state to a gas–crystal coexistence state.
Interestingly, the stability domain of the percolating network increases monotonously with decreasing rotational diffusion coefficient. In all investigated cases, it appears first at 1/![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ≈ 0.15, with the value increasing slightly with decreasing Drτ.
≈ 0.15, with the value increasing slightly with decreasing Drτ.
We conclude this section by commenting on finite size effects. In order to ensure that the behaviour we observed in Fig. 3 was robust with respect to the system size, we simulated a few state points for larger and smaller systems, consisting of N = 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 and 2197 particles respectively. First of all, we found that the identification of the states does not change, e.g. we observe fluid, liquid–gas, crystal and the percolating network independent of system size. Additionally, the density of the dense phase (percolating network of liquid clusters, liquid or crystal) was only slightly affected by the system size. Substantial deviations occurred only for the low-density phase. These deviations are expected, since the first peak of the local density histogram is complicated by the presence of surface particles in addition to the gas particles. Nevertheless, this effect does not affect the conclusions drawn above.
952 and 2197 particles respectively. First of all, we found that the identification of the states does not change, e.g. we observe fluid, liquid–gas, crystal and the percolating network independent of system size. Additionally, the density of the dense phase (percolating network of liquid clusters, liquid or crystal) was only slightly affected by the system size. Substantial deviations occurred only for the low-density phase. These deviations are expected, since the first peak of the local density histogram is complicated by the presence of surface particles in addition to the gas particles. Nevertheless, this effect does not affect the conclusions drawn above.
B. Percolating cluster state
One of the most striking differences between a gas–liquid coexistence state and the novel percolating network state is the compactness of the dense clusters. In a gas–liquid coexistence state, the system evolves in order to minimize the surface area of the cluster, resulting in compact spherical or cylindrical geometries. In the percolating network, the active system appears to almost attempt to maximize the surface area, resulting in a highly branched network. One way to characterize this difference is by looking at the ratio of surface to volume of these large aggregates. In Fig. 4 we plot the average ratio NS/NV of surface particles over the total number of particles for the largest cluster, as a function of the rotational diffusion coefficient. In all cases, the density ρσ3 = 0.191, self-propelling force![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) = 50 and interaction strength
= 50 and interaction strength ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = 12.5 are chosen such that nearly all particles are part of one large cluster (>90%). We have found that for the parameters used in Fig. 4 the fluctuations of the number of particles in the biggest cluster NV as well as of the ratio NS/NV are small. Thus, the size of the largest cluster does not fluctuate significantly, and the dynamic changes in the shape of the percolating network do not seem to affect the presented results.
= 12.5 are chosen such that nearly all particles are part of one large cluster (>90%). We have found that for the parameters used in Fig. 4 the fluctuations of the number of particles in the biggest cluster NV as well as of the ratio NS/NV are small. Thus, the size of the largest cluster does not fluctuate significantly, and the dynamic changes in the shape of the percolating network do not seem to affect the presented results.
In the fast rotational diffusion regime, the liquid cluster is indeed compact, resulting in a small surface-to-volume ratio, which decreases further with increasing system size, as expected. On the other hand, for low rotational diffusion, i.e. in the percolating network state, we observe a much larger fraction of surface particles, which is independent of the system size. For the system parameters studied in Fig. 4 we find that the transition between the network state and the gas–liquid separation occurs at a rotational diffusion of around Drτ ∼ 2. Note that this transition becomes sharper with increasing system size, characteristic of a phase transition.
To gain further insight into the properties of the percolating network state, we study the pairwise correlations between particles. In Fig. 5(a), we plot the radial distribution function g(r) for four different values of Drτ, at the same density and interaction strength as was used for Fig. 4. For the highest value of Drτ, the system exhibits a gas–crystal phase separation, and the radial distribution function shows sharp peaks characteristic of the crystalline order. For Drτ = 9 and 3, the system forms a gas–liquid separation, resulting in much weaker peaks in g(r). Finally, for Drτ = 0.3, we observe the percolating network state, for which the radial distribution function looks essentially the same as that of the gas–liquid separation.
Additionally, we calculate the normalized orientation correlation function C1(r), defined as
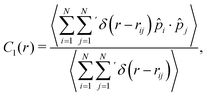 | (8) |
In light of the above conclusions, we propose here a possible mechanism that accounts for the formation of the percolating network state. Consider a dilute system of self-propelled particles with an attraction strength at least strong enough to cause gas–liquid phase separation in the absence of self-propulsion. Now assume that the magnitude of self-propulsion is stronger than the attractions ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) >
> ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) , and that the axis of self-propulsion associated with each particle is pointing in a fixed, random direction (Drτ = 0). When two particles collide there are two possible scenarios – if their axes of self-propulsion are pointing in a similar direction, then the attraction will cause them to aggregate and travel together. In contrast, if the axes of self-propulsion are pointing in sufficiently different directions, the particles will overcome the attraction and move away from each other. After a large number of collisions, this process will ultimately create a collection of clusters, with each cluster containing particles with similar orientations. By performing a small number of simulations (not shown in the present article) in very low densities ρσ3 = 0.001–0.01 and for
, and that the axis of self-propulsion associated with each particle is pointing in a fixed, random direction (Drτ = 0). When two particles collide there are two possible scenarios – if their axes of self-propulsion are pointing in a similar direction, then the attraction will cause them to aggregate and travel together. In contrast, if the axes of self-propulsion are pointing in sufficiently different directions, the particles will overcome the attraction and move away from each other. After a large number of collisions, this process will ultimately create a collection of clusters, with each cluster containing particles with similar orientations. By performing a small number of simulations (not shown in the present article) in very low densities ρσ3 = 0.001–0.01 and for ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) >
> ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) > 1, we have indeed verified that the above process creates a collection of small clusters in which particle orientations are highly correlated.
> 1, we have indeed verified that the above process creates a collection of small clusters in which particle orientations are highly correlated.
Now, if we increase the system density and instead of a fixed direction of self-propulsion we allow the particles to slowly rotate (corresponding to a low rotational diffusion coefficient), then this argument should continue to hold, e.g. particles that are in similar orientations aggregate more easily than particles pointing in opposite directions. This results in highly dynamic aggregates with groups of particles frequently attaching and detaching, and neighbouring particles displaying high degrees of orientational correlation as seen in Fig. 5. For sufficiently high density (such as those studied in this paper), these aggregates become completely system spanning, and the majority of particles are connected to a single network, as seen in our simulations. This picture agrees well with movies from our simulations (see ESI† Movies S1 and S2) and accounts for both the local alignment of particles (Fig. 5) and the lack of system size dependence of the structural properties of the percolating network (Fig. 4).
As Drτ increases, the persistence length of the self-propelled motion of the particles decreases. In this case, the attractive force is able to aggregate particles with larger differences in the orientation of the axes of self-propulsion. This process ultimately leads to a transition to the (bulk) gas–liquid phase coexistence region (Fig. 4). A similar transition from the percolating network state to a gas–liquid coexistence state can take place by fixing the persistence length of the particles and increasing the attraction (Fig. 3(b) and (c)).
C. Clustering properties
In a recent publication, Mognetti et al.33 showed that the aggregation, i.e. clustering, in a system of self-propelled attractive particles depended only on the ratio Pagg =![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) /
/![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) . To examine whether this collapse also occurs in our system, we calculated the degree of clustering Θ, introduced in ref. 33, as
. To examine whether this collapse also occurs in our system, we calculated the degree of clustering Θ, introduced in ref. 33, as | (9) |
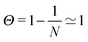 when all particles belong to the same cluster. The results are plotted in Fig. 6.
when all particles belong to the same cluster. The results are plotted in Fig. 6.
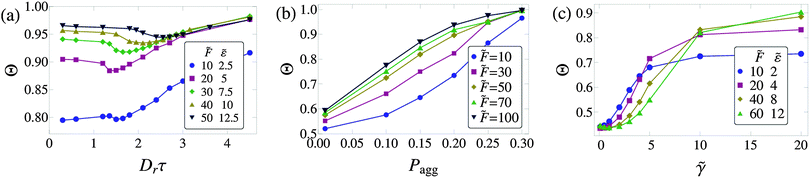 | ||
Fig. 6 Degree of clustering Θ as a function of (a) the rotational diffusion coefficient Drτ for different values of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) and and ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) , but at a constant ratio Pagg = 0.25, (b) Pagg for different values of , but at a constant ratio Pagg = 0.25, (b) Pagg for different values of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) , and fixed Drτ = 3 and (c) the dimensionless damping parameter , and fixed Drτ = 3 and (c) the dimensionless damping parameter ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) for different values of for different values of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) and and ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) , but at a constant ratio Pagg = 0.20 and constant Drτ = 3. The density of the system is ρσ3 = 0.191, same as in ref. 33. , but at a constant ratio Pagg = 0.20 and constant Drτ = 3. The density of the system is ρσ3 = 0.191, same as in ref. 33. | ||
In Fig. 6(a) we plot the degree of clustering Θ as a function of the rotational diffusion coefficient Drτ at constant Pagg near the percolating network to gas–liquid transition. We do not see a collapse in the degree of clustering here. Similarly, in Fig. 6(b) we do not see a collapse when plotting Θ as a function of Pagg at fixed rotational diffusion Drτ for a wider range of state points. Finally, we checked to see if the collapse would occur if we use underdamped dynamics in place of overdamped dynamics for the translational degrees of freedom. As shown in Fig. 6(c), we also do not find a value of the damping parameter ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) for which a collapse occurred. We conclude that the data collapse found by Mognetti et al.33 does not occur in our system. We attribute this discrepancy to the difference in the applied dynamics, and more specifically to the different mechanisms that rotate the particles in the two different systems.
for which a collapse occurred. We conclude that the data collapse found by Mognetti et al.33 does not occur in our system. We attribute this discrepancy to the difference in the applied dynamics, and more specifically to the different mechanisms that rotate the particles in the two different systems.
IV. Conclusions and outlook
In the present work, we employed computer simulations to study the self-assembly of a system of self-propelled Brownian particles that interact via the truncated and shifted Lennard-Jones potential.We determined state diagrams of the overdamped system for various rates of rotational diffusion of the self-propelled motion of the particles. We found that for fast rotational diffusion, the properties of the state diagram bore strong similarities to the phase diagram of the equilibrium Lennard-Jones system. However, as the rotational diffusion was decreased, new features arose due to the interplay between self-propulsion and attraction. That is, a new state was observed between the fluid phase and gas–liquid coexistence, which we identified as a highly dynamic, percolating network state. That state consisted of interconnected but mobile clusters that created a system-spanning network. Finally, for slow rotational diffusion the (bulk) gas–liquid coexistence disappeared and the system transitioned from the percolating network state directly to gas–crystal coexistence.
We subsequently discussed the unique properties of the percolating state, and presented evidence of a transition from gas–liquid to a percolating network with decreasing rotational diffusion. By examining the correlations between the orientations of the axes of self-propulsion of the particles, we found significant local alignment in the percolating state. A possible mechanism was proposed in order to explain the formation of the percolating network.
Finally, we noted that the ratio of the strength of attraction over the magnitude of self-propulsion does not solely characterize our system. This is in contrast to what was found in ref. 33, and may be due to differences in the applied dynamics.
We would like to comment here on the significance of the percolating network state. First, we note once more that this state is caused by the synergy between attraction and self-propulsion, so we expect it to be present in three dimensional systems for a wide variety of attractive potentials and propulsion mechanisms. Moreover, our simulations suggest that this novel state is present for low density systems and experimentally relevant rotational diffusion, so a search for this state in real colloidal systems is feasible. As earlier work has shown, hydrodynamic interactions may also cause local alignment of particles, an effect that may enhance the formation of the percolating network state in experimental systems.43
Last but not least, as demonstrated in Section IIIC, the exact dynamics of a theoretical model are of importance not only for the quantitative but also for the qualitative results it generates. Detailed comparisons between different theoretical models, as well as actual experimental systems, such as ref. 31, are thus extremely valuable and needed, in order to deepen our understanding of active matter systems.
Acknowledgements
V.P. and L.F. acknowledge funding from the Dutch Sector Plan Physics and Chemistry, and L.F. acknowledges funding from a NWO-Veni grant. We thank Wiebke Albrecht, Guido Avvisati, Tommaso Comparin and Frank Smallenburg for careful reading of the manuscript.References
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323 CrossRef PubMed.
- P. Romanczuk, M. Bär, W. Ebeling, B. Lindner and L. Schimansky-Geier, Eur. Phys. J.: Spec. Top., 2012, 202, 1 CrossRef CAS.
- M. Marchetti, J. Joanny, S. Ramaswamy, T. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- I. S. Aranson, C. R. Phys., 2013, 14, 518 CrossRef CAS PubMed.
- W. F. Paxton, K. C. Kistler, C. C. Olmeda, A. Sen, S. K. St. Angelo, Y. Cao, T. E. Mallouk, P. E. Lammert and V. H. Crespi, J. Am. Chem. Soc., 2004, 126, 13424 CrossRef CAS PubMed.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 862 CrossRef CAS PubMed.
- J. R. Howse, R. A. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef.
- Y. Hong, N. M. Blackman, N. D. Kopp, A. Sen and D. Velegol, Phys. Rev. Lett., 2007, 99, 178103 CrossRef.
- J. Deseigne, O. Dauchot and H. Chaté, Phys. Rev. Lett., 2010, 105, 098001 CrossRef.
- A. Kudrolli, G. Lumay, D. Volfson and L. S. Tsimring, Phys. Rev. Lett., 2008, 100, 058001 CrossRef.
- V. Schaller, C. Weber, C. Semmrich, E. Frey and A. R. Bausch, Nature, 2010, 467, 73 CrossRef CAS PubMed.
- G. Volpe, I. Buttinoni, D. Vogt, H.-J. Kümmerer and C. Bechinger, Soft Matter, 2011, 7, 8810 RSC.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936 CrossRef CAS PubMed.
- A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95 CrossRef CAS PubMed.
- H. C. Berg, E. coli in Motion, Springer, 2004 Search PubMed.
- R. Thar and M. Kühl, FEMS Microbiol. Lett., 2005, 246, 75 CrossRef CAS PubMed.
- V. Narayan, S. Ramaswamy and N. Menon, Science, 2007, 317, 105 CrossRef CAS PubMed.
- Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chaté and K. Oiwa, Nature, 2012, 483, 448 CrossRef CAS PubMed.
- L. Baraban, M. Tasinkevych, M. Popescu, S. Sanchez, S. Dietrich and O. Schmidt, Soft Matter, 2011, 8, 48 RSC.
- N. Koumakis, A. Lepore, C. Maggi and R. Di Leonardo, Nat. Commun., 2013, 4, 2588 CAS.
- F. C. Keber, E. Loiseau, T. Sanchez, S. J. DeCamp, L. Giomi, M. J. Bowick, M. C. Marchetti, Z. Dogic and A. R. Bausch, Science, 2014, 345, 1135 CrossRef CAS PubMed.
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226 CrossRef CAS.
- H. Chaté, F. Ginelli, G. Grégoire and F. Raynaud, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 046113 CrossRef.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489 RSC.
- J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2013, 111, 145702 CrossRef.
- T. Speck, J. Bialké, A. M. Menzel and H. Löwen, Phys. Rev. Lett., 2014, 112, 218304 CrossRef.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef.
- J. Bialké, T. Speck and H. Löwen, J. Non-Cryst. Solids, 2015, 407, 367 CrossRef PubMed.
- G. S. Redner, A. Baskaran and M. F. Hagan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012305 CrossRef.
- B. M. Mognetti, A.
![[S with combining breve]](https://www.rsc.org/images/entities/char_0053_0306.gif) arić, S. Angioletti-Uberti, A. Cacciuto, C. Valeriani and D. Frenkel, Phys. Rev. Lett., 2013, 111, 245702 CrossRef CAS.
arić, S. Angioletti-Uberti, A. Cacciuto, C. Valeriani and D. Frenkel, Phys. Rev. Lett., 2013, 111, 245702 CrossRef CAS. - J. Schwarz-Linek, C. Valeriani, A. Cacciuto, M. Cates, D. Maren-duzzo, A. Morozov and W. Poon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4052 CrossRef CAS PubMed.
- Y. Fily, S. Henkes and M. C. Marchetti, Soft Matter, 2014, 10, 2132 RSC.
- R. Ni, M. A. C. Stuart and M. Dijkstra, Nat. Commun., 2013, 4, 2704 Search PubMed.
- X. Yang, M. L. Manning and M. C. Marchetti, Soft Matter, 2014, 10, 6477 RSC.
- D. Higham, SIAM Rev., 2001, 43, 525 CrossRef.
- N. Grønbech-Jensen and O. Farago, Mol. Phys., 2013, 111, 983 CrossRef.
- C. H. Rycroft, Chaos, 2009, 19, 041111 CrossRef PubMed.
- Y. Wang, S. Teitel and C. Dellago, J. Chem. Phys., 2005, 122, 214722 CrossRef PubMed.
- B. Smit, J. Chem. Phys., 1992, 96, 8639 CrossRef CAS PubMed.
- I. Llopis and I. Pagonabarraga, Europhys. Lett., 2006, 75, 999 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm00127g |
| This journal is © The Royal Society of Chemistry 2015 |





