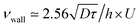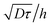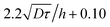Velocimetry in microchannels using photobleached molecular tracers: a tool to discriminate solvent velocity in flows of suspensions
Florinda
Schembri†
,
Hugues
Bodiguel
* and
Annie
Colin
Univ. Bordeaux, CNRS, Solvay, LOF UMR 5258, France. E-mail: hugues.bodiguel@u-bordeaux.fr
First published on 23rd October 2014
Abstract
We report the development and analysis of a velocimetry technique based on the short time displacement of molecular tracers, tagged thanks to photobleaching. We use confocal microscopy to achieve a good resolution transverse to the observation field in the direction of the velocity gradient. The intensity profiles are fitted by an approximate analytical model which accounts for hydrodynamic dispersion, and allow access to the local velocity. The method is validated using pressure driven flow in microfluidic slits having a thickness of a few tens of micrometers. We discuss the main drawbacks of this technique which is an overestimation of the velocity close to the walls due to the combination of molecular diffusion and shear. We demonstrate that this error, limited to a near wall region of a few micrometers thick, could be controlled by limiting the diffusion of fluorophore molecules or minimizing the bleaching time. The presented technique could be combined with standard particle imaging velocimetry to access velocity differences and allow particle trajectory analysis in microflows of suspensions.
1 Introduction
A suspension is a system where particles are dispersed throughout a solvent.1 These systems are ubiquitous in nature and are encountered in many areas ranging from cement and concrete technology, ceramic processing, coating and pigment technology, propellants and explosive science, mineral processing, soil science, composite processing and various slurry flow technologies. Precise predictive models of flow of such complex fluids are crucial in many applications from food to aeronautical industry. Accurate simulation of suspension flows is a crucial enabler for industrial process optimization. Composite material fabrication, propergol paste into a mould, injection or ejection of suspensions through nozzles in biomedical practice represent archetypical applications. In all these applications, suspensions are submitted to flow. Hence the rheology of suspensions is the object of intense research from the theoretical, experimental and numerical points of view. In this area, a well-known and long-standing problem in fluid mechanics has been the calculation of the effective viscosity of a suspension. The dilute and semi-dilute regimes have been well understood since the pioneering studies of Einstein (1905) and Batchelor and Green (1972). In the past decades, many studies have been focused on the concentrated regime where the average distance between the particles is less than the mean size of a particle. As suggested by dimensional analysis and confirmed by numerical simulations and experiments, dense suspensions of hard spheres are Newtonian: the shear stress is proportional to the shear rate. However, in this regime shocks between particles and short-range forces give rise to concentration inhomogeneities2 that may be misinterpreted as non-Newtonian effects. Indeed, numerous authors reported experimental data of relative suspension viscosity apparently showing shear rate dependence. Nevertheless, Ovarlez et al.3 showed that this phenomenon is rather related to a heterogeneous distribution of the particle concentration in the rheometer. Understanding the flow of a dispersion requires thus to address the question of the particle migration and of the building of concentration heterogeneities. The migration flux is directly related to the difference between liquid and particle velocities.4 At this stage, the simultaneous measurement of both velocities in the flow direction has never been performed. In this article, we display an experimental setup allowing such a characterization of the flow.Particle velocity is classically measured using micro-particle tracking velocimetry (PTV). This technique is widely used as it allows acquiring, with a great resolution time and space, resolved velocity profiles.5–7 The sample is illuminated so that the particles are visible. A camera records their movements. The analysis of the movies involves two basic steps. The first is segmentation, in which multiple particles in a field of view are identified and discriminated. Subsequently, an algorithm tracks the particles individually to monitor their displacement between successive video frames.8 Tracking algorithms used to date have included cross-correlation of subsequent images,9 calculation of the center-of-mass (centroid) of the object of interest10 and direct Gaussian fits to the intensity profile.11 Some groups have claimed nanometer resolution.
The solvent measurement velocity is less developed. The use of molecular tracers has been proposed in previous studies (see ref. 12 for a review of a pioneer study). Caged-fluorescent dye molecules have proven to be very powerful13,14 but require the use of UV-light (and consequently adequate materials for device fabrications) and expensive sensors. In contrast, photobleaching of fluorescent dyes uses visible wavelengths and moreover it is a standard option in confocal microscopy equipments.
Two main strategies have been developed to take advantage of photobleaching to measure flow velocities. The first one is based on the fact that the fluorescence intensity under a given illumination monotonically increases with the flow velocity. This technique, designed as laser induced fluorescence photobleaching anemometry (LIFPA),15,16 has been extended to single-point measurements17 allowing the determination of velocity profiles. Successively, the same group showed that it can be coupled with stimulated emission depletion (STED) microscopy in order to achieve a spatial resolution below the micron scale.18 The main drawback of this method is the need of light intensity calibration prior to the measurements. One can thus anticipate that, although very powerful for some applications, this drawback could limit its use with heterogeneous and complex fluids.
The second class of the molecular tracer velocimetry (MTV) techniques based on photobleaching take advantage of direct spatial measurement of the displacement of a photobleached region in the flow19–24 with a bright fluorescent background. It is thus similar to the principle of μ-PIV, but with tagged molecules as tracers. The disadvantage of such a size reduction is an increase of tracer diffusivity, which rapidly broadens the band created by the laser. To overcome this issue, Molho et al.19 and Mosier et al.20 used fluorescein grafted on macromolecules to reduce its diffusivity. Furthermore, the use of macromolecular probes suffers from similar limitations to particle probes. Nevertheless, hydrodynamic dispersion remains an important drawback and it has been concluded that it was better adapted to electroosmotic flows than pressure-driven ones. In the work of Cuenca and Bodiguel,22 it was shown that a small fluorescent molecule could be used even in the Taylor–Aris dispersion regime, focusing on a very short time regime just after the bleaching. This study was devoted to very thin channels, so that the velocity field along the thickness was averaged. A method was proposed in recent studies of Ponjavic et al.23 and of Wexler et al.24 to obtain information on the velocity field in the transverse direction, based on the fact that the dispersion of the photobleached spot is strongly related to the velocity gradients. However, this approach is only valid where the features of transverse velocity profiles are known, as it only gives access to the global shear rate.
In this work, we show that 2D-velocimetry is possible using photobleaching based MTV, with a spatial resolution on the order of a few micrometers, and with small molecular dyes. The idea is very simple since it takes advantage of confocal microscopy to achieve the required resolution in the vorticity direction. We focus on short times following a bleached region of fluid, similar to ref. 22, in order to reduce dispersion and diffusion issues. The main advantage of this technique is the use of molecular tracers. Moreover the presented technique does not require any calibration. We explain in the following that due to the short time limit required, a detailed analysis of the intensity curves is often necessary. Then, we validate the measurement in Poiseuille flow, and discuss the systematic error occurring in the near-wall region. Finally, we propose an application of the technique to the velocity calculation of both fluids and particles in semi-dilute and dense regimes for suspensions of hard spheres, by combining our technique with μ-PTV.
2 Experimental details
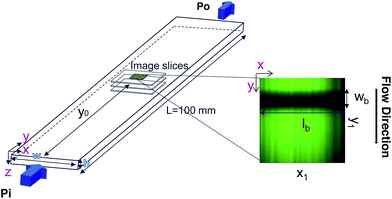
Confocal photobleaching velocimetry is developed and validated using pressure driven flows in microchannels. Since we only focus here on 2D velocimetry, we use microchannels having a large aspect ratio, as depicted in Fig. 1: the channel width is ten times the height. Two microchannels are used, of heights 50 and 100 μm, and of length 100 mm. They are fabricated in borosilicate and were purchased from Vitrocom. The inlet and outlet of the capillary are directly immersed in a plastic reservoir of controlled pressure, set using a pressure-control regulator (MFCS 4C, Fluigent). This simple setup allows us to impose a well defined and stable pressure gradient, with an accuracy smaller than 1%.The capillary is placed just above a Zeiss LSM 5 inverted confocal microscope, with an oil immersion 40× objective of numerical aperture 1.3. In full resolution, the imaging frequency is limited to 60 frames per second. The pinhole aperture has been set at its minimum (1 μm). The same laser (λ = 488 nm) is used to bleach and image the flow. During the bleaching step, the laser power is set at its maximum (100 mW) and illuminates a small portion of the observation field as shown in Fig. 1. Since we only focus here on 2D velocimetry, we chose for the bleached region a rectangular zone oriented along the x-axis, perpendicular to both the flow direction (y) and the velocity gradient (z). Two parameters could be easily varied: the width of the bleaching line, and the duration of the bleaching step. Just after this step the imaging sequence starts, in which the laser intensity is lowered at about 70% of the maximum intensity.
The experiment requires the bleaching to be highly efficient to improve the signal to noise ratio. Indeed, as will be explained and illustrated in the following, on one hand the bleaching duration needs to be small in order to reduce the diffusion of the bleached dyes, and on the other hand the signal to noise ratio needs to be increased in order to be able to determine accurately the intensity profile. Optimal conditions for bleaching and illumination are thus required. For that purpose, we use aqueous solutions of fluorescein isothiocyanate (FITC) purchased from Sigma-Aldrich at a concentration of 0.1 × 10−3 mol L−1 and adjust the pH of the mixture to a value of 7 by adding some drops of NaOH. Within these conditions (and without flow), the fluorescence intensity drops approximately by a factor of 2 in 0.25 s, at the maximum laser power.
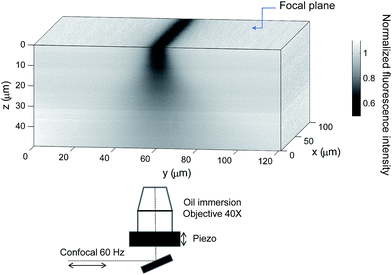
In order to characterize the bleaching resolution in the vorticity direction, we performed a vertical (z) scan of an immobile sample of fluorescein in a water–glycerol mixture at a mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, just after photobleaching a region aligned in the x direction at z = 0 μm (channel center) in a microchannel with h = 100 μm. The resulting fluorescence intensity is displayed in Fig. 2. The diffusion coefficient of fluorescein in this solution is on the order of 10−12 m2 s−1, so that the distance travelled due to diffusion is about 1 μm, given the experimental time scale. Thus the image reflects spatial variations of the photobleaching in the z direction due to the numerical aperture of the used objective. It is clear from this measurement that photobleaching is rather poorly resolved in the vertical direction, in contrast to the resolution in the focal plane. The typical decay of the photobleaching occurs at about 10 μm. When departing from the initial focal plane, the bleached line becomes smoother and wider reflecting the Gaussian beam of the laser with maximum intensity in the focal plane. An important consequence of this is the fact that we can assume in a first approximation that the photobleaching is independent of z, providing that vertical displacements within the experimental time scale are also smaller than 10 μm and by choosing the minimum pinhole for the confocal measurements.
9, just after photobleaching a region aligned in the x direction at z = 0 μm (channel center) in a microchannel with h = 100 μm. The resulting fluorescence intensity is displayed in Fig. 2. The diffusion coefficient of fluorescein in this solution is on the order of 10−12 m2 s−1, so that the distance travelled due to diffusion is about 1 μm, given the experimental time scale. Thus the image reflects spatial variations of the photobleaching in the z direction due to the numerical aperture of the used objective. It is clear from this measurement that photobleaching is rather poorly resolved in the vertical direction, in contrast to the resolution in the focal plane. The typical decay of the photobleaching occurs at about 10 μm. When departing from the initial focal plane, the bleached line becomes smoother and wider reflecting the Gaussian beam of the laser with maximum intensity in the focal plane. An important consequence of this is the fact that we can assume in a first approximation that the photobleaching is independent of z, providing that vertical displacements within the experimental time scale are also smaller than 10 μm and by choosing the minimum pinhole for the confocal measurements.
3 Intensity curve analysis
3.1 Intensity curve measurements
We focus in this paper on flows that are invariant in the x-direction (see Fig. 1). This allows to increase of the signal to noise ratio by averaging the image along x. The resulting intensity curves I(y) are however not uniform, even without bleaching, and their shapes depend on the flow rate and optical conditions. This is mainly due to the progressive bleaching of the solution, which occurs even with the low intensity laser power used for the observation. Without flow, the intensity decreases slightly with time. As soon as the flow is set, the image reaches rapidly a steady state exhibiting an intensity gradient, in the opposite direction to that of the flow. In order to suppress this effect, we systematically acquire a reference image I0(y), with the same imaging parameters as the image sequence used for the velocity measurement. Then the corresponding reference image I0(y) (image before bleaching) is systematically used to normalize each one of the bleached sequence. In the following, we define as “intensity” the quantity (I0 − I)/I0. The intensity vanishes when the bleached molecule concentration is much smaller than the total dye concentration, and this is a monotonic function of the bleached molecule concentration. For the laser power used and the fluorescein concentration, we have verified that the relationship between (I0 − I)/I0 and the bleached dye concentration is linear.22Fig. 3 shows examples of the resulting intensity profiles for different microflow conditions. Depending on the experimental parameters (fluid velocity and viscosity, bleaching width wb and duration τb), these profiles can exhibit various shapes, which might be classified into three categories, as illustrated in Fig. 3. The profiles are often Gaussian-like (see e.g.Fig. 3, top). The symmetry reveals an equilibrium between convection and diffusion. By increasing the velocity (or by increasing the bleaching duration), they become asymmetric, long-tailed in the flow direction, denoting an increase of convection with respect to molecular diffusion. When increasing the fluid viscosity at small velocities, the longer tail switches to the opposite side (see Fig. 3, bottom) and the curves try to maintain the shape of the rectangular source. We propose in the following an analysis aiming to describe these shapes, to extract from their dynamics the local fluid velocity to reconstruct the 2D velocity profiles.
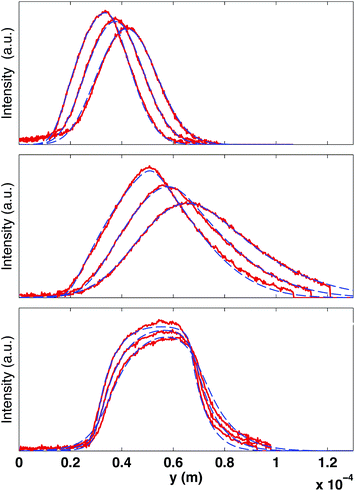 | ||
Fig. 3 Examples of intensity curves in the observation window after photobleaching for different experimental conditions. The signals are obtained by row-averaging in the x-direction and after normalizing by the background signal (image before bleaching). The solid lines are the experimental data (displayed each 116 ms) while the dash-dotted curves are the best fits to the experimental data, by using eqn (8) and (9). The fitting parameters are the velocity v(z0), the local shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and the curve center x0. (Top) Gaussian-like profiles obtained at ΔP = 0.8 mbar with a fluid of viscosity of η = 0.0059 Pa s (D = 7.1 × 10−11 m2 s−1); bleaching parameters: τb = 0.32 s, wb = 11 μm; fitting parameters v = 40 μm s−1, and the curve center x0. (Top) Gaussian-like profiles obtained at ΔP = 0.8 mbar with a fluid of viscosity of η = 0.0059 Pa s (D = 7.1 × 10−11 m2 s−1); bleaching parameters: τb = 0.32 s, wb = 11 μm; fitting parameters v = 40 μm s−1, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≃ 0. (Middle) Asymmetric triangular profiles are obtained by increasing the applied pressure to ΔP = 2.4 mbar, and increasing the bleaching time and width (τb = 0.5 s, wb = 18 μm); fitting parameters v = 77 μm s−1, ≃ 0. (Middle) Asymmetric triangular profiles are obtained by increasing the applied pressure to ΔP = 2.4 mbar, and increasing the bleaching time and width (τb = 0.5 s, wb = 18 μm); fitting parameters v = 77 μm s−1, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 6.6 s−1. (Bottom) Increasing the viscosity to η = 0.0388 Pa s (D = 1.1 × 10−11 m2 s−1), the profiles become asymmetric with the maximum value shifted toward the flow direction; bleaching parameters: τb = 0.5 s, wb = 18 μm; fitting parameters y = 16 μm s−1, = 6.6 s−1. (Bottom) Increasing the viscosity to η = 0.0388 Pa s (D = 1.1 × 10−11 m2 s−1), the profiles become asymmetric with the maximum value shifted toward the flow direction; bleaching parameters: τb = 0.5 s, wb = 18 μm; fitting parameters y = 16 μm s−1, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 9.6 s−1. = 9.6 s−1. | ||
3.2 Theoretical analysis of the intensity measurements
Let us consider the transport properties of the bleached molecules in a pressure driven flow in parallel plate geometry. The velocity v is aligned with the y-direction, parallel to the plates, and the velocity gradient is perpendicular along the z direction. The concentration field c(y, z) of the bleached molecules is solution of the convection–diffusion equation: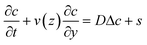 | (1) |
As shown in the previous section, the bleaching efficiency is maximal in the focal plane but only slightly decreases when moving along the z-direction. Therefore, as a first-order approximation, we could assume the source term s to be independent of z. As will be detailed in the following, we cannot neglect the finite duration and the finite width of the bleaching process. The solution of eqn (1) corresponding to the real source term could be easily derived by convolving the latter with the impulse response, i.e. when s is a simple pulse in time and in the flow direction. We will thus first focus on the Green function of the problem, c0, before proceeding with its convolution. This situation corresponds to the classical dispersion phenomenon in Poiseuille flows, first studied by Taylor25 and Aris,26 and then refined and generalized by tens of authors due to its practical importance in many fields, including analytical chemistry. For the velocimetry application that is the purpose of this work, we need to focus on the short time response as the asymptotic concentration profile at long times is independent of z. Unfortunately there is no simple analytical solution available at all times, so we will use a numerical solution.
A simple way to compute it is to solve the corresponding stochastic equation. For this purpose, we consider 105 tracer particles homogeneously distributed in the z direction. The particles are launched at t = 0 from position y = 0. The particles are convected by the flow and diffuse randomly; their positions ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t) are computed according to:
i(t) are computed according to:
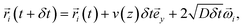 | (2) |
![[small omega, Greek, vector]](https://www.rsc.org/images/entities/i_char_e13e.gif) i is a unit vector with a random direction in the plane (
i is a unit vector with a random direction in the plane (![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) y,
y, ![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) z). Fig. 4 displays the evolution of the concentration field in dimensionless coordinates (ỹ = 2y/h,
z). Fig. 4 displays the evolution of the concentration field in dimensionless coordinates (ỹ = 2y/h, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 2z/h,
= 2z/h, ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = t2U/h) for a Peclet number Pe = Uh/D = 133. At the short and moderate times displayed, the concentration field reflects roughly the parabolic profile of the velocity. We note however that close to the wall, the maximum of the concentration does not remain immobile as it would be the case in the absence of shear and diffusion. We will come back to this point later.
= t2U/h) for a Peclet number Pe = Uh/D = 133. At the short and moderate times displayed, the concentration field reflects roughly the parabolic profile of the velocity. We note however that close to the wall, the maximum of the concentration does not remain immobile as it would be the case in the absence of shear and diffusion. We will come back to this point later.
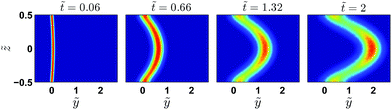 | ||
Fig. 4 Numerical solutions of the Green function of eqn (1), for Pe = 133 at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0.06, 0.66, 1.32 and 2. = 0.06, 0.66, 1.32 and 2. | ||
From the experimental intensity profiles and using the above detailed numerical approach, one could use an inverse method to deduce the velocity profile. However, this strategy is time consuming and we propose in the following a more direct and robust approach to obtain the velocity field, based on an approximate analytical solution.
Let us recall the main features of the classical dispersion problem of diffusing probes in pipe flow or in between parallel plates. Three regimes of spreading of a very thin line could be distinguished.27 At very short times, for t ≪ h4/3U2/3/D1/3 (i.e. ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ≪ Pe1/3), dispersion due to molecular diffusion dominates over the effect of shear. The probes are convected according to the velocity profile and the line width scales as
≪ Pe1/3), dispersion due to molecular diffusion dominates over the effect of shear. The probes are convected according to the velocity profile and the line width scales as 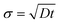 . At longer times, but before the characteristic time to diffuse along the whole thickness τd = h2/D (i.e. Pe1/3 ≪
. At longer times, but before the characteristic time to diffuse along the whole thickness τd = h2/D (i.e. Pe1/3 ≪ ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ≪ Pe), the dispersion is due to the combination of transverse diffusion and longitudinal shear. In this regime of so-called anomalous diffusion,28 the dispersion increases more rapidly with time, and scales as UD1/2t3/2/h. The well-known Taylor dispersion only occurs at long times, i.e. for t ≫ τD. Clearly, this regime is not interesting for velocimetry applications since the diffusion process homogenizes the concentration along the thickness, and the traveling velocity of the bleached line equals the mean value of the velocity field, as in the case of ref. 22 where the considered thicknesses were smaller than a few micrometers. Note that in channel flows, a fourth regime exists at longer times,29 for t ≫ w2/D, where hydrodynamic dispersion along the channel width takes place. There is no need to consider it in this study and we can model the flow geometry by two infinite parallel plates.
≪ Pe), the dispersion is due to the combination of transverse diffusion and longitudinal shear. In this regime of so-called anomalous diffusion,28 the dispersion increases more rapidly with time, and scales as UD1/2t3/2/h. The well-known Taylor dispersion only occurs at long times, i.e. for t ≫ τD. Clearly, this regime is not interesting for velocimetry applications since the diffusion process homogenizes the concentration along the thickness, and the traveling velocity of the bleached line equals the mean value of the velocity field, as in the case of ref. 22 where the considered thicknesses were smaller than a few micrometers. Note that in channel flows, a fourth regime exists at longer times,29 for t ≫ w2/D, where hydrodynamic dispersion along the channel width takes place. There is no need to consider it in this study and we can model the flow geometry by two infinite parallel plates.
For the experiments presented here, τd is always greater than 25 s for the solutions studied (diffusion coefficient of fluorescein of 4 × 10−10 m2 s−1 in water30), whereas the experiment duration is less than 1 s. We thus focus on the solution of the convection–diffusion equation in the diffusive and anomalous regime, where the characteristic transverse distance traveled by the tracers is much smaller than the channel thickness. In our experiments, the concentration profile is measured in the focal plane, located at z0. It is then convenient to rewrite eqn (1) in the moving frame v(z0), and in the vicinity of the observation plane
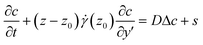 | (3) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the velocity gradient at z = z0. Note that we only keep the first term of Taylor expansion of the velocity field since the transverse displacement due to diffusion remains small.
is the velocity gradient at z = z0. Note that we only keep the first term of Taylor expansion of the velocity field since the transverse displacement due to diffusion remains small.
The impulse response of eqn (3) is given by:31
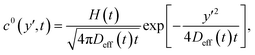 | (4) |
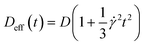 | (5) |
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) centered at v(z0). Note that this solution is not valid close to the wall since the no-flux boundary condition is satisfied for z = ±∞ and not for z = ±h/2. We can thus anticipate some deviations from this solution in the near-wall region, but also in the center where the first term of the Taylor expansion vanishes.
centered at v(z0). Note that this solution is not valid close to the wall since the no-flux boundary condition is satisfied for z = ±∞ and not for z = ±h/2. We can thus anticipate some deviations from this solution in the near-wall region, but also in the center where the first term of the Taylor expansion vanishes.
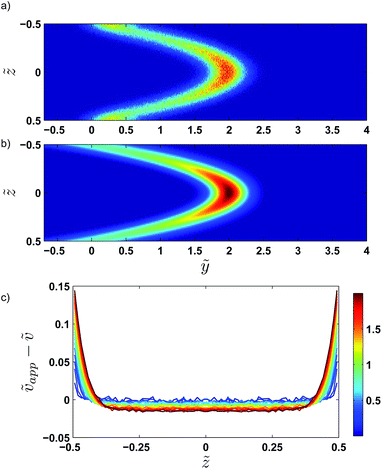
Fig. 5 shows examples of the concentration profiles corresponding to the numerical solution of eqn (1) and to the approximate analytical solution displayed eqn (4). The two sets of data agree quite well in the typical range of time scales corresponding to the experiments. Slight discrepancies are however evidenced close to the wall. The numerical simulation does not predict spreading in the negative ỹ region whereas the analytical formula does. To go further in the comparison of the two methods, we use the analytical expression to fit the numerical solution at fixed heights with effective dispersion coefficient Deff and apparent velocity vapp as fitting parameters. The fits are excellent as the concentration profiles of the numerical solution are Gaussian-like for a given height. The difference between the local velocity and the best fit parameter vapp is shown in Fig. 5c. We note that it exists a discrepancy between the two sets of data in a thin region close to the wall which increases with time. The analytical approximate solution underestimates the longitudinal displacement in the vicinity of the wall and slightly overestimates it in the center of the channel. These differences are easily explained by considering the longitudinal transverse displacement due to molecular diffusion which averages the convective displacement on a distance on the order of 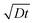 . In the center of the gap, the difference between the two approaches is less than 1% of the maximal velocity so that we neglect it in the following. Close to the wall however it is worthwhile to quantify it. We have verified that the above scaling argument applies, i.e. the apparent velocity at the wall increases as
. In the center of the gap, the difference between the two approaches is less than 1% of the maximal velocity so that we neglect it in the following. Close to the wall however it is worthwhile to quantify it. We have verified that the above scaling argument applies, i.e. the apparent velocity at the wall increases as 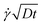 . More precisely, we find that it is within 1% given by
. More precisely, we find that it is within 1% given by
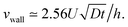 | (6) |
Both the bleaching duration τb and spatial width wb cannot be neglected since they are on the order of the acquisition time scale. From the approximate Green function c0 displayed in eqn (4), the solution for an arbitrary source could be calculated using a convolution, which reads
| c(y′, z, t) = ∫c0(λ, τ)s(y′ + v0(t − τ) − λ, t − τ)dτdλ, | (7) |
We assume that the source s is given by s(y, t) = s0⊓(y/wb)⊓(t/τb), where ⊓ is the rectangular function. We obtain for t > τb/2:
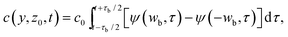 | (8) |
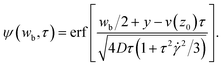 | (9) |
Eqn (8) and (9) are of great practical interest since we could use them directly to fit the experimental intensity profiles, and to extract the apparent velocity. In order to obtain a robust fitting procedure, we proceed as follows. For a given height z0, the whole time series of 15 images is fitted simultaneously, with the local velocity v0, the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and the constant c0 as fitting parameters. Examples of the resulting intensity profiles are displayed in Fig. 3. The good agreement obtained shows that the assumption of a rectangular source term both in time and in space is valid, and validates the method. It is worth noting that the model accounts well for the asymmetric shapes of the intensity curves. We also find that the fitting procedure is rather sensitive to the diffusion coefficient, and it would also be possible to deduce it from the experiments. The value of the molecular diffusion coefficient set in our fitting procedure was calculated assuming that D = Dwηw/η, where η is the liquid viscosity, Dw is the fluorescein diffusion coefficient in water (4 × 10−10 m2 s−1, according to ref. 30), and ηw the water viscosity.
and the constant c0 as fitting parameters. Examples of the resulting intensity profiles are displayed in Fig. 3. The good agreement obtained shows that the assumption of a rectangular source term both in time and in space is valid, and validates the method. It is worth noting that the model accounts well for the asymmetric shapes of the intensity curves. We also find that the fitting procedure is rather sensitive to the diffusion coefficient, and it would also be possible to deduce it from the experiments. The value of the molecular diffusion coefficient set in our fitting procedure was calculated assuming that D = Dwηw/η, where η is the liquid viscosity, Dw is the fluorescein diffusion coefficient in water (4 × 10−10 m2 s−1, according to ref. 30), and ηw the water viscosity.
To conclude this section, two additional comments should be made.
First, we recall that the above solution is only valid for t ≪ τd. At longer times, the transverse displacement would be large and the modeling of the velocity field by a single local shear rate (see eqn (3)) would not be valid. In principle, one should also include an extra term in the Taylor expansion in the center of the channel since the shear rate vanishes, but profiles acquired in this region still show good agreement with the proposed model. Furthermore the influence of the no-flux boundary conditions at the wall would at longer times affects the whole concentration field.
Second, although the impulse response (eqn (4)) exhibits a maximum at y = v(z0)t, this is generally not true for a source of finite duration (eqn (8)). The corresponding solutions are asymmetric, and the curve shape evolves with the observation time. They eventually reach a Gaussian-like profile. Therefore, by looking simply at the displacement of the maxima of the intensity curves it would lead to systematic errors, whenever the profiles are non-symmetric.
4 Velocity measurements
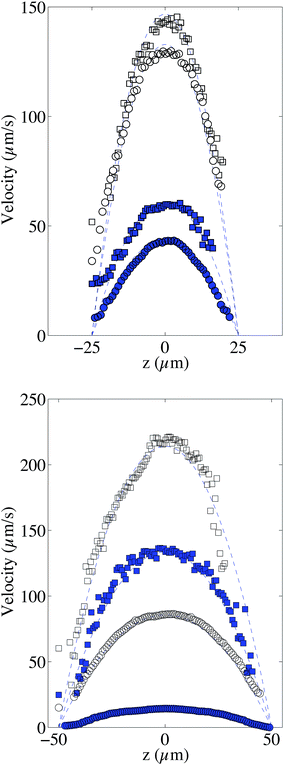
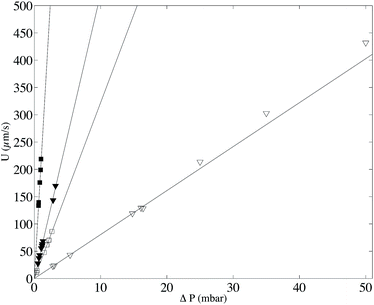
In order to validate the proposed velocimetry method, we apply it on pressure-driven flows. We recorded videos of the flow at successive heights covering the whole channel depth. It is necessary to wait a few seconds between two bleaching steps at different z in order to ensure that bleached molecules have traveled out of the observation window. We apply this experimental procedure for two different channels with h1 = 50 μm and h2 = 100 μm and two different viscosities η1 = 0.0059 Pa s and η2 = 0.0388 Pa s by controlling accurately the inlet–outlet pressure ΔP. As discussed in the previous section, different families of intensity curves are obtained from experiments. The flow profiles are obtained by fitting simultaneously 15 experimental curves, captured at each focal plane and corresponding to an observation time of τ0 = 0.25 s, with eqn (8) and (9), and having the local velocity, shear rate, and curve center x0 as fitting parameters. Fig. 6 displays the corresponding results in channels of heights 50 (top, Fig. 6) and 100 μm (bottom, Fig. 6). They are compared with the theoretical profiles, corresponding to Poiseuille flow, i.e. v = U(1 − 4z2/h2), where U = h2ΔP/8ηL. There are no fitting parameters; the viscosity η has been determined for the two fluids by using a cone–plate rheometer.For the sets of experiments we calculate the velocity at the channel center. This procedure is rather easy because the intensity curves are almost Gaussian-like at z0 = 0 and the dynamics of the intensity curves is not affected by the local shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) as it will be explained in the following. In Fig. 7 the maximum velocity versus the applied pressure ΔP is shown.
as it will be explained in the following. In Fig. 7 the maximum velocity versus the applied pressure ΔP is shown.
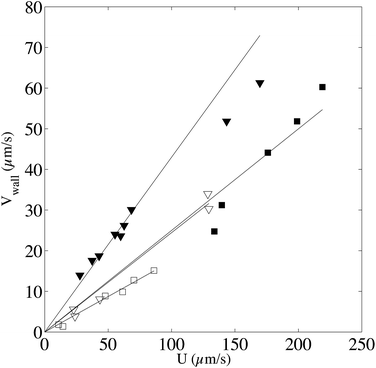
From this graph we can conclude that the method is well suited to calculate the maximum velocity with and error below 1%. The limit in the maximum velocity calculation lies mainly on the acquisition frame rate and on the size of the observation window (space available to have at least two intensity curves) because the displacement of the profile becomes too fast to be monitored. We can conclude that, with our optical setup, the limit in the maximum velocity is about 485 μm s−1 (see light triangles in Fig. 7). It would be possible to extend the experiments to higher velocities by using an objective of lower magnification, but the confocal depth would then be higher, lowering the z-resolution of the transverse profile. As for the low velocity limit, the band displacement would become too small as compared to the line diffusion. We did not test this low velocity limit in this work, but since dispersion due to shear is in this case negligible, it is possible to refer to our previous work,22 where velocities as low as 0.1 μm s−1 were reported. Coming back to the reconstructed velocity profiles, it is however clear from the profiles in Fig. 6 that there is a deviation between experimental and theoretical profiles close to the walls. The experimental results overestimate the theoretical velocity at the walls and this overestimation is proportional to the maximum velocity (see Fig. 8). Since we do not expect at these length scales any deviations from the Poiseuille law, there is a bias coming from the experimental technique itself. For the experimental conditions of the data reported in Fig. 6, the near-wall region represents a maximum value of about 5 μm at the lower viscosity value. As detailed in the previous section, the theoretical predictions are not valid near the walls, since the used solution does not respect the no-flux boundary conditions at the wall. In the data displayed in Fig. 6, the experimental time τ, which is the sum of the bleaching time and the observation time, is about 0.5 s, and the local shear rates on the order of 1 s−1, so the |![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) |τ is on the order of unity. Therefore, in eqn (9), it is not possible to neglect the advection term due to the local shear rate. During the experimental time, the transverse displacement due to diffusion is given by
|τ is on the order of unity. Therefore, in eqn (9), it is not possible to neglect the advection term due to the local shear rate. During the experimental time, the transverse displacement due to diffusion is given by 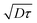 . Therefore, in the plane located in z0, the bleached molecules observed at time τ have explored by diffusion a layer of height
. Therefore, in the plane located in z0, the bleached molecules observed at time τ have explored by diffusion a layer of height 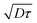 centered at z0. Due to local shear, there is thus an additional displacement in the flow direction of the order of
centered at z0. Due to local shear, there is thus an additional displacement in the flow direction of the order of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) D1/2τ3/2. In a simple shear flow and away from the wall, it is straightforward by symmetry that this displacement does not have any consequences on the mean displacement. Only the spreading is affected, as captured in the analysis, eqn (5). However, the wall breaks the vertical symmetry, and the additional positive displacement due to the local shear is not counterbalanced in the vicinity of the solid surface. Therefore, the velocity is overestimated in a near-wall region of extent
D1/2τ3/2. In a simple shear flow and away from the wall, it is straightforward by symmetry that this displacement does not have any consequences on the mean displacement. Only the spreading is affected, as captured in the analysis, eqn (5). However, the wall breaks the vertical symmetry, and the additional positive displacement due to the local shear is not counterbalanced in the vicinity of the solid surface. Therefore, the velocity is overestimated in a near-wall region of extent 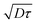 , by a quantity
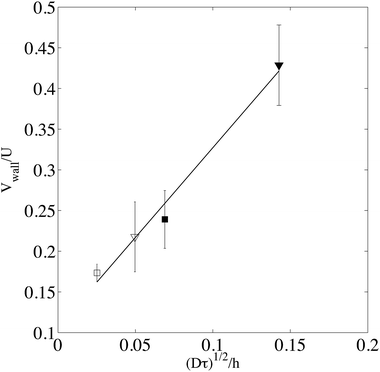
, by a quantity 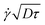 . As a practical consequence, the overestimation of the velocity near the wall could be smaller by reducing the experimental time or by decreasing the diffusion D of molecules thus increasing the fluid viscosity. This is checked in Fig. 9, where the apparent measured wall velocities normalized by the maximum velocity U and plotted versus
. As a practical consequence, the overestimation of the velocity near the wall could be smaller by reducing the experimental time or by decreasing the diffusion D of molecules thus increasing the fluid viscosity. This is checked in Fig. 9, where the apparent measured wall velocities normalized by the maximum velocity U and plotted versus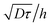 are reported. The spreading of the points for fixed
are reported. The spreading of the points for fixed 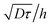 in the vertical direction is due to the increase of
in the vertical direction is due to the increase of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) with the imposed pressure gradient. The scaling is well captured for the size of channels and viscosities of fluids tested. In fact, looking for prefactors, we obtain quantitative agreement for the data displayed in Fig. 8. In Fig. 9 the normalized apparent velocity at the wall is shown from lower to higher diffusion rate and is equal to
with the imposed pressure gradient. The scaling is well captured for the size of channels and viscosities of fluids tested. In fact, looking for prefactors, we obtain quantitative agreement for the data displayed in Fig. 8. In Fig. 9 the normalized apparent velocity at the wall is shown from lower to higher diffusion rate and is equal to 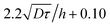 . From numerical simulations, we expect (see text in Section 3.2) that
. From numerical simulations, we expect (see text in Section 3.2) that 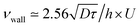 .
.
We can thus conclude that using the proposed model, detailed in the previous section, we have validated the velocimetry technique using pressure-driven flows. It is precise and robust, but can lead to a systematic error near the wall, in a layer which extend for a maximum of 5 μm from the solid surface for dye of high diffusion coefficient in a low viscous fluid. Although it does not seem possible to lower this error, it is however possible to improve it by decreasing the observation time. Indeed, the layer where the velocity is overestimated is on the order of 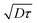 .
.
The velocity range accessibility is limited in the low speed limit by the dye molecular diffusion. The displacement due to diffusion should be not too large as compared to advection. With FITC in water, the minimum measurable velocity is about a few micrometers per second.22 The high speed limit comes from the scanning speed of the confocal microscope and from the image size related to the objective. For the conditions used in this work, this corresponds to 1 mm s−1. This high speed limit could be increased by using an objective of lower magnification. It is important to mention that the bleached line displacement between two successive images should be low enough to be able to neglect the disturbance caused by the scanning nature of confocal microscopy, or alternatively, to correct the apparent displacement.32
As compared to PTV and PIV methods, photobleaching under flow remains limited to uni-dimensional flows, although extensions to 2D are in principle possible using a bleached spot instead of a bleached line. Due to smaller diffusion coefficient, these particle-based velocimetry techniques do not suffer directly from the wall effect discussed above, but also exhibit a bias on a length scale on the order of the particle size, similar to the overestimation near the wall of the presented method.
5 Application to complex flows
As explained in the Introduction, the main interest of the present technique lies on the use of molecular tracers, which do not perturb the flow and allow particle-fluid velocity measurements. Many complex fluids contain rather large objects on the order of tens of microns in diameter that could be observed using confocal microscopy. In this case, the technique presented in this paper could be of great interest, because it is possible to measure simultaneously the fluid velocity together with the observation of particle trajectories.As an illustration of such a possibility, we disperse PMMA particles (spheromers CA6, purchased from Microbeads) in a mixture of thioglycerol and deionized water (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
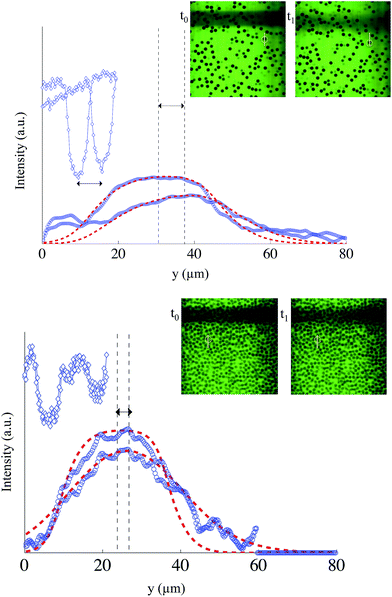
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight fraction) containing fluorescein at 0.1 × 10−3 mol L−1. The suspension is both buoyancy and refractive index matched. Two suspensions at different volume fractions (0.11 and 0.53) are flowed in our device (h = 50 μm), and the suspending fluid velocity is characterized thanks to photobleaching experiments. Since the particles appear in black on the images (see examples displayed in Fig. 10), we first segmented the particles in each image to create a mask so that we can focus only on particle-free regions to determine the fluid velocity minimizing the noise due to the black particles. At the same time we locate the particles and subsequently we measure the mean velocity using a standard tracking algorithm.8 For the fluid velocity measurement, we use exactly the same procedure described in Section 3 deducing the velocity of the liquid phase in each focal plane through the channel depth.
1 weight fraction) containing fluorescein at 0.1 × 10−3 mol L−1. The suspension is both buoyancy and refractive index matched. Two suspensions at different volume fractions (0.11 and 0.53) are flowed in our device (h = 50 μm), and the suspending fluid velocity is characterized thanks to photobleaching experiments. Since the particles appear in black on the images (see examples displayed in Fig. 10), we first segmented the particles in each image to create a mask so that we can focus only on particle-free regions to determine the fluid velocity minimizing the noise due to the black particles. At the same time we locate the particles and subsequently we measure the mean velocity using a standard tracking algorithm.8 For the fluid velocity measurement, we use exactly the same procedure described in Section 3 deducing the velocity of the liquid phase in each focal plane through the channel depth.
Fig. 10 shows two different examples of velocity measurements. In the first example (see Fig. 10, top), we imaged a plane located at z0 = −17 μm where the local particle volume fraction of 0.11 is rather low and the liquid velocity is found to be 20.2 μm s−1 while the mean particle velocity calculated by means of PTV is 19.7 μm s−1 with a standard deviation of 0.8 μm s−1. Thus, in this case the fluid and particle velocity could be considered the same.
By increasing the volume fraction of the suspension to 0.53, we observe a partial clogging of the channel due to particle accumulation. The local volume fraction reaches a value of 0.61 (see Fig. 10, bottom). Friction forces between particles are able, at this stage, to balance the drag force, so that the particle velocity is almost zero. It is much lower than the liquid velocity, estimated in this example to be 5.7 μm s−1 thanks to the photobleaching procedure. This state is not very different from the flow of a liquid in a porous medium made of solid particles. In this case, and whenever there exists a velocity difference between the fluid and the particles, the wall effect discussed in the previous section prevents an accurate spatial resolution of the velocity between arrested particles. Only the mean velocity difference can be measured given the small distance between particles.
These two examples show that the technique presented here is adequate to measure velocity differences between small scale particles and their suspending liquid in microfluidic devices. As explained in the introduction, this has some direct applications for lab-scale studies of flow properties of concentrated suspensions. Moreover, the presented velocimetry technique could also be useful for studies focusing on emulsions, transport properties in porous systems, extrusion processes of micro-particulate paste where liquid maldistribution33 and liquid phase migration34 has been found to play a major role in the final product properties.
6 Conclusion
In conclusion, we have studied the possibility of using confocal microscopy and photobleaching under flow as a velocimetry technique in microchannels. The method basically consists of following the displacement in time of bleached molecules at different focal planes through the channel depth. Despite this apparent simplicity, it is not straightforward as the resulting intensity curves could be asymmetric depending on the bleaching conditions and on the importance of convection and diffusion effects, together with the finite duration and width of the bleaching. We provide a fast method to account for this effect based on the convolution of approximate analytical solutions of the convection–diffusion equation. For pressure-driven flows, the measurement is rather accurate, and validated using various channel heights, liquid viscosities and pressure drops.The main limitation of this technique comes from wall effects. Due to diffusion and in the presence of a solid surface, the velocity is overestimated in the vicinity of the wall. This drawback is typically important in a 5 μm layer for the lower viscosity considered in this study. The only possibility to reduce this effect is to decrease the duration of the bleaching or the diffusion coefficient. Although the first one is in principle feasible but limited by the signal to noise ratio, the second one would remove the main advantage of the presented technique which relies on the use of small molecular dyes as tracers.
Applications of this technique concern any flows which could be perturbed by tracer particles. For example, we have applied it to flows of suspensions below and above the jamming, and we have proved the possibility of measuring simultaneously the particle and liquid velocity. We restrict ourselves in this study to flows that are invariant in the vorticity direction, and we use for that purpose a bleaching region which is a band aligned to this direction. However, the extension of this technique to fully 3-D flow profiles is rather straightforward, but would require from an experimental point of view an increase of the signal to noise ratio, since it is not possible to benefit from the light intensity average in the vorticity direction. In a steady flow, this could be achieved by repeating a few times the experiments.
References
- C. W. Macosko and J. Mewis, Suspension Rheology, VCH, 1994 Search PubMed.
- J. J. Stickel and R. L. Powell, Annu. Rev. Fluid Mech., 2005, 37, 129–149 CrossRef.
- G. Ovarlez, F. Bertrand and S. Rodts, J. Rheol., 2006, 50, 259–292 CrossRef CAS.
- D. Lhuillier, Phys. Fluids, 2009, 21, 023302 CrossRef PubMed.
- J. G. Santiago, S. T. Wereley, C. D. Meinhart, D. J. Beebe and R. J. Adrian, Exp. Fluids, 1998, 25, 316–319 CrossRef CAS.
- R. Lindken, M. Rossi, S. Große and J. Westerweel, Lab Chip, 2009, 9, 2551–2567 RSC.
- S. J. Lee and S. Kim, Microfluid. Nanofluid., 2009, 6, 577–588 CrossRef CAS.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- J. Gelles, B. J. Schnapp and M. P. Sheetz, Nature, 1988, 331, 450–453 CrossRef CAS PubMed.
- R. N. Ghosh and W. W. Webb, Biophys. J., 1994, 66, 1301–1318 CrossRef CAS.
- C. M. Anderson, G. N. Georgiou, I. Morrison, G. Stevenson and R. J. Cherry, J. Cell Sci., 1992, 101, 415–425 Search PubMed.
- D. Sinton, Microfluid. Nanofluid., 2004, 1, 2–21 CrossRef CAS.
- D. Ross, T. J. Johnson and L. E. Locascio, Anal. Chem., 2001, 73, 2509–2515 CrossRef CAS.
- J. P. Shelby and D. T. Chiu, Anal. Chem., 2003, 75, 1387–1392 CrossRef CAS.
- G. R. Wang, Lab Chip, 2005, 5, 450–456 RSC.
- G. R. Wang, I. Sas, H. Jiang, W. P. Janzen and C. Hodge, Electrophoresis, 2008, 29, 1253–1263 CrossRef CAS PubMed.
- C. Kuang, W. Zhao, F. Yang and G. Wang, Microfluid. Nanofluid., 2009, 7, 509–517 CrossRef.
- C. F. Kuang and G. R. Wang, Lab Chip, 2010, 10, 240–245 RSC.
- J. I. Molho, A. E. Herr, B. P. Mosier, J. G. Santiago, T. W. Kenny, R. A. Brennen, G. B. Gordon and B. Mohammadi, Anal. Chem., 2001, 73, 1350–1360 CrossRef CAS.
- B. Mosier, J. Molho and J. Santiago, Exp. Fluids, 2002, 33, 545–554 CrossRef CAS PubMed.
- C. S. Garbe, Pattern Recognit. Lect. Notes Comput. Sci., 2007, 4713, 92–101 Search PubMed.
- A. Cuenca and H. Bodiguel, Lab Chip, 2012, 12, 1672–1679 RSC.
- A. Ponjavic, M. Chennaoui and J. S. Wong, Tribol. Lett., 2013, 50, 261–277 CrossRef.
- J. Wexler, I. Jacobi and H. A. Stone, 66th Annual Meeting of the APS Division of Fluid Dynamics, 2013 Search PubMed.
- G. I. Taylor, Proc. R. Soc. London, Ser. A, 1954, 67, 857–869 Search PubMed.
- R. Aris, Proc. R. Soc. London, Ser. A, 1956, 235, 67–77 CrossRef.
- M. Latini and A. J. Bernoff, J. Fluid Mech., 2001, 441, 399–411 CAS.
- M. J. Lighthill, J. Inst. Math. Its Appl., 1966, 2, 97–108 CrossRef CAS PubMed.
- A. Ajdari, N. Bontoux and H. A. Stone, Anal. Chem., 2006, 78, 387–392 CrossRef CAS PubMed.
- K. Pappaert, J. Biesemans, D. Clicq, S. Vankrunkelsven and G. Desmet, Lab Chip, 2005, 5, 1104–1110 RSC.
- P. B. Rhines and W. R. Young, J. Fluid Mech., 1983, 133, 133–145 CrossRef.
- P. Jop, V. Mansard, P. Chaudhuri, L. Bocquet and A. Colin, Phys. Rev. Lett., 2012, 108, 148301 CrossRef.
- A. Yu, J. Bridgwater, A. Burbidge and Z. Saracevic, Powder Technol., 1999, 103, 103–109 CrossRef CAS.
- S. Rough, J. Bridgwater and D. Wilson, Int. J. Pharm., 2000, 204, 117–126 CrossRef CAS.
Footnote |
| † Present address: Laboratoire Photonique, Numérique et Nanosciences (LP2N) UMR 5298, CNRS – IOGS – Université Bordeaux, Institut d'Optique d'Aquitaine 33400 Talence, France. |
| This journal is © The Royal Society of Chemistry 2015 |