Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The rheology of aqueous solutions of ethyl hydroxy-ethyl cellulose (EHEC) and its hydrophobically modified analogue (hmEHEC): extensional flow response in capillary break-up, jetting (ROJER) and in a cross-slot extensional rheometer†
Vivek
Sharma
*ab,
Simon J.
Haward
bc,
James
Serdy
d,
Bavand
Keshavarz
b,
Asa
Soderlund
e,
Phil
Threlfall-Holmes
f and
Gareth H.
McKinley
b
aDepartment of Chemical Engineering, University of Illinois at Chicago, IL 60607, USA. E-mail: viveks@uic.edu
bHatsopoulos Microfluids Laboratory, Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139-4307, USA
cOkinawa Institute of Science and Technology Graduate University, 1919-1 Tancha, Onna-son, Kunigami-gun, Okinawa 904-0495, Japan
dLaboratory of Manufacturing and Productivity, Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139-4307, USA
eAkzoNobel Functional Chemicals, Hamnvägen 2, Stenungsund 444 85, Sweden
fAkzoNobel Research, Development and Innovation, Stoneygate Lane, Felling, Gateshead, NE10 0JY, UK
First published on 27th January 2015
Abstract
Cellulose derivatives containing associating hydrophobic groups along their hydrophilic backbone are used as rheology modifiers in the formulation of water-based spray paints, medicinal sprays, cosmetics and printable inks. Jetting and spraying applications of these materials involve progressive thinning and break-up of a fluid column or sheet into drops. Strong extensional kinematics develop in the thinning fluid neck. In viscous Newtonian fluids, inertial and viscous stresses oppose the surface tension-driven instability. In aqueous solutions of polymers such as Ethyl Hydroxy-Ethyl Cellulose (EHEC), chain elongation provides additional elastic stresses that can delay the capillary-driven pinch-off, influencing the sprayability or jettability of the complex fluid. In this study, we quantify the transient response of thinning filaments of cellulose ether solutions to extensional flows in a Capillary Break-up Extensional Rheometer (CaBER) and in a forced jet undergoing break-up using Rayleigh Ohnesorge Jetting Extensional Rheometry (ROJER). We also characterize the steady state molecular deformations using measurements of the flow-induced birefringence and excess pressure drop in an extensional stagnation point flow using a Cross-Slot Extensional Rheometer (CSER). We show that under the high extension rates encountered in jetting and spraying, the semi-dilute solutions of hydrophobically modified ethyl hydroxy-ethyl cellulose (hmEHEC) exhibit extensional thinning, while the unmodified bare chains of EHEC display an increase in extensional viscosity, up to a plateau value. For both EHEC and hmEHEC dispersions, the low extensibility of the cellulose derivatives limits the Trouton ratio observed at the highest extension rates attained (close to 105 s−1) to around 10–20. The reduction in extensional viscosity with increasing extension rate for the hydrophobically modified cellulose ether is primarily caused by the disruption of a transient elastic network that is initially formed by intermolecular association of hydrophobic stickers. This extensional thinning behavior, in conjunction with the low extensibility of the hydrophobically modified cellulose ether additives, makes these rheology modifiers ideal for controlling the extensional rheology in formulations that require jetting or spraying, with minimal residual stringiness or stranding.
1. Introduction
Multicomponent complex fluids containing long polymer molecules are found to provide a much larger resistance to extensional flow than expected on the basis of their shear viscosity. For a Newtonian fluid, the extensional viscosity is a factor of three times larger than the shear viscosity (as was first shown by Trouton1); however it can be several orders of magnitude higher for polymeric fluids.1–3 A stretching or extensional deformation is established when streamwise velocity gradients are present in a flow. Such extensional components arise in virtually all relevant processing flows,2–4 including capillary contraction/expansion flows, flows through bifurcations (e.g. ‘T’ or ‘Y’ junctions), flow around obstacles and near stagnation points,5–7 as well as in common industrial processes such as spraying, jet break-up, drop formation and filament stretching.8–11 Extensional viscosity enhancement can dramatically influence the flow characteristics of fluids in these processes.2,4–11 Designing fluids with appropriate characteristics (which are commonly expressed in heuristic terms such as sprayability, spinnability, printability and jettability) requires systematic control over the response of a complex fluid to both shear and extensional deformations. Polysaccharides or carbohydrate polymers12–14 are among the most common constituents of industrial and natural complex fluids and thus contribute to the measurable flow resistance in many extensional deformations, influencing spraying and coating of paints,15 inkjet printing, filament spinning,16 porous media flow,17 enhanced oil recovery,18 and turbulent drag reduction as well as in natural systems such as synovial fluid, mucus and deadly viscoelastic fluids found in carnivorous plants.19,20In this work we contrast the shear and extensional rheology of model aqueous solutions of cellulose ether, EHEC (Ethyl Hydroxy-Ethyl Cellulose), and its hydrophobically modified analogue, hmEHEC. The hmEHEC chains have hydrophobic stickers distributed along the backbone. In aqueous dispersion, the hydrophobic stickers associate together as temporary junctions that break and reform continuously under the action of thermal fluctuations and in response to applied deformations.21–25 Since these cellulose ethers are used as rheology modifiers in multi-component fluids, we probe their response over the wide range of shear and extensional rates that characterize typical process flows. In a companion study, we discuss the shear-rate-dependent response of EHEC and hmEHEC dispersions as manifested by the shear viscosity and first normal stress difference measurements for different polymer concentrations. Interchain hydrophobic associations between the multisticker hmEHEC polymers lead to the formation of transient physical gels that provide enhancement to the low shear-rate viscosity when compared with dispersions of bare EHEC chains. At high shear rates, the gel-like microstructure breaks down and the high shear rate viscosity of the sticky, hydrophobically modified chains becomes quite similar to that of the bare polymer. We infer that the enhancement in viscosity due to stickers at low shear rates provides the requisite high viscosity for controlling sagging and slumping behavior of paints,26 while the high degree of shear thinning associated with the break-down of the microstructure leads to a much lower shear viscosity at the high shear rates most relevant to coating applications. We also characterize the linear viscoelasticity of the physical networks formed by the sticky hmEHEC polymers using a Fractional Maxwell Model (FMM). Additionally we contrasted the measured concentration-dependent response of the linear viscoelasticity of these sticky polymer networks with the theoretical predictions of Rubinstein and Semenov.27,28 In the present paper, we focus exclusively on a comparison between the extensional behavior of aqueous dispersions of cellulose ether, EHEC and the corresponding multisticker associative polymer, hmEHEC. We probe the influence of transient extensional rheology at moderate extensional rates during capillary thinning break-up and at higher deformation rates using the free-surface flow during jetting. We also measure extensional contributions to the bulk pressure drop and the corresponding molecular deformation in a steady extensional flow field generated within a cross-slot flow extensional rheometer. We specifically consider the rheological properties from the perspective of design and application of water-based paints, to put into context the role of associative polymers as rheology modifiers in industrial applications.
The application of paint to surfaces commonly involves the use of either roller-coating devices or spraying equipment.29,30 Both of these application processes involve the formation of elongated fluid filaments that spontaneously break into droplets, due to a capillary-driven instability that seeks to minimize the total surface area of the fluid sample. This surface-tension-driven instability is manifested as sinusoidal perturbations to the initial cylindrical shape of the fluid column, and this creates a uniaxial extensional flow field within the necking filament, as the enhanced local capillary pressure squeezes fluid out of the narrow neck.8,9,31 The process of capillary thinning eventually leading to pinch-off is opposed by the presence of viscous and inertial stresses.32–34 In polymeric complex fluids, microstructural changes and the associated increase in the total viscous drag on the elongating polymer chains provide extra elastic stresses that can substantially delay the capillary-driven pinch-off as well as modify the drop size and the distribution of drop sizes.8,31,35–44 In spite of the widespread use of polysaccharides or cellulose derivatives (with and without associative stickers) as rheology modifiers in applications where the response to extensional flows determines their utility, their response to extensional deformation, especially in the context of jetting and spraying, remains a less well-studied problem.12 The lack of requisite characterization at high deformation rates for viscoelastic fluids is due to the difficulties and limitations inherent to the techniques commonly used for measuring the response to extensional flow fields, as we describe next.
Extension-free simple shear flows can be readily generated in cone-and-plate or Couette geometries on a torsional rheometer4 in order to measure the rate-dependent shear viscosity, η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), as well as the first and second normal stress differences, N1(
), as well as the first and second normal stress differences, N1(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) and N2(
) and N2(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ). Likewise, it is desirable to measure the extensional viscosity, ηE(
). Likewise, it is desirable to measure the extensional viscosity, ηE(![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ), of a complex fluid as the material response to a shear-free, purely extensional deformation where the imposed extensional rate,
), of a complex fluid as the material response to a shear-free, purely extensional deformation where the imposed extensional rate, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , is controlled to be constant. However, the extensional response of complex fluids in any geometry or device exhibits a strong dependence on flow parameters9 including both the strain rate,
, is controlled to be constant. However, the extensional response of complex fluids in any geometry or device exhibits a strong dependence on flow parameters9 including both the strain rate, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , and the total fluid strain, ε. Thus the measured extensional viscosity is a deformation-history dependent material function, and the underlying flow kinematics in most techniques result in measurement of a transient extensional viscosity or η†E(
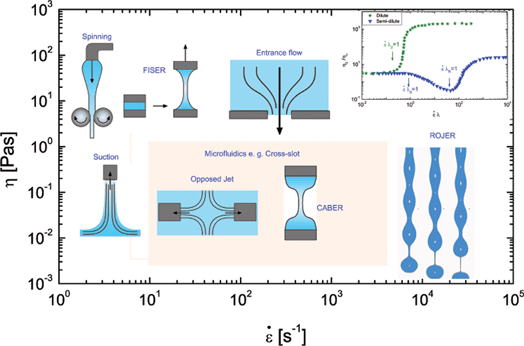
, and the total fluid strain, ε. Thus the measured extensional viscosity is a deformation-history dependent material function, and the underlying flow kinematics in most techniques result in measurement of a transient extensional viscosity or η†E(![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , t).45Fig. 1 summarizes various techniques2,4 that can be used for studying polymer solution extensional rheology. The typical range of zero shear viscosity and extensional rates accessed by each device are shown qualitatively. Though the comparison of different measures of extensional viscosity characterized using different techniques can show a great disparity,45,46 understanding the dynamics of the response from a given method is extremely useful in designing complex fluids with the requisite processability, or alternatively in controlling the processing parameters for a given complex fluid. The use of experimental techniques with well-controlled flow fields and deformation histories is also important for developing constitutive models for complex fluids. There is also considerable growth in recent interest in designing suitable, polymeric complex fluids for additive manufacturing processes where relating the processability to the underlying fluid rheology will be necessary for realizing economics of scale and quality in 3-D printing, ink-jet printing-based biomaterials, print electronics and print photovoltaics.10,47–49
, t).45Fig. 1 summarizes various techniques2,4 that can be used for studying polymer solution extensional rheology. The typical range of zero shear viscosity and extensional rates accessed by each device are shown qualitatively. Though the comparison of different measures of extensional viscosity characterized using different techniques can show a great disparity,45,46 understanding the dynamics of the response from a given method is extremely useful in designing complex fluids with the requisite processability, or alternatively in controlling the processing parameters for a given complex fluid. The use of experimental techniques with well-controlled flow fields and deformation histories is also important for developing constitutive models for complex fluids. There is also considerable growth in recent interest in designing suitable, polymeric complex fluids for additive manufacturing processes where relating the processability to the underlying fluid rheology will be necessary for realizing economics of scale and quality in 3-D printing, ink-jet printing-based biomaterials, print electronics and print photovoltaics.10,47–49
Steady extension-dominated flows that enable control over both the local strain rate and the total accumulated strain can be realized by incorporating a stagnation point in the flow field.50–53 At such a singular point, the local fluid velocity approaches zero but the strain rate can be large. Hence macromolecules contained in the fluid elements that pass through the stagnation point become trapped in the elongational flow field for an extended time period and can accumulate significant strain provided the characteristic deformation rate exceeds ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) > 1/λ, where λ is the longest relaxation time of the polymeric fluid. The relative magnitude of the relaxation rate (1/λ) and deformation rate (
> 1/λ, where λ is the longest relaxation time of the polymeric fluid. The relative magnitude of the relaxation rate (1/λ) and deformation rate (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ) is characterized by the Weissenberg number, Wi = λ
) is characterized by the Weissenberg number, Wi = λ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , and extensional flows with Wi > 1 are characterized as strong flows. Stagnation point flows can be generated using macroscopic techniques like four-roll mills and opposed jet or cross-slot devices,54 and the measurements can be extended to higher rates by using microfluidic devices50,55 such as T-junctions,56,57 four-roll mill analogues58–61 and cross-slots,6,53,62–68 where the small length scales and lower flow rates required to achieve high Weissenberg numbers result in reduced inertial contributions to the flow. By a suitable choice of geometry, such microfluidic devices allow measurements up to extension rates of at least 104 s−1 and most of these techniques also allow the use of rheo-optical methods for visualizing both flow kinematics and the polymer orientation and stretch.50 In the present study, we use a Cross-Slot Extensional Rheometer (CSER) to measure both the change in birefringence and the extra pressure drop near a stagnation point to characterize the extensional deformation of the cellulose ether solutions.
, and extensional flows with Wi > 1 are characterized as strong flows. Stagnation point flows can be generated using macroscopic techniques like four-roll mills and opposed jet or cross-slot devices,54 and the measurements can be extended to higher rates by using microfluidic devices50,55 such as T-junctions,56,57 four-roll mill analogues58–61 and cross-slots,6,53,62–68 where the small length scales and lower flow rates required to achieve high Weissenberg numbers result in reduced inertial contributions to the flow. By a suitable choice of geometry, such microfluidic devices allow measurements up to extension rates of at least 104 s−1 and most of these techniques also allow the use of rheo-optical methods for visualizing both flow kinematics and the polymer orientation and stretch.50 In the present study, we use a Cross-Slot Extensional Rheometer (CSER) to measure both the change in birefringence and the extra pressure drop near a stagnation point to characterize the extensional deformation of the cellulose ether solutions.
Quantitative analysis of the capillary-thinning dynamics of complex fluids can also provide a measure of the transient extensional viscosity and chain unraveling timescale relevant for capillary-driven flows.9,40,68–75 Measurement of the capillary-driven self-thinning dynamics of a stretched liquid bridge is the underlying principle of the Capillary Break-up Extensional Rheometer (CaBER).9,42,76,77 In this device, the practical limit to the measurable response is set by the time required to stretch the liquid bridge77 and more specialized bespoke instrumentation must be developed for low viscosity systems.73,74 We have recently developed a jetting-based rheometry technique, called the Rayleigh Ohnesorge Jetting Extensional Rheometer (ROJER) that provides access to the typically unchartered regime of very short relaxation time, low viscosity complex fluids,70,71 corresponding to the bottom right corner of Fig. 1. The rheometry technique is based on the understanding of the nonlinear fluid dynamics underlying the jetting process, as described in the text later, and is motivated by a method originally suggested by Schümmer and Tebel.78 In the present study, we examine the capillary break-up dynamics in both CaBER and ROJER devices in order to understand the extensional behavior of cellulose ethers in free-surface flow configurations that closely mimic the deformation history and stresses encountered in jetting and spraying applications.
The typical characteristics of extensional viscosity responses for dilute and semi-dilute polymer solutions are shown in the inset to Fig. 1. The enhanced resistance to extensional deformation is most pronounced and well-studied for dilute polymer solutions where a macromolecular conformational change from a random coil to a highly stretched state underlies the observed increase in resistance to elongational flow. Extensional viscosities up to 102 to 104 times larger than the zero shear viscosity have been reported for dilute solutions75 and the values increase with molecular weight, as indicated schematically by the inset (Fig. 1). In semi-dilute solutions, due to the overlap between different chains, the effective strain encountered by any individual coil is lower. Entangled semi-dilute solutions (blue triangles) thus typically show a regime of extensional thinning followed by extensional thickening at higher rates.79–83 However, depending on the entanglement density and chain rigidity, some dilute and semi-dilute solutions show an extensional thickening regime followed by extensional thinning at high rates (see open symbols).5,22,84,85 In this paper, the measured response of polymer chains with self-associating or ‘sticky’ side groups (hmEHEC dispersions) is contrasted with the corresponding response of bare polymer chains (EHEC dispersions). The understanding of the response of multisticker polymer chains is a necessary step to arrive at a rational basis for choosing or designing optimal water-soluble rheology modifiers for jetting and spraying applications.
2. Materials and methods
2.1 Materials
In this study, we use a hydrophobically modified ethyl hydroxyethyl cellulose ether (hmEHEC) with the degree of substitution (DS) occupied by the ethyl group given by DSEt ≈ 0.8; the molar degree of substitution (MS) by ethylene oxide groups is MSEO ≈ 2.5, and the degree of substitution by the hydrophobic sticker distributed along the chain is MSC14 ≈ 0.008.15 The hmEHEC was provided in a purified form by Åsa Söderlund, AkzoNobel Cellulosic Specialties and has a degree of polymerization DP ≈ 800, which corresponds to a molecular weight Mw ≈ 240![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Daltons. The molecular weight of the individual unsubstituted anhydrous glucose unit is M0 = 162 Daltons. In addition to hmEHEC, which we often refer to as a ‘sticky’ polymer in the rest of this paper, we also use the corresponding unmodified or ‘bare’ polymer (EHEC), which has no hydrophobic stickers along the chain but has a similar molecular weight and degree of substitution. The shear rheology of both the polymers is described in detail in a companion paper.
000 Daltons. The molecular weight of the individual unsubstituted anhydrous glucose unit is M0 = 162 Daltons. In addition to hmEHEC, which we often refer to as a ‘sticky’ polymer in the rest of this paper, we also use the corresponding unmodified or ‘bare’ polymer (EHEC), which has no hydrophobic stickers along the chain but has a similar molecular weight and degree of substitution. The shear rheology of both the polymers is described in detail in a companion paper.
2.2 Cross-slot extensional rheometer (CSER)
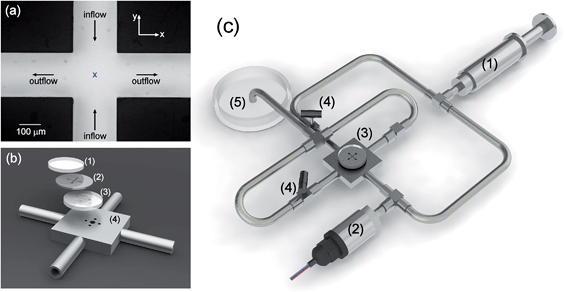
We studied the steady extensional flow of three representative EHEC and hmEHEC solutions in a microfluidic cross-slot device. Cross-slot devices consist of orthogonal, mutually bisecting channels with opposing inlets and outlets, which, by virtue of their symmetry, generate a stagnation point at the exact center of the flow domain.86 The strain rate (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CS) is controlled by the volumetric flow rate through the device and we can perform measurements of flow-induced birefringence in the vicinity of the stagnation point together with the macroscopic pressure loss across the channel as the flow rate is progressively increased. An optical micrograph of the cross-slot geometry used in the study is shown in Fig. 2a. We define the x and y axes as shown in the figure, with the stagnation point (marked by the blue ‘x’ at the centre of the intersecting channels) taken as the coordinate origin and the z-axis normal to the plane of the page. The slots are precision machined with a width of w = 0.2 mm, and a depth in the z-direction of d = 1050 ± 10 μm, providing an aspect ratio α = d/w ≈ 5 and hence a quasi-2D flow. The length of the inlet/outlet channels is l = 1.2 mm. In all the results presented herein the inflow and outflow directions are as marked in Fig. 2a.
CS) is controlled by the volumetric flow rate through the device and we can perform measurements of flow-induced birefringence in the vicinity of the stagnation point together with the macroscopic pressure loss across the channel as the flow rate is progressively increased. An optical micrograph of the cross-slot geometry used in the study is shown in Fig. 2a. We define the x and y axes as shown in the figure, with the stagnation point (marked by the blue ‘x’ at the centre of the intersecting channels) taken as the coordinate origin and the z-axis normal to the plane of the page. The slots are precision machined with a width of w = 0.2 mm, and a depth in the z-direction of d = 1050 ± 10 μm, providing an aspect ratio α = d/w ≈ 5 and hence a quasi-2D flow. The length of the inlet/outlet channels is l = 1.2 mm. In all the results presented herein the inflow and outflow directions are as marked in Fig. 2a.
The cross-slots are fabricated from stainless steel discs by the technique of wire electrical discharge machining (wire-EDM). This method provides highly parallel, non-tapering walls and a smooth surface finish; both of which are essential features for producing a stable, symmetric flow. Annealed soda glass viewing windows are glued to the front and rear surfaces of the stainless steel flow channel (see Fig. 2b), allowing optical access to the region near the stagnation point. The rear window first has four holes drilled through it ultrasonically, to allow flow into/out of each arm of the device. Finally, the stainless steel/glass sandwich assembly is glued onto a monolithic stainless steel back-plate, which provides connections to the external plumbing and flow loop, as shown in Fig. 2c. All bonds are made using silicone aquarium adhesive. The continuous flow through the cross-slot device is driven at a controlled rate using a precision syringe pump (Harvard PHD-Ultra). The flow from the syringe pump, labeled (1) in Fig. 2c, is split into two channels to provide the flow into the opposing inlets of cross-slot (3). The two outlets are connected together so they remain at equal pressure and do not generate an unbalanced flow. One of the inlet channels is fitted with a 35 kPa gauge pressure transducer (GE Druck) (2) to measure the pressure drop across the flow cell. Effluent is ejected to a Petri dish (5) and discarded to waste.
The syringe pump delivers volume flow rates in the range 0.1 mL min−1 ≤ Q ≤ 10 mL min−1. This provides nominal extension rates at the stagnation point of 40 s−1 ≤ ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CS ≤ 4000 s−1, that are calculated according to the expression:
CS ≤ 4000 s−1, that are calculated according to the expression:
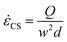 | (1) |
The Reynolds number for flow in the cross-slot device is calculated using Re = ρUDh/η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), where Dh is the hydraulic diameter, Dh = 2wd/(w + d), and η(
), where Dh is the hydraulic diameter, Dh = 2wd/(w + d), and η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) is the shear rate-dependent shear viscosity. Within the cross-slot, assuming an ideal planar extensional flow given by u = [
) is the shear rate-dependent shear viscosity. Within the cross-slot, assuming an ideal planar extensional flow given by u = [![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CSx, −
CSx, −![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CSy, 0]T the corresponding value of the characteristic shear rate is
CSy, 0]T the corresponding value of the characteristic shear rate is 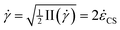 , where II(
, where II(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) is the second invariant of the deformation rate tensor
) is the second invariant of the deformation rate tensor ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = ∇u + ∇uT. For the range of volume flow rates investigated we obtain a range of 0.03 ≤ Re ≤ 40, depending on the particular fluid.
= ∇u + ∇uT. For the range of volume flow rates investigated we obtain a range of 0.03 ≤ Re ≤ 40, depending on the particular fluid.
Broadly speaking, elastic effects are expected to become significant as the Weissenberg number (Wi = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) λ) exceeds unity, i.e. as material elements are being stretched faster than the dissolved polymers can relax. Hence, observation of elastic effects such as the onset of birefringence near the stagnation point or an enhanced pressure drop across the flow cell at a specific strain rate
λ) exceeds unity, i.e. as material elements are being stretched faster than the dissolved polymers can relax. Hence, observation of elastic effects such as the onset of birefringence near the stagnation point or an enhanced pressure drop across the flow cell at a specific strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c indicates the coil–stretch transition9,54,87–90 and can be used to estimate the relaxation time of the test fluid as λ = 1/
c indicates the coil–stretch transition9,54,87–90 and can be used to estimate the relaxation time of the test fluid as λ = 1/![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c.
c.
The flow-induced birefringence arising in the fluid due to macromolecular orientation in the vicinity of the stagnation point is measured by using an ABRIO birefringence microscope system (CRi, Inc.).91,92 The cross-slot flow cell is placed on the imaging stage of an inverted microscope (Nikon Eclipse TE 2000-S) and the mid-plane of the flow cell is brought into focus using a 20 × 0.5 NA objective. Circularly polarized monochromatic light (λ = 546 nm) is passed first through the sample, then through a liquid crystal compensator optical element and finally onto a CCD array. To acquire a flow birefringence image, five individual frames are captured with the liquid crystal compensator configured in a specific polarization state in each frame, and data from the five individual frames are converted into a full-field map of optical retardation and orientation angle.91,92 The system can measure the optical retardation (R) of the polarized light to a nominal accuracy of ∼0.02 nm, with a spatial resolution corresponding to a pixel size ∼0.5 μm (with a 20× objective lens). The relationship between the retardation and the birefringence of the sample is given by R = dΔn, where d is the depth of the flow cell.
By closing the two needle valves, labeled (4), the pressure drop can also be measured for steady viscous shearing flow of fluid around a single corner of the cross-slot (ΔPshear). Subsequently, the pressure drop is measured with the two needle valves open (ΔPtotal) to generate a stagnation point flow and the excess pressure drop (ΔPexcess = ΔPtotal − ΔPshear) arising as a result of the additional extensional component in the flow field is computed. It has previously been shown that the extensional stress difference Δτ in the stretching fluid is proportional to the excess pressure drop5,64 or Δτ ∝ ΔPexcess. We can therefore obtain a measure of the apparent extensional viscosity of the fluid thus:
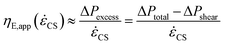 | (2) |
The Trouton ratio of the fluid is the ratio of the measured extensional viscosity to shear viscosity and is calculated from the definition Tr(![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CS) = ηE,app(
CS) = ηE,app(![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CS)/η(
CS)/η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), where η(
), where η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) is the value of shear viscosity found from cone-and-plate rheometry and
) is the value of shear viscosity found from cone-and-plate rheometry and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2
= 2![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CS, as described above. The expected Trouton ratio for Newtonian fluids undergoing planar elongational flow is Tr = 4.93
CS, as described above. The expected Trouton ratio for Newtonian fluids undergoing planar elongational flow is Tr = 4.93
2.3 Extensional rheometry based on capillary break-up dynamics
In addition to the extensional viscosity measurements performed in the microfluidic cross-slot rheometer, we carried out capillary thinning and jetting measurements to identify and characterize the response of cellulose ether solutions to the rapid transient extensional deformations that arise in free-surface flows realized in actual jetting, printing and spraying processes. The underlying physics and the methods are described next.The CaBER technique enables the assessment of the longest molecular unraveling times and extensional stresses of viscoelastic fluids through monitoring of the capillary thinning and breakup dynamics of a fluid thread that is formed between two circular rigid end-plates.76,77 As the fluid neck thins locally over time under the action of capillary pressure, the dynamics of the thinning process depend upon the magnitude of the viscous, inertial and elastic stresses that oppose the pinch-off. The relative magnitudes of these four contributions to the stress, and the absence of external forcing, result in similarity solutions that determine the rate of thinning.9 The self-similar thinning dynamics can then be used to compute material parameters, such as the relaxation time for elastic fluids, as discussed in the next sub-section.
We now consider the capillary thinning dynamics in the jetting geometry used in the ROJER technique. An inviscid fluid jet issuing out of a nozzle is unstable to a range of different perturbations. The characteristic growth rate, α, for a perturbation of wavelength, λp (or wavenumber, k = 2π/λp), is given by an expression first derived and discussed by Rayleigh94–96 to be
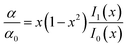 | (3) |
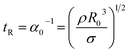 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α0 appear at xmax = kmaxR0 = 0.69. The break-up length, LB, of the jet is predicted by linear stability analysis to be shortest for the frequency kmax at which the maximum growth rate αmax is achieved. The break-up length LB of inviscid or low viscosity Newtonian fluid jets97 is linearly proportional to the jet velocity, Vj, and can be written as LB/D0 = CWe0.5. Here, the Weber number, We = ReCa = ρVj2D0/σ is the dimensionless ratio of the stagnation pressure in the jet to the capillary pressure (which acts to break the jet into drops) and typically the constant C ≈ 12. The presence of viscous effects changes both the dispersion curve and the break-up length97 to an expression of the form LB/D0 = CWe0.5(1 + 3Oh). Here the Ohnesorge number, which contrasts the relative importance of viscosity to inertio-capillary effects, is defined as Oh−2 = Re/Ca = ρσD/η02. The Ohnesorge number scales linearly with viscosity and does not depend upon the jet velocity. In contrast to free jets, for a harmonically vibrated jet, the dominant perturbation on the jet is selected by the choice of perturbation frequency, fp, and the velocity of the jet, Vj (so that wavenumber, k = 2πfp/Vj). In this case, the break-up length can be measured directly as a function of imposed perturbation frequency, and for low viscosity fluids, the shortest break-up length corresponds to the wavenumber xmax = kmaxR0 = 0.69.
α0 appear at xmax = kmaxR0 = 0.69. The break-up length, LB, of the jet is predicted by linear stability analysis to be shortest for the frequency kmax at which the maximum growth rate αmax is achieved. The break-up length LB of inviscid or low viscosity Newtonian fluid jets97 is linearly proportional to the jet velocity, Vj, and can be written as LB/D0 = CWe0.5. Here, the Weber number, We = ReCa = ρVj2D0/σ is the dimensionless ratio of the stagnation pressure in the jet to the capillary pressure (which acts to break the jet into drops) and typically the constant C ≈ 12. The presence of viscous effects changes both the dispersion curve and the break-up length97 to an expression of the form LB/D0 = CWe0.5(1 + 3Oh). Here the Ohnesorge number, which contrasts the relative importance of viscosity to inertio-capillary effects, is defined as Oh−2 = Re/Ca = ρσD/η02. The Ohnesorge number scales linearly with viscosity and does not depend upon the jet velocity. In contrast to free jets, for a harmonically vibrated jet, the dominant perturbation on the jet is selected by the choice of perturbation frequency, fp, and the velocity of the jet, Vj (so that wavenumber, k = 2πfp/Vj). In this case, the break-up length can be measured directly as a function of imposed perturbation frequency, and for low viscosity fluids, the shortest break-up length corresponds to the wavenumber xmax = kmaxR0 = 0.69.
The break-up of non-Newtonian or viscoelastic jets is markedly different from viscous jets because elastic effects are typically important. The relative contribution of elastic and viscous effects is characterized through an elasticity number, El = η0λ/ρD02, which does not depend upon the process kinematics. Since the elasticity number depends inversely on the square of the length scale, viscoelastic effects are bound to become more significant with any decrease in the diameter of a filament undergoing thinning. For weakly elastic jets, where El ≪ (1 + 3Oh)2, Middleman98 used linear stability analysis to show
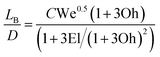 | (5) |
This expression suggests that the break-up length is lower for weakly elastic fluids. Furthermore linear stability analysis shows that viscoelastic jets initially have faster disturbance growth than a Newtonian fluid of the same viscosity.98–103 However, in the case of strongly strain-hardening polymer solutions, the capillarity-driven thinning is opposed at large strains by the presence of an extra stress due to polymer stretching, and this can subsequently stabilize the jet against pinch-off.33,37,38,99,101 In some cases, the build-up of extra elastic stresses during filament thinning can lead to the development of extremely stable beads-on-a-string morphologies, and consequently lead to much longer break-up lengths.39,43
Experimentally, the delay in pinch-off due to contributions of elastic stresses can be used to determine the apparent extensional viscosity,9,40,104 and this underlies the basis for both CaBER and ROJER techniques. In the elasto-capillary regime, the transient extensional properties of the fluid can be determined by measuring the rate of evolution in the mid-filament diameter and by using the balance between elastic and capillary forces, as described in eqn (6)–(9) below. For a cylindrical fluid filament, we can define the instantaneous strain rate (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ) and the accumulated Hencky strain (εH), as follows:42,104
) and the accumulated Hencky strain (εH), as follows:42,104
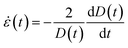 | (6) |
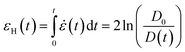 | (7) |
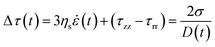 | (8) |
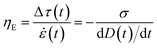 | (9) |
For an aqueous polymer solution such as the cellulosic system studied in the present work, Entov and Hinch104 argued that in the elasto-capillary thinning regime, the mid-plane diameter of the filament decays exponentially as
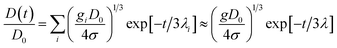 | (10) |
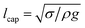 , where σ is the surface tension, ρ = 1.0 g cm−3 is the solvent (water) density, and g = 9.81 m s−2 is the acceleration due to gravity.77 The surface tension of the aqueous cellulose ether solutions was measured to be σ = 60 mN m−1 using a Krüss K10ST digital tensiometer, resulting in lcap ≈ 2.2 mm.
, where σ is the surface tension, ρ = 1.0 g cm−3 is the solvent (water) density, and g = 9.81 m s−2 is the acceleration due to gravity.77 The surface tension of the aqueous cellulose ether solutions was measured to be σ = 60 mN m−1 using a Krüss K10ST digital tensiometer, resulting in lcap ≈ 2.2 mm.
At time t = −50 ms the top endplate was displaced upwards following an exponential profile L(t) = L0e![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) 0t to achieve a final plate separation of Lf = 6 mm at time t = 0 s (final aspect ratio Λf = Lf/D0 = 1.0). The subsequent evolution of the liquid filament diameter (D(t)) was monitored at the midplane between the endplates (i.e. at L = Lf/2) using a laser micrometer. The dynamics of the liquid bridge thinning and break-up process were also recorded at 60 frames per second using a 6 megapixel CCD camera (Casio Exilim EX-F1), with a resolution of approximately 7 μm per pixel. In uniaxial extensional flow Newtonian fluids (with rate-independent shear viscosity) display an extensional viscosity that is three times the shear viscosity. Thus for Newtonian fluids, the ratio of extensional viscosity to shear viscosity, defined as the Trouton ratio is Tr = ηE/η0 = 3.
0t to achieve a final plate separation of Lf = 6 mm at time t = 0 s (final aspect ratio Λf = Lf/D0 = 1.0). The subsequent evolution of the liquid filament diameter (D(t)) was monitored at the midplane between the endplates (i.e. at L = Lf/2) using a laser micrometer. The dynamics of the liquid bridge thinning and break-up process were also recorded at 60 frames per second using a 6 megapixel CCD camera (Casio Exilim EX-F1), with a resolution of approximately 7 μm per pixel. In uniaxial extensional flow Newtonian fluids (with rate-independent shear viscosity) display an extensional viscosity that is three times the shear viscosity. Thus for Newtonian fluids, the ratio of extensional viscosity to shear viscosity, defined as the Trouton ratio is Tr = ηE/η0 = 3.
 | (11) |
The first equality relates the apparent velocity uapp to the parameters from the image analysis, where M is the magnification (related to the ratio of nozzle size in microns to its size in pixels), upix is a velocity defined in terms of pixels moved per frame, and F is the frame rate. The second equality describes the stroboscopic effect. The higher the driving frequency, the greater is the apparent slowing down of the jet. Typical operating frequencies are in the range of a few kHz, the field of view ranges from 0.5 mm to a few mm, and the typical observable feature size is in the size range of 5–200 μm. For a driving frequency of fp = 4 kHz and a frequency delay of Δfp = 0.1 Hz, the fluid is observed at 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times slower speed, allowing us to resolve the dynamics of jet thinning in a low viscosity complex fluid using conventional video imaging hardware. A charge-coupled device (CCD) camera (BlueFox, Matrix Vision) with an attached zoom lens collects the images at a rate of around F = 40 fps, and the movies are stored in digital, unprocessed form on an external hard-disk connected to the computer. Some of the jetting experiments are alternatively acquired using a JetXpert (ImageXpert, Nashua, NH) imaging system, where the frame rate is restricted to 6 fps. Air pressure or a precision syringe pump (Harvard PhD Ultra) is used to control the flow rate but the precision required in the uniformity of the flow rate limits us to fluids with viscosity below 20 mPa s. Image analysis is carried out using ImageJ105 (an imaging program developed by NIH, available freely), and custom programs specifically written for this purpose in MATLAB (Mathworks, Natick, MA). The thinning dynamics are quantified by using a MATLAB program that follows the material deformation of a Lagrangian fluid element as it moves along the jet.
000 times slower speed, allowing us to resolve the dynamics of jet thinning in a low viscosity complex fluid using conventional video imaging hardware. A charge-coupled device (CCD) camera (BlueFox, Matrix Vision) with an attached zoom lens collects the images at a rate of around F = 40 fps, and the movies are stored in digital, unprocessed form on an external hard-disk connected to the computer. Some of the jetting experiments are alternatively acquired using a JetXpert (ImageXpert, Nashua, NH) imaging system, where the frame rate is restricted to 6 fps. Air pressure or a precision syringe pump (Harvard PhD Ultra) is used to control the flow rate but the precision required in the uniformity of the flow rate limits us to fluids with viscosity below 20 mPa s. Image analysis is carried out using ImageJ105 (an imaging program developed by NIH, available freely), and custom programs specifically written for this purpose in MATLAB (Mathworks, Natick, MA). The thinning dynamics are quantified by using a MATLAB program that follows the material deformation of a Lagrangian fluid element as it moves along the jet.
3 Results and discussion
3.1 Cross-slot flow extensional rheometry
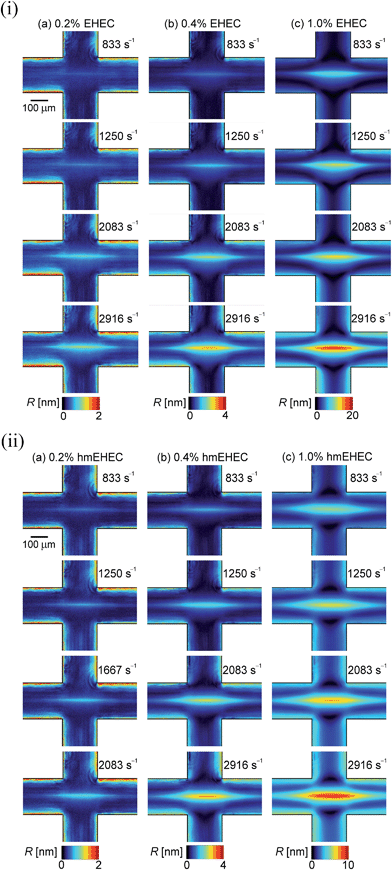
In Fig. 3 we present images of the flow-induced birefringence observed near the stagnation point of the cross-slot for solutions of EHEC and hmEHEC over a representative range of strain rates. The flow-induced birefringence provides a measure of the segmental anisotropy of macromolecules as they deform and align in the flow field and thus provides an indicator of the degree of macromolecular strain.51,106,107 Qualitatively all of the fluids display similar behavior as the strain rate is increased. At low strain rates, a narrow birefringent strand is observed that is highly localized along the central outflow axis passing through the stagnation point. Macromolecules that follow fluid elements along this streamline are the first to stretch since they experience the highest fluid strain. As the strain rate is increased the magnitude of the birefringence also increases and, while remaining quite localized, the birefringent strand grows in length and breadth. Similar responses are observed in PEO solutions and in worm-like micellar solutions.5,64,66 The birefringence is greater in the more concentrated solutions, as expected.
Fig. 4 provides a quantitative measure of the maximum birefringence (assessed at the stagnation point) as a function of the imposed strain rate for all six fluids. We find that the birefringence increases gradually, starting from very low extensional strain rates and approaches plateau values at high rates. This behavior is typical of that expected for rigid or semi-rigid macromolecules such as cellulose-based polymers, which readily align in extensional flow fields. One notable difference between the data from the EHEC and the hmEHEC solutions occurs at the 1% concentration, where a much higher birefringence is recorded in the EHEC at high deformation rates. We note that for ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CS < 300 s−1 both fluids show a similar response, however for
CS < 300 s−1 both fluids show a similar response, however for ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CS > 300 s−1 the birefringence in the hmEHEC increases more slowly than in the EHEC, due to the sticker-mediated microstructural changes in the hmEHEC solutions. The rheo-optical responses of the multisticker hmEHEC polymer dispersion and the bare EHEC dispersions both show a large absolute value of birefringence. High degrees of chain stretching at the stagnation point for
CS > 300 s−1 the birefringence in the hmEHEC increases more slowly than in the EHEC, due to the sticker-mediated microstructural changes in the hmEHEC solutions. The rheo-optical responses of the multisticker hmEHEC polymer dispersion and the bare EHEC dispersions both show a large absolute value of birefringence. High degrees of chain stretching at the stagnation point for ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CS > 1/λ have been demonstrated in cross-slot geometries by studies of flow induced birefringence51,64,106–108 and by direct observation of fluorescently labeled DNA.7,109,110 This stretching has been shown to coincide with a significant increase in the pressure drop measured across the cross-slot, consistent with the predicted increase in the extensional viscosity.51,64,106–108
CS > 1/λ have been demonstrated in cross-slot geometries by studies of flow induced birefringence51,64,106–108 and by direct observation of fluorescently labeled DNA.7,109,110 This stretching has been shown to coincide with a significant increase in the pressure drop measured across the cross-slot, consistent with the predicted increase in the extensional viscosity.51,64,106–108
 | ||
| Fig. 4 Flow birefringence as a function of imposed strain rate, measured in the cross-slot extensional rheometer. Top: EHEC dispersion, bottom: hmEHEC dispersions. | ||
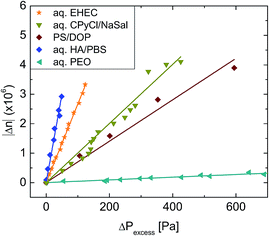
In Fig. 5, we show the measured extensional flow birefringence versus excess pressure drop data For EHEC solutions. The optical birefringence from macromolecular stretching is linearly proportional to the excess pressure drop measured at low extensional rates, and this provides an estimate of the stress-optical coefficient, CSOR, as the fluid appears to obey the stress optical rule Δn = CSORΔτ. The estimated value for the stress-optical coefficient from the data in Fig. 5 is CSOR = 2.8 × 10−8 Pa−1. Also shown in Fig. 5 are measurements of extensional flow birefringence versus excess pressure drop data obtained in the same geometry for two flexible polymers, polyethylene oxide in water and polystyrene in DOP, an aqueous solution of wormlike micelles and an aqueous solution of hyaluronic acid (HA), which is also a polysaccharide. The measured stress-optical coefficient for the EHEC solution is comparable to values known for other polysaccharides. For example, for HA in PBS solution CSOR = 1.82 × 10−8 Pa−1 was reported by Kulicke and coworkers111 while Haward et al. reported CSOR = 5.9 × 10−8 Pa−1 using cross-slot extensional rheometry measurements.5 Kulicke et al.112 have reported concentration-dependent values 2 × 10−8 Pa−1 < CSOR < 8 × 10−8 Pa−1 for sodium carboxymethyl cellulose. The values of flow birefringence and corresponding optical anisotropy of polymer segments in solutions of cellulose derivatives are noticeably greater than for the solutions of flexible chain polymers. The data shown in Fig. 5 clearly illustrate that the EHEC segments align in the direction of flow quite easily and the behavior qualitatively illustrates the fact that the chains behave as semi-rigid polymers.
In Fig. 6a we present the apparent extensional viscosity as a function of the strain rate for the EHEC solutions in the cross-slot device. The extensional viscosity is derived from pressure drop measurements using eqn (1) and (2) and the Trouton ratio is computed using Tr(![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CS) = ηE,app(
CS) = ηE,app(![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CS)/η(
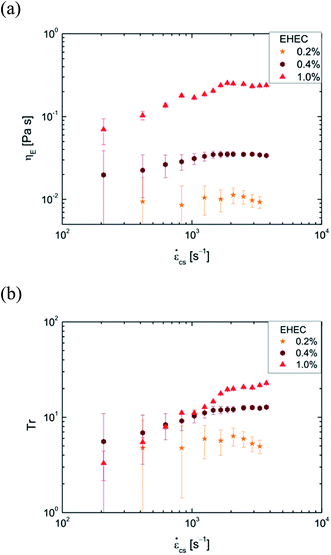
CS)/η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ). The corresponding raw pressure data are presented in the ESI.† At low flow rates, the pressure due to the extensional component of the flow field is computed as a difference of two small numbers, and hence the error bars in the low deformation rate region are relatively high. At the lowest concentration the apparent extensional viscosity is approximately constant at ηE,app ≈ 0.01 Pa s, which equates to a Trouton ratio (Tr) very close to the expected value for Newtonian fluids in planar extensional flow of Tr = 4 (Fig. 6b). As the EHEC concentration is increased we observe a non-Newtonian increase in the extensional viscosity, starting from very low strain rates, and settling to plateau values at strain rates beyond 2000 s−1. The extensional viscosity increase provides a significant increase in the Trouton ratio to Tr ≈ 10 and Tr > 20 for the 0.4% and 1.0% EHEC solutions, respectively. A similar plateau in extensional viscosity of hydroxypropyl-ether guar gum solutions was reported previously by Duxenneuner et al.113
). The corresponding raw pressure data are presented in the ESI.† At low flow rates, the pressure due to the extensional component of the flow field is computed as a difference of two small numbers, and hence the error bars in the low deformation rate region are relatively high. At the lowest concentration the apparent extensional viscosity is approximately constant at ηE,app ≈ 0.01 Pa s, which equates to a Trouton ratio (Tr) very close to the expected value for Newtonian fluids in planar extensional flow of Tr = 4 (Fig. 6b). As the EHEC concentration is increased we observe a non-Newtonian increase in the extensional viscosity, starting from very low strain rates, and settling to plateau values at strain rates beyond 2000 s−1. The extensional viscosity increase provides a significant increase in the Trouton ratio to Tr ≈ 10 and Tr > 20 for the 0.4% and 1.0% EHEC solutions, respectively. A similar plateau in extensional viscosity of hydroxypropyl-ether guar gum solutions was reported previously by Duxenneuner et al.113
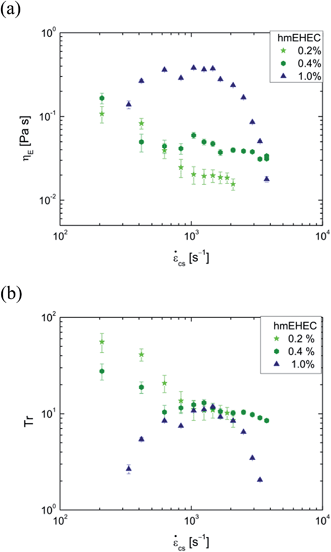
The apparent extensional viscosity and Trouton ratio data for the hydrophobically modified hmEHEC solutions are shown in Fig. 7a and b, respectively. We observe markedly different behavior from that seen with the corresponding EHEC solutions. At the lower concentrations of hmEHEC, we observe apparent extensional thinning behavior as the strain rate is increased. The Trouton ratio for these fluids initially (at low extension rates) exhibits fairly high values of around Tr ≈ 56 and Tr ≈ 40 for the 0.2% and 0.4% solution respectively. However, the Trouton ratio of both fluids drops to a low plateau value of around 10 at a strain rate of about 1000 s−1. In contrast, the 1.0% hmEHEC solution displays an initially increasing apparent extensional viscosity, which subsequently decreases for strain rates ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) CS > 103 s−1. This equates to a Trouton ratio that initially rises from a value Tr ≈ 3 up to a maximum of around 10, followed by a rapid reduction.
CS > 103 s−1. This equates to a Trouton ratio that initially rises from a value Tr ≈ 3 up to a maximum of around 10, followed by a rapid reduction.
Similar extensional thinning in associative polymers with stickers distributed along the chain was also seen in studies of a hydrophobically modified alkali soluble associative (HASE) system by Tan et al.114 Solutions of associating HASE polymers with C-12 (12 carbon long) hydrophobic stickers showed extensional thickening at intermediate extension rates followed by a large extensional thinning at the highest rates that could be achieved using an opposed-jet rheometer. In their study, the bare hydrophilic chain exhibited a plateau value in extensional viscosity at high extension rates, qualitatively similar to our observations for EHEC solutions. These authors also studied the effect of increasing the strength of association by comparing C-12 with C-16 and C-20 modified chains and determined that chains with stronger intermolecular association show only extensional thinning as a result of the progressive disruption of the microstructure at high deformation rates.
The physics underlying extensional thinning of multisticker polymer dispersions in response to strong elongation flows can be broadly understood by using arguments from nonlinear network models developed for describing the steady and transient shear and extensional response of associative polymer solutions, including for telechelic polymers in which hydrophobic stickers are present only at the chain ends.22,25,115 In a quiescent state, the temporary associations are formed and destroyed with a disassociation time, λdo ≈ Ω−1 exp(ΔG/kBT) which depends on the activation energy ΔG that in turn depends upon the number of carbon atoms (or methylene groups) present in the hydrophobic group. Under strong extensional flow conditions, the sticky chains are stretched and aligned which leads to an anisotropic enhancement in the frequency and duration of encounters between hydrophobic stickers as well as resulting in an enhanced stretching or pull-out force on the stickers that acts to break down the transient junctions. As the hmEHEC solutions are exposed to an extensional flow field, the data in Fig. 7 show that the chain alignment and stretching result in an increase in the number of associations between the bridging segments and consequently to an extensional thickening at intermediate rates. A further increase in extension rate and the onset of finite chain extensibility effects leads to a breakdown of the physical network structure and correspondingly to a large extensional thinning. In addition to associative polymers where break-up of the transient network structure leads to a decrease in extensional viscosity, extensional thinning is also observed in dilute and semi-dilute polymer solutions in experiments84,116–118 as well as simulations.88,118,119 In such cases, the extensional thinning can be described using constitutive models like the Wiest model85 and the Primitive Chain Network model81,82 that incorporate finite extensibility along with anisotropic hydrodynamic drag.81–83,85,120
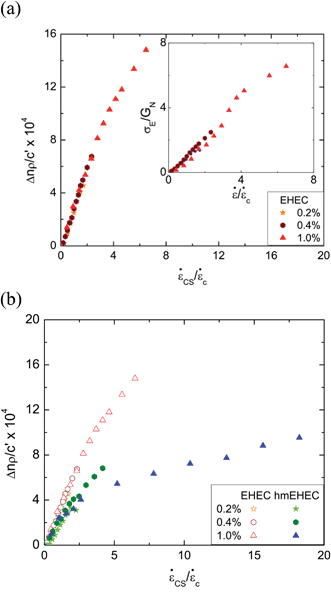
The concentration-dependent birefringence measured at a given extension rate represents the effective orientation and stretching of macromolecules in EHEC and hmEHEC solutions in response to the extensional deformation, in addition to the competition between relaxation of chains and their deformation. Rescaling the birefringence with the polymer concentration, and also rescaling the extension rate by a critical extension rate, enables the data to be superimposed as shown in Fig. 8. The scaled birefringence or specific extensional flow birefringence Δn/(c′/ρ) captures the average conformational anisotropy, while the rescaled extension rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) /
/![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c can be considered to be equivalent to an effective Weissenberg number Wi, which provides a measure of the flow strength. Here the birefringence Δn is scaled with a dimensionless ratio of concentration c′ and density, ρ (calculated with mass/volume units). The inset of Fig. 8a also displays extensional stress scaled by modulus, τE/GN = τE/c′RT for EHEC solutions, as a function of the effective Weissenberg number, and the extensional response from different EHEC solutions is remarkably similar. The superposition of normalized extensional stress and effective Weissenberg number shows that the observed nonlinear response arises from macromolecules that align and stretch in a self-similar fashion in response to applied deformation of similar strength. Similar plots of specific birefringence defined as Δn/c′ and reduced extension rate defined as r =
c can be considered to be equivalent to an effective Weissenberg number Wi, which provides a measure of the flow strength. Here the birefringence Δn is scaled with a dimensionless ratio of concentration c′ and density, ρ (calculated with mass/volume units). The inset of Fig. 8a also displays extensional stress scaled by modulus, τE/GN = τE/c′RT for EHEC solutions, as a function of the effective Weissenberg number, and the extensional response from different EHEC solutions is remarkably similar. The superposition of normalized extensional stress and effective Weissenberg number shows that the observed nonlinear response arises from macromolecules that align and stretch in a self-similar fashion in response to applied deformation of similar strength. Similar plots of specific birefringence defined as Δn/c′ and reduced extension rate defined as r = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) /
/![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c − 1 have also been presented by Sasaki et al.121 for collagen dispersions (rod-like polymers) and Fujii et al.122 for semi-dilute solutions of hydroxypropylcellulose in water–glycerol mixtures (semi-flexible polymers). The scaling carried out here for extensional flow-induced birefringence is similar in principle to the plots of specific birefringence versus reduced extension rate for dilute solutions,5,51 where
c − 1 have also been presented by Sasaki et al.121 for collagen dispersions (rod-like polymers) and Fujii et al.122 for semi-dilute solutions of hydroxypropylcellulose in water–glycerol mixtures (semi-flexible polymers). The scaling carried out here for extensional flow-induced birefringence is similar in principle to the plots of specific birefringence versus reduced extension rate for dilute solutions,5,51 where ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c = 1/λcs is based on the relaxation time for coil–stretch transition. Similarly the specific birefringence measured in response to shear flow of polydisperse semi-flexible and rodlike polymers in solution overlaps with each other when plotted as a function of shear rate normalized by the rotational diffusion coefficient.123,124
c = 1/λcs is based on the relaxation time for coil–stretch transition. Similarly the specific birefringence measured in response to shear flow of polydisperse semi-flexible and rodlike polymers in solution overlaps with each other when plotted as a function of shear rate normalized by the rotational diffusion coefficient.123,124
The superposition that follows from rescaling the birefringence by concentration suggests that the underlying fundamental contributions to the observed birefringence arise from conformational changes of individual macromolecules in EHEC dispersions. By contrast, the specific birefringence of hmEHEC dispersions in Fig. 8b exhibits a lower slope at low extension rates and the scaled data for c = 1% hmEHEC dispersion show a much lower specific birefringence when compared to the corresponding EHEC solutions. This suggests the onset of interchain effects (arising from hydrophobic stickers) that limit the molecular extension and result in the decrease in the extensional viscosity observed in Fig. 7b.
3.2 Capillary break-up extensional rheometry of cellulose ether dispersions
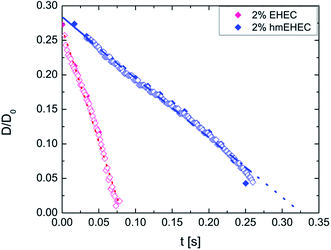
In the Capillary Break-up Extensional Rheometer (CaBER) experiment, 2% by weight aqueous dispersions of EHEC and hmEHEC both exhibit a linear decrease in filament radius with time as shown in Fig. 9. A linear decrease in radius with time suggests that a visco-capillary response, visible when Oh ∼ O(1), is observed here. This viscocapillary response can be described by the following expression:9,125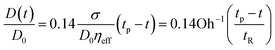 | (12) |
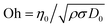 is the Ohnesorge number and the numerical pre-factor is found from the solution for the self-similar shape of capillary-driven thinning of a viscous fluid filament.125 Using the zero shear viscosity of EHEC η0 = 0.26 Pa s and hmEHEC η0 = 1.85 Pa s, the estimates for the Ohnesorge number (Oh) are Oh = 0.5 and Oh = 3.6 respectively. The longer pinch-off time, tp, for the hmEHEC dispersion (tp = 0.33 s) compared with EHEC solution (tp = 0.08 s) is due to the higher shear viscosity of the hydrophobically modified polymer dispersion. The slope of the radius versus time plots shown in Fig. 9 can be used to estimate the effective shear viscosity, and for viscous, Newtonian fluids, the estimated viscosity is within 5% of the values obtained in shear measurements.125 However, in the present experiments, the slopes correspond to ηeff = 0.021 Pa s (i.e. Oh = 0.04) for EHEC and ηeff = 0.08 Pa s (i.e. Oh = 0.16) for hmEHEC dispersions, implying that the effective solution viscosity during capillary thinning is an order of magnitude lower than the zero shear viscosity. Both solutions are highly shear thinning and the lower effective viscosity is a result of this deformation rate-dependent viscosity. The presence of associating hydrophobic stickers in hmEHEC dispersions as well as the possibility of association through hydrogen bonding and hydrophobic side-groups in EHEC solutions provides these dispersions with a complex microstructure. The initial deformation of the sample required to generate the liquid bridge in the CaBER device leads to microstructural changes that result in lower values of the effective solution viscosity. A similar effect of initial step-strain is also observed for wormlike micelles and immiscible polymer blends;126,127 however the measurements for dilute polymer solutions are found to be insensitive to the amplitude and rate of step strain.
is the Ohnesorge number and the numerical pre-factor is found from the solution for the self-similar shape of capillary-driven thinning of a viscous fluid filament.125 Using the zero shear viscosity of EHEC η0 = 0.26 Pa s and hmEHEC η0 = 1.85 Pa s, the estimates for the Ohnesorge number (Oh) are Oh = 0.5 and Oh = 3.6 respectively. The longer pinch-off time, tp, for the hmEHEC dispersion (tp = 0.33 s) compared with EHEC solution (tp = 0.08 s) is due to the higher shear viscosity of the hydrophobically modified polymer dispersion. The slope of the radius versus time plots shown in Fig. 9 can be used to estimate the effective shear viscosity, and for viscous, Newtonian fluids, the estimated viscosity is within 5% of the values obtained in shear measurements.125 However, in the present experiments, the slopes correspond to ηeff = 0.021 Pa s (i.e. Oh = 0.04) for EHEC and ηeff = 0.08 Pa s (i.e. Oh = 0.16) for hmEHEC dispersions, implying that the effective solution viscosity during capillary thinning is an order of magnitude lower than the zero shear viscosity. Both solutions are highly shear thinning and the lower effective viscosity is a result of this deformation rate-dependent viscosity. The presence of associating hydrophobic stickers in hmEHEC dispersions as well as the possibility of association through hydrogen bonding and hydrophobic side-groups in EHEC solutions provides these dispersions with a complex microstructure. The initial deformation of the sample required to generate the liquid bridge in the CaBER device leads to microstructural changes that result in lower values of the effective solution viscosity. A similar effect of initial step-strain is also observed for wormlike micelles and immiscible polymer blends;126,127 however the measurements for dilute polymer solutions are found to be insensitive to the amplitude and rate of step strain.
The typical concentration of the cellulose ethers used in sprayable paints (<1%) is usually lower than the 2% concentration examined here. However as the lower concentration EHEC and hmEHEC solutions have viscosity η < 100 mPa s, the time required to initially establish the stretched liquid bridge in the CaBER device (∼50 ms) is longer than that required for the capillary-driven pinch-off. Rodd et al.77 examined the practical limits of the capillary break-up rheometer (with a CaBER device) and note that the device cannot be used for weakly elastic (De = 1 or λ < 1 ms) or low viscosity fluids (Oh < 0.1). For the range of cellulose concentrations studied (0.2 < c < 2.4%), only solutions with c > 2% are sufficiently viscous to sustain a viscocapillary balance. Shear thinning further reduces the effective viscosity of the solutions implying that capillary break-up of typical water-borne cellulose solutions occurs in a low Oh regime, where elastocapillary effects are hard to observe on experimentally accessible length-scales.
However, it is well-established that the response of highly elastic fluids can be measured for lower viscosity fluids (Ohnesorge number Oh < 0.1),77 if the Deborah number, De ∼ O(1). For a dilute polymer solution, the relaxation time can be estimated using Zimm's theory, using the following expression:
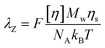 | (13) |
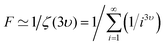 in which υ represents the solvent quality exponent, and it varies from ν = 0.5 for an ideal chain in a theta solvent to ν = 0.588 for a coil in a good solvent.128 Using [η] = 3.33 dL g−1 and Mw = 240
in which υ represents the solvent quality exponent, and it varies from ν = 0.5 for an ideal chain in a theta solvent to ν = 0.588 for a coil in a good solvent.128 Using [η] = 3.33 dL g−1 and Mw = 240![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Daltons (from our shear characterization), we get λZ = 0.014 ms. The characteristic time for relaxation as determined in extensional experiments using techniques like CaBER is typically found to be concentration-dependent even for solutions considered to be dilute i.e. c < c*.18,69,129 The overlap concentration for the EHEC dispersions is estimated using c* ≈ 1/[η] to be c = 0.3% by weight (where c in weight percent is equivalent to the absolute value in units of g dL−1). Above the overlap concentration, the relaxation time for flexible coils in an unentangled semi-dilute solution in a good solvent increases with concentration, c or volume fraction ϕ (ref. 128) as
000 Daltons (from our shear characterization), we get λZ = 0.014 ms. The characteristic time for relaxation as determined in extensional experiments using techniques like CaBER is typically found to be concentration-dependent even for solutions considered to be dilute i.e. c < c*.18,69,129 The overlap concentration for the EHEC dispersions is estimated using c* ≈ 1/[η] to be c = 0.3% by weight (where c in weight percent is equivalent to the absolute value in units of g dL−1). Above the overlap concentration, the relaxation time for flexible coils in an unentangled semi-dilute solution in a good solvent increases with concentration, c or volume fraction ϕ (ref. 128) as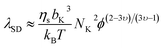 | (14) |
Only a few studies have probed the extensional response of dilute and semi-dilute polysaccharide solutions using CaBER. In contrast to the aqueous cellulose ether dispersions examined here, either higher molecular weights or more viscous solvents were used to make measurements possible. In capillary break-up studies of semi-dilute dispersions made with methylhydroxyethyl cellulose (MHEC), Plog et al.130 used aqueous NaOH solutions to suppress associations citing experimental difficulties with pure aqueous solutions. In their study, the MHEC solutions in aqueous NaOH contained a cellulose backbone with a higher degree of polymerization and higher intrinsic viscosity (3.56–17.38 dL g−1 compared to 3.33 dL g−1 for hmEHEC), and therefore 2% by weight solutions provided a measurable extensional viscosity and relaxation time. We have also probed the capillary break-up of cellulose (DP = 800) in an ionic liquid – 1-ethyl-3-methylimidazolium acetate (EMIAc) – for which the solvent viscosity was ηs = 0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pa s (i.e. 100 times higher than the viscosity of water), and found relaxation times in the range 30–1700 ms for concentrations in the range 0.5–8% by weight.16 Since the relaxation time scales with the solvent viscosity, a simple scaling estimate for an aqueous solution of any cellulose ether with similar DP would give a relaxation time of 0.6 ms for a 2% solution. Duxenneuner et al.113 reported CaBER measurements for another polysaccharide, hydroxypropyl ether guar gum (HPEGG) in aqueous solutions with concentrations as low as c = 0.17c*. Again the much higher molecular weight (Mw = 2.3 × 106 Daltons) and a higher intrinsic viscosity of 13.2 dL g−1 for the HPEGG dispersions facilitated CaBER measurements of the extensional relaxational time, with relaxation times λ > 1 ms and Tr > 10 for both dilute and semi-dilute dispersions.
Pa s (i.e. 100 times higher than the viscosity of water), and found relaxation times in the range 30–1700 ms for concentrations in the range 0.5–8% by weight.16 Since the relaxation time scales with the solvent viscosity, a simple scaling estimate for an aqueous solution of any cellulose ether with similar DP would give a relaxation time of 0.6 ms for a 2% solution. Duxenneuner et al.113 reported CaBER measurements for another polysaccharide, hydroxypropyl ether guar gum (HPEGG) in aqueous solutions with concentrations as low as c = 0.17c*. Again the much higher molecular weight (Mw = 2.3 × 106 Daltons) and a higher intrinsic viscosity of 13.2 dL g−1 for the HPEGG dispersions facilitated CaBER measurements of the extensional relaxational time, with relaxation times λ > 1 ms and Tr > 10 for both dilute and semi-dilute dispersions.
Like the cellulose ethers studied here, many of the complex fluids that are used in spraying applications or in inkjet printing are only very weakly elastic, i.e. the relaxation times of such fluids are small (typically significantly less than 1 ms), and most sprayable or jettable fluids possess viscosities less than 100 mPa s, which makes extensional rheology measurements with the CaBER instrument very difficult. Furthermore, the extension rates encountered in a real processing application can be as large as 106 s−1 and are much higher than the values that can be established in a capillary thinning experiment, where the maximum extension rate resolved in elasto-capillary thinning is limited77 to around 1000 s−1. Therefore, we turn to detailed studies of capillary-driven thinning and break-up during jetting as a means of observing pinch-off dynamics for low viscosity and weakly elastic fluids, as described in the next section.
3.3 Jetting and break-up of associative cellulose ethers
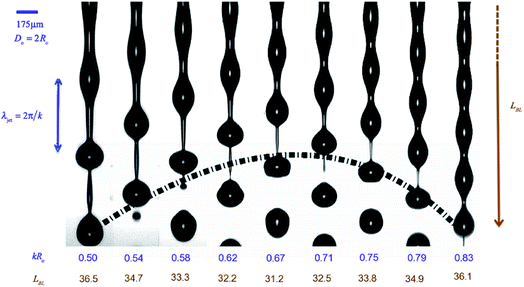
A representative set of images showing instability growth and pinch-off dynamics for jets of a 0.23% hmEHEC solution as a function of perturbation frequency (proportional to dimensionless wavenumber, kR0) are shown in Fig. 10 and 11. The images incorporate detailed information about the nature of viscoelastic jet break-up (symmetric at high wavenumbers, k becoming progressively more asymmetric at lower wavenumbers) and the formation of satellite drops (Movies M1–M3 added as ESI† showing kR0 = 0.53, 0.64 and 0.78).The dotted line shown in Fig. 10 superimposes the dispersion curve for an inviscid fluid (computed using eqn (3)). A particularly simple and symmetric mode of break-up is observed for frequencies above the critical frequency, f*, at which the shortest breakup length is measured. In this regime, jet break-up can be used to extract extensional viscosity information.70,71 The critical frequency corresponds to the wavenumber, kmaxR0 = 0.69 for an inviscid jet, and the peak shifts to a slightly lower value for low viscosity, weakly viscoelastic jets.71,102 At lower perturbation frequencies (longer wavelength modes), additional higher frequency modes with higher growth rates compete with the primary excitation mode that corresponds to the applied frequency. Computational analysis shows that these higher frequency modes lead to the formation of finer scale features such as satellite drops. However, if the excitation frequency is higher than the critical frequency, so that f > f* the shorter wavelength modes that correspond to the development of asymmetries now grow more slowly than the primary varicose mode and are thus suppressed. In Fig. 11 we show a sequence of images of the temporal evolution of the capillary thinning process observed during jetting. In contrast to low viscosity, Newtonian fluid jets (at the same We and Oh), the jets of the cellulose ether solutions examined in this study, show no satellite drop formation. Thus it is clear that nonlinear effects due to tensile stresses generated by the deformation of polymer chains in response to the elongational flow within the neck delay pinch-off sufficiently to suppress satellite formation.
The spatiotemporal evolution of a viscoelastic jet can be described in terms of the jet radius R(z, t) where z represents the distance from the nozzle and t is the time. A Lagrangian observer “P” located on the jet moving with velocity Vj reports the change in radius as R = RP(z = Vjt). From the sequence of images in Fig. 11, the progressive decrease in the radius of the neck R = RP(z = Vjt) is extracted for an excitation with kR0 = 0.78 and the data are shown, plotted as a function of dimensionless time in Fig. 12. The corresponding extensional rates computed using eqn (6) are also shown. We note that the Rayleigh time used for non-dimensionalizing the abscissa is tR = 0.11 ms, and thus the whole capillary pinch-off event is effectively complete in a time of 1.8 ms. This is much faster than the typical time required in our CaBER experiment for establishing a stretched liquid bridge. Though Schümmer and Tebel78 were probably the first to motivate the use of a jetting-based elongational rheometer, their own data show large variability with perturbation amplitude and imposed frequency (which was varied using a speaker) and jet velocity. By identifying the significant role of perturbation wavenumbers in dictating the kinematics of capillary-driven thinning and break-up during jetting, and by limiting ourselves to forcing frequencies in the range f > f* for analysis, we were able to create repeatable measurements of the transient extensional viscosity and relaxation time, and we obtained similar values with different perturbation frequencies, jet velocities and perturbation amplitudes. By using high driving frequencies and jet velocity, we can apply extensional deformations at rates that are higher than the estimated Zimm relaxation rate of the chain, and also faster than the disassociation rate of stickers present on the hmEHEC chains. We note that in Fig. 12 the neck radius decreases linearly with time close to break-up. In the previous section, we noted that a linear decrease of radius with time is characteristic of the visco-capillary response of Newtonian fluids.125 If we use eqn (12) and the measured slope (0.09) of the curve shown in Fig. 12, we obtain an effective viscosity ηeff = 22η0 that is substantially larger than the value of the zero shear viscosity, η0 value measured for 0.23% hmEHEC solution. The apparent Ohnesorge number Oh = 0.55 is computed to be 22 times higher than the value based on zero shear viscosity, Oh = 0.025. Unlike the CaBER observations with the 2% cellulose ether solutions that yielded a lower apparent Oh than computed on the basis of zero-shear viscosity, the value of Oh measured during jetting is substantially larger, and clearly, the presence of the hmEHEC chains has modified the final stage of the pinch-off dynamics.
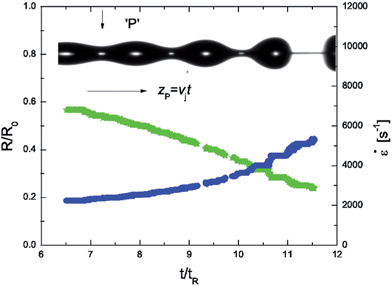 | ||
| Fig. 12 Jetting analysis of 0.23% hmEHEC solution showing scaled radius R(t)/R0vs. scaled time for Langragian point ‘P’ on the thinning neck (green symbol, left axis). The forcing frequency is kR0 = 0.78. The blue circles on the right hand axis show the extension rate (see eqn (6)) as a function of scaled time. | ||
In contrast to the Oldroyd-B model in which only an elasto-capillary regime with exponentially slow thinning is predicted, nonlinear models that include anisotropy in the drag acting on polymer (e.g. the Giesekus model) or finitely extensible dumbbell models (such as the FENE-P model) allow a finite time break-up accompanied by a linear decrease in radius close to the pinch-off time i.e. the minimum radius in the neck should scale as R(t)/R0 ≈ B(tc − t).9,131,132 In the FENE-P model, the polymer chains reach a fully stretched state during elastocapillary thinning and behave as a dilute suspension of rigid rods that increase the total effective viscosity of the fluid.132,133 Entov and Hinch104 used the FENE model to predict a linear decrease in radius with time of the form given above with B = σ/6ηeffR0 where ηeff is the effective viscosity of the fully stretched dumbbells. Renardy, and Fontelos and Li argued that the prefactor B is dependent on the constitutive model used for describing finite extensibility effects and the conformation-induced change in the magnitude of drag coefficient.9,131,134,135 The evolution and break-up of jets of viscoelastic fluids of Giesekus and FENE-P type both predict a self-similar and linear decrease in neck diameter close to pinch-off, quite similar to the dynamics observed in Fig. 11c and d and 12. The fore–aft symmetry of the thin thread or ligament connecting the large primary drops indicates that fluid inertia is not important during the break-up process.
The extensional flow induced stretching of polymer chains results in a linear decrease in radius of the thinning ligament with time which can be written in the following dimensionless form:
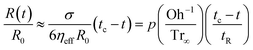 | (15) |
Fitting the linear decrease in radius with time observed in Fig. 12 with eqn (15) gives a slope of 0.05(Tr∞Oh)−1 = −0.09, and consequently the limiting value of Trouton ratio obtained for fully stretched chains is Tr∞ = 22. Irrespective of the details of the model used, the observation of such a linear scaling implies that the limiting value of Trouton ratio, Tr∞, associated with a high strain, and high extension rate (i.e. large Wi) flow is being measured in this experiment. Due to the enhanced resistance to pinch-off, the cylindrical ligament remains slender for a longer time than the value expected from the visco-capillary scaling based on the zero shear viscosity. The enhanced viscoelastic resistance to pinch-off also leads to the absence of satellite drops at different perturbation frequencies, as shown in Fig. 11 and 12.
In recent work using drop on demand inkjet printing with weakly elastic fluids,72,73,136 it has been observed that the macromolecules approach their maximum elongation in the thinning neck between drops. Macromolecules reach a high degree of extension in a transient flow when two conditions:5,90 1) a critical rate condition and 2) the accumulated strain condition are satisfied. The first condition requires the velocity gradient (or deformation rate), ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , to exceed the relaxation rate of the macromolecules, 1/λ. For dilute solutions, the simplest estimate of this rate is based on
, to exceed the relaxation rate of the macromolecules, 1/λ. For dilute solutions, the simplest estimate of this rate is based on ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) > λZ or Zimm relaxation time,137 which is the longest relaxation time of the molecule in its coiled state. The accumulated strain condition requires a large strain rate to be maintained for long enough for large molecular strains to develop (flexible high molecular weight polymers can require stretching by 100-fold to become fully stretched). According to the relaxation times given above and the magnitudes of the measured extension rates shown in Fig. 12 and 13, condition (1) is satisfied in the jetting experiments. The experimental results indicate that the observed pinch-off dynamics are characteristic of fully stretched and oriented chains, and the maximum observable fluid strain in the current set-up is estimated using eqn (7) to be εH ≈ 7. To determine whether the cellulose ethers are likely to become fully stretched in these jetting experiments, we need to estimate the extensibility of the polymer chains.
> λZ or Zimm relaxation time,137 which is the longest relaxation time of the molecule in its coiled state. The accumulated strain condition requires a large strain rate to be maintained for long enough for large molecular strains to develop (flexible high molecular weight polymers can require stretching by 100-fold to become fully stretched). According to the relaxation times given above and the magnitudes of the measured extension rates shown in Fig. 12 and 13, condition (1) is satisfied in the jetting experiments. The experimental results indicate that the observed pinch-off dynamics are characteristic of fully stretched and oriented chains, and the maximum observable fluid strain in the current set-up is estimated using eqn (7) to be εH ≈ 7. To determine whether the cellulose ethers are likely to become fully stretched in these jetting experiments, we need to estimate the extensibility of the polymer chains.
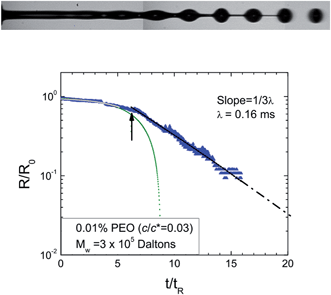 | ||
Fig. 13 Jetting analysis for 0.01% PEO solution (Mw = 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Daltons) in glycerol–water (46/54 wt%) with Oh = 0.05, We = 20, tR = 0.11 ms, and De = 0.5 showing evolution in the scaled neck radius vs. scaled time. The forcing frequency is kR0 = 0.78. The dotted green line shows that initially the thinning dynamics follow the expected inertio-capillary scaling, and the black line (dash-dotted) shows that beyond the point denoted by arrow, the elastocapillary scaling (see eqn (10)) is observed. 000 Daltons) in glycerol–water (46/54 wt%) with Oh = 0.05, We = 20, tR = 0.11 ms, and De = 0.5 showing evolution in the scaled neck radius vs. scaled time. The forcing frequency is kR0 = 0.78. The dotted green line shows that initially the thinning dynamics follow the expected inertio-capillary scaling, and the black line (dash-dotted) shows that beyond the point denoted by arrow, the elastocapillary scaling (see eqn (10)) is observed. | ||
For the Kuhn chain, the maximum extension or finite extensibility limit of a chain can be estimated by
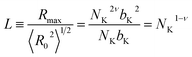 | (16) |
| 〈R02〉 = ([η]Mw/Φ∞)2/3 | (17) |
To further test the validity of these arguments, we carried out additional jetting-based rheometry studies on a dilute polyethylene oxide (PEO) solution (Mw = 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Daltons) dissolved in a glycerol–water (46
000 Daltons) dissolved in a glycerol–water (46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54) mixture (viscosity matched with cellulose ether solution). The molecular weight of the PEO is chosen to be comparable to the cellulose ethers, and the concentration chosen, c = 0.01%, corresponds to an extremely dilute solution (c[η] ≈ 0.03). Because of the flexibility of PEO chains, we obtain NK = 3750, in contrast to NK = 62 for the cellulose ethers. The corresponding extensibility for PEO chains is L ≈ 27, which is nearly five times larger than the extensibility of the cellulose ethers. The capillary-driven thinning behavior exhibited by this dilute viscoelastic solution is shown in Fig. 13. The more flexible, extensible PEO solution displays exponential thinning dynamics, a signature feature of the elastocapillary scaling discussed previously (see eqn (10)). For PEO solutions, a relaxation time of λ = 0.16 ms = 3λZ, and a Trouton ratio as high as Tr = 300 can be computed. In the context of spraying applications, it is clearly an advantage to have cellulose-based thickeners or rheology modifiers as their limited extensibility ensures that extensional viscosity effects are bounded.
54) mixture (viscosity matched with cellulose ether solution). The molecular weight of the PEO is chosen to be comparable to the cellulose ethers, and the concentration chosen, c = 0.01%, corresponds to an extremely dilute solution (c[η] ≈ 0.03). Because of the flexibility of PEO chains, we obtain NK = 3750, in contrast to NK = 62 for the cellulose ethers. The corresponding extensibility for PEO chains is L ≈ 27, which is nearly five times larger than the extensibility of the cellulose ethers. The capillary-driven thinning behavior exhibited by this dilute viscoelastic solution is shown in Fig. 13. The more flexible, extensible PEO solution displays exponential thinning dynamics, a signature feature of the elastocapillary scaling discussed previously (see eqn (10)). For PEO solutions, a relaxation time of λ = 0.16 ms = 3λZ, and a Trouton ratio as high as Tr = 300 can be computed. In the context of spraying applications, it is clearly an advantage to have cellulose-based thickeners or rheology modifiers as their limited extensibility ensures that extensional viscosity effects are bounded.
Analysis of capillary break-up during jetting of 0.4% EHEC and hmEHEC solutions shown in Fig. 14 also shows a qualitatively similar response to the 0.23% hmEHEC solutions. The radius versus time data are shown along with the corresponding extension rate for both the solutions. Using eqn (15), we can again estimate limiting Trouton ratios of Tr∞ = 10 for 0.4% EHEC solution and Tr∞ = 8 for hmEHEC solutions. The 0.4% EHEC and hmEHEC solutions can be considered semi-dilute, but since the intrinsic viscosity of these solutions is 3.88 dL g−1 and 3.33 dL g−1 respectively, the effect of stickers is hardly visible in the extensional response of the hmEHEC solutions.
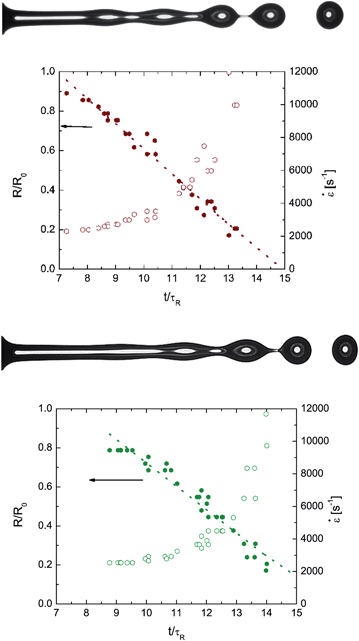 | ||
| Fig. 14 Neck radius vs. time comparison of 0.4% EHEC & 0.4% hmEHEC solutions, obtained by analyzing ROJER data. The data are based on images acquired using the JetXpert system. | ||
An estimate for the upper bound of the extensional viscosity or Trouton ratio for fully extended EHEC chains can be made by assuming that the fully extended chains behave like rods of length Rmax. The estimated value of the Trouton ratio TrB∞ computed using Batchelor's theory for rods88,143 gives:
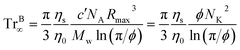 | (18) |
| ηFPE∞ = 3ηs + 2ηPL2 | (19) |
For the cellulose ether chains at c*, using the appropriate values of extensibility, L = 5.5 and the measured polymer contribution to shear viscosity, ηP = 0.7 mPa s we find the expected maximum value of the Trouton ratio to be TrFP∞ ≈ 64. The experimental value of Tr∞ ≈ 22 for 0.23% HMEHEC measured using jet rheometry is thus reasonably close to the estimate given that the polymer samples used in our study are polydisperse.
4. Conclusions
The rheological response of EHEC and hmEHEC solutions to a range of extensional deformations was studied by using excess pressure drop and flow induced birefringence measurements during steady planar extensional flow in a microfluidic cross-slot device and by a recently developed technique referred to as Rayleigh Ohnesorge Jetting Extensional Rheometry or ROJER that follows the capillary thinning and break-up of thin fluid ligaments that form between drops during jetting of weakly viscoelastic fluids. The reduction of the characteristic geometric dimensions down to the microscale in both the ROJER and cross-slot instruments, together with the use of electro-optic imaging techniques, enables accurate measurements of the extensional viscosities of these polymer solutions using relatively small scales, and allows access to the high extension rates that are of most relevance to applications such as paint spraying and coating operations. The ROJER technique can be used with opaque fluids and access comparatively higher extensional rates than cross-slot extensional rheometry, which requires optically transmissive fluids. Both techniques are ideal for use with other polysaccharide-based biological samples and industrial fluids, as the evaporation of volatile solvents is negligible and temperature control can be implemented relatively simply. We hope that the techniques and methodology described here will find widespread use in formulating and studying specialized inks for electronic, photovoltaic and biomedical print-based manufacturing technologies.47,48,144Quantitative comparison between the extensional rheology of EHEC solutions and the hydrophobically modified analogue, hmEHEC, shows that the presence of additional C-14 hydrophobic groups as stickers provides the hmEHEC dispersions with a much larger extensional viscosity at low extension rates. The extensional viscosity and flow-induced birefringence of the semiflexible EHEC solutions increase monotonically with extensional rate and with concentration. By contrast, the hmEHEC solutions exhibit extensional thinning behavior and a reduction in the specific birefringence at higher concentrations, indicative of inter-chain effects. The dramatic extensional thinning behavior at high extension rates shown by hmEHEC dispersions is quite reminiscent of their response to high shear rates. At the highest shear and extensional rates, the physical associations between the chains are no longer effective and the hydrophobically modified cellulose ethers display low viscosities, which make hmEHEC dispersions ideal for use in jetting and spraying applications. In the jetting experiments, analysis of the pinch-off dynamics exhibited by the cellulose ether solutions reveals a linear decay of neck radius with time, which is a scaling characteristic of finite extensibility. The EHEC and hmEHEC solutions display quite moderate values of the limiting Trouton ratio (typically no more than Tr∞ ≈ 20), and the experimental values are in agreement with estimates based on finite extensible nonlinear elastic (FENE-P) models. Again this bounded increase in the extensional viscosity is favorable for spraying and coating operations as it eliminates the stringiness and beads-on-strings structures that plague many other systems such as dilute solutions of flexible long chain macromolecules.136,145,146
Of course, the jetting or spraying behavior of a complex multicomponent fluid such as paint is influenced not only by the polymer viscoelasticity and extensibility, but also by the combined and coupled effects of colloidal particles, surfactants and other additives that are present in the dispersion.32,33,136 However the present study illustrates that the flow-induced destruction of the transient network that is initially established in solutions of associative polymer thickeners can help produce the requisite low viscosities required for drop formation in jetting or spraying. The creation of a physical network at low deformation rates provides the dispersions with the high viscosity and large gel strength needed to stick to surfaces and confers such paints and coatings with desirable leveling and sagging properties. In spite of the extensional thinning effects, the cellulose ether dispersions still present a greater extensional resistance to pinch-off than corresponding Newtonian fluids with similar shear viscosities, and this delays the final pinch-off event substantially, therefore reducing the size of satellite drops (if present at all) below experimental resolution. Tailoring the number of stickers and the strength of the association in the transient junctions and controlling the distance between hydrophobic stickers along the hydrophilic backbone each provide possible mechanisms for the design of a stable and sprayable multicomponent complex fluid. In each case, an understanding of the rate-dependent response of the fluid to the very large imposed shear and extensional deformation rates characteristic of coating operations is essential. The different extensional rheometer configurations presented in this paper show that both the transient and steady extensional rheological response of weakly viscoelastic fluids can now accurately be measured at deformation rates up to ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ≈ 104 s−1.
≈ 104 s−1.
Acknowledgements
VS designed the experiments, analyzed the data and wrote the paper in collaboration with and under supervision of GHM and PTH. SJH designed and performed the cross-slot rheometry and contributed to the related sections of the manuscript. VS and JS designed the ROJER set-up. AkzoNobel provided the project funding. AS supplied the cellulose ethers and, together with PTH, provided overall project guidance as well as questions and insights into the application needs in the paint industry. The jetting images for the 0.4% cellulose ether were obtained using the JetXpert with the assistance of BK. SJH gratefully acknowledges financial support from NASA Microgravity Fluid Sciences (Code UG) grant NNX09AV99G, the European Commission under Marie Curie action FP7-PEOPLE-2011-IIF grant 298220 and the Okinawa Institute of Science and Technology Graduate University (OIST).References
- F. T. Trouton, Proc. R. Soc. London, Ser. A, 1906, 77, 426–440 CrossRef.
- C. J. S. Petrie, Elongational Flows, Pitman, London, 1979 Search PubMed.
- C. J. S. Petrie, J. Non-Newtonian Fluid Mech., 2006, 137, 15–23 CrossRef CAS PubMed.
- C. W. Macosko, Rheology: Principles, Measurements and Applications, VCH Publishers Inc, New York, 1994 Search PubMed.
- S. J. Haward, V. Sharma and J. A. Odell, Soft Matter, 2011, 7, 9908–9921 RSC.
- G. Juarez and P. E. Arratia, Soft Matter, 2011, 7, 9444–9452 RSC.
- D. J. Mai, C. Brockman and C. M. Schroeder, Soft Matter, 2012, 8, 10560–10572 RSC.
- A. L. Yarin, Free Liquid Jets and Films: Hydrodynamics and Rheology, Longman Scientific & Technical, 1993 Search PubMed.
- G. H. McKinley, Rheol. Rev., 2005, 1–48 CAS.
- E. Tekin, P. J. Smith and U. S. Schubert, Soft Matter, 2008, 4, 703–713 RSC.
- G. Bhatara, E. S. G. Shaqfeh and B. Khomami, J. Rheol., 2005, 49, 929–962 CrossRef CAS.
- R. Lapasin and S. Pricl, Rheology of Industrial Polysaccharides: Theory and Applications, Chapman & Hall, London, 1995 Search PubMed.
- Polysaccharides: Structural Diversity and Functional Versality, ed. S. Dumitriu, Marcel Dekker, New York, 2nd edn, 2005 Search PubMed.
- B. Nyström, A.-L. Kjøniksen, N. Beheshti, K. Zhu and K. D. Knudsen, Soft Matter, 2009, 5, 1328–1339 RSC.
- L. Karlson, F. Joabsson and K. Thuresson, Carbohydr. Polym., 2000, 41, 25–35 CrossRef CAS.
- S. J. Haward, V. Sharma, C. P. Butts, G. H. McKinley and S. S. Rahatekar, Biomacromolecules, 2012, 13, 1688 CrossRef CAS PubMed.
- J. P. Tatham, S. Carrington, J. A. Odell, A. C. Gamboa, A. J. Muller and A. E. Saez, J. Rheol., 1995, 39, 961–986 CrossRef CAS.
- D. A. Z. Wever, F. Picchioni and A. A. Broekhuis, Prog. Polym. Sci., 2011, 36, 1558–1628 CrossRef CAS PubMed.
- E. Puchelle, J. Zahm and C. Duvivier, Biorheology, 1983, 20, 239 CAS.
- P. Erni, M. Varagnat, C. Clasen, J. Crest and G. H. McKinley, Soft Matter, 2011, 7, 10889–10898 RSC.
- M. S. Green and A. V. Tobolsky, J. Chem. Phys., 1946, 14, 80–92 CrossRef CAS PubMed.
- A. Tripathi, K. C. Tam and G. H. McKinley, Macromolecules, 2006, 39, 1981–1999 CrossRef CAS.
- T. Annable, R. Buscall, R. Ettelaie and D. Whittlestone, J. Rheol., 1993, 37, 695–726 CrossRef CAS.
- M. A. Winnik and A. Yekta, Curr. Opin. Colloid Interface Sci., 1997, 2, 424–436 CrossRef CAS.
- F. Tanaka, Polymer Physics: Applications to Molecular Association and Thermoreversible Gelation, Cambridge Univ Press, 2011 Search PubMed.
- R. R. Eley, Rheol. Rev., 2005, 173–240 CAS.
- M. Rubinstein and A. N. Semenov, Macromolecules, 1998, 31, 1386–1397 CrossRef CAS.
- M. Rubinstein and A. N. Semenov, Macromolecules, 2001, 34, 1058–1068 CrossRef CAS.
- Paint and Surface Coatings: Theory and Practice, ed. R. Lambourne and T. A. Striven, Woodhead Publishing Ltd, Cambridge, U. K., 2nd edn, 1999 Search PubMed.
- S. Paul, Surface Coatings: Science and Technology, John Wiley & Sons, New York, 1985 Search PubMed.
- O. A. Basaran, H. Gao and P. P. Bhat, Annu. Rev. Fluid Mech., 2013, 45, 85–113 CrossRef.
- J. Eggers, Rev. Mod. Phys., 1997, 69, 865–929 CrossRef CAS.
- J. Eggers and E. Villermaux, Rep. Prog. Phys., 2008, 71, 036601 CrossRef.
- H. A. Stone, Annu. Rev. Fluid Mech., 1994, 26, 65–102 CrossRef.
- C. Clasen, J. Eggers, M. A. Fontelos, J. Li and G. H. McKinley, J. Fluid Mech., 2006, 556, 283–308 CrossRef CAS.
- J. Li and M. A. Fontelos, Phys. Fluids, 2003, 15, 922–937 CrossRef CAS PubMed.
- Y. Christanti and L. M. Walker, J. Non-Newtonian Fluid Mech., 2001, 100, 9–26 CrossRef CAS.
- Y. Christanti and L. M. Walker, J. Rheol., 2002, 46, 733–748 CrossRef CAS.
- R. P. Mun, J. A. Byars and D. V. Boger, J. Non-Newtonian Fluid Mech., 1998, 74, 285–297 CrossRef CAS.
- A. Bazilevsky, V. Entov and A. Rozhkov, in Third European Rheology Conference and Golden Jubilee Meeting of the British Society of Rheology, Elsevier, Edinburgh, UK, 1990, pp. 41–43 Search PubMed.
- Y. Amarouchene, D. Bonn, J. Meunier and H. Kellay, Phys. Rev. Lett., 2001, 86, 3558–3561 CrossRef CAS.
- S. L. Anna and G. H. McKinley, J. Rheol., 2001, 45, 115–138 CrossRef CAS.
- R. Sattler, S. Gier, J. Eggers and C. Wagner, Phys. Fluids, 2012, 24, 023101 Search PubMed.
- Y. Christanti and L. M. Walker, Atomization Sprays, 2006, 16, 777–790 CrossRef CAS.
- D. F. James and K. Walters, in Techniques of Rheological Measurement, ed. A. A. Collyer, Elsevier, New York, 1994, pp. 33–53 Search PubMed.
- T. Sridhar, J. Non-Newtonian Fluid Mech., 1990, 35, 85–92 CrossRef CAS.
- P. Calvert, Chem. Mater., 2001, 13, 3299–3305 CrossRef CAS.
- B. Derby, Annu. Rev. Mater. Res., 2010, 40, 395–414 CrossRef CAS.
- C. A. Wolden, J. Kurtin, J. B. Baxter, I. Repins, S. E. Shaheen, J. T. Torvik, A. A. Rockett, V. M. Fthenakis and E. S. Aydil, J. Vac. Sci. Technol., A, 2011, 29, 030801 Search PubMed.
- F. Galindo-Rosales, M. Alves and M. Oliveira, Microfluid. Nanofluid., 2013, 14, 1–19 CrossRef CAS.
- J. A. Odell and S. P. Carrington, J. Non-Newtonian Fluid Mech., 2006, 137, 110–120 CrossRef CAS PubMed.
- W. B. Zimmerman, J. M. Rees and T. J Craven, Microfluid. Nanofluid., 2006, 2, 481–492 CrossRef CAS.
- J. A. Pathak and S. D. Hudson, Macromolecules, 2006, 39, 8782–8792 CrossRef CAS.
- A. Keller and J. Odell, Colloid Polym. Sci., 1985, 263, 181–201 CAS.
- C. J. Pipe and G. H. McKinley, Mech. Res. Commun., 2009, 36, 110–120 CrossRef PubMed.
- D. R. Link, S. L. Anna, D. A. Weitz and H. A. Stone, Phys. Rev. Lett., 2004, 92, 054503 CrossRef CAS.
- J. Soulages, M. S. N. Oliveira, P. C. Sousa, M. A. Alves and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2009, 163, 9–24 CrossRef CAS PubMed.
- S. D. Hudson, F. R. Phelan, M. D. Handler, J. T. Cabral, K. B. Migler and E. J. Amis, Appl. Phys. Lett., 2004, 85, 335–337 CrossRef CAS PubMed.
- J. S. Lee, E. S. G. Shaqfeh and S. J. Muller, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 040802 CrossRef.
- J. S. Lee, R. Dylla-Spears, N. P. Teclemariam and S. J. Muller, Appl. Phys. Lett., 2007, 90, 074103 CrossRef PubMed.
- J. Deschamps, V. Kantsler, E. Segre and V. Steinberg, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 11444–11447 CrossRef CAS PubMed.
- R. Dylla-Spears, J. E. Townsend, L. Jen-Jacobson, L. L. Sohn and S. J. Muller, Lab Chip, 2010, 10, 1543–1549 RSC.
- P. A. Stone, S. D. Hudson, P. Dalhaimer, D. E. Discher, E. J. Amis and K. B. Migler, Macromolecules, 2006, 39, 7144–7148 CrossRef CAS.
- S. J. Haward, J. A. Odell, Z. Li and X.-F. Yuan, Rheol. Acta, 2010, 49, 633–645 CrossRef CAS.
- S. J. Haward, Rheol. Acta, 2010, 49, 1219–1225 CrossRef CAS PubMed.
- S. J. Haward, T. J. Ober, M. S. N. Oliveira, M. A. Alves and G. H. McKinley, Soft Matter, 2012, 8, 536–555 RSC.
- P. E. Arratia, L. Cramer, J. P. Gollub and D. J. Durian, New J. Phys., 2009, 11, 115006 CrossRef.
- P. E. Arratia, J. P. Gollub and D. J. Durian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 036309 CrossRef CAS.
- V. Tirtaatmadja, G. H. McKinley and J. J. Cooper-White, Phys. Fluids, 2006, 18, 043101 CrossRef PubMed.
- V. Sharma, A. M. Ardekani and G. H. McKinley, in 5th Pacific Rim Conference on Rheology (PRCR-5), Sapporo, Japan, 2010 Search PubMed.
- A. M. Ardekani, V. Sharma and G. H. McKinley, J. Fluid Mech., 2010, 665, 46–56 CrossRef.
- D. C. Vadillo, W. Mathues and C. Clasen, Rheol. Acta, 2012, 51, 755–769 CrossRef CAS.
- D. C. Vadillo, T. R. Tuladhar, A. C. Mulji, S. Jung, S. D. Hoath and M. R. Mackley, J. Rheol., 2010, 54, 261 CrossRef CAS.
- L. Campo-Deano and C. Clasen, J. Non-Newtonian Fluid Mech., 2010, 165, 1688–1699 CrossRef CAS PubMed.
- G. H. McKinley and T. Sridhar, Annu. Rev. Fluid Mech., 2002, 34, 375–415 CrossRef.
- M. Stelter and G. Brenn, J. Rheol., 2000, 44, 595–616 CrossRef CAS.
- L. E. Rodd, T. P. Scott, J. J. Cooper-White and G. H. McKinley, Appl. Rheol., 2005, 15, 12–27 CAS.
- P. Schümmer and K. H. Tebel, Rheol. Acta, 1982, 21, 514–516 CrossRef.
- P. K. Bhattacharjee, D. A. Nguyen, G. H. McKinley and T. Sridhar, J. Rheol., 2003, 47, 269–290 CrossRef CAS.
- P. K. Bhattacharjee, J. P. Oberhauser, G. H. McKinley, L. G. Leal and T. Sridhar, Macromolecules, 2002, 35, 10131–10148 CrossRef CAS.
- T. Yaoita, T. Isaki, Y. Masubuchi, H. Watanabe, G. Ianniruberto and G. Marrucci, Macromolecules, 2011, 44, 9675–9682 CrossRef CAS.
- T. Yaoita, T. Isaki, Y. Masubuchi, H. Watanabe, G. Ianniruberto and G. Marrucci, Macromolecules, 2012, 45, 2773–2782 CrossRef CAS.
- P. S. Desai and R. G. Larson, J. Rheol., 2014, 58, 255–279 CrossRef CAS.
- R. K. Gupta, D. A. Nguyen and T. Sridhar, Phys. Fluids, 2000, 12, 1296–1318 CrossRef PubMed.
- J. M. Wiest, Rheol. Acta, 1989, 28, 4–12 CrossRef CAS.
- O. Scrivener, C. Berner, R. Cressely, R. Hocquart, R. Sellin and N. S. Vlachos, J. Non-Newtonian Fluid Mech., 1979, 5, 475–495 CrossRef CAS.
- C. E. Sing and A. Alexander-Katz, Macromolecules, 2010, 43, 3532–3541 CrossRef CAS.
- R. G. Larson, J. Rheol., 2005, 49, 1–70 CrossRef CAS.
- A. Peterlin, J. Polym. Sci., Part B: Polym. Lett., 1966, 4, 287–291 CrossRef CAS.
- S. Somani, E. S. G. Shaqfeh and J. R. Prakash, Macromolecules, 2010, 43, 10679–10691 CrossRef CAS.
- M. Shribak and R. Oldenbourg, Appl. Opt., 2003, 42, 3009–3017 CrossRef.
- T. J. Ober, J. Soulages and G. H. McKinley, J. Rheol., 2011, 55, 1127–1159 CrossRef CAS.
- M. R. Mackley, Rheol. Acta, 2010, 49, 443–458 CrossRef CAS.
- L. Rayleigh, Proc. Lond. Math. Soc., 1878, s1–10, 4–13 CrossRef.
- L. Rayleigh, Proc. R. Soc. London, 1879, 29, 71–97 CrossRef.
- L. Rayleigh, Proc. R. Soc. London, 1882, 34, 130–145 CrossRef.
- S. Middleman, Modeling Axisymmetric Flows: Dynamics of Films, Jets and Drops, Academic Press, San Diego, 1995 Search PubMed.
- F. W. Kroesser and S. Middleman, AIChE J., 1969, 15, 383–386 CrossRef CAS.
- V. M. Entov, Arch. Mech., 1978, 30, 435–442 Search PubMed.
- S. Middleman, Chem. Eng. Sci., 1965, 20, 1037–1040 CrossRef.
- D. W. Bousfield, R. Keunings, G. Marrucci and M. M. Denn, J. Non-Newtonian Fluid Mech., 1986, 21, 79–97 CrossRef CAS.
- G. Brenn, Z. B. Liu and F. Durst, Int. J. Multiphase Flow, 2000, 26, 1621–1644 CrossRef CAS.
- Z. H. Liu and Z. B. Liu, Int. J. Multiphase Flow, 2008, 34, 42–60 CrossRef CAS PubMed.
- V. M. Entov and E. J. Hinch, J. Non-Newtonian Fluid Mech., 1997, 72, 31–54 CrossRef CAS.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS.
- J. Odell, A. Keller and M. Miles, Polymer, 1985, 26, 1219–1226 CrossRef CAS.
- G. G. Fuller, Optical Rheometry of Complex Fluids, Oxford Univ. Press, 1995 Search PubMed.
- S. J. Haward, J. A. Odell, Z. Li and X.-F. Yuan, Rheol. Acta, 2010, 49, 781–788 CrossRef CAS.
- T. T. Perkins, D. E. Smith and S. Chu, Science, 1997, 276, 2016–2021 CrossRef CAS.
- D. E. Smith and S. Chu, Science, 1998, 281, 1335–1340 CrossRef CAS.
- F. Meyer, D. Lohmann and W. M. Kulicke, J. Rheol., 2009, 53, 799 CrossRef CAS.
- W. M. Kulicke, U. Reinhardt, G. G. Fuller and O. Arendt, Rheol. Acta, 1999, 38, 26–33 CrossRef CAS.
- M. R. Duxenneuner, P. Fischer, E. J. Windhab and J. J. Cooper-White, Biomacromolecules, 2008, 9, 2989–2996 CrossRef CAS PubMed.
- H. Tan, K. C. Tam, V. Tirtaatmadja, R. D. Jenkins and D. R. Bassett, J. Non-Newtonian Fluid Mech., 2000, 92, 167–185 CrossRef CAS.
- F. Tanaka and S. J. Edwards, J. Non-Newtonian Fluid Mech., 1992, 43, 247–271 CrossRef CAS.
- C. A. Cathey and G. G. Fuller, J. Non-Newtonian Fluid Mech., 1988, 30, 303–316 CrossRef CAS.
- D. M. Jones, K. Walters and P. R. Williams, Rheol. Acta, 1987, 26, 20–30 CrossRef CAS.
- L. M. Quinzani, R. C. Armstrong and R. A. Brown, J. Rheol., 1995, 39, 1201–1228 CrossRef CAS.
- X. F. Li and M. M. Denn, J. Rheol., 2004, 48, 805–821 CrossRef CAS.
- J. K. Nielsen, H. K. Rasmussen, O. Hassager and G. H. McKinley, J. Rheol., 2006, 50, 453–476 CrossRef CAS.
- N. Sasaki, E. D. T. Atkins and W. S. Fulton, J. Appl. Polym. Sci., 1991, 42, 2975–2985 CrossRef CAS.
- S. Fujii, N. Sasaki and M. Nakata, Colloid Polym. Sci., 2003, 281, 823–831 CAS.
- A. W. Chow and G. G. Fuller, Macromolecules, 1985, 18, 786–793 CrossRef CAS.
- A. W. Chow, G. G. Fuller, D. G. Wallace and J. A. Madri, Macromolecules, 1985, 18, 793–804 CrossRef CAS.
- G. H. McKinley and A. Tripathi, J. Rheol., 2000, 44, 653–670 CrossRef CAS.
- E. Miller, C. Clasen and J. P. Rothstein, Rheol. Acta, 2009, 48, 625–639 CrossRef CAS.
- N. J. Kim, C. J. Pipe, K. H. Ahn, S. J. Lee and G. H. McKinley, J. Rheol., 2010, 22, 31–41 Search PubMed.
- M. Rubinstein and R. Colby, Polymer Physics, Oxford Univ. Press, New York, 2003 Search PubMed.
- C. Clasen, J. P. Plog, W. M. Kulicke, M. Owens, C. Macosko, L. E. Scriven, M. Verani and G. H. McKinley, J. Rheol., 2006, 50, 849–881 CrossRef CAS.
- J. Plog, W. Kulicke and C. Clasen, Appl. Rheol., 2005, 15, 28–37 CAS.
- M. A. Fontelos and J. Li, J. Non-Newtonian Fluid Mech., 2004, 118, 1–16 CrossRef CAS PubMed.
- P. P. Bhat, O. A. Basaran and M. Pasquali, J. Non-Newtonian Fluid Mech., 2008, 150, 211–225 CrossRef CAS PubMed.
- R. Bird, P. Dotson and N. Johnson, J. Non-Newtonian Fluid Mech., 1980, 7, 213–235 CrossRef CAS.
- M. Renardy, J. Non-Newtonian Fluid Mech., 2002, 104, 65–74 CrossRef CAS.
- M. Renardy, Rheol. Rev., 2004, 2, 171–196 Search PubMed.
- D. C. Vadillo, S. D. Hoath, W.-K. Hsiao and M. R. Mackley, NIP & Digital Fabrication Conference, 2011 Search PubMed.
- B. H. Zimm, J. Chem. Phys., 1956, 24, 269–278 CrossRef CAS PubMed.
- P. J. Flory and T. G. Fox, J. Am. Chem. Soc., 1951, 73, 1904–1908 CrossRef CAS.
- P. J. Flory, O. K. J. Spurr and D. K. Carpenter, J. Polym. Sci., 1958, 27, 231–240 CrossRef CAS.
- K. Saalwachter, W. Burchard, P. Klufers, G. Kettenbach, P. Mayer, D. Klemm and S. Dugarmaa, Macromolecules, 2000, 33, 4094–4107 CrossRef.
- V. Tsvetkov, Russ. Chem. Rev., 1969, 38, 755–773 CrossRef PubMed.
- K. Kamide, Cellulose and Cellulose Derivatives: Molecular Characterization and its Applications, Elsevier, Amsterdam, 2005 Search PubMed.
- D. F. James and T. Sridhar, J. Rheol., 1995, 39, 713–724 CrossRef CAS.
- C. N. Hoth, S. A. Choulis, P. Schilinsky and C. J. Brabec, Adv. Mater., 2007, 19, 3973–3978 CrossRef CAS.
- M. S. N. Oliveira and G. H. McKinley, Phys. Fluids, 2005, 17, 071704 CrossRef PubMed.
- P. P. Bhat, S. Appathurai, M. T. Harris, M. Pasquali, G. H. McKinley and O. A. Basaran, Nat. Phys., 2010, 6, 625–631 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm01661k |
| This journal is © The Royal Society of Chemistry 2015 |