Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Manipulating shear-induced non-equilibrium transitions in colloidal films by feedback control
Tarlan A.
Vezirov
a,
Sascha
Gerloff
b and
Sabine H. L.
Klapp
b
aInstitut für Theoretische Physik, Technische Universität Berlin, Hardenbergstr. 36, D-10623 Berlin, Germany. E-mail: tarlan.a.vezirov@tu-berlin.de
bInstitut für Theoretische Physik, Technische Universität Berlin, Hardenbergstr. 36, D-10623 Berlin, Germany
First published on 13th November 2014
Abstract
Using Brownian Dynamics (BD) simulations we investigate non-equilibrium transitions of sheared colloidal films under controlled shear stress σxz. In our approach the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is a dynamical variable, which relaxes on a time scale τc such that the instantaneous, configuration-dependent stress σxz(t) approaches a pre-imposed value. Investigating the dynamics under this “feedback-control” scheme we find unique behavior in regions where the flow curve σxz(
is a dynamical variable, which relaxes on a time scale τc such that the instantaneous, configuration-dependent stress σxz(t) approaches a pre-imposed value. Investigating the dynamics under this “feedback-control” scheme we find unique behavior in regions where the flow curve σxz(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) of the uncontrolled system is monotonic. However, in non-monotonic regions our method allows to select between dynamical states characterized by different in-plane structure and viscosities. Indeed, the final state strongly depends on τc relative to an intrinsic relaxation time of the uncontrolled system. The critical values of τc are estimated on the basis of a simple model.
) of the uncontrolled system is monotonic. However, in non-monotonic regions our method allows to select between dynamical states characterized by different in-plane structure and viscosities. Indeed, the final state strongly depends on τc relative to an intrinsic relaxation time of the uncontrolled system. The critical values of τc are estimated on the basis of a simple model.
1. Introduction
Soft matter under shear flow can display rich nonlinear behaviour involving transitions between different dynamical states,1,2 spontaneous spatial symmetry-breaking,3 shear-banding4–7 (for recent reviews, see ref. 8–12), rheochaos13–15 and heterogeneous local dynamics.16,17 These intriguing phenomena often strongly affect the rheological properties of the system. Understanding shear-induced effects in, e.g., complex surfactant solutions18 or liquid crystals,1,2 colloids,19–21 soft glasses,16,17,22 and active fluids,23 is thus a major current topic connecting non-equilibrium physics and soft material science.A quantity of particular interest is the flow (or constitutive) curve,7,12 that is, the shear stress σ as function of the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , both of which can serve as experimental control parameters. In many examples, the curve σ(
, both of which can serve as experimental control parameters. In many examples, the curve σ(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) behaves not only nonlinear (indicating shear-thinning,24,25 shear-thickening,25,26 sometimes connected irregular (chaotic) rheological response15,27), but becomes also multivalued, i.e. different shear rates lead to the same stress. In complex fluids of e.g. wormlike micelles, this multivalued property is in fact a universal indicator of a shear-banding instability, specifically, gradient banding, where the (formerly homogeneous) system separates in gradient direction into coexisting bands characterized by a smaller and a larger local shear rate12 (note that this is different from the more exotic vorticity banding, i.e., the formation of bands along the vorticity direction as discussed e.g., in ref. 11, 12 and 28). In soft (colloidal) glasses, multivalued functions σ(
) behaves not only nonlinear (indicating shear-thinning,24,25 shear-thickening,25,26 sometimes connected irregular (chaotic) rheological response15,27), but becomes also multivalued, i.e. different shear rates lead to the same stress. In complex fluids of e.g. wormlike micelles, this multivalued property is in fact a universal indicator of a shear-banding instability, specifically, gradient banding, where the (formerly homogeneous) system separates in gradient direction into coexisting bands characterized by a smaller and a larger local shear rate12 (note that this is different from the more exotic vorticity banding, i.e., the formation of bands along the vorticity direction as discussed e.g., in ref. 11, 12 and 28). In soft (colloidal) glasses, multivalued functions σ(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) occur as transient phenomena after a sudden switch-on of shear stress (Bauschinger effect),29 or in the vicinity of the so-called yield stress;30 in these systems one observes strong dynamical heterogeneities.17 A further intriguing feature is that close to such nonmonotonicities, the system's behaviour strongly depends on whether one uses the shear stress or the shear rate as a control parameter.14,31 In fact, both choices are common in rheological experiments.22,32,33
) occur as transient phenomena after a sudden switch-on of shear stress (Bauschinger effect),29 or in the vicinity of the so-called yield stress;30 in these systems one observes strong dynamical heterogeneities.17 A further intriguing feature is that close to such nonmonotonicities, the system's behaviour strongly depends on whether one uses the shear stress or the shear rate as a control parameter.14,31 In fact, both choices are common in rheological experiments.22,32,33
Here we present BD computer simulation results of yet another system with multivalued stress–shear curve, that is, a thin colloidal film sheared from an (equilibrium) state within in-plane crystalline order in a planar Couette geometry. As shown in previous experimental34 and simulation21,35 studies, such films can display successive non-equilibrium transitions from square crystalline over molten into hexagonal states. Here we demonstrate that the structural transitions lead again to non-monotonic flow curves, with a shape reminding that of materials which perform a solid-to-liquid transition beyond a critical (yield) stress.36
Based on this nonlinear behaviour, we then investigate the films in presence of controlled shear stress. In fact, so far most simulations of sheared colloids have been done under fixed shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , exceptions being e.g.ref. 17, 30 and 37, where constant σ has been realized by fixing the force acting on the atoms forming the walls. Here we introduce an alternative, easy-to-apply scheme to control σ which has been previously used by us in continuum approaches of sheared liquid crystals.31 In that scheme
, exceptions being e.g.ref. 17, 30 and 37, where constant σ has been realized by fixing the force acting on the atoms forming the walls. Here we introduce an alternative, easy-to-apply scheme to control σ which has been previously used by us in continuum approaches of sheared liquid crystals.31 In that scheme ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (which directly enters the BD equations of motion) becomes a dynamical variable whose time dependence is governed by a relaxation equation involving a time scale τc. The relaxation is based on the difference between the instantaneous (configuration-dependent) stress σ(t) and a preimposed value σ0. The idea of adapting the shear rate
(which directly enters the BD equations of motion) becomes a dynamical variable whose time dependence is governed by a relaxation equation involving a time scale τc. The relaxation is based on the difference between the instantaneous (configuration-dependent) stress σ(t) and a preimposed value σ0. The idea of adapting the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is inspired by experiments of stress-controlled systems.32,38 Our scheme differs from earlier schemes17,30,37 where the desired value σ0 is imposed instantaneously. Moreover, due to the coupling to the particle positions our method corresponds to a “feedback” (closed-loop) control scheme, which is similar in spirit to e.g. a Berendsen thermostat for temperature control.39 However, here the choice for τc is found to be crucial for the observed dynamical behaviour. In particular we demonstrate that, if our scheme is applied within the multivalued regime of σ(
is inspired by experiments of stress-controlled systems.32,38 Our scheme differs from earlier schemes17,30,37 where the desired value σ0 is imposed instantaneously. Moreover, due to the coupling to the particle positions our method corresponds to a “feedback” (closed-loop) control scheme, which is similar in spirit to e.g. a Berendsen thermostat for temperature control.39 However, here the choice for τc is found to be crucial for the observed dynamical behaviour. In particular we demonstrate that, if our scheme is applied within the multivalued regime of σ(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), the final state strongly depends on the magnitude of τc relative to important intrinsic time scales of the system. Thus, the stress-control can be used to deliberately select a desired dynamical state.
), the final state strongly depends on the magnitude of τc relative to important intrinsic time scales of the system. Thus, the stress-control can be used to deliberately select a desired dynamical state.
2. Model and simulation details
We consider a model colloidal suspension where two particles with distance rij interact via a combination of a repulsive Yukawa potential, uYuk(rij) = W exp[−κrij]/rij and a repulsive soft-sphere potential uSS(rij) = 4εSS(d/rij)1/2 involving the particle diameter d.21 The interaction parameters are set in accordance to a real suspension of charged silica macroions [for details, see ref. 40 and 41]. Specifically, at the density considered (see below), the interaction strength W/(kBTd) ≈ 123 (where kBT the thermal energy) and the inverse screening length κ ≈ 3.2d. Spatial confinement is modeled by two plane parallel, smooth, uncharged surfaces separated by a distance Lz along the z direction and of infinite extent in the x–y plane. We employ a purely repulsive fluid-wall decaying as z−9 [see ref. 21]. This is motivated by previous investigations of the equilibrium layer structure, where we found a very good agreement with experiments.40,41Our investigations are based on standard BD simulations in three dimensions, where the position of particle i is advanced according to42
 | (1) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . We note that, despite the application of a linear shear profile, the real, steady-state flow profile can be nonlinear.43 This approximation has also been employed in other recent simulation studies of sheared colloids;19,44,45 the same holds for the fact that we neglect hydrodynamic interactions.
. We note that, despite the application of a linear shear profile, the real, steady-state flow profile can be nonlinear.43 This approximation has also been employed in other recent simulation studies of sheared colloids;19,44,45 the same holds for the fact that we neglect hydrodynamic interactions.
One quantity of prime interest in our study is the x–z component of the stress tensor,
 | (2) |
Thus, we consider only the configuration-dependent contribution to σxz; the kinematic contribution (which involves the velocity components in x- and z-direction) is negligible under the highly confined conditions here. We note that, apart from the kinematic contribution, eqn (2) also neglects higher-order contributions involving gradients.46,47 In continuum approaches, one typically includes non-local terms which are essential for the description of interfaces between shear-bands.7,14 The importance of such terms in our highly confined system, which is characterized by pronounced layer formation, remains to be investigated.
Based on the shear stress, we introduce a feedback scheme as follows. Starting from an initial value for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) we calculate, in each time step, the configuration-dependent stress σxz from eqn (2) and adjust
we calculate, in each time step, the configuration-dependent stress σxz from eqn (2) and adjust ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) via the relaxation equation
via the relaxation equation
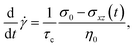 | (3) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0 (Newtonian regime). This control scheme is inspired by experiments under fixed stress [see, e.g.ref. 32], where the adaptation of the shear rate to a new stress value always takes a finite time.
→ 0 (Newtonian regime). This control scheme is inspired by experiments under fixed stress [see, e.g.ref. 32], where the adaptation of the shear rate to a new stress value always takes a finite time.
From a more formal point of view, we note that through eqn (3), ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) becomes an additional dynamical variable. Therefore, and since σxy(t) depends on the instantaneous configuration {ri(t)} of the particles, simultaneous solution of the N + 1 equations of motion (1) and (3) forms a closed feedback loop with global coupling. Interestingly, this feedback scheme is in accordance with the common view that, in a stable system, the shear stress σxz should increase with the applied shear rate. This can be shown (at least for a homogeneous system) by a linear stability analysis of eqn (3) as outlined in Appendix A.
becomes an additional dynamical variable. Therefore, and since σxy(t) depends on the instantaneous configuration {ri(t)} of the particles, simultaneous solution of the N + 1 equations of motion (1) and (3) forms a closed feedback loop with global coupling. Interestingly, this feedback scheme is in accordance with the common view that, in a stable system, the shear stress σxz should increase with the applied shear rate. This can be shown (at least for a homogeneous system) by a linear stability analysis of eqn (3) as outlined in Appendix A.
In our numerical calculations, we focus on systems at high density, specifically ρd3 = 0.85, and strong confinement, Lz = 2.2d. The corresponding equilibrium system forms a colloidal bilayer with crystalline in-plane structure.41 We also show some data with Lz = 3.2d, yielding three layers. The values Lz = 2.2 and 3.2 have been chosen because the equilibrium lattice structure is square41 (other values would lead to hexagonal equilibrium structures which do not show the shear-induced transitions discussed here). The number of particles was set to N = 1058 and 1587, the width of the shear cell to L ≈ 23.8d and 24.2d for Lz = 2.2d and 3.2d, respectively. Periodic boundary conditions were applied in flow (x) and vorticity (y) direction. The time step was set to δt = 10−5τ where τ = d2/D0 the time unit.
The system was equilibrated for 10 × 106 steps (i.e. 100τ). Then the shear force was switched on. After the shearing was started the simulation was carried out for an additional period of 100τ. During this time the steady state was reached. Only after these preparations we started to analyze the considered systems.
3. Shear-induced transitions
We start by considering flow curves for systems at constant![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . The functions σxz(
. The functions σxz(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) for both, two- and three layer systems are plotted in Fig. 1, where we have included data for the viscosities η = σxz/
) for both, two- and three layer systems are plotted in Fig. 1, where we have included data for the viscosities η = σxz/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . Note that we have defined η via the externally applied rate
. Note that we have defined η via the externally applied rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) rather than via the effective shear rate within the system (characterized by the average velocity of the layers21), which can show significant deviations from
rather than via the effective shear rate within the system (characterized by the average velocity of the layers21), which can show significant deviations from ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . As seen from Fig. 1, both the bi- and the trilayer systems are characterized by a nonmonotonic flow curve, accompanied by pronounced shear-thinning. At small shear rates, the systems display linear stress, related to an Newtonian response of the square in-plane lattice structure. An exemplary simulation snapshot for the three-layer system is shown in Fig. 2a [see ref. 21 for corresponding results for the bilayer]. In fact, within the Newtonian regime (square state) the layer velocities are zero, i.e., the particles are “locked”.21 In this state the lattice structure persists and the system reacts to the displacement of the particles in elastical manner. Further increase of the shear rate then destroys the square order. In the bilayer, the system then enters a “shear-molten” state characterized by the absence of translational order within the layers (as indicated, e.g., by a non-zero long-time diffusion constant in lateral directions21). At the same time, the entire system starts to flow, that is, the layer velocities increase from zero to non-zero values.21 From the function σxz(
. As seen from Fig. 1, both the bi- and the trilayer systems are characterized by a nonmonotonic flow curve, accompanied by pronounced shear-thinning. At small shear rates, the systems display linear stress, related to an Newtonian response of the square in-plane lattice structure. An exemplary simulation snapshot for the three-layer system is shown in Fig. 2a [see ref. 21 for corresponding results for the bilayer]. In fact, within the Newtonian regime (square state) the layer velocities are zero, i.e., the particles are “locked”.21 In this state the lattice structure persists and the system reacts to the displacement of the particles in elastical manner. Further increase of the shear rate then destroys the square order. In the bilayer, the system then enters a “shear-molten” state characterized by the absence of translational order within the layers (as indicated, e.g., by a non-zero long-time diffusion constant in lateral directions21). At the same time, the entire system starts to flow, that is, the layer velocities increase from zero to non-zero values.21 From the function σxz(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) plotted in Fig. 1a, the appearance of the shear-molten state is indicated by a sudden decrease of σxz, implying the onset of shear-thinning. In fact, with the shear-molten regime the slope of the flow curve is negative. For bulk systems, such a behavior implies that the system is mechanically unstable.48,49 Here we are considering a strongly confined system, where the macroscopic arguments cannot be immediately applied. Nevertheless, it is an interesting question to which extent the flow curve pertains to a true steady state in the regime where the shear rate has values corresponding to shear-molten configurations. Investigating the shear stress as function of strain (see Appendix B) we find that σxz assumes indeed a constant value on the time scale of our simulations; however, the relaxation time is extremely long (see next section). We also mention that our observation of shear-molten (long-time) configurations in the regime, where σxz decreases with
) plotted in Fig. 1a, the appearance of the shear-molten state is indicated by a sudden decrease of σxz, implying the onset of shear-thinning. In fact, with the shear-molten regime the slope of the flow curve is negative. For bulk systems, such a behavior implies that the system is mechanically unstable.48,49 Here we are considering a strongly confined system, where the macroscopic arguments cannot be immediately applied. Nevertheless, it is an interesting question to which extent the flow curve pertains to a true steady state in the regime where the shear rate has values corresponding to shear-molten configurations. Investigating the shear stress as function of strain (see Appendix B) we find that σxz assumes indeed a constant value on the time scale of our simulations; however, the relaxation time is extremely long (see next section). We also mention that our observation of shear-molten (long-time) configurations in the regime, where σxz decreases with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , is consistent with findings in an earlier theoretical study of a colloidal suspension under shear.50
, is consistent with findings in an earlier theoretical study of a colloidal suspension under shear.50
Somewhat different behaviour is found in the trilayer system which displays, before melting, an intermediate state [see Fig. 2b]: this state is characterized by a non-zero layer velocity. In addition, the middle layer separates into two sublayers, in which the particles are ordered in “lanes” [see inset of Fig. 2b] and move with the velocity of the corresponding outer layer (a more detailed discussion of this “laned” state will be given elsewhere51). Only further increase of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) then yields a shear-molten state characterized by a decreasing flow curve (in analogy to the bilayer). Finally, both systems transform into a state with in-plane hexagonal ordering [see Fig. 2c] and low viscosity. In this hexagonal state the layer velocity is non-zero,21 that is, the systems flows. As demonstrated earlier by us21 the mechanism of relative motion involves collective oscillations of the particles around lattice sites, consistent with recent experiments of 3D sheared colloidal crystals.20 Regarding the stress, we see that the hexagonal regime is (in both systems) characterized by a slight increase of σxz with
then yields a shear-molten state characterized by a decreasing flow curve (in analogy to the bilayer). Finally, both systems transform into a state with in-plane hexagonal ordering [see Fig. 2c] and low viscosity. In this hexagonal state the layer velocity is non-zero,21 that is, the systems flows. As demonstrated earlier by us21 the mechanism of relative motion involves collective oscillations of the particles around lattice sites, consistent with recent experiments of 3D sheared colloidal crystals.20 Regarding the stress, we see that the hexagonal regime is (in both systems) characterized by a slight increase of σxz with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . As a consequence, there is a parameter range (indicated as region “II” in Fig. 1) where the flow curve is multivalued, that is, different
. As a consequence, there is a parameter range (indicated as region “II” in Fig. 1) where the flow curve is multivalued, that is, different ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) lead to the same σxz. In many contexts (such as for worm-like micelles), multivalued flow curves are associated with the phenomenon of shear-banding, that is, the separation of the system into spatial regions with different shear rates. In our case, where the system consists of two or three layers such a separation can not occur. Instead, the non-monotonic stress curve is a consequence of the structural transitions of the system induced by the shear.
lead to the same σxz. In many contexts (such as for worm-like micelles), multivalued flow curves are associated with the phenomenon of shear-banding, that is, the separation of the system into spatial regions with different shear rates. In our case, where the system consists of two or three layers such a separation can not occur. Instead, the non-monotonic stress curve is a consequence of the structural transitions of the system induced by the shear.
4. Intrinsic time scales
Before exploring the impact of shear–stress control, which involves a time scale itself through the parameter τc [see eqn (3)], we take a closer look at the intrinsic time scales characterizing the uncontrolled systems. We focus on the bilayer (the same findings apply qualitatively on the trilayer) and consider the response of the unsheared equilibrium system, which is in a square state, to a sudden switch-on at time τon of shear with rate![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) new. The resulting time dependence of the instantaneous stress is plotted in Fig. 3.
new. The resulting time dependence of the instantaneous stress is plotted in Fig. 3.
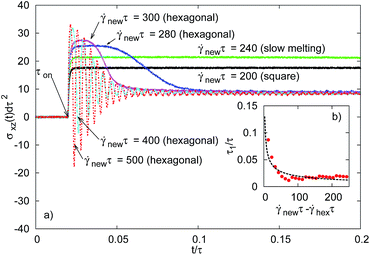 | ||
Fig. 3 (Color online) response of σxz(t) to a sudden switch-on (at time τon) of shear with different rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) newτ. The simulations were started from the equilibrium (square) state in a bilayer system. The inset shows the fit of the relaxation times τ1 according to eqn (4). newτ. The simulations were started from the equilibrium (square) state in a bilayer system. The inset shows the fit of the relaxation times τ1 according to eqn (4). | ||
If ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) newτ has a value pertaining to the square state, the shear stress jumps at τon to a non-zero value but then settles quickly to its steady-state value [see Fig. 1]. At shear rates corresponding to the shear-molten state we can also observe a relaxation at some non-zero value. However, it should be emphasized that this value is transient in character. The true, steady state value is only achieved at much longer simulation times (see the stress–strain relations presented in Appendix B). Finally, for shear rates related to the hexagonal steady state (
newτ has a value pertaining to the square state, the shear stress jumps at τon to a non-zero value but then settles quickly to its steady-state value [see Fig. 1]. At shear rates corresponding to the shear-molten state we can also observe a relaxation at some non-zero value. However, it should be emphasized that this value is transient in character. The true, steady state value is only achieved at much longer simulation times (see the stress–strain relations presented in Appendix B). Finally, for shear rates related to the hexagonal steady state (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) newτ >
newτ > ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) hexτ ≈ 257, [see Fig. 1]), we observe a well-pronounced stress overshoot, similar to what is observed e.g. in soft glassy systems,29 wormlike micelles52 and polymer melts.53 Closer inspection shows that the actual value of τ1 as well as the functional behavior of σxz(t) strongly depends on the distance between
hexτ ≈ 257, [see Fig. 1]), we observe a well-pronounced stress overshoot, similar to what is observed e.g. in soft glassy systems,29 wormlike micelles52 and polymer melts.53 Closer inspection shows that the actual value of τ1 as well as the functional behavior of σxz(t) strongly depends on the distance between ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) newτ and the threshold between shear-molten and hexagonal state,
newτ and the threshold between shear-molten and hexagonal state, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) hexτ: the smaller this distance is, the larger becomes τ1, and the more sensitive it is against small changes of the shear rate. Moreover, a sudden quench deep into the hexagonal state leads to an oscillatory relaxation of the stress σxz(t) [see curves
hexτ: the smaller this distance is, the larger becomes τ1, and the more sensitive it is against small changes of the shear rate. Moreover, a sudden quench deep into the hexagonal state leads to an oscillatory relaxation of the stress σxz(t) [see curves ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) newτ = 400, 500], with τ1 (which now corresponds to the relaxation time of the envelope) being still quite large. Taken together, for
newτ = 400, 500], with τ1 (which now corresponds to the relaxation time of the envelope) being still quite large. Taken together, for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) newτ >
newτ > ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) hexτ, τ1 can be fitted according to (see inset in Fig. 3)
hexτ, τ1 can be fitted according to (see inset in Fig. 3)
 | (4) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 1τ =
1τ = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) hexτ). The oscillations occurring at large
hexτ). The oscillations occurring at large ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) new induce yet a different time scale τos, which is smaller than τ1. Specifically, we find τos/τ =
new induce yet a different time scale τos, which is smaller than τ1. Specifically, we find τos/τ = ![[scr O, script letter O]](https://www.rsc.org/images/entities/i_char_e52e.gif) (10−3). The physical reason for these oscillations is the “zig-zag” motion of particles in adjacent layers.21 This motion is accompanied by periodic variations of nearest-neighbor distances, and thus, pair forces, which eventually leads to oscillations of σxz(t).
(10−3). The physical reason for these oscillations is the “zig-zag” motion of particles in adjacent layers.21 This motion is accompanied by periodic variations of nearest-neighbor distances, and thus, pair forces, which eventually leads to oscillations of σxz(t).
Furthermore it is interesting to relate the relaxation times emerging from Fig. 3 to the structural transition from square to hexagonal state in Fig. 1. To this end we consider the Peclet number Pe ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τPe where τPe is a “typical” relaxation time.54 Identifying τPe with τ1 and considering shear rates
τPe where τPe is a “typical” relaxation time.54 Identifying τPe with τ1 and considering shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) close to the transition from the quadratic into the shear-molten state, we find Pe =
close to the transition from the quadratic into the shear-molten state, we find Pe = ![[scr O, script letter O]](https://www.rsc.org/images/entities/i_char_e52e.gif) (100). In other words, the shear-induced structural transitions happen at Pe ≧ 1, consistent with our expectations.54
(100). In other words, the shear-induced structural transitions happen at Pe ≧ 1, consistent with our expectations.54
For comparison we have also investigated the reverse situation, where the system is initially in a hexagonal steady state at shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init = 400. We then suddenly change the shear rate towards a much smaller value and consider the relaxation towards the square equilibrium state. The corresponding behaviour of σxz(t) is shown in Fig. 4. Again we find that, the smaller the difference
init = 400. We then suddenly change the shear rate towards a much smaller value and consider the relaxation towards the square equilibrium state. The corresponding behaviour of σxz(t) is shown in Fig. 4. Again we find that, the smaller the difference ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) newτ −
newτ − ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 2τ is, the larger τ2 becomes (and the more pronounced is the sensitivity to small changes in
2τ is, the larger τ2 becomes (and the more pronounced is the sensitivity to small changes in ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) new). The resulting relaxation times can be also fitted viaeqn (4) with a2/τ = 22.58, b2 = 1.73 and
new). The resulting relaxation times can be also fitted viaeqn (4) with a2/τ = 22.58, b2 = 1.73 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 2τ = 215, whereby
2τ = 215, whereby ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 2τ =
2τ = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) sqτ denotes the threshold between the square and the molten states. The result for this fit is visualized in the inset of the Fig. 4.
sqτ denotes the threshold between the square and the molten states. The result for this fit is visualized in the inset of the Fig. 4.
 | ||
Fig. 4 (Color online) response of σxz(t) to a sudden change (at time τon) of shear. The new shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) newτ result in a relaxation in the square state. The simulations were started from the hexagonal steady state at newτ result in a relaxation in the square state. The simulations were started from the hexagonal steady state at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ = 400 in a bilayer system. The inset shows the fit of the relaxation times τ2 according to eqn (4). τ = 400 in a bilayer system. The inset shows the fit of the relaxation times τ2 according to eqn (4). | ||
5. Impact of feedback control
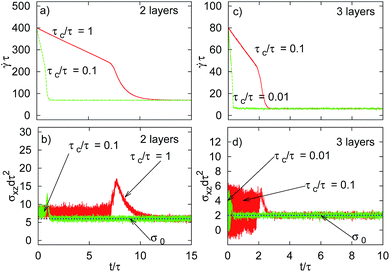
We now discuss the impact of our shear stress control scheme defined in eqn (3). The latter involves the zero-shear viscosity, η0, which is estimated from Fig. 1 to η0 = 0.086/dτ and 0.323/dτ for the bilayer and trilayer, respectively.The overall dynamical behaviour under feedback control strongly depends on the value of σ0 (imposed shear stress) relative to the flow curve of the original system [see Fig. 1]. We can differentiate between regimes I, II, and III, which are indicated in Fig. 1.
For a σ0 chosen in region I, the response of the system is unique, that is, the final state is independent of the control time scale τc, as well as of the initial shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init and the initial microstructure. Thus, when starting from a square state, with a corresponding initial shear rate
init and the initial microstructure. Thus, when starting from a square state, with a corresponding initial shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init, the system immediately settles at this state. As a more critical test of the injectivity of the flow curve in region I, we plot in Fig. 5a and b the functions
init, the system immediately settles at this state. As a more critical test of the injectivity of the flow curve in region I, we plot in Fig. 5a and b the functions ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) and σxz(t) for the bilayer system at σ0dτ2 = 6 and various τc, starting from a hexagonal configuration (and
(t) and σxz(t) for the bilayer system at σ0dτ2 = 6 and various τc, starting from a hexagonal configuration (and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) initτ = 400). In all cases, the shear rate decreases towards the value
initτ = 400). In all cases, the shear rate decreases towards the value ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ ≈ 70 and the structure relaxes into the square state pertaining to the value σxzdτ2 = 6 in the uncontrolled system. This indicates that the square state in region I is indeed the only fixed point of the dynamics. We also see from Fig. 5a that the relaxation time into this steady state increases with τc. Fig. 5b additionally shows that σxz(t) displays a pronounced peak. The peak indicates the time window in which the initial hexagonal ordering transforms into a square one. In fact, the high values of σxz at the peak reflect the large friction characterizing the intermediate molten state. Similar behaviour occurs in region I of the trilayer system [see Fig. 5c and d] where, however, fluctuations of σxz(t) are generally larger.
τ ≈ 70 and the structure relaxes into the square state pertaining to the value σxzdτ2 = 6 in the uncontrolled system. This indicates that the square state in region I is indeed the only fixed point of the dynamics. We also see from Fig. 5a that the relaxation time into this steady state increases with τc. Fig. 5b additionally shows that σxz(t) displays a pronounced peak. The peak indicates the time window in which the initial hexagonal ordering transforms into a square one. In fact, the high values of σxz at the peak reflect the large friction characterizing the intermediate molten state. Similar behaviour occurs in region I of the trilayer system [see Fig. 5c and d] where, however, fluctuations of σxz(t) are generally larger.
We now choose σ0 within region II of the flow curve, where there are three different shear rates (and thus, three fixed points) pertaining to the same stress [see Fig. 1]. We focus on systems which are initially in a square configurations, whereas the initial shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init has a value pertaining to the hexagonal state (other initial conditions will be discussed below). The impact of τc on the time dependence of
init has a value pertaining to the hexagonal state (other initial conditions will be discussed below). The impact of τc on the time dependence of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) and σxz(t) is shown in Fig. 6. For small values of the control time scale the systems stays in the initial lattice configuration, i.e.,
(t) and σxz(t) is shown in Fig. 6. For small values of the control time scale the systems stays in the initial lattice configuration, i.e., ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) relaxes towards the value pertaining to the square state (
relaxes towards the value pertaining to the square state (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ ≈ 90). Different behaviour occurs at larger values of τc/τ: although the initial structure is square, the final state is hexagonal, and the shear rate essentially remains at its high initial value. We stress that these findings crucially depend on the choice of
τ ≈ 90). Different behaviour occurs at larger values of τc/τ: although the initial structure is square, the final state is hexagonal, and the shear rate essentially remains at its high initial value. We stress that these findings crucially depend on the choice of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init. In particular, the dependency of the long-time behaviour on τc/τ only arises for large values of
init. In particular, the dependency of the long-time behaviour on τc/τ only arises for large values of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init; for small values the system remains in the square state irrespective of τc. An overview of the final dynamical states in the feedback-controlled bilayer at σ0dτ2 = 8 and various combinations of
init; for small values the system remains in the square state irrespective of τc. An overview of the final dynamical states in the feedback-controlled bilayer at σ0dτ2 = 8 and various combinations of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init and τc/τ (assuming a square initial structure) is given in Fig. 7. The colour code indicates the ratio of local bond-order parameters 〈Ψ6/Ψ4〉 [for a definition of the Ψn see e.g., ref. 21]. The restriction to values 〈Ψ6/Ψ4〉 ≤ 6 is related to the actual values observed in the simulations. From Fig. 7 one clearly sees that for initial shear rates
init and τc/τ (assuming a square initial structure) is given in Fig. 7. The colour code indicates the ratio of local bond-order parameters 〈Ψ6/Ψ4〉 [for a definition of the Ψn see e.g., ref. 21]. The restriction to values 〈Ψ6/Ψ4〉 ≤ 6 is related to the actual values observed in the simulations. From Fig. 7 one clearly sees that for initial shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) initτ >
initτ > ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) hexτ ≈ 257, the final state of the feedback-controlled system depends on τc/τ. This is in contrast to the uncontrolled system which becomes hexagonal for all
hexτ ≈ 257, the final state of the feedback-controlled system depends on τc/τ. This is in contrast to the uncontrolled system which becomes hexagonal for all ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init >
init > ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) hex. For a hexagonal initial configuration the diagram (not shown here) looks similar from a qualitative point of view; however, the range of control times where the system retains a hexagonal state despite of
hex. For a hexagonal initial configuration the diagram (not shown here) looks similar from a qualitative point of view; however, the range of control times where the system retains a hexagonal state despite of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init <
init < ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) quad (with
quad (with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) quad being the threshold between square/molten states) is much smaller.
quad being the threshold between square/molten states) is much smaller.
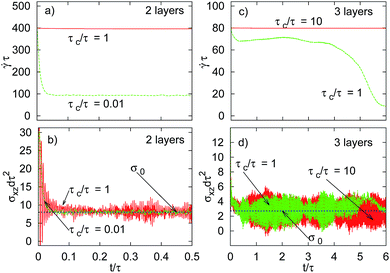 | ||
| Fig. 6 (Color online) same as Fig. 5, but for σ0dτ2 = 8(2.7) for the bilayer (trilayer) system (region II). The initial configuration is square. | ||
 | ||
| Fig. 7 (Color online) state diagram indicating long-time lattice structures. All simulations were started from a square initial structure and the imposed shear stress was set to σ0dτ2 = 8. The line shows the result from eqn (8). | ||
We conclude that, by varying τc and the initial structure, we can “switch” between the two stable, steady-state configurations arising in the multivalued region of the uncontrolled system. That these states are stable also under feedback (stress) control is supported by the linear stability analysis presented in Appendix A. Indeed, the dynamics under feedback control never evolves towards the intermediate, shear-molten states, consistent with the view that these states are mechanically unstable. This holds also in region III of the flow curve of the uncontrolled system, e.g., for σ0dτ2 = 16(5) for the bilayer (trilayer): here, a small value of τc yields relaxation towards the square state, whereas for large τc, the system evolves into a hexagonal state. Finally, we note that completely analogous behaviour is found in the trilayer system [see Fig. 6b and c] for a σ0 pertaining to the regime where square, molten and hexagonal states exist.
6. Transition line
The most significant observation from Fig. 7 is that at high values of![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init, the feedback-controlled system can achieve either the hexagonal or the square configuration, provided that we start from a square configuration and choose τc/τ accordingly. We now propose a simple model which allows us to estimate the transition values of the control time, τtransc.
init, the feedback-controlled system can achieve either the hexagonal or the square configuration, provided that we start from a square configuration and choose τc/τ accordingly. We now propose a simple model which allows us to estimate the transition values of the control time, τtransc.
The physical idea behind our model is that, with the initial conditions described above, relaxation into the hexagonal state only occurs if the reorganization time τreorg required by the system to transform from a square into a hexagonal configuration, is smaller than the time τdecay in which ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) decays to a value pertaining to the square state. We can estimate τdecay from eqn (3) if we assume, for simplicity, a linear relationship σxz(t) = m
decays to a value pertaining to the square state. We can estimate τdecay from eqn (3) if we assume, for simplicity, a linear relationship σxz(t) = m![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) (note that such a relationship is indeed nearly fulfilled within the square and hexagonal states, see Fig. 1). Under this assumption eqn (3) can be easily solved, yielding
(t) (note that such a relationship is indeed nearly fulfilled within the square and hexagonal states, see Fig. 1). Under this assumption eqn (3) can be easily solved, yielding
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) = m−1e−mt/η0τc(m (t) = m−1e−mt/η0τc(m![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init − σ0 + emt/η0τcσ0). init − σ0 + emt/η0τcσ0). | (5) |
From eqn (5) we find that the decay time of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) to the threshold value
to the threshold value ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) hexτ ≈ 257 (below which the hexagonal state of the uncontrolled system is unstable) is given by
hexτ ≈ 257 (below which the hexagonal state of the uncontrolled system is unstable) is given by
 | (6) |
To estimate the reorganization time τreorg (from the initial square into a hexagonal configuration), we assume that its dependence on ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init is analogous to that of the relaxation time τ1 introduced for the uncontrolled system [see eqn (4)]. Specifically, we make the ansatz
init is analogous to that of the relaxation time τ1 introduced for the uncontrolled system [see eqn (4)]. Specifically, we make the ansatz
 | (7) |
As stated above, a crucial assumption of our model is that the system can only reach the hexagonal state if τreorg does not exceed τdecay. Note that the latter involves (in fact, is proportional to) the time τc. By equating expressions (6) and (7) for τdecay and τreorg, respectively, we can therefore find an expression for the minimal control time, τtransc, above which the system reaches the hexagonal state, that is
 | (8) |
Due to the square initial configuration, we set m = η0 and σxz(t) = m![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) as defined in our ansatz. The remaining parameters a′ and b′ are determined by fitting the numerical results for τc/τ at the boundary [see Fig. 7] to expression (8), yielding a′/τ = 54.127 and b′ = 1.503. The resulting line τtransc(
(t) as defined in our ansatz. The remaining parameters a′ and b′ are determined by fitting the numerical results for τc/τ at the boundary [see Fig. 7] to expression (8), yielding a′/τ = 54.127 and b′ = 1.503. The resulting line τtransc(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) init) is included in Fig. 7, showing that our estimate describes the transition between square and hexagonal states very well.
init) is included in Fig. 7, showing that our estimate describes the transition between square and hexagonal states very well.
Similar considerations are possible, when we use a hexagonal initial lattice structure. Choosing then a small value of γinitτ we find that we can switch between hexagonal and square state. This is illustrated in Fig. 8. To obtain the corresponding transition values of τc, we use the same strategy as before, but take a different ansatz for the stress. Specially, we set σxz(t) = n + m![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) which approximately describe the flow curve in the hexagonal state of the uncontrolled system. From the results plotted in Fig. 1 we find n = 7.0477/dτ2 and m = 0.0025. The analog of the eqn (8) then reads
(t) which approximately describe the flow curve in the hexagonal state of the uncontrolled system. From the results plotted in Fig. 1 we find n = 7.0477/dτ2 and m = 0.0025. The analog of the eqn (8) then reads
 | (9) |
 | ||
| Fig. 8 (Color online) state diagram indicating long-time lattice structures. All simulations were started from the hexagonal initial structure and the imposed shear stress was set to σ0dτ2 = 8. | ||
7. Conclusions
Using numerical simulation we have studied the complex dynamical behaviour of sheared colloidal films under a specific type of shear–stress control. Our approach involves relaxation of the shear rate in a finite relaxation time τc, until the instantaneous stress matches its desired value. This approach is inspired by rheological experiments32 where the instantaneous shear rate as function of time can be measured. Focusing on systems with multivalued flow curves (resulting from successive non-equilibrium transitions) we have found that, by tuning τc and the initial conditions, it is possible to select a specific dynamical state. In the present system these are either a state with square in-plane ordering and high viscosity, or a hexagonal state with low viscosity. Therefore, our study suggests a way to stabilize states with desired rheological properties, particularly shear viscosities. Moreover, we have proposed a model which relates the transition values of τc to relevant intrinsic relaxation times under sudden change of![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.
Although most of our results pertain to a colloidal bilayer, the fact that we found analogous results for trilayers suggests that the proposed technique can also be applied for systems with larger number of layers. In fact, we think that this method, after some minor adaptations such as consideration of the kinematic (and, possibly, also the non-local) contributions in eqn (2), should also be applicable and fruitful in bulk systems. Indeed, we expect the method to allow for state selection in any shear-driven system with multivalued flow curve. For example, in an earlier study we have used an analogous approach (based, however, on continuum equations) to select states and even suppress chaos in shear-driven nematic liquid crystals.31 It therefore seems safe to assume that the capabilities of the present scheme are quite wide. For colloidal layers one may envision, e.g., stabilization of time-dependent structures such as oscillatory density excitation, which may have profound implications for lubrication properties.55
Finally, our findings are quite intriguing in the broader context of manipulating nonlinear systems by feedback control. In our case, the feedback character stems from the fact that the stress control involves the configuration-dependent instantaneous stress. Mathematically, this scheme can be viewed as feedback control with exponentially distributed time-delay56 (as can be seen by formally integrating eqn (3) and inserting it into eqn (1)). Similar schemes are used to stabilize dynamical patterns in laser networks,57 neural systems,58 and more generally, coupled oscillator systems.59 The implications of these connections are yet to be explored.
Appendix
A. Stability of the feedback controlled system
In this Appendix we investigate the stability of the solutions of eqn (3). Specifically, we consider the impact of small variations of the shear rate from its steady state value![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 related to the imposed stress σ0. Expanding the right side of eqn (3) with respect to the difference
0 related to the imposed stress σ0. Expanding the right side of eqn (3) with respect to the difference ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −
− ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 yields
0 yields | (10) |
For long times we expect the first term on the right side of eqn (10) to vanish, since σxz(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0,t) → σ0. To linear order, eqn (10) then reduces to
0,t) → σ0. To linear order, eqn (10) then reduces to
 | (11) |
Noting that the values of τc and η0 are both positive, we can follow that the feedback controlled shear rate approaches a steady-state value only if
 | (12) |
This corresponds to the usual criterion of mechanical stability.48
B. Strain–stress relation under constant shear rate
In this Appendix we present results for stress–strain relations at different fixed values of![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . These can be obtained from the data shown in Fig. 3 by rescaling the time axis with the applied shear rate. Numerical results are shown in Fig. 9. Similar to the stress–time relations shown in Fig. 3, one observes simple, monotonic behavior for the case
. These can be obtained from the data shown in Fig. 3 by rescaling the time axis with the applied shear rate. Numerical results are shown in Fig. 9. Similar to the stress–time relations shown in Fig. 3, one observes simple, monotonic behavior for the case ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) newτ = 200 (quadratic regime), while the curves for larger shear rates display pronounced stress overshoots. The width of these overshoots is largest at
newτ = 200 (quadratic regime), while the curves for larger shear rates display pronounced stress overshoots. The width of these overshoots is largest at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) newτ = 240, where the system is in the molten state. This is consistent with the appearance of a particularly large intrinsic relaxation time as discussed in Section 4.
newτ = 240, where the system is in the molten state. This is consistent with the appearance of a particularly large intrinsic relaxation time as discussed in Section 4.
 | ||
| Fig. 9 (Color online) stress–strain relations in the colloidal bilayer for different shear rates, starting from the equilibrium (square) configuration. | ||
Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft through SFB 910 (project B2).References
- M. Ripoll, P. Holmqvist, R. G. Winkler, G. Gompper, J. K. G. Dhont and M. P. Lettinga, Phys. Rev. Lett., 2008, 101, 168302 CrossRef CAS.
- D. Strehober, H. Engel and S. H. L. Klapp, Phys. Rev. Lett., 2013, 88, 012505 Search PubMed.
- M. Das, B. Chakrabarti, C. Dasgupta, S. Ramaswamy and A. Sood, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 021707 CrossRef.
- R. Moorcroft and S. M. Fielding, Phys. Rev. Lett., 2013, 110, 086001 CrossRef.
- R. Besseling, L. Isa, P. Ballesta, G. Petekidis, M. E. Cates and W. C. K. Poon, Phys. Rev. Lett., 2010, 105, 268301 CrossRef CAS.
- R. L. Moorcroft, M. E. Cates and S. M. Fielding, Phys. Rev. Lett., 2011, 106, 055502 CrossRef.
- C.-Y. D. Lu, P. D. Olmsted and R. C. Ball, Phys. Rev. Lett., 2000, 84, 642 CrossRef CAS.
- P. T. Callaghan, Rheol. Acta, 2008, 47, 243–255 CrossRef CAS.
- J. K. G. Dhont and W. J. Briels, Rheol. Acta, 2008, 47, 257–281 CrossRef CAS PubMed.
- S. Manneville, Rheol. Acta, 2008, 47, 301–318 CrossRef CAS.
- P. D. Olmsted, Rheol. Acta, 2008, 47, 283–300 CrossRef CAS PubMed.
- S. M. Fielding, Soft Matter, 2007, 3, 1262 RSC.
- A. Aradian and M. E. Cates, Europhys. Lett., 2005, 70, 397 CrossRef CAS.
- A. Aradian and M. E. Cates, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041508 CrossRef CAS.
- D. Lootens, H. V. Damme and P. Hebraud, Phys. Rev. Lett., 2003, 90, 178301 CrossRef.
- J. Zausch and J. Horbach, Europhys. Lett., 2009, 88, 60001 CrossRef.
- P. Chaudhuri and J. Horbach, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 040301 CrossRef.
- M. E. Cates and S. M. Fielding, Adv. Phys., 2006, 55, 799 CrossRef CAS.
- T. H. Besseling, M. Hermes, A. Fortini, M. Dijkstra, A. Imhof and A. van Blaaderen, Soft Matter, 2012, 8, 6931 RSC.
- D. Derks, Y. L. Wu, A. v. Blaaderen and A. Imhof, Soft Matter, 2009, 5, 1060 RSC.
- T. A. Vezirov and S. H. L. Klapp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052307 CrossRef.
- J. S. Raynaud, P. Moucheront, J. C. Baudez, F. Bertrand, J. P. Guilbaud and P. Coussot, J. Rheol., 2002, 46, 709 CrossRef CAS.
- M. E. Cates, S. M. Fielding, D. Marenduzzo, E. Orlandini and J. M. Yeomans, Phys. Rev. Lett., 2008, 101, 068102 CrossRef CAS.
- G. L. Burrell, N. F. Dunlop and F. Separovic, Soft Matter, 2010, 6, 2080 RSC.
- X. Cheng, J. H. McCoy, J. N. Israelachvili and I. Cohen, Science, 2011, 333, 6047 Search PubMed.
- A. Fall, A. Lematre, F. Bertrand, D. Bonn and G. Ovarlez, Phys. Rev. Lett., 2010, 105, 268303 CrossRef.
- R. Bandyopadhyay and A. K. Sood, Europhys. Lett., 2001, 56, 447 CrossRef CAS.
- K. Kang, M. P. Lettinga and J. K. G. Dhont, Rheol. Acta, 2008, 47, 499–508 CrossRef CAS.
- F. Frahsa, A. K. Bhattacharjee, J. Horbach, M. Fuchs and T. Voigtmann, J. Chem. Phys., 2013, 138, 12A513 CrossRef PubMed.
- F. Varnik, L. Bocquet and J. L. Barrat, J. Chem. Phys., 2004, 120, 2788 CrossRef CAS PubMed.
- S. H. L. Klapp and S. Hess, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 051711 CrossRef.
- Y. T. Hu, P. Boltenhagen and D. J. Pine, J. Rheol., 1998, 42, 1185 CrossRef CAS.
- V. S. Rudraraju and C. M. Wyandt, Int. J. Pharm., 2005, 292, 53–61 CrossRef CAS PubMed.
- R. Biehl and T. Palberg, Europhys. Lett., 2004, 66, 291–295 CrossRef CAS.
- R. Messina and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 011405 CrossRef.
- P. H. T. Uhlherra, J. Guoa, C. Tiua, X.-M. Zhanga, J. Z.-Q. Zhoua and T.-N. Fang, J. Non-Newtonian Fluid Mech., 2005, 125, 101–119 CrossRef PubMed.
- V. Mansard, A. Colin, P. Chaudhuri and L. Bocquet, Soft Matter, 2013, 9, 7489 RSC.
- J. Paredes, N. Shahidzadeh-Bonn and D. Bonn, J. Phys.: Condens. Matter, 2011, 23, 284116 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS PubMed.
- S. H. L. Klapp, Y. Zeng, D. Qu and R. von Klitzing, Phys. Rev. Lett., 2008, 100, 118303 CrossRef.
- S. Grandner and S. H. L. Klapp, J. Chem. Phys., 2008, 129, 244703 CrossRef PubMed.
- D. L. Ermak, J. Chem. Phys., 1975, 62, 4189 CrossRef CAS PubMed.
- J. Delhommelle, J. Chem. Phys., 2003, 119, 21 CrossRef PubMed.
- B. Lander, U. Seifert and T. Speck, J. Chem. Phys., 2013, 138, 224907 CrossRef PubMed.
- J. Rottler and D. J. Srolovitz, Phys. Rev. Lett., 2007, 98, 175503 CrossRef.
- J. H. Irving and J. G. Kirkwood, J. Chem. Phys., 1950, 18, 817 CrossRef CAS PubMed.
- B. D. Todd, D. J. Evans and R. J. Daivis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 1627 CrossRef CAS.
- R. I. Tanner, Engineering Rheology, Oxford Engineering Science Series, 2002, vol. 52, p. 493 Search PubMed.
- S. M. Fielding and P. D. Olmsted, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 036313 CrossRef CAS.
- P. Harrowell, Phys. Rev. A, 1990, 42, 3421–3431 CrossRef.
- T. Vezirov, S. Gerloff and S. H. L. Klapp, to be published.
- J. T. Padding, E. S. Boek and W. J. Briels, J. Phys.: Condens. Matter, 2005, 17, S3347–S3353 CrossRef CAS.
- J. M. Delay and R. G. Larson, Structure and Rheology of Molten Polymers, Hanser, Munich, 2006 Search PubMed.
- M. J. Stevens and M. O. Robbins, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 5 CrossRef.
- A. Vanossi, N. Manini and E. Tosatti, PNAS, 2012, 109, 16429 CrossRef CAS PubMed.
- P. Hoevel and E. Schöll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 046203 CrossRef.
- T. Juengling, A. Gjurchinovski and V. Urumov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 046213 CrossRef.
- Y. Song, Y. Han and Y. Peng, Neurocomputing, 2013, 121, 442 CrossRef PubMed.
- Y. N. Kyrychko, K. B. Blyuss and E. Schöll, Eur. Phys. J. B, 2011, 84, 307 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |