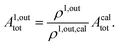DOI:
10.1039/C4SC03955F
(Edge Article)
Chem. Sci., 2015,
6, 2968-2978
Expanding discriminative dimensions for analysis and imaging†‡
Received
19th December 2014
, Accepted 18th February 2015
First published on 18th March 2015
Abstract
Eliminating the contribution of interfering compounds is a key step in chemical analysis. In complex media, one possible approach is to perform a preliminary separation. However purification is often demanding, long, and costly; it may also considerably alter the properties of interacting components of the mixture (e.g. in a living cell). Hence there is a strong interest for developing separation-free non-invasive analytical protocols. Using photoswitchable probes as labelling and titration contrast agents, we demonstrate that the association of a modulated monochromatic light excitation with a kinetic filtering of the overall observable is much more attractive than constant excitation to read-out the contribution from a target probe under adverse conditions. An extensive theoretical framework enabled us to optimize the out-of-phase concentration first-order response of a photoswitchable probe to modulated illumination by appropriately matching the average light intensity and the radial frequency of the light modulation to the probe dynamics. Thus, we can selectively and quantitatively extract from an overall signal the contribution from a target photoswitchable probe within a mixture of species, photoswitchable or not. This simple titration strategy is more specifically developed in the context of fluorescence imaging, which offers promising perspectives.
Introduction
One of the main challenges for chemists remains being able to quantify a specific analyte in highly complex systems such as biological or medical samples.1–3 A crude sample (e.g. cell extract), like those found in diagnostics assays,4 drug screening,5,6 or metabolites quantification,7 may contain up to 104 to 105 rather similar components at concentrations covering ten orders of magnitude. Analysis requires in general challenging sample conditioning and preliminary purifications. Selective detection is even more challenging when the sample has to remain in its native state (e.g. living cells). Non-invasive methods have thus to be adopted. The archetype of such methods is fluorescence microscopy, which has revolutionised the way one observes biological samples.8,9 However relying on fluorescence as read-out presents several limitations. Hence multiplexed observations of more than a few fluorescent species are difficult because of spectral crowding resulting from the large emission bandwidth of most fluorophores. Moreover biological media often produce high levels of scattering and autofluorescence at optical wavelengths, which interfere with the signals of interest and diminish the contrast. There is therefore a strong need for approaches enabling to circumvent the selectivity issue in the context of both analysis and imaging.
To detect a target in a complex medium, one needs a probe. This probe can be intrinsic, i.e. present in the target (atoms or functional groups). However it is often difficult to find an intrinsic probe that is unique for a target. For instance, biomolecules (e.g. proteins, nucleic acids) are essentially composed of the same functionalities. Alternatively, exogenous probes with unnatural chemical functions or singular spectroscopic properties can be used to give a unique signature and act as contrast agents. Additional selectivity can be observed if the exogenous probe is engaged in a reactive process. This is typically the strategy of titration experiments, where one observes a reagent specifically probing the analyte of interest thanks to a chemical reaction. Selectivity classically results from the difference between the equilibrium constants associated to the titration reaction. Relying on kinetics10 opens further dimensions to improve selectivity by increasing the number of discriminating parameters: in the most simple case, two independent rate constants instead of only one thermodynamic constant are associated to the titration reaction for each system component. In this account, we exploit chemical kinetics to introduce a simple and cheap protocol for selective analysis or imaging of a probe used either as a label (Fig. 1a) or as a titrating reagent (Fig. 1b).
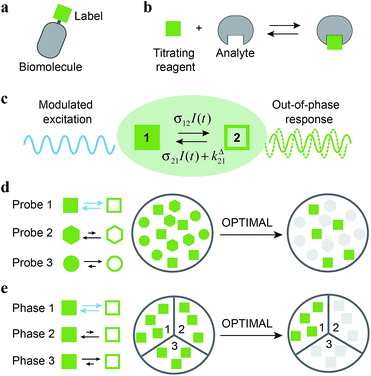 |
| | Fig. 1 Out-of-Phase TItration after Modulation of Activating Light (OPTIMAL) for selective detection of a photoswitchable probe. When illuminated, a photoswitchable probe (green square) used either (a) as a label or (b) as a titrating reagent exchanges between two distinguishable states 1 and 2 (c). With a periodic modulated light, its response signal is modulated with a phase shift. The amplitude of the out-of-phase (or quadrature-delayed) first-order component of its response is optimal when the average intensity and the angular frequency of the modulated light match the dynamic parameters of the probe. Accordingly, when the modulated light is tuned to its dynamics, the photoswitchable probe is the only species giving a significant signal in quadrature detection. This enables its selective detection in (d) a mixture of interfering probes or species displaying different dynamics or, if its dynamics is environment-sensitive, in (e) a specific phase of a heterogeneous multiphasic medium. | |
Kinetic information can be uncovered by relaxation methods,11 where an externally driven excitation forces the system out-of-equilibrium.12–17 Recently, selective imaging protocols relying on kinetic filtering have been implemented upon modulating the probe signal using light18–31 or temperature32–34 as external triggers. In this work, we adopted light as a non-invasive and easily modulatable trigger. We additionally chose photo-switchable probes, which interconvert between two states upon light illumination and correspondingly exhibit several discriminating parameters that can be used to optimize an efficient dynamic contrast (Fig. 1c).35 As we already showed in the context of selective analysis and separation,32,34,36–38 modulation of a control parameter can reveal intrinsic chemical kinetics upon periodically forcing the system out-of-equilibrium. By analogy, we adopted a periodically oscillating monochromatic light excitation, which modulates the extent of the photochemical reaction, thereby modulating the reporting signal. Beyond favoring discrimination against background noise by means of a lock-in detection39 such a modulation enables subsequent kinetic filtering. More precisely, we show theoretically how tuning both the average intensity and the frequency of the modulated monochromatic light excitation permits to simply and selectively extract from the overall signal the contribution from a photoswitchable probe of interest within a mixture of species, photoswitchable or not. Hence it will be possible to specifically retrieve the contribution from a targeted probe in a mixture of interfering probes (Fig. 1d), or the contribution originating from a specific compartment when a medium-sensitive probe is incorporated in a heterogeneous multiphasic medium (Fig. 1e). We correspondingly dubbed our approach OPTIMAL for Out-of-Phase TItration after Modulation of Activating Light. In particular, it generalizes the fluorescence imaging approach OPIOM (Out-of-Phase Imaging after Optical Modulation) we recently introduced,40 which enables selective and quantitative imaging of photoswitchable fluorescent proteins.
Optimizing the response of a photoswitchable probe to periodic illumination
The model
The dynamic behavior of a photoswitchable probe P illuminated with a light of intensity I(t) can be described by the two-state exchange (1)| | 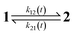 | (1) |
where the thermodynamically more stable state 1 is photochemically converted to the thermodynamically less stable state 2 at rate constantfrom which it can relax back to the initial state 1 either by a photochemically- or a thermally-driven process at rate constant| | | k21(t) = σ21I(t) + kΔ21, | (3) |
where σ21I(t) and kΔ21 are respectively the photochemical and the thermal contributions of the rate constant. In that case, the molecular action cross-sections for photoisomerization σ12 and σ21 and the thermal rate constant kΔ21 fully define the behavior of the photoswitchable probe.
It is worth to mention that the following theoretical development involving a truncation of the kinetic equations to various orders of the light intensity could be applied to other mechanisms possibly involving non-linearities. However the scheme (1) provides simple expressions. Furthermore it is already relevant to model several multi-step mechanisms, which can be dynamically reduced to light-driven exchanges between two states.41–43 Hence, in ESI,† we first demonstrate that this scheme satisfactorily accounts for the behavior of photochromic probes. Then we show that it describes as well the dynamics of (i) a chromophore yielding singlet and triplet states upon illuminating and (ii) a photoswitchable probe sensing an analyte present in excess as long as photochemical steps are rate-limiting.
Concentration response to constant illumination
When the system is submitted to a constant illumination defined by the intensity I(t) = I0, the forward and backward rate constants become| | | k21(t) = k021 = σ21I0 + kΔ21. | (5) |
After a transient regime defined by the relaxation time τ012 = 1/(k012 + k021), the system reaches a photostationary state characterized by the apparent photoisomerization constant K012 = k012/k021. The concentrations of 1 and 2, noted respectively 10 and 20, are then given by
| | 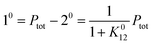 | (6) |
where
Ptot is the total concentration of
P.
Concentration response to sinusoidal modulation of small amplitude
To evaluate the behavior of such system upon illumination with a periodically modulated light, we first consider a sinusoidally modulated illumination oscillating around the averaged value I0 at angular frequency ω and with a small amplitude εI0 (ε ≪ 1) such that| | I(t) = I0[1 + ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ωt)]. (ωt)]. | (7) |
Temporal dependence of the concentrations.
After introducing the expression (7) into eqn (2) and (3), the system of differential equations governing the temporal evolution of the concentrations in 1 and 2 is solved at the first-order expansion in the light perturbation (see ESI†). Beyond the relaxation time τ012, one enters into the forced and permanent regime where the concentration i = i0 + εi1(t) in each species i (i = 1 or 2) oscillates around a mean value i0 (corresponding to the concentration of i at steady-state associated to the photon flux I0; see eqn (6)) at the angular frequency ω but with a phase delay of ϕ12 = arctan(ωτ012)| | 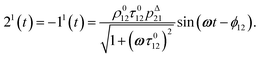 | (8) |
In eqn (8), ρ012 = k01210 = k02120 and pΔ21 = kΔ21/(σ21I0 + kΔ21) respectively designate the steady-state rate of reaction (1) and the relative thermal contribution to the relaxation of state 2 upon illuminating at I0.
The phase-delayed oscillating concentrations i can also be written
| | i(t) = i0 + ε[i1,in![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) + i1,out sin(ωt) + i1,out![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt)] cos(ωt)] | (9) |
where
εi1,in![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin(
ωt) and
εi1,out![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos(
ωt) are in-phase and out-of-phase (or quadrature-delayed) oscillating terms at angular frequency
ω. The amplitudes
i1,in and
i1,out of the in-phase and out-of-phase oscillating terms are (see ESI
†)
| | 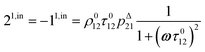 | (10) |
| | 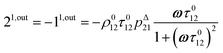 | (11) |
or similarly
| | 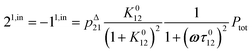 | (12) |
| | 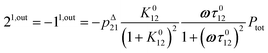 | (13) |
to make explicit the proportionality of 2
1,in and 2
1,out with the total
P concentration.
Optimal out-of-phase response.
Fig. 2a and b displays the dependence of the normalized in-phase |11,innorm| = |11,in/Ptot| and out-of-phase |11,outnorm| = |11,out/Ptot| amplitudes on the control parameters I0 and ω for a given photoswitchable probe P characterized by the triplet of parameters (σ12, σ21, kΔ21). In contrast to the in-phase amplitude, the out-of-phase amplitude exhibits a single optimum when the control parameters (I0, ω) verify| | 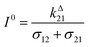 | (14) |
with full widths at half-maximum 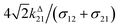 along I0 and
along I0 and 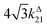 along ω. The normalized out-of phase amplitude |11,outnorm| is then equal to σ12/[8(σ12 + σ21)].
along ω. The normalized out-of phase amplitude |11,outnorm| is then equal to σ12/[8(σ12 + σ21)].
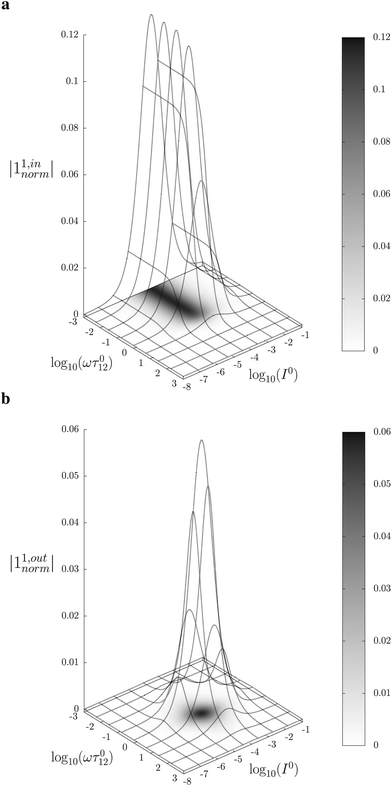 |
| | Fig. 2 Theoretical computation of the response of a photoswitchable fluorophore 1 ⇌ 2 submitted to light harmonic forcing of small amplitude. The absolute values of the normalized amplitudes of the in-phase and out-of-phase oscillations in 1 concentration, |11,innorm| (a) and |11,outnorm| (b) respectively, are plotted versus the light flux I0 (in ein s−1 m−2) and the adimensional relaxation time ωτ012. σ12 = 73 m2 mol−1, σ21 = 84 m2 mol−1, kΔ21 = 1.5 × 10−2 s−1. See eqn (12) and (13). | |
The optimization of 11,out results from the independent optimisation of the terms pΔ21K012Ptot/(1 + K012)2 and ωτ012/[1 + (ωτ012)2] in eqn (13). From the expression (6) using eqn (4) and (5), one can calculate d20/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I0 to show that εpΔ21K012Ptot/(1 + K012)2 measures the composition shift δ20 from the steady-state 20 after a light intensity jump of amplitude εI0. It depends on I0 and is maximized in a regime of intermediate illumination, in which thermally- and photochemically-driven reactions occur at the same rate such that kΔ21 = (σ12 + σ21)I0 (see eqn (14)). When the light intensity is too low, the thermal relaxation dominates the photoisomerization and the light intensity jump εI0 cannot significantly shifts the photoswitchable probe from the state 1. Conversely, when the light intensity is too large, the thermal relaxation does not contribute anymore to the dynamics of the exchange (1): the relative proportions in states 1 and 2 become independent of the light intensity, so there is no composition shift induced by the light jump. The second optimized term, ωτ012/[1 + (ωτ012)2], is maximized upon matching the radial frequency of the light modulation ω with the exchange relaxation time τ012 so that ωτ012 = 1 (see eqn (14) and (15)). When ω ≫ 1/τ012, the exchange is slow compared to the light variations and the couple {1, 2} has not enough time to respond: both i1,in and i1,out vanish. Conversely, when ω ≪ 1/τ012, i1,out cancels, so the concentrations of 1 and 2 oscillate in phase with the light modulation.
I0 to show that εpΔ21K012Ptot/(1 + K012)2 measures the composition shift δ20 from the steady-state 20 after a light intensity jump of amplitude εI0. It depends on I0 and is maximized in a regime of intermediate illumination, in which thermally- and photochemically-driven reactions occur at the same rate such that kΔ21 = (σ12 + σ21)I0 (see eqn (14)). When the light intensity is too low, the thermal relaxation dominates the photoisomerization and the light intensity jump εI0 cannot significantly shifts the photoswitchable probe from the state 1. Conversely, when the light intensity is too large, the thermal relaxation does not contribute anymore to the dynamics of the exchange (1): the relative proportions in states 1 and 2 become independent of the light intensity, so there is no composition shift induced by the light jump. The second optimized term, ωτ012/[1 + (ωτ012)2], is maximized upon matching the radial frequency of the light modulation ω with the exchange relaxation time τ012 so that ωτ012 = 1 (see eqn (14) and (15)). When ω ≫ 1/τ012, the exchange is slow compared to the light variations and the couple {1, 2} has not enough time to respond: both i1,in and i1,out vanish. Conversely, when ω ≪ 1/τ012, i1,out cancels, so the concentrations of 1 and 2 oscillate in phase with the light modulation.
Concentration response to square wave modulation of small amplitude
As an experimentally relevant extension of the previous case, we analyzed the behavior of the system upon illumination with a square wave light modulation of weak amplitude around the averaged value I0. We adopted its Fourier series expansion| | 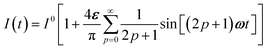 | (16) |
with ε ≪ 1 upon choosing the starting time (t = 0) halfway through the first pulse.
Concentration response to periodic modulations of large amplitude
The use of a modulation of small amplitude is favorable to derive simple analytical expressions. However, it generates only small variations of the probe signal because of the small modulation, which is a drawback to reliably extract the out-of-phase amplitude of the first order response from the experimental signal. To overcome this limitation, we analyzed the response of a photoswitchable probe to the preceding periodic illuminations but with a large modulation amplitude α. Thus we adopted| | I(t) = I0[1 + α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt)] sin(ωt)] | (20) |
and| | 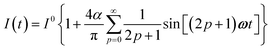 | (21) |
for the sinusoidal and square wave modulation respectively. In particular, the latter periodic illumination is of simple experimental implementation (on–off illumination switching).
Temporal dependence of the concentrations.
The ESI† details the calculations referring to these two modulations of large amplitude. In this paragraph, we only introduce the calculation guideline, which is common to both types of modulations. The light intensity can be written| | | I(t) = I0[1 + αh(ωt)] | (22) |
where h(ωt) designate a periodic function with fundamental radial frequency ω. Eqn (22) was used to express the rate constants with eqn (2) and (3). Then, upon expanding the concentration expressions asthe system of differential equations governing the temporal evolution of the concentrations in 1 and 2 becomes| | 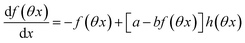 | (25) |
where| | 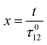 | (26) |
| | | b = α(σ12 + σ21)I0τ012 | (28) |
Beyond the relaxation time τ012, one enters into a permanent regime in which f(θx) is a continuous periodic function. In contrast to the situation of light modulation of small amplitude, one cannot anymore restrict the f(θx) analysis to the first-order. The f(θx) function has to be expressed as a Fourier series
| | 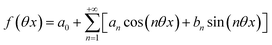 | (30) |
where
an and
bn designate the amplitudes of the
n-th components of the Fourier series. The
an and
bn terms can be extracted from
eqn (25) upon identifying the amplitudes of the components of same order. Then one can obtain the expressions of the concentrations in
1 and
2:
| | 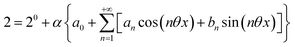 | (31) |
| | 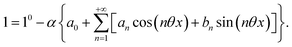 | (32) |
Consequently, at steady-state, a large periodic modulation of illumination now causes modulation of the concentrations in 1 and 2 at an infinite number of radial frequencies. Eqn (31) and (32) can be transformed to explicit the amplitudes 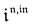 and
and 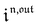 of the in-phase and out-of phase terms oscillating at the radial frequency nω. The concentration of i can be now written
of the in-phase and out-of phase terms oscillating at the radial frequency nω. The concentration of i can be now written
| | 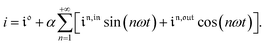 | (33) |
Interestingly, 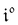 ,
, 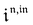 and
and 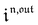 are proportional to Ptot. Indeed eqn (25) can be transformed into
are proportional to Ptot. Indeed eqn (25) can be transformed into
| | 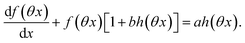 | (34) |
Neither b nor h(θx) depend on Ptot (see eqn (20), (21) and (26–29)). In contrast, a is proportional to Ptot (see eqn (6) and (27)). Derivation being a linear operation, eqn (34) then implies that f(θx) is proportional to Ptot. The system of equations giving access to an and bn being linear (see ESI†), all the an and bn amplitudes are individually proportional to Ptot. Finally, we use eqn (31–33) to deduce that 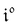 ,
, 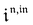 and
and 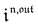 are proportional to Ptot.
are proportional to Ptot.
We showed that, in the case of light modulation of small amplitude, the out-of-phase amplitudes of the concentration modulation at radial frequency ω are optimal when the resonance conditions (14) and (15) are fulfilled. In the absence of analytical expressions for 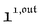 and
and 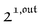 , such conclusions cannot be directly derived in the case of periodic light modulation of large amplitude. We correspondingly evaluated their relevance by means of numerical calculations (see ESI†). For harmonic forcing as well as square wave modulation in a regime of large amplitude modulation, we could show that |
, such conclusions cannot be directly derived in the case of periodic light modulation of large amplitude. We correspondingly evaluated their relevance by means of numerical calculations (see ESI†). For harmonic forcing as well as square wave modulation in a regime of large amplitude modulation, we could show that |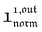 | exhibits an optimum in the space (I0, ω), which position and amplitude are very close to those observed with a sinusoidal modulation of small amplitude. In fact, the error done when taking the analytical expression of the resonance conditions valid only for a modulation of small amplitude is always less than 20%, no matter which amplitude α is used. Such an error would be of the order of magnitude of the experimental errors done when fixing the average light intensity and radial frequency to their values at resonance, I0,R and ωR.
| exhibits an optimum in the space (I0, ω), which position and amplitude are very close to those observed with a sinusoidal modulation of small amplitude. In fact, the error done when taking the analytical expression of the resonance conditions valid only for a modulation of small amplitude is always less than 20%, no matter which amplitude α is used. Such an error would be of the order of magnitude of the experimental errors done when fixing the average light intensity and radial frequency to their values at resonance, I0,R and ωR.
Application to selective and quantitative detection of a photoswitchable probe
In the preceding section, we demonstrated that, for a photoswitchable probe submitted to a periodic modulated light, the out-of-phase first-order response of the concentration could be maximized by appropriately choosing both the average light intensity and the radial frequency of the light modulation. However, in general, concentrations are retrieved from a signal. In this section, we analyze whether the out-of-phase response of the signal can be used for selective detection of a photoswitchable probe.
Out-of-phase response of the overall observable
The overall observable O (e.g. absorbance, electrophoretic mobility, …) from the photoswitchable probe results from the individual contributions of the states 1 and 2. We assume that this observable varies linearly with the concentrations in 1 and 2. We note Qi the response factor of i linking signal and concentration (hereafter considered as constant). We can write| | | O(t) = Q11(t) + Q22(t). | (35) |
In the general case of a periodic modulation of large amplitude, using the expressions of 1(t) and 2(t) given in eqn (33), the expression of the signal O(t) becomes
| | 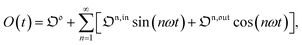 | (36) |
where (see ESI
†)
| | 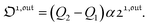 | (37) |
As shown in eqn (37), 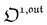 is directly proportional to
is directly proportional to 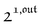 , which was shown above to be optimal when the resonance conditions (14) and (15) are fulfilled. Hence, the analysis of the out-of-phase first-order response
, which was shown above to be optimal when the resonance conditions (14) and (15) are fulfilled. Hence, the analysis of the out-of-phase first-order response 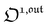 of the overall observable O(t) allows for the selective and quantitative detection of a photoswitchable probe. Note that
of the overall observable O(t) allows for the selective and quantitative detection of a photoswitchable probe. Note that 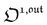 can be easily extracted from the overall signal O(t) via lock-in amplification, which enables to further improve the signal to noise ratio (see ESI†).
can be easily extracted from the overall signal O(t) via lock-in amplification, which enables to further improve the signal to noise ratio (see ESI†).
Out-of-phase response of the fluorescence intensity
Fluorescence emission is a particularly relevant observable to apply the present protocol.44 In small molecules, combining fluorescence emission and photochromism is difficult since both processes are often competitive mechanisms for relaxation of the excited states.45 In contrast, such a combination is widely found in photochromic fluorescent proteins which have recently led to powerful techniques including time-resolved protein tracking,46 super-resolution microscopy47–50 and high contrast imaging.19,20 Moreover we recently showed that hybrid systems composed of a photoconvertible fluorogen that fluoresces upon binding to an acceptor provide an attractive two-component approach.51
Compared to other observables, the fluorescence intensity IF(t) includes an additional signal convolution since it is not only proportional to concentrations, but also proportional to the light intensity. Thus, considering that both concentrations of the states 1 and 2, and light intensity are modulated, the fluorescence emission IF(t) can be written
with
Qi being the molecular brightness of
i. In the general case of a periodic modulation of large amplitude, one obtains
| | 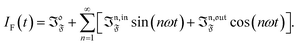 | (39) |
where (see ESI
†)
| | 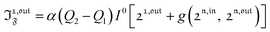 | (40) |
with
n ≥ 1. For a sinusoidal or square wave modulation of small amplitude,
g(
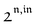
,
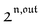
) = 0 but it is non-vanishing in the case of a periodic modulation of large amplitude.
In a regime of sinusoidal or square wave modulation of small amplitude, the out-of-phase amplitude of the fluorescence emission, 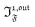 , is proportional to 21,out and exhibits a resonant behavior. In contrast, such a conclusion cannot be directly drawn in the case of periodic modulation of large amplitude since analytical expressions are cumbersome. We therefore evaluated its relevance by means of numerical calculations using typical values found for photoswitchable fluorescent proteins.52–56 To evaluate the possible interference originating from the second order term g(
, is proportional to 21,out and exhibits a resonant behavior. In contrast, such a conclusion cannot be directly drawn in the case of periodic modulation of large amplitude since analytical expressions are cumbersome. We therefore evaluated its relevance by means of numerical calculations using typical values found for photoswitchable fluorescent proteins.52–56 To evaluate the possible interference originating from the second order term g(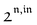 ,
, 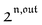 ), we used eqn (40) to numerically compute the dependence of
), we used eqn (40) to numerically compute the dependence of 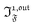 on ω and I0 (see ESI†). Hence we showed that the position and the amplitude of its optimum are similar independently on the nature and amplitude of the light modulation.
on ω and I0 (see ESI†). Hence we showed that the position and the amplitude of its optimum are similar independently on the nature and amplitude of the light modulation.
Therefore, the out-of-phase first-order fluorescence emission enables the selective and quantitative detection of a photoswitchable probe. Easily extracted from the overall signal IF(t) with the benefit of synchronous detection (see ESI†), it additionally provides an improved spatial resolution compared to usual fluorescence detection (see ESI†), which is an advantage for imaging.
Discussion
Our theoretical framework suggests that the out-of-phase first-order response to a periodically modulated light excitation under resonant conditions is appropriate to isolate the contribution of a photoswitchable probe of interest when the observable linearly depends on concentrations. Compared to a classical analysis that relies on an observation in absence of concentration modulation, this feature provides a simple protocol to perform selective and quantitative analyses in complex media without any preliminary separation.
A separation-free selective and quantitative analytical protocol
Instead of analyzing the behavior of a given photoswitchable probe upon varying the values of the control parameters I0 and ω, we now examine which photoswitchable probe can be specifically addressed at fixed values of I0 and ω.
Dynamic contrast.
In a mixture of photoswitchable probes, dynamic contrast will originate from differences in the triplet of parameters (σ12, σ21, kΔ21). At fixed values of I0 and ω, the optimized out-of-phase first-order response to a periodically modulated light excitation originates from matching (i) the rate constants for the thermally- and photochemically-driven reactions (see eqn (14)) and (ii) the exchange relaxation time τ012 with the radial frequency of the light modulation ω (see eqn (14) and (15)). We correspondingly use the (σ12 + σ21, kΔ21) dynamic set to characterize the dynamic behavior of the photoswitchable probes illuminated at average intensity I0 and radial frequency ω. Fig. 3a and b displays the dependence of the normalized in-phase |11,innorm| = |11,in/Ptot| and out-of-phase |11,outnorm| = |11,out/Ptot| amplitudes on (σ12 + σ21)I0/ω and kΔ21/ω for a weak sinusoidal light modulation. In contrast to the in-phase amplitude, the out-of-phase amplitude exhibits a single optimum centered on| | 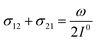 | (41) |
| | 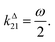 | (42) |
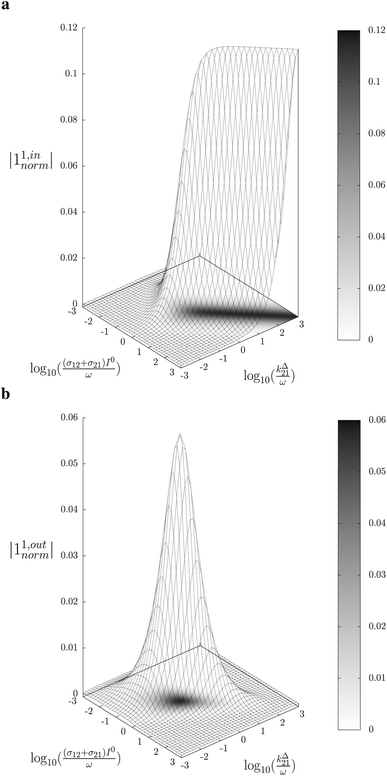 |
| | Fig. 3 Theoretical computation of the response of a photoswitchable probe 1 ⇌ 2 submitted to light harmonic forcing of small amplitude at fixed values of I0 and ω. The normalized amplitudes of the in-phase and out-of-phase oscillations in 1 concentration, |11,innorm| (a) and |11,outnorm| (b) respectively, are plotted versus (σ12 + σ21)I0/ω and kΔ21/ω for σ12/(σ12 + σ21) = 0.46. See eqn (12) and (13). | |
At fixed values of I0 and ω, eqn (41) and (42) show that one can selectively isolate the contribution from the monodimensional 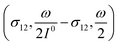 manifold in the three-dimensional (σ12, σ21, kΔ21) space of photoswitchable probes. Among the manifold members, the |11,outnorm| = σ12/[8(σ12 + σ21)] amplitude is ruled by the σ12/(σ12 + σ21) photochemical parameter. |11,outnorm| is maximal
manifold in the three-dimensional (σ12, σ21, kΔ21) space of photoswitchable probes. Among the manifold members, the |11,outnorm| = σ12/[8(σ12 + σ21)] amplitude is ruled by the σ12/(σ12 + σ21) photochemical parameter. |11,outnorm| is maximal 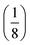 for the
for the 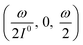 photoswitchable probe. However the amplitude of all the manifold members notably remains of the same order of magnitude as long as σ12 does not drop much below the σ21 range.
photoswitchable probe. However the amplitude of all the manifold members notably remains of the same order of magnitude as long as σ12 does not drop much below the σ21 range.
Selective and quantitative detection.
The above discussion shows that optimizing the out-of-phase response by choosing a couple (I0, ω) that verifies the resonance conditions (14) and (15) opens an interesting way to selectively image and quantify a photoswitchable probe P in the presence of interfering compounds X (of total concentrations Xtot), each defined by a different set of parameters (σ12,X, σ21,X, kΔ21,X). Note that X can be non-photoswitchable: in that case σ12,X = σ21,X = 0 and kΔ21,X = 0. To illustrate this, we take a simplified case of a mixture containing photoswitchable probes, whose only the state 1 yields an observable signal, and possessing all the same brightness Q1. In that case, a protocol relying on illumination at constant light intensity I0 leads to a signal S0 which is proportional to the sum of the contributions of the different probes such that:| | 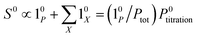 | (43) |
where| | 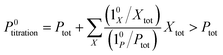 | (44) |
When the signal S0 is used to titrate the concentration of P upon assuming that only the reactant of interest is present, the titration result P0titration always overestimates the total concentration Ptot because of the contributions of the interfering compounds (see Fig. 4a).
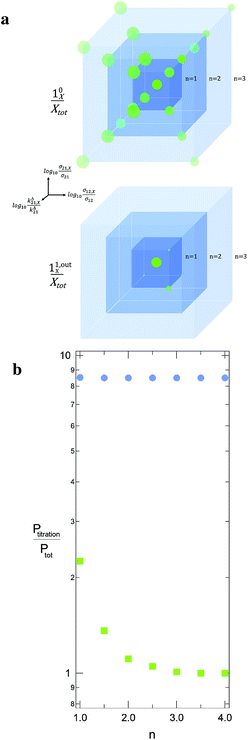 |
| | Fig. 4 Theoretical computation of Ptitration in seven different equimolar mixtures, which include the targeted triplet (σ12, σ21, kΔ21) plus eight other interfering ones. In each sample labelled n, the latter species correspond to the eight (σ12,X, σ21,X, kΔ21,X) sets placed on the nodes of a cube centered on (σ12, σ21, kΔ21) and which mesh size is n in decimal logarithmic units (a; the individual responses (10X/Xtot) and (11,outX/Xtot) have been used to define the sphere radius associated to each (σ12,X, σ21,X, kΔ21,X) set in (10/Ptot) and (11,out/Ptot) units). The n-dependence of the ratio of Ptitration to the effective target concentration Ptot is displayed in b for both the constant light intensity (disks) and the OPTIMAL (squares) methods. σ12 = 73 m2 mol−1, σ21 = 84 m2 mol−1, kΔ21 = 1.5 × 10−2 s−1; I0 = kΔ21/(σ12 + σ21) = 9.6 × 10−5 ein s−1 m−2, ω = 2kΔ21 = 3 × 10−2 rad s−1. | |
In contrast, the corresponding out-of-phase first-order response to light modulation 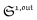
| | 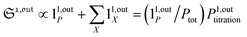 | (45) |
where
| | 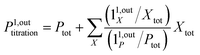 | (46) |
enables to determine
Ptot when the light parameters (
I0,
ω) are tuned to the resonance conditions of
P. Indeed, the term 1
1,outP is then maximal while the terms 1
1,outX are negligible (
Fig. 3b). Thus, the signal from
P now dominates those of the other probes, and the titration result
P1,outtitration is approximatively equal to
Ptot (see
Fig. 4a).
Fig. 4b illustrates for various mixtures the superiority of this second strategy over measurements performed at constant light intensity: whereas all the
P0titration are several times larger than the actual
Ptot concentration, the discrepancy between
P1,outtitration and
Ptot becomes negligible as soon as (
σ12,
σ21,
kΔ21) deviates from (
σ12,X,
σ21,X,
kΔ21,X).
Experimental implementation
This theoretical analysis suggests that it is possible to selectively and quantitatively visualize a given photoswitchable probe defined by the triplet of parameters (σ12, σ21, kΔ21) by simply analysing the out-of-phase (or quadrature-delayed) first-order component of the overall signal resulting from an illumination with a light of average intensity I0 and periodically modulated at fundamental angular frequency ω so as to fulfil the resonance conditions (14) and (15) (Fig. 1).
To selectively address a photoswitchable probe of interest used for analyte labelling necessitates to preliminarily measure the sum of its molecular action cross-sections for photoisomerization σ12 + σ21 and its thermal rate constant kΔ21, which can be easily performed, for instance, with a series of simple light jump experiments.40,51 Once the parameters σ12 + σ21 and kΔ21 are known, one fixes the parameters I0 and ω of the modulated illumination so as to fulfil the resonance conditions (14) and (15) of the photoswitchable probe. Then one extracts the out of phase first-order response 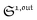 from the acquired probe signal S(t) (possibly contaminated by the contribution of interfering compound). One subsequently aims at extracting from
from the acquired probe signal S(t) (possibly contaminated by the contribution of interfering compound). One subsequently aims at extracting from 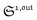 the total probe concentration P1,outtot, which quantifies the labelled analyte. Although theoretical expressions could make possible to directly retrieve the concentrations of the photoswitchable probe from the observed signal, it is probably easier to proceed by calibration upon acquiring the signal from the pure photoswitchable probe at a reference concentration Pcaltot under the same illumination conditions (see ESI†). Then
the total probe concentration P1,outtot, which quantifies the labelled analyte. Although theoretical expressions could make possible to directly retrieve the concentrations of the photoswitchable probe from the observed signal, it is probably easier to proceed by calibration upon acquiring the signal from the pure photoswitchable probe at a reference concentration Pcaltot under the same illumination conditions (see ESI†). Then
| | 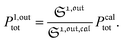 | (47) |
When the photoswitchable probe is used as a titrating reagent, to fulfil the resonance conditions for the parameters I0 and ω first requires an initial guess since the apparent molecular action cross-sections for photoisomerization and thermal rate constant now depend on the concentration of the targeted analyte Atot (see ESI†). In fact, as usually encountered in any titration protocol, one should have an order of magnitude of the latter value before proceeding. Moreover, in contrast to the previous situation, the information sought for is not anymore Ptot but Atot, which is contained in the amplitude of the P response to the light modulation (see ESI†). However, the latter amplitude is also proportional to Ptot and one has first to remove this dependence, for instance by relying on a ratiometric analysis, where one collects the overall signal upon adopting a same illumination but under two conditions of observation (e.g. by recording the fluorescence emission at two different wavelengths). Hence, the analyzed observable is now the ratio 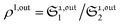 of the out-of-phase first-order amplitudes of the signal collected under the two observation conditions (see ESI†). Calibration now requires to preliminarily investigate the dependence of ρ1,out on Atot. Then quantification can be simply achieved by recording the observable from a calibrating solution where the photoswitchable probe is used to sense a known concentration Acaltot. The concentrations of the analyte, which is retrieved at first-order, is eventually
of the out-of-phase first-order amplitudes of the signal collected under the two observation conditions (see ESI†). Calibration now requires to preliminarily investigate the dependence of ρ1,out on Atot. Then quantification can be simply achieved by recording the observable from a calibrating solution where the photoswitchable probe is used to sense a known concentration Acaltot. The concentrations of the analyte, which is retrieved at first-order, is eventually
| | 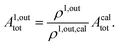 | (48) |
Fields of application
The possibility to selectively and quantitatively retrieve the signal from a probe of interest without any separation is especially attractive when dealing with complex unknown systems.
Selective and quantitative detection in a mixture of probes.
As a first field of application, one can think of selectively and quantitatively detecting a probe of interest in a system containing multiple probes or interfering compounds. This application could be especially useful in living cells, both to perform multiplexed observations as well as to overcome the contribution of endogenous components (Fig. 1a).
Selective and quantitative detection in a heterogeneous system.
Another attractive field of application deals with the analysis or imaging of heterogenous systems. Indeed the brightness as well as the thermokinetic features of a probe often strongly depend on its environment. Thus, in a highly heterogeneous system (e.g. a living cell), it may be especially hazardous to retrieve a quantitative information from the probe signal acquired at constant illumination, when one has no information on the probe location. Indeed the collected signal depends on the concentration, the brightness and the thermokinetic features of the probe. In contrast, the out-of-phase first-order probe response strongly depends on the probe thermokinetic properties, which permits to selectively address the probe molecules located in a given phase, in which preliminary experiments for setting resonance conditions and calibration should have been performed. Therefore, the present analytical protocol could be fruitfully used to selectively analyze concentrations in a phase of interest within a multiphasic media (Fig. 1b), without requiring any extensive structural modification of the probe (as it is usually done to drive the probe location) or fluctuation-based protocols57 to achieve calibration-free concentration measurements.
New challenges for probe development
The relevance and efficiency of the OPTIMAL/OPIOM protocols rely on the availability of appropriate photoswitchable probes. Many photoswitchable organic58 as well as inorganic59 platforms are presently available, so as to make promising the development of OPTIMAL labels with different types of observables. Moreover, these platforms have been already extensively implemented in the context of photocontrollable receptors,60 so as to consider as well their use as OPTIMAL sensors. In the specific OPIOM context, photoswitchable fluorescent proteins are already highly significant probes. However, even in this case developing photoswitchable fluorescent probes fully optimised for OPIOM would enable to increase both the temporal resolution and the signal-to-noise ratio of this new imaging protocol. Indeed, although the above arguments are favorable, the extensive use of the OPTIMAL/OPIOM protocols may be hampered by the lack of a library of suitable engineered photoswitchable probes. This point has already motivated specific developments of photoswitchable fluorescent proteins in the context of SAFIRe.61 In fact, most available reversibly photoswitchable fluorescent proteins (e.g. Dronpa52) have been engineered to exhibit extremely slow thermal return after photoconversion. In the context of OPIOM, such a feature is particularly detrimental in terms of fluorescence signal and temporal resolution: at resonance, intensity of light excitation as well as frequency of light modulation are proportional to the rate constant for thermal return (see eqn (14) and (15)). Even upon relying on the fastest Dronpa-3 mutant,56 we only reached 20 s for the period of light modulation – typically leading to the minute range to record an image.40 Such conditions are not optimal with respect to dynamic analysis of biological phenomena.62 A slow thermal return also requires working at low average light intensity, which is not favorable to get a satisfactory signal to noise ratio.48,63 We currently estimate that temporal resolution in the second range at a satisfactory few tens of W cm−2 average light power could be reached with photoswitchable probes exhibiting a relaxation time for thermal return in the 0.1–1 s range. Moreover, in relation to multiplex applications, Fig. 4 shows that it would be relevant to generate libraries of photoswitchable probes with values of their relevant dynamic parameters kΔ21 and σ12 + σ21 spread over at least two orders of magnitude ranges. Both photoswitchable fluorescent proteins as well as photoswitchable fluorescence turn-on probes are favorable candidates to implement such an engineering.51,64,65
Conclusion
By relying on the out-of-phase first-order response to periodic light modulation, OPTIMAL can discriminate – without any separation or washing step – a targeted photoswitchable probe among various interfering compounds, photoswitchable or not. Its experimental implementation is expected to be simple and cheap, just involving one-day preliminary investigations and appropriate tuning of two control parameters, the average intensity and the radial frequency of the modulated illumination, in order to fulfil robust resonance conditions. In particular, the OPTIMAL approach holds promises for selective and quantitative analyses in complex media such as encountered in biology: with optimized photoswitchable probes, the OPTIMAL protocol should make possible to titrate minor or signal-buried components as well as to facilitate multiplexed observations, as we recently demonstrated upon introducing the OPIOM fluorescence imaging approach in integral cells and organisms.40
References
- C. M. Beck II, Anal. Chem., 1994, 66, 224A–239A CrossRef.
- J. A. Pérez-Bustamante, Fresenius' J. Anal. Chem., 1997, 357, 151–161 CrossRef.
-
D. Harvey, Modern Analytical Chemistry, McGraw-Hill, Boston, 2000 Search PubMed.
- T. R. Gingeras, R. Higuchi, L. J. Kricka, Y. M. D. Lo and C. T. Wittwer, Clin. Chem., 2005, 51, 661–671 CAS.
- R. L. Nicholson, M. Welch, M. Ladlow and D. R. Spring, ACS Chem. Biol., 2007, 2, 24–30 CrossRef CAS PubMed.
- J. L. Duffner, P. A. Clemons and A. N. Koehler, Curr. Opin. Chem. Biol., 2007, 11, 74–82 CrossRef CAS PubMed.
- B. D. Bennett, E. H. Kimball, M. Gao, R. Osterhout, S. J. Van Dien and J. D. Rabinowitz, Nat. Chem. Biol., 2009, 5, 593–599 CrossRef CAS PubMed.
- B. Giepmans, S. Adams, M. Ellisman and R. Tsien, Science, 2006, 312, 217–224 CrossRef CAS PubMed.
- B. Wu, K. D. Piatkevich, T. Lionnet, R. H. Singer and V. V. Verkhusha, Curr. Opin. Cell Biol., 2011, 23, 310–317 CrossRef CAS PubMed.
- R. Winkler-Oswatitsch and M. Eigen, Angew. Chem., Int. Ed., 1979, 18, 20–49 CrossRef.
-
M. Eigen and L. de Mayer, Relaxation Methods in Techniques of Organic Chemistry, Interscience Publishers, John Wiley and Sons, New York, London, 2nd edn, 1963, vol. VIII, pp. 895–1054 Search PubMed.
- H. Berthoumieux, C. Antoine and A. Lemarchand, J. Chem. Phys., 2009, 131, 084106 CrossRef CAS PubMed.
- H. Berthoumieux, L. Jullien and A. Lemarchand, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 056112 CrossRef CAS.
- A. Lemarchand, H. Berthoumieux, L. Jullien and C. Gosse, J. Phys. Chem. A, 2012, 116, 8455–8463 CrossRef CAS PubMed.
- F. Closa, C. Gosse, L. Jullien and A. Lemarchand, J. Chem. Phys., 2013, 138, 244109 CrossRef CAS PubMed.
- D. Baurecht and U. P. Fringeli, Rev. Mod. Sci. Inst., 2001, 72, 3782–3792 CrossRef CAS.
-
I. Noda and Y. Osaki, Two-Dimensional Spectroscopy Applications in Vibrational and Optical Spectroscopy, Wiley, Chichester, 2004 Search PubMed.
- D. Boyer, P. Tamarat, A. Maali, B. Lounis and M. Orrit, Science, 2002, 297, 1160–1163 CrossRef CAS PubMed.
- G. Marriott, S. Mao, T. Sakata, J. Ran, D. K. Jackson, C. Petchprayoon, T. J. Gomez, E. Warp, O. Tulyathan, H. L. Aaron, E. Y. Isacoff and Y. Yan, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17789–17794 CrossRef CAS PubMed.
- Y. Yan, M. E. Marriott, C. Petchprayoon and G. Marriott, Biochem. J., 2011, 433, 411–422 CrossRef CAS PubMed.
- C. I. Richards, J.-C. Hsiang, D. Senapati, S. Patel, J. Yu, T. Vosch and R. M. Dickson, J. Am. Chem. Soc., 2009, 131, 4619–4621 CrossRef CAS PubMed.
- C. I. Richards, J.-C. Hsiang and R. M. Dickson, J. Phys. Chem. B, 2010, 114, 660–665 CrossRef CAS PubMed.
- C. I. Richards, J.-C. Hsiang, A. M. Khalil, N. P. Hull and R. M. Dickson, J. Am. Chem. Soc., 2010, 132, 6318–6323 CrossRef CAS PubMed.
- C. Fan, J.-C. Hsiang, A. E. Jablonski and R. M. Dickson, Chem. Sci., 2011, 2, 1080–1085 RSC.
- C. Fan, J.-C. Hsiang and R. M. Dickson, ChemPhysChem, 2012, 13, 1023–1029 CrossRef CAS PubMed.
- A. E. Jablonski, J.-C. Hsiang, P. Bagchi, N. Hull, C. I. Richards, C. J. Fahrni and R. M. Dickson, J. Phys. Chem. Lett., 2012, 3, 3585–3591 CrossRef CAS PubMed.
- S. Sarkar, C. Fan, J.-C. Hsiang and R. M. Dickson, J. Phys. Chem. A, 2014, 117, 9501–9509 CrossRef PubMed.
- J.-C. Hsiang, A. E. Jablonski and R. M. Dickson, Acc. Chem. Res., 2014, 47, 1545–1554 CrossRef CAS PubMed.
- A. D. Q. Li, C. Zhan, D. Hu, W. Wan and J. Yao, J. Am. Chem. Soc., 2011, 133, 7628–7631 CrossRef CAS PubMed.
- Z. Tian, W. Wu, W. Wan and A. D. Q. Li, J. Am. Chem. Soc., 2011, 133, 16092–16100 CrossRef CAS PubMed.
- Z. Tian and A. D. Q. Li, Acc. Chem. Res., 2013, 46, 269–279 CrossRef CAS PubMed.
- H. Berthoumieux, C. Antoine, L. Jullien and A. Lemarchand, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 021906 CrossRef CAS.
- I. Schoen, H. Krammer and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 21649–21654 CrossRef CAS PubMed.
- K. Zrelli, T. Barilero, E. Cavatore, H. Berthoumieux, T. Le Saux, V. Croquette, A. Lemarchand, C. Gosse and L. Jullien, Anal. Chem., 2011, 83, 2476–2484 CrossRef CAS PubMed.
- Q. Wei and A. Wei, Chem.–Eur. J., 2011, 17, 1080–1091 CrossRef CAS PubMed.
- L. Jullien, A. Lemarchand and H. Lemarchand, J. Chem. Phys., 2000, 112, 8293–8301 CrossRef CAS.
- D. Alcor, V. Croquette, L. Jullien and A. Lemarchand, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 8276–8280 CrossRef CAS PubMed.
- D. Alcor, J.-F. Allemand, E. Cogné-Laage, V. Croquette, F. Ferrage, L. Jullien, A. Kononov and A. Lemarchand, J. Phys. Chem. B, 2005, 109, 1318–1328 CrossRef CAS PubMed.
- J. H. Scofield, Am. J. Phys., 1994, 62, 129–133 CrossRef.
- J. Querard, T.-Z. Markus, M.-A. Plamont, C. Gauron, P. Wang, A. Espagne, M. Volovitch, S. Vriz, V. Croquette, A. Gautier, T. Le Saux and L. Jullien, Angew. Chem., Int. Ed., 2015, 54, 2633–2637 CrossRef CAS PubMed.
- G. Marriott, R. M. Clegg, D. J. Arndt-Jovin and T. M. Jovin, Biophys. J., 1991, 60, 1374–1387 CrossRef CAS PubMed.
- T. Sanden, G. Persson, P. Thyberg, H. Blom and J. Widengren, Anal. Chem., 2007, 79, 3330–3341 CrossRef CAS PubMed.
- J. Vogelsang, C. Steinhauer, C. Forthmann, I. H. Stein, B. Person-Skegro, T. Cordes and P. Tinnefeld, ChemPhysChem, 2010, 11, 2475–2490 CrossRef CAS PubMed.
-
B. Valeur, Molecular fluorescence: principles and applications, Wiley-VCH, 2001 Search PubMed.
- T. Fukaminato, J. Photochem. Photobiol., C, 2011, 12, 177–208 CrossRef CAS.
- D. M. Chudakov, T. V. Chepurnykh, V. V. Belousov, S. Lukyanov and K. A. Lukyanov, Traffic, 2006, 7, 1304–1310 CrossRef CAS PubMed.
- M. Fernandez-Suarez and A. Y. Ting, Nat. Rev. Mol. Cell Biol., 2008, 9, 929–943 CrossRef CAS PubMed.
- M. Hofmann, C. Eggeling, S. Jakobs and S. W. Hell, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17565–17569 CrossRef CAS PubMed.
- E. Betzig, G. H. Patterson, R. Sougrat, O. W. Lindwasser, S. Olenych, J. S. Bonifacino, M. W. Davidson, J. Lippincott-Schwartz and H. F. Hess, Science, 2006, 313, 1642–1645 CrossRef CAS PubMed.
- J. Lippincott-Schwartz and G. H. Patterson, Trends Cell Biol., 2009, 19, 555–565 CrossRef CAS PubMed.
- P. Wang, J. Querard, S. Maurin, S. S. Nath, T. Le Saux, A. Gautier and L. Jullien, Chem. Sci., 2013, 4, 2865–2873 RSC.
- R. Ando, H. Mizuno and A. Miyawaki, Science, 2004, 306, 1370–1373 CrossRef CAS PubMed.
- S. Habuchi, R. Ando, P. Dedecker, W. Verheijen, H. Mizuno, A. Miyawaki and J. Hofkens, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9511–9516 CrossRef CAS PubMed.
- M. Andresen, A. C. Stiel, S. Trowitzsch, G. Weber, C. Eggeling, M. C. Wahl, S. W. Hell and S. Jakobs, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 13005–13009 CrossRef CAS PubMed.
- A. C. Stiel, S. Trowitzsch, G. Weber, M. Andresen, C. Eggeling, S. W. Hell, S. Jakobs and M. C. Wahl, Biochem. J., 2007, 402, 35–42 CrossRef CAS PubMed.
- R. Ando, C. Flors, H. Mizuno, J. Hofkens and A. Miyawaki, Eur. Biophys. J., 2007, L97–L99 CrossRef CAS PubMed.
- S. Charier, A. Meglio, D. Alcor, E. Cogné-Laage, J.-F. Allemand, L. Jullien and A. Lemarchand, J. Am. Chem. Soc., 2005, 127, 15491–15505 CrossRef CAS PubMed.
- H. Bouas-Laurent and H. Dürr, Pure Appl. Chem., 2001, 73, 639–665 CrossRef CAS.
- M.-S. Wang, G. Xu, Z.-J. Zhang and G.-C. Guo, Chem. Commun., 2010, 46, 361–376 RSC.
- M. Natali and S. Giordani, Chem. Soc. Rev., 2012, 41, 4010–4029 RSC.
- A. E. Jablonski, R. B. Vegh, J.-C. Hsiang, B. Bommarius, Y.-C. Chen, K. M. Solntsev, A. S. Bommarius, L. M. Tolbert and R. M. Dickson, J. Am. Chem. Soc., 2013, 135, 16410–16417 CrossRef CAS PubMed.
- R. Milo, P. Jorgensen, U. Moran, G. Weber and G. M. Springer, Nucleic Acids Res., 2010, 38, D750–D753 CrossRef CAS PubMed.
-
R. Y. Tsien, L. Ernst and A. Waggoner, Fluorophores for Confocal Microscopy: Photophysics and Photochemistry, Springer Science + Business Media, 3rd edn, 2006 Search PubMed.
- D. Bourgeois and V. Adam, IUBMB Life, 2012, 64, 482–491 CrossRef CAS PubMed.
- X. X. Zhou and M. Z. Lin, Curr. Opin. Chem. Biol., 2013, 17, 682–690 CrossRef CAS PubMed.
Footnotes |
| † This article is dedicated to Prof. Manfred Eigen. |
| ‡ Electronic supplementary information (ESI) available: Reduction of photo-(physical)chemical mechanisms to a two-state exchange, kinetic analysis of the two-state model, retrieval of concentrations from the observables, improvement of the spatial resolution. See DOI: 10.1039/c4sc03955f |
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article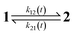
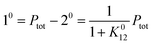
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ωt)].
(ωt)].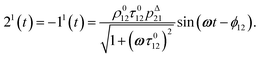
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) + i1,out
sin(ωt) + i1,out![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt)]
cos(ωt)]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) and εi1,out
sin(ωt) and εi1,out![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) are in-phase and out-of-phase (or quadrature-delayed) oscillating terms at angular frequency ω. The amplitudes i1,in and i1,out of the in-phase and out-of-phase oscillating terms are (see ESI†)
cos(ωt) are in-phase and out-of-phase (or quadrature-delayed) oscillating terms at angular frequency ω. The amplitudes i1,in and i1,out of the in-phase and out-of-phase oscillating terms are (see ESI†)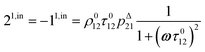
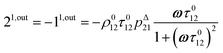
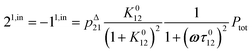
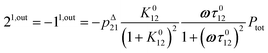
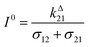
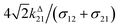 along I0 and
along I0 and 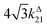 along ω. The normalized out-of phase amplitude |11,outnorm| is then equal to σ12/[8(σ12 + σ21)].
along ω. The normalized out-of phase amplitude |11,outnorm| is then equal to σ12/[8(σ12 + σ21)].

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I0 to show that εpΔ21K012Ptot/(1 + K012)2 measures the composition shift δ20 from the steady-state 20 after a light intensity jump of amplitude εI0. It depends on I0 and is maximized in a regime of intermediate illumination, in which thermally- and photochemically-driven reactions occur at the same rate such that kΔ21 = (σ12 + σ21)I0 (see eqn (14)). When the light intensity is too low, the thermal relaxation dominates the photoisomerization and the light intensity jump εI0 cannot significantly shifts the photoswitchable probe from the state 1. Conversely, when the light intensity is too large, the thermal relaxation does not contribute anymore to the dynamics of the exchange (1): the relative proportions in states 1 and 2 become independent of the light intensity, so there is no composition shift induced by the light jump. The second optimized term, ωτ012/[1 + (ωτ012)2], is maximized upon matching the radial frequency of the light modulation ω with the exchange relaxation time τ012 so that ωτ012 = 1 (see eqn (14) and (15)). When ω ≫ 1/τ012, the exchange is slow compared to the light variations and the couple {1, 2} has not enough time to respond: both i1,in and i1,out vanish. Conversely, when ω ≪ 1/τ012, i1,out cancels, so the concentrations of 1 and 2 oscillate in phase with the light modulation.
I0 to show that εpΔ21K012Ptot/(1 + K012)2 measures the composition shift δ20 from the steady-state 20 after a light intensity jump of amplitude εI0. It depends on I0 and is maximized in a regime of intermediate illumination, in which thermally- and photochemically-driven reactions occur at the same rate such that kΔ21 = (σ12 + σ21)I0 (see eqn (14)). When the light intensity is too low, the thermal relaxation dominates the photoisomerization and the light intensity jump εI0 cannot significantly shifts the photoswitchable probe from the state 1. Conversely, when the light intensity is too large, the thermal relaxation does not contribute anymore to the dynamics of the exchange (1): the relative proportions in states 1 and 2 become independent of the light intensity, so there is no composition shift induced by the light jump. The second optimized term, ωτ012/[1 + (ωτ012)2], is maximized upon matching the radial frequency of the light modulation ω with the exchange relaxation time τ012 so that ωτ012 = 1 (see eqn (14) and (15)). When ω ≫ 1/τ012, the exchange is slow compared to the light variations and the couple {1, 2} has not enough time to respond: both i1,in and i1,out vanish. Conversely, when ω ≪ 1/τ012, i1,out cancels, so the concentrations of 1 and 2 oscillate in phase with the light modulation.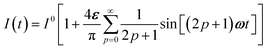
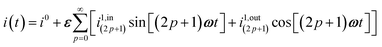
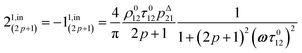
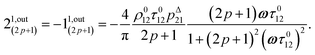
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt)]
sin(ωt)]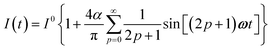
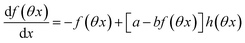
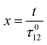
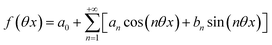
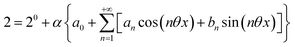
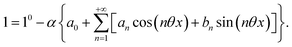
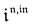 and
and 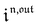 of the in-phase and out-of phase terms oscillating at the radial frequency nω. The concentration of i can be now written
of the in-phase and out-of phase terms oscillating at the radial frequency nω. The concentration of i can be now written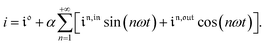
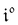 ,
, 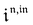 and
and 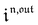 are proportional to Ptot. Indeed eqn (25) can be transformed into
are proportional to Ptot. Indeed eqn (25) can be transformed into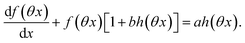
 ,
, 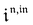 and
and 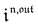 are proportional to Ptot.
are proportional to Ptot.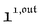 and
and 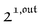 , such conclusions cannot be directly derived in the case of periodic light modulation of large amplitude. We correspondingly evaluated their relevance by means of numerical calculations (see ESI†). For harmonic forcing as well as square wave modulation in a regime of large amplitude modulation, we could show that |
, such conclusions cannot be directly derived in the case of periodic light modulation of large amplitude. We correspondingly evaluated their relevance by means of numerical calculations (see ESI†). For harmonic forcing as well as square wave modulation in a regime of large amplitude modulation, we could show that |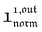 | exhibits an optimum in the space (I0, ω), which position and amplitude are very close to those observed with a sinusoidal modulation of small amplitude. In fact, the error done when taking the analytical expression of the resonance conditions valid only for a modulation of small amplitude is always less than 20%, no matter which amplitude α is used. Such an error would be of the order of magnitude of the experimental errors done when fixing the average light intensity and radial frequency to their values at resonance, I0,R and ωR.
| exhibits an optimum in the space (I0, ω), which position and amplitude are very close to those observed with a sinusoidal modulation of small amplitude. In fact, the error done when taking the analytical expression of the resonance conditions valid only for a modulation of small amplitude is always less than 20%, no matter which amplitude α is used. Such an error would be of the order of magnitude of the experimental errors done when fixing the average light intensity and radial frequency to their values at resonance, I0,R and ωR.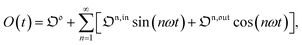
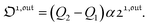
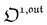 is directly proportional to
is directly proportional to 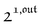 , which was shown above to be optimal when the resonance conditions (14) and (15) are fulfilled. Hence, the analysis of the out-of-phase first-order response
, which was shown above to be optimal when the resonance conditions (14) and (15) are fulfilled. Hence, the analysis of the out-of-phase first-order response 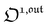 of the overall observable O(t) allows for the selective and quantitative detection of a photoswitchable probe. Note that
of the overall observable O(t) allows for the selective and quantitative detection of a photoswitchable probe. Note that 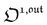 can be easily extracted from the overall signal O(t) via lock-in amplification, which enables to further improve the signal to noise ratio (see ESI†).
can be easily extracted from the overall signal O(t) via lock-in amplification, which enables to further improve the signal to noise ratio (see ESI†).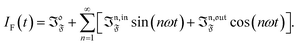
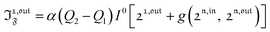
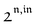 ,
, 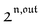 ) = 0 but it is non-vanishing in the case of a periodic modulation of large amplitude.
) = 0 but it is non-vanishing in the case of a periodic modulation of large amplitude.
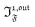 , is proportional to 21,out and exhibits a resonant behavior. In contrast, such a conclusion cannot be directly drawn in the case of periodic modulation of large amplitude since analytical expressions are cumbersome. We therefore evaluated its relevance by means of numerical calculations using typical values found for photoswitchable fluorescent proteins.52–56 To evaluate the possible interference originating from the second order term g(
, is proportional to 21,out and exhibits a resonant behavior. In contrast, such a conclusion cannot be directly drawn in the case of periodic modulation of large amplitude since analytical expressions are cumbersome. We therefore evaluated its relevance by means of numerical calculations using typical values found for photoswitchable fluorescent proteins.52–56 To evaluate the possible interference originating from the second order term g(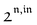 ,
, 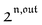 ), we used eqn (40) to numerically compute the dependence of
), we used eqn (40) to numerically compute the dependence of 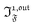 on ω and I0 (see ESI†). Hence we showed that the position and the amplitude of its optimum are similar independently on the nature and amplitude of the light modulation.
on ω and I0 (see ESI†). Hence we showed that the position and the amplitude of its optimum are similar independently on the nature and amplitude of the light modulation.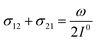
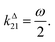

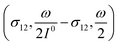 manifold in the three-dimensional (σ12, σ21, kΔ21) space of photoswitchable probes. Among the manifold members, the |11,outnorm| = σ12/[8(σ12 + σ21)] amplitude is ruled by the σ12/(σ12 + σ21) photochemical parameter. |11,outnorm| is maximal
manifold in the three-dimensional (σ12, σ21, kΔ21) space of photoswitchable probes. Among the manifold members, the |11,outnorm| = σ12/[8(σ12 + σ21)] amplitude is ruled by the σ12/(σ12 + σ21) photochemical parameter. |11,outnorm| is maximal 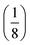 for the
for the 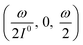 photoswitchable probe. However the amplitude of all the manifold members notably remains of the same order of magnitude as long as σ12 does not drop much below the σ21 range.
photoswitchable probe. However the amplitude of all the manifold members notably remains of the same order of magnitude as long as σ12 does not drop much below the σ21 range.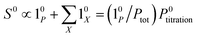
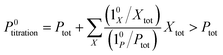
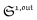
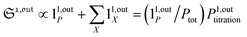
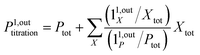
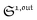 from the acquired probe signal S(t) (possibly contaminated by the contribution of interfering compound). One subsequently aims at extracting from
from the acquired probe signal S(t) (possibly contaminated by the contribution of interfering compound). One subsequently aims at extracting from 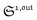 the total probe concentration P1,outtot, which quantifies the labelled analyte. Although theoretical expressions could make possible to directly retrieve the concentrations of the photoswitchable probe from the observed signal, it is probably easier to proceed by calibration upon acquiring the signal from the pure photoswitchable probe at a reference concentration Pcaltot under the same illumination conditions (see ESI†). Then
the total probe concentration P1,outtot, which quantifies the labelled analyte. Although theoretical expressions could make possible to directly retrieve the concentrations of the photoswitchable probe from the observed signal, it is probably easier to proceed by calibration upon acquiring the signal from the pure photoswitchable probe at a reference concentration Pcaltot under the same illumination conditions (see ESI†). Then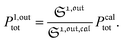
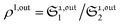 of the out-of-phase first-order amplitudes of the signal collected under the two observation conditions (see ESI†). Calibration now requires to preliminarily investigate the dependence of ρ1,out on Atot. Then quantification can be simply achieved by recording the observable from a calibrating solution where the photoswitchable probe is used to sense a known concentration Acaltot. The concentrations of the analyte, which is retrieved at first-order, is eventually
of the out-of-phase first-order amplitudes of the signal collected under the two observation conditions (see ESI†). Calibration now requires to preliminarily investigate the dependence of ρ1,out on Atot. Then quantification can be simply achieved by recording the observable from a calibrating solution where the photoswitchable probe is used to sense a known concentration Acaltot. The concentrations of the analyte, which is retrieved at first-order, is eventually