Open Access Article
Open Access ArticleMolecular recognition in curved π-systems: effects of π-lengthening of tubular molecules on thermodynamics and structures†‡
Taisuke
Matsuno
ab,
Sota
Sato
ab,
Ryosuke
Iizuka
b and
Hiroyuki
Isobe
*ab
aJST, ERATO, Isobe Degenerate π-Integration Project, Aoba-ku, Sendai 980-8577, Japan
bAdvanced Institute for Materials Research (AIMR) and Department of Chemistry, Tohoku University, Aoba-ku, Sendai 980-8578, Japan. E-mail: isobe@m.tohoku.ac.jp
First published on 14th October 2014
Abstract
The thermodynamics and molecular structure of a supramolecular complex between a tubular molecule, (P)-(12,8)-[4]cyclo-2,8-anthanthrenylene, and fullerene were investigated. The enthalpy-driven characteristics of the association were enhanced upon lengthening of the curved sp2-carbon networks in the tubular molecule as a result of an increase in the C–C contact areas in addition to the emergence of CH–π contacts with aliphatic chains. The involvement of CH–π interactions in the molecular recognition consequently increased the entropy cost for the association, and the importance of molecular structures at the edge of tubular molecules was revealed. An inflection-free, smooth surface inside the tubular molecule was revealed by crystallographic analysis, which allowed for dynamic motions of the encapsulated fullerene molecule in solution. This study provided a new example of a molecular peapod with a smoothly curved π-interface to be examined in the structure–thermodynamics relationship study and led to an in-depth understanding of peapods in general.
Introduction
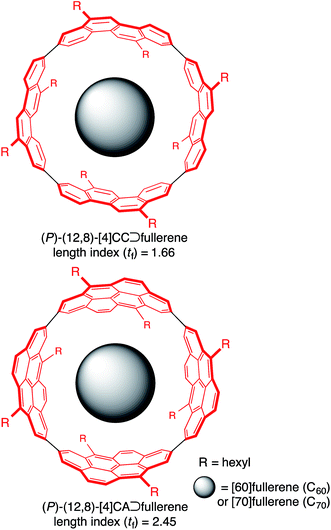
A supramolecular combination of single-wall carbon nanotubes (SWNT) and fullerenes, the so-called peapod, constitutes a unique class of molecular assemblies.1 The structure of this complex is composed of curved π-systems with a concave–convex interface, and its assembly is driven solely by van der Waals interactions.2 The complemental interface with a non-directional association force further allows for dynamic motions of the encapsulated guests, which is also of interest to researchers in the field of molecular machines.3,4 A range of methods for assembling this complex are being explored, and a solution-phase method is becoming one of the most popular and important methods because of its mild conditions.5 Although the exploration of solution-phase methods has provided phenomenological insights on the assembly, the fundamental thermodynamics and structures are poorly understood due to the available SWNT being inhomogeneous.The host–guest chemistry at the curved π-interface is currently being exploited through the introduction of finite tubular molecules that possess segmental structures of SWNT.6 The encapsulation of fullerenes in finite nanorings was first demonstrated by Kawase with sp2/sp-carbon nanorings7 and recently demonstrated by Yamago, Jasti and Itami with sp2-carbon nanorings.8 Simultaneously, we introduced belt-persistent tubular molecules, [4]cyclochrysenylenes ([4]CC; Fig. 1), with sp2-carbons9,10 and showed that the unique structural features of SWNT, such as a persistent “wall”, are critically important for the molecular assembly of peapods. The belt-persistent molecules resulted in a several-million-fold higher equilibrium constant for the association of C60 in comparison to the flexible nanorings, and the fundamental thermodynamics have been investigated.11,12 The presence of a smoothly curved surface without inflection nodes in the molecular peapod (12,8)-[4]CC⊃C60 was observed and was beneficial for the dynamic motions of fullerene guests even in the solid state.13 We herein report the thermodynamics and structures of molecular peapods with a π-lengthened tubular molecule, (12,8)-[4]cyclo-2,8-anthanthrenylene ([4]CA; Fig. 1).10,14 The thermodynamics study revealed that the molecular assembly has an enthalpy-driven nature, and the comparison between tubular molecules with different lengths showed that the entropy term has an unexpected effect on the association. The atomic-level structure of the molecular peapod was investigated through crystallographic analysis, which revealed the presence of an inflection-free concave surface inside the peapod, and dynamic motions of the fullerene guest were also revealed through solution-phase NMR analysis. The fundamental thermodynamics and the molecular structure will be informative for designing elaborate functional peapods in the future.
Results and discussion
Thermodynamics of fullerene encapsulation in (P)-(12,8)-[4]CA
The thermodynamics of a molecular peapod, (P)-(12,8)-[4]CA⊃fullerene, was first investigated using the fluorescence-quenching titration method in o-dichlorobenzene (oDCB). As shown in Fig. 2, the fluorescence of [4]CA was quenched upon the introduction of fullerenes, and the quenching behavior was analyzed using the Weber curve-fitting method to determine the association constant (Ka; see also Fig. S1‡).11,15,16 The one-to-one stoichiometry of [4]CA and fullerene in the complex was separately confirmed by the Job plot of the UV-vis spectra (see also Fig. S2‡). The Gibbs free energy gain (ΔG) for the formation of the peapod was thus derived at 25 °C using the Ka value. The contribution of the enthalpy terms (ΔH) to the association was analyzed using isothermal titration calorimetry (ITC; Fig. S3‡), which, together with the ΔG values, revealed the contribution of the entropy terms (ΔS).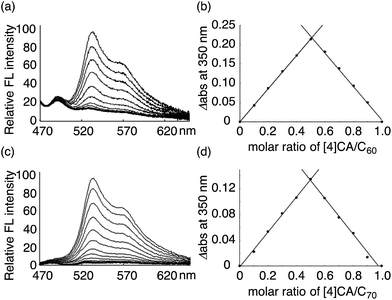 | ||
| Fig. 2 Analysis of (P)-(12,8)-[4]CA⊃fullerene complexation in oDCB at 25 °C. The fluorescence spectra were recorded with excitation at 442 nm, and the change in the fluorescence intensities were monitored at 531 nm (Fig. S1‡). The intensities were calibrated and corrected using the competitive absorbance of fullerenes.11,16 The Job plot was obtained from the absorbance at 350 nm in the UV-vis spectra (Fig. S2‡). (a) Fluorescence-quenching titration for (P)-(12,8)-[4]CA⊃C60. The concentration of (P)-(12,8)-[4]CA was 3.53 × 10−9 M, and the concentration of C60 for the titration was 3.57 × 10−8 M. (b) Job plot analysis for (P)-(12,8)-[4]CA⊃C60 at a total concentration of 3.89 × 10−6 M. (c) Fluorescence-quenching titration for (P)-(12,8)-[4]CA⊃C70. The concentration of (P)-(12,8)-[4]CA was 2.75 × 10−9 M, and the concentration of C70 for the titration was 2.76 × 10−8 M. (d) Job plot analysis for (P)-(12,8)-[4]CA⊃C70 at a total concentration of 3.10 × 10−6 M. | ||
The thermodynamics data for the association of C60 and C70 are summarized in Table 1 along with the reference data for shorter peapods, (P)-(12,8)-[4]CC⊃fullerene.11,17 The association constants, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka, and the resulting free energy gains (ΔG, 25 °C) were not affected by the length of the tubular molecules and were the highest levels (log
Ka, and the resulting free energy gains (ΔG, 25 °C) were not affected by the length of the tubular molecules and were the highest levels (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka ∼ 9, ΔG ∼ −13 kcal mol−1) for host–guest complexes in organic solvents.18 However, the content of the association energy changed depending on the lengths of the tubular molecules. The contribution of the enthalpy terms for the association was pronounced with longer [4]CA molecules, and the enthalpy gains were increased to ca. −14 kcal mol−1. The differences of the enthalpy gains between [4]CA and [4]CC were 1.8-fold for C60 and 1.4-fold for C70. The contribution of the entropy terms, therefore, changed its nature for the association: for the shorter [4]CC, the entropy term operated favorably for the association (−TΔS = −5.3 kcal mol−1 for C60 and −3.0 kcal mol−1 for C70; 25 °C), whereas for the longer [4]CA, the entropy term negligibly or unfavorably contributed to the association (−TΔS = +0.5 kcal mol−1 for C60 and +1.2 kcal mol−1 for C70; 25 °C).
Ka ∼ 9, ΔG ∼ −13 kcal mol−1) for host–guest complexes in organic solvents.18 However, the content of the association energy changed depending on the lengths of the tubular molecules. The contribution of the enthalpy terms for the association was pronounced with longer [4]CA molecules, and the enthalpy gains were increased to ca. −14 kcal mol−1. The differences of the enthalpy gains between [4]CA and [4]CC were 1.8-fold for C60 and 1.4-fold for C70. The contribution of the entropy terms, therefore, changed its nature for the association: for the shorter [4]CC, the entropy term operated favorably for the association (−TΔS = −5.3 kcal mol−1 for C60 and −3.0 kcal mol−1 for C70; 25 °C), whereas for the longer [4]CA, the entropy term negligibly or unfavorably contributed to the association (−TΔS = +0.5 kcal mol−1 for C60 and +1.2 kcal mol−1 for C70; 25 °C).
| Peapod | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka Ka |
ΔG (kcal mol−1) | ΔH (kcal mol−1) | ΔS (cal mol−1 K−1) |
|---|---|---|---|---|
| a The data are obtained from triplicate experiments, and the errors in s.d. are shown. b The data for [4]CC were originally reported in ref. 11 and were slightly corrected in this study.17 | ||||
| (P)-(12,8)-[4]CA⊃C60 | 9.7 ± 0.1 | −13.2 ± 0.1 | −13.7 ± 0.3 | −1.5 ± 1.5 |
| (P)-(12,8)-[4]CA⊃C70 | 9.6 ± 0.3 | −13.1 ± 0.4 | −14.3 ± 0.1 | −4.1 ± 1.7 |
| (P)-(12,8)-[4]CC⊃C60b | 9.5 ± 0.2 | −13.0 ± 0.3 | −7.7 ± 0.2 | 17.6 ± 1.6 |
| (P)-(12,8)-[4]CC⊃C70b | 9.6 ± 0.1 | −13.1 ± 0.1 | −10.1 ± 0.2 | 10.0 ± 1.1 |
Solid-state crystal structure of (P)-(12,8)-[4]CA⊃C60
The molecular structures of (P)-(12,8)-[4]CA⊃C60 in the crystalline solid state were determined by crystallographic analysis of a single crystal. The diffraction analysis was performed with monochromated X-rays (beamline BL-1A, Photon Factory, KEK) to determine the structures with confident R factors [R1 (observed data) = 0.1420 and wR2 (all data) = 0.3849]. Residual chloroform molecules in the crystal were beneficial for reducing the Flack parameter to a reliable level of 0.25(12) through anomalous dispersion effects from chlorine atoms. The absolute configuration of [4]CA in the C2 space group was thus confirmed as (P)-helicity,10,19 which confirmed the previous assignment through theoretical analyses of CD spectra.14The representative features of the molecular structures are described. Two non-identical structures of [4]CA were found in a unit cell. As shown in the overlaid structures (Fig. 3a),21 two molecules shared similar tubular structures with small structural deviations. The average diameter of [4]CA was measured at the carbon atoms closest to the equator (2- and 8- positions) and was equal to 14.00 ± 0.06 Å. Each of the [4]CA molecules encapsulated two disordered C60 molecules, and as a result, four different structures of C60 molecules were found. Although the structures of the disordered C60 molecules showed various orientations, a pair of hexagons on the opposite faces occupied the same position in the [4]CA molecules (see the side view in Fig. 3a). Because the hexagon–hexagon distance is slightly shorter than the pentagon–pentagon distance (∼97%) in an ideal truncated icosahedron,22 we believe that this orientation may minimize the energy for the encapsulation in the crystalline solid state.
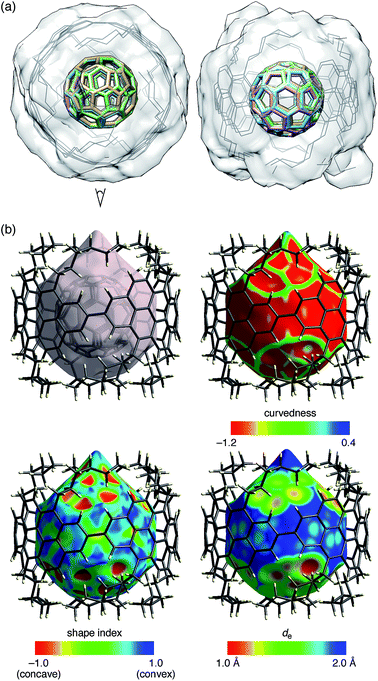 | ||
| Fig. 3 Crystallographic analysis of the molecular structures of (P)-(12,8)-[4]CA⊃C60. Two sets of non-identical peapod structures were found in a unit cell, and two disordered structures of C60 molecules were found for each peapod. (a) Top (left) and side (right) views of the molecular structure of (P)-(12,8)-[4]CA⊃C60. Using four 2,8-carbon atoms at the linkage as the matching atoms, the two coordinates of the non-identical structures were overlaid. The root-mean-square deviation (RMSD) for the positions of the matching atoms was 0.036 Å.21 The structure thus shows four structures of C60 molecules (colored sticks) and two structures of (P)-(12,8)-[4]CA (gray lines) with a transparent solvent-excluded molecular surface of [4]CA molecules.20 Hydrogen atoms are omitted for clarity. See Fig. S4‡ for the separate structures. (b) Hirshfeld surfaces of (P)-(12,8)-[4]CA⊃C60 for one of the non-identical structures. See Fig. S5‡ for the other structure. Color mappings are shown for curvedness, shape index and de. | ||
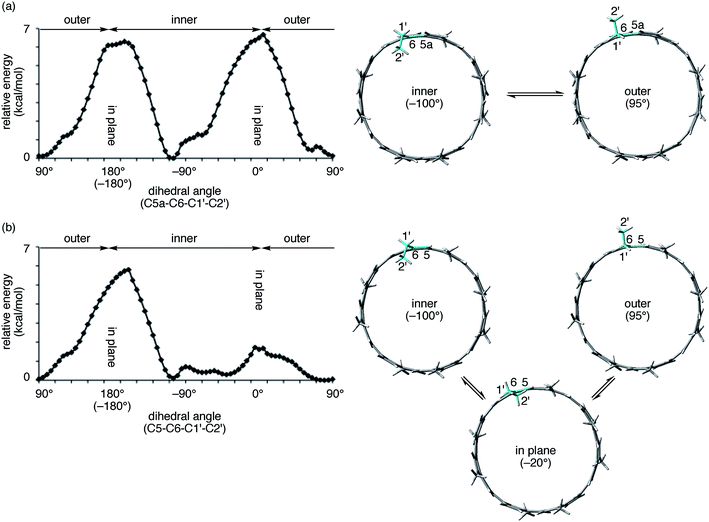
The aliphatic hexyl chains at the edge of the [4]CA molecules were folded to wrap the C60 molecules in the crystal, which is different from the interdigitated structures found in the shorter [4]CC peapods.13 The dihedral angle at the linkage between the hexyl chain and the anthanthrenylene base was −83.55 ± 3.08° (C5a–C6–C1′–C2′; cf.Fig. 4 and 5) and most likely directed the hexyl chains to the inner side of the tubular molecule and hence to the folding orientations (vide infra).23 In addition to this directed orientation, the helical environment of (12,8)-[4]CA with (P)-helicity aligned the hexyl chains in a left-handed spiral on each end of the tubular molecule to cover the encapsulated C60 molecules. In contrast, the dihedral angles of (M)-(12,8)-[4]CC⊃C60 at the same position (C5–C6–C1′–C2′; cf.Fig. 5) varied over the range of 87° to −113°,24 which varied the pointing directions of hexyl chains from the inner, in-plane and outer sides of the tubular molecule.
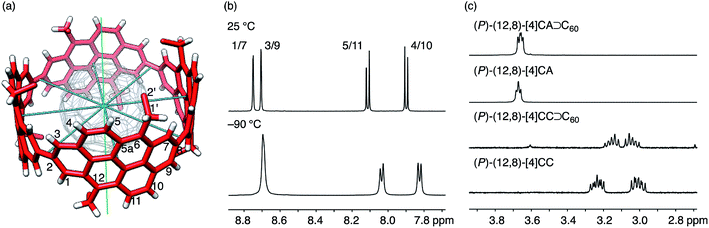 | ||
| Fig. 4 NMR analysis of dynamic structures. (a) The molecular structure of (P)-(12,8)-[4]CA⊃C60 showing symmetry axes (four C2 axes in blue and one C4 axis in green) and position numbers for representative atoms. Representative coordinates from the crystallographic analysis are used, and a part of the hexyl chains are omitted for clarity. (b) Representative spectra from variable temperature NMR analyses of (P)-(12,8)-[4]CA⊃C60 for the aromatic region in CD2Cl2 at 25 °C and −90 °C. See Fig. S7 and S8‡ for the spectra of the whole region and for the spectra for vacant (P)-(12,8)-[4]CA, respectively. (c) Representative spectra for 1′-proton resonances of (P)-(12,8)-[4]CA⊃C60, (P)-(12,8)-[4]CA, (P)-(12,8)-[4]CC⊃C60 and (P)-(12,8)-[4]CC at 25 °C in CD2Cl2. See Fig. S9‡ for the whole region. | ||
A detailed analysis of the atomic contacts in the molecular peapod was performed using Hirshfeld surfaces.25,26 The Hirshfeld surface provides a unique and convenient method for structural analysis: the surface of a molecule provides graphical information about the shape of the space dominated by the electron distribution of the internal molecule. The surface can be further mapped with colors with measures for curvedness, shape index and distances from the surface to the external atoms (de) to provide information about the environment surrounding the surface.
As shown in Fig. 3b, the Hirshfeld surface showed that the C60 molecule was confined in an inner tubular space of the [4]CA molecule. Except for the presence of the aliphatic lids at both ends of the tubular molecule, the Hirshfeld surfaces and the color mappings well resemble those of the shorter [4]CC peapod (Fig. S5‡).13 The curvedness mapping showed no inflection nodes in the contacting areas with [4]CA and revealed a smoothly curved surface inside the [4]CA molecule. The shape index showed no indication of π–π stacking but rather indicated the presence of a unique tube-sphere recognition. The de mapping showed the presence of intimate C–C contacts that distributed over the smooth concave–convex interface.
Surface areas with C–C contacts were compared between peapods with the longer [4]CA peapod and the shorter [4]CC peapod (Fig. S6‡). The surface areas of the C60 molecule that possessed C–C contacts with the tubular molecule were 35.9% for the [4]CA peapod and 27.8% for the [4]CC peapod, and a 1.3-fold increase in the contact areas was observed for [4]CA. This increase in the experimental contact areas is well expected from the geometry of finite SWNT molecules: the geometrical increase in the length of [4]CA is 1.5-fold, the atom-filling rate of [4]CA is 85%,27 and an increase of 1.3-fold (1.5 × 0.85) is thus expected from the geometry of the molecules.10 Note that this good correlation between the mathematical geometries and experimental structural features confirmed a tubular character of [4]CA and [4]CC that allows for a vector description of the molecular structures.10
Solution-phase structures of (P)-(12,8)-[4]CA⊃C60
The spectral pattern of resonances did not change upon cooling the sample to −90 °C, which indicated that the dynamic motions were maintained at this temperature. A comparable analysis of the shorter (P)-(12,8)-[4]CC⊃C60 also showed similar spectral behaviors,11 and no noticeable effect of π-lengthening on the dynamic motions of the C60 guest was detected under the present conditions in spite of the presence of a higher enthalpic constraint for the association.
The spectral change of the 1′-protons in [4]CA should originate from the steric variance due to the additional sp2-carbon atoms at the edge of the tubular structure, and theoretical calculations of model molecules suggested a structural origin for this change. As shown in Fig. 5, we investigated the rotational preference of alkyl chains on [4]CA and [4]CC, using one ethyl substituent as the model for the rotating alkyl group. The other seven substituents were simplified as methyl groups, and energy profiles for the rotation at the linkage of the ethyl group (C5a–C6–C1′–C2′ for [4]CA and C5–C6–C1′–C2′ for [4]CC) were obtained using the semiempirical PM3 method.
Two structures were found as global minima, and the orientations of these structures were identical for [4]CA and [4]CC: the ethyl group pointed toward either inner or outer sides with a dihedral angle of ca. −100° or 95° (Fig. 5). On the other hand, a difference between [4]CA and [4]CC was observed at an orientation for in-plane conformations. The two in-plane orientations were saddle points for [4]CA, whereas one of them for [4]CC was located near a second global minimum with a dihedral angle of −20°. The presence of this second global minimum as well as an associated barrier with a low energy height indicate that the ethyl group on [4]CC oscillates through this point to set the time-average structure at the biased in-plane orientation at 0°. This different dynamic behavior of alkyl groups should be the structural origin of the NMR spectra, which originates from a subtle structural difference at the edge of the tubular molecules. Spectroscopically, two 1′-methylene protons of [4]CA should simultaneously be located in the same environments on the same side of the tube, either inner or outer, whereas two 1′-methylene protons of [4]CC should be located separately in the different environments on the different sides.29,30 This conclusion is also supported by the alkyl orientations observed in the crystal structures (vide supra).23,24 The orientations were scattered among the inner, in-plane or outer directions for [4]CC and were fixed at the inner directions for [4]CA. The CH–π contact between alkyl chains and fullerene in the crystal structure may further indicate that such inner orientations were preferred, even in the solution phase.
Conclusion
Analysis of the thermodynamics for the formation of a peapod in a π-lengthened tubular molecule revealed an enthalpy-driven association, resulting in large enthalpy values of −14 kcal mol−1. Crystallographic analysis of (P)-(12,8)-[4]CA⊃C60 provided precise, atomic-level structures of the molecular peapod, which further provided an important structural basis for understanding the details for peapod formation. The 1.8-fold increase in the enthalpy gains with the longer [4]CA⊃C60 peapod compared to the shorter [4]CC⊃C60 peapod can primarily be attributed to the 1.3-fold increase in the C–C contact areas at the concave–convex interface of curved π-systems. The discrepancy from a commensurate increase in the enthalpy gain is best explained by the addition of CH–π interactions between alkyl chains and fullerene in the longer [4]CA peapods.31,32 Effects of π-lengthening on the electronic communications between host and guest is of interest for future studies.33 The lengthening structure with additional sp2-carbon atoms at the edges not only increased the C–C contact areas but also helped direct the alkyl chains to wrapping orientations, most likely even in the solution phase. The asymmetric environment, arising both from an sp2-carbon wall and wrapping alkyl chains around the encapsulated fullerenes, is of great interest for its effect exerted on the dynamic motions of the guest. The forced orientations of alkyl chains, on the other hand, should accompany a large entropy cost for the association, which has indeed been observed. The favorable entropy contribution that was observed in the shorter [4]CC peapod consequently diminishes in the longer [4]CA peapod.34 Molecular design at the edge of tubular molecules should thus be important for enabling synergetic and favorable contributions of enthalpy and entropy. The structural and thermodynamic bases obtained in this study should also be useful for exploring the solution-phase method for the preparation of infinite SWNT peapods. Consideration of the molecular structures at the edge, for instance, may be important for further development.35,36Experimental section
Materials
The tubular molecules, (P)-(12,8)-[4]CA and (P)-(12,8)-[4]CC, were synthesized following the methods reported in the literature,9,14 and the molar amounts of specimens were determined by combustion elemental analysis. Fullerenes, C60 and C70, were purchased from Kanto and Aldrich, respectively.Physical measurements and instrumentation
The experiments were performed following the methods reported in the literature.11 Fluorescence spectra were recorded on a Hitachi High-Tech F7000 spectrometer equipped with a thermostatic cell holder and a stirrer, UV-vis spectra were recorded on a JASCO V-670 spectrophotometer equipped with a JASCO ETC-717 temperature controller, and NMR spectra were recorded on a Bruker AVANCE 400 (400 MHz for 1H) or JEOL ECA-600 (600 MHz for 1H) spectrometer. ITC analysis was performed using a GE Healthcare MicroCal iTC200 microcalorimeter.Preparation of (P)-(12,8)-[4]CA⊃C60 for NMR analysis
A solution of the molecular peapod, (P)-(12,8)-[4]CA⊃C60, for 1H NMR analysis was prepared with (P)-(12,8)-[4]CA (8.00 mg, 4.52 μmol) and C60 (3.26 mg, 4.52 μmol) in CD2Cl2. The solution was degassed using the freeze–thaw method prior to analysis.Crystallographic analysis
A solution of the molecular peapod, (P)-(12,8)-[4]CA⊃C60 (ca. 0.5 mg), for crystallographic analysis was prepared in chloroform (ca. 0.6 mL), and ethanol was introduced as a poor solvent. The solution was left at 25 °C for 3 days in a loosely sealed vial to afford a single crystal. A single crystal was mounted on a thin polymer tip with cryoprotectant oil and frozen at −178 °C via flash-cooling. The diffraction analysis of a single crystal with a synchrotron X-ray source was conducted at −178 °C at the beamline BL-1A at the KEK Photon Factory using a diffractometer equipped with a Dectris PILATUS 2M-F PAD detector. The collected diffraction data were processed with the HKL2000 software program.37 The structure was solved using the charge-flipping method38 and refined by full-matrix least-squares on F2 using the SHELX program suite39 running on the Yadokari-XG 2009 software program.40 In the refinements, fullerene molecules were treated as rigid body models and restrained by SIMU, and alkyl groups and solvent molecules were restrained by SIMU, DFIX, and DANG. The non-hydrogen atoms were analyzed anisotropically, and hydrogen atoms were input at calculated positions and refined with a riding model. Due to disordering solvents, the electron density distributed to some solvent molecules was not properly modeled, and the structures were refined without these solvents using the PLATON squeeze technique.41,42 The details of the crystal data are summarized in Table S2.‡Theoretical calculations
The Gaussian 09 program suite was used,43 and the semiempirical calculations for the scan analysis were performed using the PM3 method.44Acknowledgements
This study was partly supported by KAKENHI (24241036, 25107708, 25102007). We thank Clariant Japan for the generous gift of Pigment Red 168 and Photon Factory KEK (Research 2013G640) for the use of the X-ray diffraction instruments. T.M. thanks JSPS for a predoctoral fellowship. We thank Dr S. Hitosugi (Tohoku Univ.), Prof. M. Kotani (Tohoku Univ.) and Prof. H. Naito (Nagoya Univ.) for helpful discussion.Notes and references
- B. W. Smith, M. Monthioux and D. E. Luzzi, Nature, 1998, 396, 323–324 CrossRef CAS; I. V. Krive, R. I. Shekhter and M. Jonson, Low Temp. Phys., 2006, 32, 1171–1194 CrossRef; M. Monthioux, Carbon, 2002, 40, 1809–1823 CrossRef; S. Iijima, Phys. B, 2002, 323, 1–5 CrossRef; A. de Juan and E. M. Pérez, Nanoscale, 2013, 5, 7141–7148 RSC.
- F. G. Klärner and T. Schrader, Acc. Chem. Res., 2013, 46, 967–978 CrossRef CAS PubMed; L. M. Salonen, M. Ellermann and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 4808–4842 CrossRef PubMed; J. W. Steed and J. L. Atwood, Supramolecular Chemistry, John Wiley & Sons, New York, 2nd edn, 2009 Search PubMed.
- J. Cumings and A. Zettl, Science, 2000, 289, 602–604 CrossRef CAS PubMed; Z. Liu, K. Yanagi, K. Suenaga, H. Kataura and S. Iijima, Nat. Nanotechnol., 2007, 2, 422–425 CrossRef PubMed; N. Solin, M. Koshino, T. Tanaka, S. Takenaga, H. Kataura, H. Isobe and E. Nakamura, Chem. Lett., 2007, 36, 1208–1209 CrossRef; M. Koshino, N. Solin, T. Tanaka, H. Isobe and E. Nakamura, Nat. Nanotechnol., 2008, 3, 595–597 CrossRef PubMed.
- E. R. Kay, D. A. Leigh and F. Zerbetto, Angew. Chem., Int. Ed., 2006, 46, 72–191 CrossRef PubMed.
- M. Yudasaka, K. Ajima, K. Suenaga, T. Ichihashi, A. Hashimoto and S. Iijima, Chem. Phys. Lett., 2003, 380, 42–46 CrossRef CAS; T. W. Chamberlain, A. M. Popov, A. A. Knizhnik, G. E. Samoilov and A. N. Khlobystov, ACS Nano, 2010, 4, 5203–5210 CrossRef PubMed.
- T. Kawase and H. Kurata, Chem. Rev., 2006, 106, 5250–5273 CrossRef CAS PubMed.
- T. Kawase, K. Tanaka, N. Fujiwara, H. R. Darabi and M. Oda, Angew. Chem., Int. Ed., 2003, 42, 1624–1628 CrossRef CAS PubMed; T. Kawase, K. Tanaka, Y. Seirai, N. Shiono and M. Oda, Angew. Chem., Int. Ed., 2003, 42, 5597–5600 CrossRef PubMed; T. Kawase, N. Fujiwara, M. Tsutumi, M. Oda, Y. Maeda, T. Wakahara and T. Akasaka, Angew. Chem., Int. Ed., 2004, 43, 5060–5062 CrossRef PubMed.
- T. Iwamoto, Y. Watanabe, T. Sadahiro, T. Haino and S. Yamago, Angew. Chem., Int. Ed., 2011, 50, 8342–8344 CrossRef CAS PubMed; T. Iwamoto, Y. Watanabe, H. Takaya, T. Haino, N. Yasuda and S. Yamago, Chem.–Eur. J., 2013, 46, 6777–6785 Search PubMed; J. Xia, J. W. Bacon and R. Jasti, Chem. Sci., 2012, 3, 3018–3021 RSC; Y. Nakanishi, H. Omachi, S. Matsuura, Y. Miyata, R. Kitaura, Y. Segawa, K. Itami and H. Shinohara, Angew. Chem., Int. Ed., 2014, 53, 3102–3106 CrossRef PubMed.
- S. Hitosugi, W. Nakanishi, T. Yamasaki and H. Isobe, Nat. Commun., 2011, 2 DOI:10.1038/ncomms1505; S. Hitosugi, W. Nakanishi and H. Isobe, Chem.–Asian J., 2012, 7, 1550–1552 CrossRef CAS PubMed; S. Hitosugi, T. Yamasaki and H. Isobe, J. Am. Chem. Soc., 2012, 134, 12442–12445 CrossRef PubMed.
- T. Matsuno, H. Naito, S. Hitosugi, S. Sato, M. Kotani and H. Isobe, Pure Appl. Chem., 2014, 86, 489–495 CrossRef CAS.
- H. Isobe, S. Hitosugi, T. Yamasaki and R. Iizuka, Chem. Sci., 2013, 4, 1293–1297 RSC.
- S. Hitosugi, R. Iizuka, T. Yamasaki, R. Zhang, Y. Murata and H. Isobe, Org. Lett., 2013, 15, 3199–3201 CrossRef CAS PubMed; S. Hitosugi, K. Ohkubo, R. Iizuka, Y. Kawashima, K. Nakamura, S. Sato, H. Kono, S. Fukuzumi and H. Isobe, Org. Lett., 2014, 16, 3352–3355 CrossRef PubMed.
- S. Sato, T. Yamasaki and H. Isobe, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8374–8379 CrossRef CAS PubMed.
- T. Matsuno, S. Kamata, S. Hitosugi and H. Isobe, Chem. Sci., 2013, 4, 3179–3183 RSC.
- D. K. Ryan and J. H. Weber, Anal. Chem., 1982, 54, 986–990 CrossRef CAS; C. L. D. Gibb and B. C. Gibb, The Thermodynamics of Molecular Recognition, in Supramolecular Chemistry: from Molecules to Nanomaterials, ed. J. W. Steed and P. A. Gale, Wiley, Chichester, 2012, vol. 1, pp. 45–65 Search PubMed.
- M. Zheng, F. Bai, F. Li, Y. Li and D. Zhu, J. Appl. Polym. Sci., 1998, 70, 599–603 CrossRef CAS.
- We noticed the presence of a minute amount of solvent in [4]CA/[4]CC specimens, and the concentration, molar absorption coefficients and association constants were corrected by using the exact molar amount estimated from the combustion elemental analysis of the specimens. In this study, all the data for [4]CC peapods was corrected, albeit slightly, from the previous values (ref. 11; see Table S1‡).
- E. M. Pérez and N. Martín, Chem. Soc. Rev., 2008, 37, 1512–1519 RSC.
- N. Komatsu, Jpn. J. Appl. Phys., 2010, 49, 02BC01 Search PubMed.
- M. F. Sanner and A. J. Olson, Biopolymers, 1996, 38, 305–320 CrossRef CAS PubMed.
- Molecular graphics and overlay analyses were performed with the UCSF Chimera package (v. 1.9). Chimera is developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco (supported by NIGMS P41-GM103311). E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- For instance, see: http://mathworld.wolfram.com/TruncatedIcosahedron.html.
- The dihedral angles at C5a–C6–C1′–C2′ were measured for all the structures including the disorders and were −76.16°, −80.04°, −80.32°, −81.82°, −81.94°, −82.55°, −84.42, −82.71°, −83.19°, −83.53°, −84.24°, −84.50°, −84.67°, −85.92°, −86.49°, −88.38° and −89.51°.
- The dihedral angles at C5–C6–C1′–C2′ were 86.64°, 85.87°, 81.64°, 78.09°, 62.95°, 3.23°, −111.53° and −112.86. Because the dihedral angles are measured with (M)-isomer, the pointing directions of the alkyl chains are opposite. The positive values indicate the inner directions, and negative values indicate the outer directions.
- J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 627–668 CrossRef PubMed.
- S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, CrystalExplorer, version 3.1.1, University of Western Australia, 2012 Search PubMed.
- The length index (tf) is 2.45 and 1.66, and the atom-filling rate is 85% and 100% for (12,8)-[4]CA and (12,8)-[4]CC, respectively. See ref. 10 for the details.
- See also Fig. S8‡ for spectra of vacant host.
- Albeit qualitatively, theoretical GIAO calculations of resonances at the PM3//B3LYP/STO-3G level of theory for the 1′-methylene protons also supported this conclusion. Proton resonances were calculated with inner and outer conformers for [4]CA and with inner, in-plane and outer conformers for [4]CC, and the Boltzmann-weighted average resonances were estimated to afford the resonances at 3.94 and 3.73 ppm for [4]CA and 3.44 ppm and 2.90 ppm for [4]CC. The difference of upfield and downfield 1′-resonances in chemical shifts (Δδ) thus resulted in 0.21 ppm for [4]CA and 0.54 ppm for [4]CC. This result qualitatively matched with the experimental observations where a difference in the 1′-resonaces was larger for [4]CC (Δδ = 0.23 ppm) than that of [4]CA (Δδ ∼ 0 ppm).
- For GIAO calculations, see: J. R. Cheeseman, G. W. Trucks, T. A. Keith and M. J. Frisch, J. Chem. Phys., 1996, 104, 5497–5509 CrossRef CAS.
- M. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 13873–13900 RSC.
- Note, however, that the CH–π interactions in this system may be suppressed by competition with solvent molecules with similar interactions. See ref. 31 and J. W. Steed, P. C. Junk, J. L. Atwood, M. J. Barnes, C. L. Raston and R. S. Burkhalter, J. Am. Chem. Soc., 1994, 116, 10346–10347 CrossRef CAS.
- The first reduction potential of C60 in the [4]CA peapod appeared at −0.83 V, whereas those of [4]CC peapod and naked C60 appeared at −0.75 V and −0.42 V, respectively (ref. 12). The enhancement in the negative shift in the [4]CA peapod indicates that partial charge transfer is emphasized upon π-lengthening. The details of the electronics will be reported in due course.
- Desolvation of oDCB from C60 should accompany a favorable entropy change of +54.6 cal mol−1 K−1 A. M. Kolker, N. I. Islamova, N. V. Avramenko and A. V. Kozlov, J. Mol. Liquids, 2007, 131–132, 95–100 CrossRef CAS Considering that ca. 28% of the C60 surface was desolvated by encapsulation in the [4]CC peapod, we may expect an entropy contribution of 15 cal mol K−1 for the association. The experimental value of ΔS = 18 cal mol−1 K−1 may largely be attributed to this desolvation effect.
- A. Hirsch, Angew. Chem., Int. Ed., 2002, 41, 1853–1859 CrossRef CAS.
- L. Tang and X. Yang, J. Phys. Chem. C, 2012, 116, 11783–11791 CAS.
- Z. Otwinowski and W. Minor, Processing of X-ray Diffraction Data Collected in Oscillation Mode, in Methods in Enzymology, Part A, Macromolecular Crystallography, Academic Press, New York, 1997, vol. 276, pp. 307–326 Search PubMed.
- L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786–790 CrossRef CAS.
- G. M. Sheldrick and T. R. Schneider, SHELXL: High-resolution Refinement, in Macromolec. Crystal. B Book Series: Methods in Enzymology, Elsevier, Amsterdam, 1997, vol. 277, pp. 319–343 Search PubMed.
- C. Kabuto, S. Akine, T. Nemoto and E. Kwon, J. Crystallogr. Soc. Jpn., 2009, 51, 218–224 CrossRef.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- P. van der Sluis and A. L. Spek, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46, 194–201 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta Jr, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- J. J. P. Stewart, J. Comput. Chem., 1989, 10, 209–220 CrossRef CAS; J. J. P. Stewart, J. Comput. Chem., 1989, 10, 221–264 CrossRef.
Footnotes |
| † Dedicated to Professor Iwao Ojima on the occasion of his 70th birthday. |
| ‡ Electronic supplementary information (ESI) available: Supplementary figures and tables. CCDC 1018830. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4sc02812k |
| This journal is © The Royal Society of Chemistry 2015 |