Expert vs. novice: approaches used by chemists when solving open-ended problems
C. A.
Randles
a and
T. L.
Overton
*b
aChemistry Department, University of Hull, Cottingham Road, Hull, HU6 7RX, UK
bSchool of Chemistry, Monash University, Victoria 3800, Australia. E-mail: tina.overton@monash.edu
First published on 7th July 2015
Abstract
This paper describes the results of a qualitative study using ground theory to investigate the different approaches used by chemists when answering open-ended problems. The study involved undergraduate, industrialist and academic participants who individually answered three open-ended problems using a think aloud protocol. Open-ended problems are defined here as problems where not all the required data are given, where there is no one single possible strategy and there is no single correct answer to the problem. Analysis of the qualitative data identified a limited number of different approaches used to solve open-ended problems. These approaches were applied to individual participants and these were collated to identify approaches used by each group. The relative quality of solutions developed by each group was also analysed. Analysis showed that undergraduates adopted a greater number of novice-like approaches and produced poorest quality solutions, academics exhibited expert-like approaches and produced the highest quality solutions, whilst industrial chemist's approaches are described as transitional.
Introduction
Krulik and Rudnick described a problem as “a situation quantitative or otherwise, that confronts an individual or group of individuals, that requires resolution, and for which the individuals see no apparent or obvious means or path to obtaining a solution” (Krulik and Rudnick, 1987). Hayes defined a problem as “whenever there is a gap between where you are now and where you want to be and you don't know how to find a way to cross that gap, you have a problem” (Hayes, 2009). Therefore, problem solving can be described as “the means by which an individual uses previously acquired knowledge, skills and understanding to satisfy the demands of an unfamiliar situation. The student must synthesise what he or she has learned, and apply it to a new and different situation” (Krulik and Rudnick, 1987). Generally, it is accepted that a problem must be unfamiliar in some way, demand cognitive processing and that it is the unfamiliarity which separates problem solving from an exercise. So is a unified theory of problem solving possible and is it possible to understand the strategies employed in problem solving? Bodner believes “it is possible to construct a unified theory of problem solving. I [he] have done so… Unfortunately, I'm afraid our unified theories will differ significantly from one another”(Bodner, 1991a).Furthermore, there is disagreement in the literature on the definition of the term “problem”. Some believe that exercises are a subset of problems, whereas others believe that exercises and problems are mutually exclusive, differing in difficulty and complexity (Smith, 1988). A further complication is whether solely algorithmic processes can be used in solving problems and whether using solely algorithmic processes demonstrates conceptual understanding. The types of problems used in examinations have been found to be predominantly algorithmic in nature because the questions require the application of familiar methods, altering only the data input (Bennett, 2004). However, “the existence of a problem implies that the individual is confronted by something he or she does not recognize, and to which he or she cannot merely apply a model. A problem will no longer be a problem once it can easily be solved by algorithms that have been previously learned” (Krulik and Rudnick, 1987). It could be the presence of well-defined algorithms combined with prior knowledge that results in a problem turning into an exercise (Johnstone and El-Banna, 1986). With this definition in mind one may eliminate from problem solving any task that can be solved solely through application of an algorithm, as this demonstrates only operational processes rather than scientific reasoning which, has been previously identified as a gap between algorithmic and conceptual problem solving ability (Cracolice et al., 2008). This is supported by Nurrenbern and Pickering who state being able to solve algorithmic problems is not equivalent to demonstrating conceptual understanding, demonstrating that a gap between algorithmic and conceptual problem solving ability exists (Nurrenbern and Pickering, 1987). This statement is supported by Bennett who suggests that many calculating-type questions in examinations in higher education are masquerading as problem solving, as examinations predominantly include ‘easy to set, easy to mark’ questions. Bennett further states that examinations focus on regurgitating of information or ‘soft’ calculations where the questions are the same year to year altering only the input data (Bennett, 2004). A report released by the Scottish Qualifications Authority has identified the need for open-ended problems to be embedded into the national examination process. While algorithmic/recall questions were to remain the mainstay of the examination process, open-ended problems were to be incorporated in order to “promote and reward creativity and analytical thinking” (Education Scotland, 2010).
In 1993 Johnstone attempted to subcategorize the different types of problems encountered in science education based around altering three different variables. The three variables were the data in a problem, the method of tackling the problem and the outcomes/goals of the problem. As a result of altering the three variables, Johnstone identified eight possible types of problem. The first, type 1, with given data, familiar method and closed outcomes, equates to routine exercises requiring lower order cognitive skills, whereas type 8 problems, with incomplete data, an unfamiliar method and open outcomes, resemble real life, complex problems that graduates may encounter in the work place (Johnstone, 1993). These types of problems are shown in Table 1.
| Type | Data | Methods | Outcomes | Skills |
|---|---|---|---|---|
| 1 | Given | Familiar | Given | Recall of algorithms. |
| 2 | Given | Unfamiliar | Given | Looking for parallels to unknown method. |
| 3 | Incomplete | Familiar | Given | Analysis of problem to decide what further data are required. |
| 4 | Incomplete | Unfamiliar | Given | Weighing up possible methods and deciding on data required. |
| 5 | Given | Familiar | Open | Decision making about appropriate goals. Exploration of knowledge networks. |
| 6 | Given | Unfamiliar | Open | Decisions about goals and choices of appropriate methods. Exploration of knowledge and technique networks. |
| 7 | Incomplete | Familiar | Open | Once goals have been specified, the data are seen to be incomplete. |
| 8 | Incomplete | Unfamiliar | Open | Suggestion of goals, methods, consequent need for additional data. All of the above skills. |
These descriptions of varying types of problems presented in Table 1 were designed to inform chemistry educators’ practice and to increase their awareness of different types of problems available to assess student understanding. However considering Johnstone published this table in 1993, 11 years later Bennett is still reporting that exams are centred around recall and basic mathematical manipulation (Bennett, 2004).
Greenbowe states that successful problem solvers exhibit more effective organisation, persistence, evaluate more often, and adopt heuristic and formal operations when compared against less successful problem solvers (Greenbowe, 1983). The first step used by successful problem solvers is the initial framing of the problem. This process can be achieved through imaging, inference, decision making and identification of information needed.
In addition to the aforementioned skills, representation continues to be an important component of problem solving (Greenbowe, 1983; Bodner and Domin, 2000). Hayes suggests that there are two separate modes of representation, the internal and external representation (Hayes, 2009). Internal representation is understanding the “information that has been encoded, modified and stored in the brain” (Simon and Simon, 1978). This closely represents the framing component associated with solving problems. External representation is the expression of the processed information to other people, either through drawing diagrams or writing symbols. Bodner and Domin (2000) related the modes of representation as they relate to problem solvers, describing internal representation as “the way in which [the] problem solver stores the internal components of the problem in his or her mind.” External representation was defined by Bodner and Domin as the “physical manifestation of this information.” They state that the characteristic differences between successful and unsuccessful problem solvers are the number of representations that they can apply to the problem. They further claim that visual representation, through the use of models and diagrams, can improve performance in problem solving. Returning to Greenbowe's study, it could be possible that there is a link between conceptual understanding and problem representation, where a synergy exists with one effecting the other (Reid and Yang, 2002).
The attributes required to solve algorithmic and open-ended problems are thought to be different. Surif et al. (2014) looked at the differences in solving algorithmic, conceptual and open-ended problems. In this study Surif et al. identified that 96% of participants engaged in algorithmic problems were successful, whereas only 14% of participants who engaged in open-ended problems were successful. Surif et al. state that the lack of success with the open-ended problem solving was probably as a result of the inability to transfer knowledge to new situations. The algorithmic problems, however, only required participants to recall a formula and input the required values. Further analysis through partial eta squared test (ηp2 = 0.912) showed that variations in achievement were based on style of question. This supports the proposal that open-ended problems and algorithmic questions are assessing different areas of understanding.
In a study of non-algorithmic problem solving in chemistry, Tsaparlis (2005) considered field dependence to be a good predictor of problem solving success. Overton and Potter have previously suggested that working memory, m-capacity and field dependence all effect student achievements in solving open-ended problems and, in particular, found correlations between field dependence and ability in open-ended problem solving (Overton and Potter, 2011). They further reported a correlation between student success at algorithmic problem solving and final degree scores, but no such correlation existed between success in open-ended problem solving and degree scores. This would indicate that different sets of skills are required for solving algorithmic and open-ended problems. Additionally, they stated that attitudes in student populations shift more positively for problem solving, when the problems are open-ended and context rich, as opposed to algorithmic in nature. In a further study by Overton and Potter they identified three separate types of problem solvers; expert, novice and transitional (Overton et al., 2013). They state that the novice participants adopt mainly negative and unhelpful approaches, unable to identify what is being asked in the question and what data they require. This resulted in an unscientific approach which was grounded solely in algorithms. The expert participants were identified as using more positive approaches, such as making appropriate estimations, evaluation of solutions and developing a logical scientific approach. These two characteristics resemble those categories of problem solver identified by Walsh et al. as ‘no clear approach’ (Novice) and ‘scientific approach’ (Expert) who tackled algorithmic physics problems (Walsh et al., 2007).
What makes an expert problem solver remains elusive and, in particular, understanding what an expert does that makes them more successful at solving problems than novices. Larkin et al., whilst studying physics problem solvers, postulated that expert problem solvers are considerably faster thinking and more accurate in their processes than novice problem solvers (Larkin et al., 1980). Expert physics problem solvers are said to have “physical intuition,” where little deliberation is spent on attacking the problem, with the appropriate strategy “just occurring” to them. Although it is recognised that specific subject knowledge is a prerequisite to expert skill, it is the retrieval process of that knowledge and patterns of recognition which guide the expert more rapidly to relevant parts of the stored knowledge. It is this formation of knowledge or complex schemata that guide an expert through the problem's interpretation and solution, resulting in terminology such as physical intuition. Although Larkin et al. focused on physics problem solvers, the underlying characteristic is that the knowledge base of the expert transforms the complex problem into an exercise because the processes are more familiar to them. This is further supported by Herron and Greenbowe who state that successful problem solvers have a good command of the facts required to answer the problem, but are also able to construct appropriate representations and employ logical strategies which connect elements of the problem (Herron and GreenBowe, 1986). They further identified that successful problem solvers used a variety of ‘verification’ or evaluation processes to ensure that representations are consistent with the problem or the task, the solution is logical and that the problem solved is the problem they have been asked to solve. Camacho and Good conducted a cross spectrum study including participants from high school, undergraduates, PhD students and academic members of faculty asking them to solve chemical equilibrium problems (Camacho and Good, 1989). They noticed that there was no absolute category of novice and expert, but more a continuum of expertise. The study further categorised the behaviours used by more successful participants when tackling their problems which included: at the start individuals read the question completely before beginning to solve the problem and frame the objectives. During the process they used appropriate representations and didn't use formulas until they were required, used multiple components without using trial and error and answering the problem in a logical manner. Whilst tackling the problem individuals evaluated their work and were not easily confused by the process.
There are many different models associated with the constituent stages of problem solving, although most submit to a multiple stage approach (Dewey, 1933; Krulik and Rudnick, 1987; Polya, 1988). Polya suggested that solving problems was a four stage process. The first stage was to try and understand the problem. Secondly, a plan was devised, followed by carrying out of the plan, before final evaluation and reflection. Bodner questions the discrete separation of stages as suggested by Polya. Bodner concedes that a considerable amount of time is spent on ‘understanding the problem,’ but questions the legitimacy of a single separate stage of devising a plan prior to solving the problem (Bodner, 1987). Bodner suggests a plan for solving the problem is founded through continual revision of the process, by “gradually exploring or playing with the question,” to get closer to the answer. A more extensive model suggested for problem solving has been proposed by Wheatley (Wheatley, 1984) which demonstrated a chaotic, non-linear and iterative approach which has been identified by some as resembling research behaviour. Exercises are often linear processes with a clearly defined path from start to finish, whereas problem solving is a cyclic, reflective and at times an irrational process (Bodner, 1991b). Consensus appears that the model for problem solving is a multistage process, initialised with an “understand the problem,” and concluding with a “reflection” component (Carson, 2007). The overall objective of educational problems is that problem solving develops theory and practice (Krulik and Rudnick, 1987), creativity (Fredriksen, 1984; Slavin, 1997), enhances a complete and organized knowledge base and develops transferable skills in order demonstrate conceptual knowledge to others (Norman and Schmidt, 1992; Stepien et al., 1993; Gallagher et al., 1994; Hmelo and Ferrari, 1997; Lunyk-Child et al., 2001).
Reports published on the business readiness of chemistry graduates state that they are entering the workplace lacking necessary transferable skills and professional skills such as communication and problem solving (Ashraf et al., 2011; Rami Ibo, 2014). One report states that although graduates have problem solving skills they lack the ability to take risks, focusing on ‘facts, figures and balances.’ (IER Report, 2008) However, although this report identifies that the graduates have problem solving skills, the skills identified in the report are more akin to those required for algorithmic problem solving. As stated earlier, Bennett surmises that assessments are based on ‘easy to set, easy to mark’ questions. Some further research suggests that many chemistry curricula at universities are more focused towards teaching discipline specific skills (Bridgestock, 2009; Herok et al., 2013) and future academics rather than the skills necessary for industry. (Runquist and Kerr, 2005; Wieman, 2007; Wood, 2009; Varsavsky et al., 2014) However, to adapt these curricula so that graduates leave with enhanced transferrable skills, further research and understanding into how students think within their subject domain and within transferable skills is required. Currently, there is insufficient known about the approaches chemistry students use to answer open-ended problems, with most research focusing on algorithmic problem solving perspectives; presumably, because as Bennett, suggests, they are easy to mark and, as such, easier to research. The aim of this study was to investigate the approaches used by undergraduate chemistry students, industrial partners and academic staff participants when solving open-ended problems and ascertain whether any differences emerged.
Method
This study used a qualitative research approach in which the data were collected through think aloud sessions and analysed for emergent themes. Themes were given codes and participant data were then ‘coded’ to produce an individual profiles. Cohort profiles were then produced by combining individual profiles. The quality of the solutions was evaluated using a semi-quantitative scale.The participants in this study were chemistry undergraduates, chemistry academic staff and graduate chemists working in industry. The 17 chemistry undergraduate participants were level 4 students (first year of study in England and second year of study in Scotland due to the different education systems) who were studying chemistry full time. The chemistry undergraduate participants were drawn from two institutions in the United Kingdom. The eight academic members of staff were all chemistry staff drawn from five universities in the United Kingdom. The chemistry academic staff participants all had at least ten years of academic experience. The six graduate chemist participants were University of Hull chemistry graduates who had at least ten years of experience working in the chemical industry in the United Kingdom. All of the participants had volunteered to take part in the study following an open call for participants within their selected groups. No discrimination or selection process was made based on gender, ethnic background or pre university academic achievements, except that all undergraduate participants should be level 4, and all academic and industrialists should be chemistry graduates. The study involved participants solving three open-ended problems, and data captured through a think aloud protocol (Ericsson and Simon, 1993).
The problems used were classified as open-ended. Open-ended problems are defined here as problems in which the participants are not provided with all the data they need, there is no single method or strategy that will lead to an answer and there is no single correct solution. The problems each participant answered were:
1. How many toilets do you need at a music festival?
2. How far does a car travel before a one atom layer is worn off the tyres?
3. What is the mass of the Earth's atmosphere?
The first question is unfamiliar, but with no scientific knowledge required. This question was used to allow the participants to become comfortable with the style of problem and a think aloud protocol. The second and third questions require greater scientific knowledge and were used to ascertain what approaches participants used when tackling scientific open-ended problems. A similar style of questions has been used at the University of Hull with second year chemistry undergraduates for eight years as part of their chemical professional skills module. The eight year piloting of similar styled questions to those used within this study has shown anecdotally that these types of problems elicit problem solving. The research team felt that a new selection of questions were required to ensure that methods were not openly available to students prior to participation in the study.
A think aloud protocol involves the participant vocalising their thought processes as they engage with a particular task, which in this study was tackling open-ended problems. Use of think aloud interviews during this study allowed the investigator to observe and capture approaches that undergraduates used when they encountered open-ended problems. Think aloud collection methods were created in the 1980s and early 1990s for use in studies of cognitive processing in psychology (Ericsson and Simon, 1993), education and cognitive sciences, particularly in disciplines requiring working memory (Jääskeläinen, 2010). However, the method is incapable of identifying unconscious processes. It should also be recognised that, due to the high cognitive load brought about through verbalisation, researchers are only provided with a glimpse of the cognitive processing rather than a “complete account” (Jääskeläinen, 2010). Kuusela and Paul (2000) suggest two separate forms of think aloud protocol, the first being concurrent think aloud where the data are collected during decision making. The second process is called retrospective think aloud protocol where the participants reflect on the decisions they have made and reasons for having done so (Kuusela and Paul, 2000). The participants in this study were encouraged to vocalise their thoughts whilst answering the problems and write as much information as possible which was concurrent think aloud. This was chosen because concurrent think aloud provides the researcher with greater insight into the decision making process, whereas retrospective think aloud generally focuses on the final outcome, in this case the problem solution (Kuusela and Paul, 2000). Care was taken to minimise the impact of the researcher upon the participant to reduce the risk of atypical behaviour in terms of the participant's chosen problem solving process. The participants were able to explore avenues of enquiry they wanted to follow with the researcher providing none-leading prompts to the participant when the think aloud process stalled e.g., “What are you thinking at the moment?” and “could you explain why you thought that?”
The data from the think aloud protocol were captured using a LiveScribe Echo device which captures both audio and visual data in synchronicity using Anoto digital paper. This capture method allows the researcher to return to the data and analyse what was being said and done at particular points in the solution.
At the start of each think aloud session the participants were informed of the intentions of the research and the following guidelines issued to each individual:
• There is no single correct method to solve these problems.
• There is no single correct answer.
• Not all the information has been provided. However, you may ask for specific pieces of information. If the information asked for is on a pre-assigned information sheet the information will be provided. (The preassigned sheet contained information that the participant would not be expected to know or reasonably estimate. For example, the depth of the atmosphere.)
• Lack of information of the pre-assigned sheet does not mean the participant's strategy is incorrect.
• Access to a calculator is allowed, but access to smart devices and the internet are prohibited.
• A maximum of 20 minutes is allowed to answer each question.
Each participant was provided with the opportunity to ask further questions before the think aloud session commenced to ensure that they understood the task required of them.
Ethical approval for this study was obtained through the University of Hull's ethical research approval panel. Participants were notified about how and what data would be obtained and that their participation was voluntary. They were informed that they were able to withdraw at any time without providing a reason and without detrimental treatment or service of any kind. Participants were also informed that where quotes were used, the individual would remain anonymous and would be referred to only by a code. The data were stored on encrypted storage devices and paper data were stored in a lockable cupboard and office. Data were only provided to members of the research team, and the identities of the individuals was only known to one individual throughout the process to maintain anonymity. Each participant's LiveScribe pencast was transcribed to ensure that no details were overlooked. All the data were initially analysed to establish a set of thematic events emerging from the data. The process of analysis used a five stage process.
The data and audio recordings were read and notes taken about the overall strategy employed by the participants. The strategy is the overall method used by the participant to solve the open-ended problem, such as calculating the load capacity of the toilets.
The transcripts and audio files were read and notes taken of any initial themes emerging from the data, e.g., little evaluation, becomes confused etc.
Having reviewed the data for the first time, the text and audio files were studied again in greater detail to establish whether there were any hidden themes which the initial stage had failed to identify. Key words were highlighted which supported these emerging themes.
The next stage was to review all the identified emergent themes and eliminate some of them using a redundancy approach where similar themes were combined together.
The final themes were then given codes ready for the subsequent coding processes.
Using this approach the themes emerged from the data rather than being identified via testing a hypothesis. Once the set of codes had been developed and the definitions provided, the individual transcripts and audio recordings were analysed and codes assigned each time one of the themes appeared. To ensure validity of this coding process four individual researchers undertook inter-rater coding. Inter-rater coding is used to establish the consistency of findings from data analysis performed by two or more researchers (Armstrong et al., 1997). This ensured that the researchers were coding themes correctly and the definitions for the codes were robust. The research group used four coders (the two authors of this paper, and a further two coders who were academics with experience of qualitative research), who took two randomly selected participant transcripts. Independently, the four coders assigned codes to the thematic events they observed using the definitions created in the code development stage. It was seen that when using the definitions for the codes, the researchers agreed with their assignment 85% of the time, demonstrating that the coding process was sufficiently robust.
Each participant's transcript was coded for where the thematic events occurred and tallied to see how many times an individual participant used that approach. Once the individuals' transcripts had been coded and tallied a cohort profile was produced by summing all participants' scores. These were visualised by plotting them as radar diagrams.
Following coding of the approaches used for each problem, each script was analysed for the quality of the solution and the success of the solution was evaluated. The success of the solution was categorised as red, amber or green (traffic lighted). Each of these categories had their own definition:
• Red: poor answer with little to no demonstration of strategy development.
• Amber: a good strategy developed but leads to a poor answer, or a good answer produced but no evidence of a specific strategy.
• Green: a good strategy developed with a good answer.
The term ‘answer’ applies to the final outcome of the solution and whether it is realistic or near to a ‘correct’ answer. The term ‘strategy’ refers to the model used to arrive at an answer. For example, a green response for the first question might employ a strategy based around how long an average festival-goer spends in a toilet per day and produce an answer of a few thousand portable toilets. An amber response may use the same strategy but come up with an answer of a few tens or many thousands of toilets. The traffic light system was used because detailed numerical scores are difficult to assign because of the variety of strategies used and range of solutions produced. To help facilitate comparisons more easily a simple numerical scale was also used in which a score was given to each traffic light colour. Red = 1, Amber = 2 and Green = 3. Using a combination of colours and numbers meant that comparisons could be more easily made.
Results
Table 2 summarises the approaches and associated codes identified from the analysis of the transcripts and pencasts using the five step process of analysis. The data shown in Tables 3 and 4 were obtained from coding of the individual pencasts and transcripts and shows the range of approaches used by each individual. The values shown in the tables are the percentage values based on the total number of codes collected for each participant. The most prominent approaches used by each participant are italicized.| Code | Definition | Example quote |
|---|---|---|
| IIN+ | The participant identified a specific piece of information they think they need. | “how many people are attending the music festival?” |
| IIN− | The participant fails to identify a specific piece of data they need. | |
| A&E+ | The participant makes realistic estimations relating to numerical values of their chosen strategy, approximations are made to ensure ease of calculations. | “The size of a car tyre is about… 30 cm???” |
| A&E− | The participant fails to make realistic estimations, or is unable to estimate required values for their strategy. Fails to make approximate values to ease calculations. | “Ok so I guess there are about 78 moles of nitrogen and 22 moles of oxygen in the atmosphere.” |
| ALG+ | The participant uses calculations and/or equations to solve the problem. | Writes “2πr” |
| ALG− | The participant does not use calculations and/or equations to solve the problem. | “I guess it is about one revolution of a tyre” |
| EVA+ | The participant evaluates their strategy and/or their final answer. | “So I used, so I calculated that and it gave me the area of one point one three times ten to the fourteen metres squared, I think that seems small. Very small actually but then I thought obviously that maybe the calculations were ok.” |
| EVA− | The participant does not evaluate either the strategy or answer. | |
| IPF+ | The participant reflects about what is being asked in the problem. | “Ok, so when you sell the tickets you're gonna know in advance sort of how many sorts of toilets you are going to need for those people. So I think also you need a sufficient amount for the people.” |
| IPF− | The participant does not reflect on the problem creating uncertainty in how to proceed. | |
| DAS+ | The participant develops a clear strategy which allows them to solve the problem. | “I want to do… the volume of a sphere which is the size of obviously the radius of the Earth plus the height of the atmosphere and then take off the volume of the Earth in the middle.” |
| DAS− | The participant does not develop a suitable strategy to solve the problem. | |
| NDIS+ | The participant does not become distracted by additional details. | |
| NDIS− | The student becomes distracted by extra details. | “that's yeah, atmosphere. that would include everything that wouldn't it… everything structural wise.” |
| LSA+ | The participant employs a logically progressive strategy and/or grounded in scientific reasoning. | Manifests with multiple stages to answer the question. |
| LSA− | The participant employs an illogical strategy, with little grounding in scientific reasoning. | “So just guess or estimate?... so about one hundred and fifty.” |
| CC+ | The participant shows no signs of lack of confidence, or becoming confused. | |
| CCP− | The participant becomes confused with how to tackle the problem. | “I don't know I have to work out a temperature but I'm not sure if that's the right equation.” |
| CCA− | The participant becomes confused with their own abilities and knowledge. | “I can't remember which way round it is (converting 1 atmosphere to pascals).” |
| Participant % distribution | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Code | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| IIN+ | 26 | 24 | 18 | 28 | 15 | 12 | 31 | 22 | 22 | 33 | 23 | 23 | 29 | 26 | 28 | 31 | 29 |
| A&E+ | 4 | 10 | 6 | 6 | 15 | 6 | 9 | 12 | 6 | 7 | 4 | 4 | 9 | 8 | 3 | 6 | 8 |
| ALG+ | 15 | 13 | 12 | 10 | 17 | 6 | 13 | 25 | 10 | 15 | 29 | 26 | 12 | 16 | 12 | 8 | 18 |
| EVA+ | 7 | 5 | 0 | 3 | 7 | 0 | 7 | 11 | 0 | 0 | 3 | 1 | 3 | 2 | 4 | 2 | 6 |
| IPF+ | 11 | 13 | 13 | 16 | 13 | 18 | 7 | 4 | 14 | 7 | 14 | 6 | 5 | 14 | 10 | 9 | 8 |
| DAS+ | 4 | 3 | 4 | 3 | 8 | 0 | 7 | 7 | 6 | 7 | 6 | 4 | 3 | 6 | 6 | 4 | 6 |
| NDIS+ | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 |
| LSA+ | 0 | 1 | 0 | 1 | 3 | 0 | 2 | 0 | 4 | 0 | 3 | 0 | 3 | 2 | 3 | 2 | 4 |
| IIN− | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 |
| A&E− | 9 | 0 | 4 | 4 | 3 | 0 | 0 | 0 | 0 | 2 | 1 | 1 | 5 | 2 | 1 | 2 | 2 |
| ALG− | 2 | 0 | 2 | 1 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 4 | 0 |
| EVA− | 2 | 1 | 6 | 3 | 0 | 6 | 5 | 2 | 6 | 7 | 3 | 1 | 2 | 4 | 1 | 4 | 0 |
| IPF− | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| DAS− | 2 | 1 | 2 | 1 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 0 |
| NDIS− | 4 | 3 | 6 | 6 | 3 | 12 | 2 | 0 | 4 | 0 | 0 | 1 | 5 | 2 | 4 | 6 | 0 |
| LSA− | 7 | 3 | 6 | 3 | 1 | 8 | 5 | 4 | 2 | 7 | 1 | 3 | 2 | 4 | 1 | 4 | 2 |
| CC+ | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 2 | 4 | 5 | 3 | 0 | 2 | 2 | 0 | 2 | 0 |
| CCP− | 7 | 13 | 19 | 10 | 11 | 6 | 5 | 9 | 20 | 10 | 6 | 21 | 11 | 8 | 18 | 6 | 10 |
| CCA− | 0 | 10 | 2 | 4 | 3 | 0 | 7 | 0 | 2 | 0 | 0 | 9 | 3 | 2 | 8 | 8 | 8 |
| Participants % distribution | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Code | E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | E9 | E10 | E11 | E12 | E13 | E14 |
| IIN+ | 19 | 8 | 32 | 23 | 15 | 20 | 19 | 29 | 25 | 19 | 18 | 14 | 28 | 19 |
| A&E+ | 6 | 8 | 7 | 13 | 9 | 13 | 12 | 3 | 8 | 7 | 6 | 7 | 0 | 9 |
| ALG+ | 17 | 8 | 5 | 3 | 9 | 20 | 8 | 7 | 11 | 15 | 13 | 21 | 10 | 17 |
| EVA+ | 15 | 6 | 5 | 3 | 11 | 7 | 12 | 3 | 8 | 6 | 4 | 10 | 4 | 5 |
| IPF+ | 15 | 12 | 7 | 13 | 9 | 5 | 8 | 5 | 16 | 13 | 18 | 12 | 25 | 21 |
| DAS+ | 6 | 4 | 7 | 8 | 6 | 7 | 5 | 10 | 4 | 6 | 6 | 3 | 1 | 4 |
| NDIS+ | 6 | 6 | 2 | 8 | 4 | 3 | 2 | 3 | 1 | 0 | 2 | 5 | 6 | 0 |
| LSA+ | 4 | 6 | 5 | 8 | 6 | 7 | 3 | 7 | 4 | 4 | 6 | 3 | 4 | 3 |
| IIN− | 0 | 4 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A&E− | 2 | 4 | 2 | 3 | 0 | 3 | 0 | 5 | 0 | 0 | 2 | 1 | 4 | 0 |
| ALG− | 0 | 4 | 2 | 5 | 2 | 0 | 0 | 5 | 1 | 4 | 0 | 0 | 2 | 0 |
| EVA− | 0 | 4 | 5 | 5 | 0 | 3 | 0 | 5 | 0 | 4 | 4 | 0 | 2 | 1 |
| IPF− | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| DAS− | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| NDIS− | 0 | 0 | 5 | 0 | 2 | 5 | 5 | 7 | 3 | 6 | 4 | 1 | 1 | 4 |
| LSA− | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 1 |
| CC+ | 2 | 0 | 2 | 8 | 2 | 7 | 0 | 5 | 0 | 4 | 0 | 0 | 1 | 1 |
| CCP− | 6 | 22 | 8 | 0 | 14 | 0 | 17 | 3 | 6 | 8 | 15 | 14 | 4 | 9 |
| CCA− | 0 | 2 | 2 | 0 | 11 | 0 | 9 | 0 | 13 | 2 | 2 | 9 | 6 | 6 |
As can be seen in Table 3, many chemistry undergraduate participants focused their approaches on identifying the information needed (IIN+), using algorithms and making calculations (ALG+) and identify and framing the problem (IPF+). The codes related to confidence and confusion have been placed at the bottom of the table as they could be described as behaviours rather than approaches. The behaviour codes occurred frequently in participant recordings. Where a participant showed bias towards one of the minus coded behaviours (CCP− & CCA−) the corresponding box was highlighted, where a participant showed no bias, whereby both codes were prominent, both boxes were highlighted. As can be seen there is a fairly even spread of participants who were confused with just the problem, and participants who were confused with their ability and the problem. Interestingly there were no participants who were just lacked confidence in their ability.
Table 4 shows the range of approaches exhibited by each of the graduate chemist participants when they were solving open-ended problems. The most prominent codes are italicized. As can be seen in Table 4 most of the participants focused their approaches on identifying the information needed (INN+), using algorithms and making calculations (ALG+) and identifying information needed (IIN+). Participants in this group can also be seen to exhibit the evaluation code, and the making approximations and estimations code. From Table 4 it can be seen that there is fairly even distribution of participants that showed confusion with the problem (CCP−) and participants who also showed a lack of confidence in their own ability (CCA−).
Table 5 shows the overall profiles of each group of participants. This table was created by combining all the occurrences for a code from every participant in each group and the percentage distribution calculated. There were 17 participants in the undergraduate group (N = 17), six industrialist participants (N = 6) and eight academic participants (N = 8). As can be observed in Table 5 the graduate chemist participant pool has been split into industrialist and academics as different profiles emerged from the data. The table further identifies primary and secondary codes within the data set. A primary code is a cluster of codes that are the most prominent to the group, and a secondary code is a cluster of codes that hold secondary prominence. Prominence is determined through groupings of codes that cluster together based on percentage distribution of approach. For example, a cluster towards the top end of their distribution, normally within 50% of the most prominent code (although not strictly set towards percentiles), would be considered the primary cluster and therefore the set of primary codes. The next cluster of codes after the primary group would be considered the secondary codes, as they represent approaches used by the group, but they are not the most prominent approaches. The use of the secondary codes was required to tease out the emerging subtle differences between the different emerging profile groups. The undergraduate profile shows that, overall, the primary codes are identifying the information needed (IIN+), using algorithms and making calculations (ALG+) and identifying and framing the problem (IPF+). The secondary codes for chemistry undergraduate students are making approximations and estimations (A&E+) and successfully developing a strategy (DAS+). For chemistry industrialist participants the overall profile shows that the primary codes are identifying the information needed (IIN+), using algorithms and making calculations (ALG+) and identifying and framing the problem (IPF+). The secondary codes for the industrialists are using approximations and estimations (A&E+) and evaluating the strategy or final solution (EVA+). As can be clearly observed in Table 5 the profiles for both undergraduate participants and industrial participants are very similar with slight elevation in the use of evaluation in the industrialist participant profile over the undergraduate participant profile. The reason for splitting the graduate participants into two separate profiles becomes apparent when we analyse the academic participants. Academic participants showed a profile where the primary codes were identifying the information needed (IIN+), making approximations and estimations (A&E+), using algorithms and making calculations (ALG+) and identifying and framing the problem (IPF+). The approaches observed showing secondary prominence in the academic participant profile are evaluating their strategy and solution (EVA+), developing a strategy (DAS+), not becoming distracted by lack of details in the question (NDIS+) and applying a logical scientific approach to their solution (LSA+). Although there is relatively little difference in primary approaches observed between undergraduate, industrialist and academic participants, it is the secondary approaches that highlight the differences between the groups. Academic participants utilise a much greater variety of approaches when solving open-ended problems when compared against industrialist participants and undergraduate participants. When we look at the behaviour codes we also observe a great similarity between undergraduate and industrialist profiles, which show they become confused with the problem and lack confidence in their own ability (CCP−, CCA−). However, the expert academic participant profile shows only confusion with the problem (CCP−) and no lack of confidence in their own ability.
| Codes | Undergraduates | Industrialists | Academics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Primary | Secondary | Primary | Secondary | Primary | Secondary | |||||||
| N | % | N | % | N | % | N | % | N | % | N | % | |
| IIN+ | 220 | 24.76 | 220 | 24.76 | 89 | 20.70 | 89 | 20.70 | 68 | 18.79 | 68 | 18.78 |
| A&E+ | 66 | 7.23 | 66 | 7.23 | 26 | 6.05 | 26 | 6.05 | 33 | 9.12 | 33 | 9.12 |
| ALG+ | 128 | 15.51 | 128 | 15.51 | 64 | 14.88 | 64 | 14.88 | 37 | 10.22 | 37 | 10.22 |
| EVA+ | 33 | 3.67 | 33 | 3.67 | 27 | 6.28 | 27 | 6.28 | 32 | 8.84 | 32 | 8.84 |
| IPF+ | 92 | 10.69 | 92 | 10.69 | 76 | 17.67 | 76 | 17.67 | 35 | 9.67 | 35 | 9.67 |
| DAS+ | 45 | 5.14 | 45 | 5.14 | 16 | 3.72 | 16 | 3.72 | 23 | 6.35 | 23 | 6.35 |
| NDIS+ | 1 | 0.42 | 1 | 0.42 | 11 | 2.56 | 11 | 2.56 | 15 | 4.14 | 15 | 4.14 |
| LSA+ | 15 | 1.78 | 15 | 1.78 | 16 | 3.72 | 16 | 3.72 | 20 | 5.52 | 20 | 5.52 |
| IIN− | 3 | 0.31 | 3 | 0.31 | 0 | 0.00 | 0 | 0.00 | 2 | 0.55 | 2 | 0.55 |
| A&E− | 20 | 2.20 | 20 | 2.20 | 5 | 1.16 | 5 | 1.16 | 7 | 1.93 | 7 | 1.93 |
| ALG− | 9 | 0.94 | 9 | 0.94 | 5 | 1.16 | 5 | 1.16 | 7 | 1.93 | 7 | 1.93 |
| EVA− | 25 | 2.83 | 25 | 2.83 | 7 | 1.63 | 7 | 1.63 | 7 | 1.93 | 7 | 1.93 |
| IPF− | 1 | 0.10 | 1 | 0.10 | 0 | 0.00 | 0 | 0.00 | 1 | 0.28 | 1 | 0.28 |
| DAS− | 9 | 0.94 | 9 | 0.94 | 2 | 0.47 | 2 | 0.47 | 1 | 0.28 | 1 | 0.28 |
| NDIS− | 31 | 3.25 | 31 | 3.25 | 12 | 2.79 | 12 | 2.79 | 11 | 3.04 | 11 | 3.04 |
| LSA− | 31 | 3.35 | 31 | 3.35 | 2 | 0.47 | 2 | 0.47 | 1 | 0.28 | 1 | 0.28 |
| CC+ | 10 | 1.26 | 10 | 1.26 | 4 | 0.93 | 4 | 0.93 | 10 | 2.76 | 10 | 2.76 |
| CCP− | 106 | 11.53 | 106 | 11.53 | 39 | 9.07 | 39 | 9.07 | 38 | 10.50 | 38 | 10.50 |
| CCA− | 39 | 4.09 | 39 | 4.09 | 29 | 6.74 | 29 | 6.74 | 14 | 3.87 | 14 | 3.87 |
The data were visualised using radar diagrams for each group of participants. The radar diagrams in Fig. 1 further support the data displayed in Table 5, showing the overall profile for each group. The radar diagrams for undergraduate and industrialist participants in Fig. 1 clearly displays the primary observed approaches from Table 5, manifesting as extension along the IIN, ALG and IPF axes, leading to some angular features. The secondary observed approaches are not as readily identifiable because of the prominence of the primary observed approaches. The radar diagram for the academic participants' profile is very different from the undergraduate and industrialist radar diagrams, with much reduced angular features, reflecting the greater abundance of secondary approaches observed in the academic participant profile.
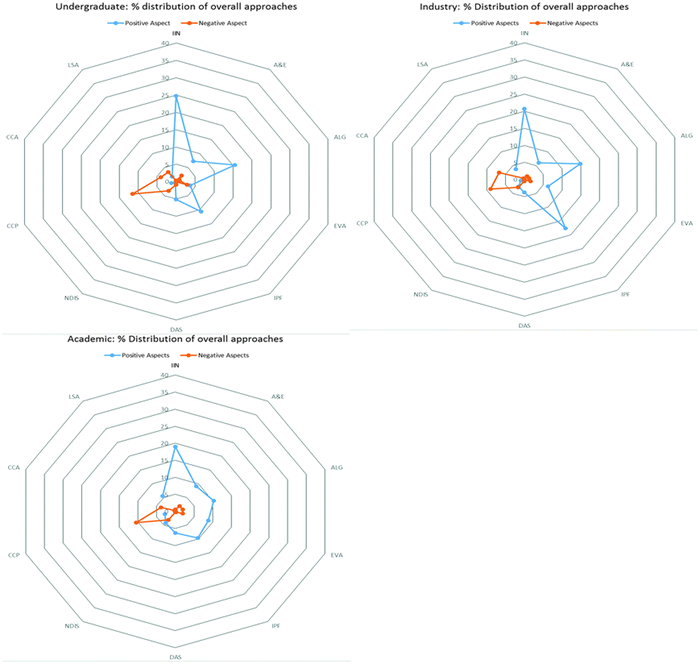 | ||
| Fig. 1 Radar diagram showing the profiles of chemistry undergraduate students, industry and academic participants. | ||
The data from the traffic lighted solutions are presented in Table 6 and show that a large proportion of solutions from all disciplines are categorised as amber with undergraduate and industrial participants achieving 43% and academic experts achieving 46%. With such similarity between groups around the amber category the largest differences were observed between the red and green traffic lighted solutions. As Table 6 shows, 37% of undergraduate solutions were categorised as red, which is a much greater proportion than the academic participants, which showed 17% red code. The industrialists showed a red code distribution of 28% which lies between the academic and undergraduate participants. The differentiation is shown again in the green solutions where undergraduate participants achieved a much lower number of green solutions (20%) than both industrialist (39%) and academic participants (37%).
| Red solutions | Amber solutions | Green solutions | Number of questions | Q-score | ||||
|---|---|---|---|---|---|---|---|---|
| N | % | N | % | N | % | N | AVG | |
| Undergraduate | 19 | 37 | 22 | 43 | 10 | 20 | 51 | 1.82 |
| Industrialists | 5 | 28 | 6 | 33 | 7 | 39 | 18 | 2.11 |
| Academic | 4 | 17 | 11 | 46 | 9 | 37 | 24 | 2.21 |
Each question was assigned a score whereby red = 1, yellow = 2 and green = 3. The scores for each group were added together and divided by the total number of questions answered by the group to give an average score for the group's performance. Undergraduate participants scored an average of 1.8 per question, industrialist participants scored an average of 2.11 per question and the academic experts scored an average of 2.21 per question. This clearly shows a differentiation in success with undergraduates performing least well, industrialists a little better and academics achieving most success.
Discussion
The objective of this study was to ascertain what approaches are used by chemistry undergraduates in their first year of study and graduates when they engage with open-ended problems. The graduate group was drawn from academics within chemistry departments in the UK and graduate professionals in the chemical industry. The analysis of the data in Table 3 show that the approaches used by the undergraduate participants were very similar to each other; indicating that identifying the information needed (IIN+), using algorithms and making calculations (ALG+) and identifying and framing the problem (IPF+) are prominent approaches used in solving open-ended problems. The analysis presented in Tables 3 and 4 is supported by previous literature with individuals identifying and framing the problem as suggested by Polya (1988) and Bodner (1987). What is unclear from these papers is whether identifying the information needed to answer the problem is grouped together with identifying the problem and framing what the problem is asking. Using an emergent approach the data presented in Tables 3 and 4 clearly show that these two components are discretely separate, particularly with academic participants. Although there are occasions when the undergraduate participants have used identifying the information needed as a method to frame the problem and develop a strategy when they are unsure how to proceed, undergraduate participants still identified/asked for discrete pieces of information. So although participants all identified the information needed, its implementation thereafter differs. In addition to identifying and framing the problem, Table 4 shows that expert participants engaged in more evaluation than the undergraduate participants (Table 3). This has been identified as a key skill in previous studies where it has been observed as the concluding approach of a problem-solving strategy (Wheatley, 1984; Bodner, 1987; Polya, 1988). In this study it appears evaluation processes did occur toward the end of a solution, although some graduate participants used an evaluation approach during their solution in a continual review process. This continual review process was observed less frequently than the end of solution review process and never occurred in undergraduate participants.A further interesting point associated with the data presented in Tables 3 and 4 is the prominence of reliance on using algorithms and making calculations associated with the questions in both undergraduate and graduate participants. These open-ended problems can be answered through verbal reasoning as well as arithmetic reasoning, yet the focus of all participants was towards an arithmetic process. This is reflected in Tables 3 and 4 were most participants held ALG+ (using algorithms and making calculations) as a prominent code. Bodner (1987) and Polya (1988) do not identify the use of algorithms and making calculations as an important component of problem solving, presumably assuming its importance was implicit in solving chemistry problems and, as such, is an intrinsic tool in scientific problem solving. Although this approach is not identified as important for problem-solving in these previous studies, it was identified in a qualitative study by Overton et al. (2013) These authors used a different terminology, stating that participants ‘seek’ an algorithmic approach. This is slightly different to the ALG+ code associated with this paper which catalogues the events and approaches of the ‘use’ of algorithms and calculations. It is not surprising that a large number of participants utilised an arithmetic process, as their previous experience in problem solving will have focussed around using algorithms and calculations to solve most problems (Bennett, 2008; Pappa and Tsaparlis, 2011). When participants encounter an unfamiliar experience they try to imprint a more familiar process, such as transforming an open-ended problem into an algorithmically structured problem.
The analysis of the data from Table 5 and Fig. 1 highlight the most interesting correlations between groups, presenting the overall profiles of the three groups. What has been identified is that the primary approaches used by undergraduate, academic and industrialist participants are very similar, but when the secondary prominent codes are identified it emerges that the academics look very different to the undergraduates and industrialists. The profile for the academic participants shows a much great number of secondary approaches. As previously stated “the means by which an individual uses previously acquired knowledge, skills and understanding to satisfy the demands of an unfamiliar situation” (Krulik and Rudnick, 1987) may result in greater success at solving the problem. As discussed earlier Camacho and Good (1989) have previously identified the behaviours required to be a successful problem solver, including approaches such as identifying and framing the problem, evaluation and logical and scientific approach and developing a strategy. The approaches identified in Camacho and Good's paper are similar to the approaches identified during this study. When the data in Table 5 is compared against the Camacho and Goods study it is clear that academic participants exhibit a greater number of similar characteristics (Camacho and Good, 1989).
Overton and Potter have suggested that there are three different profiles of problem solvers in open-ended problem solving, which are novice, expert and transitional (Overton et al., 2013). The definitions of each of those groups are:
Novice: Participants who adopted negative and unhelpful approaches, lacking scientific strategy and unable to define the problem, little to no evaluation occurs. Furthermore they are unable to detach themselves from the context of the problem and seek an arithmetic approach. ‘No clear approach.’
Transitional: Participants who employ a wide range of approaches depending on the problem, dependent on whether they could identify the problem and contextualise the data they needed. These participants evaluated their solutions, but still usually sought an algorithmic approach.
Expert: Participants who adopt predominantly positive approaches, understanding the problem and employing a logical scientific method. Participants in this group can handle the lack of data and evaluate their solutions.
Participants in this study did not adhere strictly to these definitions, as all participants used an arithmetic approach (ALG+) and all participants were able to identify and frame the problem (IPF+). However, what should be noted is the use of evaluation. The undergraduate participants rarely used evaluation in their approach, and where it did occur it was superficial, surface evaluation. The undergraduate participants also became confused with the problem and lacked the confidence in their ability. Industrial participants engaged in much more meaningful evaluation than their undergraduate counterparts, which materialises in Table 5 as secondary code. Academic participants also engage in evaluation, and to a greater extent than both the industrialist and undergraduate groups. The academics' use of evaluation emerges as a secondary code in Table 5 in addition to three other secondary codes. As such the academic group could be identified as experts under the definition by Overton et al. because they were able to engage in a wider variety of positive approaches and achieved greater success in the process. The undergraduate participants can be categorised as novices due to their lack of meaningful evaluation, resulting in low success rate as reflected Table 6. This in-turn means that industrialists are transitional, because although they achieved greater success than the undergraduate participants because of their approaches and evaluation of their strategies and solution. Industrialists still focused on developing an arithmetic procedure and became confused with the problem and their ability, even after clearly defining the problem.
The traffic lighted solutions in Table 6 shows the percentage distribution for the quality of participants solution and answers. The percentage distribution for the green solutions shows that the undergraduate solutions have a lower percentage of success (20%) than the academics (37%) and industrialists (39%), with the academics achieving the highest percentage of green solutions. Undergraduate chemistry participants further showed most unsuccessful solutions (37%) followed by industrialists (28%) with the academics showing the least percentage of unsuccessful solutions (17%). The numerical scores provide another way of evaluating relative success. The score data in Table 6 clearly show that there is an increasing score from the undergraduate participants who scored an average of 1.80 per question, industrialists who scored 2.11 and academics who scored 2.21. These numbers were derived from a semi-qualitative analysis of the solutions so statistical analysis is inappropriate. However, the data do appear to indicate increasing quality of the solutions from undergraduates to industrialists to academics. This further supports the description of undergraduate participants as novices, industrial participants as transitional and the academic participants as experts, not only in their approaches used but also their success in answering the open-ended problems.
Of course this study has limitations that must be taken into account. The sample sizes were modest, particularly the academic and industrialist cohorts. Thus a larger sample size may lead to more diversity with a cohort. All participants were volunteers and there are always concerns around self-selecting samples. Volunteers may be particularly interested in the research study or in problem solving itself, and so may be atypical of the normal population. The academic cohort stands out here as being quite different to the undergraduate and industrialist participants. This is not surprising as they are a self-selecting group from the entire graduate population. Their research training and the fact they are research-active may be what leads to expert-like behaviour. We must also consider cognitive factors. Several studies have indicated that field dependence is a predictor of success in solving open-ended problems and it may be that academics are naturally field independent. We did not measure this cognitive skill but it would be interesting to do so.
Conclusions
An emergent process for data analysis using a think aloud protocol was used to conduct a qualitative study to identify the approaches used by undergraduate, industrialist and academic chemistry participants.Undergraduate students conform to a very specific profile when they answer open-ended problems. Undergraduate students focus their approaches towards identifying the information needed (IIN+), using algorithms and making calculations (ALG+) and identify and framing the problem (IPF+). Their approaches and success are categorised as those used by novices.
Industrialist participants have a profile of approaches which is similar to undergraduate chemistry participants focusing towards identifying the information needed (IIN+), using algorithms and making calculations (ALG+) and identifying and framing the problem (IPF+). The main differences between industrial participants and undergraduate chemistry participants emerges with the secondary coding with an increase in the occurrences of evaluation. Their approaches and success are categorised as transitional.
The academic participants show a more rounded profile when compared to both the undergraduate chemistry participants and industrial experts, showing further use of approximations and estimations (A&E+), evaluation of solutions and answers (EVA+), developing a strategy (DAS+), not becoming distracted by information (NDIS+) and developing a logical and scientific approach (LSA+). Academic participants used much more evaluation than both other groups. The approaches and success of academic participants would classify them as experts.
Despite the limitations of this study, the findings have implications for undergraduate education. It is clear that success in solving open-ended problems in aided by the use of evaluation. Undergraduates should be encouraged to evaluate throughout the problem solving process, not just for the final solution, developing problem solvers with a more reflective mind set. In addition, expert problem solvers utilise a wider range of approaches. This expert behaviour is exhibited by academics and it could be the extensive experience of research that inculcates such behaviours. In order to enhance undergraduates' problem solving abilities and move them towards expert-like behaviour a curriculum with a bias towards undergraduate research and problem solving activities could be beneficial.
Acknowledgements
We acknowledge undergraduate participants from the University of Hull and the University of Strathclyde and the academic and industrialist participants who were drawn from various academic institutions and companies in the UK. We thank Dr Debbie Willison for organising participants at the University of Strathclyde. We further thank Dr Ross Galloway and Dr Marsali Wallace for their valuable supporting in developing the qualitative coding method.Notes and references
- Armstrong D., Glosling A. Weinman J. and Marteau T., (1997), The Place of Inter-Rater Reliability in Qualitative Research: An Empirical Study, Sociology, 31(3), 597–606.
- Ashraf S. S., Marzouk, S. A. M., Shehadi, I. A., Murphy B. M., (2011), An intergrated professional and transferable skills course for undergraduate chemistry students, J. Chem. Educ., 88, 44–48.
- Bennett S. W., (2004), Assessment in chemistry and the role of examinations, Chem. Educ. Res. Pract., 8, 52–57.
- Bennett S. W., (2008), Problem solving: can anybody do it? Chem. Educ. Res. Pract., 9, 60–64.
- Bodner G. M., (1987), The Role of Algorithms in Teaching Problem Solving, J. Chem. Educ., 64, 513–514.
- Bodner G., (1991a), Toward a unified theory of problem solving: a view from chemistry, Hillesdale, NJ: Lawrence Erlbaum Associates.
- Bodner G. M., (1991b), A View from Chemistry, in Smith M. U. (ed.), Toward a Unified Theory of Problem Solving, 1st edn, Hillsdale, NJ: Lawrence Erlbaum Associates Inc., pp. 21–34.
- Bodner G. M. and Domin D. S., (2000), Mental models: the role of representations in problem solving in chemistry, Univ. Chem. Educ., 4, 22–28.
- Bridgestock R., (2009), The graduate attributes we've overlooked: enhancing graduate employability through career management skills, High. Educ. Res. Dev., 28, 31–44.
- Camacho M. and Good R., (1989), Problem solving and chemical equilibrium: successful versus unsuccessful performance, J. Res. Sci. Teach., 26, 251–272.
- Carson J., (2007), A Problem with Problem Solving: Teaching Thinking Without Teaching Knowledge, Math. Educ., 17, 7–14.
- Cracolice M. S., Demming J. C. and Ehlert B., (2008), Concept learning versus problem solving: a cognitive difference, J. Chem. Educ., 85, 873–878.
- Dewey J., (1933), How we think, Boston: D.C. Heath.
- Education Scotland (SQA), (2010), Chemistry: Open-ended problems, online available from http://www.educationscotland.gov.uk/resources/nq/c/nqresource_tcm4628999.asp, accessed 11th June 2015.
- Ericsson K. A. and Simon H. A., (1993), Protocol Analysis: Verbal Reports as Data, Cambridge, MA: MIT Press.
- Fredriksen N., (1984), Implications of Cognitive Theory for Instruction in Problem Solving, Rev. Educ. Res., 54, 363–407.
- Gallagher S. A., Stepien W. J. and Rosenthal H., (1994), The effects of problem-based learning on problem solving, Gifted Child Quart., 36, 195–200.
- Greenbowe T. J., (1983), An investigtion of variables in chemistry problem solving, Purdue University.
- Hayes J. R., (2009), The complete problem solver, New York: Routledge (Digital Printing Edition).
- Herok G. H., Chuck, J. and Millar T. J., (2013), Teaching and Evaluating Graduate Attributes in Science Based Disciplines, Creative Educ., 4, 42–49.
- Herron J. D. and GreenBowe T. J., (1986), What can we do about Sue: a case study of competence, J. Chem. Educ., 63, 528–531.
- Hmelo C. E. and Ferrari M., (1997), The problem-based learning tutorial: cultivating higher order thinking skills, J. Educ. Gifted, 20, 401–422.
- Ibo R., (2014), Investigating the Relevance of the Graduate Attributes to Australian Tertiary Chemistry Education: A Staff, Student and Industry Perspective, BSc, Australian National University, Australia.
- Institute for Employment Research (IER), (2008), An Investigation of the Factors Affecting the Post-University Employment of Chemical Science Graduates in the UK, report to the Royal Society of Chemistry, available at http://www.rsc.org/images/IERFullReport_tcm18-159366.pdf, accessed 10 June 2015.
- Jääskeläinen R., (2010), Think-aloud Protocols, in Gambier Y. and Doorslaer L., (ed.), Handbook of Translation Studies, Amsterdam: John Benjamins Publishing Company.
- Johnstone A. H., (1993), Introduction, in Wood C. and Sleet R. (ed.), Creative Problem Solving in Chemistry, London: The Royal Society of Chemistry.
- Johnstone A. H. and El-Banna H., (1986), Capacities, demands and processes – a predictive model for science education, Educ. Chem., 80–84.
- Krulik S. and Rudnick J. A., (1987), Problem solving: a handbook for teachers, Boston: Allyn and Bacon.
- Kuusela H. and Paul P., (2000), A comparison of concurrent and retrospective verbal protocol analysis, Am. J. Psychol., 113, 387–404.
- Larkin J., McDermott J., Simon D. P. and Simon H. A. (1980), Expert and Novice Performance in Solving Physics Problems, Science, 208, 1335–1342.
- Lunyk-Child O., Crooks D., Ellis P. J., Ofosu C., O'Mara L. and Rideout E., (2001), Self-Directed Learning: Faculty and Student Perceptions, J. Nurs. Educ., 40, 116–123.
- Norman G. R. and Schmidt H. G., (1992), Psychological basis of problem-based learning: a review of the evidence, Acad. Med., 67, 557–565.
- Nurrenbern S. C. and Pickering M., (1987), Concept learning versus problem solving: is there a difference, J. Chem. Educ., 64, 508–510.
- Overton T. L. and Potter N. M., (2011), Investigating students' success in solving and attitudes towards content-rich open-ended problems, Chem. Educ. Res. Pract., 12, 294–302.
- Overton T. L., Potter N. M. and Leng C., (2013), A study of approaches to solving open-ended problems in chemistry, Chem. Educ. Res. Pract., 14, 468–475.
- Pappa E. T. and Tsaparlis G., (2011), Evaluation of questions in general chemistry textbooks according to the form of the questions and the question-answer relationship (QAR): the case of intra- and intermolecular chemical bonding, Chem. Educ. Res. Pract., 12, 262–270.
- Polya G., (1988), How to solve it: a new aspect of mathematical method, Princeton: Princeton University Press.
- Reid N. and Yang M., (2002), The solving of problems in chemistry: the more open-ended problems, Res. Sci. Tech. Educ., 20, 83–98.
- Runquist O. and Kerr S., (2005), Are we serious about Preparing Chemists for the 21st Century Workplace or Are We Just Teaching Chemistry, J. Chem. Educ., 82, 231–233.
- Simon D. P. and Simon H. A., (1978), Individual differences in solving physics problems, in Siegler R. S. (ed.), Childrens thinking: what develops? Hillsdale, NJ: Lawrence Erlbaum Associates.
- Slavin R. E., (1997), Educational Psychology: Theory and Practice, Boston: Allyn and Bacon.
- Smith M. U., (1988), Toward a unified theory of problem solving: a view from biology, Annual Meeting of the American Educational Research Association, New Orleans.
- Stepien W. J., Gallagher S. A. and Workman D., (1993), Problem Based Learning for traditional and interdisciplinary classrooms, J. Educ. Gifted, 16, 338–357.
- Surif J., Ibrahim N. H. and Dalim S. F., (2014), Problem Solving: Algorithms and Conceptual and Open-ended Problems in Chemistry, Soc. Behav. Sci., 116, 4955–4963.
- Tsaparlis, G. (2005), Non-algorithmic quantitative problem solving in university physical chemistry: a correlation study of the role of selective cognitive factors, Research in Science and Technological Education, 23, 125–148.
- Varsavsky C., Matthews K. E. and Hodgson Y., (2014), Perceptions of Science Graduating Students on their Learning Gains, Int. J. Sci. Educ., 36, 929–951.
- Walsh L. N., Howard R. G. and Bowe B., (2007), Phenomenographic study of students' problem solving approaches in physics, Phys. Rev. Spec. Top. Phys. Educ. Res., 3, 1–12.
- Wieman C., (2007) Why Not Try a Scientific Approach to Science Education? Change: The Magazine of Higher Learning, 39, 9–15.
- Wheatley G. H., (1984), Problem Solving in school Mathematics, MEPS Technical Report No. 84.01, West Lafayette: Purdue University.
- Wood W. B., (2009), Revising the AP Biology Curriculum, Science, 325, 1627–1628.
| This journal is © The Royal Society of Chemistry 2015 |
