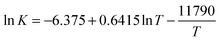Chemical engineering students' ideas of entropy

Abstract

Thermodynamics, and in particular entropy, has been found to be challenging for students, not least due to its abstract character. Comparisons with more familiar and concrete domains, by means of analogy and metaphor, are commonly used in thermodynamics teaching, in particular the metaphor ‘entropy is disorder’. However, this particular metaphor has met major criticism. In the present study, students (N = 73) answered a questionnaire before and after a course on chemical thermodynamics. They were asked to: (1) explain what entropy is; (2) list other scientific concepts that they relate to entropy; (3) after the course, describe how it had influenced their understanding. The disorder metaphor dominated students' responses, although in a more reflective manner after the course. The view of entropy as the freedom for particles to move became more frequent. Most students used particle interaction approaches to entropy, which indicates an association to the chemistry tradition. The chemistry identification was further illustrated by enthalpy and Gibbs free energy being the concepts most often mentioned as connected to entropy. The use of these two terms was particularly pronounced among students at the Chemical Engineering programme. Intriguingly, no correlation was found between the qualitative ideas of entropy and the results of the written exam, primarily focusing on quantitative problem solving. As an educational implication, we recommend that students are introduced to a range of different ways to interpret the complex concept entropy, rather than the use of a single metaphor.

---

Introduction

The field of thermodynamics in general and the concept of entropy in particular are central to our understanding of nature, and how to come to terms with challenges that we are confronted with as a society, such as global warming. The centrality and personal interest vested in entropy is epitomised by Ludwig Boltzmann, whose gravestone has engraved: S = k log W, in commemoration of his ground-breaking formula, which relates entropy to the number of microstates of a system.

In the early 1980s, science educators came to realise that doing well on paper-and-pencil problem-solving exams is no guarantee for a deep conceptual understanding of the topic at hand. Early focus was on investigating students' understanding of Newtonian mechanics (Clement, 1982; McCloskey, 1983), but has later expanded to other fields, including thermodynamics (e.g.Yeo and Zadnik, 2001). In this tradition, science education research has shown that thermodynamics is challenging to grasp – see Bain et al. (2014) and Dreyfus et al. (2015) for recent reviews on teaching and learning in the field. Consequently, in an international questionnaire study, Ugursal and Cruickshank (2014) concluded that engineering students found thermodynamics to be more difficult than most other engineering subjects, and – unfortunately – not very interesting to learn. This challenge in learning is particularly pronounced for the concept of entropy (e.g.Sözbilir, 2003; Sözbilir and Bennett, 2007), not least due to its abstract nature. We cannot readily probe the entropy of a system with our senses, and there is no ‘entropymeter’; rather we derive its value from measurements of a set of other quantities.

In the present study, we set out to explore how engineering students interpret and understand the entropy concept and its role in thermodynamics, before and after a course in chemical thermodynamics. In particular, we attended to what metaphors students use, what other concepts they associate with entropy, and how this relates to their exam results on the course. In what follows, we first review the literature of students' understanding of entropy, and teaching approaches to come to terms with students' challenges in relation to entropy.

Students' conceptions of entropy

In a study of upper secondary students' responses to a test in chemical thermodynamics, Johnstone et al. (1977) found that students generally interpreted entropy vaguely as a measure of disorder, but were left with the impression that they “have little or no conception of entropy” (p. 249). The students also had a tendency to confuse entropy with kinetic energy.

Carson and Watson (2002) interviewed students in order to probe their qualitative understanding of entropy and Gibbs free energy before and after a first-year course in chemical thermodynamics. The students were presented with three chemical reactions, asked to explain what happened and why, and to describe how they understood the concepts entropy and Gibbs free energy. Few of the students had been introduced to entropy in their prior secondary chemistry education, but many ideas had formed after the course. The majority of students had grasped that the entropy of a system and its surroundings cannot decrease, along with ways in which the entropy of a system can increase, e.g. through change of state from solid to liquid to gas. Other aspects of entropy were found to be more challenging, including its relation to the number of microstates or energy distribution across energy levels, or differentiating between the system and its surroundings. Some explanations involved entropy as a ‘form of energy’, which was hard to disambiguate from enthalpy or Gibbs free energy. The term was also vaguely identified with disorder or randomness. Overall, Carson and Watson argue that the course focused on teaching quantitative problem solving through symbol manipulation, as reflected in the problem solving exercises and the nature of the exam. In this way, the students were given little opportunity to develop a conceptual understanding of involved concepts, such as entropy and Gibbs free energy.

In a similar vein, Sözbilir and Bennett (2007) studied third-year chemistry undergraduates' understanding and misconceptions of entropy before and after courses in physical chemistry. They gathered data from pre- and post-tests with conceptual questions – some of which involved entropy – and interviews before and after the course. The results reveal that students have many challenges with regard to entropy, due to, e.g.: identification of entropy with disorder, interpreted as movement, collisions and ‘mixed-upness’, and disambiguation of the system and its surroundings. Some identified misunderstandings were actually more prevalent after the course than before, and the rather discouraging conclusion is that after the course most of the students were still unable to explain the change in entropy of a system using thermodynamic principles.

Turning to studies of physics students' understanding of entropy, Brosseau and Viard (1992) interviewed physics PhD students regarding what happens to the entropy of a thermally isolated gas during reversible expansion. Although the majority of the students mentioned that the relation dS = dQ/T applies to the situation, only one of them concluded that the entropy remains unchanged. Instead, the dominating line of reasoning built on the idea of entropy as disorder: as the volume increases, the disorder increases; hence the entropy increases. In their interpretation, seeing entropy as disorder made the students focus exclusively on spatial configuration, but ignore the decrease in internal energy. Similarly, physics teacher students concluded, in small-group exercises, that the entropy of an ideal gas should increase during reversible adiabatic expansion (Haglund and Jeppsson, 2014), while a pair of physical chemistry PhD students arrived at constant entropy, but found it to be counterintuitive (Jeppsson et al., 2013). Furthermore, physics undergraduate students have been found to have difficulties applying the second law of thermodynamics in assessing the feasibility of given thermal processes (Cochran and Heron, 2006), and believe that the entropy of a system and its surroundings typically remains unchanged throughout thermal processes (Christensen et al., 2009).

As part of a course in engineering thermodynamics, Gustavsson et al. (2013) studied students' conceptions of entropy. The students were given a questionnaire where they were asked to rate how strongly, on a 0–5 scale, they related entropy to a list of notions: probability, temperature, work, disorder, heat, and energy. The result was that the students associated entropy most strongly with disorder, and least strongly with work. There was further a strong correlation between relating entropy to heat and relating it to temperature (indicating an awareness of the formula dS ≥ dQ/T), but also between relating it to disorder and to probability. The students were further asked to read four short texts involving entropy and summarise them in groups of 4–5 students. The texts represented different aspects of the topic, including a microscopic approach, macroscopic cyclic processes, and relating entropy to human, social matters. Out of these, the students' summaries of the microscopic, statistical accounts, some of which involved disorder, reflected a more complex understanding of entropy.

Teaching approaches to thermodynamics and entropy

Many different teaching approaches have been suggested in order to come to terms with students' challenges with thermodynamics in general, and entropy in particular. In introductory physics and physical chemistry teaching, respectively, Reif (1999) and Kozliak (2004) argue for a microscopic approach to the concept, engaging Boltzmann's interpretation of entropy in relation to the number of microstates. In contrast, due to students' difficulties in interpreting such microscopic models, Loverude et al. (2002) prefer the introduction of thermal concepts by relating them to macroscopic phenomena with which the students are familiar, such as the increasing temperature when using a bicycle pump. From another point of view, Geller et al. (2014) have experienced that when introducing entropy to life science students, who are more familiar with Gibbs free energy than entropy, it may be productive to start with pointing out how the entropy contributes to Gibbs free energy. Other suggested approaches rely on connecting the second law of thermodynamics to our intuition that energy tends to degrade and dissipate (Duit, 1984; Ross, 1988; Daane et al., 2014).

Eventually, however, students would need both a foundational, microscopic understanding of entropy, and practical skills in applying it in calculations of thermal processes and chemical reactions. There remains a particular challenge for students to see how such diverse aspects of entropy relate to one single physical quantity (Baierlein, 1994; Kozliak, 2004). For instance, Baierlein (1994) sees a risk that students do not get an in-depth understanding of what entropy is with macroscopic approaches to the topic. In the light of Johnstone's (1991) triangle model of levels of thought in chemistry and chemistry education, at the macroscopic level, we find heat engine and chemical reaction applications, while notions such as microstates and probabilities which may be interpreted in terms of disorder are introduced at the submicroscopic level. However, this divide across the macro and submicro levels is also inherited at the symbolic level, where it is hard for students to see how macroscopic quantities, such as heat, temperature, enthalpy or Gibbs free energy, relate to microstates and probabilities from the world of statistical mechanics.

Theoretical framework

Our data analysis and discussion relies on a theoretical framework, comprising three aspects: the interpretation of entropy in different disciplinary traditions, with an emphasis on chemistry; the use of metaphors and analogies in understanding entropy; and the use of teleological reasoning in seeing how entropy is related to the second law of thermodynamics.

Views of thermodynamics and entropy in different disciplinary traditions

Using thermodynamics as a case, Christensen and Rump (2008) bring forth the idea that students' challenges in learning may derive partly from differences in the epistemological frameworks they encounter in different disciplinary traditions. In their comparison of how thermodynamics is approached in courses in physics, physical chemistry and engineering thermodynamics, respectively, Christensen and Rump acknowledge that they cover partly different content. For instance, chemical potential or enthalpy changes are central in chemistry, but less so in the other disciplines. More interestingly, however, there are also differences in how central, shared concepts are interpreted. For instance, whereas physicists and chemists typically study systems in equilibrium with constant mass or in open vessels, mechanical engineers often model scenarios with a flow of matter through a ‘control volume’, which yields completely different mathematical formulations, even of central relations, such as the first law of thermodynamics. Furthermore, while a physicist may approach thermodynamics macroscopically without considering the microscopic nature of matter (even though statistical mechanics does provide such microscopic explanations), a chemist will always take into account molecular interaction. The importance of considering molecular interaction in chemistry found support in a study of students' argumentation in small-group work in a physical chemistry study by Becker et al. (2013), where the students' justification of claims in relation to particle-level structures and processes was identified as a prevalent sociochemical norm across topics and context. In particular, Haglund et al. (2010) show that the term ‘entropy’ is assigned different interpretations in different contexts, such as macroscopic thermodynamics, statistical mechanics, or information theory.

Qualitative interpretations of and metaphors for entropy

One potential approach to come to terms with the abstract nature of entropy is to introduce the concept by comparison to something more concrete and familiar, by means of metaphor or analogy. However, the use of metaphor and analogy in science education has been identified as a ‘double-edged sword’ (Glynn, 1989). Students may indeed interpret metaphors and analogies in ways that lead towards an understanding in line with the current understanding in science, but poorly chosen or interpreted metaphors and analogies can completely lead students astray. Jeppsson et al. (2011) provide an overview and analysis of metaphors for entropy that have been suggested for science teaching, but also criticised for failing to convey crucial aspects of the concept or for their potential for misinterpretation.

The metaphor that has dominated teaching is entropy is disorder, often exemplified by the analogy to an untidy room, where scattered toys and clothes are assigned high entropy, in contrast to the tidy room's low entropy. The analogy is meant to illustrate Boltzmann's microscopic approach to entropy, in that there are more disordered configurations of the child's belongings – corresponding to a system's microstates – than there are ordered ones; hence higher entropy. The use of the disorder metaphor has, however, met with considerable criticism (e.g.Styer, 2000; Lambert, 2002). Styer (2000) points out a range of weaknesses of the disorder metaphor, including that disorder is vague and emotionally charged. Most importantly, the messy room analogy focuses on a snapshot view of a system's spatial configuration, and fails to recognise the importance of the energy involved. As we have seen above, empirical findings that students have difficulties in problem solving involving entropy have often been explained by overreliance on disorder. Wei et al. (2014, p. 330) even see the use of the disorder metaphor and the confusion it has induced as the main cause of the marginalised position of the second law of thermodynamics in K-12 teaching:

“Ultimately, however, it is the pervasive yet inappropriate use of the disorder metaphor for entropy that has prevented more widespread incorporation of the second law into student thinking. /…/ Because the metaphor of entropy as disorder has been so pervasive, most of students' misconceptions – that have documented regarding entropy, the second law and spontaneous processes – are directly or indirectly related to this metaphor.”

The personal engagement vested in this issue may be illustrated by Lambert's (2014) list of textbooks (36, and counting!), from which the disorder metaphor has been removed.

Realising the need for conceptualising entropy beyond mathematical formalism, but finding the disorder metaphor “entirely mysterious” in relation to Clausius' macroscopic interpretation, Leff (1996, p. 1260) instead proposes the introduction of entropy in terms of spreading of energy. He argues that “entropy is a function that represents a measure of spatial spreading of energy and a temporal spreading over energy states” (Leff, 2007, p. 1760) and concludes that “it is appropriate to view entropy's symbol S as shorthand for spreading” (p. 1744). Consequently, Wei et al. (2014) propose that we replace the disorder metaphor with the idea of entropy as energy dispersal also in K-12 teaching of energy. In contrast, Jeppsson et al. (2011) argue that, like all metaphors, the spreading metaphor is not unproblematic. For instance, ‘spreading’ as a verb in the gerund form may lead students to think that it is a process variable, parallel to for instance ‘heating’. Although more neutral than disorder, spreading is also likely to be given primarily spatial interpretations. Furthermore, it would not be unreasonable to interpret the ‘spreadoutness’ of energy mathematically in terms of a derivative of the internal energy with respect to the volume: dU/dV, which relates closer to an ‘energy density’ or the pressure of a system than its entropy. Such merits and shortcomings have to be pointed out explicitly to students for every metaphor that is engaged in teaching.

Similar to Leff (1996), Styer (2000) argues that we need qualitative, metaphorical ways to introduce entropy. However, in line with the reasoning above, where Leff and Wei et al. (2014) suggest wholesale replacement of the disorder metaphor with entropy as spreading, Styer recognises that every metaphor – including, but not only, entropy as disorder – has shortcomings. Consequently, he thinks that the disorder metaphor may be retained, as long as we acknowledge its drawbacks. Furthermore, as a way to counteract the idiosyncrasies of the disorder metaphor, Styer suggests that we complement it with another: entropy is freedom, which admittedly is just as vague as disorder, but positively charged emotionally, and better at capturing the range of microstates a system can be in. The merit of the freedom metaphor in going beyond the typical snapshot view of the disorder metaphor is emphasised also by Amin et al. (2012). The approach of deliberately combining the freedom metaphor with other metaphors in the teaching of entropy is adopted also by Brissaud (2005), even though he settles for entropy is information, relating to its use in information theory.

A quite different qualitative interpretation, entropy as heat, has been suggested within macroscopic approaches to thermal physics (Fuchs, 1987; Herrmann, 2000) and in engineering thermodynamics (Gaggoli, 2010). Here, entropy is seen as a substance-like (although not conserved) entity that may be contained in and flow between objects, i.e. corresponding to how we typically use ‘heat’ in everyday language. Note, however, that this approach may entail problems for students who later encounter more traditional interpretations of heat as a process variable in thermodynamics (Strnad, 2000).

Teleological and anthropomorphic reasoning in relation to the second law of thermodynamics

There has been a debate in science education regarding the use and potential merits or shortcomings in teaching of teleological reasoning, i.e. explaining phenomena by pointing to their purposes, or effects, rather than causes, and anthropomorphic reasoning, where non-human entities are ascribed human characteristics, such as having emotions or a free will. On one hand, such lines of reasoning may be productive in making use of our everyday experience as humans when we want to understand the nature. On the other hand, teleological or anthropomorphic reasoning may also lead our thoughts to inappropriate conclusions, such as the tempting Lamarckian view on evolution (Rudolph and Stewart, 1998): giraffes have stretched their necks in order to get taller; therefore giraffes are taller now than their previous generations.

Taber and Watts (1996) investigated students' use of anthropomorphic language in relation to chemical bonding, and identified two different classes of anthropomorphism. In the case of ‘weak’ anthropomorphism, a student realises that an atom does not actually ‘want’ or ‘feel’ anything, but uses such language metaphorically as if the atom were a sentient being. Weak anthropomorphism might be a powerful communicative device, in breaking the rules of the otherwise impersonal, detached language in science class (Lemke, 1990). However, in the case of ‘strong’ anthropomorphism, typically expressed as teleological reasoning, such desires are actually ascribed to inanimate entities. In chemistry, this sometimes results in misunderstandings, for example in the context of the ‘full outer shell’ heuristic, i.e. that atoms ‘try’ to achieve stable noble-gas electronic configurations. As part of their further investigation of students' ideas of chemical bonds, Taber and Watts (2000) have developed a framework of students' explanations. They bring forward teleology and anthropomorphism as examples of pseudoexplanations, i.e. statements that look like explanations on the surface, but do not logically fit the studied phenomenon. Relating to the anthropomorphism example of a student who says that an atom is trying to become stable, they argue that: “Such language has explanatory currency only when the implied actor is actually animate and capable of ‘trying’” (Taber and Watts, 2000, pp. 347–348).

Talanquer (2007) identified and analysed teleological explanations in chemistry textbooks. He found that teleological lines of reasoning are used to explain rules and laws, which have been found empirically to have high generality. According to these rules and laws, chemical changes occur in order to optimise some characteristic or quantity. As an example, Talanquer also refers to the full outer shell heuristic, in the form of the octet rule, according to which bonds form in order to achieve increased stability. Novice students are often not aware that the octet rule is a quite rough rule-of-thumb, and tend to overgeneralise it in situations where it does not apply. Other examples relate to the second law of thermodynamics, where students are told that changes occur in order to maximise the entropy of the universe, or minimise the Gibbs free energy of the studied system; teleological explanations of causes, in reference to their effects. Here, in contrast to the case of the octet rule, however, the teleological reasoning gains force and educational legitimacy from the generality and consistency of the second law of thermodynamics. The confidence in the second law of thermodynamics has been expressed eloquently by Eddington (1928, p. 74):

“The law that entropy always increases, holds, I think, the supreme position among the laws of Nature. If someone points out to you that your pet theory of the universe is in disagreement with Maxwell's equations – then so much the worse for Maxwell's equations. If it is found to be contradicted by observation – well, these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of thermodynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation.”

Once we are convinced that the second law of thermodynamics holds universally, we may see the increase of entropy as a ‘driving force’, a ‘tendency’, or giving directions for change along ‘time's arrow’. From this perspective, anthropomorphic reasoning represents another step in understanding the second law of thermodynamics, as expressed, for example, in “nature abhors a gradient” (Schneider and Sagan, 2005). Indeed, such anthropomorphic language was also adopted by Clausius (1865, p. 400), as he ended the seminal paper in which he coined ‘entropy’ by stating the laws of thermodynamics in terms of:

(1) Die Energie der Welt ist Constant.

(2) Die Entropie der Welt strebt einem Maximum zu.†

Then again, we seek for deeper explanations, and would prefer to understand the underlying mechanical causation. Why does the entropy tend to increase? Explanations of the underlying mechanisms are provided probabilistically in statistical mechanics. But this does not automatically discredit the educational legitimacy of teleological explanations at earlier stages in the educational system. The question is whether teleological explanations are valuable for helping students to understand aspects of the second law of thermodynamics, without introducing obstacles for grasping more fundamental explanations, should they decide to specialise in the subject.

As recognised by Amin et al. (2012) and Wei et al. (2014), this search for teaching approaches that fit a particular age group and prepare for further studies also applies to the issue of the relative merits and shortcomings of different metaphors for entropy – in particular the still widely used, yet contended disorder metaphor. So far, however, this pedagogical debate has been largely limited to theoretical arguments, and we believe that empirical study of how students respond to different teaching approaches is required to cast further light on these matters.

Purpose of the study

The purpose of the present study was to investigate engineering students' interpretation of the entropy concept and how it is related to other scientific concepts, in relation to a course in chemical thermodynamics. Another ambition was to be able to assess the usefulness of students' ideas of entropy, and the metaphors they employ, in relation to learning thermodynamics.

In particular, the study served to respond to the following research questions:

• What scientific concepts do engineering students relate to entropy, prior to and after a chemical thermodynamics course, and how are these concepts related to one another?

• How do engineering students explain what entropy is, prior to and after a chemical thermodynamics course?

• How do engineering students' explanations of and associations to entropy relate to their exam results on a chemical thermodynamics course?

Methodology

Context of the study

The study was conducted in the spring term 2014 in relation to the course Chemical Thermodynamics given to second-year engineering students, specialising in study programs such as Chemical Engineering, Environmental and Water Engineering, and Molecular Biotechnology Engineering at Uppsala University. There is an admission requirement for students to have passed at least one course in chemistry.

Atkins' physical chemistry, 9th edn (Atkins and De Paula, 2010) was used as course literature, and the course had a traditional structure with lectures, problem-solving sessions, and laboratory exercises. The lecturer told – in a subsequent interview – that emphasis was placed on students' development of conceptual understanding, for instance by use of qualitative problems to be discussed in small-group settings, as well as quantitative problem-solving skills. Furthermore, adhering to the chemistry disciplinary tradition (Christensen and Rump, 2008), students' development of microscopic explanations was given priority, rather than the relation to macroscopic examples, such as heat engine cycles. In particular, Boltzmann's approach to entropy, involving the number of microstates, was adopted more commonly than Clausius' macroscopic approach. When teaching about entropy, the lecturer explained that there are limitations to the disorder metaphor that students had encountered in previous courses. For example, crystals may form into layers where molecules have high freedom to move in the layer (high ‘order’ going together with high entropy).

After the course, the students took a paper-and-pencil problem-solving exam in Swedish, where some of the items involved entropy. Most items were of a predominately quantitative character, but some involved qualitative reasoning, such as whether the entropy in a given reaction is likely to increase, decrease, or remain the same. The seven items were graded from 1 to 10, based on the correctness and justifications given, and an overall score of 35 out of a maximum 70 was required to pass the exam. English translations of the exam items that relate explicitly to entropy are provided in Appendix A.

Data collection

Paper-and-pen questionnaires in Swedish were given to students in conjunction with the first (N = 130) and last lectures (N = 96) of the course. The students were asked to specify their secondary school science courses taken, study program, and names. The names were used to match questionnaires before and after the course (N = 73), and with examination results for students that answered both questionnaires (N = 64).

For ethical reasons, students were introduced orally to the purpose of the study and how data would be used and reported, informed that participation was voluntary, and that the teachers of the course would not have access to individual students' responses. By signing their questionnaires, students provided written consent to participation.

In both questionnaires, the students were asked two open-answer questions:

• What is entropy? Give a brief explanation that reflects your understanding.

• Which are the most important other scientific concepts that relate to entropy, according to you?

In the questionnaire after the course, the following item was added:

• How has the course influenced your understanding of the entropy concept? Please give concrete examples.

Research on students' conceptual understanding of a broad range of science topics, including thermodynamics and entropy, has typically been performed by use of clinical interviews or multiple choice questions. Interviews have the benefit that an in-depth understanding can be gained of the interviewed student's line of reasoning, but involves an asymmetrical power relationship between the interviewer and the interviewee. In addition, since conducting interviews and analysing the outcome is time consuming, there are practical constraints on how many interviews can be conducted. With multiple choice questions, in turn, many more students can be included, but the students' qualitative understanding can only be inferred indirectly. By asking the students to write down their explanations of what entropy is, we strived to approach all students of the course in order to be able to say something about how prevalent different ideas were among them, and to gain some insight into their qualitative understanding of entropy. This exploratory approach was adopted in the light of the scarcity of empirical studies on the metaphors students use in relation to entropy. We also considered that the approach should be reasonable for practicing teachers to adopt in getting an overview of their students' understanding of a particular topic or concept, based on positive experience from asking students in a similar population to provide free-text explanations (Gustavsson et al., 2013).

The second item was used against the background of previous research on the connection between students' achievement and their responses to word association tests in physics. High school students who are currently taking a physics course have been found to generate more concepts and more strongly interrelated concepts, when asked to associate freely to a word when given a list of 18 terms from the topic of mechanics, in comparison to students who took the course a year ago, or have not taken the course (Johnson, 1964). Similarly, Shavelson (1972) found that high school students' achievement increases from a pretest to a posttest after instruction in mechanics came together with increased interrelation between key concepts at word association tests. As mentioned above, Gustavsson et al. (2013) have used word association tasks for engineering thermodynamics students, although with a given set of concepts to choose from.

Data analysis

Answers from the questionnaires were entered into a spreadsheet. Individual students' answers before and after were matched, and we focused our analysis on the 73 students who answered both.

The students' answers to what entropy is (before and after) and how the course had changed their ideas (after) were first categorised by one of the researchers, deductively as the categories were formed against the background of previous research described in the Theoretical framework, but also inductively as new patterns of reasoning were identified (e.g. coming to problematise one's previous understanding). These ideas vary in the degree to which they align with the current view in science. Next, two of the researchers refined the categories, gave them descriptions in English, and coded the students' responses. The resulting classification scheme, with relative frequencies and examples of students' answers, which have been translated into English, are detailed in Table 1. These categories are not mutually exclusive, and many student responses were classified as involving several of them. Suitable grain sizes of the categories were also discussed. For instance, we chose to form one category of teleological and anthropomorphic reasoning since many expressions involved both, such as systems ‘striving’ for disorder. Lastly, the categories were grouped into overarching themes.

Table 1 Percentages of categories within six overarching themes before and after the course (out of a total of 73 students), with example responses to the item: “What is entropy? Give a brief explanation that reflects your understanding”

Category	Percentage of students (%) (before/after)	Description	Example student explanations
Microscopic interpretation of entropy (38/68)
Microscopic	34/59	Relating to the state of a system's particles, atoms, molecules, etc.	How many ways the particles can distribute across different energy levels… (after). Probabilities for molecules to move in a particular way (after).
Movement	10/19	Connection to the movement of particles	The disorder of molecules, how much they move (before).
Freedom	3/30	The freedom or possibility for a system or its particles to change states, move, etc.	Entropy is the molecules' possibility to move freely. E.g. gas has high entropy, solids have lower (after).
Probability	7/7	The probability for a system or its particles to be in a particular state	ΔS, it deals with how probable it is that a certain substance will be in a certain state (before).
The disorder metaphor for entropy (67/77)
Disorder	67/77	Relating entropy to disorder	Entropy describes the disorder in a system (after). Entropy is a measure of disorder. How free the molecules are to move (after).
Problematising	0/19	Reflection on or questioning own understanding of entropy prior to the course (in responses after the course)	Last time I answered that I thought it was order. Apparently, that was a dumb way to see things. How atoms distribute (after). In the beginning of the course I saw entropy as ‘disorder’. Now I have a more nuanced view on entropy [in terms of the possibility for molecules to move and spread out] (after).
The spreading metaphor for entropy (7/30)
Spatial configuration	7/25	The location, mixing or spreading of particles	Order, high entropy → high disorder, i.e. the molecules are spread out in a room, a beaker, etc. (before). Entropy is disorder, how “messy” or mixed up it is in a gas/liquid (before).
Spreading of energy	0/5	The spreading or distribution of energy in space or across particles	A measure of how energy is distributed among molecules in a system (after).
Problematic connection between entropy and energy (26/7)
Energy	26/7	Identification of entropy with energy, or a part or form of it	Entropy is the heat in a system that does not transform into work (before).
Teleological understanding of the second law of thermodynamics (26/20)
Second law of thermodynamics	25/18	Entropy as an increasing quantity	Everything strives for high entropy (before).
Teleology/anthropomorphism	23/11	Attribution of purposefulness, sentience or volition to physical phenomena	Entropy – disorder. All systems strive for disorder in all processes. The entropy is thereby the driving force for reactions to happen (before). Atoms/molecules strive to reach disorder, since they want most to be as spread out from each other as possible (before).
Other categories
Literal	15/19	Statements that entropy is a state function, use of denotations (e.g. S, ΔS) or formulae (e.g. dS = dQrev/T)	A physical state function. Denoted with S (before). You can calculate it like this: S = U/T + k ln Q (after). dS = dQrev/T. S increases for every spontaneous process in an isolated system (after).
Concrete examples	14/22	Specific physical processes, or the third law of thermodynamics	A measure of order/disorder, e.g. a gas has higher entropy than a solid, as the molecules in the gas are free (before). A substance at 0 K and with perfect crystalline structure cannot be ordered in different ways and the entropy is then 0 (after).

---

In order to describe how the classification was done, we provide an example of the coding of a student's explanation of what entropy is:

“Order, high entropy → high disorder, i.e. the molecules are spread out in a room, vessel, etc. The universe strives for, like, high entropy…”

This statement was coded as involving microscopic explanations and spatial configuration, since it relates to the relative locations of molecules. It further makes use of the disorder metaphor, which is used to express the second law of thermodynamics. Since the word ‘strives’ was used, the expression was also coded as making use of teleology/anthropomorphism.

Following Johnson (1964) and Shavelson (1972), we took interest in the interrelations that the students attributed to scientific concepts. The concepts associated to entropy and our categorisation of the student explanations of entropy were uploaded into SPSS, and descriptive statistics (absolute frequencies) were generated. An overview of correlations between the categories was provided by means of Spearman's rho, and individual pairs singled out for one-tailed Fisher's exact tests, for which the significances are given in the results. The correlations were calculated in order to identify clusters of ideas that tended to come together. Some of the responses were further subjected to qualitative analysis, with a particular focus on how individual students had developed their understanding of entropy between the pre- and post-tests.

In a second round of analysis, the students' responses to the questionnaires were matched with their overall exam results. Correlations were calculated between the exam results on one hand, and the concepts students relate to entropy and categories of students' explanations on the other, in order to identify patterns of qualitative understanding of entropy that are useful or detrimental to problem solving.

After the data analysis, preliminary results were shared with the lecturer of the course, in order to check whether our interpretations were reasonable, and might be useful for the teaching practice.

Results

Analysis of scientific concepts related to entropy

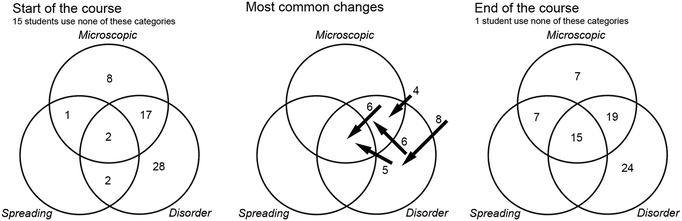
Fig. 1 depicts the number of students who relate entropy to certain scientific concepts. The students are characterised as ‘stable’ if they state a concept both before and after the course, ‘leavers’ if they state a concept before, but not after the course, and ‘adopters’ if they state a concept after, but not before the course. The first thing to notice is the large number of students who mention enthalpy and Gibbs free energy, both before and after the course. In our view, this identifies the students as largely belonging to a chemistry disciplinary tradition (Christensen and Rump, 2008), where they are used to calculating the changes in entropy, enthalpy and Gibbs free energy involved in chemical reactions. We imagine that the responses would be quite different among students who have encountered entropy primarily in a physics or information theory context.

Fig. 1 Number of students that relate entropy to certain concepts, before or after the course, or both.

This connection to enthalpy and Gibbs free energy is further reinforced by the correlation analysis. Students who relate entropy to Gibbs free energy prior to the course tend to relate it also to enthalpy prior to the course (p = 0.0004, significance of one-tailed Fisher's exact test), and to Gibbs free energy after the course (p = 0.0007). Relating entropy to enthalpy and Gibbs free energy was found to be particularly common among students at the Chemical Engineering programme, which has the most extensive chemistry content prior to the course.

Whereas 18 of the students relate entropy to energy before the course, their responses are more differentiated after the course, distributed between internal energy, temperature, heat, and heat capacity. Out of these, relating entropy to energy before the course is significantly positively correlated to relating entropy to heat after the course (p = 0.005). Similarly, relating entropy to energy (undifferentiated) and Gibbs free energy after the course is significantly negatively correlated (p = 0.003).

A remarkable finding was that none of the students (before or after) bring up disorder as a scientific concept that is related to entropy. This is interesting for many reasons. First, there is the international research pointing to dominance of the disorder metaphor in teaching (e.g.Lambert, 2002). Second, there is a stark contrast with the results of Gustavsson et al. (2013), where engineering thermodynamics students connected entropy most strongly with disorder, when given a list of notions to choose from. Third, as we will see, the majority of the students in the present study mention disorder in their explanations of what entropy is to them. In our view, this unwillingness to bring up disorder as a scientific concept connected to entropy suggests that the students were aware that the notion should be interpreted figuratively rather than literally.

Analysis of explanations of entropy

We now turn to the students' responses to the questionnaire item where they were asked to explain what entropy means to them. Table 1 provides an overview of the categories that emerged from the analysis, grouped in their overarching themes. Illustrative examples are given from student responses, which are expanded upon in what follows. On average, the students' responses were coded as involving 1.90 of the categories in their explanations before the course, compared to 2.44 after the course, which illustrates an overall trend towards richer responses.

Microscopic explanations are influenced by the chemistry disciplinary tradition. Many of the students (34% before, and 59% after the course) describe microscopic aspects of entropy. This involves bringing up, for instance, the configuration or movement of atoms and molecules, or the multiplicity of microstates. Even though the course does not provide an in-depth statistical mechanics account, it fits within the chemistry disciplinary tradition of focusing on the molecular level of description (Christensen and Rump, 2008), aiming for explanations involving particle interaction (Becker et al., 2013).

Another identified category within the microscopic theme, which is more common in the answers after the course than before, is the connection between entropy and movement of particles. Prior to the course, this connection is typically quite direct, for instance: “The disorder of molecules, how much they move”. As we have seen, such an interpretation of disorder as a microscopic movement in relation to entropy has been reported previously (Sözbilir and Bennett, 2007), and may indicate confusion between entropy and kinetic energy (Johnstone et al., 1977). After the course, however, entropy is not typically connected to movement as such, but to the potential or freedom for particles to move about: “Entropy is the molecules' possibility to move freely. E.g. gas has high entropy. Solids have lower”, or “The ability for atoms/molecules to move/change places/how locked they are”. Indeed, in the responses after the course, there is a significant positive correlation between the movement and freedom categories (p = 0.00004). Overall, responses involving freedom are much more prevalent after the course than before (from 3% to 30%). Styer (2000) suggests using entropy as freedom in conjunction with the disorder metaphor. In our data, however, even though many of the descriptions involve both freedom and disorder, there is a significant negative correlation between these categories after the course (p = 0.005).

Overall, several of the qualitative, figurative descriptions of entropy we have come across in the literature are mentioned by one or more of the students, including disorder, freedom to move about, spreading of energy, teleological striving, etc. The chemistry profile of these engineering students is once again emphasised by the fact that only one of them indirectly alludes to entropy as information (“how ‘well’ we can know where molecules are located”), and none sees entropy as a substance-like entity that flows into and out of a system, which could have been expected in other scientific disciplines (Christensen and Rump, 2008).

Students come to problematise the disorder metaphor. An overwhelming impression from the analysis of the students' responses is the high proportion of them (67% before the course, and 77% afterwards) that, in some way or another, relate to the disorder metaphor. The strength in the conceived connection between entropy and disorder aligns with students that were studied by Gustavsson et al. (2013), but, as we have seen, contrasts with the students' own sets of scientific concepts related to entropy. The responses in relation to disorder are rather diverse. Some of them involve unspecified identification, e.g.: “The entropy describes the disorder in a system”, or “entropy means disorder”, but most of them use disorder in conjunction with other categories. For instance, some exemplify entropy as disorder by use of concrete examples, such as phase changes: “A measure of order/disorder, e.g. a gas has higher entropy than a solid, as the molecules in the gas are free”. It should be noted that entropy as disorder typically – although not infallibly (Styer, 2000) – gives adequate predictions of entropy changes in phase changes. As expected, some responses focus on spatial configuration, e.g.: “Disorder, high entropy → high disorder, i.e. the molecules are spread out in a room, a beaker, etc. …”. Furthermore, although Leff (1996, p. 1262) points out that the disorder metaphor is “entirely mysterious” from a macroscopic point of view, we found no correlation between students' use of microscopic explanations and the disorder metaphor. We will come back to how the other categories connect to entropy as disorder as they are brought up below.

We can further follow the change that some of the students undergo in relation to the disorder metaphor from before to after the course, in terms of problematising their previous understanding. In their responses, some of the students relate explicitly to the lecturer's given limitations of the disorder metaphor. In the light of examples where visual order goes along with high entropy, some of these students draw the same conclusion as Lambert (2002): the disorder metaphor is no good. For instance, Lisa, who wrote that entropy is disorder prior to the course, relates to her previous response after the course: “Last time I answered that I thought it was order. Apparently, that was a dumb way to see things. How atoms distribute.” Still, her feeling that she has not quite grasped the concept remains: “Now, I know how to do calculations with it, but I still feel that it's not very clear to me.” Similarly Anna has come to abandon the disorder metaphor, where the course has “clarified, taken away ‘disorder’ explanations”.

However, more students express that they have now a more nuanced view on the disorder metaphor. There are cases when it does not work very well: “I have realised that entropy cannot always be described as the degree of disorder in a system”, or “That entropy cannot be described only as a measure of disorder”. In particular, Karolina adopted the idea of entropy as the possibility for molecules to move and spread out. She reflects: “In the beginning of the course I saw entropy as ‘disorder’. Now I have a more nuanced view on entropy, according to [her description].” In all these cases, the disorder metaphor is problematised, and the students have developed an awareness that it does not always apply. There are good reasons to provide other, complementary explanations, but in line with Styer (2000), that does not necessarily mean that the disorder metaphor has to be avoided and completely abandoned.

Students relate spreading to particles, not to energy. The category spatial configuration involves the relative location of the constituent particles of a system, e.g. the volume in which they reside, the particles being near each other or spread out, or mixed up. The percentage of students who relate entropy to spatial configuration increased in the responses after the course compared to before the course (7% before the course, and 25% afterwards). As mentioned, one drawback of the disorder metaphor pointed out in the literature (Brosseau and Viard, 1992; Styer, 2000) is that it may provide an exclusive focus on spatial configuration. In our data, however, we see no such strong connection. Involving disorder in the descriptions before or after the course has no significant correlation with involving spatial configuration either before or after it.

As we have seen, Leff (1996, 2007) has proposed the introduction of entropy in terms of spreading of energy, which is adopted in the course literature (Atkins and De Paula, 2010). However, only four of the students make use of descriptions relating to entropy as spreading of energy in terms of the distribution or dispersal of energy across energy levels after the course. In fact, all cases where students use expressions involving “spread” or “spreading” relate to the spreading of particles rather than energy, supporting the view that it is tempting to give the metaphor a spatial interpretation (Jeppsson et al., 2011); these instances were thus coded in the spatial configuration category. It may be the case that the interpretation of entropy as spreading of particles is particularly tempting within chemistry, with its focus on particle interactions (Becker et al., 2013).

Students' progress towards microscopic explanations has a systematic pattern. As we have seen, many students involve more of the identified categories in their explanations of entropy after the course. This increased richness primarily relates to increased use of the categories within the three themes covered so far: microscopic reasoning, disorder and spreading. An analysis of these themes was carried out utilising the broader categorical groupings from Table 1. Fig. 2 shows Venn diagrams for how the uses of the categories within these themes relate and overlap before and after the course. Only one student does not relate to any of these categories after the course. Changes in themes related to in the explanations were observed for 54 of the 73 students. The five most common change patterns observed are presented in the middle diagram. We see a systematic pattern of students going from an exclusive focus on disorder towards incorporating features of microscopic explanations and spreading. In addition, other students come to adopt disorder-based explanations they did not use before the course. In this regard, the disorder metaphor may be seen as a stepping stone towards a more complex understanding of entropy.

Fig. 2 Venn diagrams showing student use of the categories within the microscopic reasoning, disorder and spreading themes in their explanations before and after the course. The middle diagram shows the five most common changes in category usage. All figures indicate number of students.

Students relate entropy to energy in problematic ways. As was identified in the analysis of the concepts that the students relate to entropy, its connection to energy was more specified after the course than before. This pattern is also reflected in the students' answers to what entropy means to them. Overall, however, the nature of the connection between entropy and energy was found to be problematic among the students. Prior to the course, similar to what was noticed by Carson and Watson (2002), quite a few of the students identify entropy vaguely as a part or form of energy: “It is part of the energy there is in a system”, some of whom mention heat and work: “Entropy is the heat in a system that does not transform into work.” Fewer examples are found among the responses after the course, but some remain, e.g.: “A measure of the energy that cannot become work, but disappears as heat.” In our view, such descriptions indicate underlying confusion of entropy and energy, or in other words misconceptions of what entropy is.

In the analysis of the concepts the students relate to entropy, we also found many of them associating entropy with enthalpy. A closer look at the descriptions of what entropy means to them reveals a variety of the nature of the connection to enthalpy prior to the course. Some of the students admit to mixing them up: “I mix it up with enthalpy, but I think it is disorder”, and one of them sees the concepts as contrary: “A measure of disorder, the opposite of enthalpy”. In these examples, the fact that the students merely do not remember which label comes with which concept does not preclude that they may have an adequate understanding of the concepts themselves. In contrast, none of the descriptions of entropy after the course involve enthalpy.

Teleological reasoning help students acknowledge the second law of thermodynamics. Teleological or anthropomorphic explanations were much more frequent before the course than after. In line with Talanquer (2007), following in the footsteps of Clausius (1865), these examples are dominated by expressions of the second law of thermodynamics, involving systems, nature, or the universe “striving” for maximum entropy or disorder, e.g.: “Entropy – disorder. All systems strive for disorder in all processes. Entropy is thereby the driving force for reactions to happen.” Other examples of teleological or anthropomorphic expressions are: “It is more favourable to have a disordered structure”, and “…all systems always want higher disorder, i.e. high entropy”.

If teleological and anthropomorphic language were seen as an indication of a more primitive understanding or of limited explanatory value, its decreasing prevalence would be welcome. In this case, we would rather side with Talanquer (2007), in his argumentation that the idea of teleological striving may be useful in grasping the second law of thermodynamics. Our data show that the teleological/anthropomorphic category is significantly positively correlated with relating to the second law of thermodynamics, both before (p < 0.00001) and after the course (p = 0.0002). In fact, 18 of the 19 students who relate to the second law of thermodynamics before the course also involve teleological or anthropomorphic reasoning in their responses. In other words, without recourse to teleological expressions, students are less likely to connect entropy to the second law of thermodynamics, which we think is a central aspect of the concept. Furthermore, before the course, both mentioning of the second law of thermodynamics (p = 0.0002) and the use of teleological/anthropomorphic reasoning (p = 0.0004) are positively correlated to the use of the disorder metaphor, forming a cluster of three categories, as captured in statements like: “Entropy – disorder. All systems strive for disorder in all processes.” These significant correlations to disorder are not retained in the responses after the course (p = 0.32 and p = 0.47, respectively). In addition, there was no significant correlation between the teleology/anthropomorphic category and the microscopic category.

Other explanations and reflections. Some of the students' responses involve quite literal descriptions of entropy and its characteristics. For instance, it is identified as: “A physical state function. Denoted with S” (before course), “You can calculate it like this: S = U/T + k ln Q”, in reference to the partition function formalism presented in the course, or “dS = dQ_rev/T. S increases for every spontaneous process in an isolated system” (after course). However, surprisingly few answers relate to Clausius's (or Boltzmann's) formalism explicitly in this way.

Finally, many of the students admitted, before and after the course, that they found entropy to be a difficult and abstract concept – particularly in the responses to the item “How has the course influenced your understanding of the entropy concept? Please give concrete examples.” –. For instance: “Now, I know how to do calculations with it, but I still feel it's not entirely clear to me.” This view of thermodynamics, and particularly entropy, as abstract and restricted to mathematical formalism, is recognised from previous research (e.g.Carson and Watson, 2002).

Relationship to examination results

64 of the 73 students took the exam, and there was a wide distribution of scores. Intriguingly, the combined exam results were not significantly correlated with any of the categories that emanated from the analysis of the pre- or post-questionnaires.

Discussion

We first reflect on to what degree the purpose of the study has been fulfilled, and then draw conclusions from the study by revisiting the research questions. Finally we turn to discussing educational implications of the study, in particular in relation to the use of metaphors for entropy in science teaching.

As for the overall purpose of the study, the students provided evidence of a broad range of explanations of what entropy is, and other scientific concepts they associate with entropy. We also see clear evidence of the involved students adopting a chemistry-specific perspective on thermodynamics. This is expressed in the phenomena and scientific concepts they bring up, but most characteristically, however, with a focus on microscopic, particle-based explanations (Becker et al., 2013; Christensen and Rump, 2008). When it comes to our ambition to evaluate the usefulness of different ideas of and metaphors for entropy, our results are less clear cut and require some elaboration.

What scientific concepts do engineering students relate to entropy, prior to and after a chemical thermodynamics course, and how are these concepts related to one another?

Many of the participating second year engineering students relate entropy to Gibbs free energy and enthalpy before and after the course, which, as mentioned, clearly shows their adoption of a chemistry perspective on thermodynamics (Christensen and Rump, 2008). This association to Gibbs free energy and enthalpy was particularly pronounced among students at the Chemical Engineering programme, where they had taken many chemistry courses before the present course.

When comparing the responses from the questionnaires before and after the course, there is a trend towards abandoning a connection between entropy and an undifferentiated energy, and instead mentioning its connection to heat, heat capacity, internal energy and temperature.

It should further be noted that no students related entropy to disorder as a scientific concept, which points to their awareness of the metaphorical interpretation of the idea of entropy as disorder. This stands in stark contrast to the students' own interpretations of what entropy is and prior research where students were found to associate entropy strongly with disorder, when it was given in a list of concepts related to entropy found in the literature (Gustavsson et al., 2013).

How do engineering students explain what entropy is prior to and after a chemical thermodynamics course?

The explanations of entropy among the students in our study are dominated by the disorder metaphor, both before and after the chemical thermodynamics course. This is in spite of the fact that the idea of entropy as disorder has been removed from the textbook used (Atkins and De Paula, 2010), in response to critique of the metaphor in the chemistry education research community (e.g.Lambert, 2002), and even though the teacher of the course explicitly pointed out some of its limitations. Some of the students, however, express a more nuanced view of the disorder metaphor, by acknowledging that it has limitations or should be complemented by other ways to conceptualise entropy.

As the course was framed in chemistry education (Christensen and Rump, 2008), it comes as no surprise that a large and increasing proportion of the students make use of microscopic, molecular interpretations of entropy. In particular, several of the participants come to adopt the view of entropy as particles' freedom to move about, relying on but also elaborating on the metaphor of entropy as freedom (Styer, 2000; Brissaud, 2005).

The proportion of students employing teleological reasoning (e.g. the universe strives for maximum entropy or disorder) decreases from the pre- to the post-questionnaire. However, the fact that reduced teleological reasoning comes along with fewer students pointing out the relevance of entropy in relation to the second law of thermodynamics – which we regard as a central aspect of entropy – confirms its usefulness for this particular topic (Talanquer, 2007).

Only a few students adopt the idea of entropy as in some way related to spreading after the course, and those who do relate it to spreading of particles, rather than spreading of energy, as suggested by Leff (1996). In other words, the spreading metaphor – just like the disorder metaphor – easily invites a focus on the spatial configuration of the constituent particles of a system, rather than constraining the focus to energy distributions.

How do engineering students' explanations of and associations to entropy relate to their exam results on a chemical thermodynamics course?

Surprisingly, and possibly somewhat discouragingly, no correlations were found between the students' total exam scores and any of the categories of the students' conceptual understanding of entropy and related concepts.

One possible interpretation aligns with the findings of Carson and Watson (2002) that thermodynamics courses tend to focus on algebraic problem-solving, and that the connection between problem-solving skills and conceptual understanding in science courses is weak (Clement, 1982); in fact, in the current study problem-solving and conceptual understanding come across as completely orthogonal dimensions. An alternative, possibly more provocative interpretation, also consistent with our findings, is that the different conceptions or metaphors of entropy are potentially equally useful or likely to be misinterpreted. For each metaphor, students need to become aware of its shortcomings as well as its merits. What is perhaps most puzzling with our findings is that problematisation of an earlier understanding of entropy has no correlation with exam results.

Then again, given the nature of the exam and the method of data collection, we should be cautious in reading too much into the lack of correlations. As seen in Appendix A, most exam items did not involve entropy explicitly. It may well be that a more fine-grained analysis of the responses to the individual test items would show correlational patterns, but they do not emerge at the aggregate score level.

Accuracy and usefulness of the students' explanations

In their framework for assessing whether a student's utterance is a scientific explanation, Taber and Watts (2000) use three criteria: it should have the formal structure of an explanation (e.g. using ‘because’, or ‘therefore’); it should be logically consistent and fit the concerned phenomenon; it should match the norms of science, i.e. be ‘right’ (Taber and Watts, 2000). Admittedly, in the case of our study, it is difficult to assess the adequacy of the students' written responses and underlying ideas, due to their brevity and vagueness. Many of them are descriptions, in the form of “entropy is…”, rather than explanations. However, the responses still make possible reflections on the relative usefulness of different perspectives on entropy.

First of all, we would like to emphasise that metaphor is a ubiquitous feature of language (Lakoff and Johnson, 1980). We use metaphors frequently – and often unconsciously – in many different contexts, including everyday language, the science classroom, and scientific texts. Metaphor is not merely an ornamental rhetorical device, but something that we cannot do without in science learning and communication. The questions are whether a particular metaphor is apt, and whether our students have understood it in the way that it was intended by an author or teacher.

As we have seen above, Taber and Watts (2000) argue that students' language involving entities ‘trying’, ‘wanting’, or ‘liking’ has explanatory power only so long as these entities literally are animate; such use of anthropomorphic or teleological lines of reasoning can only provide pseudoexplanations. From another perspective, Boyer (1996) points to research that has found that infants are able to distinguish between animate and inanimate objects and that pre-schoolers are able to make reasonable inferences based on such categories. Since even young children do not tend to confuse animate and inanimate entities, Boyer sees the prevalence of animistic and anthropomorphic reasoning across cultures as counter-intuitive and puzzling at first glance. However, he argues that it is precisely this counter-intuitive character that makes anthropomorphic reasoning attractive and attention grabbing. In this regard, he resonates with Duit's (1991, p. 650) take on the use of metaphors in science education: “Metaphors always have an aspect of surprise; they provoke anomaly”, and Lemke's (1990) view that metaphorical language in the science classroom is attractive just because of its rule-breaking character.

In our view, when one of the student writes: “The universe strives for, like, high entropy…”, we think that he is aware of the figurative nature of the expression, in relation to an inanimate quality of nature, i.e. a case of ‘weak’ anthropomorphism (Taber and Watts, 1996). In fact, this may help to remind students that entropy is not a conserved quantity, a mistake many students have been found to make (Christensen et al., 2009). In this regard, we argue that anthropomorphic and teleological reasoning may be useful for students' understanding of science, in particular in relation to theoretically and empirically well-grounded ideas as the second law of thermodynamics (Talanquer, 2007).

On the other hand, in line with Taber and Watts (1996), we acknowledge that the enticement of anthropomorphic and teleological reasoning makes novices vulnerable to overgeneralisation. For instance, from our human experience at the macroscopic scale, it is tempting to infer – erroneously – that heat is generated and accumulated when atoms collide with each other, or that energy is needed as an ingredient, rather than released, when a chemical bond is formed. In this regard, we find some problematic student statements in our data, such as: “Atoms/molecules strive to reach disorder, since they want most to be as spread out from each other as possible.” From this sentence, we suspect that the student has not fully grasped the randomness of the spatial distribution of the particles, implying that the particles are repelled from each other, as if they were equally charged particles. Students also have to be made aware of the difference between ‘weak’ anthropomorphism used as a pedagogical tool, and ‘strong’ anthropomorphism, which might be relevant for instance in a biological context. More fundamentally, from the point of view of the nature of science, students need to understand the relation between cause and effect, and thereby the difference between teleological and properly causal explanations. Teleological explanation may serve as a useful intermediate stepping stone in education, but students should be encouraged to eventually grasp the underlying causal mechanisms.

In contrast to these ambiguous cases of metaphorical language, some of the students' explanations involving the relation between entropy and aspects of energy are more unequivocally inaccurate. For instance, the statement: “Entropy is the heat in a system that does not transform into work”, provided before the course, reveals a poor understanding of entropy, but also of heat and work as process variables. Confusion of entropy and energy may be an underlying reason for believing that entropy is a conserved quantity (Christensen et al., 2009). In this regard, we were happy to see that the prevalence of such statements decreased considerably in the responses after the course.

Implication for the chemistry education research and practice

As a reflection on the methods of data collection and data analysis assumed in the present study, we strived for gathering relatively rich, qualitative data, involving the majority of the students taking a course. This can be seen as an exploratory approach to collecting initial empirical data to shed light on a matter which hitherto has been debated from a theoretical perspective. In addition, although the study is framed as educational research, parts of the approach might be suitable for course development purposes or as diagnostic tests, in order to probe the range of students' ideas within the regular teaching practice.

As we have seen, the disorder metaphor has received considerable criticism in science education research (Leff, 1996; Lambert, 2002; Wei et al., 2014), and there is a deliberate effort to convince textbook authors and teachers not to use it (Lambert, 2014). Although acknowledging many of the drawbacks of identifying entropy as disorder, we would like to call for some moderation. Data from the present study show that students' use of the disorder metaphor or not in coming to understand entropy has no correlation with problem-solving ability in a chemical thermodynamics course. This does not support the view that the metaphor is detrimental for thermodynamics teaching (Lambert, 2002; Wei et al., 2014), but it is not very useful in its own right either.

In our view, the disorder metaphor serves well in early introductions of entropy. In particular, it may be used to explain the possibility of spontaneous endothermic reactions, or that a substance typically increases in entropy as it changes from solid, through liquid, to gas phase, although as emphasised by Styer (2000) and others not without exceptions. In addition, we found that students' connection of entropy to the second law of thermodynamics before the course was positively correlated to seeing entropy in terms of disorder, and the use of teleological reasoning; a valuable contribution of the otherwise criticised ways of approaching the concept. In fact, in the interview with the lecturer where we presented the main outcomes of the study, he found it valuable to get to know that fewer students connected entropy to the second law of thermodynamics after the course than before it. He explained this as a consequence of the microscopic focus of the course, and thought, in line with Baierlein (1994), that more effort might be spent towards the end of the course to connect the microscopic interpretations to the macroscopic level.

Admittedly, as pointed out by Leff (1996), the disorder metaphor may seem mysterious from the point of view of macroscopic thermodynamics, in relation to Clausius's formalism: dS = dQ_rev/T. However, the metaphor is probably less cryptic within a chemistry tradition, with its inherent focus on molecular interactions (Christensen and Rump, 2008). Furthermore, in order to encourage a more nuanced interpretation of the disorder metaphor, Pflug (1983) proposes distinguishing between a static, configurational ‘desk type disorder’ and a more dynamic ‘disco type disorder’. With the disco type disorder in mind, there is a better opportunity to illustrate the influence of a system's energy on its entropy.

Some of the students express that they have come to problematise the disorder metaphor as they engaged with the course, in response to the lecturer pointing out its limitations. This is encouraging. As pointed out by Glynn (1989), analogies and metaphors are double-edged swords, and every metaphor breaks down at some point. As some of these students realise, however, awareness of a metaphor's limitations does not mean that it has to be abandoned altogether. It is also interesting to note that the students bring up limitations only of the disorder metaphor. Ideally, all metaphors or models that are introduced in teaching should undergo the same type of scrutiny with regard to the scope of their applicability.

As a final word, previous recommendations for teaching about entropy have sometimes focused on finding the best metaphor, be it freedom, spreading or something else. The present study, in contrast, shows that students are able to coordinate several metaphors simultaneously, including entropy as disorder, freedom and movement. Each of these metaphors has the potential to illustrate different aspects of the topic at hand. In this way, we would encourage the introduction of several ways to conceive the highly complex concept of entropy, rather than using one approach only.

Appendix A

English translations of the exam items that explicitly involve entropy

1. (a) Specify for the following reaction, with justification, whether ΔH^θ and ΔS^θ, respectively, should be negative or positive.

Na₂SO₄·10H₂O(s) → Na₂SO₄(s) + 10H₂O(g)

3. (a) 0.750 moles of hexane evaporates at its normal boiling point (69 °C). The enthalpy of vaporization is 331.8 J g⁻¹ and the vapour phase is assumed to be ideal. Calculate ΔH, ΔS, and ΔG.

7. For the gas phase reaction

2HBr ↔ H₂ + Br₂

the equilibrium constant has been measured at different temperatures, which has yielded the following expression (where T is the temperature in Kelvin)

Use this expression to calculate ΔH^θ, ΔS^θ, ΔG^θ, and ΔC^θ_p for the reaction at 80 °C.

Acknowledgements

We would like to thank the lecturer of the course and the students for their participation in the study. The study was partly funded by the Centre for Discipline-Based Education Research in Mathematics, Engineering, Science, and Technology at Uppsala University.

References

1. Amin T. G., Jeppsson F., Haglund J. and Strömdahl H., (2012), The arrow of time: metaphorical construals of entropy and the second law of thermodynamics, Sci. Educ., 96(5), 818–848.
2. Atkins P. W. and De Paula J., (2010), Atkins' physical chemistry, 9th edn, Oxford, UK: Oxford University Press.
3. Baierlein R., (1994), Entropy and the second law: a pedagogical alternative, Am. J. Phys., 62(1), 15–26.
4. Bain K., Moon A., Mack M. R. and Towns M. H., (2014), A review of research on the teaching and learning of thermodynamics at the university level, Chem. Educ. Res. Pract., 15(3), 320–335.
5. Becker N., Rasmussen C., Sweeney G., Wawro M., Towns M. and Cole R., (2013), Reasoning using particulate nature of matter: an example of a sociochemical norm in a university-level physical chemistry class, Chem. Educ. Res. Pract., 14(1), 81–94.
6. Boyer P., (1996), What makes anthropomorphism natural: Intuitive ontology and cultural representations, The Journal of the Royal Anthropological Institute, 2(1), 83–97.
7. Brissaud J.-B., (2005), The meanings of entropy, Entropy, 7(1), 68–96.
8. Brosseau C. and Viard J., (1992), Quelques réflexions sur le concept d'entropie issues d'un enseignement de thermodynamique [Some reflections on the entropy concept from thermodynamics teaching], Enseñanza de las ciencias, 10(1), 13–16.
9. Carson E. M. and Watson J. R., (2002), Undergraduate students' understandings of entropy and Gibbs' free energy, Univ. Chem. Educ., 6(1), 4–12.
10. Christensen F. V. and Rump C., (2008), Three conceptions of thermodynamics: Technical matrices in science and engineering, Res. Sci. Educ., 38(5), 545–564.
11. Christensen W. M., Meltzer D. E. and Ogilvie C. A., (2009), Student ideas regarding entropy and the second law of thermodynamics in an introductory physics course, Am. J. Phys., 77(10), 907–917.
12. Clausius R., (1865), Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie [On several convenient forms of the fundamental equations on the mechanical theory of heat], Ann. Phys., 201(7), 353–400.
13. Clement J., (1982), Students' preconceptions in introductory mechanics, Am. J. Phys., 50(1), 66–71.
14. Cochran M. J. and Heron P. R. L., (2006), Development and assessment of research-based tutorials on heat engines and the second law of thermodynamics, Am. J. Phys., 74(8), 734–741.
15. Daane A. R., Vokos S. and Scherr R. E., (2014), Goals for teacher learning about energy degradation and usefulness, Physical Review Special Topics - Physics Education Research, 10(2), 020111.
16. Dreyfus B. W., Geller B. D., Meltzer D. E. and Sawtelle V., (2015), Resource letter TTSM-1: Teaching thermodynamics and statistical mechanics in introductory physics, chemistry, and biology, Am. J. Phys., 83(1), 5–21.
17. Duit R., (1984), Is the second law of thermodynamics easier to understand than the first law? Tijdschrift Didactiek Natuurwetenschappen, 2(2), 102–111.
18. Duit R., (1991), On the role of analogies and metaphors in learning sciences, Sci. Educ., 75(6), 649–672.
19. Eddington A. S., (1928), The nature of the physical world, Cambridge, UK: Cambridge University Press.
20. Fuchs H. U., (1987), Entropy in the teaching of introductory thermodynamics, Am. J. Phys., 55(3), 215–219.
21. Gaggoli R. A., (2010), Teaching elementary thermodynamics and energy conversions: Opinions, Energy, 35(2), 1047–1056.
22. Geller B. D., Dreyfus B. W., Gouvea J., Sawtelle V., Turpen C. and Redish E. F., (2014), Entropy and spontaneity in an introductory physics course for life science students, Am. J. Phys., 82(5), 394–402.
23. Glynn S. M., (1989), The teaching with analogies model, in Muth K. D. (ed.), Children's comprehension of text: research into practice, Newark, DE: International Reading Association, pp. 185–204.
24. Gustavsson C., Weiszflog M. and Andersson S., (2013), Engineering physics students' conceptions of entropy, paper presented at the 4:e utvecklingskonferensen för Sveriges ingenjörsutbildningar, Umeå, 27–28 November.
25. Haglund J. and Jeppsson F., (2014), Confronting conceptual challenges in thermodynamics by use of self-generated analogies, Sci. Educ., 23(7), 1505–1529.
26. Haglund J., Jeppsson F. and Strömdahl H., (2010), Different senses of entropy – implications for education, Entropy, 12(3), 490–515.
27. Herrmann F., (2000), The Karlsruhe Physics Course, Eur. J. Phys.21(1), 49–58.
28. Jeppsson F., Haglund J. and Strömdahl H., (2011), Exploiting language in teaching of entropy, Journal of Baltic Science Education, 10(1), 27–35.
29. Jeppsson F., Haglund J., Amin T. G. and Strömdahl H., (2013), Exploring the use of conceptual metaphors in solving problems on entropy, J. Learn. Sci., 22(1), 70–120.
30. Johnson P. E., (1964), Associative meaning of concepts in physics, J.Educ. Psychol., 55(2), 84–88.
31. Johnstone A. H., (1991), Why is science difficult to learn? Things are seldom what they seem, J. Comput. Assist. Lear., 7(2), 75–83.
32. Johnstone A. H., MacDonald J. J. and Webb G., (1977), Misconceptions in school thermodynamics, Phys. Educ., 12(4), 248–251.
33. Kozliak E. I., (2004), Introduction of entropy via the Boltzmann distribution in undergraduate physical chemistry: a molecular approach, J. Chem. Educ., 81(11), 1595–1598.
34. Lakoff G. and Johnson M., (1980), Metaphors we live by, Chicago, IL: The University of Chicago Press.
35. Lambert F. L., (2002), Disorder – A cracked crutch for supporting entropy discussions, J. Chem. Educ., 79(2), 187–192.
36. Lambert F. L., (2014), Entropysite, retrieved 23 September, 2014, from entropysite.oxy.edu.
37. Leff H. S., (1996), Thermodynamic entropy: the spreading and sharing of energy, Am. J. Phys., 64(10), 1261–1271.
38. Leff H. S., (2007), Entropy, its language and interpretation, Found. Phys., 37(12), 1744–1766.
39. Lemke J. L., (1990), Talking science. Language, learning and values, Norwood, NJ: Ablex.
40. Loverude M. E., Kautz C. H. and Heron P. R. L., (2002), Student understanding of the first law of thermodynamics: Relating work to the adiabatic compression of an ideal gas, Am. J. Phys., 70(2), 137–148.
41. McCloskey M., (1983), Intuitive physics, Sci. Am., 248(4), 122–130.
42. Pflug A., (1983), Real systems on the oneway road towards disorder (What you always wanted to know about entropy but never dared to ask II), in Marx G. (ed.), 6th Danube Seminar on Physics Education - Entropy in the School, Budapest, Hungary: Roland Eötvös Physical Society, pp. 323–341.
43. Reif F., (1999), Thermal physics in the introductory physics course: why and how to teach it from a unified atomic perspective, Am. J. Phys., 67(12), 1051–1062.
44. Ross K. A., (1988), Matter scatter and energy anarchy: The second law of thermodynamics is simply common sense, Sch. Sci. Rev., 69(248), 438–445.
45. Rudolph J. L. and Stewart J., (1998), Evolution and the nature of science: on the historical discord and its implications for education, J. Res. Sci. Teach., 35(10), 1069–1089.
46. Schneider E. D. and Sagan D., (2005), Into the cool: energy flow, thermodynamics, and life, Chicago, IL: University of Chicago Press.
47. Shavelson R. J., (1972), Some aspects of the correspondence between content structure and cognitive structure in physics instruction, J. Educ. Psychol., 63(3), 225–234.
48. Sözbilir M., (2003), What students' understand from entropy?: a review of selected literature, Journal of Baltic Science Education, 2(1), 21–27.
49. Sözbilir M. and Bennett J. M., (2007), A study of Turkish chemistry undergraduates' understanding of entropy, J. Chem. Educ., 84(7), 1204–1208.
50. Strnad J., (2000), On the Karlsruhe physics course, Eur. J. Phys., 21(4), L33–L36.
51. Styer D. F., (2000), Insight into entropy, Am. J. Phys., 68(12), 1090–1096.
52. Taber K. S. and Watts M., (1996), The secret life of the chemical bond: students' anthropomorphic and animistic references to bonding, Int. J. Sci. Educ., 18(5), 557–568.
53. Taber K. S. and Watts M., (2000), Learners' explanations for chemical phenomena, Chem. Educ.: Res. Prac. Eur., 1(3), 329–353.
54. Talanquer V., (2007), Explanations and teleology in chemistry education, Int. J. Sci. Educ., 29(7), 853–870.
55. Ugursal V. I. and Cruickshank C. A., (2014), Student opinions and perceptions of undergraduate thermodynamics courses in engineering, European Journal of Engineering Education, DOI: http://10.1080/03043797.2014.987646.
56. Wei R., Reed W., Hu J. and Xu C., (2014), Energy spreading or disorder? Understanding entropy from the perspective of energy, in Chen R. F., Eisenkraft A., Fortus D., Krajcik J., Neumann K., Nordine J., and Scheff A. (ed.), Teaching and learning of energy in K – 12 education, Cham, Switzerland: Springer, pp. 317–335.
57. Yeo S. and Zadnik M., (2001), Introductory thermal concept evaluation: assessing students' understanding, Phys. Teach., 39(8), 496–504.

---

Footnote

† This translates literally into: “(1) The energy of the world is constant. (2) The entropy of the world strives towards a maximum”, although the formulation “The entropy of the universe tends to a maximum” is more widely spread.

---