Use of representation mapping to capture abstraction in problem solving in different courses in chemistry

Abstract

A perspective is presented on how the representation mapping framework by Hahn and Chater (1998) may be used to characterize reasoning during problem solving in chemistry. To provide examples for testing the framework, an exploratory study was conducted with students and professors from three different courses in the middle of the undergraduate chemistry curriculum. Each participant's reasoning while solving exam problems was characterized by comparing the stored knowledge representation used as a resource and the new instance representation associated with the problem being solved. Doing so required consideration of two ways in which abstraction occurs: abstractness of representations, and abstracting while using representations. The representation mapping framework facilitates comparison of the representations and how they were used. This resulted in characterization of reasoning as memory-bank or rule-based (rules processes), or similarity-based or prototype (similarity processes). Rules processes were observed in all three courses. Similarity-based reasoning seldom occurred in students, but was common to all of the professors’ problem solving, though with higher abstractness than in students. Examples from the data illustrate how representation mapping can be used to examine abstraction in problem solving across different kinds of problems and in participants with different levels of expertise. Such utility could permit identifying barriers to abstraction capacity and may facilitate faculty assessment development.

---

Introduction

Problem solving plays a major role in science, technology, engineering and mathematics (STEM) curricula, both at school and university level. It is important to train students in problem solving so they can become competitive when joining the workforce (Jonassen, 2011). However, students often encounter difficulties in problem solving because they lack the ability to relate new problems to their previous experiences and because they do not recognize appropriate steps to take to solve problems (Sweller, 1988). “The point is that there is an obstacle or barrier in the path from problem to solution… problem solving is overcoming obstacles or barriers, or bridging this gap by using information and reasoning” (Cardellini, 2010, p. 43).

Many researchers have analyzed different facets of problem solving in order to identify obstacles or barriers. On the one hand, typologies or taxonomies of problem features that impact students’ success in problem solving have been the subject of many studies. Problems have been classified according to information provided (i.e., data, methods, and outcomes; Johnstone, 1993), activities involved in the problem (Jonassen, 2003), whether they require conceptual or quantitative knowledge (Nurrenbern and Pickering, 1987; Stamovlasis et al., 2005), levels of understanding chemistry (Johnstone, 1991), or higher- and lower-order cognitive skills (Zoller, 2002). Several researchers note that the majority of students' experiences with problem solving is algorithmic and structured (Bennett, 2008; Pappa and Tsaparlis, 2011).

On the other hand, much research has focused on studying the process of problem solving, including investigation of specific strategies (Gabel and Bunce, 1994; Bodner and Herron, 2002), transformations between levels (Dori and Hameiri, 2003), mental effort (Overton et al., 2013), and the use of representations (Schwartz, 1995). These aspects have been analyzed under the expert-novice paradigm (McDermott and Larkin, 1978; Chi et al., 1981). Students often seem to adhere to simple, algorithmic rules without questioning their intention and justification (Mason et al., 1997; Reid and Yang, 2002).

Both strands of research on problem solving, i.e. work on categorizing types of problems and studies on strategies and approaches during problem solving, have led to many successes, including the development of approaches that students can use to get started on problems and to use when they get stuck (cf.Taconis et al., 2001), algorithmic representations of problem solving (McMillan and Swadener, 1991), and understanding roles of procedural knowledge and domain knowledge in problem solving (Litzinger et al., 2010).

We surmise that an important aspect of problem solving is the capacity for abstraction. The types of problems posed in disciplinary courses within a particular undergraduate STEM discipline evolve from ones that require understanding of a few laws or principles and the mastery of common approaches to more complex problems requiring students to abstract the problem at hand onto one or more generalized problems, or classes of problems, and then translate the techniques and results from the generalized problem back to the specific problem. Students may not be prepared to deal with such complex problems and may turn to “unhelpful” approaches, particularly when solving open-ended problems (Overton et al., 2013). Consequently, students’ abstraction capacity might be an important factor for their success in problem solving, especially in STEM subjects where abstraction is a foundational feature of the discipline. In this paper, we seek to address how to measure abstraction capacity in problem solving by employing a cognitive processing framework to distinguish among reasoning processes used by students when solving problems in chemistry in terms of the abstractness inherent in the representations used to solve the problems, and the abstracting applied to utilize the representations. After clarifying the major theoretical foundations of the framework, data from interviews will be used to illustrate the use of the framework, as well as to illustrate the potential conclusions that can be derived from its application regarding students' problem solving processes.

Problem solving in chemistry

Problem solving has been studied with many approaches and frameworks. Regarding cognitive processing during problem solving, two main approaches have been used in science and engineering: mental effort and types of reasoning. The former is useful in understanding the extent to which different measurable cognitive factors affect problem solving and may explain why some strategies are preferred by some individuals over other, more successful, strategies. The latter incorporates the notion of abstraction explicitly, and therefore can provide a method for measuring its extent. That is, examining reasoning processes allows for a comparison of how abstract different representations of knowledge are, and makes it possible to quantify how much abstraction a person performs.

Problems and problem solving in chemistry

Raker and Towns (2010) examined the types of problems in four second-year university organic chemistry courses (nearly 800 problems). Using the typology of eleven types of problems characterized by Jonassen (2003), they found the majority (61%) required rule usage, while 17% needed algorithms to solve, and smaller percentages required recall (7%), trouble-shooting (7%), diagnosis (5%), story (3%) and designs (1%). No problems necessitated case analysis, decision making, dilemmas, logic, or strategic performance.

Reasoning in problem solving by graduate students taking organic chemistry was examined in a study about organic synthesis problems (Kraft et al., 2010). Graduate students were provided with problems that required them to complete a mechanism or determine the product of a reaction. The researchers assessed the ways in which the students solved the problems by studying the cues that students took from the problems when approaching solutions, and the reasoning processes they used to solve the problems. It was found that each student primarily used one of three types of reasoning: case-based reasoning, rule-based reasoning or models-based reasoning. Case-based reasoning occurred when specific instances from the student's past experiences were used to solve the problem. In rule-based reasoning, several rules were used to deduce the solution. Models-based reasoning involved constructing models of the situations in a problem and using these models to solve the problem.

Christian and Talanquer (2012) studied the reasoning approaches used by undergraduate students during study groups while they were enrolled in the first semester of organic chemistry (typically taken in the second year of the undergraduate program). They observed four reasoning approaches in students: (1) model-based reasoning refers to models with different scales (e.g., distance) and variables (e.g., compositional/structural, time), used either conceptually or quantitatively, that have explanatory and predictive power, (2) case-based reasoning focuses on (often interconnected) classifications of entities and processes, (3) rule-based reasoning relies on patterns of behavior induced from experiences or mental models, and (4) symbol-based reasoning has recognizable symbols manipulated to arrive at decisions without necessarily associating those symbols with deeper meaning. Similar to the results of Kraft et al. (2010), the majority (56.7%) of students' content-based talk used rule-based reasoning, a smaller percent (26.1%) was case-based reasoning, even less (8.5%) was model-based reasoning, and the remainder (8.7%) was symbol-based reasoning.

Cognitive processes during problem solving

Cognitive processing models provide a means of representing mental mechanisms according to assumptions about how knowledge is organized and accessed in the mind. Two long-standing research traditions exist. The classical approach to cognition posits that cognitive activity occurs by mental rules involving facts about the world applied to specific instances. This tradition holds that knowledge is stored as collections of rules, and these rules are organized into theories. Many formalisms, including Piagetian development theory, are based on this tradition. From a Piagetian perspective, the ability to abstract is generally considered a core characteristic of formal reasoning ability in the sciences (Cavallo, 1996; Niaz, 1996).

An alternative tradition in cognitive processing research proposes that similarity processes, in combination with past situations that are stored in a relatively unprocessed form, can model cognition. Again, many formalisms are based on this tradition, such as case-based reasoning in artificial intelligence (Kolodner, 1992). These formalisms are most closely associated with behaviorist theories of learning, which rely on generalization as the activity on which behavior depends, when comparing a new stimulus to a previously experienced one.

Cognitive scientists have long debated whether cognitive processes are better modeled by rules or similarity (Hahn and Chater, 1998a), and there has been vivid argument in cognition literature pointing to reasoning processes being able to be modeled by both (e.g., Smith and Medin, 1981; Reed and Bolstad, 1991). In fact, some cognitive scientists argue for a hybrid model of the structure of knowledge (Keil et al., 1998), and dual-processing has been proposed as a promising model for understanding this (e.g., Amsel et al., 2008).

Abstraction in problem solving

Abstraction is elusive and its measures are indirect. While most researchers who study problem solving agree that abstraction is critical to solving problems, it is usually defined within a framework that is used to study how people solve problems. When considering abstraction as a memory item, involving storing the meaning of ideas without storing the exact ideas, abstraction depends on the model of how memory is constructed or organized. In terms of cognitive processes, abstraction tends to be considered in two ways: the degree of abstraction present in the way in which a person is imagining a problem (i.e., a representation or mental model of the problem or situation), and the act of abstraction as an ability, such as simplifying or generalizing. We organize these into two categories, respectively: abstractness and abstracting.

Abstractness. In a study comparing group vs. individual cognition, Schwartz (1995) considered the level of abstraction in problem-solving representations generated by students. He identified degrees of abstraction present in them by comparing representations. For example, when students were reasoning about problems involving sequences of gears, he considered “the ability to reason about the numerical attributes of the problem without modeling the gears themselves” (p. 327) to be a more abstract representation than concrete representations in which hand gestures were used to simulate gears moving. When students were presented with tasks that involved visualizing relationships (e.g., structure–function or cause-effect) in the domain of biology, three properties were considered in determining whether a visualization was abstract or not: (1) the visualization had to be sufficiently removed, in terms of surface features, from the original text presentation as to not be able to recover the original problem, (2) linkages had to be distilled to a more general form, such as associating all relating verbs (e.g., give, get, send, receive) as a transmission of some sort, and (3) referents to original entities could not be used, such as representing particular organisms as specific concrete pictures.

Representations of situations or problem spaces have also been a subject of study. Building upon McDermott and Larkin (1978), Chi and collaborators (1981) investigated differences in ways that novice and expert physicists developed representations of physics problems. Experts differed from novices both in the amount of knowledge brought to solving problems as well as the organization of knowledge that allowed experts to build different kinds of representations than novices. Concerning the latter, Chi et al. (1981) marshaled evidence from their own, as well as others' studies to support the assertion that representations for solving problems are formed on the basis of categories or patterns that the problem at hand is judged to resemble. Domin and Bodner (2012) considered abstraction in representations constructed by chemistry graduate students during successful vs. unsuccessful problem solving in the context of problems about 2D-NMR. They found that successful problem-solvers had more accurate, more complete, and more abstract representations than unsuccessful problem-solvers. They considered representations to be the ways in which students constructed interpretations of a problem based on perceptions of the systems of symbols (text, visuals, charts, tables, etc.) presented in the problem. Once a student's representation was described, its abstractness was measured as “the degree to which the constructed representation incorporates additional symbol systems that were not part of the original presented instructional episode… [presuming] that these elements are prior knowledge contributions from the student's cognitive schema.” This measurement of abstraction in a representation builds from the characterization of abstract vs. grounded of Koedinger and collaborators (2008), who considered lack of specificity vs. specificity to a person's experience as the main latent variable of abstractness.

Abstracting. Working in the field of artificial intelligence, with the purpose of modeling reasoning with abstraction in people using common sense and in artificial intelligence programs that try to approximate such reasoning, Giunchiglia and Walsh (1992) described abstraction as a mapping between formal systems. They defined the act of abstraction as “the process of mapping a representation of a problem onto a new representation” (p. 323). This sets two conditions for reasoning with abstraction (p. 329): the resultant mapping (1) “helps deal with the problem in the original search space by preserving certain desirable properties”, and (2) “it is simpler to handle as it is constructed from the ground representation by ‘throwing away details’.” Reed (2012) has analyzed a broad array of literature and considered whether representations may be mapped in a variety of ways, not just one-to-one, but also one-to-many, and mapping parts of representations.

Ellis (2007) has studied abstraction as it occurs in the act of generalizing among students while learning about linear growth problems in mathematics. She found that students engaged in three major categories of generalizing actions: they relate by forming associations between situations or objects, they search for elements of similarity in relationships, procedures, patterns, or solutions, and they extend by expanding patterns or relations to form more general structures that have wider ranges of applicability, have particulars removed, can generate new cases through an operation or by continuing a pattern.

Prain and Tytler (2012) integrated several perspectives on how representations are formed in order to develop a framework that explains how and why the construction of representations by students supports their learning in science. Next to a semiotic and a epistemic perspective, the third epistemological perspective in their framework considers how students provide causal accounts using their representations. The activity of abstracting occurs most prominently within this third perspective, in which students apply constraints on their representations in order to provide causal accounts. They do so by limiting a case or making generalizations, comparing to simulations, basing arguments on similar cases through pattern identification, and evaluating the coherence of claims.

Representation mapping to capture abstraction

As noted in the introduction, much research in science and engineering education has focused on studying types of problems, strategies for solving them, mental effort exerted when problem solving, and the role of representations when solving problems. However, few have studied relationships between abilities in abstraction and approaches to solving problems, and, to our knowledge, there have not been any investigations of abstraction and problem solving approaches across an undergraduate curriculum. In the interest of quantifying the abstraction brought to problem solving across an undergraduate curriculum, we apply an approach that examines reasoning in terms of the use of representations formed and used by students as mental resources when solving problems. Recognizing that varying degrees of abstractness are present in representations, while abstracting also may occur when using representations to solve problems, we present here a framework that considers the mapping of the representation of a new instance (the problem) to the student's own representations (the individual's cognitive resources) via different mechanisms. In this way, the degrees of abstractness in the representations (new instance vs. stored knowledge), and the action of abstracting that occurs when mapping the new instance representation to the stored knowledge representation to generate the problem's solution through reasoning may be examined.

Mapping representations

Hahn and Chater (1998b) proposed a representation mapping model based on stored representations and how they are applied, that distinguishes the two main classes of cognitive processes – rules and similarity – and accounts for other types of reasoning, particularly prototype reasoning and use of memory bank (i.e., applying memorized matching or algorithms). Although there are other types of reasoning that do not necessarily fit in this domain-general scheme, such as input–output mapping, the model accounts for types of reasoning and degree of abstraction as follows. Reasoning can be mapped as representations of information stored in the mind and logic processes applied to those ideas. The core distinction between rules and similarity processes is accounted for by the ways in which representations are used, as illustrated in Table 1. In particular, they differ in how the representation of a new item is integrated with existing knowledge. In rules processes, existing knowledge is stored as rules (e.g., if a straight-chain carbon-backbone molecule has a C–C double bond, then it is an alkene). If the antecedent of a rule is satisfied (a molecule has a chain of carbons, and there is a double bond), then the category in the consequent applies (it is an alkene). In similarity processes, knowledge is stored as a set of past instances with category labels (e.g., the student is familiar with many examples of alkenes). A new item is classified as an alkene if the past instance it resembles the most has this classification.

Table 1 Comparison of a new item to existing knowledge in rules vs. similarity processes, with a paradigmatic case of reasoning within each type of process illustrated using an example of naming an organic compound that has a carbon–carbon double bond

	How strictly the new item matches the existing knowledge	Paradigmatic case of reasoning based on how specifically the new item is compared to the existing knowledge
Rules processes	Matching is strict, the condition of the rule must be satisfied or not, and no intermediate value is allowed. Ex: if the compound has a chain of carbons AND there is a C–C double bond, then it is always an alkene.	Rule-based reasoning: representation of the new instance is compared to a representation of different abstractness in the antecedent of the rule (in this case more general). In the example of the alkene, “chain of carbons” and “C–C double bond” are abstracted away from the details of the particular instance.
Similarity processes	Matching is partial and is a matter of degree, so correspondence between the representation of new and stored knowledge can be a matter of degree. Ex: a new straight-chain carbon compound with a C–C double bond might be compared to known structures of ethane or cyclohexene. Although not a ring shape, the double bond occurs in the known instances which have suffix “–ene”, so the new instance is deemed an alkene.	Similarity-based reasoning: representations of the new instance and the existing knowledge that it is compared to are equally specific abstractness. In the example of the alkene, the new compound is compared to specific instances of other structures (e.g., ethene, butene, cyclohexene).

---

Fig. 1 maps a representation space according to the further differentiation of these processes motivated by degree of abstractness the representations differ by, which thereby defines four types of reasoning. This scheme explains memory bank reasoning as an antecedent of a rule being equally specific as the existing knowledge to which it is compared, thus providing no basis for generalization. On the opposite extreme, the class of reasoning that involves partial matching to an abstraction can explain prototype reasoning. The most commonly investigated types of reasoning, rule-based reasoning and similarity-based reasoning, are explained as opposites in terms of strictness of matching and of specificity involved in comparing the two representations. Rule-based reasoning occurs when there is a difference between abstractness in the representations of stored knowledge and the new instance, but the matching between representations is strict. Similarity-based reasoning occurs when the two representations are similarly abstract (i.e., both could have low levels of abstractness, or both could have high levels of abstractness), and when the matching is partial.

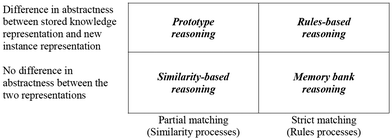Fig. 1 Possibility space for representation mapping (adapted from Fig. 2 of Hahn and Chater, 1998b, p. 206). The horizontal axis is strictness of matching, which defines the cognitive process used (similarity is partial matching while rules is strict matching). The vertical axis is the comparison between the two representations measured as the difference in abstractness between the new instance representation and the stored knowledge representation (bottom = no difference, top = difference exists).

The representation mapping framework of Hahn and Chater (1998b) provides a possible means for distinguishing different reasoning approaches, and explaining how they arise from separable constructs: (a) levels of abstractness in the new instance vs. stored knowledge representations, corresponding to the vertical axis in Fig. 1, and (b) underlying cognitive processes in which the mechanism of abstracting differs, corresponding to the horizontal axis in Fig. 1. Thus, the representation mapping framework might be more flexible and comprehensive to capture the diversity of students' cognitive processes than other typologies, as described above.

We expect this framework to be sufficiently flexible to apply across different kinds of problems (e.g., easy vs. difficult by various typologies and frameworks, quantitative vs. conceptual, analytical vs. design), with a variety of strategies for solving problems.

Testing the usability of representation mapping

We are interested in examining how students' problem solving processes and degrees of abstraction in different STEM disciplines can be characterized. Therefore, we must investigate whether the representation mapping framework is useful for characterizing students' problem solving approaches and the degree of abstraction students bring to them. So far, no application of this framework can be found in the literature. The framework of Hahn and Chater is the result of a comprehensive consolidation of different lines of research on students' problem solving processes. This portends an opportunity that aspects of this problem solving process that were covered by different frameworks in the literature might converge under this proposed framework. This perspective paper therefore intends to provide evidence for the usability and the benefit of its application.

Thus, we examined the following question: How can the representation mapping framework be used to examine abstraction capacity? We intend to address this question by analyzing the problem solving process of a wide choice of students, selected from different courses, and different professors, working on diverse problems.

Methods

Settings and participants

Participants were recruited from a medium-sized non-traditional university in the northeastern United States. Data were collected from the professors and student volunteers in three courses that occur during the sophomore (2nd) and junior (3rd) years of the undergraduate chemistry program. The three courses were selected because they occur in the middle of the undergraduate chemistry curriculum and have very different kinds of problems. Furthermore, students in these courses have demonstrated at least a basic understanding of chemistry by having passed prior courses in the curriculum. Courses were chosen from both the traditional and the off-semester (explained below) conditions in the undergraduate program, in order to include participants with a wide range of academic performance. The number of participants in each course, gender distribution, and mean SAT scores of students who took the SAT, are shown in Table 2.†

Table 2 Student participants by course, and SAT percentile mean and standard deviation based on students who took the SAT (number of students indicated in parentheses)

Course	Female	Male	SAT percentile (national scale) as mean (SD)
Organic 1 (O1)	5	2	M = 50, SD = 21 (6 of 7)
Organic 2 (O2)	2	3	M = 90, SD = 4 (4 of 5)
Thermochemistry (T)	2	1	M = 97, SD = N/A (1 of 3)

---

In accordance with the institution's IRB approval, student participants were volunteers contacted via announcements in laboratory or lecture, with the instructor's consent, and were offered small denomination gift cards. Race/ethnicity of participants was a typical sampling of the university's population: 46% Caucasian, 7% African American, 11% Asian, and 36% from other ethnicities. The SAT percentiles of the participants who took the SAT generally fell within the typical range of students accepted to the university; the middle two quartiles of students admitted to the university fall between the 47th and 85th percentiles of SAT-takers on a national scale. The Organic 1 course was in its off-semester when data were collected. Generally, one-third of students at this university who take the off-semester organic chemistry courses are students who did not pass the course once before. This is likely related to the lower mean for SAT percentile in Organic 1. For reference and privacy purposes, a label was assigned to each student indicating the course in which the student was enrolled (O1, O2, T) and the student's position on the interview list in that course. For example, the third person interviewed in the Organic 2 course was labeled O2-3. All three professors were male. The O1 professor had 11 years of experience teaching, the O2 professor had 2 years, and the T professor had 1 year.

Data collection

The principal strategy for data collection was semi-structured interviews. The interview protocol was designed to elicit professors' and students' approaches to solving problems that are central to the material covered in their courses. Interviews were conducted using a LiveScribe pen to be able to associate drawn solutions with spoken explanations.

The professors were interviewed shortly after giving Exam 1 (the first of two or three midterm exams in each course) and prior to interviewing the students. During the interview, professors were asked to think aloud through the major ideas in all of the problems on the exam, and then to select the one problem that they judged to be a good indicator of a student's general understanding of the material covered on the exam, if it were perhaps necessary to evaluate every student's general understanding based on a single problem. We then asked the professor to show us how he would expect a proficient student to solve the problem. We elicited a comparison of how an expert would solve the problem vs. how a proficient student should be able to solve the problem, which lent us insight into differences between expert reasoning and the reasoning expected by these faculty of students who should be on their way toward expert reasoning. Professors were also asked to provide an additional similar problem that had not been seen by students in the present course. They provided these either from a prior year's exam, a test bank, or their own design. The exam problem and alternative problem for each course are provided in Table 3. The objectives of the three courses from which participants were recruited, and the professors’ explanations (from their interviews) of what they intended their exam problems to test, and why they considered that the alternative problems they provided tested the same material, are provided in the Appendix.

Table 3 Exam problem and alternative problem about which participants were interviewed in each course

Course	Exam problem	Alternative problem
Organic 1	How much of the R enantiomer is present in 10 g of a mixture which has an enantiomeric excess of 60% of the R isomer?	A 0.2 g mL^−1 solution containing a mixture of enantiomers rotates light by −2° in a 1 dm polarimeter. A pure sample of the R enantiomer has a specific rotation of +20°. Determine the enantiomeric excess (and which enantiomer) present in the solution.
Organic 2	Make this from the provided cyclopentane and any other carbon species or reagents that you would like. List all reagents and species used. Mechanisms not necessary.	Make the following substance from the provided propane and any other carbon species that you would like. List all reagents and species used. Mechanisms not necessary.
Thermochemistry	A sample of a monatomic perfect gas occupies 1.00 L at 25 °C and 1 atm. (a) What pressure is needed to compress the sample to 100 mL at this temperature? (b) If this compression is reversible, how much work is done on (or by) the sample? (i.e., calculate w for this process.) (c) Once the process is complete, what will the change in the internal energy of the system be? (calculate ΔU) (d) What is the heat flow into (or out of) the sample? (calculate q) (e) If the system is allowed to reversibly and adiabatically expand back to its original volume, what will the final temperature be? (f) For this second step, what is the change in the internal energy of the system? (equation sheet provided)	A sample containing 3.00 mol of a diatomic perfect gas initially at 300 K and 2 atm is heated at constant-volume to twice its initial temperature. Calculate q, w, ΔU, and ΔH for each step and overall. (equation sheet provided)

---

Each student was interviewed about two problems written by the professor: one from the exam that the student took one to four days prior to the interview, and a second problem that was provided by the professor as an alternative to that problem. The first problem allowed the interviewer to gauge what kinds of prompts worked best to uncover the student's reasoning, representations of stored knowledge, and how the student views problems. Since students had already taken the exam, they had had more time to think about the problem on the exam, and may have talked with others about how to solve it. In some cases, the solution to the exam had already been posted as well. Therefore, we also interviewed students about the problem that they had not previously seen, but which tested similar material to the exam problem. Our expectation was that some students might use some elements from the exam problem as the stored knowledge resource, while other students might see the second problem as substantially different and rely on different stored knowledge as a resource to solve it.

Data analysis

Interviews were transcribed from audio recordings taken using the LiveScribe pen. Videos with voice audio were generated from the LiveScribe data. The transcripts and videos were considered simultaneously during coding, applying an iterative, non-linear constant comparison method of analysis (Charmaz, 2006), with qualitative analysis software (Dedoose) used to code the transcripts and facilitate the process of analysis. Interview transcripts were first parsed into episodes of reasoning, which usually comprised the entire reasoning about solving a problem, i.e., there were two episodes per transcript. Episodes were then analyzed initially to describe the pathway taken to solve the problem, e.g., identifies X and Y as given, clarifies Z as unknown, then applies equation Q by substituting X and Y to generate Z; or recognizes the problem as a W-type of problem, recalls a similar problem from the homework, and fits the exam problem to the homework problem solution.

After generating these descriptions, we paid attention to the cues noticed by the student when solving the problem, which aided in characterizing the stored knowledge representation used as the main resource in solving the problem. For example, some students relied on remembered equations while others began with a mental image of what the concept means in the laboratory. The stored knowledge representations used in each course were grouped into categories, for example: (a) conceptual picture of enantiomeric excess as unequal balance, (b) percentages of enantiomers as two equations and two unknowns, or (c) equation for enantiomeric excess in terms of path length, observed rotation and concentration. Frequently, the student did not describe the new instance representation in as much detail as the stored knowledge representation, so we relied on the problem-solving process followed by the student to infer the new instance representation. To do so, we characterized the process used in solving the problem, particularly what actions were taken by the student, and then grouped these into categories, for example: (a) describes a pictorial representation with light rotating as it passes through the sample, or (b) recognizes values of relevant variables and substitutes them into an equation. Based on the comparison of the solution process/new instance representation and the stored knowledge representation, we determined what was matched and evaluated whether matching was strict or partial, and whether level of abstractness in the stored knowledge representation was substantially similar to the new instance representation, greater than it, or less than it.

The first author coded all interviews in the data set. To test inter-rater reliability, six students' answers to problems were randomly selected from the 30 problem-solving activities in the entire student data set (20% of the student data). The second author independently determined the stored knowledge and new instance representations, and coded these for the type of matching (partial or strict) and the difference in abstractness of representations (minimal-both low, minimal-both high, new > stored, or stored > new). There was 100% agreement on matching. Since difference in abstractness involved separate evaluation of the abstractness of the representations and then determination of the difference, we paid attention to whether the abstractness evaluations were aligned or not (i.e., effectively two codes per student answer). Agreement between the raters in this was 75%.

Comparisons illustrating representation mapping

Analysis of the types of matching and the abstractness level differences between stored knowledge vs. new instance representations allowed us to identify the reasoning processes used, according to representation mapping. Following the presentation of examples in the full possibility space of Fig. 1, key comparisons are made to illustrate the capability of the representation mapping framework to capture abstraction through classifying reasoning processes, noting characteristics that seem to differ by reasoning process, and illustrating how these reasoning patterns appeared in problems in the three courses. For each problem solution that is discussed, we provide an icon that refers to Fig. 1, in which the reasoning on that problem is indicated by a grayed box representing the quadrant in Fig. 1. For example, when the lower left quadrant is gray (), it indicates similarity-based reasoning, which is a similarity process (partial and specific matching) with nearly equal levels of abstractness of the representations.

The possibility space

Table 4 presents a summary of illustrative comparisons in each of the four quadrants in Fig. 1. The vertical axis in Fig. 1 represents a difference between the degree of abstractness of the new instance and the stored knowledge representations. Thus, in each quadrant, two possibilities exist. In the lower half of the figure, where abstractness difference is near zero, this difference could result from two representations with high abstractness or two representations with low abstractness. Similarly, in the upper half of the figure, where abstractness difference is large, this could results from the abstractness of the new representation being greater than the abstractness of the stored knowledge representation, or vice versa. Therefore, eight possibilities exist for ways in which reasoning could be categorized. While not all of these were observed in the data that were collected, sufficient examples exist to make comparisons to illustrate the versatility and potential of the representation mapping framework for examining abstraction in problem solving.

Table 4 Summary of reasoning patterns observed and examples of data illustrating cases of reasoning during problem solving in each quadrant of Fig. 1, with two possibilities of difference between abstractness of representations in each quadrant

Prototype reasoning	Rule-based reasoning
• Abstractness (new instance) > Abstractness (stored) Comparing, contrasting, analyzing specific cases (values, substances, structures etc.; stored knowledge) in order to generalize across these cases and to derive a functional or conceptual relation (new instance) O1-3 on alternative problem – Selected two variables, concentration and (0.2 g mL^−1) observed rotation (−2°) – Fitted into a remembered equation relating specific rotation, observed rotation, path length, and concentration – Compared the obtained values to values obtained for an ideal case of concentration (1 g mL^−1) and a different ideal case of observed rotation (pure S enantiomer; −20°) – Used proportions to derive a general equation giving the observed rotation in relation to the concentration ratio of the enantiomers	• Abstractness (new instance) > Abstractness (stored) Establishing new relations (functional, causal; new instance) by combining and/or replacing remembered or given values or relations (stored knowledge), thus creating a more general and complex mathematical equation or conceptual relation T-3 on alternative problem – Translated given information into mathematical equations – Searched for unknowns, combining and substituting different equations to cancel out unknowns – Calculated the result by substituting the given values
• Abstractness (stored) > Abstractness (new instance) Particular features (relevant for the problem) of a general category or relation (stored knowledge) are selected and applied as a specific example to the problem at hand (new instance). O2-4 on exam problem – Reverse synthesis, considered product as two attached parts, cyclopentane and phenol – Determined attachment point and applied category of Grignard reactions to make attachment – Constrained Grignard mechanism by preference for secondary to tertiary carbon, which set conditions for how to set up mechanism	• Abstractness (stored) > Abstractness (new instance) Searching for values or key features in the problem statement (new instance) that fit (specifically, 1 : 1) into a remembered or derived general mathematical formulae, functional representation or conceptual relation (stored knowledge) O1-1 on exam problem – Sees enantiomeric excess as a function of concentration ratios – Extends the equation (by substituting) to contain all given variables – Fits values into the generated equation

---

Similarity-based reasoning	Memory bank reasoning
• Abstractness (new instance) and Abstractness (stored) both high Extracting and focusing on specific functional features of the problem or key features of the solution process. Arguing on the most general level (e.g. a class of substances or reactions) that still meets all relevant key features O2-P on alternative problem – Identifies condensation reaction as the relevant category of reactions – Matches the target species to the starting material – Fills in reaction steps according to general class of condensation reactions	• Abstractness (new instance) and Abstractness (stored) both high Not observed in the data
• Abstractness (stored) and Abstractness (new instance) both low Extracting and focusing on specific functional features of the problem or key features of the solution process (stored knowledge). Trying to match a specific case to these key features (new instance) O2-3 on exam problem – Identifies “leaving group” as a key feature of the mechanism and “double bond” as a key feature of the target molecule – Applies specific reaction steps to establish a good leaving group – Applies specific reaction steps to establish a double bond	• Abstractness (stored) and Abstractness (new instance) both low Using a sequence of remembered steps to transform the given information (values, starting material etc.) towards the requested or assumed target (value of a specific variable, target species etc.; new instance). Both the steps and the sequence are either given or remembered (stored knowledge), but no rationale for the overall process is requested or applied O2-5 on exam problem – Remembers first step to add a moiety to cyclopentane – Remembers next step to form a double bond – Remembers next step to form a hydroxyl group, etc.

---

Categories of actions were observed in students' reasoning and use of stored knowledge and new instance representations in solving problems. For example, students were observed comparing representations, establishing new relations, searching for features, extracting features, and remembering steps. There were insufficient data to compare classes of representations used when solving problems (e.g., Treagust et al., 2003), but this would be an important consideration when more data are available.

Rules vs. similarity processes

According to the representation mapping framework, the characteristic of reasoning that differentiates similarity and rules processes (the horizontal axis in Fig. 1) is whether matching is partial, or strict, respectively (see Table 1). This difference is illustrated here for the alternative problem in the Organic 1 course (see Table 3 for the problem statement).

One student, O1-1, began solving the problem using a stored knowledge representation represented by Fig. 2. It has enantiomeric excess symmetrically laid across the center of a distance from 0 to 100, such that to either side, half the difference between 100 and the enantiomeric excess rests.

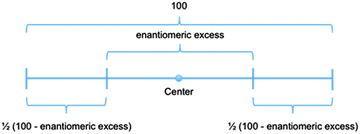Fig. 2 The stored knowledge representation of O1-1 when solving the alternative problem in the Organic 1 course.

She tried to find matches in the problem statement to the enantiomeric excess variable in the representation she had in mind, but quickly discovered that her representation did not have enough variables:

That is too much. I don't know what that means. But what is the enatiomeric excess. Oh I think it's like the same formula. Enantiomer excess but this time instead of the r minus s. Or hmm. I don't know why they have the density there but hmm. I know if the r is plus 20, I know the s is negative 20 I think. But I'm not so sure because um they didn't say it's like racemic form. Okay I'll just try and see what happens. I guess 20 minus 20 okay divide by, oh you can't divide by 0. No. For 20 plus this actually get 0 times 100. So that's not right. So this can't be right. (O1-1)

She tried to remember a formula with two additional variables that appeared to be in the problem statement, concentration (c) and path length (l), and then continued to try to fit the given information (using the rotation of −2 degrees) into her stored knowledge representation:

O1-1: There's 100, what's in the formula you write something like… Over c l. Yea I think it's something like this. So. SO plus 20. Oh God. I forgot what the c stands for … The c. Like I, I don't get this point. Like I think I'm supposed to change that into something.

Int: The 0.2 grams per milliliter?

O1-1: Yea I think that, but it doesn't cancel out with anything here. And the m…. I don't know. A solution containing a mixture of enantiomers rotates polarized light by… Hmm wait let me see. I'll try this. (Laughing) I'll keep trying it. I'm gonna minus, minus 2. And then that so that's um 22 divided by 18 times 100…Oh like dividing by 2 by 2 and then like trying to get a good number. That's probably gonna be like um…Hmmmm. Yea. 1100 minus 192. Would give you an answer of 2.2 so that 122.22 huh that's a big number. Percent. Hmm. I don't know. I don't like this formula. I like this one. I'd rather change it to this one. But I mean if I was doing an exam and I was stuck here and there was no time I would probably give this answer.

The approach taken by O1-1 is characteristic of rules processes. She sought to find the values in the new instance of each of the more general variables that she knew were present in her stored knowledge representation. Matching is strict.

Another student, O1-3, initially approached this problem in a manner involving strict matching. This initial approach involved identifying the known and unknown values given in the problem, then trying to fit them into an equation she remembered (her stored knowledge representation):

So when I just saw specific rotation and this I automatically thought of the equation that he gave us, um observed rotation over the concentration times the length. And then when he said that the specific rotation is 20° I know this is gonna be the specific rotation. So I know that this is gonna be 20°. And then I don't have any other information so far. And then a solution containing, so right now it's giving us the concentration. And then it rotates the plane by −2° so I know that this is gonna be −2°. And then it tells us that the length is 1 D which is standard. What is the enter, enty, enantiomeric excess of the mixture. Um so I would solve it just normally and say 20° equals −2° over 0.2 multiplied by one. So then I would do, multiplied by 0.2 gives me the negative oh no wait, −2°. (Long silence) (O1-3)

The equation from class that she was referring to is:

where [α] is specific rotation, α is observed rotation, l is path length, and c is concentration. She tried to locate values in the problem statement and substitute them, but realized that this representation was insufficient because the necessary values were not provided to solve it.

When this did not work, she began instead to generate a new instance representation based on comparison to this stored knowledge representation using proportions. She selected two variables, concentration (0.2 g mL⁻¹) and observed rotation (−2°), and made specific comparisons of the values of these in the sample to an ideal case of concentration (1 g mL⁻¹) and a different ideal case of observed rotation of pure S enantiomer (−20°), respectively:

So what I do note is that the concentration is usually 1 gram per milliliter. So I know that this is one-fifth. So I know whatever um excess, I'm gonna multiply it by 5… So I know that, so whatever the excess is I'm gonna multiply by 5 and then get it, the percentage. (Silence) Oh. (long silence) 2° over 20° I think that gives me a tenth. Yea it gives me a tenth. So that's 10%. And then if I multiply it by 5, cancel this and get 50%… Excess… And that's specific rotation but its, yea because if it's actually rotating it 2° out of the 20° it's supposed to it's a tenth of it. So it would be 10% of what it's supposed to do. And then because the concentration is only a fifth of what it's supposed to be I'll take the 10%, multiply it by the 5 to get 50% excess supply. Yea. (O1-3)

O1-3's approach is characteristic of similarity processes, in which matching is partial.

Abstractness in stored knowledge vs. new instance representation

Abstractness differences between the stored knowledge and new instance representations determine the vertical position in the representation space of Fig. 1. If there is a large difference, then the reasoning is rule-based (if strict matching) or prototype (partial matching). If there is a small or no difference, then the reasoning is memory-bank (if strict matching) or similarity-based (partial matching). Small or no difference can occur if the stored knowledge and new instance representations both have low levels of abstractness, or if they both have high levels of abstractness.

Let us consider the case of a student, O2-5, whose reasoning on both problems demonstrated strict matching, and who exhibited a small difference in abstractness in her representations (both low levels of abstractness) when solving the exam problem, but a large difference in abstractness in representations when solving the alternative problem. According to the representation mapping framework, then, she demonstrated memory-bank reasoning on the exam problem, and rule-based reasoning on the alternative problem. (See Table 3 for the two problem statements.)

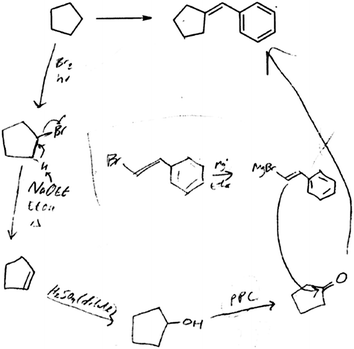
This student's solution to the exam problem is shown in Fig. 3. Her stored knowledge representation consisted of various remembered one-step reactions that connect alkanes, usually beginning with bromination, as she explained here:

Fig. 3 The solution of O2-5 to the exam problem in Organic 2.

So basically when I was practicing it would generally with these kinds of like connecting alkanes are kinda just generating new carbon chains from whatever you start out with usually just like neutral carbon species. Um they would, like a lot of the problems I just kind of right off the bat started off with Br ₂ and light because it was easy for me to add things after that to whatever I was making. (O2-5)

She solved the problem with a common mistake made by students who solved this problem incorrectly: she located the Grignard attack incorrectly. She performed many reaction steps involving small changes to the symbolic structure of the compound in an attempt to reach the product using the steps she knew. This student's representations of remembered reactions were used in strictly matched ways: bromination performed on a carbon in an alkane (cyclopentane) to make a bromide, elimination of bromine performed via sodium ethoxide to form a double bond, the double bond converted to an alcohol by acid hydrolysis, an alcohol oxidized to a carbonyl with PPC. She did not remember how the reactions worked, she only remembered what they did:

O2-5: Uh then I guess I used PPC and I don't even really remember, I should've studied before I came here.

Int: And what is PPC? Can you remind me?

O2-5: I don't even remember what it stands for. Um.

Int: Where did you come up with the PPC?

O2-5: It was, I was just going through notes in my notebook before I came to class I have it with me if I can show you actually. It might be easier for me to explain if I do look and I probably did that wrong also. Trying to uh, what was that reduction, reduction? Is that reduction? I don't even know. Turning OH into the double bond O, carbonyl.

When she reached the carbonyl, cyclopentanone, she got stuck: “It said that I can use any kind, any other carbon species that I would like so I just took the main part and made it into the Grignard um thing here.”

In contrast, the student's new instance representation for the alternative problem was more abstract than her stored knowledge representation (see Table 3 for problem statement). She began with the same stored knowledge representation of lots of remembered one-step reactions for connecting alkanes: “Okay so it's kinda the same exact approach actually because there's this part and then it's connected to the new part with a double bond.” She added to this that the key step in the synthesis should involve a nucleophilic attack. She realized that her stored knowledge representation would not suffice:

So my first thought is that I need to make this here um a maybe electrophilic so that it can undergo a nucleophilic attack or vice versa it doesn't really matter as long as one can attack the other. Um so um let me think about this. I guess I could just do S _N 2 when I think about it. Maybe not no that doesn't work. Um I would actually just do the same thing that I started out with oh wait that wouldn't work ‘cause that's secondary. Hmm, um. I can do oh wait no that does work. I'm sorry that does work. As the primary, uh the major product. The other one is negligible. Um and then I don't even remember what it does. Uh. Damn. I guess then I would just make up something to add like I would do this but instead of this uh alkene substrate I would put hmmm I'm sorry. (O2-5)

She then began thinking about how the mechanism might work – a shift from applying remembered one-step reactions – and reasoned that she could create a nucleophilic attack:

And then maybe I would take this cyclohexane and I feel like I could do a Grignard to make it nucleophilic. Give it a nucleophilic center. Um so it would have to already have a Br and Mg. MgBr so then that is equiv… or practically equivalent to uh this. I'm sorry wait it's the other way around, this is negative … Actually now that I think about it. Maybe I could even instead of this I could do alternatively like that instead. And turn that into the Grignard.

After several more trial-and-error cycles, she decided on the synthesis shown in Fig. 4.

Fig. 4 The solution of O2-5 to the alternative problem in Organic 2.

Her solution had an error in not recognizing that bromination of the product near the “X” would result in many possible products, as there are two tertiary carbons and five secondary carbons in the structure. Nevertheless, she generated this solution by a process of adding abstractness to her stored knowledge, stretching her knowledge about nucleophilic attack mechanisms to figure out how to create the double bond:

I wanna make a double bond here is what I want ultimately. One way I can do that is by elimination, but I don't have a good leaving group. So I can turn, I can do another one of these and that will select the tertiary position and give me that. And I have a hydrogen here, which is, thank God, ‘cause otherwise I'd be totally stuck. Um. And then I can do an E2 process, this is E2. Um with a base, and I don't want it to be very sterically hindered because it's all, there's a lot of sterics goin’ on here. Um so just NaMeOH, MeOH, heat and, uh, that will… hold on a sec… well first this has to go, and then the hydrogen will add across here. Oh well. Ultimately I'm getting this. Double bond. Sorry it's so sloppy. Double bond! And that's pretty much it.

Low–low vs. high–high abstractness

According to the representation mapping framework, both memory-bank and similarity-based reasoning can occur with either similarly low levels of abstractness in the stored knowledge and new instance representations, or similarly high levels of abstractness. The following two examples show how this looked in the data. One student, O2-3, and the professor both solved the exam problem in Organic 2 using similarity-based reasoning. However, the student demonstrated similarly low levels of abstractness in both representations, while the professor demonstrated similarly high levels.

The first thing the student noticed was that the cyclopentane had a phenyl group attached to it by a double bond. He keyed in on the double bond (partial matching, specific) and all of the other features of the problem fell away. His sole aim then became figuring out how to create the double bond through generating a good leaving group. During the interview, he described many mechanisms in the category of “leaving groups”, his stored knowledge representation. He tried creating an alcohol group on the cyclopentane so that it would be a leaving group. He tried creating an “OH hoop” (his words) epoxide mechanism, and also considered trying to make an alkyne (considering it a leaving group) into the alkene. Eventually, he was able to make cyclopentanone. He remained fixated on leaving groups:

This is when I started thinking about Grignard. So the thing I know about Grignard is, I mean he [the professor] didn't say you couldn't do it so I just said okay I'll just make a phenyl group with a bromine um. I don't know what this is called but you know I just made a Grignard reagent here. I was like that will just attach to this alco, uh this oxygen here. It will create this OH here. Then I can make it a good leaving group, pop it off. Which is the step here, OTs [tosylate]. And then from there treat it with, I don't even know what this is, sodium methoxide. And then I'm not sure if this is correct but I was hoping that the double bond would go here as opposed to here. My reason for this was here, that this is already stabilized through resonance so if I add something here it, it's just not gonna stick so it's going to go here. And that's when I start breathing again. (O2-3)

Both the stored knowledge representation (leaving groups) and the new instance representation (cylopentanone attached to a phenyl group by a double bond) had similar degrees of abstractness (leaving groups was a narrow set of attachments that can be replaced, double bond was a type of connectivity). The matching of these representations was partial with comparable abstractness. The reasoning was similarity-based.

By contrast, the professor solved the problem by comparing the final product to the starting material:

When I look at this problem here I look at the final product first, and the final product has in it a benzene ring, so here's what I look at, I look at the very beginning and I see ok, what do I have to start with? I have to start with cyclopentane. Alright, so start with cyclopentane, do I have cyclopentane in my final product at all? And I do, I have it right there ok? That's important because this is something that's definitely used from the starting material, and more so this phenyl moiety is a new species, new entity. (O2-P)

He explained that the process then involves

a four-step synthesis with chlorination followed by Grignard formation and alternate Grignard attack, benzaldehyde attack, and then water, and then protonation using acid water followed by an elimination type of process, either an E1 or E2, depending on how you want to look at it, so four steps.

Later in the interview, when he was explaining his solution to the alternative problem, he referred to the exam problem in calling the alternative problem “another condensation reaction”, indicating that the stored knowledge representation he used to solve the problem was a category of reactions that all have in common that they are condensation reactions, which is a larger class of mechanisms than Grignard reactions. Like O2-3, he used partial matching to compare the new instance (a starting material structure with a moiety attached) to his stored knowledge representation (condensation reactions). Both representations contain high levels of abstractness, and the reasoning was similarity-based.

Abstractness in stored knowledge > new instance representation vs. the reverse

According to the representation mapping framework, prototype and rule-based reasoning can occur when there is a difference in the levels of abstractness of the representations; however, the difference can occur in either direction. The following two examples, from two students' solutions to the alternative problem in the Thermochemistry course (see Table 3 for problem statement), illustrate both of these for problem solving on the alternative problem that involved rule-based reasoning. The professor provided an equations sheet with the exam, so we also provided the equation sheet during the interviews.

One student, T-2, paid attention to relevant cues and their consequences in order to simplify the general case of a perfect gas to the situation of the problem posed:

Ok, so the first thing I'm thinking is that I'm heating this, so I'm changing q, so ΔU would not be 0 and neither will ΔH. ΔH is equal to q so it won't be 0. So I have constant volume, I'd do ΔU = C _v ΔT, it's constant volume heat capacity. It's a diatomic perfect gas, so that means it's linear, which is (5/2)R, so ΔU = (5/2)R. 600 minus 300, twice its initial temperature, its initial temperature is 300, so, ΔU… so I have, ΔU… so now I'm looking for an equation for w, but w is gonna be 0, because w depends on the change in volume, and there's no change in volume, so ΔV = 0 so w = 0. (T-2)

After he set up all of the equations, he plugged in the numbers and solved for each value requested in the problem. In this example, the student held the general case of a perfect gas, which could be monatomic, diatomic, or something else, as the stored knowledge representation, along with general equations, such as ΔU = q + w from the First Law of Thermodynamics. He methodically looked for the complete set (strict matching) of the cues necessary for simplifying the general case – what type of gas, what variable is held constant during the change (e.g., volume, temperature, heat) – in order to simplify. Only after producing the equations did he substitute the numbers. In this case, then, the stored knowledge representation has greater abstractness than the new instance representation, while the matching is strict. He also used the equation sheet to confirm his derivations, rather than to find equations to use:

T-2: so I have, ΔU (thinking) so now I'm looking for an equation for w, but w is gonna be 0, because w depends on the change in volume, and there's no change in volume, so ΔV = 0 so w = 0.

Int: and where did you learn that from? something that you learned in class or?

T-2: it's just looking at the sheet, I was looking for an equation to find w so that I can then find q because I know that I could find q with ΔU and w, so all the equations for w have a change in volume and if volume is constant then these are all multiplied by 0, and become 0.

Another student, T-3, used a different approach to the same problem. She began by writing down the given information and translating sentences to equations where possible, e.g., T_final = 2T_initial. She then searched for unknowns for which she had sufficient information to solve, and charted a path through calculating their values:

This question, contain 3 moles, so and …and then … so temperature is T = 300, and then we have pressure, is 2 atm, heated at constant volume, so needs constant and ΔT, ΔV equal zero. Two times its initial temperature so this is T _final , and then we got T _final equals 2 times T _initial , 600, and then we calculate q equals, I'm looking for equation for heat, we don't have heat capacity, q, need to do work first ok… for T _initial …so work is zero, total V equal zero … q, q, q … I don't know, q, so q equals total T and then V is constant so ΔT equals … I don't know how to do this one… oh I don't remember (laughing). So C _v equals … dU, Δq ok, I just know the relationship between them, I don't know how to calculate the heat, I just jump this part. (T-3)

After “jumping” that part, she began writing down all of the equations she could remember that related to the cues she had noticed. The interviewer then asked her to explain:

Int: ok and where did you get this from?

T-3: from the class and I don't remember is 6 over 2 or 3 over 2 or half ‘cause it's diatomic… diatomic… and then … I'm not sure

Int: ok how about this, where did you get this from?

T-3: because Δenergy equals the heat

Int: oh you have it here

T-3: actually, yeah and the work because ΔV equals zero so work is zero

Int: so then you have that relationship ok

T-3: yeah

Int: but you don't know the values, you just know the formulas

T-3: yeah, I don't know, ‘cause I don't know how to calculate q, but if I have q then I have the following.

Although she could not remember the value of C_v for a diatomic gas, she successfully wrote down all of the equations necessary for calculating the requested values, which could then be calculated once C_v was known. This student's stored knowledge representation consisted of lots of equations corresponding to different situations, which was a lower level of abstractness than the new instance required, and she strictly matched the equations to the situation of the new instance (diatomic gas, heated at constant volume). Although she could not remember the value of a constant that was needed to solve the problem, C_v, she was able to produce all of the equations necessary and placed them in terms of the constant. Thus, her new knowledge representation was on a higher level of abstractness than the stored knowledge. Although the problem was set up as a step-wise process, and equations were provided on an equation sheet, this student did not use the equation sheet.

Summary of results

The reasoning processes used by students in each course and by professors are shown in Table 5. All three professors demonstrated their own solutions to both problems in their courses using similarity-based reasoning with high levels of abstractness in both representations. In all three cases, this was different than the rule-based reasoning they described to us that they expected a proficient student to use in solving each problem. Across all problems, students predominantly (90%) used strict matching, i.e., rules processes, the right half of the possibility space of Fig. 1. Out of 30 problem solving processes, 18 were categorized as rule-based reasoning (60%) and 9 as memory-bank reasoning (30%). Prototype reasoning occurred only twice, and similarity-based reasoning only once. There are insufficient numbers of students to make any claims from these data about what kind of processes or reasoning tend to be used by students in one course or another; more participants and more variety of problems solved per student would need to be included in order to examine such questions. The aim of the present study was to determine whether and how the representation mapping framework can be used to study students' abstraction capacity. In this light, it is valuable to consider the variety of approaches to problem solving taken by students solving different kinds of problems, the variety of stored representations and new instance representations inferred, and the differences in abstraction capacity that can be illuminated through application of the representation mapping framework to analyze problem solving.

Table 5 Types of reasoning exhibited by students (N = 15) and professors (N = 3) in each course. Each person is counted twice: once for the problem on the exam, and a second time for the alternative problem. Row-wise percentages of the type of reasoning are shown in parentheses

Course	Memory-bank	Rule-based	Similarity-based	Prototype
Organic 1	6 (43%)	7 (50%)	—	1 (7%)
Organic 2	1 (10%)	7 (70%)	1 (10%)	1 (10%)
Thermochemistry	2 (33%)	4 (67%)	—	—
Total (students)	9 (30%)	18 (60%)	1 (3%)	2 (7%)
Professors	—	—	6 (100%)	—

---

In the Organic 1 course, the most common strategy (9 out of 15) involved attempting to identify and substitute the given information into a remembered equation to solve for the unknown. Five different stored knowledge representations were used among the seven students. Generally, the stored knowledge occurred in the form of an equation, though represented in various ways (with symbols, pictorially, as a number line). The one case of a conceptually stored knowledge representation (the meaning of enantiomeric excess) was used by only one student, and only for the alternative problem. In all cases of memory bank reasoning, both the stored knowledge and new instance representations had low levels of abstractness.

Differences arose between how students approached the exam problem and the alternative problem. For the alternative problem, twice as many Organic 1 students as in the exam problem approached the problem with memory-bank reasoning. Since students had not seen the alternative problem previously, and the problem was quite different than the exam problem, the representation formed in the exam problem was of limited use, so this problem may have been a better probe of capacity for abstraction. Only one student solved the alternative problem correctly. This student employed prototype reasoning to do so. She recognized that the stored knowledge representation had insufficient abstractness necessary to solve the problem, and generated additional abstraction for the new instance representation. Two other students also attempted to generate new instance representations with a higher level of abstractness than the stored knowledge representation, but did so within strict matching, i.e., rule-based reasoning.

In the Organic 2 course, most students (4 of 5) used “lots of little chemistries” (term from O2-P's interview, meaning memorized mechanisms to perform small changes to the symbolic structure of a compound) as the stored knowledge from which they drew to solve the problems. There were four different stored knowledge representations used; some students used a combination of two representations: (1) Parts can be joined via a Grignard reaction (used in 8 of 10 instances), (2) Lots of “little chemistries” can be combined in sequence (4 of 10 instances), and (3) Lots of mechanisms can be combined in sequence (1 instance). The latter two were differentiated by the way in which students held the representations of reactions in mind, as remembered patterns (without the mechanism underneath it), or as remembered mechanisms (from which the reaction patterns derive).

There were also some differences between approaches to the exam problem and the alternative problem. There was a variety of reasoning processes used on the Organic 2 exam problem, but all five students used rule-based reasoning on the alternative problem. Of these five, in three cases students simplified a more general rule to the specific case of the new instance, and two students generalized a specific example to a more general rule in order to solve the problem. The two students who demonstrated the greatest abstractness in representations also solved the alternative problem correctly.

In the Thermochemistry course, stored knowledge occurred in only two forms, either as sets of remembered equations, or as more general equations that could be simplified to fit the circumstances specified by conditions. The former case corresponded to memory-bank reasoning, while the latter corresponded to rule-based reasoning. Two students had low levels of abstractness in both stored knowledge and new instance representations (corresponding to memory-bank reasoning), and one of these students relied on the equations sheet, for example, using a trial-and-error approach with each equation for work, w, until she found one that worked. One of the four instances of rule-based reasoning involved generating greater abstractness (to derive a new equation), and three involved simplifying more general equations to the special case specified by the conditions.

There were also some differences between how the Thermochemistry students solved the exam problem and the alternative problem. Both cases of memory-bank reasoning occurred with the exam problem, and all reasoning on the alternative problem was rule-based. All three students solved the alternative problem partially correctly. The student who solved it almost entirely correctly only missed noticing that the problem statement indicated that there were 3.00 moles of the substance (he used 1.00 mole in the calculations). This student also demonstrated the most abstractness in his representations.

Discussion and conclusions

Examining Table 5, rules processes appear to be more dominant than similarity processes in all courses. There are many possible explanations for such an observation. For example, it may be an indication that throughout their educations, students are taught to follow rules processes more often than similarity processes. This is in alignment with the results of Raker and Towns (2010), who found that the majority of problems assigned in Organic 2 required rule-usage. An alternative explanation could be that rules processes are easier than similarity processes to use. In our continuing work, we will pay attention to the reasoning processes that professors use when demonstrating example problems to their classes, as unspoken value statements can certainly be communicated through inferences taken by students from such emphases. A first hint can be found in contrasting the professors’ problem solutions in this study with their expectations a proficient student would solve the problems. While the professors themselves solved the problems using similarity-based reasoning, they expected rule-based reasoning from their students. Of the similarity processes, similarity-based reasoning occurred in both students' and professors’ problem solving. However, in students it always occurred in low–low abstractness (stored knowledge vs. new instance representations), while in professors it occurred in high–high combination. In considering an arc to utility, this research may be able to guide ways to develop interventions that bridge students within similarity-based reasoning to develop increasingly higher levels of abstractness in both stored knowledge and new instance representations. Such an intervention would necessitate making professors aware of differences between their own reasoning processes, which were similarity-based in all of the professors who participated in our study, and the reasoning that they teach students to use, which appeared to be rule-based for all of the professors in our study. This differentiation of expectation might already be a first aspect of awareness (maybe not totally conscious), but the question is how to bridge these differences and to provide students' with a broader range of reasoning capabilities.

Finally, it appears that representation mapping provided a sound base for analyzing students' and professors' reasoning processes on a variety of problems, stemming from different courses in the chemistry curriculum. All approaches, both by students and professors, to all problems could be coded reliably, providing first evidence for the usability of this framework in practice. The following sections provide further evidence on the question how the data analyzed in this study can be seen in the light of relevant literature.

Comparison of representation mapping reasoning processes to prior studies in chemistry

Both Kraft et al. (2010) and Christian and Talanquer (2012) observed three types of reasoning in graduate students and undergraduate students, respectively, in solving problems in organic chemistry. They called these rule-based, case-based, and models-based reasoning. Common to both studies was that rule-based reasoning was most prevalent. A synthesis of the findings of both studies would characterize rule-based reasoning as the use of rules or patterns induced from experiences or mental models to deduce a problem's solution. This appears to be consistent with many of the cases of rule-based reasoning classified through the representation mapping framework in our study. In cases where the stored knowledge representation was simplified to a new instance representation in order to solve the problem, students deduced their solutions from rules. However, it was also the case that some students generated additional abstraction from simpler representations, while matching variables strictly. For example, T-3 above generated more abstract equations when she was unable to remember the value for C_v. This appears, then, to add to the characterization of rule-based processing.

The second most prevalent reasoning type seen by both Kraft et al. (2010) and Christian and Talanquer (2012) was case-based reasoning. A synthesis of the findings of both studies would characterize this type of reasoning as classifications of specific remembered, experienced or learned instances into (often interconnected) categories, which are then used as resources to solve a problem. This appears to be consistent with the cases of similarity-based reasoning that we observed. It may be that the difference between low–low and high–high abstractness levels within similarity-based reasoning are related to the degree of interconnectedness of categories. Hahn and Chater (1998b) point out, however, that while categories are the prototypical way of considering similarity-based reasoning, other mechanisms also would theoretically fall under similarity-based reasoning. According to Hahn and Chater, similarity is completely characterized by three conditions (p. 206): “(1) similarity is some function of common properties (including binary attributes, continuous valued dimensions, and relations), (2) similarity is graded, and (3) similarity is maximal for identity.” They point out that instance-based approaches, such as case-based reasoning, are similarity, but there are other approaches that count as similarity as well, including geometric (Shepard, 1980) and contrast (Tversky, 1977) models in psychology, and nearest-neighbor algorithms in machine learning (Cost and Salzberg, 1993). As we continue to pursue this line of research, we will remain open to observing situations of similarity-based reasoning that do not necessarily rely on categories as the type of representation.

The least prevalent reasoning type observed by both prior studies was models-based reasoning. The characterizations of this type of reasoning in both studies are not easily merged into a common description. Kraft et al. considered it to involve construction of models of the situations and subsequent use of the models to solve a problem. Christian and Talanquer describe the models as having different scales and variables, having both explanatory and predictive power, and being used either conceptually or quantitatively. Both of these explanations could correspond to either rule-based or prototype reasoning in the representation mapping framework. However, the description by Kraft et al. seems to be about the new instance representation having greater abstractness than the stored knowledge representation, while the description by Christian and Talanquer seems to be the reverse. If it were possible to obtain the interview transcripts from the study by Christian and Talanquer, it might be fruitful to analyze them using the representation mapping framework.

Abstractness

The abstractness of representations was compared in order to assess whether there was a small or large difference in abstractness, and whether one representation had greater abstractness than the other. Representations occurred in many forms that depended on the problems, the experiences students had in class and with homework, and, probably, individual differences that would lead students to prefer some forms of representations over others. Categorizing the types of representations, their affordances, and associations with individual factors is beyond the scope of this study, and more complex methods of categorizing problems have been developed that take into account both student-specific factors and problem attributes (e.g., Dori and Sasson, 2013). However, some general patterns in abstractness emerged from our analyses which were useful to us in applying representation mapping across students' problem solving approaches.

Stored knowledge representations occurred in many forms, including pictorial representations of relationships among variables (such as that of O1-1), equations with variables represented by symbols and mathematical relations among variables (such as the equation used by O1-3) or sets of equations and unknowns that would be simultaneously solved, remembered examples or cases, and stories describing the meaning of particular constructs (such as enantiomeric excess) or causal pathways (such as reaction mechanisms). In each of these, we were able to identify factors or variables. The amount of abstractness of a student's stored knowledge representation and her new instance representation could then be compared by determining whether there were more or fewer variables or factors in the new instance than in the stored knowledge. In some cases, more variables were added to a stored knowledge representation, such as when O1-3 used two variables in the equation for enantiomeric excess to develop comparisons via proportions. In other cases, a new element was added to a story, such as when O2-3 made a leaving group leave via a Grignard reaction. In some cases, variables could be removed, such as through simplification. For example, T-2 reduced the number of variables in equations upon recognizing that there was zero change of volume.

In comparison to prior studies in which abstractness was a focus of either the analysis or of the model building, we consider this focus on variables or factors to correspond more closely to the approach of Domin and Bodner (2012), who examined abstractness in terms of what is present or absent in a representation. Other approaches, such as that of Schwartz (1995), considered abstractness in terms of how removed the representation was from the case at hand. Such an approach may be relevant primarily to the specific situation of rule-based reasoning in the representation mapping framework.

Abstracting

In many cases, the stored knowledge representation was more clearly described by the student than the new instance representation. In these cases, the latter had to be inferred through considering what the student described doing in order to solve the problem. Again, it is likely that there are many more factors associated with different abstracting actions than what we explored in this study, such as experiences in class and individual factors. However, some general patterns in abstracting actions occurred. A pictorial representation could be created as the new instance based on conceptual understanding in stored knowledge. For example, on the enantiomeric excess problem in Organic 2, based on a stored knowledge representation of a conceptual understanding of the meaning of enantiomeric excess, one student (O1-4) generated a mental picture that was something like bar graphs, where the higher bar corresponded to the enantiomer present in excess. New variables could be created through comparison to an ideal case, such as when O1-3 developed proportions. Many students attempted to add variables to existing equations or pictures. Students also made representations fit situations. A common approach was to recognize specific values of variables present in the stored knowledge representation, substitute those values, and then calculate an outcome variable. Representations were also narrowed by constraining them. For example, O2-P constrained the more general representation of condensation reactions by regioselectivity imparted through the choice of a class of reagents.

Most prior work reviewed earlier on abstracting has been concerned with examining how students generate more general abstractions, and approaches that should be useful in classrooms for helping students to do this. Many of the actions previously studied were present in our data: making drawings, idealizing, and generating equations (Larkin, 1983); and forming associations, searching for patterns, and extending patterns to wider ranges of applicability (Ellis, 2007). Less apparent to us, perhaps because it occurred to lesser extent, were the actions specified by Roschelle and Greeno (1987) of envisioning alternatives, reformulating problems, imagining alternative contexts, and recovering from errors. Two of the activities specified by Prain and Tytler (2012) were observed in our data: limiting a case or making generalizations, and basing arguments on similar cases through pattern identification. Two were not: comparing to simulations, and evaluating the coherence of claims. It may simply be that students did not have many experiences with simulations that could have been used as stored knowledge resources. None of the problems we examined made claims and asked students to evaluate their worthiness, so there was no direct mandate to do so, nor did we observe occurrences of students doing this on their own.

General conclusions

With regard to the goal of testing the representation mapping framework in capturing abstraction during problem solving in chemistry, we have shown that the framework can be used flexibly to examine abstraction capacity and to characterize types of reasoning provided by students and professors as they solved a variety of problems stemming from three different courses in the undergraduate chemistry curriculum. The framework permits analyzing both conceptual and quantitative problems. We observed differences among the small populations of students studied in each of the three courses, and these appear to suggest that, with greater numbers of participants and analysis of more problems solved by each student, we may be able to uncover trends in abstraction capacity and reasoning that occur as students traverse the entire undergraduate chemistry curriculum. Given that the framework is able to be used with a variety of problems in chemistry, it may be possible to expand this analysis to other STEM disciplines. With regard to the sample of data we collected, the results are mainly illustrative for the applicability of the representation mapping framework to analyze different students in different courses and different kinds of problems. Due to the small sample size of the qualitative study, a generalization of trends, e.g. across the three courses or the whole curriculum, or of relations between the students abstraction capacity or reasoning approaches to other factors (e.g. SAT scores) is not possible.

However, as the framework proved to be a useful and reliable lens for analyzing students' problem solving approaches, this study represents a first step toward our larger goal of determining where in an undergraduate STEM curriculum the capacity for abstraction presents a barrier to student success. In our continuing research, we hypothesize that undergraduate STEM curricula have an abstraction threshold at which point a typical student's innate capacity for abstraction is not matched to the complexity of the problems being posed, and that this threshold impacts student performance. We are motivated by the belief that students can gain the flexibility and metacognitive awareness necessary to choose reasoning approaches that are most efficient in solving problems, and that this will facilitate increased success and, ultimately, retention of students in the STEM career pipeline. The representation mapping framework was not designed for studying only chemistry problem solving. Thus, our findings may have implications not only for chemistry, but also for examining abstraction in problem solving in other domains, as aspects of abstraction in problem solving that are domain-general may be addressed in a course or courses that are common across several undergraduate STEM curricula.

Appendix

Presented here are objectives of the three courses from which students and their professors were recruited, and the professors' explanations (from their interviews) of what they intended their exam problems to test, and why they considered that the alternative problems they provided tested the same material.

Organic 1 course

Introduction to structure and synthesis of organic molecules, reactions of principal functional groups, and basis theory of organic chemistry. Focus on prediction of reaction products using reaction mechanisms, and the determination of organic structure using spectroscopy. Underlying role of stereochemistry in organic structure and reactions is emphasized.

Exam problem and professor's explanation of what it tests

Alternative problem and professor's explanation of why it tests the same material as the exam problem

How much of the R enantiomer is present in 10 g of a mixture which has an enantiomeric excess of 60% of the R isomer? — “If you just look at it, and you think a little then you should be able to get it in 30 seconds without using the calculator… this problem is about enantiomeric purity… I wanted to show them it's not just about memorizing.”

A 0.2 g mL^−1 solution containing a mixture of enantiomers rotates light by −2° in a 1 dm polarimeter. A pure sample of the R enantiomer has a specific rotation of +20°. Determine the enantiomeric excess (and which enantiomer) present in the solution. — “The other [alternative] problem that I gave you is basically related to this one… very similar, the question is about determining the enantiomeric excess so there are some data given, and their job was or would be to determine the enantiomeric excess of the mixture, again they have to know the concept of optical rotation and enantiomeric excess.”

Organic 2 course

Fundamental principles and advanced topics in organic chemistry. Carbonyl chemistry is covered in particular detail, using principles of stereochemistry, stereoelectronic theory, and molecular orbital theory as a foundation. Students learn about strategies in multi-step organic synthesis and an introduction into organometallic chemistry.

Exam problem and professor's explanation of what it tests

Alternative problem and professor's explanation of why it tests the same material as the exam problem

Make this from the provided cyclopentane and any other carbon species or reagents that you would like. List all reagents and species used. Mechanisms not necessary. — “This one was what I would call on a scale of 1 to 10, 10 being a very difficult synthesis problem, this is a roughly a 6 or a 7. In terms of synthesis, this is one of the typical build a simple molecule with no stereochemistry. That's an important thing to know, from a given starting material. So I say given this starting material and any other carbon species or any reagent that you want to use, make the final molecule and they just have to give me, and there was an endless number of ways to do it… so it was a good diagnostic.”

Make the following substance from the provided propane and any other carbon species that you would like. List all reagents and species used. Mechanisms not necessary. — “This is a good catch-all question… [it] assays the students' abilities to understand how to link up little, understand little chemistries, like little acid/base chemistry, very small reactions, even Grignard small, not very complicated. It's not like an ozonolysis problem where you have like a gigantic mechanism, it's a very simple straightforward thing.”

Thermochemistry course

Introductory course in chemical thermodynamics, kinetic theory and classical chemical kinetics. Topics include the First, Second, and Third Laws of Thermodynamics with special application to chemical transformations. Phase equilibria and the phase rule are discussed in detail. Discussion of chemical kinetics includes rate laws, order, molecularity, and activation parameters.

Exam problem and professor's explanation of what it tests

Alternative problem and professor's explanation of why it tests the same material as the exam problem

A sample of a monatomic perfect gas occupies 1.00 L at 25 °C and 1 atm. (a) What pressure is needed to compress the sample to 100 mL at this temperature? (b) If this compression is reversible, how much work is done on (or by) the sample? (i.e., calculate w for this process.) (c) Once the process is complete, what will the change in the internal energy of the system be? (calculate ΔU) (d) What is the heat flow into (or out of) the sample? (calculate q) (e) If the system is allowed to reversibly and adiabatically expand back to its original volume, what will the final temperature be? (f) For this second step, what is the change in the internal energy of the system? (equation sheet provided) — “[This] problem was a long one… it did a number of things. I think it tied together a number of different concepts that we touched upon and we covered in class, like the gas law, perfect gases and how things simplify in isothermal conditions or when the process is reversible, and then it took them through another step, well if you turn things around and take another step but it's adiabatic and go back to where you started, then how do things change. And what equations do you use and how do they, why are you using them this way. And so the whole problem is long and there's multiple parts because I wanted them to be able to see that when you come across some problem you can dissect it and break it up into bits and solve each little part individually.”

A sample containing 3.00 mol of a diatomic perfect gas initially at 300 K and 2 atm is heated at constant-volume to twice its initial temperature. Calculate q, w, ΔU, and ΔH for each step and overall. (equation sheet provided) — “It's similar, but this one's a little more involved in the things you have to do. There's more things you have to calculate so to start out. It's a similar problem; we're dealing with perfect gas, but in this case it's a diatomic which changes things a little.”

Acknowledgements

This paper was based, in part, on the undergraduate thesis of one of the authors (SA). The authors are grateful to Yehudit Judy Dori and Melissa Weinrich for providing critical feedback on drafts of the manuscript during its preparation. The authors wish to acknowledge the funding sources, US National Science Foundation awards 1348722 and 1348632, that supported part of our work. Any opinions, conclusions, or recommendations expressed in this paper are those of the authors, and do not necessarily reflect the views of the funding sources.

Notes and references

1. Amsel, E., Klaczynski, P. A., Johnston, A., Bench, S., Close, J., Sadler, E. and Walker R., (2008), A dual-process account of the development of scientific reasoning: The nature and development of metacognitive intercession skills, Cognitive Dev., 23, 452–471.
2. Bennett S. W., (2008), Problem solving: can anybody do it? Chem. Educ. Res. Pract., 9(1), 60–64.
3. Bodner G. M. and Herron J. D., (2002), Problem-solving in chemistry, in Gilbert J. K. et al. (ed.), Chemical education: Towards research-based practice, Netherlands: Kluwer Academic Publishers, pp. 235–266.
4. Cardellini L., (2010), Multi-national approach to teaching and learning, in Lovitt C. F. and Kelter P. (ed.), Chemistry as a second language: Chemical education in a globalized society, Washington, DC: American Chemical Society, pp. 43–65.
5. Cavallo A. M. L., (1996), Meaningful learning, reasoning ability and students' understanding and problem solving of genetics topics, J. Res. Sci. Teach., 33(6), 625–656.
6. Charmaz K., (2006), Constructing grounded theory, London: Sage.
7. Chi M., Feltovich P. and Glaser R., (1981), Categorization and representation of physics problems by experts and novices, Cognitive Sci., 5, 121–152.
8. Christian K. and Talanquer V., (2012), Modes of reasoning in self-initiated study groups in chemistry, Chem. Educ. Res. Pract., 13, 286–295.
9. Cost S. and Salzberg S., (1993), A weighted nearest neighbour algorithm for learning with symbolic features, Mach. Learn., 10(1), 57–78.
10. Domin D. and Bodner G., (2012), Using students' representations constructed during problem solving to infer conceptual understanding, J. Chem. Educ., 89(7), 837–843.
11. Dori Y. J. and Hameiri M., (2003), Multidimensional analysis system for quantitative chemistry problems: symbol, macro, micro and process aspects, J. Res. Sci. Teach., 40(3), 278–302.
12. Dori Y. J. and Sasson I., (2013), A three-attribute transfer skills framework – part I: establishing the model and its relation to chemical education, Chem. Educ. Res. Pract., 14, 363–375.
13. Ellis A. B., (2007), A taxonomy for categorizing generalizations: Generalizing actions and reflection generalizations, J. Learn. Sci., 16(2), 221–262.
14. Gabel D. and Bunce D. M., (1994), Research on chemistry problem solving, in Gabel D. (ed.), Handbook of research on teaching and learning science, New York: MacMillan, pp. 301–326.
15. Giunchiglia F. and Walsh T., (1992), A theory of abstraction, Artif. Intell., 57, 323–389.
16. Hahn U. and Chater N., (1998a), Understanding similarity: a joint project for psychology, case-based reasoning and law, Artif. Intell. Rev., 12, 393–427.
17. Hahn, U. and Chater, N., (1998b), Similarity and rules: Distinct? Exhaustive? Empirically distinguishable? Cognition, 65, 197–203.
18. Johnstone A. H., (1991), Why is science difficult to learn? Things are seldom what they seem, J. Comput. Assist. Lear., 7, 75–83.
19. Johnstone A. H., (1993), Introduction, in Wood C. and Sleet R. (ed.), Creative problem solving in chemistry, London: The Royal Society of Chemistry, pp. 4–6.
20. Jonassen D., (2003), Learning to solve problems: an instructional design guide, Hoboken, NJ: Wiley.
21. Jonassen D., (2011), Designing for problem solving, in Reiser R. and Dempsey J. (ed.), Trends and issues in instructional design and technology, Boston, MA: Pearson Education, pp. 64–74.
22. Keil F. C., Smith W. C., Simons D. J. and Levin D. T., (1998), Two dogmas of conceptual empiricism: implications for hybrid models of the structure of knowledge, Cognition, 65(2/3), 103–135.
23. Koedinger K. R., Alibali M. W. and Nathan M. J., (2008), Trade-offs between grounded and abstract representations: evidence from algebra problem solving, Cognitive Sci., 32(2), 366–397.
24. Kolodner J., (1992), An introduction to case-based reasoning, Artif. Intell. Rev., 6(3), 3–34.
25. Kraft A., Strickland A. M. and Bhattacharyya G., (2010), Reasonable reasoning: Multi-variate problem-solving in organic chemistry, Chem. Educ. Res. Pract., 11, 281–292.
26. Larkin J. H., (1983), Expert representations of physics problems, in Gentner D. and Stevens A. (ed.), Mental models, Hillsdale, NJ: Lawrence Eribaum Associates.
27. Litzinger T. A., Van Meter P., Firetto C. M., Passmore L. J., Masters C. B., Turns S. R., Gray G. L., Costanzo F. and Zappe S. E., (2010), A cognitive study of problem solving in statics, J. Eng. Educ., 99(4), 337–352.
28. Mason D. S., Shell D. F. and Crawley F. E., (1997), Differences in problem solving by nonscience majors in introductory chemistry on paired algorithmic-conceptual problems, J. Res. Sci. Teach., 34(9), 905–923.
29. McDermott J. and Larkin J. H., (1978), Re-representing textbook physics problems, Proceedings of the 2nd Conference of the Canadian Society for Computational Studies of Intelligence, Toronto: University of Toronto Press, pp. 156–164.
30. McMillan C. and Swadener M., (1991), Novice use of qualitative versus quantitative problem solving in electrostatics, J. Res. Sci. Teach., 28(8), 661–670.
31. Niaz M., (1996), Reasoning strategies of students in solving chemistry problems as a function of developmental level, functional M-capacity and disembedding ability, Int. J. Sci. Educ., 18(5), 525–541.
32. Nurrenbern S. C. and Pickering M. J., (1987), Concept learning versus problem solving: Is there a difference? J. Chem. Educ., 64, 508–510.
33. Overton T., Potter N. and Leng C., (2013), A study of approaches to solving open-ended problems in chemistry, Chem. Educ. Res. Pract., 14, 468–475.
34. Pappa E. T. and Tsaparlis G., (2011), Evaluation of questions in general chemistry textbooks according to the form of the questions and the Question-Answer Relationship (QAR): the case of intra- and intermolecular chemical bonding, Chem. Educ. Res. Pract., 12, 262–270.
35. Prain V. and Tytler R., (2012), Learning through constructing representations in science: a framework of representational construction affordances, Int. J. Sci. Educ., 34(17), 2751–2773.
36. Raker, J. R. and Towns M. H., (2010), Benchmarking problems used in second year level organic chemistry instruction, Chem. Educ. Res. Pract., 11(1), 25–32.
37. Reed S. K., (2012), Learning by mapping across situations, J. Learn. Sci., 21(3), 353–398.
38. Reed S. K. and Bolstad C. A., (1991), Use of examples and procedures in problem solving, J. Exp. Psychol. Learn., 17(4), 753–766.
39. Reid N. and Yang M.-J., (2002), Open-ended problem solving in school chemistry: A preliminary investigation, Int. J. Sci. Educ., 24(12), 1313–1332.
40. Roschelle J. and Greeno J. G., (1987), Mental models in expert physics reasoning (Technical Report No. GK-2), Berkeley: University of California Press, retrieved from http://www.dtic.mil/dtic/tr/fulltext/u2/a184106.pdf, Feb. 1, 2015.
41. Schwartz D. L., (1995), The emergence of abstract representations in problem solving, J. Learn. Sci., 4(3), 321–354.
42. Shepard R., (1980), Multidimensional scaling, tree-fitting, and clustering, Science, 210(4468), 390–399.
43. Smith E. and Medin D., (1981), Categories and concepts, Cambridge, MA: Harvard University Press.
44. Stamovlasis D., Tsaparlis G., Kamilatos C., Papaoikonomou D. and Zaratiadou E., (2005), Conceptual understanding vs. algorithmic problem solving: further evidence from a national chemistry examination, Chem. Educ. Res. Pract., 6, 104–118.
45. Sweller J., (1988), Cognitive load during problem solving: effects on learning, Cognitive Sci., 12, 257–285.
46. Taconis R., Ferguson-Hessler M. G. M. and Broekkamp H., (2001), Teaching science problem solving: an overview of experimental work, J. Res. Sci. Teach., 38(4), 442–468.
47. Treagust D. F., Chittleborough G. and Mamiala T. L., (2003), The role of submicroscopic and symbolic representations in chemical explanations, Int. J. Sci. Educ., 25(11), 1353–1368.
48. Tversky A., (1977), Features of similarity, Psychol. Rev., 84(4), 327–352.
49. Zoller U., (2002), Algorithmic LOCS and HOCS (chemistry) exam questions: performance and attitudes of college students, Int. J. Sci. Educ., 24(2), 185–203.

---

Footnote

† SAT scores are compared via national percentiles according to the year in which the exam was taken, as the years in which students took the SAT varied from 2000 to 2011, and the maximum SAT score changed from 1600 to 2400 during this period.

---