Multiple thermal magnetic relaxation in a two-dimensional ferromagnetic dysprosium(III) metal–organic framework

Abstract

A new two-dimensional (2D) lanthanide metal–organic framework, {[Dy₂(HCAM)₃(H₂O)₄]·2H₂O}_n (1, H₃CAM = 4-hydroxypyridine-2,6-dicarboxylic acid) has been hydrothermally synthesized and structurally characterized using single-crystal X-ray diffraction. There are two crystallographically independent dysprosium atoms in 1, displaying spherical tricapped trigonal prism geometry and square antiprism geometry, respectively. The dysprosium(III) ions are connected with each other through the bridging HCAM²⁻ anions, generating a classical 2D (4, 4) grid structure. Magnetic investigations revealed that intramolecular ferromagnetic interactions exist among the dysprosium(III) ions in 1, which shows field-induced two-step thermal magnetic relaxation, with the effective thermal barriers of 63.5 K and 57.1 K, respectively.

---

Introduction

Recently, the architecture of lanthanide metal–organic frameworks (LnMOFs) has been an effective and exciting approach to novel functional molecule-based materials. This research motivation has roots in the LnMOFs’ structural diversity and their extensive applications in areas such as lighting, optical communications, photonics, magnetic materials, adsorption, separation, catalysis, chemical sensors, and biomedical devices.¹ Photoluminescence is the main focus of a study of this kind of molecular material, however, the existence of large magnetic moments and remarkable magnetic anisotropy in the lanthanide ions, particularly the Dy³⁺ ion, allows the design of single-molecule magnets (SMMs) to be carried out in the LnMOF systems,² because both a large spin ground state (S) and a negative uniaxial magnetic anisotropy (D) are prerequisites for a molecule to be a SMM.³ The lanthanide ions thus become excellent components of the SMMs, even the LnMOFs showing SMM behaviours. The SMMs show magnetic bistability associated with the hysteresis cycle, below the blocking temperature (T_B), and can therefore be utilized for high-density information storage.^2–4 Furthermore, the SMMs have potential applications in other high-technique fields such as quantum computer and spintronics.⁵ Notably, association of the SMMs into coordination networks has provided a unique opportunity to investigate new behaviours at the frontier between the SMMs and classical bulk magnets, and thus be considered as a promising approach to a new generation of molecular magnetic materials.⁶ However, in contrast to abundant luminescent LnMOFs and numerous cluster-type lanthanide-based SMMs (LnSMMs), LnMOFs displaying SMM behaviours are documented less in the literature.²

Although most LnSMMs behave as single-ion magnets (SIMs) due to the very weak magnetic exchange interaction between the lanthanide ions, the occasional presence of a ferromagnetic interaction may enhance the SMMs’ properties.^2b,7 Enlightened by the popular 2D nanomaterial graphene, we believe that the highly ordered 2D (4, 4) grid motif LnMOFs displaying SMM behaviours are extremely attractive as a layered quantum dot arrangement of the SIMs (corresponding to the lanthanide ion node) in such molecular materials becomes feasible, which is in favour of their practical applications as molecular devices. Furthermore, an effective ferromagnetic arrangement of the SMM or the SIM units in coordination networks is known to favour ‘enhanced’ SMM properties or magnet behaviours.^6,8 However, reports of 2D LnMOFs exhibiting SMM behaviours are limited,^2b,i,k and only few examples show obvious ferromagnetic interactions.^2b,i

Our current research is also focused on the construction of new LnMOFs^2k,9 and new LnSMMs.¹⁰ Recently, we used a semi-rigid ligand, 4,4′-dicarboxybiphenyl sulfone (H₂dcps), to hydrothermally assembly a novel 2D DyMOF, [Dy₂(dcps)₃(H₂O)₅]_n,^2k which shows both polyrotaxane and polycatenane topology features and field-induced two-step magnetic relaxation.^2k However, its thermal barrier value of 12.5 K is relatively low and the 2D layers are entangled.^2k Therefore, we chose other multidentate ligands to synthesize new 2D LnMOFs with better SMM behaviours. Herein, we describe the hydrothermal synthesis, crystal structure and magnetic properties of a new DyMOF derived from 4-hydroxypyridine-2,6-dicarboxylic acid (H₃CAM), {[Dy₂(HCAM)₃(H₂O)₄]·2H₂O}_n (1), which shows an excellent 2D (4, 4) grid structure. Interestingly, complex 1 possesses an obvious intramolecular ferromagnetic interaction, displaying field-induced two-step thermal magnetic relaxation.

Experimental

Materials and methods

All chemicals are commercially available and were utilized without further purification. The elemental analyses were carried out on a FLASH EA1112 elemental analyzer. The infrared spectrum was determined on a BRUKER TENSOR-27 spectrophotometer with a pressed KBr pellet. The X-ray powder diffraction (XRD) pattern was recorded on a PANalytical Empyrean-1 diffractometer with Cu-Kα (λ = 1.5418 Å) radiation. The magnetic susceptibility measurements were performed on a polycrystalline sample on a Quantum Design MPMS-XL5 SQUID magnetometer. Pascal’s constants for all constituent atoms were used to estimate diamagnetic corrections.

Synthesis of 1

A mixture of H₃CAM (0.5 mmol), Dy(NO₃)₃·5H₂O (0.25 mmol), 1,10-phenanthroline·H₂O or 2,2′-bipyridine (0.25 mmol) and 15 mL of H₂O in a Teflon-lined stainless steel autoclave (25 mL) was kept at 170 °C for 6 days. After the autoclave had cooled to room temperature overnight, colourless plate crystals of 1 were harvested, these crystals were then washed with water and dried at ambient temperature. 65–75% yield based on Dy. Elemental analysis (%): calc. for C₂₁H₂₁Dy₂N₃O₂₁ (1): C, 25.83; H, 2.17; N, 4.30. Found: C, 25.80; H, 2.21; N 4.28. IR (KBr pellet, cm⁻¹): 3520(s), 3454(b, s), 3152(b, s), 1590(vs), 1441(s), 1375(m), 1340(m), 1241(w), 1122(w), 1029(m), 973(w), 947(w), 893(w), 810(w), 730(m), 645(m), 579(w), 515(w), 496(w), 448(w).

Crystallography

A single crystal with dimensions of 0.12 × 0.25 × 0.35 mm³ for 1, was chosen to collect data on a Bruker SMART APEX-CCD diffractometer with Mo-Kα radiation (λ = 0.71073 Å) at 293(2) K. Empirical absorption corrections from φ scan were applied. Cell parameters were obtained by the global refinement of the positions of all collected reflections. The direct method was used to solve the structure, which was then refined by a full matrix least-squares technique based on F² using a SHELXL 97 program.¹¹ All non-hydrogen atoms were refined anisotropically, and all hydrogen atoms were refined as riding atoms. Selected crystallographic data and structure determination parameters for complex 1 are given in Table 1.

Table 1 Crystal data and structural refinement parameters for complex 1

a R 1 = ∑‖Fo| − |Fc‖/∑|Fo|. b wR2 = ∑{[w(Fo^2 − Fc^2)^2]/∑[wFo^2]^2}^1/2.
Chemical formula	C21H21Dy2N3O21
Formula weight	976.41
Crystal system	Monoclinic
Space group	P21/c
a/Å	9.0067(18)
b/Å	14.524(3)
c/Å	23.390(6)
β/°	111.54(3)
V/Å^3	2846.0(12)
Z	4
T/K	293(2)
λ(Mo-Kα)/Å	0.71073
ρ calc/g cm^−3	2.279
µ(Mo-Kα)/mm^−1	5.312
θ range	1.69° ≤ θ ≤ 27.48°
Limiting indices	−9 ≤ h ≤ 11, −18 ≤ k ≤ 18, −30 ≤ l ≤ 30
Reflections collected	19 849
Unique reflections	6473
R 1 ^a [I > 2σ(I)]	0.0271
wR2^b [I > 2σ(I)]	0.0566
R 1 ^a [all data]	0.0284
wR2^b [all data]	0.0572
S	1.176

---

Results and discussion

Synthetic procedure, thermogravimetric analysis and XPD spectra of 1

In 2006, Cheng’s group used H₃CAM to hydrothermally synthesize two classes of 2D LnMOFs: one class with the formula {[Ln₂(HCAM)₃(H₂O)₄]·2H₂O}_n (Ln = Nd and Er) shows a 2D (4, 4) grid structure; while the other class with the formula {[Ln(CAM) (H₂O)₃]·H₂O}_n (Ln = Gd, Dy and Er) belongs to a 2D coordination polymer with a 3³4² uniform net.¹² Their research revealed that the use of Ln(III) salts [LnCl₃ and Ln(ClO₄)₃] or Ln₂O₃ as the lanthanide ion source has a great influence on the final products.¹² Unfortunately, no magnetic properties of these complexes were reported.¹² In this study, we utilized Dy(NO₃)₃·6H₂O as the Ln(III) salt to treat with H₃CAM in the presence of 1,10-phenanthroline or 2,2′-bipyridine under suitable hydrothermal conditions, and obtained complex 1 as the only product. It is somewhat surprising that the reported complex {[Dy(CAM) (H₂O)₃]·H₂O}_n¹² is not the product. Alternatively, complex 1, the isomorphous compound of other reported complexes {[Ln₂(HCAM)₃(H₂O)₄]·2H₂O}_n (Ln = Nd and Er), was prepared. Interestingly, when Gd(NO₃)₃·6H₂O was used instead of Dy(NO₃)₃·6H₂O, the reported 2D LnMOF {[Gd(CAM) (H₂O)₃]·H₂O}_n¹² was obtained. Notably, although it is not incorporated into the structure of 1, 1,10-phenanthroline or 2,2′-bipyridine is necessary to yield complex 1, because no crystalline products could be obtained when it was absent from the reaction mixture. We guess that 1,10-phenanthroline or 2,2′-bipyridine could adjust the pH value of the reaction system.

Thermogravimetric analysis (TGA) of the polycrystalline samples of 1 revealed that this compound begins to lose solvent hydrate molecules at about 60 °C, and the loss of total two solvent water molecules is completed at 210 °C (calcd 3.68%, found 3.7%) (Fig. S1, ESI†). Then the four coordination hydrate molecules start to escape, resulting in the weight loss of 7.4% until 270 °C (calcd 7.36%). After that, the other parts of the complex start to decompose, and the remaining network collapses.

The powder XRD pattern of 1 is shown in Fig. 1, which is utilized to compare with the pattern simulated on the basis of the single-crystal structure. The diffraction peaks from both simulated and experimental patterns coincide well in terms of position, indicating the excellent phase purity of the synthesized sample.

Fig. 1 The simulated (black) and experimental (blue) powder X-ray diffraction patterns for 1.

Crystal structure of 1

Complex 1 crystallizes in the monoclinic P2₁/c space group. As shown in Fig. 2, the asymmetric unit of 1 is composed of the [Dy(HCAM)₃]³⁻ anion and the [Dy(H₂O)₄]³⁺ cation. Therefore, two crystallographically independent dysprosium(III) atoms exist in 1 (Fig. 2a): the Dy1 atom is nine-coordinated, bonded by six oxygen atoms and three nitrogen atoms from three HCAM²⁻ anions; while the Dy2 atom is eight-coordinated, completed by four carboxylate oxygen atoms from four HCAM²⁻ anions and four oxygen atoms from four coordinated water molecules. Exact geometry analysis by Shape software¹³ reveals that the geometry of the nine-coordinated Dy1 ion is the spherical tricapped trigonal prism with a deviation of 1.210 from the ideal D_3h symmetry, while the eight-coordinated Dy2 ion is the square antiprism with a deviation of 0.366 from the ideal D_4d symmetry (Table S1, ESI†). The Dy1⋯Dy2 separation is 6.058 Å, which is a little shorter than the Nd1⋯Nd2 separation of 6.344 Å in {[Nd₂(HCAM)₃(H₂O)₄]·2H₂O}_n.¹² As can be seen from Table 2, the average Dy–O and Dy–N bond distances of 1 are 2.390 Å and 2.475 Å, respectively, which are a little larger than the mean Ln–O and Ln–N bond lengths of {[Er₂(HCAM)₃(H₂O)₄]·2H₂O}_n (2.382 Å and 2.452 Å, respectively),¹² but obviously smaller than the corresponding values of {[Nd₂(HCAM)₃(H₂O)₄]·2H₂O}_n (2.478 and 2.566 Å, respectively)¹² owing to the lanthanide contraction effect.

Fig. 2 (a) Coordination environments of the Dy atoms in 1, symmetry codes: a: −1 + x, y, z; b: −1 − x, 1/2 + y, 1/2 − z; c: −x, 1/2 + y, 1/2 − z; and (b) 2D (4, 4) grid layer of 1.

Table 2 Selected bond distances (Å) and angles (°) for complex 1^a

a Symmetry codes: ^#1 −1 + X, Y, Z; ^#2 −1 − X, 1/2 + Y, 1/2 − Z; ^#3 −X, 1/2 + Y, 1/2 − Z.
Dy1–N1	2.473(3)	Dy1–N2	2.486(3)
Dy1–N3	2.465(3)	Dy1–O1	2.441(3)
Dy1–O3	2.428(3)	Dy1–O6	2.397(3)
Dy1–O8	2.408(3)	Dy1–O11	2.382(3)
Dy1–O13	2.386(3)	Dy2–O1W	2.383(3)
Dy2–O2W	2.374(3)	Dy2–O2^#1	2.341(3)
Dy2–O3W	2.400(3)	Dy2–O4W	2.417(3)
Dy2–O9^#2	2.370(3)	Dy2–O12	2.385(3)
Dy2–O14^#3	2.352(3)
N1–Dy1–N2	115.25(10)	N3–Dy1–N1	122.71(10)
N3–Dy1–N2	121.87(10)	O1–Dy1–N1	63.97(10)
O3–Dy1–N1	64.62(9)	O6–Dy1–N2	63.97(9)
O8–Dy1–N2	63.66(10)	O11–Dy1–N3	64.22(9)
O13–Dy1–N3	64.77(9)	O1W–Dy2–O12	80.70(10)
O2W–Dy2–O12	72.56(10)	O2^#1–Dy2–O12	140.50(9)
O9^#2–Dy1–O12	115.65(9)	O14^#3–Dy2–O12	77.34(10)
O1W–Dy2–O4W	106.91(11)	O2W–Dy2–O4W	81.86(11)
O2^#1–Dy2–O4W	73.09(10)	O3W–Dy2–O4W	143.48(10)
O9^#2–Dy2–O4W	78.51(9)	O12–Dy2–O4W	143.64(10)
O14^#3–Dy2–O4W	72.22(10)	O9^#2–Dy2–O2W	71.64(10)
O14^#3–Dy2–O2W	77.78(10)	O14^#3–Dy2–O1W	70.87(10)
O2^#1–Dy2–O1W	71.52(10)	O2^#1–Dy2–O9^#2	77.91(10)

---

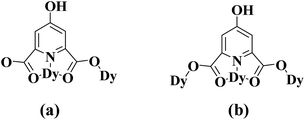
The HCAM²⁻ anions in 1 fall into two categories according to the coordination modes. One acts as a µ²-bridge to link two adjoining Dy atoms, in which two carboxylato oxygen atoms and one pyridine nitrogen atom bond the Dy1 atom with the chelating mode, whereas one of two carboxylato groups links the Dy1 atom and the Dy2 atom as a bismonodentate bridge (Scheme 1a). The other also adopts the same chelating mode involving two carboxylato oxygen atoms and one pyridine nitrogen atom, but uses both carboxylato groups as bismonodentate bridges to respectively link the Dy1 atom and the Dy2 atom, so it totally connects with three adjacent Dy atoms in a µ³-bridging fashion (Scheme 1b). The Dy1 atom and the Dy2 atom alternatively link to each other through these two kinds of HCAM²⁻ bridges along two approximately vertical directions, generating a highly ordered 2D (4, 4) grid network (Fig. 2b).

Scheme 1 Coordination modes of the HCAM²⁻ ligands.

The hydroxyl oxygen atoms in all the HCAM²⁻ anions do not coordinate to the Dy atoms, however, they form intramolecular hydrogen bonds between O10 and the symmetry equivalent of O15, and between O15 and the symmetry equivalent of O10. Furthermore, the hydroxyl oxygen atom also interacts with the intermolecular hydrogen bonds between it and the solvent water molecule, and between it and the carboxylate O atom. In addition, there are not only intermolecular hydrogen bonds between the solvent hydrate molecule and the coordinated water molecule, and between the solvent water molecule and the carboxylate O atom, but also an intramolecular hydrogen bond between the coordinated hydrate molecule and the carboxylate O atom. Such extensive hydrogen bonding extends the 2D grid layers into a 3D supramolecular framework, which are similar to those observed in the structure of {[Nd₂(HCAM)₃(H₂O)₄]·2H₂O}_n.¹²

Magnetic properties of 1

Direct current (dc) magnetic susceptibilities of 1 were determined in the range of 2–300 K in a 1 kOe applied field. As depicted in Fig. 3a, the χT value at 300 K is 28.35 cm³ K mol⁻¹, in good agreement with the theoretical value (28.34 cm³ K mol⁻¹) of two isolated Dy³⁺ ions (S = 5/2, L = 5, ⁶H_15/2, g = 4/3). When the temperature is dropped, the χT product increases slightly to about 75 K, then increases quickly to a maximum value of 29.23 cm³ K mol⁻¹ at 30 K. Upon further cooling, it falls abruptly to reach a minimum value of 27.05 cm³ K mol⁻¹ at 2 K. The protuberance around 40 K in the χT versus T plot suggests that intramolecular ferromagnetic interactions exist among the Dy³⁺ ions in 1, which are strong enough to counteract the χT decline with decreased temperature resulting from the magnetic anisotropy and the thermal depopulation of the Dy³⁺ excited states (Stark sublevels of the ⁶H_15/2 state). The magnetic data in the range of 50–300 K obeys the Curie–Weiss law, 1/χ = (T − θ)/C, and the best fit afforded the values of C = 28.22 cm³ K mol⁻¹ and θ = 1.1 K. The positive Weiss constant value confirms the existence of intramolecular ferromagnetic interactions in 1. To the best of our knowledge, there are only a few carboxylate-based 2D dysprosium(III) MOFs showing remarkable intramolecular ferromagnetic interactions.^2b,i The combination of the bridging roles of the carboxylate anion and the hydroxide anion has been proven to be an important approach to the ferromagnetic interaction among the Dy³⁺ ions,^2b,i which can be suitable for the situation where only one type of Dy³⁺ coordination geometry exists. For complex 1, there exists two types of Dy³⁺ coordination geometries (the spherical tricapped trigonal prism and the square antiprism), which are bridged by the carboxylate anion only, with the bismonodentate bridging mode. Therefore, our work suggests that using the bismonodentate carboxylate bridge to link two types of Dy³⁺ ions with different coordination geometries is another effective method by which the 2D dysprosium(III) MOFs display ferromagnetic properties. While the magnetic anisotropy and/or low-lying excited states are verified by the field dependence of the magnetization measured at 2–6 K, as shown in Fig. 3b, the produced M versus H/T curves at different temperatures are not superimposed.

Fig. 3 (a) Plots of χT versus T (□) and 1/χ versus T (○) of 1 (a); the solid line represents the best theoretical fitting with the Curie–Weiss law. (b) M versus H/T plots at 2–6 K.

Alternating-current (ac) magnetic susceptibilities were then measured in a 2.5 Oe oscillating field at different frequencies to explore the magnetization dynamics of 1. As shown in Fig. 4, the out-of phase (χ″) component of the ac susceptibilities versus T plots of 1 are somewhat frequency dependent below 6 K, but no peaks could be seen even at a high frequency of 1399 Hz. However, after application of a 2000 Oe dc field, the χ″ signals of 1 become strongly frequency dependent below 8 K, and peaks could be observed clearly at all indicated frequencies (1–1399 Hz, Fig. 5a). The improvement of the χ″ signals under a dc field indicates that obvious quantum-tunnelling effects exist in 1, which could be effectively suppressed by a dc field by removing the ground-state degeneracy.^2k,10d,f,14 As seen in the high frequency region, there exists two thermally activated relaxation phases in the low-temperature signal region and in the high-temperature signal region, corresponding to the fast relaxation phase (FR) and the slow relaxation phase (SR), respectively.

Fig. 4 Ac susceptibilities measured in a 2.5 Oe ac field with a zero dc field for 1.

Fig. 5 (a) Plots of χ″ versus T measured in a 2.5 Oe oscillating field with a 2 kOe dc field for 1. (b) Plots of ln(τ) versus 1/T for 1, the solid lines represent the best fit with the Arrhénius law.

The nature of ac susceptibility frequency dependence is generally judged by a parameter, ϕ = (ΔT_f/T_f)/Δ(log f); here f is the frequency: ϕ > 0.1 for a superparamagnet and ϕ ≈ 0.01 for a spin glass.¹⁵ The ϕ value of 1 equals 0.31, indicating the SMM behaviours of 1. The effective thermal barriers can be derived using the Arrhenius law, τ = τ₀ exp(U_eff/kT) (here τ = 1/2πf). As shown in Fig. 5b, two ln(τ)–1/T plots corresponding to the FR and the SR, respectively, were fitted to the formula ln τ = ln τ₀ + U_eff/kT, extracting two sets of magnetization relaxation parameters: U_eff/k = 57.1 K and τ₀ = 2.1 × 10⁻¹⁰ s for the FR as well as U_eff/k = 63.5 K and τ₀ = 5.0 × 10⁻⁹ s for the SR. Both τ₀ values are in the normal range of 10 × 10⁻⁶ to 10 × 10⁻¹¹ s for the SMMs or the SIMs,^2–7 and the two U_eff/k values are remarkably larger than that of [Dy₂(dcps)₃(H₂O)₅]_n (12.5 K).^2k As the two U_eff/k values are close, and the two τ₀ values are similar, both thermally activated relaxation processes are ascribed to the Orbach process.^10d,e,16

The presence of two thermally activated relaxation phases in 1 was further validated by the frequency-dependent ac susceptibilities performed at 2–6 K under a dc field of 2000 Oe, which are depicted in the format of χ″ versus χ′ plots (Fig. 6). Each Cole–Cole plot is composed of two half-baked semicircles, which are superimposed at the connection point, forming a hook-shaped curve: the left part of the curve corresponds to the FR, whereas the right part to the SR. The two separate thermal magnetic relaxation processes could be described by the sum of two modified Debye functions (eqn (1)):^10d–f,17

Fig. 6 Cole–Cole plots at 2–6 K for 1 (H_ac = 2.5 Oe and H_dc = 2 kOe). The solid lines represent the best fit with the sum of the two modified Debye functions.

Both the χ″ versus T plot and the χ′ versus T plot were fitted to eqn (1) synchronously, affording seven parameters χ₁, χ₂, χ₀, α₁, α₂, τ₁ and τ₂ at each temperature. The results are listed in Table S1† and depicted as Fig. 6 and S2–S6.† The α₁ values are in the range of 0.24–0.44 and the α₂ values in the range of 0.04–0.48. These distribution coefficient values are not very small, suggesting that the distribution of the relaxation time for both the FR phase and the SR phase is not narrow. The two-step thermal magnetic relaxation is associated not only with the existence of two types of dysprosium(III) ions, which adopt the square antiprism (D_4d) geometry and the tricapped trigonal prism (D_3h) geometry, respectively, but also more specifically with the associated energies of the excited states.¹⁸ Similar multiple thermal magnetic relaxation was also observed in other SMMs or SIMs.^10d,f,19 It is worth noting that complex 1 is the first example of ferromagnetic LnMOFs displaying a 2D (4, 4) grid network and two steps of thermal magnetic relaxation processes. In addition, no hysteresis effect is formed in the M versus H plot of 1 at 1.9 K (Fig. S7†).

In order to better understand the slow relaxation of the magnetization of 1, we applied the electrostatic model implemented in the Magellan program²⁰ to determinate the magnetic anisotropy in 1. The directionality of the magnetic axes of the two types of dysprosium(III) ions in 1 is shown in Fig. 7, which shows an almost collinear arrangement, with an angle deviation of 23.48°. Undoubtedly, such a nearly parallel arrangement of the magnetic axes does favour the SMM properties of 1, as shown by its slow thermal magnetic relaxation.²¹

Fig. 7 Magnetic axes of the Dy³⁺ ions calculated by an electrostatic method.

Due to the full treatment of the 2D lanthanide system exceeding the ability of modern precise ab initio calculations, we approximate the structure to be a two-core cluster. The individual Dy(III) fragment was extracted from the full 2D layer crystal structure (Fig. S8†). The complete-active-space self-consistent field (CASSCF) and RASSI (to compute spin–orbit coupling) calculations were performed using a MOLCAS 8 program package²² and SINGLE_ANISO programs.

During the calculations, the other Dy(III) ions were replaced by diamagnetic Lu(III) ions. The atomic natural orbitals from the MOLCAS ANO-RCC library are used as basis sets: ANO-RCC-VTZP for the Dy(III) ion, ANO-RCC-VTZ for the direct coordinate atoms of the Dy(III) ion, and ANO-RCC-VDZ for the other atoms in the fragment. The active space was 7 with all f electrons of the Dy(III) ion in the CASSCF calculation (CAS (9 in 7)). During the calculation of spin–orbit coupling in the framework of active space state interaction (RASSI-SO), the number of spin-free state mixed was almost the maximum for our hardware (all from 21 sextets, 128 from 224 quadruplets and 130 from 490 doublets for the Dy(III) fragment).

The lowest Kramers doublets and the g tensors of the two kinds of Dy(III) ions in the model are shown in the Table 3. The energy gap between the ground state doublet and the first-excited state doublet is about 33 K for Dy1 and 121 K for Dy2. The calculated energy gap for Dy1 is smaller than the experimental one, which may be due to the model being not accurate enough. A better model is a {DyLu₄} cluster, i.e. four Lu(III) ions were calculated together with each Dy(III) ion, and the cluster will be not the same for each kind of Dy(III) ion. However, the calculation of such a model is beyond the ability of our hardware.

Table 3 Lowest Kramers doublets (cm⁻¹) and the g (g_x, g_y, g_z) tensors on individual Dy(III) fragments of the two-core cluster model

Dy1	E	0	23.7	82.0	133.0	183.6	217.9	255.6	286.6
	g (S̃ = 1/2)	0.792	1.708	0.537	1.875	8.844	1.810	1.768	0.702
		3.892	2.130	3.746	6.012	7.064	3.459	2.770	2.339
		15.508	12.824	13.284	10.535	0.390	9.244	13.061	16.236
Dy2	E	0	86.7	169.3	236.3	284.6	347.5	436.8	840.6
	g (S̃ = 1/2)	0.028	0.152	0.757	1.949	4.047	0.652	0.041	0.000
		0.051	0.155	1.195	3.993	5.026	0.970	0.076	0.000
		19.629	16.804	13.638	9.427	9.322	15.134	17.429	19.860

---

The planar components (g_x, g_y) of g for Dy1 are not small, indicating failures of the Ising model, while Dy2 could be described using an Ising model. This means that the Lines model is no longer accurate for this system. Furthermore, the direction of g_z of the two kinds of Dy(III) ions is not completely collinear (Fig. 7 and S8†). Above all, the magnetic coupling in such a 2D (4 × 4) system will be very complex to fit. Combining the calculation results and the χT vs. T measurements of the complex, we think that the main magnetic coupling interactions are possibly ferromagnetic in the present system. However, antiferromagnetic coupling cannot be excluded.

Conclusions

In summary, we have hydrothermally synthesized a new 2D dysprosium(III) MOF (1) derived from 4-hydroxypyridine-2,6-dicarboxylic acid. It contains two kinds of dysprosium atoms, exhibiting the tricapped trigonal prism geometry and the square antiprism geometry, respectively. They are alternatively connected with each other through 4-hydroxypyridine-2,6-dicarboxylate bridges, generating a highly ordered 2D (4, 4) grid network. An intramolecular ferromagnetic interaction was observed in 1, which displays two-step thermal magnetic relaxation under a 2 kOe dc field, with U_eff/k values of 63.5 K and 57.1 K, respectively. Complex 1 represents the first ferromagnetic LnMOF displaying both the (4, 4) grid network and multiple thermal magnetic relaxation. This work demonstrates that LnMOFs with a highly ordered 2D (4, 4) grid network can be explored to exhibit SMM behaviours, and we think that such molecular materials are promising for practical applications as molecular devices.

Acknowledgements

This work was supported by the National Key Basic Research Program of China (2013CB933403), the National Natural Science Foundation of China (21471154 and 91022014), and the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB12010103).

Notes and references

1. (a) J. Rocha, L. D. Carlos, F. A. A. Paza and D. Ananias, Chem. Soc. Rev., 2011, 40, 926; (b) Y. Cui, B. Chen and G. Qian, Coord. Chem. Rev., 2014, 273, 76; (c) Y. Hasegawa and T. Nakanishi, RSC Adv., 2015, 5, 338.
2. (a) P. F. Shi, Y. Z. Zheng, X. Q. Zhao, G. Xiong, B. Zhao, F. F. Wan and P. Cheng, Chem.–Eur. J., 2012, 18, 15086; (b) D.-D. Yin, Q. Chen, Y.-S. Meng, H.-L. Sun, Y.-Q. Zhang and S. Gao, Chem. Sci., 2015, 6, 3095; (c) D. Savard, P. H. Lin, T. J. Burchell, I. Korobkov, W. Wernsdorfer, R. Clérac and M. Murugesu, Inorg. Chem., 2009, 48, 11748; (d) F. R. Fortea-Perez, J. Vallejo, M. Julve, F. Lloret, G. de Munno, D. Armentano and E. Pardo, Inorg. Chem., 2013, 52, 4777; (e) M. Chen, E. C. Sañudo, E. Jiménez, S.-M. Fang, C.-S. Liu and M. Du, Inorg. Chem., 2014, 53, 6708; (f) X. Yi, G. Calvez, C. Daiguebonne, O. Guillou and K. Bernot, Inorg. Chem., 2015, 54, 5213; (g) X. Yi, K. Bernot, G. Calvez, C. Daiguebonne and O. Guillou, Eur. J. Inorg. Chem., 2013, 5879; (h) Q. Li and S. Du, RSC Adv., 2015, 5, 9898; (i) X. Ma, N. Xu, C. Gao, L. Li, B. Wang, W. Shi and P. Cheng, Dalton Trans., 2015, 44, 5276; (j) Q.-Y. Liu, Y.-L. Li, Y.-L. Wang, C.-M. Liu, L.-W. Ding and Y. Liu, CrystEngComm, 2014, 16, 486; (k) C.-M. Liu, D.-Q. Zhang and D.-B. Zhu, RSC Adv., 2014, 4, 36053; (l) C.-M. Liu, D.-Q. Zhang and D.-B. Zhu, RSC Adv., 2015, 5, 63186.
3. R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141.
4. For examples: (a) G. Christou, D. Gatteschi, D. N. Hendrickson and R. Sessoli, MRS Bull., 2000, 25, 66; (b) C. Benelli and D. Gatteschi, Chem. Rev., 2002, 102, 2369; (c) D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268; (d) L. M. C. Beltran and J. R. Long, Acc. Chem. Res., 2005, 38, 325; (e) G. Aromi and E. K. Brechin, Struct. Bonding, 2006, 122, 1; (f) R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328; (g) V. Chandrasekhar and B. Murugesapandian, Acc. Chem. Res., 2009, 42, 1047; (h) R. Bagai and G. Christou, Chem. Soc. Rev., 2009, 38, 1011; (i) G. E. Kostakis, A. M. Akoab and A. K. Powell, Chem. Soc. Rev., 2010, 39, 2238; (j) M. Murrie, Chem. Soc. Rev., 2010, 39, 1986; (k) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110; (l) B.-W. Wang, X.-Y. Wang, H.-L. Sun, S.-D. Jiang and S. Gao, Philos. Trans. R. Soc. A, 2013, 371, 20120316; (m) P. Zhang, Y.-N. Guo and J. k. Tang, Coord. Chem. Rev., 2013, 257, 1728; (n) K. Liu, W. Shi and P. Cheng, Coord. Chem. Rev., 2015, 289–290, 74.
5. (a) R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357; (b) T. Komeda, H. Isshiki, J. Liu, Y.-F. Zhang, N. Lorente, K. Katoh, B. K. Breedlove and M. Yamashita, Nat. Comm., 2011, 2, 217.
6. I.-R. Jeona and R. Clérac, Dalton Trans., 2012, 41, 9569.
7. (a) P.-H. Lin, T. J. Burchell, R. Clérac and M. Murugesu, Angew. Chem., Int. Ed., 2004, 43, 707; (b) Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. k. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948; (c) Z. Chen, B. Zhao, P. Cheng, X.-Q. Zhao, W. Shi and Y. Song, Inorg. Chem., 2009, 48, 3493; (d) Y. Wang, T. W. Wang, Y. Song and X. Z. You, Inorg. Chem., 2010, 49, 969; (e) W. T. Xu, Y. F. Zhou, D. C. Huang, W. Xiong, M. Y. Su, K. Wang, S. Han and M. C. Hong, Cryst. Growth Des., 2013, 13, 5420; (f) P. I. Girginova, L. C. J. Pereira, J. T. Coutinho, I. C. Santos and M. Almeida, Dalton Trans., 2014, 43, 1897; (g) W.-H. Zhu, Y. Zhang, Z. Guo, S. Wang, J. Wang, Y.-L. Huang, L. Liu, Y.-Q. Fan, F. Cao and S.-W. Xiang, RSC Adv., 2014, 4, 49934; (h) C.-B. Han, Y.-L. Wang, Y.-L. Li, C.-M. Liu and Q.-Y. Liu, Inorg. Chem. Commun., 2015, 58, 91; (i) Y. Z. Zheng, Y. H. Lan, W. Wernsdorfer, C. E. Anson and A. K. Powell, Chem.–Eur. J., 2009, 15, 12566.
8. H. Miyasaka, K. Nakata, K.-i. Sugiura, M. Yamashita and R. Clérac, Angew. Chem., Int. Ed., 2004, 43, 707.
9. (a) C.-M. Liu, J.-L. Zuo, D.-Q. Zhang and D.-B. Zhu, CrystEngComm, 2008, 10, 1674; (b) C.-M. Liu, M. Xiong, D.-Q. Zhang, M. Du and D.-B. Zhu, Dalton Trans., 2009, 5666.
10. (a) C.-M. Liu, D.-Q. Zhang and D. B. Zhu, Dalton Trans., 2010, 39, 11325; (b) X.-L. Li, C.-L. Chen, Y.-L. Gao, C.-M. Liu, X.-L. Feng, Y.-H. Gui and S.-M. Fang, Chem.–Eur. J., 2012, 18, 14632; (c) C.-M. Liu, D.-Q. Zhang, X. Hao and D.-B. Zhu, Cryst. Growth Des., 2012, 12, 2948; (d) C.-M. Liu, D.-Q. Zhang and D. B. Zhu, Inorg. Chem., 2013, 52, 8933; (e) C.-M. Liu, D.-Q. Zhang and D. B. Zhu, Dalton Trans., 2013, 42, 14813; (f) C.-M. Liu, D.-Q. Zhang, X. Hao and D.-B. Zhu, Chem.–Asian J., 2014, 9, 1847.
11. G. M. Sheldrick, SHELXL-97, Program for refinement of crystal structures, University of Göttingen, Germany, 1997.
12. H.-L. Gao, L. Yi, B. Zhao, X.-Q. Zhao, P. Cheng, D.-Z. Liao and S.-P. Yan, Inorg. Chem., 2006, 45, 5980.
13. D. Casanova, M. Llunell, P. Alemany and S. Alvarez, Chem.–Eur. J., 2005, 11, 1479.
14. (a) A. Mishra, W. Wernsdorfer, K. A. Abboud and G. Christou, J. Am. Chem. Soc., 2004, 126, 15648; (b) L. Lecren, W. Wernsdorfer, Y. Li, O. Roubeau, H. Miyasaka and R. Clérac, J. Am. Chem. Soc., 2005, 127, 11311; (c) M. Moragues-Canovas, E. Riviere, L. Ricard, C. Paulsen, W. Wernsdorfer, G. Rajaraman, E. K. Brechin and T. Mallah, Adv. Mater., 2004, 16, 1101; (d) S. Koizumi, M. Nihei, T. Shiga, M. Nakano, H. Nojiri, R. Bircher, O. Waldmann, S. T. Ochsenbein, H. U. Güdel, F. Fernandez-Alonso and H. Oshio, Chem.–Eur. J., 2007, 13, 8445; (e) S.-J. Liu, J.-P. Zhao, W.-C. Song, S.-D. Han, Z.-Y. Liu and X.-H. Bu, Inorg. Chem., 2013, 52, 2103; (f) J.-L. Liu, K. Yuan, J.-D. Leng, L. Ungur, W. Wernsdorfer, F.-S. Guo, L. F. Chibotaru and M.-L. Tong, Inorg. Chem., 2012, 51, 8538; (g) J. Kan, H. Wang, W. Sun, W. Cao, J. Tao and J. Jiang, Inorg. Chem., 2013, 52, 8505; (h) S.-Q. Wu, Q.-W. Xie, G.-Y. An, X. Chen, C.-M. Liu, A.-L. Cui and H.-Z. Kou, Dalton Trans., 2013, 42, 11043; (i) D.-K. Cao, R.-H. Wei, Y.-W. Gu, Y. Zhao and M. D. Ward, RSC Adv., 2014, 4, 43064.
15. J. A. Mydosh, Spin Glasses, An Experimental Introduction, Taylor and Francis, London, 1993.
16. S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730.
17. (a) M. Grahl, J. Kotzler and I. Sessler, J. Magn. Magn. Mater., 1990, 90–91, 187; (b) Y.-N. Guo, G.-F. Xu, P. Gamez, L. Zhao, S.-Y. Lin, R. Deng, J. Tang and H.-J. Zhang, J. Am. Chem. Soc., 2010, 132, 8538.
18. (a) F. Habib, J. Long, P.-H. Lin, I. Korobkov, L. Ungur, W. Wernsdorfer, L. F. Chibotaruc and M. Murugesu, Chem. Sci., 2012, 3, 2158; (b) C.-M. Liu, D.-Q. Zhang, X. Hao and D.-B. Zhu, RSC Adv., 2015, 5, 92980.
19. (a) Z. Sun, D. Ruiz, N. R. Dilley, M. Soler, J. Ribas, K. Folting, M. Brian Maple, G. Christou and D. N. Hendrickson, Chem. Commun., 1999, 1973; (b) I. J. Hewitt, J. Tang, N. T. Madhu, C. E. Anson, Y. Lan, J. Luzon, M. Etienne, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2010, 49, 6352; (c) J. Long, F. Habib, P.-H. Lin, I. Korobkov, G. Enright, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 5319; (d) K. Katoh, T. Kajiwara, M. Nakano, Y. Nakazawa, W. Wernsdorfer, N. Ishikawa, B. K. Breedlove and M. Yamashita, Chem.–Eur. J., 2011, 17, 117; (e) M.-X. Yao, Q. Zheng, F. Gao, Y.-Z. Li, Y. Song and J.-L. Zuo, Dalton Trans., 2012, 41, 13682; (f) Y.-X. Wang, W. Shi, H. Li, Y. Song, L. Fang, Y. Lan, A. K. Powell, W. Wernsdorfer, L. Ungur, L. F. Chibotaru, M. Shen and P. Cheng, Chem. Sci., 2012, 3, 3366; (g) R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673; (h) S. K. Langley, N. F. Chilton, B. Moubaraki and K. S. Murray, Inorg. Chem., 2013, 52, 7183; (i) F. Gao, Y.-Y. Li, C.-M. Liu, Y.-Z. Li and J.-L. Zuo, Dalton Trans., 2013, 42, 11043; (j) S. Das, A. Dey, S. Biswas, E. Colacio and V. Chandrasekhar, Inorg. Chem., 2014, 53, 3417; (k) M. Feng, F. Pointillart, B. Lefeuvre, V. Dorcet, S. Golhen, O. Cador and L. Ouahab, Inorg. Chem., 2015, 54, 4021.
20. N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551.
21. K. H. Zangana, E. Moreno Pineda and R. E. P. Winpenny, Dalton Trans., 2015, 44, 12522.
22. G. Karlström, R. Lindh, P. Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P. O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222.

---

Footnote

† Electronic supplementary information (ESI) available: X-ray crystallographic data for complex 1 in CIF format. Additional magnetic characterization (Fig. S1–S8 and Table S1). CCDC 1408951. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5ra23638j

---