Smallest deltahedra silicon dicarbide: C₂Si₃²⁻

Abstract

The composition and valence electrons of molecules usually have a great impact on the eventual topology. With a high tendency to form sp/sp²-hybridized multiple bonding of C₂, the main-group dicarbides (C₂X_n) usually adopt a non-closo (or open) topology. By contrast, naked Zintl ions (e.g., Si₅²⁻) usually feature deltahedral structures. In this paper, we report an unexpected example of a pentatomic carbon-silicon cluster C₂Si₃²⁻ which has the global minimum C₂Si₃²⁻-01 featuring a closo-structure with all deltahedras. The global minimum nature of C₂Si₃²⁻-01 was confirmed by various sophisticated methods including G3B3, G4, CBS-QB3 and W1BD as well as CCSD(T) extrapolated up to the complete basis set limit based on the CCSD(T)/aug-cc-pVTZ, CCSD(T)/aug-cc-pVQZ and CCSD(T)/aug-cc-pV5Z calculations. The AdNDP analysis revealed that C₂Si₃²⁻-01 possesses a lone pair of electrons on each of the three silicon atoms, four 2c–2e bonds and four 3c–2e bonds, among which the two 2c–2e bonds between the two carbons indicate the existence of a multiply bonded C₂ (1.320 Å) that carries the most negative charges. With a total of 22 valence electrons, C₂Si₃²⁻-01 formally resembles the known Wade–Mingos clusters with (n + 1) polyhedral skeletal electron pairs (PSEPs). Replacement of Si₂ by the highly electron-withdrawing C₂ does not break the deltahedral topology of the Zintl ion Si₅²⁻. To the best of our knowledge, C₂Si₃²⁻ represents the smallest deltahedral main-group dicarbide and also the first deltahedral main-group dicarbide with (n + 1) PSEPs. To direct its organometallic applications, we designed the hetero-deckered sandwich compounds CpMg(C₂Si₃²⁻)MgCp, in which the C₂Si₃²⁻-01 unit can be nicely maintained.

---

1. Introduction

In general, the topological structure of a chemical compound depends on its inherent elemental composition and electronic structure. Various conceptual rules have been developed to effectively connect the topology and electron number.¹ Among them is the famous Wade–Mingos rule, which is usually applied to judge the structures of boranes and carboranes by the skeletal electron pairs, i.e., the n-vertex clusters with (n + 1) polyhedral skeletal electron pairs (PSEPs) prefer to be arranged into closo-deltahedra.^1a,b On the other hand, the Zintl ions composed of heavier main-group or transition metal elements feature deltahderal structures, and their topology can in most cases be accounted for by the Wade–Mingos rule.²

The ligand-free dicarbides (C₂X_n) usually contain a multiply bonded C₂ unit. The simplest tri-atomic dicarbides, i.e., C₂X, have been the earlier focus of numerous studies.^3–6 They have played important roles in various fields. For example, the well-known C₂Ca can not only be used as the basic material to synthesize the organic compounds, but also be applied to the nonferrous metals and steel industry.⁴ The actinide dicarbides as the appropriate fuels of nuclear reactors, have also received much attention.⁶ Besides, some of them have been detected in space.³

Concerning the topological structures, the simplest C₂X usually take the chainlike or T-shaped ground states.^3,5,6 With more than one X-atom, the structure and bonding within the dicarbide are expected to be complicated since the C–C, C–X and X–X bonds may undergo interactive competition. It has now been found that some transition metals (e.g., X = Co,^7a Fe,^7b Ni (ref. 7b)) can effectively allow the multiply bonded C₂ to be positioned as one edge of a closo-structure, forming the deltahedral topology. However, in spite of a large body of published research articles on the main-group dicarbides,^8,9 only the hexatomic cluster C₂Si₄ has been firmly shown to have a deltahedral structure.⁸ The rather limited examples of the main-group dicarbides must be ascribed to the strong preference of the C₂-moiety to drive the whole or part of the molecule to be open in chainlike or planar forms.

Can other ligand-free main-group dicarbides possess a deltahedral structure besides C₂Si₄? In this paper, based on a global isomeric search strategy and various sophisticated quantum chemical methods including G3B3, G4, CBS-QB3, W1BD and CCSD(T)/CBS, we report the smallest main-group dicarbide molecule C₂Si₃²⁻ with all deltahedras. With 22 valence electrons, the pentatomic C₂Si₃²⁻ formally has (n + 1) PSEPs, differing from C₂Si₄ with (n) PSEPs. Using C₂Si₃²⁻ as a decker, we designed novel hetero-deckered sandwich compounds.

2. Theoretical methods

In order to explore the global structure of C₂Si₃²⁻, we introduced a locally developed grid-based comprehensive isomeric search strategy for both the singlet and triplet systems.¹⁰ For each system, a three-dimensional cubic boxes consisting of the uniformly distributed 125 candidate sites were constructed. The two C and three Si-atoms were placed into these candidate sites to get diversified structural forms. Eventually, a total of 138 effective grid-based structures were generated as the input for B3LYP¹¹/6-31G(d)¹² optimizations followed by the harmonic vibrational calculations. All the B3LYP/6-31G(d) local minimum structures without imaginary frequencies were further subject to the B3LYP/aug-cc-pVTZ¹³ re-optimization followed by the frequency calculations. The single-point energies were performed at the CCSD(T)¹⁴/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ level with inclusion of the zero-point vibrational energy (ZPVE) correction from the B3LYP/aug-cc-pVTZ calculations. For the key isomers of C₂Si₃²⁻, we applied the composite G3B3,¹⁵ G4,¹⁶ CBS-QB3 (ref. 17) and W1BD¹⁸ calculations that have been developed for reliable “model chemistry”. In addition, the CCSD(T) calculations with extrapolation up to the complete basis set limit (denote as CCSD(T)/CBS¹⁹) were carried out based on the aug-cc-pVTZ, aug-cc-pVQZ¹³ and aug-cc-pV5Z^13c,d-CCSD(T) single-point energies. The natural charge populations and Wiberg bond index were obtained at the B3LYP/aug-cc-pVTZ level using the natural bond orbital (NBO) analysis. Chemical bonding partition of global minimum structure was performed utilizing the Adaptive Natural Density Partitioning (AdNDP) method.²⁰ For the hetero-deckered sandwich compound, we used the PBE0 (ref. 21)/cc-pVTZ//B3LYP/6-31G(d) to calculate the single-point energies. The calculation in tetrahydrofuran (THF) solution were carried out using the SMD solvent model of Gaussian09.²² All calculations were performed with the Gaussian03 (ref. 23) and Gaussian09 (ref. 24) program packages.

3. Results and discussions

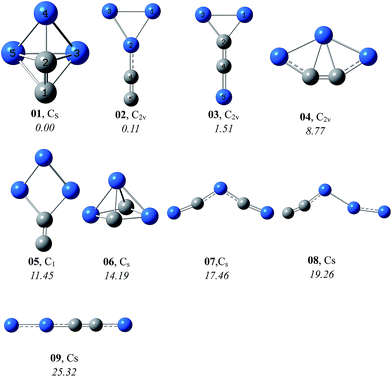
By means of the grid isomeric search, a total of 20 for singlet and 36 for triplet C₂Si₃²⁻ were obtained at the B3LYP/aug-cc-pVTZ level. For simplicity and for easier discussion, we only presented the selected singlet (in Fig. 1) and triplet (in Fig. 2) isomers within 30 kcal mol⁻¹. Note that the total energy of the closo isomer 01 was set to be 0.00 kcal mol⁻¹ as the energy reference. In general, the singlet isomers are more stable than the triplet ones. The lowest-energy triplet isomer ³01 is higher than the lowest-energy singlet isomer by 15.04 kcal mol⁻¹, and is the seventh in the energy order of all the singlet and triplet isomers. So in the following context we only discuss the properties of singlet isomers. The information of all the isomers can be found in ESI† (SI).

Fig. 1 Representative singlet isomers (ΔE < 30 kcal mol⁻¹) of C₂Si₃²⁻ with their symmetry and relative energies (kcal mol⁻¹) at CCSD(T)/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ+ZPVE level. The gray and blue balls are used for carbon and silicon atoms, respectively.

Fig. 2 Representative triplet isomers (ΔE < 30 kcal mol⁻¹) of C₂Si₃²⁻ with their symmetry and relative energies (kcal mol⁻¹) at CCSD(T)/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ+ZPVE level. The total energy of the singlet isomer 01 was set to be 0.00 kcal mol⁻¹ as the energy reference. The left superscript number “3” denotes the triplet state. The gray and blue balls are used for carbon and silicon atoms, respectively.

3.1 Structural properties

At the CCSD(T)/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ+ZPVE level, the lowest-energy isomer 01 has a closo-structure, which is a result of the vertical attack of the C₂-moiety to the Si₃ ring, forming six deltahedras. Interestingly, the two carbon atoms occupy different sites, one is equatorial whereas the other is apex. In topology, 01 is quite analogous to the isoelectronic triagonal bipyramidal cluster Si₅²⁻, which was synthesized in form of the (Rb-crypt)₂Si₅·4NH₃ crystal.²⁵ The equatorial Si–Si (2.503 Å) and axial Si–Si (2.393 Å) bond lengths of C₂Si₃²⁻-01 are in accordance with the experimental values 2.535 and 2.350 Å of Si₅²⁻,²⁵ respectively. Additionally, the C–C distance of 01, i.e., 1.320 Å, lies around the experimental value of the conventional C=C double bond (1.34 Å)²⁶ and is supported by the large Wiberg bond index (WBI) of C–C (1.938). In Table 1, the natural charge population analysis indicates that the negative charge of C₂Si₃²⁻ is mainly distributed on C₂ (−1.589e) with minor on Si₃ (−0.411e).

Table 1 The natural charge (e) of the three lowest-energy isomers of C₂Si₃²⁻ at the B3LYP/aug-cc-pVTZ level

	1	2	3	4	5
01	−0.639	−0.950	−0.127	−0.156	−0.127
02	−0.527	0.345	−0.527	−0.974	−0.316
03	−0.073	−0.991	−0.073	−0.803	−0.060

---

The species 02 and 03 in C_2v symmetry both exhibit a planar structure. The C₂ moiety connects terminally with the Si₃ ring in 02, while it is inserted into the Si₃ ring in 03. Alternatively, 03 can be viewed as a result of the SiC-terminal connection with the CSi₂ ring. The C–C bond length of 02 is very short (1.252 Å) with the WBI value 2.725, indicative of the triple bonding. In 03, the internal C–C bond distance is 1.340 Å (WBI is 1.608), consistent with a double bond. The natural charge population analysis of 02 and 03 are similar to that of 01, i.e., the negative charge is mostly localized on C₂. The almost doubly bonded C₂ unit in 03 carries more charge (−1.794e) than the triply bonded one in 02 (−1.290e).

3.2 Energetics

As shown in Fig. 1, the relative energies of the former three isomers 01, 02 and 03 are close within 2 kcal mol⁻¹, i.e., 0.00, 0.11 and 1.51 kcal mol⁻¹, respectively at the CCSD(T)/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ+ZPVE level. 01 and 02 are almost isoenergetic. It's thus quite desirable to study their energetic competition at more sophisticated levels (see Table 2). First, we carried out the composite G3B3, G4, CBS-QB3 and W1BD calculations, which have been well defined for the purpose of accurately predicting the thermochemical properties of chemical systems. All the four composite methods showed the lowest-energy nature of 01. Interestingly, the energetic competition between the two planar isomers 02 and 03 are not consistent at different levels. G3B3 and G4 place 03 to be more stable than 02, whereas CBS-QB3 and W1BD show 02 to be more stable than 03. Moreover, the relative energy of 02 with reference to 01 at the G3B3, G4 and CBS-QB3 levels are higher than that at W1BD by more than 2 kcal mol⁻¹. The W1BD method was designed to be computationally much more expensive and more accurate than the CBS-QB3 and G3 methods. It should be noted that the above four composite methods comprising a set of optimal parameters have been largely tested on diversified chemical systems. Alternatively, the CCSD(T) method extrapolated to the complete basis set (namely CCSD(T)/CBS) is also an easy-to-use and a powerful tool for predicting energetics of chemical systems especially in the case where the exotic structures that have not been included in the test of composite methods or the desired basis sets are not involved in the composite methods. Using the aug-cc-pVTZ, aug-cc-pVQZ and aug-cc-pV5Z-CCSD(T) calculations based on the B3LYP/aug-cc-pVTZ geometries, we derived the CCSD(T)/CBS relative energies of 02 and 03 as 0.49 and 2.95 kcal mol⁻¹, respectively above 01. It's of interest to note that the CCSD(T)/CBS results are close to the W1BD values. We thus concluded that the global minimum of C₂Si₃²⁻ is a closo-structure 01 with all deltahedras.

Table 2 Relative energies (kcal mol⁻¹) of the three lowest-energy isomers of C₂Si₃²⁻ at different levels

	01	02	03
G3B3	0.00	2.77	1.02
G4	0.00	3.73	1.78
CBS-QB3	0.00	3.64	4.14
W1BD	0.00	0.69	2.17
CCSD(T)/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ+ZPVE	0.00	0.11	1.51
CCSD(T)/aug-cc-pVQZ//B3LYP/aug-cc-pVTZ+ZPVE	0.00	0.26	1.96
CCSD(T)/aug-cc-pV5Z//B3LYP/aug-cc-pVTZ+ZPVE	0.00	0.38	2.44
CCSD(T)_CBS	0.00	0.49	2.95

---

In consideration of the reliability of the B3LYP functional used in the electronically complex systems, we utilized the other two functionals (M06-2X²⁷ and PBE0) to assess the computed structural parameters of the key isomers. The results indicated that the M06-2X and PBE0 functionals produce essentially the same structure for the former three low-lying isomers with only minor difference in bond lengths (see Table 3).

Table 3 The bond lengths (Å) of the 01, 02 and 03 at the B3LYP/aug-cc-pVTZ, M06-2X/aug-cc-pVTZ and PBE0/aug-cc-pVTZ

01	C1–C2	C1–Si3	C1–Si5	C2–Si3	C2–Si4	C2–Si5	Si3–Si4	Si3–Si5	Si4–Si5
B3LYP	1.320	2.176	2.176	2.143	1.842	2.143	2.503	2.393	2.503
M06-2X	1.318	2.117	2.117	2.165	1.843	2.165	2.467	2.368	2.467
PBE0	1.331	2.127	2.127	2.113	1.834	2.113	2.471	2.370	2.471

---

02	Si1–Si2	Si1–C3	Si2–C3	C3–C4	C4–Si5
B3LYP	2.286	1.876	1.876	1.340	1.703
M06-2X	2.275	1.859	1.859	1.351	1.689
PBE0	2.272	1.866	1.866	1.344	1.696

---

03	Si1–Si2	Si1–Si3	Si2–Si3	Si3–C4	C4–C5
B3LYP	2.405	2.251	2.251	1.792	1.252
M06-2X	2.376	2.234	2.234	1.796	1.248
PBE0	2.385	2.242	2.242	1.789	1.252

---

3.3 Bonding characteristics

To explore in detail the bonding situation within isomer C₂Si₃²⁻-01, we applied the AdNDP analysis.²⁰ The deduced localized molecular orbitals of 01 were given in Fig. 3. In 01, there are three silicon lone pairs, four 2c–2e, bonds and four 3c–2e bonds. The occupation numbers (ON) of the silicon lone pairs in equator and apex are 1.96|e| and 1.95|e|, respectively. For the 2c–2e bonds, the ON (2.00|e| and 1.97|e|) of two C₁–C₂ bonds indicate that 01 retains the multiple bonding within C₂. The other two 2c–2e bonds are Si₃–Si₅ (ON = 1.95|e|) and C₂–Si₄ (ON = 1.94|e|). In addition, 01 possesses four 3c–2e bonds, i.e., C₁–C₂–Si₃, C₁–C₂–Si₅, C₂–Si₃–Si₄ and C₂–Si₄–Si₅. The former C₁–C₂–Si₃, C₁–C₂–Si₅ have higher occupancy (ON = 1.98|e|) compared to the latter two identical 3c–2e bonds (ON = 1.83|e|). The existence of four 3c–2e bonds within C₂Si₃²⁻-01 is reminiscent of the well-known boranes and carboranes that are electron deficient and typically characterized by the 3c–2e bonding.^1a–c

Fig. 3 The localized molecular orbitals of C₂Si₃²-01 obtained by AdNDP analysis. The ON denotes the occupation numbers on the localized orbital.

3.4 Sandwich compounds based on C₂Si₃²⁻

The dianionic C₂Si₃²⁻ belongs to the family of charged ligand-free clusters, which can play important roles in the organometallic or cluster-assembled chemistry.²⁸ They can effectively take part in the “sandwiching” interaction with metal ions together with the counter deckers, forming novel sandwich compounds. And vice versa, during the sandwiching, the charged ligand-free clusters can be stabilized electronically (by removal of the Coulomb repulsion) and sterically (by crowded substituents) by the metal ions and counter deckers.

In the sandwiching stabilization of C₂Si₃²⁻, either C₂Si₃²⁻ itself or other stable anionic clusters can be the counter decker, resulting in the “homo-deckered” or “hetero-deckered” sandwich compounds, respectively. To avoid the cluster fusion between nonstoichiometric deckers, the hetero-deckered sandwich strategy is a more favorable choice by introducing a stable decker such as cyclopentadienyl anion (Cp⁻).²⁹ Nowadays, Cp⁻ is one of the versatile ligand in organometallic chemistry, and has been considered as the most commonly used reagent for the synthesis of many metallocenes that are important in a wide range of applications.³⁰

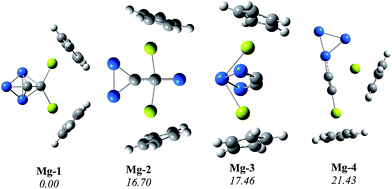
As an example, we studied CpM(C₂Si₃²⁻)MCp with M being the alkali-earth Mg. To reduce the computational cost, the PBE0 method was chosen for sandwich-like compounds since the relative energies of C₂Si₃²⁻ at PBE0/cc-pVTZ//B3LYP/aug-cc-pVTZ+ZPVE are generally in accordance with the CCSD(T)/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ+ZPVE values as listed in ESI† (SI). Fig. 4 shows the representative isomers obtained at the PBE0/cc-pVTZ//B3LYP/6-31G(d)+ZPVE level. Others isomers can be found in ESI† (SI). The hetero-deckered sandwich compound of Mg-1 (closo-C₂Si₃²⁻) is more stable than the second low-lying isomer Mg-2 (open-C₂Si₃²⁻) by 16.70 kcal mol⁻¹. From the structural parameters listed in Table 4, we can see that the six bond distances of the closo-C₂Si₃²⁻ vary little before and after the hetero-deckered sandwiching. Thus, the dianionic closo-01 can be nicely retained within the sandwich compounds.

Fig. 4 Representative isomers of CpMg(C₂Si₃²⁻)MgCp with their relative energies (kcal mol⁻¹) at the PBE0/cc-pVTZ//B3LYP/6-31G(d)+ZPVE level. The gray, blue, white and yellow balls are used for carbon, silicon, hydrogen and magnesium, respectively.

Table 4 The bond lengths (Å) of the closo-C₂Si₃²⁻ in the 01 and Mg-1

	C1–C2	C1–Si3	C1–Si5	C2–Si3	C2–Si4	C2–Si5	Si3–Si4	Si3–Si5	Si4–Si5
01	1.320	2.176	2.176	2.143	1.842	2.143	2.503	2.393	2.503
Mg-1	1.355	2.200	2.200	2.150	1.771	2.150	2.577	2.316	2.577

---

To investigate whether the designed sandwich compound Mg-1 is stable or not against fragmentation, we studied various dissociation pathways as follows:

CpMg(C₂Si₃)²⁻MgCp → CpMgCCMgCp + Si₃ (1)

CpMg(C₂Si₃)²⁻MgCp → CpMgMgCp + C₂Si₃ (2)

CpMg(C₂Si₃)²⁻MgCp → CpMgCp + C₂Si₃Mg (3)

The easiest pathway is (3) with the dissociation energy of 57.25 kcal mol⁻¹. The pathways (1) and (2) need to absorb much more energy. The corresponding endothermicities are 80.41 and 88.23 kcal mol⁻¹. Clearly, due to the very high dissociation energies, the hetero-deckered sandwich compounds CpMg(C₂Si₃²⁻)MgCp are quite stable against fragmentation.

Due to the exposure of the highly electron-withdrawing C₂ moiety within CpMg(C₂Si₃²⁻)MgCp, the solvent effect might have an influence on the isomeric stability. The tetrahydrofuran (THF) solution was chosen for our study. The relative energies of Mg-1, Mg-2, Mg-3 and Mg-4 in gas phase are 0.00, 16.70, 17.46 and 21.43 kcal mol⁻¹, respectively. Their corresponding energies in the THF solution are 0.00, 20.36, 24.54 and 16.20 kcal mol⁻¹. Although the relative energy order of the latter three isomers in solution is different from that in gas phase, the global minimum structure of CpMg(C₂Si₃²⁻)MgCp in both phases remains to be Mg-1 with closo C₂Si₃²⁻.

3.5 Implications

Besides the easy accessibility for spectroscopic study, small-sized clusters are relevant to the growth or assembly into larger systems. The p-block first-row elements (e.g., B, C, N) are prone to form strongly π-bonded structure. Thus, when incorporated into the heavier main-group clusters, they have strong trend to destabilize the formation of a closo or deltahedral structure, especially in small clusters.³¹ Understandably, the structure of C₂X_n is usually fully or partially open instead of being closo, resulting in the formation of the multiply bonded C₂. Thus, our computational finding at various sophisticated levels that the global structure of the small C₂Si₃²⁻ features a closo polyhedra is quite unexpected.

In sharp contrast, the deltahedra is known to be the characteristics of the Zintl ions. Deltahedral Zintl ions composed of the group 14 elements have been known for more than 100 years.³² Many such compounds have been prepared including the smallest E₅²⁻ (E = Si, Ge, Sn, Pb).³³ The bonding of these ligand-free clusters cannot be accounted for by classical octet rule, i.e., 2c–2e bond. Instead, they feature the delocalized 3c–2e bonds and their topologies can usually be explained in terms of the Wade–Mingos rule as for boranes and carboranes. Clearly, replacement of Si₂ moiety within Si₅²⁻ by the highly electron-withdrawing C₂ does not break the closo topology. To our best knowledge, C₂Si₃²⁻ is the smallest main-group dicarbide. The carried two additional electrons render C₂Si₃²⁻ to be applicable in organometallic chemistry, e.g., to form sandwich compounds. Also, with the multiply bonded C₂, the C₂Si₃²⁻ compounds are expected to have particular applications such as in catalysis and cycloaddition reactions.

4. Conclusions

In this paper, we reported the smallest silicon dicarbide with all deltahedras, which is also the first main-group dicarbide with (n + 1) polyhedral skeletal electron pairs (PSEPs). In addition, to counteract the coulomb repulsion within the dianion C₂Si₃²⁻, we introduced the Cp⁻ to design the hetero-deckered sandwich compounds, in which the closo unit 01 can be nicely kept. Due to the strong preference of the C₂-moiety in making the whole or partial molecule be open, the main-group dicarbides with no ligands usually adopt a non-closo topology. The presently disclosed closo-C₂Si₃²⁻ really represents an exception, and its sandwich-like compounds warmly welcome future laboratory studies.

Acknowledgements

This work was funded by the National Natural Science Foundation of China (No. 21273093, 21473069, 21073074). The authors are very thankful for the reviewers' helpful comments and suggestions.

References

1. (a) K. Wade, Chem. Commun., 1971, 792; (b) D. M. P. Mingos, Acc. Chem. Res., 1984, 17, 311; (c) A. C. Tang and Q. S. Li, Int. J. Quantum Chem., 1986, 29, 579; (d) P. V. R. Schleyer and A. I. Boldyrev, J. Chem. Soc., Chem. Commun., 1991, 22, 1536.
2. (a) S. C. Sevov and J. M. Goicoechea, Organometallics, 2006, 25, 5678; (b) R. S. P. Turbervill and J. M. Goicoechea, Chem. Rev., 2014, 114, 10807.
3. (a) K. Tucker, M. Kutner and P. Thaddeus, Astrophys. J., 1974, 193, L115; (b) A. Largo and C. Barrientos, Chem. Phys., 1989, 138, 291; (c) J. El-Yazal, J. M. L. Martin and J.-P. François, J. Phys. Chem. A, 1997, 101, 8319; (d) D. Halfen, D. Clouthier and L. M. Ziurys, Astrophys. J., Lett., 2008, 677, L101; (e) A. Largo, C. Barrientos, X. Lopez and J. M. Ugalde, J. Phys. Chem., 1994, 98, 3985; (f) F. X. Sunahori, J. Wei and D. J. Clouthier, J. Am. Chem. Soc., 2007, 129, 9600; (g) S. Saito, K. Kawaguchi, S. Yamamoto, M. Ohishi, H. Suzuki and N. Kaifu, Astrophys. J., 1987, 317, L115; (h) A. J. Schoeffler, H. Kohguchi, K. Hoshina, Y. Ohshima and Y. Endo, J. Chem. Phys., 2001, 114, 6142; (i) J. Cernicharo, C. Kahane, J. Gomez-Gonzalez and M. Guélin, Astron. Astrophys., 1986, 167, L9; (j) J. Flores and A. Largo, Chem. Phys., 1990, 140, 19; (k) D. Michalopoulos, M. Geusic, P. Langridge-Smith and R. Smalley, J. Chem. Phys., 1984, 80, 3556; (l) L. Snyder, C. Henkel, J. Hollis and F. Lovas, Astrophys. J., 1985, 290, L29; (m) P. Thaddeus, S. Cummins and R. Linke, Astrophys. J., 1984, 283, L45.
4. (a) S. Bresler, G. Zakharov and S. Kirillov, Polym. Sci. U.S.S.R., 1962, 3, 832; (b) H. S. Knight and F. T. Weiss, Anal. Chem., 1962, 34, 749; (c) J. J. Mu and R. A. Hard, Ind. Eng. Chem. Res., 1987, 26, 2063; (d) C. Jaturapitakkul and B. Roongreung, J. Mater. Civ. Eng., 2003, 15, 470.
5. (a) A. Largo, P. Redondo and C. Barrientos, J. Am. Chem. Soc., 2004, 126, 14611; (b) V. M. Rayón, P. Redondo, C. Barrientos and A. Largo, Chem.–Eur. J., 2006, 12, 6963; (c) B. Xiao, J. Feng, J. Chen and L. Yu, Chem. Phys. Lett., 2007, 448, 35; (d) V. M. Rayón, P. Redondo, C. Barrientos and A. Largo, J. Chem. Phys., 2010, 133, 124306.
6. (a) S. Imoto and K. Fukuya, J. Less-Common Met., 1986, 121, 55; (b) M. F. Zalazar, V. C. M. Rayón and A. Largo, J. Phys. Chem. A, 2012, 116, 2972; (c) X. Wang, L. Andrews, D. Ma, L. Gagliardi, A. P. Gonçalves, C. C. L. Pereira, J. Marçalo, C. Godart and B. Villeroy, J. Chem. Phys., 2011, 134, 244313; (d) X. Wang, L. Andrews, P. Å. Malmqvist, B. O. Roos, A. P. Gonçalves, C. C. L. Pereira, J. Marçalo, C. Godart and B. Villeroy, J. Am. Chem. Soc., 2010, 132, 8484; (e) P. Pogány, A. Kovács, Z. Varga, F. M. Bickelhaupt and R. J. M. Konings, J. Phys. Chem. A, 2012, 116, 747; (f) I. Shein and A. Ivanovskii, J. Nucl. Mater., 2009, 393, 192; (g) A. Kovács and R. Konings, J. Nucl. Mater., 2008, 372, 391; (h) D. D. Jackson, G. W. Barton, O. H. Krikorian and R. S. Newbury, J. Phys. Chem., 1964, 68, 1516; (i) S. K. Gupta and K. A. Gingerich, J. Chem. Phys., 1980, 72, 2795; (j) P. Pogány, A. Kovács, D. Szieberth and R. J. Konings, Struct. Chem., 2012, 23, 1281; (k) N. Sasaki, K. Kubo and M. Asano, J. Nucl. Sci. Technol., 1971, 8, 614; (l) W. Huang and L. Yang, Can. J. Phys., 2014, 93, 409; (m) D. Wandner, P. Link, O. Heyer, J. Mydosh, M. A. Ahmida, M. M. Abd-Elmeguid, M. Speldrich, H. Lueken and U. Ruschewitz, Inorg. Chem., 2010, 49, 312; (n) S. K. Gupta and K. A. Gingerich, J. Chem. Phys., 1979, 71, 3072.
7. (a) J.-Y. Yuan, H.-G. Xu and W.-J. Zheng, Phys. Chem. Chem. Phys., 2014, 16, 5434; (b) B. Zhang, B. Cao, C. Chen, J. Zhang and H. Duan, J. Cluster Sci., 2013, 24, 197.
8. (a) G. Froudakis, A. Zdetsis, M. Mühlhäuser, B. Engels and S. D. Peyerimhoff, J. Chem. Phys., 1994, 101, 6790; (b) A. Nakajima, T. Taguwa, K. Nakao, M. Gomei, R. Kishi, S. Iwata and K. Kaya, J. Chem. Phys., 1995, 103, 2050; (c) S. Hunsicker and R. O. Jones, J. Chem. Phys., 1996, 105, 5048; (d) Z. Y. Jiang, X. H. Xu, H. S. Wu, F. Q. Zhang and Z. H. Jin, Chem. Phys., 2003, 290, 223; (e) H. Wang, W.-C. Lu, J. Sun, Z.-S. Li and C.-C. Sun, Chem. Phys. Lett., 2006, 423, 87; (f) J. L. Deng, K. H. Su, X. Wang, Q. F. Zeng, L. F. Cheng, Y. D. Xu and L. T. Zhang, Eur. Phys. J. D, 2008, 49, 21; (g) M. Savoca, A. Lagutschenkov, J. Langer, D. J. Harding, A. Fielicke and O. Dopfer, J. Phys. Chem. A, 2013, 117, 1158.
9. (a) M. M. Ghouri, L. Yareeda and D. S. Mainardi, J. Phys. Chem. A, 2007, 111, 13133; (b) S. Becker and H. J. Dietze, Int. J. Mass Spectrom. Ion Processes, 1988, 82, 287; (c) R.-X. Wang, D.-J. Zhang, R.-X. Zhu and C.-B. Liu, Acta Chim. Sin., 2007, 65, 2092; (d) Y. Pei and X. C. Zeng, J. Am. Chem. Soc., 2008, 130, 2580; (e) C. Wang, W. Cui, J. Shao, X. Zhu and X. Lu, Comput. Theor. Chem., 2013, 1006, 19; (f) G. Pascoli and H. Lavendy, Int. J. Mass Spectrom., 2001, 206, 153; (g) M. Chen, L. Zheng, Q. Zhang, M. Liu and C. Au, J. Phys. Chem. A, 2003, 107, 10111; (h) M. Chen, H. Liang, M. Liu, Q. Zhang and C. Au, Int. J. Mass Spectrom., 2004, 232, 165; (i) X. Li, L.-S. Wang, N. A. Cannon and A. I. Boldyrev, J. Chem. Phys., 2002, 116, 1330; (j) F. Y. Naumkin, J. Phys. Chem. A, 2008, 112, 4660; (k) Y.-B. Wu, H.-G. Lu, S.-D. Li and Z.-X. Wang, J. Phys. Chem. A, 2009, 113, 3395; (l) F. Dong, S. Heinbuch, Y. Xie, J. J. Rocca and E. R. Bernstein, Phys. Chem. Chem. Phys., 2010, 12, 2569; (m) B. I. Loukhovitski, A. S. Sharipov and A. M. Starik, J. Phys. Chem. A, 2015, 119, 1369.
10. (a) C. B. Shao and Y. H. Ding, Grid-Based Comprenhensive Isomeric Search Algorithm, Jilin University, Changchun, China, 2010; (b) Z. H. Cui, M. Contreras, Y. H. Ding and G. Merino, J. Am. Chem. Soc., 2011, 133, 13228; (c) S. M. Gao and Y. H. Ding, RSC Adv., 2012, 2, 11764; (d) X. Y. Tang, Z. H. Cui, C. B. Shao and Y. H. Ding, Int. J. Quantum Chem., 2012, 112, 1299; (e) S. M. Gao and Y. H. Ding, RSC Adv., 2012, 2, 11764; (f) C. Guo, Z. H. Cui and Y. H. Ding, Struct. Chem., 2013, 24, 263; (g) C. Guo, Z. H. Cui and Y. H. Ding, Int. J. Quantum Chem., 2013, 113, 2213; (h) C. Guo, C. Wang and Y. H. Ding, Struct. Chem., 2014, 25, 1023; (i) X. Y. Zhang and Y. H. Ding, Comput. Theor. Chem., 2014, 1048, 18; (j) X. Y. Zhang and Y. H. Ding, RSC Adv., 2015, 5, 27134.
11. (a) R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, Oxford, 1989; (b) A. D. Becke, J. Chem. Phys., 1992, 96, 2155; (c) J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671.
12. (a) M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D.J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654; (b) T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007; (c) V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223; (d) V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976.
13. (a) R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796; (b) D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358; (c) D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975; (d) N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107.
14. (a) J. Cizek, Adv. Chem. Phys., 1969, 14, 35; (b) G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910; (c) G. E. Scuseria, C. L. Janssen and H. F. Schaefer, J. Chem. Phys., 1988, 89, 7382; (d) G. E. Scuseria and H. F. Schaefer, J. Chem. Phys., 1989, 90, 3700.
15. A. G. Baboul, L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 1999, 110, 7650.
16. L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108.
17. (a) J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822; (b) J. A. Montgomery Jr, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532.
18. (a) J. M. L. Martin and G. de Oliveira, J. Chem. Phys., 1999, 111, 1843; (b) S. Parthiban and J. M. L. Martin, J. Chem. Phys., 2001, 114, 6014; (c) E. C. Barnes, G. A. Petersson, J. A. Montgomery Jr, M. J. Frisch and J. M. Martin, J. Chem. Theory Comput., 2009, 5, 2687.
19. K. A. Peterson, D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1994, 100, 7410.
20. (a) D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207; (b) D. Y. Zubarev and A. I. Boldyrev, J. Org. Chem., 2008, 73, 9251; (c) D. Y. Zubarev and A. I. Boldyrev, J. Phys. Chem. A, 2009, 113, 866.
21. (a) C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158; (b) C. Adamo, M. Cossi and V. Barone, J. Mol. Struct.: THEOCHEM, 1999, 493, 145; (c) M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029.
22. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision E.01, Gaussian, Inc., Wallingford, CT, 2004.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009.
25. (a) J. M. Goicoechea and S. C. Sevov, J. Am. Chem. Soc., 2004, 126, 6860; (b) D. Y. Zubarev, A. I. Boldyrev, X. Li, L.-F. Cui and L.-S. Wang, J. Phys. Chem. A, 2005, 109, 11385.
26. J. Dowling and B. P. Stoicheff, Can. J. Phys., 1959, 37, 703.
27. (a) E. G. Hohenstein, S. T. Chill and C. D. Sherrill, J. Chem. Theory Comput., 2008, 4, 1996; (b) M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, J. Phys. Chem. A, 2013, 117, 12590.
28. (a) J. Frunzke, M. Lein and G. Frenking, Organometallics, 2002, 21, 3351; (b) E. Urne˙žius, W. W. Brennessel, C. J. Cramer, J. E. Ellis and P. v. R. Schleyer, Science, 2002, 295, 832; (c) R. Wolf, A. W. Ehlers, M. M. Khusniyarov, F. Hartl, B. de Bruin, G. J. Long, F. Grandjean, F. M. Schappacher, R. Pöttgen and J. C. Slootweg, Chem.–Eur. J., 2010, 16, 14322; (d) S. Scharfe, F. Kraus, S. Stegmaier, A. Schier and T. F. Fässler, Angew. Chem., Int. Ed., 2011, 50, 3630.
29. (a) L. M. Yang, Y. H. Ding and C. C. Sun, ChemPhysChem, 2006, 7, 2478; (b) L. M. Yang, Y. H. Ding and C. C. Sun, Chem.–Eur. J., 2007, 13, 2546; (c) L. M. Yang, J. Wang, Y. H. Ding and C. C. Sun, Organometallics, 2007, 26, 4449; (d) L. M. Yang, Y. H. Ding, W. Q. Tian and C. C. Sun, Phys. Chem. Chem. Phys., 2007, 9, 5304; (e) L. M. Yang, Y. H. Ding and C. C. Sun, J. Am. Chem. Soc., 2007, 129, 658; (f) L. M. Yang, Y. H. Ding and C. C. Sun, J. Am. Chem. Soc., 2007, 129, 1900; (g) L. M. Yang, Y. H. Ding and C. C. Sun, Theor. Chem. Acc., 2008, 119, 335; (h) L. M. Yang, J. Wang, Y. H. Ding and C. C. Sun, J. Phys. Chem. A, 2007, 111, 9122; (i) L. M. Yang, Y. H. Ding and C. C. Sun, J. Phys. Chem. A, 2007, 111, 10675.
30. (a) X. Wu and X. C. Zeng, J. Am. Chem. Soc., 2009, 131, 14246; (b) D. Senthilnathan, S. Vaideeswaran, P. Venuvanalingam and G. Frenking, J. Mol. Model., 2011, 17, 465.
31. (a) G. H. Chen, Y. H. Ding, X. R. Huang and C. C. Sun, J. Phys. Chem. A, 2005, 109, 5619; (b) G. H. Chen, Y. H. Ding, X. H. Huang, H. X. Zhang, Z. S. Li and C. C. Sun, J. Phys. Chem. A, 2002, 106, 10408; (c) G. Maier, H. P. Reisenauer and J. Glatthaar, Organometallics, 2000, 19, 4775; (d) M. Zhou, L. Jiang and Q. Xu, J. Phys. Chem. A, 2004, 108, 9521; (e) M. J. Maclean, P. C. H. Eichinger, T. Wang, M. Fitzgerald and J. H. Bowie, J. Phys. Chem. A, 2008, 112, 12714.
32. (a) A. C. R. Joanis, C. R. Hebd. Seances Acad. Sci., 1891, 113, 795; (b) E. Zintl and A. Z. Harder, Z. Phys. Chem., Abt. A, 1931, 154, 47; (c) E. Zintl and W. Z. Dullenkorf, Z. Phys. Chem., Abt. B, 1932, 16, 183.
33. (a) J. D. Corbett, Struct. Bonding, 1997, 87, 157; (b) T. F. Fässler, Coord. Chem. Rev., 2001, 215, 377.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra22310e

---