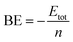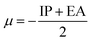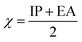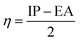Structural evolution, electronic and magnetic manners of small rhodium Rh_n^+/− (n = 2–8) clusters: a detailed density functional theory study

Abstract

A systematic investigation on the lowest energy electronic structure of neutral, cationic and anionic Rh_n (n = 2–8) clusters in the gas phase is performed with an all electron relativistic method using density functional theory within the generalized gradient approximation. The lowest energy structures of neutral and ionic rhodium clusters are evaluated with different multiplicities. Neutral clusters with even atoms of rhodium and ionic clusters containing odd atoms of rhodium are optimized with multiplicities M = 1, 3 and 5, while neutral clusters containing odd rhodium atoms and ionic clusters with even atoms of rhodium are allowed to relax with multiplicities M = 2, 4 and 6. The bond length, binding energy, coordination number, bond dissociation energy, stability function, ionization potential, electron affinity, electrophilicity, LUMO–HOMO gap, chemical hardness, dipole moment and magnetic moment are evaluated from the lowest energy geometry. These studies reveal that even atom rhodium clusters are more stable than odd atom clusters. Calculated electronic properties such as the LUMO–HOMO gap, bond dissociation energy, stability function, electron affinity and electrophilicity suggest that Rh₄ with a tetrahedral geometry is the most stable among all Rh_n (n = 2–8) clusters. Hence, tetrahedral Rh₄ may be considered as the magic number cluster.

---

Introduction

Atomic clusters are a very vital class of materials which are composed of a few to hundreds of atoms. Clusters show different physical¹ and chemical properties^2–4 from their bulk counterparts due to quantum size effects. Studies of small metal clusters provided a connecting link between molecular and bulk states. The high surface to volume ratio of smaller clusters lead to the properties differing from the bulk. The properties of nanoclusters change drastically even after the addition of a single extra atom. In recent years, transition metal clusters have been widely studied due to their unique catalytic and magnetic properties. In particular, nanoclusters of Pt, Pd and Rh are used as heterogeneous catalysts for hydrogenation as well as for the reduction of NO and oxidation of CO and unburned hydrocarbons.⁵ Rh on the other hand, is a vital heterogeneous catalyst used for hydrogenation as well as dehydrogenation reactions of alcohols⁶ and also for removing harmful gases.⁷ The variation of the magnetic moment with cluster size and high catalytic activity are the most significant characteristics of transition metal clusters. Many theoretical and experimental studies on the magnetic properties of 3d transition metal clusters such as Fe, Co and Ni have been extensively performed to date.^8–13 These investigations suggest that 3d transition metal clusters have nonzero magnetic moments, while the bulk form shows no magnetic moment.^11,14 Due to the reduced coordination and high symmetry, clusters develop a narrow d-band width that gives the possibility of larger spin multiplicities in the ground state. However, very few theoretical and experimental studies on 4d transition metal clusters are reported.¹⁵ Out of them, Rh metal clusters have been the subject of a number of experimental and theoretical studies because of their catalytic and magnetic properties. Two very important aspects are considered when investigating the magnetic properties of metal clusters: the first is to study the lowest energy geometrical structures and the second is to determine their electronic properties. Most of the electronic calculations on Rh clusters have been performed either by assuming fixed geometries^16–18 or just optimizing bond lengths.^15,19–21 Investigation of the electronic structure of rhodium clusters is very challenging due to a huge number of electrons and large number of achievable geometric isomers. However, some low energy rhodium clusters are derived using density functional theory calculations. Reddy et al.²² combined the techniques of MD (molecular dynamics) with DFT and anticipated that a 13 atom Rh cluster would be magnetic with a magnetic moment of 1.62 μ_B, while the observed value of magnetic moment per atom of Rh₁₃ was found to be 0.48 μ_B.^23,24 Jinglong et al.^15,25 examined different small rhodium clusters and Li et al.¹⁹ evaluated the magnetic properties of Rh_n (n = 6, 9, 13, 19 and 43). Cox et al. reported the permanent magnetic moment of rhodium clusters with n ≤ 60–90, while ruthenium along with palladium clusters showed nonmagnetic behavior at least for a cluster size greater than 13.^24,26 Rh is the first case where magnetism is observed in the nanoclusters of a nonmagnetic solid. A remarkable size dependence of the magnetic moment per atom of rhodium is observed from experimental studies. The magnetic moment of nanoclusters oscillates as a function of cluster size along with the number of atoms. The magnetic moment of a rhodium cluster seems to be different from other ferromagnetic transition metal clusters such as Fe, Co and Ni, where the magnetic moments are extended over wide ranges.^27–31 A finite size effect in the electronic structure and reduction of the local coordination number qualitatively reflect the enhancement of magnetism in small clusters.²⁴ A spin-polarized DFT study^32,33 of Ru, Rh, and Pd clusters shows a large magnetic moment for small clusters, while the magnetic moment of Ru and Rh clusters decreases gradually with increasing cluster size.

Some theoretical works^22,23 revealed that Rh₄ with a tetrahedral geometry is stabilized in the singlet state; while Bae et al.³⁴ showed that high spin rhombus Rh₄ is the ground state. The magnetic moment of metal clusters changes with changes in their geometry. The magnetic moment of a Rh₁₃ cluster is found to be 1.3 μ_B per atom with a cage like structure,³⁴ while Stern–Gerlach evaluated a magnetic moment of 0.48 μ_B per atom.^24,26 Different geometrical assumptions can clarify the obvious inconsistency between different theoretical and experimental works. Thus it is obvious that obtaining the ground state geometry is very much crucial for explaining the magnetic properties of metal clusters.

Most of the recent investigations related to Rh clusters are motivated by the theoretical studies of Galicia³⁵ and Reddy et al.²³ and the experimental works of Cox et al.^24,26 A wide range of magnetic moments of rhodium nanoclusters are observed from theoretical studies.^15,19,36,37 This indicates a quite strong understanding of the calculated magnetic properties of Rh with a theoretical method approximation. Due to indirect experimental information and insufficient precise structural determination, the correct properties of free-standing clusters are hard to pin down. Metals do not always follow the good proportionality of magnetism with coordination number and interatomic distances which is observed from the ab initio calculation of Rh₂ supported on Ag (001).³⁸ Therefore, a methodical exploration of both the geometric and magnetic properties of isolated rhodium clusters with respect to size is vital.

The magnetism as well as the bonding nature in correlation with the atomic structures of Rh nanoclusters is found to be significant for catalysis.³⁹ Hence, it is challenging to fully recognize the magnetic properties to understand their role in catalytic applications. The correct representation of the electronic correlation for the large number of open shell electronic states which arise due to incomplete 4d states of Rh is a challenging aspect in theoretical study.⁴⁰

To the best of our knowledge, probably for the first time a detailed systematic investigation on the electronic, structural and magnetic properties of neutral and ionic Rh_n (n = 2–8) clusters has been done. The main focus of this study is to correlate different properties such as bond length, coordination number, binding energy, bond dissociation energy, ionization potential, electron affinity, LUMO–HOMO gap, global hardness, etc., with the size and stability of the clusters. The DOS and spin density values are evaluated in order to study the electronic and magnetic contribution of each atom to a cluster. A systematic survey on small rhodium clusters is done to determine their most stable or reactive cluster on the basis of calculated reactivity parameters. Geometry optimization of different possible structural isomers of neutral Rh_n (n = 2–8) clusters is carried out with different multiplicities i.e., M = 2, 4 and 6 for odd atom clusters and M = 1, 3 and 5 for even atom clusters to evaluate the stable geometry. The geometries of Rh_n⁺ and Rh_n⁻ clusters are also fully optimized with multiplicities of 2, 4, and 6 for even atom ionic clusters, and 1, 3 and 5 for odd atom ionic clusters, in order to determine the most stable geometry.

Computational details

All the isomers of rhodium clusters are fully optimized using a double numerical plus polarization (DNP) basis set implemented in a DMol3 program package.^41,42 DFT calculations are performed under a generalized gradient approximation (GGA) with a BLYP exchange correlation functional^43,44 which incorporates the exchange functional of Becke with the gradient corrected functional of Lee–Yang–Parr. A DNP⁴⁵ basis set is chosen for geometry optimization. The DNP basis set is comparable to a Gaussian split-valence 6-31G** basis set. Relativistic calculations are very important for heavy metal atoms. Hence, all electron relativistic corrections to valence orbitals via a local pseudo potential are carried out for direct inversion in a subspace method (DIIS) without symmetry constraints. In this study self consistent field (SCF) procedures are adopted with a convergence criteria of energy 1 × 10⁻⁵ Ha, maximum force gradient 2 × 10⁻³ Ha Å⁻¹ and displacement convergence 5 × 10⁻³ Å on the total energy and 10⁻⁶ a.u. on electron density are the boundary conditions applied. All neutral and charged isomers of rhodium clusters are optimized corresponding to low spin configurations. In order to compare the energy values of ground state clusters with their higher multiplicities, symmetry restricted calculations are done at higher spin states. Vibrational frequency calculations are done to ensure an energy minima. A zero point vibrational energy correction is incorporated in all the calculated energies. From further study of higher multiplicities most of the clusters are found to retain their ground state. An absence of imaginary frequencies for all geometries suggests their energy minima. To evaluate the stability of the clusters with respect to size, the binding energy per atom, second difference of binding energy, first vertical ionization potential, electron affinity and chemical hardness of the stable structures are determined.

The average binding energy per atom is computed from the following equation

where E_tot is the total energy of a cluster which is defined as E_tot = E_n − nE₁ where E₁ and E_n are the energies of a single atom and the optimized cluster, respectively, and n is the number of atoms in the cluster.

For ionic clusters, the binding energy is evaluated as

BE = −E_tot^±/n

where E_tot^± = E_n^± − (n − 1)E₁ − E₁^± is the total energy of an ionized cluster where E₁^± and E_n^± are the energies of a single charged atom (Rh₁^±) and Rh_n cluster, respectively.

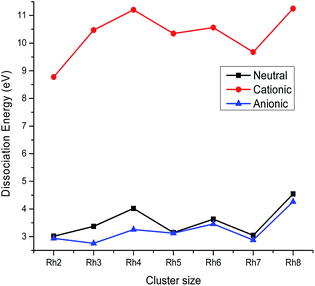
The dissociation energy of a cluster of size n has been calculated from

D(n, n − 1) = E(Rh_n − 1) + E(Rh₁) − E(Rh_n)

where E(Rh₁) is the energy of a single atom and E(Rh_n) is the energy of n optimized rhodium atoms.

Chemical hardness (η) can be defined as the second derivative of the energy (E) with respect to the number of electrons (N) at a constant external potential ν(r⃑)

where μ, the chemical potential, is defined as the negative of electronegativity by Iczkowski and Margrave.⁴⁶

Using the finite difference approach⁴⁶ the chemical potential, electronegativity and chemical hardness can be computed from the vertical ionization potential (IP) and electron affinity (EA).

According to Parr’s prescription, the electrophilicity index⁴⁷ is defined as

Results and discussion

Geometries and energetics

In order to find out the best exchange-correlation functional to be used for the calculation, we carried out a comparative study of the bond length, vibrational frequency and binding energy of a rhodium dimer using various functionals with the available experimental results.⁴⁸ The comparative results are presented in Table 1. It is noticed from Table 1 that among all the GGA functionals used, the BLYP functional provides the best assessment of all three experimental parameters considered. Hence, we chose the BLYP functional for this study.

Table 1 Binding energy, vibrational frequency and bond length of the Rh₂ dimer evaluated with different functionals

Method	Binding energy (eV)	Frequency (cm^−1)	Bond length (Å)
GGA-BLYP	3.013	268	2.308
GGA-PW91	0.524	287	2.269
GGA-BOP	2.203	277	2.312
GGA-BP	2.462	286	2.288
GGAVWN_BP	2.484	286	2.286
GGA-HCTH	2.021	284	2.309
GGA-RP	2.336	279	2.308
GGA-PBE	3.321	287	2.286
Experiment	2.92 ± 0.22	267	2.280

---

Neutral Rh_n clusters

The ground state for Rh atoms is found to be a quartet, ⁴F (4d⁸5s¹), with an energy of 131 524.7615 eV. The ground state geometries of neutral Rh_n (n = 2–8) clusters evaluated at the BLYP/DNP level are shown in Fig. 1 and all other isomers with their point groups are given in Fig. S1 of the ESI.† Singlet multiplicity is the lowest energy state for neutral Rh₂ with a symmetric point group D_∞h and a bond length of 2.308 Å. The binding energy per atom of all the neutral clusters with different multiplicities is given in Table 2 and the bond lengths are mentioned in Table S1 of the ESI.† It is observed from Table 2 that the binding energy per atom of Rh₂ is calculated to be 1.5067 eV. The energy values of the singlet and triplet states of the Rh₂ cluster are determined to be comparable i.e. the triplet state possesses an energy 0.3660 eV higher than the singlet state. The variation of the binding energy per atom of neutral clusters with cluster size is shown in Fig. 2. For a neutral Rh₃ cluster, a triangular geometry with a quartet state is the lowest energy isomer with a bond length of 2.448 Å and a symmetric point group, D_3h. The energy difference between the doublet and the quartet state is found to be only 0.1659 eV. The binding energy per atom for the most stable Rh₃ cluster with a triangular shape is 2.1276 eV. A singlet state with a tetrahedral geometry is the ground state for the neutral Rh₄ cluster with an average bond length and binding energy per atom of 2.518 Å and 2.5315 eV, respectively. The energy difference between the triplet and singlet state is evaluated to be 0.3798 eV. The calculated binding energy per atom of Rh₄ is found to be lower than the corresponding values reported by Jinlong et al.¹⁵ and Reddy et al.²² However, the DFT evaluated average bond length is found to be closer to the corresponding value (2.48 Å) reported by them. For a cluster containing five rhodium atoms, a doublet state with a square pyramidal geometry and symmetric point group C_4v is the lowest energy state. The average bond length and binding energy per atom of the stable Rh₅ cluster are 2.532 Å and 2.7091 eV, respectively. The energy difference between the singlet and triplet state of the Rh₅ cluster is 0.0778 eV only. The binding energy value is very close to the reported value of 2.70 eV per atom predicted by Chien³⁷ (GGA-DFT) but lower than the values (3.06 and 3.13 eV per atom) showed by Jinlong et al.¹⁵ and Reddy et al.²² with the symmetric point groups D_3h and C_4v, respectively. The bond length of 2.532 Å obtained in this study is closer to the reported values (2.52 and 2.54 Å) by Jinlong et al.¹⁵ and Chien.³⁴ A trigonal prismatic geometry for a Rh₆ neutral cluster in the singlet state with a symmetric point group D_3h is observed to be the ground state with an average bond length of 2.491 Å and binding energy of 2.8809 eV per atom. The energy difference between the singlet state and triplet state is found to be 0.0797 eV. The binding energy and bond length values are evaluated to be lower than the corresponding values reported by Jinlong et al.¹⁵ (DV-LSDA) and Li¹⁹ (DV-LSDA). However, the calculated binding energy value is exactly the same as the binding energy obtained by Chien et al.³⁷ For a Rh₇ cluster, a quartet state with a capped prism structure is found to be the most stable isomer with a symmetric point group (C_2v). The binding energy per atom and the average bond length of this stable cluster are evaluated to be 2.9045 eV and 2.539 Å, respectively. The binding energy value of Rh₇ obtained is lower than the binding energy values of Jinlong et al.¹⁵ (3.43 eV per atom) and Reddy et al.²² (3.33 eV per atom). The average bond distance of 2.77 Å evaluated in this study is higher than the corresponding values reported by Jinlong et al.¹⁵ and Reddy et al.²² The energy difference between the doublet and quartet state of the Rh₇ cluster is found to be 0.0218 eV. A cubic geometry of Rh₈ with a singlet state is evaluated to be most stable isomer. This isomer has a symmetric point group (O_h), with an average bond length and binding energy per atom of 2.459 Å and 3.1092 eV, respectively. The triplet state is recorded to be slightly higher in energy (0.00370 eV) than the singlet state. The binding energy as well as the average bond distance is calculated to be lower than the values suggested by Jinlong et al.¹⁵ and Reddy et al.²²

Fig. 1 Stable geometries of neutral, cationic and anionic clusters derived at the BLYP/DNP level.

Table 2 Binding energies (E_b) per atom in eV of neutral, cationic and anionic Rh_n (n = 2–8) with different multiplicities (M)

	Multiplicity
	M = 1	M = 2	M = 3	M = 4	M = 5	M = 6
Neutral cluster size
Rh2	1.5067		1.3235		1.5060
Rh3_1		1.6584		1.666		1.6644
Rh3_2		2.0722		2.1276		2.0649
Rh4_1	2.5315		2.5055		2.4251
Rh4_2	2.3471		2.3565		2.3713
Rh5_1		2.6337		2.6282		2.6082
Rh5_2		2.7091		2.6935		2.6583
Rh5_3		2.7086		2.6935		2.6640
Rh5_4		2.7084		2.6935		2.6817
Rh6_1	2.7393		2.7392		2.7333
Rh6_2	2.8307		2.8306		2.8365
Rh6_3	2.8307		2.8319		2.8365
Rh6_4	2.7135		2.7121		2.7001
Rh6_5	2.8809		2.8676		2.8381
Rh7_1		2.5676		2.5645		2.5660
Rh7_2		2.8867		2.8917		2.8903
Rh7_3		2.9014		2.9045		2.9026
Rh7_4		2.8133		2.8119		2.7964
Rh7_5		2.7869		2.7866		2.8217
Rh7_6		2.8868		2.8917		2.8903
Rh8_1	2.9728		2.9541		2.9612
Rh8_2	2.6068		2.6092		2.6103
Rh8_3	2.9884		2.9868		2.9825
Rh8_4	3.1092		3.1087		3.0796
Rh8_5	2.9543		2.9492		2.9403
Rh8_6	2.9632		2.8432		2.7890
Rh8_7	2.6789		2.6794		2.5978
Ionic clusters
Rh2^+		0.7862		0.9506		1.0707
Rh2^−		1.5784		1.7128		1.4433
Rh3^+	1.9935		1.9207		1.9935
Rh3^−	2.2245		2.2143		2.2176
Rh4^+		2.6381		2.5449		2.4901
Rh4^−		2.6048		2.5297		2.4852
Rh5^+	2.8531		2.8412		2.8082
Rh5^−	2.8054		2.7948		2.8069
Rh6^+		3.0262		2.9965		2.9557
Rh6^−		2.9966		2.9850		2.9627
Rh7^+	3.0288		3.0278		3.0284
Rh7^−	3.0491		3.0447		3.0473
Rh8^+		3.2271		3.2171		3.1987
Rh8^−		3.2619		3.2404		3.2285

---

Fig. 2 Binding energy (eV per atom) of neutral, cationic and anionic Rh_n clusters.

Cationic (Rh_n⁺) and anionic (Rh_n⁻) clusters

In the literature, very few reports on cationic and anionic clusters of rhodium are accessible. The ground state geometries and average bond lengths evaluated at the BLYP/DNP level are shown in Fig. 1 and Table S1 of the ESI,† respectively. Cationic and anionic rhodium clusters are generated by removing and adding one electron to the lowest energy neutral Rh_n clusters. Spin unrestricted geometry optimization of these ionic clusters with different multiplicities is performed. The variation of the binding energies per atom of these ionic clusters with cluster size is shown in Fig. 2 and the binding energy values (eV per atom) are listed in Table 2. A cationic (Rh₂⁺) cluster in a sextet state is the lowest energy state with the symmetric point group D_∞h, while, the ground state for an anionic (Rh₂⁻) cluster is a quartet with the point group D_∞h. It is seen that the average bond distance and binding energy per atom for the Rh₂⁺ and Rh₂⁻clusters are 2.355 and 2.353 Å and 1.0707 and 1.7128 eV, respectively. The sextet Rh₂⁺ is stabilized more by 0.56912 eV than the doublet state, while, the quartet Rh₂⁻ is stabilized more by 0.26884 eV than the geometry with doublet multiplicity. The lowest energy triangular geometry with the symmetry point group D_3h is found for Rh₃⁺ and Rh₃⁻ in the singlet state. It is seen from Table S1† that the average bond distances (Rh–Rh) in Rh₃⁺ and Rh₃⁻ are found to be 2.448 Å and 2.494 Å, respectively. The binding energy per atom for the cationic cluster is 1.9935 eV, while for the anionic cluster it is calculated to be 2.2245 eV. The energies of Rh₃⁻, in the singlet as well as in the triplet state, are found to be closer. Again, the doublet states of Rh₄⁺ and Rh₄⁻ with tetrahedral geometry are found to be the ground state with a T_d symmetry point group. The average bond distances of the tetrahedral cationic and anionic rhodium clusters are 2.512 Å and 2.550 Å, respectively. While for cationic and anionic Rh₄, a quartet multiplicity is found to be the least stable. The binding energies per atom for the ground state of Rh₄⁺ and Rh₄⁻ are evaluated to be 2.6381 and 2.6048 eV, respectively. Cationic and anionic Rh₅ clusters with singlet and pentet multiplicities are evaluated to be the ground state with average bond lengths of 2.538 and 2.543 Å, respectively. The structure of anionic and cationic Rh₅ is evaluated to be square pyramidal with the symmetric point group C_4v. The binding energy values per atom for Rh₅⁺ and Rh₅⁻ are 2.8531 and 2.8069 eV, respectively. The energy difference between the triplet and singlet states of Rh₅⁺ is 0.05932 eV, while, between the pentet and singlet states of Rh₅⁻ it is 0.0080 eV. A doublet state with a trigonal prismatic geometry for both Rh₆⁺ and Rh₆⁻ clusters with a point group D_3h is stabilized. The average bond lengths for Rh₆⁺ and Rh₆⁻ are calculated to be 2.484 Å and 2.497 Å, respectively. While, the quartet states of Rh₆⁺ and Rh₆⁻ are less stabilized by 0.17796 and 0.06911 eV, respectively, with respect to the doublet state of respective ionic Rh₆. The binding energy per atom values of the lowest energy Rh₆⁺ (3.0262 eV) and Rh₆⁻ (2.9966 eV) are noticed to be close. Rh₇⁺ and Rh₇⁻ with a singlet multiplicity and a capped prism geometry with C_2v symmetry are found to be the lowest energy structures. The triplet states of Rh₇⁺ and Rh₇⁻ are evaluated to be less stable than the corresponding singlet states. The binding energies per atom for Rh₇⁺ and Rh₇⁻ are 3.0288 and 3.0491 eV, respectively. A cubic geometry in the doublet state with the symmetric point group D_3h is the ground state for cationic and anionic Rh₈ clusters. Table S1† reports that the average Rh–Rh bond lengths for Rh₈⁺ and Rh₈⁻ are 2.474 and 2.461 Å respectively. The binding energy per atom for the Rh₈⁺ cluster (3.2271 eV) is found to be lower than for Rh₈⁻ (3.2619 eV). The quartet states of the Rh₈⁺ and Rh₈⁻ clusters are the least stable. However, the quartet and doublet states of ionic Rh₈ clusters are found to possess very close energy values.

Trends

The variation of the average bond length with cluster size for the most stable cluster is shown in Fig. 3. It is observed from the figure that the average bond lengths increase with size in the case of smaller clusters, while no regular variation of geometrical parameters is noticed in the case of larger clusters. The variation of binding energy with cluster size is shown in Fig. 2. It is quite visible from Fig. 2 that the binding energy per atom of neutral and ionic (cationic and anionic) clusters increases with the increasing number of atoms and number of bonds. Hence, the energy stability of a rhodium cluster increases with the cluster size, while this variation is less prominent in the case of larger clusters. The coordination number (α) of all the clusters is evaluated at the DNP/BLYP level. The coordination number of the neutral as well as the ionic clusters is evaluated to be the same. The coordination numbers (α) of the Rh₃, Rh₄, Rh₅, Rh₆, Rh₇ and Rh₈ clusters are found to be 2.00, 3.00, 3.20, 3.00, 3.71, and 3.00, respectively. That is the Rh₄, Rh₆, and Rh₈ clusters in the neutral as well as in the ionic form possess the same coordination number.

Fig. 3 Bond length of neutral, cationic and anionic Rh_n clusters.

Relative stability

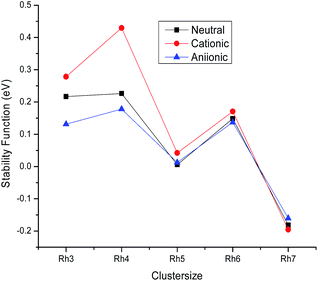
To understand the relative stability of the rhodium clusters, we have evaluated the second finite difference of total energies Δ²E_b(n), which is the measure of the stability function. The stability function is calculated from the following mathematical formulation:

Δ²E_b(n) = 2E_b(n) − E_b(n + 1) − E_b(n − 1)

where E_b(n) is the binding energy per atom of a cluster with n atoms. The variation of the stability function with the cluster size of rhodium is shown in Fig. 4. It is noticed from Fig. 4 that the highest peak is observed at n = 4 for the neutral as well as the ionic form indicating a maximum stability for neutral and ionic Rh₄ among all other clusters. The bond dissociation energies (the energy required for fragmenting a Rh_n cluster to Rh_n−1 and Rh) of the most stable neutral and ionic rhodium clusters are plotted against the cluster size as shown in Fig. 5. Fig. 5 suggests that neutral and cationic Rh₄ and Rh₈ clusters have higher bond dissociation energies and hence, reveals a higher stability. However, anionic clusters show noticeable peaks at n = 4, 6 and 8. It is also seen from Fig. 5 that even atom rhodium clusters are comparatively more stable than the odd atom clusters. Cationic clusters are found to possess higher dissociation energies than the neutral as well as anionic clusters. Hence, a larger interaction between electrons and the nucleus is observed in the case of cationic clusters compared to their neutral clusters. While anionic clusters with lower dissociation energy present more electron–electron repulsion than nuclear electronic attraction.

Fig. 4 Stability function of neutral, cationic and anionic Rh_n.

Fig. 5 Dissociation energy of neutral, cationic and anionic Rh_n.

Electronic properties and reactivity parameters

A. Ionization potentials and electron affinity. The vertical ionization potential (IP) and electron affinity (EA) of rhodium clusters are evaluated based on the following mathematical expressions

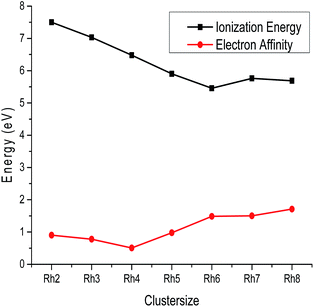
IP = E_n⁺ − E_n

EA = E_n − E_n⁻

where E_n⁺ and E_n⁻ are the energies of the cationic and anionic rhodium clusters at the optimized geometry of the neutral cluster. The calculated ionization potential and electron affinity values of all the clusters are summarized in Table S3 of the ESI† and variations of these parameters with cluster size are plotted in Fig. 6. From Fig. 6, it is observed that the ionization potential decreases from Rh₂ to Rh₆ and then slightly increases for Rh₇ and again decreases towards Rh₈. The higher ionization potential values of smaller clusters reveal that the nucleus holds their electrons tightly giving extra stability due to a closed shell electronic arrangement. It is also observed from Fig. 6 that the electron affinity values decrease from Rh₂ to Rh₄ and then steadily increase from Rh₅ to Rh₈. Hence, Rh₄ has a lower electron affinity than other clusters. The lower electron affinity of Rh₄ suggests a higher stability due to the stable electronic configuration. Therefore, larger clusters have the tendency to attract more electrons for acquiring extra stability. Thus, the larger atomic clusters have a higher affinity to accept electrons to form a negatively charged species compared to the smaller clusters.

Fig. 6 Ionization energy and electron affinity of Rh_n (n = 2–8).

B. LUMO–HOMO gap, global hardness, electrophilicity and electronegativity. The variation of the LUMO–HOMO gap of the lowest energy isomers with cluster size is plotted in Fig. 7 and the calculated values are listed in Table S2 of the ESI.† An even–odd oscillation of the LUMO–HOMO gap is observed with respect to the cluster size (Fig. 7). Neutral Rh_n exhibit a larger LUMO–HOMO gap in comparison to their corresponding ionic clusters. It is also noticed that even atom clusters have a higher LUMO–HOMO energy gap than odd atom clusters. Among all the rhodium clusters investigated in this study, neutral as well as ionic Rh₄ are found to have a larger LUMO–HOMO energy difference. A larger LUMO–HOMO energy gap is the measure of higher global hardness (η) which in return reveals a higher stability. The change in global hardness with respect to cluster size is presented in Fig. 8. Higher hardness values are observed for Rh₂, Rh₃ and Rh₄ (Table S3 of the ESI†). Larger clusters have lower hardness values because the band gap in higher atomic clusters is smaller due to a linear combination of more atomic orbitals for which the electrons in the Fermi regions are loosely bound, that is why larger clusters always have the tendency to change their electronic structure.⁴⁹ Electrons flow in clusters from a higher potential region to a lower potential region due to the chemical potential difference. The chemical potential is the negative value of the electronegativity. In this study, it is observed that among all the stable rhodium clusters, the Rh₂ cluster has the lowest chemical potential value (−4.201 eV), whereas Rh₄ (−3.492 eV) has the highest potential, which indicates that Rh₂ has a higher electron accepting power than Rh₄. The higher chemical potential of a cluster indicates a lower stability because a larger number of electrons may be released when it interacts with a species with a lower chemical potential.

Fig. 7 HOMO–LUMO gap of neutral, cationic and anionic clusters.

Fig. 8 Chemical hardness, electronegativity and electrophilicity plot of Rh_n (n = 2–8).

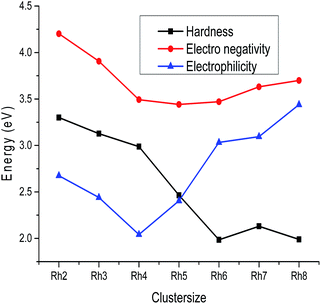
The variation of electronegativity with cluster size is plotted in Fig. 8. It is seen from Fig. 8 that the electronegativity values decrease from Rh₂ to Rh₅ and then increase up to Rh₈ (Table S3 of the ESI†). In the case of larger clusters the electronegativity values increase with the increase of the number of metal atoms because the attraction between the nucleus and inner core electrons increases, as with the increase of atoms in a cluster the nuclear charge also increases. Electrophilicity is the measure of the stabilization energy required by clusters when they acquire an extra electronic charge. It is observed from Table S3 of the ESI† and Fig. 8 that Rh₄ has lower electrophilicity values than the others i.e. it is less prone to get electrons from its surroundings, which supports the higher stability of the Rh₄ cluster compared to its neighbours.

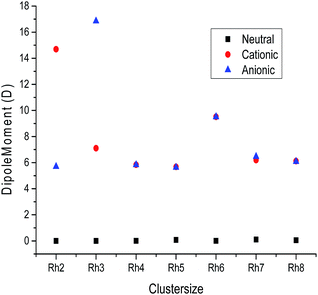
Magnetic properties

A. Magnetic dipole moments. The calculated magnetic moments per atom as a function of cluster size are shown in Table 3. It is observed from Table 3 that the magnetic moment of Rh_n clusters changes discontinuously with size. Rh₄, Rh₆ and Rh₈ clusters show zero magnetic moment per atom. However, odd atomic rhodium clusters show a small magnetic moment. In Table 3, we present the magnetic moment per atom for the lowest energy structures of Rh_n (n = 4–8) clusters. The magnetic moment of even atom rhodium clusters is found to be zero or nearly zero because the spin up electron of one atom couples with the spin down electron of another atom, where as odd atom clusters have a non-zero magnetic moment due to the absence of such coupling.

Table 3 Magnetic moment values (μ_B) of Rh_n (n = 4–8) clusters calculated at the BLYP/DNP level

	Magnetic moment in this study	Magnetic moment study by Jinlonget et al.^16	Magnetic moment study by Reddy et al.^20	Magnetic moment study by F. Aguilera-Granja et al.^50
Rh4	0	0	0	0.06
Rh5	0.20	0.60	1.40	0.22
Rh6	0	0	0	1.48
Rh7	0.43	1.28	1.28	0.05
Rh8	0	1.25	0.75	0.89

---

B. Electronic dipole moment. The variation of the electronic dipole moment (in Debye) of all the stable rhodium metal clusters as a function of cluster size is shown in Fig. 9 and the calculated dipole moment values are mentioned in Table S4 of the ESI.† It is observed from Fig. 9 that the neutral clusters have dipole moment values closer to zero, which suggests a spherical charge distribution in all neutral clusters. In the case of ionic clusters the dipole moment values are found to be higher than their corresponding neutral clusters because ionic clusters have a higher delocalization of electrons due to the addition or removal of electrons from neutral clusters. The polarity of the ionic rhodium clusters is also evaluated to be higher than the neutral clusters.

Fig. 9 Dipole moment values of neutral, cationic and anionic rhodium clusters.

Molecular orbital study

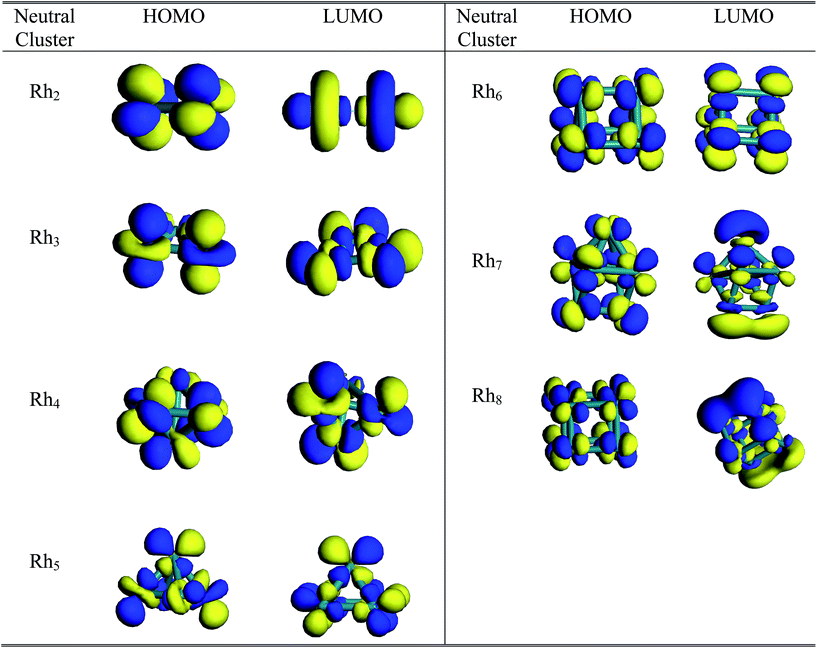
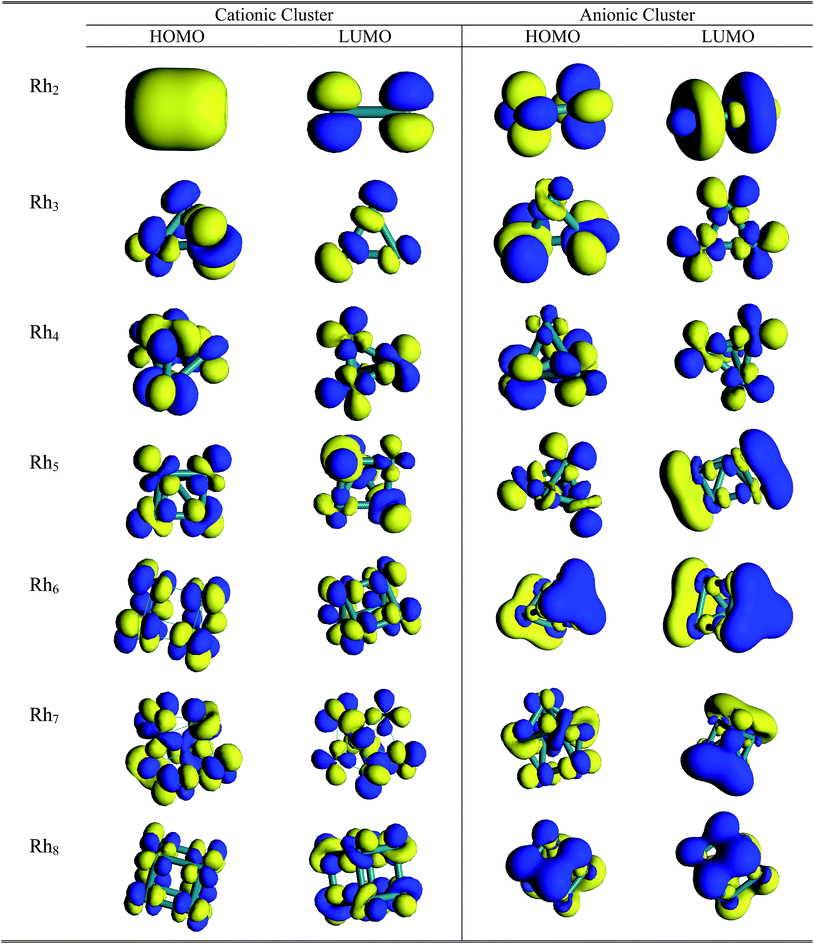
A pictorial representation of molecular orbitals can be used to understand the structural properties along with the stability and bonding properties of the nanoclusters. The 3D isosurface diagrams (LUMO and HOMO) of the most stable Rh_n clusters (neutral and ionic) evaluated at the BLYP/DNP level are presented in Fig. 10 and 11. The isosurface diagrams of the LUMO and HOMO indicate the types of orbitals involved in the formation of the nanoclusters, that is which type of orbitals are responsible for bond formation. Analysis of the isosurface diagrams reveals that in most of the cases there is always sideways or π overlap between the d orbitals of the rhodium atoms. In some cases constructive or sigma overlapping is also observed among the bonding orbitals. The HOMO of neutral Rh₂ (b_2u) consists of a non-bonding d_xy orbital but in the LUMO (a_2u) hybridization is noticed with an anti-bonding d_z² orbital along the bond axis. The HOMO of the cationic Rh₂ cluster suggests sigma bond overlapping while in the anionic cluster nonbonding overlap is observed similar to that of the neutral cluster. It is observed from the HOMO diagram of neutral Rh₃ (e′) that dd_π bonding occurs from the hybridization of the d_z² orbital oriented perpendicular to the triangular framework where as in the LUMO (a′′₂) some constructive overlapping is observed between the four lobes of the d orbitals. In the cationic cluster of Rh₃, there is anti-symmetric overlapping between the d_z² orbital of one atom with the four lobes of the d orbitals of the other atoms on the HOMO isosurface. The HOMO of anionic Rh₃ reveals pi bonding with the d_z² orbitals but in the LUMO limited region overlapping is noticed among the orbitals. The HOMO (t₁) of Rh₄ consists of four lobed either d_yz or d_zx orbitals where as in the LUMO (t₂) dd_π occurs in between the d_z² orbitals. The isosurface diagrams of the HOMO of cationic and anionic Rh₄ show bonding as well as perpendicular nonbonding overlap. In the neutral Rh₅ cluster the HOMO (a₂) is formed by the overlapping of either a d_yz or d_zx orbital with a d_z² orbital. In cationic Rh₅ limited region overlapping with a d_z² orbital is observed in the HOMO, whereas a mismatch of overlapping among d_x²−y² and d_z² is seen in the LUMO. The LUMO of neutral Rh₅ possesses b₁ symmetry. In neutral clusters of Rh₇ (a₁) and Rh₈ (e_u), the LUMO is composed of sigma bonding overlap whereas in Rh₆, both the HOMO (e′′) and LUMO (a′′₁) are composed of nonbonding overlap between four lobe d orbitals. In anionic Rh₆, positive bonding overlap is observed in the HOMO as well as in the LUMO. For cationic Rh₇ the HOMO and LUMO and for Rh₈ the HOMO consists of sideways limited region overlap among perpendicular d orbitals whereas in the LUMO of anionic Rh₇ and Rh₈, dd_σ bonding occurs. The HOMO of Rh₇ and Rh₈ clusters has (t_1u) and (a₂) symmetry.

Fig. 10 3D isosurface HOMO and LUMO diagrams of neutral Rh_n (n = 2–8) clusters.

Fig. 11 3D isosurface HOMO and LUMO diagrams of cationic and anionic Rh_n (n = 2–8) clusters.

Density of states study

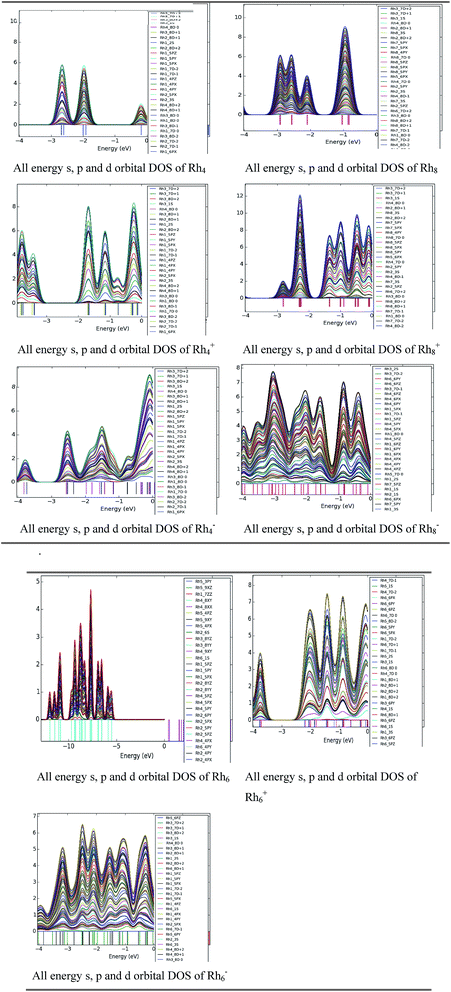
To investigate the orbital occupation per energy interval a DOS study was performed for neutral and ionic rhodium clusters. A few cases are picked up for our analysis purpose viz. neutral and ionic Rh_n clusters (n = 4, 6 and 8). The DOS of the d orbitals of a rhodium atom are partially noticeable near the zero energy level which is hybridized with the s and p orbitals of rhodium. The zero energy is related to the Fermi energy level. For cationic Rh₄ and Rh₈ clusters, the density of states is at a maximum nearer the Fermi level than it is for the corresponding neutral clusters. For cationic clusters the intensity of the peak density is high at certain energy levels which means that there are many states available for occupation at that energy level. Hybridization along with the band width is higher for all neutral and ionic clusters of Rh₈ than for Rh₄. Rh₆⁻ clusters have higher mixing of orbitals whereas no DOS is observed for neutral Rh₆ near the Fermi level. With the increase in the number of atoms in the cluster more overlapping occurs between the orbitals of rhodium. The width of the orbital band is noticed to be higher in anionic clusters than in cationic and neutral clusters (Fig. 12).

Fig. 12 DOS of all higher and lower energy s, p and d orbitals of rhodium atoms for neutral and ionic Rh_n (n = 4, 6 and 8) clusters. (all D ± n orbitals refer to upper and lower energy orbitals of D state, n = 0, 1 and 2).

Spin density and deformation density analysis

The spin density and deformed electron density are shown in Fig. 13 and 14, respectively. It is seen from Fig. 13 that the magnetic moment of Rh₄ is found to be zero because the spin up density is neutralized by the spin down density. Again, the spin down density is high on each vertex which is cancelled out by the high spin up density in the middle region of the cluster which is the reason for the zero magnetic moment of Rh₆. The odd atom clusters of Rh₅ and Rh₇ show nonzero magnetic moments because the spin up density is found to be higher than the spin down density. The deformation density reveals that the electron density is more deformed in cationic Rh₄ than in its neutral and anionic clusters. The electron density of neutral and anionic Rh₅ clusters is evaluated to be more deformed than in the cationic cluster. Again, the electron density of cationic Rh₆ is more deformed than in the neutral and anionic cluster of Rh₆. That is, the electron density is more deformed in the cationic clusters of Rh₄ and Rh₆ and in the anionic Rh₅ cluster. The electron density in the cationic cluster is more deformed because of the greater nuclear charge which pulls the electrons more tightly than the anionic and neutral rhodium nanoclusters.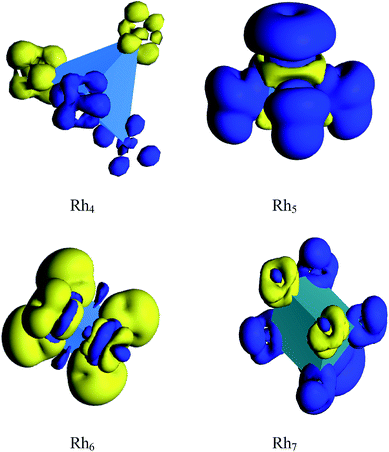

Fig. 13 Calculated spin density of Rh_n (n = 4, 5, 6 and 7) clusters. (Blue and yellow colour represent spin up and spin down density.)

Fig. 14 DFT evaluated deformation electron density of neutral and ionic Rh_n (n = 4, 5 and 6) clusters.

Conclusion

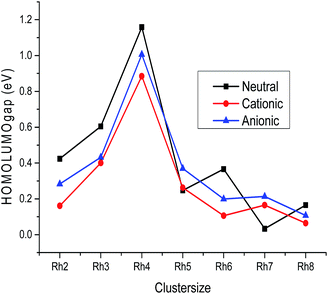
We have investigated systematically the electronic, structural and magnetic properties of neutral and ionic Rh_n (n = 2–8) clusters with different multiplicities. In this study, we have evaluated different parameters such as bond length, binding energy, coordination number, stability function, bond dissociation energy, ionization potential, electron affinity, LUMO–HOMO gap, electrophilicity, electronegativity, global hardness and magnetic properties of different possible isomers of rhodium clusters. Based on the calculated reactivity parameters such as the binding energy, LUMO–HOMO gap, bond dissociation energy and electron affinity, an important inference can be drawn on the stability of the clusters. These results reveal that even atom rhodium clusters are more stable than odd atom clusters and hence, suggest the highest stability for Rh₄. It is found that larger clusters have a higher binding energy than smaller clusters in all of their neutral and ionic Rh_n clusters. Cationic clusters possess a higher stability function than neutral and anionic rhodium clusters. The highest LUMO–HOMO gap, the lowest electron affinity and electrophilicity, the highest stability function, the high ionization potential and high bond dissociation energy suggest that Rh₄ is the magic cluster as these parameters are hallmarks to predict the magic cluster.⁵¹ Molecular orbital analysis suggests that the bonding in Rh_n clusters in most of the cases is π overlapping between the d orbitals.

Acknowledgements

Authors thank Department of Science and Technology (DST), New Delhi, India for financial support (SB/EMEQ-214/2013).

References

1. U. Sarkar and S. A. Blundell, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 125441.
2. M. Che and C. O. Bennett, Adv. Catal., 1989, 36, 55.
3. K. Judai, S. Abbet, A. S. Worz, U. Heiz and C. R. Henry, J. Am. Chem. Soc., 2004, 126, 2732.
4. G. Qiu, M. Wang, G. Wang, X. Diao, D. Zhao, Z. Du and Y. Li, J. Mol. Struct.: THEOCHEM, 2008, 861, 131.
5. B. Kalita and R. C. Deka, J. Chem. Phys., 2007, 127, 244306.
6. D. A. Hickman and L. D. Schmidt, Science, 1993, 259, 343.
7. V. P. Zhdanov and B. Kasemo, Surf. Sci. Rep., 1997, 29, 31.
8. D. R. Salahub and R. P. Messmer, Surf. Sci., 1981, 106, 415.
9. K. Lee, J. Callaway and S. Dhar, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 30, 1724.
10. A. Rosen and T. T. Rantala, Z. Phys. D: At., Mol. Clusters, 1986, 3, 205.
11. G. M. Pastor, J. Dorantes-Davila and K. H. Benneman, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 7642.
12. N. Fujima and T. Yamaguchi, J. Phys. Soc. Jpn., 1989, 58, 3290.
13. B. I. Dunlap, Phys. Rev. A, 1990, 41, 5691.
14. F. Liu, S. N. Khanna and P. Jena, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 8179.
15. Y. Jinlong, F. Toigo and W. Kelin, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 7915.
16. K. Lee, Z. Phys. D: At., Mol. Clusters, 1997, 40, 164.
17. R. Guirado-López, D. Spanjaard, M. C. Desjonqueres and F. Aguilera-Granja, J. Magn. Magn. Mater., 1998, 186, 214.
18. J. Guevara, A. M. Llois, F. Aguilera-Granja and J. M. Montejano- Carrizales, Solid State Commun., 1999, 111, 335.
19. Z. Q. Li, J. Z. Yu, K. Ohno and Y. Kawazoe, J. Phys.: Condens. Matter, 1995, 7, 47.
20. B. Piveteau, M. C. Desjonqueres, A. M. Olés and D. Span-jaard, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 9251.
21. G. W. Zhang, Y. P. Feng and C. K. Ong, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17208.
22. B. V. Reddy, S. K. Nayak, S. N. Khanna, B. K. Rao and P. Jena, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 5214.
23. B. V. Reddy, S. N. Khanna and B. I. Dunlap, Phys. Rev. Lett., 1993, 70, 3323.
24. A. J. Cox, J. G. Louderback and L. A. Bloomfield, Phys. Rev. Lett., 1993, 71, 923.
25. Y. Jinlong, F. Toigo, W. Kelin and Z. Manhong, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 7173.
26. A. J. Cox, J. G. Louderback, S. E. Apsel and L. A. Bloomfield, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 12295.
27. I. M. L. Billas, J. A. Becker, A. Châtelain and W. A. de Heer, Phys. Rev. Lett., 1993, 71, 4067.
28. I. M. L. Billas, A. Châtelain and W. A. de Heer, Science, 1994, 265, 1662.
29. J. P. Bucher, D. C. Douglass and L. A. Bloomfield, Phys. Rev. Lett., 1991, 66, 3052.
30. J. P. Bucher, D. C. Douglass and L. A. Bloomfield, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 6341.
31. D. C. Douglass, A. J. Cox, J. P. Bucher and L. A. Bloomfield, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 12874.
32. V. Kumar and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 144413.
33. V. Kumar and Y. Kawazoe, Eur. Phys. J. D, 2003, 24, 81.
34. Y.-C. Bae, H. Osanai, V. Kumar and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 195413.
35. R. Galicia, Rev. Mex. Fis. S, 1985, 32, 51.
36. G. W. Zhang, Y. P. Feng and C. K. Ong, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17208.
37. C.-H. Chien, E. Blaisten-Barojas and M. R. Pederson, Phys. Rev. A, 1998, 58, 2196.
38. V. S. Stepanyuk, W. Hergert, P. Rennert, J. Izquierdo, A. Vega and L. C. Balbás, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 14020.
39. J. Wei and E. Iglesia, J. Catal., 2004, 225, 116.
40. C. H. Chien, E. B. Barojas and M. R. Pederson, Phys. Rev. A, 1998, 58, 3.
41. B. Delley, J. Chem. Phys., 2000, 113, 7756.
42. B. Delley, J. Chem. Phys., 1990, 92, 508.
43. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
44. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
45. B. Delly and D. E. Ellis, J. Chem. Phys., 1982, 76, 1949.
46. R. P. Iczkowski and J. L. Margrave, J. Am. Chem., Soc., 1961, 83, 3547–3551.
47. P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065–2091.
48. K. A. Gingerich and D. L. Cocke, J. Chem. Soc., Chem. Commun., 1972, 1, 536.
49. A. H. Larsen, J. Kleis, K. S. Thygesen, J. K. Norskov and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 245429.
50. F. Aguilera-Granja, J. L. Rodríguez-López, K. Michaelian, E. O. Berlanga-Ramírez and A. Vega, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 224410.
51. B. K. Rao, P. Jena, S. Burkart, G. Gantefor and G. Seifert, Phys. Rev. Lett., 2001, 86, 692.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra21600a

---