A facile approach for fabrication of mechanically strong graphene/polypyrrole films with large areal capacitance for supercapacitor applications

Abstract

Substantial progress has been made in free-standing flexible graphene-based films for flexible supercapacitors. However, there are limited reports on the areal capacitance of these electrodes, which is an important parameter for practical applications, especially in miniaturized electronic devices. Herein we report the facile fabrication of robust flexible graphene/polypyrrole nanoparticle films. PPy NPs act as the “spacer” between graphene layers creating hierarchical structures. This free-standing film shows excellent mechanical properties with a fracture strength of 16.89 MPa and Young's modulus of 11.77 MPa. The resulting film electrode delivers a large areal specific capacitance of 216 mF cm⁻², which is higher or comparable to other graphene/conducting polymer composite films. Moreover, this composite film exhibits a high capacitance retention rate of 87% after 5000 charge/discharge cycles and a fast relaxation time constant of 2.51 s. These excellent properties all suggest their prospective use in flexible energy storage devices.

---

Introduction

The growth of flexible/bendable electronic equipment such as collapsible displays and wearable devices urgently demands the development of flexible energy storage devices.^1–3 As an important class of energy storage devices, supercapacitors have received extensive interest due to large capacitance, high power density and long cycle life.^4,5 The use of free-standing, binder-free films, to produce flexible supercapacitors simplifies the device fabrication process. Also, the free-standing films can be easily processed into different shapes and sizes for various types of devices. Two-dimensional (2D) graphene is a promising candidate for such electrodes due to its high electrical conductivity, large theoretical specific surface area, high mechanical strength and good thermal and chemical stability.^6,7 Most importantly, graphene can be fabricated into macroscopic free-standing films with high mechanical robustness and flexibility.^8–11

The main challenge in the fabrication of macroscopic graphene-based films is that the graphene sheets are prone to restacking into graphite-like structures due to the strong π–π interactions and van der Waals attraction between the planar basal plane sheets.¹² This drawback is fatal for supercapacitors because the formed films suffer from extensive loss of specific surface area which massively reduces the accessibility of electrolyte into the inner structures of the films. Assembling graphene into three-dimensional (3D) structures, graphene aerogels or hydrogels is an effective way to prevent graphene sheets from restacking. They are fabricated through self-assembly^13,14 or template-assisted assembly.^15,16 However, these graphene-based 3D structures usually exhibit poor mechanical properties that could easily fracture or collapse because of the highly porous internal structure and insufficient backbones, which considerably limited their practical application.

Another commonly used approach to prevent graphene sheets from restacking is to introduce redox active “spacers” between graphene sheets. Spacers, such as carbon nanomaterials,^17–19 metal oxides^20,21 and conducting polymers^22,23 can not only expand the distance between graphene sheets, but also provide additional charge storage leading to greatly improved electrochemical performance. The use of solvent as the spacer to prevent graphene sheets from restacking also results in good electrochemical performance.²⁴ However, this gel-like graphene films may bring difficulties in fabrication of devices or transportation for practical applications.

Polypyrrole (PPy), a common conducting polymer, is considered to be a promising supercapacitor material due to its high pseudocapacitance, relatively high electrical conductivity, ease of synthesis and low cost.^25,26 The use of PPy–graphene composites harnesses the synergistic effect from these two components, the high surface area and conductivity of graphene and high pseudocapacitance of PPy.^27–30 In situ polymerization of PPy on the surface of graphene sheets can prevent the restacking of graphene nanosheets and boost the capacitance, such as 500 F g⁻¹ for graphene oxide–PPy fiber composite²⁷ and 360 F g⁻¹ for PPy–sulfonated graphene composites.³¹ However, these composites are not free-standing films but are in powder form, which requires the use of a binder and a substrate to prepare electrodes. Also no capacitances in areal units are mentioned. Free-standing PPy/graphene composite films have also been reported with high specific capacitances of 211–243 F g⁻¹. They include the pulse-electrodeposited PPy on free-standing graphene films,³² and cellulose³³ or carbon nanotubes³⁴ enhanced graphene/PPy. However, most of these reports have focused on the study of gravimetric capacitance to date, although the areal capacitance is a more practical indicator for applications, in either small scale electronics or stationary energy storage devices.³⁵ Recently, a flexible composite membrane of reduced graphene oxide and polypyrrole nanowire was reported to offer an areal capacitance of 175 mF cm⁻².³⁶

In this work, we fabricated free-standing flexible robust graphene/PPy composite films through vacuum filtration. The highly water-dispersible PPy NPs were mixed with graphene oxide (GO) dispersions and functioned as spacers to prevent GO sheets from restacking during the filtration process. Although there are quite a few reports about graphene-based flexible electrodes, reports on free-standing graphene-based films with very high mechanical strength and flexibility (e.g. 16.89 MPa for fracture strength, 11.77 MPa for Young's modulus), high areal capacitance (216 mF cm⁻² at a current density of 0.2 mA cm⁻²), and good cycling stability are limited. This work provides a step forward to the practical application of graphene-based electrodes for flexible supercapacitors.

Experimental

Materials

Intercalated graphite was sourced from Asbury Carbon. Pyrrole was purchased from Merck, and other chemicals were obtained from Sigma-Aldrich. Pyrrole was freshly distilled before use, and all the other chemicals were used as received.

Synthesis of graphene oxide (GO)

Intercalated graphite was thermally expanded at 1000 °C under argon atmosphere. The volume expansion was over 800 times. The expanded graphite (4 g) was oxidised with concentrated H₂SO₄ (200 mL) and KMnO₄ (25.6 g) under the conditions as described in our previous report.³⁷ The contents were washed with H₂O₂ and HCl for removal of manganese from the graphene oxide. The contents were carefully neutralised till pH 3 for treatment of mineral acid with dilute ammonia using auto titration equipment from Metrohm. The salts were removed by repeated centrifugation till the pH was close to neutral.

Synthesis of PPy NPs

The synthetic route of PPy NPs was based on a previous report.³⁸ Briefly, 0.75 g PVA (M_w 31 000–50 000, 0.5 wt%) was added and dissolved into 150 mL Milli-Q water under magnetic stirring. Then 9.32 g FeCl₃·6H₂O (0.23 M) was added into this solution and stirred for 1 h to reach a state of equilibrium forming a viscous orange mixture, followed by an addition of 1.04 mL pyrrole (0.1 M). The polymerization proceeded under stirring in ice bath for 4 h. The resulting dispersion was centrifuged at 10 000 rpm for 30 min to collect the nanoparticles. The product was further rinsed several times with hot water to remove excessive PVA and other impurities. The obtained PPy NPs were dried in vacuum at room temperature.

Fabrication of Er-GO and Er-GO–PPy films

In this work, GO–PPy composites with different weight ratio of PPy to GO (1 : 3, 1 : 2 and 1 : 1) were prepared. The amount of GO was kept same in all these samples. The fabrication procedure is described using the 1 : 2 films as an example. PPy NPs (5 mg) were dispersed in 10 mL Milli-Q water with the assistance of sonication. The formed dispersion was mixed with 10 mL 1 mg mL⁻¹ GO, and subjected to another 10 min sonication. Thereafter the mixture was directly filtered on a membrane (pore size: 0.22 μm). The wet films were peeled off and dried in a vacuum oven at 60 °C overnight. The same procedures were followed to prepare GO film using 10 mL 1 mg mL⁻¹ GO dispersion. The areal mass loading of these composite films increased with PPy NPs content. It is 1.79, 1.92 and 2.28 mg cm⁻² for 1 : 3, 1 : 2 and 1 : 1 film, respectively. They demonstrated an improved specific capacitance as well, 118, 164 and 201 mF cm⁻² at a scan rate of 50 mV s⁻¹ in 1 M Li₂SO₄ (Fig. S1†). However, their flexibility and mechanical strength dropped. It became brittle and difficult to handle for fabrication of supercapacitors at the ratio of 1 : 1. Thus only the 1 : 2 samples were investigated for the electrochemical and mechanical properties, and data are presented in this work.

The electrochemical reduction of the films was performed in a three-electrode system. The GO or GO/PPy films were attached onto a piece of nickel foam as working electrode. Stainless steel mesh and Ag/AgCl (3 M NaCl) were used as counter and reference electrode, respectively. The reduction was conducted at −1.1 V (vs. Ag/AgCl) in PBS solution for 30 min, followed by rinsing with water.³⁰ The resultant films were denoted as Er-GO or Er-GO–PPy films, and they were dried in vacuum oven at 60 °C for fabrication of supercapacitors.

Assembly of supercapacitors and electrochemical measurements of the devices

Symmetrical supercapacitors were assembled into two-electrode Swagelok type cells for test. The films were cut into pieces with a dimension of 0.5 cm × 0.5 cm, the mass loading was about 1.92 mg cm⁻² for Er-GO–PPy films and 1.61 mg cm⁻² for Er-GO films. A filter paper was used as the separator, and 1 M Li₂SO₄ was used as electrolyte.

Cyclic voltammetry (CV) of the devices was conducted from 0 to 1 V using CHI 650D (CHI instruments). Electrochemical impedance spectra were obtained using a Gamry EIS 3000 system in the frequency range of 100 kHz to 0.01 Hz with an AC perturbation of 10 mV at open circuit potential. Galvanostatic charge/discharge tests of the devices were performed using a battery test system (Neware electronic Co.) between 0 and 1 V.

Structure and morphology characterization

The morphology of Er-GO and Er-GO–PPy films was characterized by FE-SEM (JEOL JSM-7500FA). Raman spectra were obtained by a confocal Raman spectrometer (Jobin Yvon HR800, Horiba) using 632.8 nm diode laser. The thermal properties of the films were tested by TGA (Q500, TA instruments) under nitrogen at a ramp rate of 10 °C min⁻¹. X-ray photoelectron spectroscopy (XPS) data was collected from a hemispherical energy PHOIBOS 100/150 analyser. Tensile tests of the films were conducted using a Shimadzu EZ mechanical tester at a cross-head speed of 1 mm min⁻¹.

Results and discussion

Vacuum filtration flow can induce an orientation of GO sheets in the dispersion to horizontally face-to-face restack on the filter membrane, forming uniform films with a compact layered structure.⁸ With the addition of spacers, such as PPy NPs, the inter-layer distances are significantly expanded and the face-to-face interactions between GO sheets are weakened, resulting in a hierarchical structure. The procedures to fabricate Er-GO and Er-GO–PPy films are illustrated in Fig. 1.

Fig. 1 Schematic procedures to fabricate Er-GO and Er-GO–PPy composite films.

A good dispersibility of PPy NPs in GO dispersions is the prerequisite for forming such hierarchical structure. A template is usually used to fabricate PPy with specific nanostructures. For example, Lu et al. used carbon nanotube (CNT) as hard template to synthesize tube-like PPy.³⁴ In this work, we chose PVA as template and stabilizer to produce highly dispersible PPy NPs. The PPy NPs exhibits good uniformity with a particle size of ∼114 nm (Fig. 2a). These particles can be easily dispersed in H₂O with the assistance of sonication forming a homogeneous dispersion at a concentration of 0.5 mg mL⁻¹ PPy NPs, which was stable for weeks (inset of Fig. 2a). PPy NPs can be uniformly distributed onto the GO sheets in their mixture dispersion, which might be attributed to the electrostatic interactions, hydrogen bond or π–π interactions. The Er-GO film that exhibited a slightly wrinkled surface, and the cross-sectional view shows a compact layered structure (Fig. 2b and d). Er-GO–PPy films formed by filtration displayed a highly crumpled and rough surface, and a hierarchical structure with loosely stacked graphene layers is obvious from the cross-sectional view (Fig. 2c and e).

Fig. 2 SEM images of PPy NPs (a) (inset: digital image of PPy NPs aqueous dispersion with a concentration of 0.5 mg mL⁻¹); surface morphology and cross-sectional view of Er-GO (b and d) and Er-GO–PPy films (c, e and f); stress–strain curves for Er-GO and Er-GO–PPy films (g); digital image of flexible Er-GO–PPy film (h).

The formation of the more open structure can be attributed to the distribution of PPy NPs between graphene sheets, effectively expanding the distance between the layers. The film thickness was increased by around 3 fold, from ∼4 nm to ∼12 nm. At a higher magnification, a wavy and crumpled structure of graphene sheets with PPy NPs decorated between layers can be clearly observed (Fig. 2f). Such expanded multi-layered structures of Er-GO–PPy films should provide a larger electrolyte–electrode interface.

The fracture strength and Young's modulus of the Er-GO–PPy films were determined to be 16.89 MPa and 11.77 MPa (Fig. 2g), respectively. This result demonstrates that the Er-GO–PPy films formed here are robust and have excellent mechanical flexibility (Fig. 2h). The mechanical strength of the Er-GO–PPy film is higher than previously reported flexible graphene–cellulose paper³⁹ with a fracture stress of 8.67 MPa, or graphene/polypyrrole nanofiber films with a fracture stress of 35.0 MPa but with much lower Young's modulus of 2.1 MPa.²³ A detailed comparison is shown in Table S1.† It was noted that the Er-GO films displayed higher fracture strength and Young's modulus (23.73 MPa and 14.47 MPa) compared to Er-GO–PPy films. This is attributed to the fact that the compact restacked structures of graphene sheets have a stronger attraction force between adjacent layers enhancing mechanical performance.

To verify the effect of electrochemical reduction, the chemical structures of Er-GO and Er-GO–PPy films were characterized by Raman spectroscopy. GO and Er-GO films displayed the characteristic D band (∼1330 cm⁻¹) and G band (∼1600 cm⁻¹) for graphene materials (Fig. 3a). The G bands are assigned to the first order scattering of the E_2g vibration mode of sp²-bonded carbon and the in-plane bond stretching motion of the sp² domains, while the D bands are attributed to the vibration of aromatic rings, which corresponds to edges and structure defects on the carbon basal planes.^40,41 The intensity ratio of D band to G band (I_D/I_G) increased after reduction (from 1.09 to 1.16), agrees with the previously reported results for reduced graphene oxide via either chemically or electrochemical route.^23,30 For pristine PPy NPs, five distinct peaks related to polypyrrole can be identified. Two strong and broad peaks at 1326 cm⁻¹ and 1550 cm⁻¹ represent the ring stretching and the polymer C–C backbone stretching, respectively. The peak at 917 cm⁻¹ corresponds to the C–H out-of-plane deformation, whilst the peak at 985 cm⁻¹ can be ascribed to the pyrrole ring deformation. The peak at 1039 cm⁻¹ arises from the C–H in-plane deformation.^26,42 These three small peaks can be clearly observed in Er-GO–PPy film, demonstrating the existence of PPy in the composite film. The two major peaks of PPy are overlapped with the D and G band of graphene. The obtained I_D/I_G intensity ratio was 1.14, which is very close to the films without PPy NPs, indicating that the similar structured graphene sheets was formed as that in pristine Er-GO film after the electrochemical reduction.

Fig. 3 (a) Raman spectra of PPy NPs, GO, Er-GO and Er-GO–PPy films; (b) TGA curves of these samples; (c) deconvoluted XPS C 1s spectra of GO, Er-GO and Er-GO–PPy films.

The thermal stability of composites was investigated using TGA (Fig. 3b). All samples were kept at 100 °C to remove surface-absorbed water before the experiment commenced. The weight loss of GO film starts at around 150 °C, and it exhibits a substantial weight loss of 26% in the temperature range of 150–220 °C. This is mainly due to the removal of oxygen-containing functional groups from GO surface.⁸ In contrast, the Er-GO film only displays a 2% weight loss in this temperature range, suggesting the significant removal of oxygen-containing functional groups using electrochemical reduction. Above 600 °C, both GO and Er-GO show a sharp weight loss with 34% and 40% retention at 800 °C, which can be ascribed to the bulk pyrolysis of the carbon skeleton of graphene. PPy NPs begin to lose weight at around 200 °C and the final weight loss is 39% at 800 °C. For Er-GO–PPy film, only a 5% weight loss can be observed at 300 °C, which is similar to Er-GO film, also indicating the massive removal of oxygenated functional groups from GO sheets during the reduction process. The steep mass decrease for Er-GO–PPy after 300 °C can be mainly attributed to the decomposition of PPy, and the final weight loss at 800 °C is 50%.

To further demonstrate the reduction of GO in composites, X-ray photoelectron spectroscopy (XPS) was applied to analyse their chemical structure changes. All curves were fitted by the Gaussian–Lorentzian shape peaks based on the Shirley background correction, as shown in Fig. 3c. In the C 1s spectrum of GO, three peaks can be observed. The peak centred at 286.8 eV represents the C–C bonding, while other two strong peaks at 289.0 eV and 290.0 eV arise from the oxygen-containing functional groups including C–O bonding and C=O bonding, respectively. For Er-GO and Er-GO–PPy films, both spectra display dominating C–C bonding peaks at 285.4 eV and 285.0 eV, respectively.⁴³ The peak located at 286.0 eV in the spectrum of Er-GO–PPy film corresponds to the C–N backbone bonding.⁴⁴ Moreover, the peaks belong to the C–O and C=O bonding decreased dramatically, suggesting that the oxygen-containing functional groups on GO sheets have been effectively removed after the electrochemical reduction. This conclusion can also be supported by the increased C/O ratio from 1.95 to 5.92 after the electrochemical reduction.

Fig. 4a and b show the CV curves of Er-GO and Er-GO–PPy electrodes at different scan rate from 5 to 100 mV s⁻¹. They all display a nearly rectangular shape even at high scan rate of 100 mV s⁻¹, demonstrating capacitive behaviour. For easy comparison, the CV curves of both these two films at the same scan rate of 50 mV s⁻¹ are shown in Fig. 4c. It can be clearly seen that Er-GO–PPy film electrode displayed a significantly larger current response than that of Er-GO film electrode, suggesting that the composite can deliver much higher capacitance.

Fig. 4 CV curves of the supercapacitor based on Er-GO or Er-GO–PPy films at different scan rate (a and b) or at a scan rate of 50 mV s⁻¹ for comparison (c) in 1 M Li₂SO₄; galvanostatic charge/discharge curves of Er-GO–PPy film electrodes supercapacitor at different current densities (d), or at 0.2 A cm⁻² in comparison to Er-GO supercapacitor (e) in 1 M Li₂SO₄; areal capacitances of the Er-GO–PPy and Er-GO electrodes supercapacitors as function of current densities (f); Ragone plot of supercapacitors based on Er-GO–PPy film electrodes in comparison to the reported graphene/conducting polymer composites supercapacitors (g); cycling stability of supercapacitors based on Er-GO and Er-GO–PPy film electrodes (h).

The energy storage performance of the film electrodes was further evaluated by galvanostatic charge/discharge experiments. As shown in Fig. 4d, all the charge and discharge curves of supercapacitors based on Er-GO–PPy films show nearly linear and symmetric shapes even at a very high current density of 8 mA cm⁻², indicating the excellent reversibility. It can be seen from the charge/discharge curves that Er-GO–PPy film electrode displayed a much larger areal capacitance than that of the Er-GO film electrode at a current density of 0.2 mA cm⁻² (Fig. 4e). This result is consistent with the CV results discussed above. The areal and gravimetric capacitances of the single electrode were calculated based on the charge/discharge curves using the equation of C_a = (2 × I × t)/(S × ΔV) and C_g = (4 × I × t)/(m × ΔV), where C_a is the areal capacitance in mF cm⁻², C_g is the gravimetric capacitance in F g⁻¹, I is the discharge current in mA, t is the discharge time in s, S is the area of the electrode in cm², m is the total mass of the films on both electrodes and ΔV is the scan potential window in V. Er-GO–PPy film electrode delivered a large areal specific capacitance (C_a) of 216 mF cm⁻² at a current density of 0.2 mA cm⁻², which is much higher than that (41.2 mF cm⁻²) of the Er-GO film electrodes at the same current density (Fig. 4f). This enhanced capacitance of Er-GO–PPy films can be attributed to two major facts: (1) the intercalation of PPy NPs expands the distance between graphene sheets which provides larger electrolyte–electrode interface for charge storage and ion transportation; (2) PPy NPs provide additional capacitance. In the gravimetric unit, the capacitance is 110 F g⁻¹, 5.6 F g⁻¹ for the composite films or Er-GO films, respectively.

At a high current density of 8 mA cm⁻², the Er-GO–PPy film electrodes could still deliver a capacitance of 160 mF cm⁻², showing a capacitance retention ratio of 74.0%. However, the C_a of Er-GO films decreased sharply to 16.0 mF cm⁻², only 38.8% of the capacitance was maintained. The greatly improved rate performance of Er-GO–PPy films can be ascribed to the intercalation of PPy NPs which effectively prevent graphene sheets from restacking, whilst the compactly restacked graphene sheets of the Er-GO films hinder the fast ion transportation between graphene layers, resulting in low capacitances at high current densities.

The areal capacitance reported in this work is higher than or comparable to the previously reported data for graphene/conducing polymer composite film electrodes, including three-dimensional porous graphene/polyaniline composite films (67.2 mF cm⁻²),⁴⁵ graphene/poly(3,4-ethylenedioxythiophene) (PEDOT) composite films (12.2 mF cm⁻²),⁴⁶ electrochemically deposited PPy/GO composite films (152 mF cm⁻²)⁴⁷ and flexible graphene–PPy composite membranes (175 mF cm⁻²).³⁶ It can be concluded that our Er-GO–PPy composite films possess better or comparable performance with respect to both the mechanical and electrochemical point of view (Table S1†). The areal energy density and power density of the devices were calculated using the equations of E = [C_a × (ΔV)²]/(2 × 3600) and P = (3600 × E)/t, where E is the areal energy density in mW h cm⁻², P is the areal power density in mW cm⁻², C_a is the areal capacitance in mF cm⁻², ΔV is the potential window in V and the t is the discharge time in s. The device in this work presented an areal energy density of 30.0 μW h cm⁻² at an areal power density of 200 μW cm⁻², while an areal energy density of 22.2 μW h cm⁻² was still delivered at an areal power density of 8000 μW cm⁻². Ragone plot of the supercapacitors based on Er-GO–PPy film electrodes and the results from the aforementioned references for comparison is shown in Fig. 4g. It clearly demonstrates that our device can provide remarkably high energy densities at relatively high power densities.

The cycling performance of Er-GO–PPy electrodes was investigated at a current density of 4 mA cm⁻². For comparison, the Er-GO film electrodes were also tested but at a much lower current density of 0.5 mA cm⁻², since it delivered a very low capacitance at 4 mA cm⁻². The areal capacitance of the Er-GO electrode showed a slight increase of capacitance during 5000 cycles. The final capacitance was 23 mF cm⁻², 115% of the initial capacitance (20 mF cm⁻²). This capacitance increase could be explained by the activation of densely packed films during the charge/discharge process that allows more ions to penetrate. For Er-GO–PPy films, a capacitance loss of 8.7% can be observed after the first 1000 cycles, and a capacitance retention rate of 87.0% after 5000 cycles (Fig. 4h). The capacitance drop is related to the volumetric swelling and shrinking of PPy polymer chains during the cyclic redox reactions. Our result is superior to that for pure PPy electrodes, such as only 84% was remained after 1000 cycles for electrodeposited PPy⁴⁸ and 70% for chemically synthesized PPy fibres.²⁷ This result is also competitive to the graphene–PPy fibre films (44% after 5000 cycles at 1 A g⁻¹).²³ The current density of 4 mA cm⁻² applied in this work is equal to 1.04 A g⁻¹ in the mass unit. This greatly improved cycling stability of Er-GO–PPy films can be ascribed to the sandwiched structures of PPy NPs and graphene sheets, which can protect PPy from volume change and mitigate the loss of capacitance. The remained areal capacitance (153 mF cm⁻²) after 5000 cycles was still much higher than that of the Er-GO film electrodes (23 mF cm⁻²) at a small current density of 0.5 mA cm⁻².

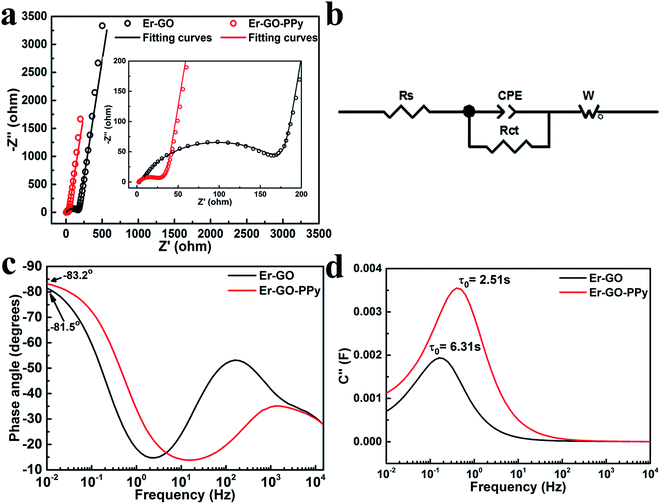
The Er-GO and Er-GO–PPy film electrodes were further studied by electrochemical impedance spectroscopy (EIS). In the Nyquist plot depicted in Fig. 5a, the intercept of the curves with real axis in the high frequency region corresponds to the bulk resistance (R_s), mainly including the resistance of electrolyte, the intrinsic resistance of the active material and contact resistances. The semi-circle part of the plot represents the charge transfer resistance (R_ct). It can be clearly seen that Er-GO films have much larger R_ct than Er-GO–PPy films in the high frequency region (inset of Fig. 5a). The Nyquist plots was further analysed using a simulated equivalent circuit (Fig. 5b). It is composed of four elements: a bulk resistance (R_s), a charge transfer resistance (R_ct), the Warburg impedance (W) and a constant phase element (CPE). The R_s values of Er-GO and Er-GO–PPy samples are 2.0 ohm and 2.7 ohm, respectively. The R_ct value for Er-GO film is 164.3 ohm. This high charge transfer resistance can be attributed to the densely compacted structures that hinder the ion transport. The R_ct for Er-GO–PPy film decreased sharply to 20.7 ohm. Such greatly reduced resistance may be mainly due to the hierarchical loosely-stacked structure facilitating fast ion transport. The phase angle of a capacitor is also an important indicator to judge its capacitive performance. The phase angle of an ideal capacitor is −90°, the closer to this angle, the device behaves more like an ideal capacitor.⁴⁹ The phase angle for Er-GO and Er-GO–PPy film electrodes are −81.5° and −83.2° (Fig. 5c), suggesting that the device based on Er-GO–PPy film electrodes has better capacitive behaviours.

Fig. 5 (a) Nyquist plots and the simulated curves of Er-GO and Er-GO–PPy based supercapacitors in 1 M Li₂SO₄ (inset: expanded views at high-frequency region); (b) the equivalent circuit diagram used to simulate the Nyquist plots; (c) plot of Bode phase angle versus frequency; (d) plot of the imaginary part of specific capacitance (C′′) versus frequency.

The relaxation time constant (τ₀) reflects the ion diffusion rate in the electrodes. τ₀ is defined as the minimum time needed to discharge all the energy from the device with an efficiency of more than 50%.⁵⁰ It can be calculated from the equation τ₀ = 1/f₀, where f₀ is the frequency at maximum imaginary capacitance (C′′). As shown in Fig. 5d, the τ₀ of Er-GO–PPy based supercapacitor is 2.51 s, which is much smaller compared to that of the Er-GO based supercapacitor (6.31 s). Such τ₀ is also faster than that of the commercial 2.7 V/1 F Maxwell supercapacitor (3.86 s).⁵¹ The fast frequency response of this device can be mainly attributed to the expanded distance between graphene layers which allows faster ion transport.

Conclusions

In summary, we have fabricated free-standing multi-layered reduced graphene oxide/polypyrrole nanoparticles films. Such Er-GO–PPy composite films possess good mechanical strength as well as high flexibility. As supercapacitor electrodes, this Er-GO–PPy film exhibited excellent performance with a large areal specific capacitance of 216 mF cm⁻² and a good cycling stability with 87% capacitance retention over 5000 cycles. It also demonstrated a fast charge/discharge property as evidenced by the short relaxation time constant (τ₀) of 2.51 s, shorter than that of the representative commercial supercapacitor. Such promising performance can be mainly attributed to the synergistic effect arising from two components: the intercalation of PPy NPs effectively prevents the graphene sheets restacking creating larger electrolyte–electrode interface for charge storage and fast ion transportation, and also provides additional capacitance; the graphene sheets structure accommodates the volume change occurring in PPy during oxidation–reduction preventing a loss in capacitance with cycling. The combination of such good capacitive performance and high mechanical stiffness/excellent flexibility makes this a promising material for high-performance flexible energy storage devices.

Acknowledgements

Funding from the Australian Research Council Centre of Excellence Scheme (Project Number CE 140100012) is gratefully acknowledged. G. G. W. is grateful to the ARC for support under the Australian Laureate Fellowship scheme (FL110100196). The authors would like to thank the Australian National Nanofabrication Facility-Materials node (ANFF) and the UOW Electron Microscopy Centre for the equipment use.

References

1. H. Nishide and K. Oyaizu, Science, 2008, 319, 737–738.
2. X. M. Lu and Y. N. Xia, Nat. Nanotechnol., 2006, 1, 163–164.
3. C. Y. Wang and G. G. Wallace, Electrochim. Acta, 2015, 175, 87–95.
4. R. Kotz and M. Carlen, Electrochim. Acta, 2000, 45, 2483–2498.
5. J. R. Miller and P. Simon, Science, 2008, 321, 651–652.
6. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
7. X. Huang, Z. Y. Zeng, Z. X. Fan, J. Q. Liu and H. Zhang, Adv. Mater., 2012, 24, 5979–6004.
8. H. Chen, M. B. Müller, K. J. Gilmore, G. G. Wallace and D. Li, Adv. Mater., 2008, 20, 3557–3561.
9. C. Y. Wang, D. Li, C. O. Too and G. G. Wallace, Chem. Mater., 2009, 21, 2604–2606.
10. C. Chen, Q.-H. Yang, Y. Yang, W. Lv, Y. Wen, P.-X. Hou, M. Wang and H.-M. Cheng, Adv. Mater., 2009, 21, 3007–3011.
11. F. Liu, S. Y. Song, D. F. Xue and H. J. Zhang, Adv. Mater., 2012, 24, 1089–1094.
12. M. D. Stoller, S. J. Park, Y. W. Zhu, J. H. An and R. S. Ruoff, Nano Lett., 2008, 8, 3498–3502.
13. Y. X. Xu, K. X. Sheng, C. Li and G. Q. Shi, ACS Nano, 2010, 4, 4324–4330.
14. S. H. Lee, H. W. Kim, J. O. Hwang, W. J. Lee, J. Kwon, C. W. Bielawski, R. S. Ruoff and S. O. Kim, Angew. Chem., Int. Ed., 2010, 49, 10084–10088.
15. X. H. Cao, Y. M. Shi, W. H. Shi, G. Lu, X. Huang, Q. Y. Yan, Q. C. Zhang and H. Zhang, Small, 2011, 7, 3163–3168.
16. B. G. Choi, M. Yang, W. H. Hong, J. W. Choi and Y. S. Huh, ACS Nano, 2012, 6, 4020–4028.
17. L. Qiu, X. W. Yang, X. L. Gou, W. R. Yang, Z. F. Ma, G. G. Wallace and D. Li, Chem.–Eur. J., 2010, 16, 10653–10658.
18. C. X. Guo and C. M. Li, Energy Environ. Sci., 2011, 4, 4504–4507.
19. Y. M. Wang, J. C. Chen, J. Y. Cao, Y. Liu, Y. Zhou, J. H. Ouyang and D. C. Jia, J. Power Sources, 2014, 271, 269–277.
20. M. Li, Z. Tang, M. Leng and J. M. Xue, Adv. Funct. Mater., 2014, 24, 7495–7502.
21. J. Kim, W. H. Khoh, B. H. Wee and J. D. Hong, RSC Adv., 2015, 5, 9904–9911.
22. Q. Wu, Y. X. Xu, Z. Y. Yao, A. R. Liu and G. Q. Shi, ACS Nano, 2010, 4, 1963–1970.
23. S. Li, C. Zhao, K. W. Shu, C. Y. Wang, Z. P. Guo, G. G. Wallace and H. K. Liu, Carbon, 2014, 79, 554–562.
24. X. Yang, J. Zhu, L. Qiu and D. Li, Adv. Mater., 2011, 23, 2833–2838.
25. A. R. Liu, C. Li, H. Bai and G. Q. Shi, J. Phys. Chem. C, 2010, 114, 22783–22789.
26. S. Biswas and L. T. Drzal, Chem. Mater., 2010, 22, 5667–5671.
27. L. L. Zhang, S. Y. Zhao, X. N. Tian and X. S. Zhao, Langmuir, 2010, 26, 17624–17628.
28. P. A. Mini, A. Balakrishnan, S. V. Nair and K. R. V. Subramanian, Chem. Commun., 2011, 47, 5753–5755.
29. H. H. Chang, C. K. Chang, Y. C. Tsai and C. S. Liao, Carbon, 2012, 50, 2331–2336.
30. Y. Yang, C. Y. Wang, B. B. Yue, S. Gambhir, C. O. Too and G. G. Wallace, Adv. Energy Mater., 2012, 2, 266–272.
31. C. Bora, J. Sharma and S. Dolui, J. Phys. Chem. C, 2014, 118, 29688–29694.
32. A. Davies, P. Audette, B. Farrow, F. Hassan, Z. W. Chen, J. Y. Choi and A. P. Yu, J. Phys. Chem. C, 2011, 115, 17612–17620.
33. A. de Adhikari, R. Oraon, S. K. Tiwari, J. H. Lee and G. C. Nayak, RSC Adv., 2015, 5, 27347–27355.
34. X. J. Lu, H. Dou, C. Z. Yuan, S. D. Yang, L. Hao, F. Zhang, L. F. Shen, L. J. Zhang and X. G. Zhang, J. Power Sources, 2012, 197, 319–324.
35. J. P. Liu, J. Jiang, M. Bosman and H. J. Fan, J. Mater. Chem., 2012, 22, 2419–2426.
36. J. T. Zhang, P. Chen, B. H. L. Oh and M. B. Chan-Park, Nanoscale, 2013, 5, 9860–9866.
37. R. Jalili, S. H. Aboutalebi, D. Esrafilzadeh, K. Konstantinov, S. E. Moulton, J. M. Razal and G. G. Wallace, ACS Nano, 2013, 7, 3981–3990.
38. J. Y. Hong, H. Yoon and J. Jang, Small, 2010, 6, 679–686.
39. Z. Weng, Y. Su, D. W. Wang, F. Li, J. H. Du and H. M. Cheng, Adv. Energy Mater., 2011, 1, 917–922.
40. L. M. Malard, M. A. Pimenta, G. Dresselhaus and M. S. Dresselhaus, Phys. Rep., 2009, 473, 51–87.
41. S. Niyogi, E. Bekyarova, M. E. Itkis, H. Zhang, K. Shepperd, J. Hicks, M. Sprinkle, C. Berger, C. N. Lau, W. A. Deheer, E. H. Conrad and R. C. Haddon, Nano Lett., 2010, 10, 4061–4066.
42. Y. C. Liu, B. J. Hwang, W. J. Jian and R. Santhanam, Thin Solid Films, 2000, 374, 85–91.
43. D. Yang, A. Velamakanni, G. Bozoklu, S. Park, M. Stoller, R. D. Piner, S. Stankovich, I. Jung, D. A. Field, C. A. Ventrice and R. S. Ruoff, Carbon, 2009, 47, 145–152.
44. S. Bose, T. Kuila, M. E. Uddin, N. H. Kim, A. K. T. Lau and J. H. Lee, Polymer, 2010, 51, 5921–5928.
45. Q. Q. Zhou, Y. R. Li, L. Huang, C. Li and G. Q. Shi, J. Mater. Chem. A, 2014, 2, 17489–17494.
46. T. Lindfors, Z. A. Boeva and R. M. Latonen, RSC Adv., 2014, 4, 25279–25286.
47. H. H. Zhou, G. Y. Han, Y. M. Xiao, Y. Z. Chang and H. J. Zhai, J. Power Sources, 2014, 263, 259–267.
48. B. B. Yue, C. Y. Wang, P. Wagner, Y. Yang, X. Ding, D. L. Officer and G. G. Wallace, Synth. Met., 2012, 162, 2216–2221.
49. K. Sheng, Y. Sun, C. Li, W. Yuan and G. Shi, Sci. Rep., 2012, 2, 247.
50. D. Pech, M. Brunet, H. Durou, P. H. Huang, V. Mochalin, Y. Gogotsi, P. L. Taberna and P. Simon, Nat. Nanotechnol., 2010, 5, 651–654.
51. S. Zhang and N. Pan, Adv. Energy Mater., 2015, 5, 1401401.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra21100j

---