DOI:
10.1039/C5RA20538G
(Paper)
RSC Adv., 2015,
5, 105889-105900
An insight into thermodynamics of adsorptive removal of fluoride by calcined Ca–Al–(NO3) layered double hydroxide†
Received
4th October 2015
, Accepted 18th November 2015
First published on 20th November 2015
Abstract
The conventional method for the estimation of ΔG0 through the van't Hoff equation was critically analysed. The development of an analytical framework for the determination of the thermodynamic parameters for the adsorption process had been attempted in this work. A calcined Ca–Al–(NO3) layered double hydroxide was employed for the adsorptive removal of fluoride. The effect of the temperature on the adsorption process was assessed through thermodynamic and statistical methods. The adsorption equilibrium was described by Freundlich and linear isotherms. The isotherm constants were used in the van't Hoff equation by the proposed method. The thermodynamic assessment revealed that the adsorption reaction is endothermic and spontaneous. Furthermore, the ΔH0, Ea, Ead, and ΔHx values confirmed that the adsorption process is in between physisorption and chemisorption in nature. The interactive effect of the temperature with other important process parameters, i.e., pH, initial fluoride concentration and adsorbent dose, was evaluated through response surface methodology. The solution pH had very little effect on the adsorption. On the contrary, the adsorbent dose and initial concentration influenced the adsorption process significantly. The interactive effect of temperature was prominent at a lower adsorbent dose and a higher initial concentration. The highest adsorption capacity, obtained in the RSM study, was 59.60 mg g−1. However, the highest Kf value from Freundlich isotherm was 8.48 (mg g−1) (L mg−1)1/n at 50 °C.
Introduction
Fluorine is the 13th most abundant element in the earth crust1 and is an essential micronutrient for human beings, helping in the formation of bone and dental enamel.2 Fluorine occurs in the form of fluoride in ground water. Fluoride is required at a low concentration for preventing tooth decay, although it is detrimental at higher concentrations as it initiates fluorosis in different proportions.3,4 As fluorosis spread over more than 35 nations,5 fluoride turn out to be an important contaminant in drinking water. The defluoridation of drinking water has enormous significance in the arena of research as well as for the drinking water industry/organizations. Adsorption is found to be a cheap and feasible technology in this regard.6,7 Extensive research on the adsorptive removal of fluoride gave rise to a number of natural and synthetic adsorbents, wherein layered double hydroxides acquired significant attention.2,8–10
Layered double hydroxides (LDHs), commonly known as hydrotalcite (HTlc)-like compounds are basically a class of synthetic or natural anionic clay. The layered structure of LDH materials is similar to brucite [Mg(OH)2]. Two or more kinds of metallic cations present in the main layers and anionic species present in the hydrated interlayer. In this material, some divalent ions are replaced by trivalent ions resulting in a net positive surface charge, which is further counterbalanced by intercalated exchangeable anions. LDHs have the general chemical formula [M(II)1−xM(III)x(OH)2]x+[(An−)x/nyH2O], where M(II) and M(III) represent bivalent metal ions and trivalent metal ions, respectively. A denotes an interlamellar anion with valency n- and x is the molar ratio, i.e., the ratio of the trivalent metal to the total metal ions (ranging between 0.2 and 0.4).11,12 The net positive surface charge and availability of the exchangeable anions in the hydrated interlayer creates the high anion trapping capacity of LDHs.13 A wide application of LDHs is documented in various fields of chemistry, engineering, materials and bio-sciences, i.e., magnetic materials,14 fluorescence and luminescence,15–18 nanocomposite hydrogels,19 polymer thermal stabilizers,20 UV-shielding composites,21 biomedical,22 environmental engineering,23 photochemistry,24 catalytic processes25 etc. In the field of water and wastewater treatment, LDHs are used as pollutant scavengers for various anions and oxyanions.13,26 The defluoridation of water was performed with various LDHs,10,27–29 of which the Mg–Al LDH was preferred by many researchers.30–33 The calcination of LDHs expels anionic species and intercalated water resulting in the formation of metal oxides. The calcined LDH may reconstruct its layered structure by trapping target anions from an aqueous anionic solution.12 A number of literatures established the enhancement of the defluoridation capacity of LDHs upon calcination.27,34 Given the affinity of calcium and aluminum towards fluoride and their wide application in the field of water treatment, a calcined Ca–Al–(NO3) LDH has been considered for the adsorption of fluoride in the present study.
The adsorption of anions by a LDH is largely dependent on the factors related to the adsorption process. The temperature of the adsorption process controls the thermodynamics of the adsorption. The study of the effect of temperature on the adsorption is essential for understanding and controlling the adsorption reaction. One of the most important parameters for adsorption thermodynamics is the Gibbs free surface energy change (ΔG0), which indicates the spontaneity of a reaction. Although experimental methods for the determination of the enthalpy of adsorption have been reported using calorimetric measurements,35 in a number of literatures the determination of thermodynamic parameters is conducted from isotherm experiments performed at different temperatures. The ΔG0 value was attained mostly from the van't Hoff equation, where the equilibrium constant is correlated with ΔG0. However, crucial issues such as the correct estimation of the equilibrium constant and the non-dimensionality of the van't Hoff constant were not adequately addressed so far.36–40 Furthermore, the change in the standard entropy and enthalpy would also be erroneously appraised without the correct assessment of the thermodynamic equilibrium constant (Keq). Correct methodology for the estimation of the van't Hoff constant is unequivocally a gap in this field.
The assessment of the combined influence of temperature with other important process parameters is necessary to understand the adsorption thermodynamics. Multivariate optimization techniques are of pivotal importance for assessing the optimal conditions of the adsorption and the interactive effects of the influencing parameters on the adsorption. The ‘one factor at a time’ approach was commonly performed for the optimization, although the interactive effect of the influencing factors and overall optima of the system were rarely achieved. A recent trend of using multivariate optimization became popular in this field to overcome this drawback. Among the different techniques of multivariate optimization, response surface methodology (RSM) is one of the efficient tools.41 The main advantages of RSM lie in the systematic design of experiments, application of statistical and mathematical models and achieving accuracy in the prediction model with the minimum number of experiments. RSM has been efficiently utilized to model the adsorption process, addressing the effect of the interactive parameters.42–49 To the best of the knowledge of the authors, the use of RSM for addressing the adsorptive removal of fluoride by LDH materials has been rarely conducted. RSM can be applied for the determination of the interactive effect of the parameters influencing the defluoridation by LDH materials as well as appraising the overall optima of the adsorption process.
In this paper, an analytical method for the estimation of the thermodynamic equilibrium constant has been introduced. The effect of the temperature on the adsorption process in the defluoridation by calcined Ca–Al–(NO3) LDH was investigated through the thermodynamic and statistical approach. The Gibbs free surface energy change was determined from the van't Hoff equation through the proposed methodology. The thermodynamic parameters, e.g., activation energy, isosteric heat of adsorption, change in standard entropy and enthalpy etc. were also addressed to describe the adsorption process. A four factor face centered central composite design (FCCD) coupled with the response surface method was attempted to appraise the combined influence of the temperature and the other parameters, viz., pH, initial fluoride concentration and adsorbent dose.
Experimental section
Materials
All chemicals used in the study, e.g., sodium fluoride (NaF), calcium nitrate tetrahydrate [Ca(NO3)2·4H2O], aluminum nitrate nonahydrate [Al(NO3)3·9H2O], sodium hydroxide (NaOH) and nitric acid (HNO3) were purchased from Merck, India. The chemicals were of analytical reagent grade and were used without further purification. Deionized (DI) water was used for the material preparation and the sorption experimentation process.
Synthesis of calcined Ca–Al–(NO3) LDH and its characterization
The preparation and subsequent characterization of the material are described elsewhere.50 Typically, the synthesis of the Ca–Al–(NO3) LDH was conducted through a co-precipitation method. The precursor salts of 0.04 M Ca(NO3)2·4H2O and 0.02 M Al(NO3)3·9H2O were dissolved in DI water. An alkali solution of 4 M NaOH was prepared in DI water. The salt solution and alkali solution were together added drop-wise at a constant pH of 11 with continuous stirring. A nitrogen atmosphere was used to avoid carbonate intercalation. The resulting solution was thermally treated in an aging process and dried in a vacuum oven to obtain the pristine LDH. The LDH was calcined at 500 °C and manually ground to a powder form to use for further experiments. The characterization of the adsorbent was performed with XRD, FTIR, EDX, SEM and N2 adsorption desorption analyses and was reported elsewhere.50
Sorption experiments
A series of batch adsorption experiments were conducted in a BOD incubator shaker at controlled temperatures and agitation rate. The working volume of the fluoride solutions was taken as 100 mL in a 300 mL polypropylene bottle. The adsorption isotherms were obtained at various temperatures (10 °C to 50 °C) by varying the adsorbent dose at a range of 0.05 to 3 g L−1 for initial concentration of 10 mg L−1. As per the preliminary experiments, the influencing parameters selected for the RSM study were temperature, pH, initial concentration and adsorbent dose. The sorption experiments for the RSM study were conducted under the designed values of these parameters. An Orion Star A214 benchtop pH/ISE meter with an Orion 9609BNWP fluoride electrode (Thermo Scientific, USA) and TISAB III buffer were used to measure the fluoride concentration. The adsorption capacity qt (mg g−1) (the amount of fluoride adsorbed per unit mass of LDH at any time t) was calculated from eqn (1) as:where C0 (mg L−1) and Ct (mg L−1) are the initial concentration and the concentration of fluoride at any time t, respectively. M is the mass (g) of the adsorbent, and V is the volume (L) of the solution.
Experimental design
RSM is a combination of statistical and mathematical tools and has become an established technique for the design of experiments (DoE). The efficiency of a DoE is represented as the ratio of the number of coefficients present in the model equation to the number of experiments required.51 The central composite design, Box–Behnken design (BBD), Doehlert matrix, 33 factorial design etc. are different RSM methods. Amongst these, BBD has the highest efficiency and 33 factorial design has the highest accuracy.51 FCCD has become a very popular technique as the accuracy of the method is comparable to 33 factorial design, however, the efficiency of FCCD is close to BBD. A four factor three level FCCD was employed to design the experiments and the optimization was performed through the generation of response surfaces. The temperature, pH, initial fluoride concentration and adsorbent dose were considered as the factors and the adsorption capacity was optimized as the response. The coded values of variables (Xi) were computed using eqn (2) for the design of experiments as follows:41| |
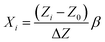 | (2) |
where Zi and Z0 represent the actual value at the ith level and the central point, respectively. ΔZ is the difference between the maximum or the minimum value and the value in the central point, and β is the major coded limit value for each variable.
The actual and coded values of independent variables are presented in Table 1. FCCD consists of a total number of 30 sets of experiments, out of which there are sixteen factorial, eight axial and six centre points (24 + 2 × 4 + 6). The experimental design was computed by Design Expert 8.0.7.1 (Stat-Ease, Inc. USA) and is represented in Table 2. A second order polynomial model [eqn (3)], appropriate for a 4-factor, 3-level design,52 was used to establish a numerical relationship between the dependent and independent variables as follows:
| |
 | (3) |
where
Y is the response;
Xi and
Xj are the coded variables;
β0 is a constant coefficient;
βi,
βii and
βij are the coefficients of the linear, quadratic and second-order interactions, respectively;
k is the number of studied factors; and
e is the error. Design Expert 8.0.7.1 (Stat-Ease, Inc. USA) was used to perform the RSM analysis of the experimental data. The significance of the independent variables and their individual and interactive effect on the adsorption capacity was identified and was expressed by
P-values and
F-values.
Table 1 Experimental range and levels of factors used in RSM
| Factors |
Level |
| −1 |
0 |
+1 |
Coded value |
| Temperature (A) |
10 |
30 |
50 |
Actual value |
| pH (B) |
6 |
8 |
10 |
| Initial fluoride concentration (C) |
5 |
20 |
35 |
| Adsorbent dose (D) |
0.5 |
1.0 |
1.5 |
Table 2 Design matrix and experimental results of FCCD
| Run order |
(A) Temperature (°C) |
(B) pH |
(C) Initial concentration (mg L−1) |
(D) Adsorbent dose (g L−1) |
Adsorption capacity (mg g−1) |
| 1 |
30 |
8 |
20 |
1 |
16.62 |
| 2 |
30 |
8 |
20 |
1.5 |
12.01 |
| 3 |
50 |
8 |
20 |
1 |
17.65 |
| 4 |
50 |
6 |
5 |
1.5 |
3.29 |
| 5 |
30 |
10 |
20 |
1 |
16.86 |
| 6 |
50 |
6 |
5 |
0.5 |
7.62 |
| 7 |
10 |
6 |
35 |
1.5 |
20.59 |
| 8 |
30 |
8 |
20 |
0.5 |
30.28 |
| 9 |
30 |
8 |
20 |
1 |
16.94 |
| 10 |
10 |
6 |
5 |
1.5 |
3.15 |
| 11 |
30 |
8 |
35 |
1 |
30.31 |
| 12 |
50 |
6 |
35 |
1.5 |
21.61 |
| 13 |
30 |
8 |
20 |
1 |
15.92 |
| 14 |
10 |
10 |
5 |
1.5 |
3.17 |
| 15 |
10 |
10 |
35 |
1.5 |
20.68 |
| 16 |
30 |
8 |
20 |
1 |
15.91 |
| 17 |
50 |
10 |
5 |
0.5 |
7.8 |
| 18 |
50 |
10 |
5 |
1.5 |
3.29 |
| 19 |
30 |
6 |
20 |
1 |
16.64 |
| 20 |
30 |
8 |
5 |
1 |
4.4 |
| 21 |
10 |
10 |
5 |
0.5 |
5.9 |
| 22 |
10 |
10 |
35 |
0.5 |
55.44 |
| 23 |
50 |
6 |
35 |
0.5 |
59.3 |
| 24 |
50 |
10 |
35 |
0.5 |
59.6 |
| 25 |
10 |
6 |
35 |
0.5 |
54.98 |
| 26 |
10 |
6 |
5 |
0.5 |
5.76 |
| 27 |
10 |
8 |
20 |
1 |
15.84 |
| 28 |
30 |
8 |
20 |
1 |
17.31 |
| 29 |
50 |
10 |
35 |
1.5 |
21.73 |
| 30 |
30 |
8 |
20 |
1 |
16.14 |
Results and discussion
Adsorption isotherm
The adsorption of fluoride on the calcined Ca–Al–(NO3) LDH was represented by the adsorption isotherms for various temperatures, viz., 10 °C, 20 °C, 30 °C, 40 °C and 50 °C. The isotherm studies were conducted for an initial fluoride concentration of 10 mg L−1 with a varied adsorbent dose from 0.05 to 3 g L−1. The Langmuir, Freundlich, linear and Dubinin–Raduskevich adsorption models were attempted in this study. In view of the inherent bias of the linearized forms of these models, a non-linear fit was performed using MATLAB, 2010a (The MathWorks, INC.). The general forms of the Langmuir, Freundlich, Dubinin–Raduskevich and linear models are represented in eqn (4)–(6) and (8), respectively, as follows:| |
 | (4) |
where qe represents the amount of the adsorbate adsorbed per unit weight of the adsorbent at the equilibrium (mg g−1), Ce is the concentration of the solute at the equilibrium (mg L−1), and qmax and b are the Langmuir constants. qmax is represented as the maximum adsorption capacity (mg g−1) and b is related to the binding energy or the affinity parameter of the adsorption system.where Kf and n are the Freundlich constants and indicate the relative adsorption capacity and adsorption intensity, respectively.| |
qe = Qm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Kadε2) exp(−Kadε2)
| (6) |
where Qm and Kad are the maximum adsorption capacity and a constant related to the adsorption energy, respectively. The parameter ε is the Polanyi potential and is represented by eqn (7) as follows:| |
 | (7) |
where R is the universal gas constant and T is the absolute temperature in K.where Kc is the isotherm constant. The isotherm curves are plotted in Fig. 1. The non-linearized plot represents the better applicability of the Freundlich isotherm. The linear isotherm was also fitting for this experimental data.
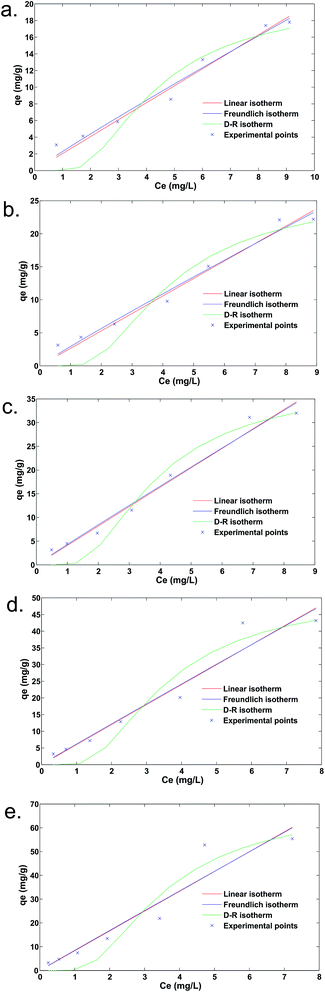 |
| | Fig. 1 Adsorption isotherms at (a) 10 °C, (b) 20 °C, (c) 30 °C, (d) 40 °C and (e) 50 °C. | |
Adsorption thermodynamics
Adsorption is a temperature dependent phenomena and the assessment of the thermodynamic parameters delineates the feasibility of the adsorption process. The spontaneity of a system is defined by evaluating ΔG0. At equilibrium conditions, ΔG0 is defined as follows:| |
ΔG0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Keq Keq
| (9) |
where Keq is the thermodynamic equilibrium constant. Substituting eqn (9) into the Gibbs Helmholz equation [eqn (10)], the van't Hoff equation is obtained [eqn (11)] as follows:| |
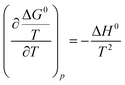 | (10) |
| |
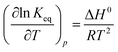 | (11) |
where ΔH0 is the change in the standard enthalpy. Integrating eqn (11) for T at a constant pressure, the following equation is attained:| |
−RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Keq = ΔH0 − TRY Keq = ΔH0 − TRY
| (12) |
where Y is the integration constant. The relationship between the standard Gibbs free surface energy change, standard enthalpy change and standard entropy change (ΔS0) is as follows:
From eqn (9), (12) and (13) the following equation is attained:
| |
 | (14) |
If ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Keq is plotted against 1/T (van't Hoff plot), multiplying the slope and intercept of the plot by R, ΔH0 and ΔS0 is obtained. The equilibrium constant should be dimensionless in accordance with the dimensionality of eqn (9) and (14).
Keq is plotted against 1/T (van't Hoff plot), multiplying the slope and intercept of the plot by R, ΔH0 and ΔS0 is obtained. The equilibrium constant should be dimensionless in accordance with the dimensionality of eqn (9) and (14).
Existing approaches for the determination of Keq
A critical literature review revealed that the determination of Keq was performed by various approaches.8,31,32,37,53–57 In this regard, the use of b as Keq was found in a number of literatures.8,36,39,54,58 Besides, the use of the isotherm constant from other adsorption isotherm models, i.e., Freundlich, Frumkin, Flory–Huggins model etc., was also practiced.40,57,59 The equilibrium constant was also derived by adopting the distribution coefficient (Kd) in terms of qe/Ce,29,60,61 the equilibrium constant (Ke) in terms of Cs/Ce (Cs is the concentration of solute adsorbed at equilibrium in mol L−1 or mg L−1),56,62,63 or other theoretical approaches.64,65 The key issue in dealing with the isotherm constant is the consideration of the dimensionality. The various approaches for the determination of the equilibrium constant from the isotherm study and other theoretical approaches are mostly incapable of explaining the ambiguity of the dimensions of the constant. Furthermore, the different methods estimated the thermodynamic parameters in various ways, which unequivocally depicts the non-uniformity and ambiguity associated with this field. Many researchers proposed a number of modifications to existing methodologies to rectify the error associated with the different approaches.
Milonjić has proposed an equation for an equilibrium constant given in L mol−1 as follows:66
| |
ΔG0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(55.5 × Keq) ln(55.5 × Keq)
| (15) |
This multiplication was used to nullify the unit of Keq (L mol−1) with 55.5 mol of water per litre of aqueous solution and if Keq is represented in L g−1, a factor of 1000 can be used, as the unit weight of water is 1000 g L−1. Albadarin et al. had adopted the same concept and developed a similar equation for the Langmuir isotherm constant as follows:38
| |
ΔG0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(55.5 × b) ln(55.5 × b)
| (16) |
However, Albadarin et al. used the unit b in L mg−1.38 Dawood and Sen attained a positive value of ΔG0 by employing Kd, taken as qe/Ce with a unit of L g−1 in the van't Hoff equation and commented on the non-spontaneity of the process.37 Canzano et al. commented on the work in terms of the erroneous estimation of the value of Kd without considering the non-dimensionality.67 Accordingly, Dawood and Sen corrected the value of Kd by multiplying by 1000 (considering the density of water as 1000 g L−1) and achieved a negative value of ΔG0 after the rectification, demonstrating the spontaneity of the adsorption reaction.68 Biggar and Cheung, Khan and Singh proposed the method for the estimation of Keq considering the effect of activity.64,65 The Keq value was determined from the intercept of the plot for ln(Cs/Ce) versus Cs, where Cs and Ce are the concentration of the adsorbate at the surface and the suspension in the equilibrium. Many researchers followed this method.55,60,69 Sawalha et al. found Keq from the above mentioned methods without considering the non-dimensionality.60 Milonjić analysed the work of Sawalha et al. and showed that the value of ΔG0 was wrongly calculated.60,66
The above mentioned approaches and the proposed modifications thereof, for the determination of the equilibrium constant, have several shortcomings due to the inadequate theoretical background or improper applications of the methods. The method of multiplying Keq by mol L−1 (or g L−1) of water is not applicable everywhere. In the existing literature, the use of Kd, Ke or the constant from the method proposed by Khan and Singh did not consider the equilibrium relationship between qe and Ce represented by the appropriate isotherm model.65 Subsequently, the non-linear relationship of qe and Ce may lead to a poor fitting of the experimental data and improper estimation of the thermodynamic parameters.
Proposed approach for the determination of Keq
In view of the drawbacks discussed above, a theoretical analysis is essential for the correct estimation of Keq. The equilibrium relation of qe and Ce shall be confirmed in order to adopt a suitable approach. In most of the literature, the equilibrium relationship is described either by the Langmuir or the Freundlich isotherm model. The linear isotherm may also be applicable for a lower range of equilibrium concentration. An adsorption equation can be represented as follows:70| | |
A(aq) + M(s) ⇔ M–A(ad)
| (17) |
where A is the adsorbate and M is the vacant site of adsorbent. M–A represents the adsorbed sites on the adsorbent. The equilibrium constant, Keq can be defined as follows:| |
 | (18) |
The molar concentration of the adsorbate and the adsorbent should be represented in terms of activity and is as follows:
| |
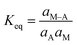 | (19) |
where
aA,
aM, and
aM–A represent the activities of A, M and M–A, respectively. The Langmuir isotherm constant,
b in mol L
−1, is numerically equal to the equilibrium constant for the non-ionic or the dilute solution of the ionic substances. However, a suitable modification of
b, represented with other units, should be performed in order to adopt it as the equilibrium constant. The influence of the activity coefficient shall also be accounted for a concentrated solution of the ionic solutes. The stated method can only be used if the Langmuir isotherm defines the adsorption process. However, a number of existing literatures also showed the applicability of the Freundlich and other isotherm models. The determination of the thermodynamic constants from the Langmuir isotherm shall not be performed in those cases. Two widely used approaches, the representation of
Keq as
Kd or
Ke, adopted in a diversified manner in the literature have to be investigated as mentioned above.
Ke and Kd may be represented by eqn (20) and (21) as follows:
| |
 | (20) |
| |
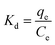 | (21) |
Now, considering the activity of the solid adsorbent aM is one in eqn (19), Keq can be represented as follows:
| |
 | (22) |
However, the activity will represent the molar concentration for the non-ionic and dilute solution of electrolytes. Hence, eqn (22) can be re-written as follows:
| |
 | (23) |
CMA is equal to the concentration in the adsorbed phase at equilibrium which is equal to Cs in mass per mass units. In the existing literature, Cs is mostly defined in mol L−1 (or mg L−1). It is customary to represent Cs as the solid phase concentration of the solute in a mass to mass ratio. As a consequence, Cs can be represented as mol g−1 (or mg g−1). Ce is represented in mol L−1 (or mg L−1). By representing the concentration in this manner one may get
The two entities, Ke and Kd have units of L g−1. However, the equilibrium constant Keq is unitless. If Ce is converted to mol (or mg) of the solute per gram of the solvent, the dimensions of Ke or Kd can be omitted. Considering the mass of water per litre is Mw(T), in g L−1 at a temperature T, Ke or Kd can be written as follows:
| |
 | (25) |
From eqn (25), one can postulate eqn (26) as follows:
| | |
Keq ≈ KeMw(T) = KdMw(T)
| (26) |
Eqn (26) is applicable if the equilibrium is defined by the linear isotherm. If the equilibrium is defined by the Freundlich isotherm model with Ce and qe in mg L−1 and mg g−1, respectively, the following equation may be developed by analysing the dimension of Kd and Kf:
| |
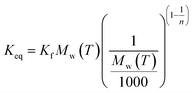 | (27) |
However, calculating the value of Keq from the slope of the plot of qe (or Cs) versus Ce may not be wise unless the linear isotherm describes the adsorption equilibrium. Similarly, the method proposed by Khan and Singh did not account for the influence of the equilibrium relationship between Cs and Ce.65 In the present paper, Keq is computed from the slope of the linear and Freundlich isotherm plots (R2 = 0.91 to 0.97) for different temperatures and modified through eqn (26) and (27), respectively. The van't Hoff plot (Fig. 2) of Keq versus 1/T provided ΔH0 and ΔS0 as the slope and intercept of the graph multiplied by R. ΔG0 was obtained from eqn (13) for different temperatures.
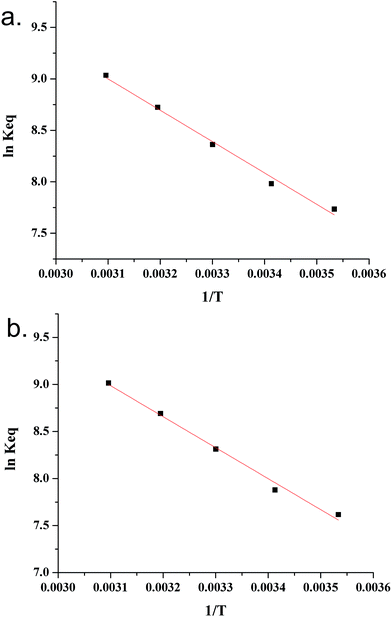 |
| | Fig. 2 van't Hoff plot using isotherm constants from (a) the Freundlich model and (b) the linear model. | |
The positive value of ΔH0 indicated that the adsorption reaction is endothermic and the increase in temperature favoured the adsorption process.71 Furthermore, the value of ΔH0 ranges between 2.1 and 20.9 kJ mol−1 and between 80 and 200 kJ mol−1 in case of physisorption and chemisorption, respectively.72 In the present study, the value of ΔH0 (Table 3) showed the nature of adsorption was in between physisorption and chemisorption. The positive value of ΔS0 (Table 3) reflected an affinity of the calcined LDH for the fluoride ion along with an increase in randomness at the interface during the sorption process and an increase in the degree of freedom of the adsorbed species.58,72 The negative value of ΔG0 confirmed that the adsorption process is spontaneous and thermodynamically feasible (Table 3). The decrease in ΔG0 with the increase in the temperature unequivocally confirmed an enhancement of the adsorption with the increase in the temperature. This is plausible due to the increase in the mobility of the fluoride ions in aqueous solution and the increase of the affinity of the fluoride ions for the calcined LDH with the increase in temperature.72
Table 3 Thermodynamic parameters from isotherm constant
| Temperature (°C) |
Freundlich isotherm |
Linear isotherm |
| ΔG0 (kJ mol−1) |
ΔH0 (kJ mol−1) |
ΔS0 (kJ mol−1 K−1) |
ΔG0 (kJ mol−1) |
ΔH0 (kJ mol−1) |
ΔS0 (kJ mol−1 K−1) |
| 10 |
−18.07 |
25.33 |
0.15 |
−17.78 |
27.38 |
0.16 |
| 20 |
−19.60 |
−19.38 |
| 30 |
−21.13 |
−20.98 |
| 40 |
−22.67 |
−22.57 |
| 50 |
−24.20 |
−24.17 |
Mean free surface energy
The Freundlich or Langmuir isotherm equations do not account the influence of temperature in the isotherm relationship. However, the D–R isotherm parameters correlate the adsorption equilibrium with the thermodynamic parameters. The adsorption constant Kad is related to adsorption energy. The D–R isotherm was computed from the adsorption data to obtain the values of Kad at different temperatures (Fig. 1). The mean free surface energy (Ead) is the free energy change when one mole of an ion is transferred from a solution to the surface of the adsorbent and is calculated by the following equation:38| |
 | (28) |
A value of Ead that is less than 8 kJ mol−1 represents physical adsorption. However, the value of Ead in ion exchange reactions ranges between 8 and 16 kJ mol−1.73 The calculated values of Ead, represented in Table 4, may be ascribed to the fact that physisorption is predominant in the present study.
Table 4 Energy parameter from thermodynamic analyses
| Temperature (°C) |
Ead (kJ mol−1) |
Ea (kJ mol−1) |
S* |
| 10 |
0.40 |
53.18 |
0.28 |
| 20 |
0.42 |
| 30 |
0.47 |
| 40 |
0.53 |
| 50 |
0.55 |
Activation energy
The effect of temperature on fluoride adsorption was further assessed by evaluating the activation energy from a modified Arrhenius type equation as follows:74| |
 | (29) |
where S* is the sticking probability and depends on the temperature of the system. Ea is the activation energy. The surface coverage (θ) is estimated by the following equation:74| |
 | (30) |
S* and Ea were calculated from the plot of (1 − θ) versus 1/T through linear regression (Fig. 3). S* is defined as a function of the adsorption system depicting the potential of an adsorbate to remain on the adsorbent. A value of S* between 0 and 1 favours sorption (Table 4). A positive value of Ea indicates an endothermic reaction. The value of Ea ranges between 5 and 40 kJ mol−1 for physisorption and between 40 and 800 kJ mol−1 for chemisorption.55 The Ea value (Table 4) indicates that the adsorption process is between physical and chemical adsorption.
 |
| | Fig. 3 Variation of surface coverage with temperature for determination of the activation energy. | |
Isosteric heat of adsorption
Isosteric heat of adsorption is an important thermodynamic parameter depicting the influence of heat on the adsorption process. The standard enthalpy of the adsorption at a constant amount of the adsorbate adsorbed is defined as the isosteric heat of adsorption. It is an indicator of the performance of an adsorptive separation process and surface energetic heterogeneity. The isosteric heat of adsorption at a constant surface coverage is obtained from the Clausius–Clapeyron equation as follows:| |
 | (31) |
where ΔHx is the isosteric heat of adsorption. Furthermore, assuming ΔHx is independent of the temperature, the following equation may be obtained upon integration:| |
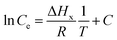 | (32) |
where C is integration constant. ΔHx can be attained from the slope of the isosteres at different surface loading values (mg g−1) in the plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce versus 1/T (Fig. 4). The isosteres for the different equilibrium concentrations at a constant amount sorbed was obtained from the adsorption isotherm data at different temperatures.
Ce versus 1/T (Fig. 4). The isosteres for the different equilibrium concentrations at a constant amount sorbed was obtained from the adsorption isotherm data at different temperatures.
 |
| | Fig. 4 Plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce for fluoride adsorption at constant amounts adsorbed as a function of 1/T. Ce for fluoride adsorption at constant amounts adsorbed as a function of 1/T. | |
The nature of the adsorption may be appraised from the value of ΔHx. The value of ΔHx is less than 80 kJ mol−1 for physisorption. However, a value of ΔHx between 80 and 400 kJ mol−1 may be found for a chemisorption reaction. In this study, the value of ΔHx (Fig. 4) is attributed to the occurrence of physisorption. Furthermore, the degree of heterogeneity of the adsorbent may be confirmed from the variation of ΔHx with the surface loading. A constant value of ΔHx, however, may be attained in the case of a homogeneous surface.72,75 The moderate variation of ΔHx (Fig. 4) confirmed a less heterogeneous adsorbent surface in the present study.
Empirical modeling through RSM
Optimization of fluoride removal. The empirical relationship between the fluoride adsorption capacity and the adsorption process parameter was established through RSM. A FCCD was employed to perform the experimental design and the polynomial model equation was developed by regression analysis. The actual adsorption capacity in accordance to the experimental run varied from 3.15 to 59.60 mg g−1 (Table 2). The substantial variation of the adsorption capacity may be attributed to the fact that the process parameters had a potential influence in the experimental domain. The quadratic model equation (eqn (3)) for the adsorption capacity with the coded values of the independent variables (i.e. temperature, pH, initial fluoride concentration and adsorbent dose) was attained as follows:| | |
q = +16.54 + 0.91A + 0.09B + 16.66C − 9.84D − 0.01AB + 0.41AC − 0.62AD + 0.04BC − 0.05BD − 8.16CD + 0.14A2 + 0.15B2 + 0.75C2 + 4.54D2
| (33) |
ANOVA was perform for the regression model [eqn (33)], which exhibited its adequacy with a considerably higher F value. A low F value for ‘lack of fit’ [Table S1 in ESI†] also demonstrated the significance of the model. It was revealed from ANOVA that the model terms with the pH showed less significance. A stepwise model reduction was performed to eliminate the insignificant model terms. Accordingly, the reduced model is given in eqn (34) as follows:
| | |
q = +16.55 + 0.91A + 16.66C − 9.84D + 0.41AC − 0.62AD − 8.16CD + 0.19A2 + 0.80C2 + 4.59D2
| (34) |
The equation of the reduced model was evaluated by Fisher's F value, P value, lack of fit, sequential model sum of squares (Table S2 in ESI†) and coefficient of determination (R2 = 0.99). The model parameters were improved after reduction (Table S2 in ESI†). The validity of the fitted quadratic model was further evaluated by graphically analysing the residual. The plot of the predicted versus actual values exhibited a reasonable agreement between the predicted values from the model equation and the experimental results (Fig. S1 in ESI†). The studentized residual was plotted against the predicted value and confirmed the adequacy of the model (Fig. S2 in ESI†). The normal distribution of the error was exhibited from the presence of scatter points in close proximity to the straight line in the normal probability plot for the studentized residual (Fig. S3 in ESI†). The random distribution of the residual without a definite pattern was depicted in the graphical analyses.
Influence of parameters. The influence of the independent variables on the fluoride adsorption capacity was assessed through the coefficient of the model equation [eqn (33)] and the perturbation curve (Fig. 5). The three dimensional surface plot provided the interactive effects of the process parameters and the overall optima of the system (Fig. 6). The adsorption capacity was mostly influenced by the initial fluoride concentration and the adsorbent dose compared to the other two parameters. The pH had the most insignificant effect and least interaction with the other three parameters. A prominent synergistic and antagonistic effect was exhibited for the initial fluoride concentration and the adsorbent dose, respectively. However, the temperature had a comparatively lower synergistic effect in the tested range. The interaction between the initial concentration and the adsorbent dose had pronounced significance whereas the combined influences of the temperature with these two parameters was comparatively less significant (Fig. 6). The effect of the temperature is more prominent at a higher initial concentration and a lower adsorbent dose. The increase in the adsorption capacity with the increase in the initial concentration at a lower adsorbent dose was greater compared to the same at a higher adsorbent dose (Fig. 6c). The greater amount of adsorbate available at the active sites of the adsorbent at a higher initial fluoride concentration facilitated the increasing trend of the adsorption capacity. The possibility of contact between the adsorbate and the adsorbent was enhanced at a higher concentration gradient due to the diffusion and mass transfer rates as well as faster transport.46,76 The decreasing trend of the adsorption capacity with the adsorbent dose may be ascribed to the fact that the availability of more active sites may reduce the amount of the utilization of the adsorbent, depending on the concentration of the adsorbate.45
 |
| | Fig. 5 Perturbation curve ((A) temperature, (B) pH, (C) initial concentration, (D) adsorbent dose). | |
 |
| | Fig. 6 Three-dimensional response surface for the interactive effects of (a) temperature and initial concentration, (b) temperature and adsorbent dose and (c) initial concentration and adsorbent dose. | |
Conclusions
A critical review for the estimation of the thermodynamic equilibrium constant has been performed, indicating discrepancy in the existing literature. An analytical approach has been proposed for the appropriate estimation of the equilibrium constant. In the present study, the thermodynamic aspects of the adsorption of fluoride onto the calcined Ca–Al–(NO3) LDH were delineated. Analysing the isotherm data at different temperatures, it was revealed that the Freundlich and linear isotherm models were appropriate for this study. The estimation of Keq was conducted with the proposed method. ΔG0 was obtained by incorporating Keq into the van't Hoff equation from both the Freundlich and linear isotherm data. The value of ΔG0 was comparable using both the isotherm constants after the proposed modification. The negative ΔG0 confirmed the spontaneity of the reaction. ΔH0, ΔS0, Ea, Ead and ΔHx were also calculated. The obtained values of the thermodynamic constant may be ascribed to the thermodynamic feasibility of the adsorption reaction. Furthermore, the thermodynamic constant confirmed that the type of sorption reaction is in between physisorption and chemisorption and is endothermic in nature. The RSM study exhibited the prominent interactive effect of the temperature at a lower adsorbent dose and a higher initial concentration. The pH of the adsorption process had an insignificant influence. However, the influence of the adsorbent dose and initial fluoride concentration has a predominant effect on the adsorption capacity. The present method for the determination of the thermodynamic parameters from the van't Hoff equation will be instrumental in appropriately delineating the adsorption process from isotherm constants.
List of abbreviations
| ANOVA | Analysis of variance |
| ΔG0 | Gibbs free surface energy change |
| ΔH0 | Change in standard enthalpy |
| ΔHx | Isosteric heat of adsorption |
| ΔS0 | Change in standard entropy |
| Ea | Activation energy |
| Ead | Mean free surface energy |
| FCCD | Face centered central composite design |
| LDH | Layered double hydroxide |
| Keq | Thermodynamic equilibrium constant |
| Ke | Equilibrium constant from Cs/Ce |
| Kd | Distribution coefficient |
| RSM | Response surface methodology |
| R | Universal gas constant |
| T | Temperature |
References
- A. K. Yadav, C. P. Kaushik, A. K. Haritash, B. Singh, S. P. Raghuvanshi and A. Kansal, J. Hazard. Mater., 2007, 142, 77–80 CrossRef CAS PubMed.
- S. Mandal and S. Mayadevi, J. Hazard. Mater., 2009, 167, 873–878 CrossRef CAS.
- World Health Organization, Guidelines for drinking-water quality, World Health Organization, Geneva, 4th edn, 2011 Search PubMed.
- S. Ayoob and A. K. Gupta, Crit. Rev. Environ. Sci. Technol., 2006, 36, 433–487 CrossRef CAS.
- S. Ayoob, A. K. Gupta and V. T. Bhat, Crit. Rev. Environ. Sci. Technol., 2008, 38, 401–470 CrossRef CAS.
- S. Ayoob and A. K. Gupta, J. Hazard. Mater., 2008, 152, 976–985 CrossRef CAS PubMed.
- A. Bhatnagar, E. Kumar and M. Sillanpää, Chem. Eng. J., 2011, 171, 811–840 CrossRef CAS.
- L. Lv, Desalination, 2007, 208, 125–133 CrossRef CAS.
- T. Zhang, Q. Li, H. Xiao, H. Lu and Y. Zhou, Ind. Eng. Chem. Res., 2012, 51, 11490–11498 CrossRef CAS.
- X. Zhao, L. Zhang, P. Xiong, W. Ma, N. Qian and W. Lu, Microporous Mesoporous Mater., 2015, 201, 91–98 CrossRef CAS.
- A. Cavani, F. Trifirò and F. Vaccari, Catal. Today, 1991, 11, 173–301 CrossRef.
- J. He, M. Wei, B. Li, Y. Kang, D. G. Evans and X. Duan, Layered Double Hydroxides, 2006, 119, 89–119 CAS.
- F. L. Theiss, S. J. Couperthwaite, G. A. Ayoko and R. L. Frost, J. Colloid Interface Sci., 2014, 417, 356–368 CrossRef CAS PubMed.
- R. Liang, R. Tian, Z. Liu, D. Yan and M. Wei, Chem.–Asian J., 2014, 9, 1161–1167 CrossRef CAS.
- Y. Zhao, H. Lin, M. Chen and D. Yan, Ind. Eng. Chem. Res., 2014, 53, 3140–3147 CrossRef CAS.
- R. Gao, M. Zhao, Y. Guan, X. Fang, X. Li and D. Yan, J. Mater. Chem. C, 2014, 2, 9579–9586 RSC.
- D. Yan, Y. Zhao, M. Wei, R. Liang, J. Lu, D. G. Evans and X. Duan, RSC Adv., 2013, 3, 4303 RSC.
- G. Wang, S. Xu, C. Xia, D. Yan, Y. Lin and M. Wei, RSC Adv., 2015, 5, 23708–23714 RSC.
- Z. Hu and G. Chen, Adv. Mater., 2014, 26, 5950–5956 CrossRef CAS PubMed.
- J. Liu, G. Chen and J. Yang, Polymer, 2008, 49, 3923–3927 CrossRef CAS.
- T. Cao, K. Xu, G. Chen and C. Guo, RSC Adv., 2013, 3, 6282 RSC.
- J. Choy, J. Oh and D. Park, in Low-Dimensional Solids, eds. W. B. Duncan, D. O'Hare and R. I. Walton, John Wiley & Sons, Ltd., 2010, pp. 163–187 Search PubMed.
- R. Rojas, in Hydroxides: Synthesis, Types and Applications, eds. A. C. Carillo and D. A. Griego, Nova Science Publishers, Inc., 2012, pp. 39–71 Search PubMed.
- S. Li, Y. Shen, M. Xiao, D. Liu, L. Fa and K. Wu, J. Ind. Eng. Chem., 2014, 20, 1280–1284 CrossRef CAS.
- Z. P. Xu, J. Zhang, M. O. Adebajo, H. Zhang and C. Zhou, Appl. Clay Sci., 2011, 53, 139–150 CrossRef CAS.
- K.-H. Goh, T.-T. Lim and Z. Dong, Water Res., 2008, 42, 1343–1368 CrossRef CAS PubMed.
- D. Kang, X. Yu, S. Tong, M. Ge, J. Zuo, C. Cao and W. Song, Chem. Eng. J., 2013, 228, 731–740 CrossRef CAS.
- S. Mandal and S. Mayadevi, Appl. Clay Sci., 2008, 40, 54–62 CrossRef CAS.
- J. Zhou, Y. Cheng, J. Yu and G. Liu, J. Mater. Chem., 2011, 21, 19353 RSC.
- P. Cai, H. Zheng, C. Wang, H. Ma, J. Hu, Y. Pu and P. Liang, J. Hazard. Mater., 2012, 213–214, 100–108 CrossRef CAS PubMed.
- Q. Chang, L. Zhu, Z. Luo, M. Lei, S. Zhang and H. Tang, Ultrason. Sonochem., 2011, 18, 553–561 CrossRef CAS PubMed.
- W. Ma, N. Zhao, G. Yang, L. Tian and R. Wang, Desalination, 2011, 268, 20–26 CrossRef CAS.
- L. Lv, J. He, M. Wei, D. G. Evans and Z. Zhou, Water Res., 2007, 41, 1534–1542 CrossRef CAS PubMed.
- Q. Guo and E. J. Reardon, Appl. Clay Sci., 2012, 56, 7–15 CrossRef CAS.
- G. Chen, B. Han and H. Yan, J. Colloid Interface Sci., 1998, 201, 158–163 CrossRef CAS.
- S. Hong, C. Wen, J. He, F. Gan and Y.-S. Ho, J. Hazard. Mater., 2009, 167, 630–633 CrossRef CAS PubMed.
- S. Dawood and T. K. Sen, Water Res., 2012, 46, 1933–1946 CrossRef CAS.
- A. B. Albadarin, C. Mangwandi, A. H. Al-Muhtaseb, G. M. Walker, S. J. Allen and M. N. M. Ahmad, Chem. Eng. J., 2012, 179, 193–202 CrossRef CAS.
- I. A. W. Tan, A. L. Ahmad and B. H. Hameed, J. Hazard. Mater., 2009, 164, 473–482 CrossRef CAS PubMed.
- D. Duranoğlu, A. W. Trochimczuk and U. Beker, Chem. Eng. J., 2012, 187, 193–202 CrossRef.
- M. A. Bezerra, R. E. Santelli, E. P. Oliveira, L. S. Villar and L. a. Escaleira, Talanta, 2008, 76, 965–977 CrossRef CAS PubMed.
- A. I. Appavoo, J. Hu, Y. Huang, S. F. Y. Li and S. L. Ong, Water Res., 2014, 57, 270–279 CrossRef PubMed.
- M. Arulkumar, P. Sathishkumar and T. Palvannan, J. Hazard. Mater., 2011, 186, 827–834 CrossRef CAS PubMed.
- C. Han, H. Pu, H. Li, L. Deng, S. Huang, S. He and Y. Luo, J. Hazard. Mater., 2013, 254–255, 301–309 CrossRef CAS PubMed.
- H. Tajernia, T. Ebadi, B. Nasernejad and M. Ghafori, Water, Air, Soil Pollut., 2014, 225, 2028 CrossRef.
- E. B. Simsek, A. O. Avcı Tuna and U. Beker, Environ. Sci. Pollut. Res., 2015, 22, 3249–3256 CrossRef PubMed.
- A. Asfaram, M. Ghaedi, S. Hajati and A. Goudarzi, RSC Adv., 2015, 5, 72300–72320 RSC.
- H. Mazaheri, M. Ghaedi, S. Hajati, K. Dashtian and M. K. Purkait, RSC Adv., 2015, 5, 83427–83435 RSC.
- H. Zhu, Y. Fu, R. Jiang, J. Yao, L. Xiao and G. Zeng, Ind. Eng. Chem. Res., 2014, 53, 4059–4066 CrossRef CAS.
- P. S. Ghosal, A. K. Gupta and S. Ayoob, Appl. Clay Sci., 2015, 116–117, 120–128 CrossRef CAS.
- P. S. Ghosal, A. K. Gupta and A. Sulaiman, J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng., 2015, 51(1), 86–96 CrossRef PubMed.
- D. C. Montgomery, Design and analysis of experiments, John Wiley & Sons Singapore Pte. Ltd., 8th edn, 2013 Search PubMed.
- D. P. Das, J. Das and K. Parida, J. Colloid Interface Sci., 2003, 261, 213–220 CrossRef CAS PubMed.
- T. Lv, W. Ma, G. Xin, R. Wang, J. Xu, D. Liu, F. Liu and D. Pan, J. Hazard. Mater., 2012, 237–238, 121–132 CrossRef CAS PubMed.
- M. N. Sepehr, V. Sivasankar, M. Zarrabi and M. Senthil Kumar, Chem. Eng. J., 2013, 228, 192–204 CrossRef CAS.
- P. Saha, S. Chowdhury, S. Gupta and I. Kumar, Chem. Eng. J., 2010, 165, 874–882 CrossRef CAS.
- S. Lyubchik, A. Lyubchik, O. Lygina, S. Lyubchik and I. Fonseca, in Thermodynamics – Interaction Studies – Solids, Liquids and Gases, ed. J. C. Moreno Pirajn, InTech, 2011, pp. 95–122 Search PubMed.
- Y.-S. Ho, Water Res., 2003, 37, 2323–2330 CrossRef CAS PubMed.
- A. S. Bhatt, P. L. Sakaria, M. Vasudevan, R. R. Pawar, N. Sudheesh, H. C. Bajaj and H. M. Mody, RSC Adv., 2012, 2, 8663 RSC.
- M. F. Sawalha, J. R. Peralta-Videa, J. Romero-González and J. L. Gardea-Torresdey, J. Colloid Interface Sci., 2006, 300, 100–104 CrossRef CAS PubMed.
- V. C. Srivastava, I. D. Mall and I. M. Mishra, Chem. Eng. J., 2007, 132, 267–278 CrossRef CAS.
- S. Mandal, S. Tripathy, T. Padhi, M. K. Sahu and R. K. Patel, J. Environ. Sci., 2013, 25, 993–1000 CrossRef CAS.
- L. You, Z. Wu, T. Kim and K. Lee, J. Colloid Interface Sci., 2006, 300, 526–535 CrossRef CAS PubMed.
- J. W. Biggar and M. W. Cheung, Soil Sci. Soc. Am. J., 1973, 37, 863 CrossRef CAS.
- A. A. Khan and R. P. Singh, Colloids Surf., 1987, 24, 33–42 CrossRef CAS.
- S. K. Milonjić, J. Serb. Chem. Soc., 2007, 72, 1363–1367 CrossRef.
- S. Canzano, P. Iovino, S. Salvestrini and S. Capasso, Water Res., 2012, 46, 4314–4315 CrossRef CAS PubMed.
- S. Dawood and T. K. Sen, Water Res., 2012, 46, 4316–4317 CrossRef CAS PubMed.
- W. Huang, J. Chen, F. He, J. Tang, D. Li, Y. Zhu and Y. Zhang, Appl. Clay Sci., 2015, 104, 252–260 CrossRef CAS.
- P. Atkins and J. de Paula, Atkins' Physical Chemistry, Oxford University Press, Oxford New York, 8th edn, 2006 Search PubMed.
- R. Chang, Physical Chemistry for the Chemical and Biological Sciences, University Science Books, USA, 3rd edn, 2000 Search PubMed.
- P. Saha and S. Chowdhury, Insight into adsorption thermodynamics, INTECH Open Access Publisher, 2011 Search PubMed.
- S. K. Swain, T. Patnaik, V. K. Singh, U. Jha, R. K. Patel and R. K. Dey, Chem. Eng. J., 2011, 171, 1218–1226 CrossRef CAS.
- N. K. Amin, J. Hazard. Mater., 2009, 165, 52–62 CrossRef CAS PubMed.
- M. R. Unnithan and T. S. Anirudhan, Ind. Eng. Chem. Res., 2001, 40, 2693–2701 CrossRef CAS.
- A. Ö. A. Tuna, E. Özdemir, E. B. Simsek and U. Beker, Water, Air, Soil Pollut., 2013, 224, 1685 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra20538g |
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. 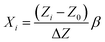


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Kadε2)
exp(−Kadε2)

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Keq
Keq
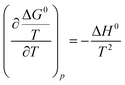
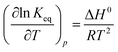
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Keq = ΔH0 − TRY
Keq = ΔH0 − TRY

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Keq is plotted against 1/T (van't Hoff plot), multiplying the slope and intercept of the plot by R, ΔH0 and ΔS0 is obtained. The equilibrium constant should be dimensionless in accordance with the dimensionality of eqn (9) and (14).
Keq is plotted against 1/T (van't Hoff plot), multiplying the slope and intercept of the plot by R, ΔH0 and ΔS0 is obtained. The equilibrium constant should be dimensionless in accordance with the dimensionality of eqn (9) and (14).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(55.5 × Keq)
ln(55.5 × Keq)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(55.5 × b)
ln(55.5 × b)

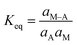

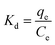



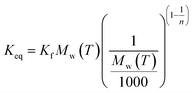





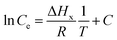
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce versus 1/T (Fig. 4). The isosteres for the different equilibrium concentrations at a constant amount sorbed was obtained from the adsorption isotherm data at different temperatures.
Ce versus 1/T (Fig. 4). The isosteres for the different equilibrium concentrations at a constant amount sorbed was obtained from the adsorption isotherm data at different temperatures.





