Core/shell-structured, covalently bonded TiO2/poly(3,4-ethylenedioxythiophene) dispersions and their electrorheological response: the effect of anisotropy†
Abstract
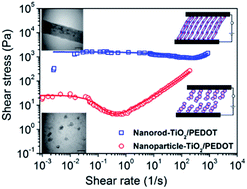
As a new electrorheological (ER) material, core/shell nanorods composed of a titania core and conducting polymer poly(3,4-ethylenedioxythiophene) (PEDOT) shell were prepared via covalent bonding to achieve a thin polymer shell and make the interfacial interactions between the two components more impressive. The successful coating of PEDOT on the nanorod-TiO2 particles was confirmed by TEM analysis. The antisedimentation stability of the core/shell nanorod-TiO2/PEDOT particles was determined to be 100%. The ER properties of the materials were studied under controlled shear, oscillatory shear and creep tests. The dielectric spectra of the dispersions were obtained to further understand their ER responses and fitted with the Cole–Cole equation. The ER behavior of the dispersions was also observed using an optical microscope. The flow curves of these ER fluids were determined under various electric field strengths and their flow characteristics examined via a rheological equation using the Cho–Choi–Jhon (CCJ) model. In addition, the results were also compared with nanoparticle-TiO2/PEDOT. It was concluded that the conducting thin polymer shell and elongated structure of the hybrid material introduced a synergistic effect on the electric field induced polarizability and colloidal stability against sedimentation, which resulted in stronger ER activity, storage modulus and higher recovery after stress loadings when compared to nanoparticle-TiO2/PEDOT.

 Please wait while we load your content...
Please wait while we load your content...