Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
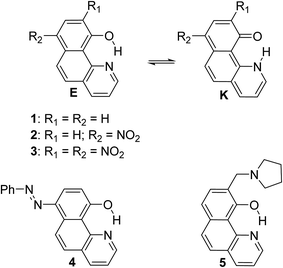
10-Hydroxybenzo[h]quinoline: switching between single- and double-well proton transfer through structural modifications†‡
S.
Hristova
a,
G.
Dobrikov
a,
F. S.
Kamounah
c,
S.
Kawauchi
b,
P. E.
Hansen
c,
V.
Deneva
a,
D.
Nedeltcheva
a and
L.
Antonov
 *a
*a
aInstitute of Organic Chemistry with Centre of Phytochemistry, Bulgarian Academy of Sciences, Acad. G. Bonchev str., bl. 9, 1113 Sofia, Bulgaria. E-mail: lantonov@orgchm.bas.bg; Web: http://www.orgchm.bas.bg/%E2%88%BCi2mp
bTokyo Institute of Technology, Department of Polymer Science, O-okayama, Meguro-ku, Tokyo 152, Japan
cRoskilde University, Department of Science, Systems and Models, DK-4000, Roskilde, Denmark
First published on 23rd November 2015
Abstract
Proton transfer in 10-hydroxybenzo[h]quinoline (HBQ) and structurally modified compounds was investigated experimentally (steady state UV-Vis absorption and emission spectroscopy, NMR and advanced chemometric techniques) and theoretically (DFT and TD-DFT M06-2X/TZVP calculations) in the ground and excited singlet state. We observed that the incorporation of electron acceptor substituents on position 7 of the HBQ backbone led to appearance of a keto tautomer in ground state and changes in the excited state potential energy surface. Both processes were strongly solvent dependent. In the ground state the equilibrium could be driven from the enol to the keto form by change of solvent. The theoretical calculations explain the substitution-determined transition from a single- to a double-well proton transfer mechanism.
Introduction
Excited state intramolecular proton transfer (ESIPT) reactions involve proton (or hydrogen atom) transfer through a pre-existing ground state hydrogen bond, giving rise to another tautomer in the excited state.1,2 Due to this structural change, the excited tautomer possesses photophysical properties, different from those of the ground state species. Large Stokes shift is a typical indication for ESIPT occurrence. The ESIPT process has been intensively studied experimentally1,3 and computationally in various systems.4 The ESIPT reactions have become a field of active research5 in the last two decades, due to the applications of ESIPT exhibiting molecules as laser dyes,6 photo stabilizers,7 photo switches3a,8 and light-emitting materials for electroluminescent devices.910-Hydroxybenzo[h]quinoline, well known also with the abbreviation HBQ (1, Scheme 1), is an extensively studied ESIPT molecular system10,11 and since the experimental verification of the occurrence of ESIPT in it,12,13 has been successfully exploited for applicative research.14,15 Further, some metal complexes of HBQ (and structurally related compounds) have been reported to exhibit high electroluminescence quantum efficiency and admirable thermal stability, whereby making them prospective materials for the development of organic light emitting devices.16 The observed orange-red fluorescence recognized as a keto-tautomer (K) emission results from the intramolecular excited-state proton transfer reaction.17 ESIPT in 1 is a direct consequence of very strong intramolecular hydrogen bonding as has been verified both experimentally and theoretically.7,13,18 The obtained results clearly show that in the case of HBQ only the enol-like form is present in the ground state, while in the excited state the keto-like form is dominating. The proton transfer in both states is barrierless proceeding through a single-well mechanism.19 Structural modifications of HBQ and their effects on the ESIPT and the spectral characteristics have been intensively studied by Gryko et al.20,21 in recent years, giving directions for the design of ESIPT chromophores. The distance between tautomeric sites (O and N) in structurally similar compounds is considered as a tool for modeling the barrier of ESIPT as well.22
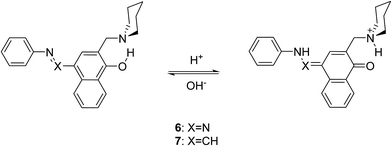
In the current paper, tautomerism and proton transfer in HBQ is studied as a function of the substitution in the aromatic system (compounds 2–5, Scheme 1) and as a function of solvent environment. In compounds 2 and 3, the ground and excited state proton transfer is investigated as a consequence of incorporating a strong electron acceptor(s),23 while in compounds 4 and 5 the influence of competitive processes takes our attention. In the case of 4, the incorporation of an azo group creates an alternative tautomeric route (azo-quinonehydrazone, Scheme 2) to the HBQ type proton transfer. Recently we have reported24 that controlled tautomerism is possible through attachment of a proton crane (antenna) to the tautomeric backbone in some azonaphthols and Schiff bases. Compound 5 is an analogue of these systems where the competition for the tautomeric proton between the nitrogen atom from the antenna (pyrrolidine moiety) and the nitrogen from the HBQ unit is studied.
Results and discussion
Structures 1–3
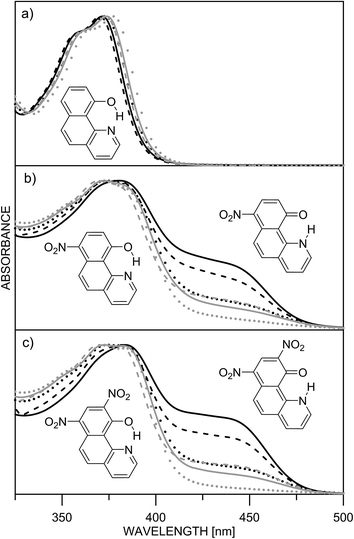
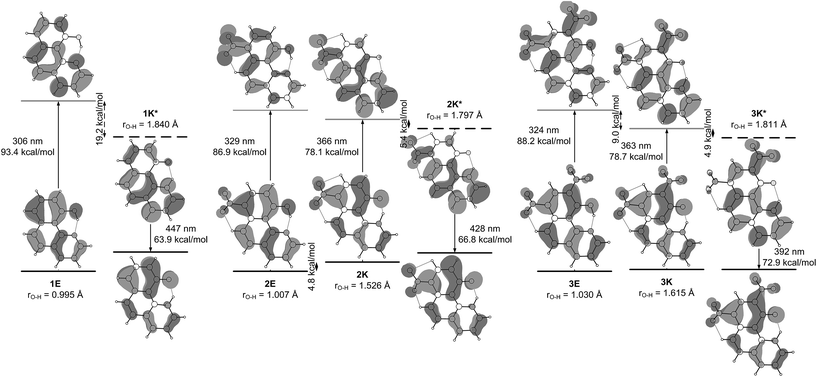
The ESIPT processes in HBQ7 can be easily recognized with spectroscopic techniques, because the tautomers behave quite differently under UV-irradiation. In the ground state, the HBQ molecule exists as enol form (E), which is stabilized by the intramolecular hydrogen bonding interactions. Upon photoexcitation, the molecule in the excited-state enol form (E*) experiences an ultrafast intramolecular proton transfer which gives rise to the excited-state keto tautomeric form (K*). Then the K* tautomer relaxes to the ground state by emission. This pathway is confirmed by the data shown in Table S1.‡ No tautomeric equilibrium is observed in compound 1, which exists only as an enol form with absorption maximum at ∼370 nm (Fig. 1a, Table S1‡). Excitation at the absorption maximum gives an emission at ∼620 nm, showing a very large Stokes shift of ∼11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1,25 which is typical for the ESIPT process.
000 cm−1,25 which is typical for the ESIPT process.
The inclusion of an electron-acceptor substituent in 2, leads to the appearance of a new absorbance band at ∼450 nm (Fig. 1b), belonging to the keto form K, whose intensity depends on the solvent. The spectral behavior of 3 (Fig. 1c) is identical to that of 2, but as seen from Table 1, the amount of the keto tautomer is slightly higher.
| Comp. | Solventsa | UV-Vis spectroscopy | Theoretical calculations M06-2X/TZVP | |
|---|---|---|---|---|
| Molar part [%] | ΔG(E→K)b [kcal mol−1] | ΔEK–Ec [kcal mol−1] | ||
| enol | ||||
| a Dielectric constants: acetonitrile – 37.5; acetone – 20.7; CH2Cl2 – 8.93; ethyl acetate – 6.02; CHCl3 – 4.81; toluene – 2.38. b Calculated using experimentally determined tautomeric constant ([K]/[E]) at room temperature. c Relative energy of the tautomeric pair taken as difference between energies of the tautomers at room temperature; positive value corresponds to more stable enol form. | ||||
| 1 | Acetonitrile | 100 | — | — |
| Acetone | 100 | — | — | |
| CH2Cl2 | 100 | — | — | |
| Ethyl acetate | 100 | — | — | |
| CHCl3 | 100 | — | — | |
| Toluene | 100 | — | — | |
| 2 | Acetonitrile | 85 | 1.03 | 4.86 |
| Acetone | 87 | 1.13 | 5.04 | |
| CH2Cl2 | 91 | 1.37 | — | |
| Ethyl acetate | 91 | 1.37 | — | |
| CHCl3 | 93 | 1.53 | — | |
| Toluene | 97 | 2.06 | — | |
| 3 | Acetonitrile | 74 | 0.62 | 0.58 |
| Acetone | 78 | 0.75 | 0.82 | |
| CH2Cl2 | 84 | 0.98 | 1.51 | |
| Ethyl acetate | 84 | 0.98 | 2.06 | |
| CHCl3 | 87 | 1.12 | 2.47 | |
| Toluene | 94 | 1.63 | 4.05 | |
The substitution in the HBQ backbone changes the fluorescence spectra as well. On Fig. 2, absorption, fluorescent emission and excitation spectra of 3 in acetonitrile are compared as an typical example for the spectral behavior of 2 and 3. Irrespective of the excitation wavelength (at absorption maxima of 3E or 3K at 385 and 446 nm, respectively), the same emission is measured, which in addition to the large Stokes shift, is a clear evidence for the occurrence of ESIPT. The excitation spectrum has a similar shape as the absorption one, but the higher proportion of the emission coming from the excited keto tautomer is evident as well. Actually this tendency in both 2/3 is clearly seen, when quantum yields (calculated upon excitation at the absorption maxima of the E or K forms) are compared in Table S1.‡ The analysis of the Stokes shifts collected in Table S1,‡ shows a decrease from 1 to the substituted 2 and 3, which will be rationalized below.
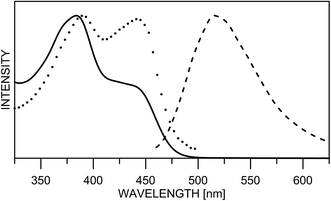 | ||
| Fig. 2 Normalized absorption (line), fluorescence emission (dashes) and excitation (dots) spectra of 3 in acetonitrile. | ||
Unfortunately, the low solubility of the studied compounds does not allow direct comparison between UV-Vis spectroscopy and NMR in the same solvents. According to the NMR results in N,N-dimethylformamide (DMF) the 7,9-dinitro derivative 3 is fully in the keto form.23 The 1H chemical shifts in DMF-d7 (H-2, Hx) of 1 (9.03, 14.80), 2 (9.15, 16.68) and 3 (9.48 and 19.87) give an estimate of 68% keto form of 2 under the assumption that HBQ is fully in the enol form and 3 exists as a keto form only. Unfortunately the interpretation of the UV-Vis spectra in DMF is not straightforward. The absorption spectra in DMF are compared with those of the remaining solvents in Fig. S1.‡ The spectra of 2 and 3 in DMF give an impression of full shift of the position of the tautomeric equilibrium towards keto tautomer. However, this impression is a result of the appearance of new bands at around 410 and 480 nm (Fig. S2‡), which belong to the deprotonated compound. Such deprotonation happens in 2 and 3 upon addition of N,N,N-triethyl amine in acetonitrile26 giving the same spectral pattern. Consequently, in the UV-Vis spectroscopy concentration range, there is an equilibrium in DMF between three components (enol and keto, and the deprotonated one), which does not allow determination of the tautomeric ratio, although according to the emission measurements and the derivative spectra (Fig. S2‡), keto and enol tautomers exist in the case of 2. The strong spectral overlapping does not allow a definite conclusion, based on derivative spectroscopy, to be made about the disappearance of the enol tautomer of 3 in DMF as well.
Two facts are clearly evident from the experimental data. Firstly, the incorporation of a second nitro group in 3 does not bring substantial stabilization of the keto tautomer as it could be expected and secondly, the keto form stabilization depends on the solvent (see also the discussion about linear solvation energy relationship below) without being a direct function of its dielectric constant.
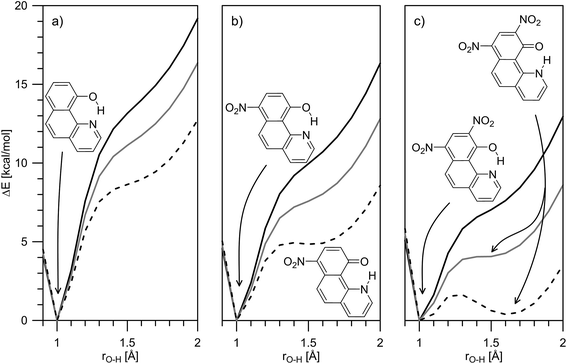
The theoretical calculations, summarized in Tables 1 and S2,‡ generally support the experimental data, showing change of the tautomerism of 2 and 3 in comparison with HBQ. In Fig. 3, the change of the ground state energies of 1–3 is shown as a function of the O–H distance and the solvent. It should be underlined that the transition of the proton from O to N atom leads to changes in the whole molecule and especially to change of the distance between them. It can be seen from Fig. S4–S6‡ that the O and N atoms get closer together at rO⋯H ∼ 1.3 Å when the proton actually is exchanged.
It is clear from Fig. 3a that in the case of 1, the keto tautomer is not present, as the experiment shows, and the proton transfer process is barrierless in the studied solvents. In 2 (Fig. 3b) no stable K tautomer is found in toluene, CH2Cl2, CHCl3 and ethyl acetate and a single-well proton transfer mechanism is at play. For 3 a keto tautomer is obtained as stable form in all the studied solvents (Fig. 3c). Considering the substitution effect, a tendency can be seen even comparing the curves in toluene – the curve becomes less sloping and in the case of 3 the energy goes to plateau in the keto form region. In acetonitrile the changes are more pronounced. According to the calculations, the 2K form exists in acetonitrile and acetone, even though there is an energy gap of around 5 kcal mol−1. Compared to 2, in 3 the amount of the K tautomer should be substantially more in all solvents, following the predicted energy gap below 1 kcal mol−1 (Table 1).
Although the experimental results and theoretical calculations qualitatively agree that the incorporation of the nitro group on 7th position in the HBQ skeleton switch the proton transfer in ground state from a single- to a double-well mechanism,27 a major disagreement can be seen comparing experimental ΔG and theoretical ΔE values in Table 1. While the keto tautomer of 2 is observed in all solvents, the theoretical calculations predict its existence only in acetone and acetonitrile with large energy gaps, which differ substantially from the experimentally determined ΔG values. The theoretical calculations predict substantial keto form stabilization in 3 in comparison with 2, as a result of the second nitro group incorporation, which is not confirmed by the experimental data.
In an attempt to rationalize these contradictions, a linear solvation energy relationship analysis28 was performed using the experimentally determined tautomeric constants (Table 1). The obtained results, removing the values in acetone as outliers, are given below:
for 2: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KT = −2.30(±0.01) + 1.16(±0.02)π* + 1.13(±0.01)α + 1.46(±0.01)β, R2 = 0.999 KT = −2.30(±0.01) + 1.16(±0.02)π* + 1.13(±0.01)α + 1.46(±0.01)β, R2 = 0.999 | (1) |
for 3: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KT = −1.97(±0.06) + 1.1(±0.1)π* + 1.10(±0.09)α + 1.42(±0.08)β, R2 = 0.992 KT = −1.97(±0.06) + 1.1(±0.1)π* + 1.10(±0.09)α + 1.42(±0.08)β, R2 = 0.992 | (2) |
Taking into account the limited number of the used solvents and the narrow range of the KT values, the fitted parameters, in spite of the good statistics, could be interpreted more as tendencies than as exact values. Nevertheless, the results clearly show structure related stabilization of the enol form (negative intercept) and solvent stabilization of the keto form (positive π*, α and β terms). The former is predicted by the theoretical calculations as well, the reduced enol stabilization from 2 to 3 is also evident (the free term becomes less negative, from −2.3 to −1.97) in line with the decreasing relative stability of the enol tautomer (comparing shapes of Fig. 3b and c).
The latter is expected as a consequence of the solvent polarity and proton donor ability of the solvent – the keto form being more polar (for dipole moments see Table S4‡) and the carbonyl group being a better proton acceptor in comparison with the enol OH group – explain the positive values of the π* and α terms respectively. Quite surprisingly, the LSER analysis shows that the keto form interacts better with proton acceptor solvents (positive β term). In general the keto N–H is a weaker proton donor compared to the enol O–H, but in this particular case the situation is not typical due to the involvement of the tautomeric proton in strong intramolecular hydrogen bonding changes. It seems that the better proton acceptor ability of the keto carbonyl group, leading to weakening of the N–H bond in the keto tautomer, is the reason for better interaction of the tautomeric proton with proton acceptor solvents and even to deprotonation as it is observed in DMF. According to the theoretical calculations, the N–H bond in 2K (1.075 Å in acetonitrile) is longer compared to the O–H bond in 2E (1.00 Å in acetonitrile), which suggests higher lability.
The LSER analysis confirms the existence of specific solute–solvent interactions which are not taken into account by the PCM solvent model and could be used as an explanation for the disagreement between the theoretical prediction of the position of the equilibrium and the experimental findings. On one side, the solvent effect is virtually the same in both 2 and 3 (almost the same solvent terms in the LSER analysis), which means that the second nitro group does not substantially influence the specific interactions. On the other hand, the theoretical description of the tautomerism in 3 using PCM model is very near to reality in almost all solvents, comparing the theoretical ΔE and experimental ΔG values. All this means that the stability of the keto tautomer in 2 is underestimated by the PCM solvent model, which could mean that the absence of the ortho nitro group facilitates the specific solute–solvent interactions. However, this contradicts the current LSER model. Obviously, at this stage we cannot explain exactly the reasons for experiment/theory disagreements. Further experimental investigations involving larger sets of solvents are needed and they must be accompanied by theoretical calculations involving explicit solvent molecules in addition to the PCM description.
It is worth mentioning that the theoretical calculations reasonably well describe the observed spectral changes in the studied compounds. Predicted absorption and emission band positions are collected in Table S2.‡ It is seen that the calculated band positions are systematically blue shifted compared to the experimental ones, but this is a typical behavior of the M06-2X/TZVP calculations as shown before.30 The tendency of red shift in the absorption maxima going from 1 to 3 is correctly predicted and as seen in Fig. S3a‡ there is very good linearity between experimental and theoretical band positions, which allows correction of the theoretical values if needed (corresponding values are given in brackets in Table S2‡). The situation with the predicted emission band positions is similar (Fig. S3b‡), which leads, as cancelation of errors, to a very good match between theory and experiment concerning the Stokes shifts.
The mechanism of ESIPT can be discussed in details when the situation in the excited state is taken into account. In Fig. 4, changes in the ground and excited state energies are presented again as a function of O–H distance in acetonitrile. The same curves, but in toluene, are given in Fig. S7–S9.‡
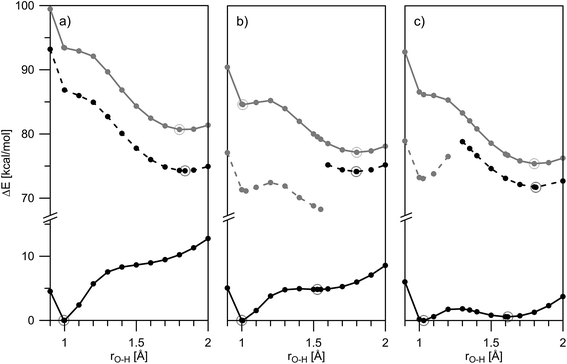 | ||
| Fig. 4 Theoretically predicted ground and excited state potential energies for proton transfer in 1 (a), 2 (b) and 3 (c) in acetonitrile presented as a function of rO–H: S0 – solid black line; S1(vertically excited) – solid grey line; S1 – black dashes; dark S1 – grey dashes. Calculated points are given with dots, corresponding stable structures are depicted with circles. The HOMO–LUMO molecular orbitals of the stable structures are shown in Fig. 5. | ||
Fig. 4a (in acetonitrile) and S7‡ (in toluene) show a typical ESIPT picture. The stable in ground state 1E form being vertically excited goes to an unstable Frank–Condon (FC) state, having then two options: relaxation to S1 state and then ESIPT to the stable 1K* (S1 channel); or ESIPT keeping ground state geometry (S1(FC) channel), followed by relaxation to 1K*. Taking into account that the rate of ESIPT in HBQ is less than 30 fs12,31 the first mechanism seems logical, but at the same time, 1 has a rigid structure, which suggests a fast relaxation as well. Of course, these two options are computationally idealistic ones; in fact, the proton transfer and structural relaxation happen simultaneously while the molecule is moving along the reaction path.13 The ESIPT is associated with a transient shortening of the O–N distance larger than in the ground state (well seen in Fig. S7‡).
Analysis of the HOMO and LUMO (Fig. 5) reveals that the HOMO is a π-orbital with almost identical electronic distribution for both the E- and K-forms. As seen, it comprises in the enol form a large electronic density projection over the oxygen atom along with bonding character along the O–H bond. The LUMO is of π* character and excitation of an electron from HOMO to LUMO in 1E leads to a localization of the π-electron density over the nitrogen atom. Actually, the ESIPT follows the process in which the nitrogen atom undergoes an enrichment of the electronic density projection simultaneously with a drastic reduction of the same over the O atom. The antibonding character along the C–O axis in 1E prevents electron delocalization involving the aromatic nucleus and thereby forbidding the reversal of the proton transfer in the excited-state.
 | ||
| Fig. 5 HOMO–LUMO molecular orbitals of the stable tautomers of 1–3 in ground and singlet excited state obtained from the theoretical calculations in acetonitrile. Taking into account that the S0–S1 transitions in the studied compounds are mainly HOMO–LUMO the relative energies of the vertical transitions from Fig. 4 are sketched. | ||
According to the calculations, the incorporation of a nitro substituent in 2 leads to a dark excited state in the enol tautomer region (grey dash line in Fig. 4b). This means that a hypothetical relaxation from S1(FC) to S1 leads back to ground state (no ESIPT to the stable K*) and, hence, no emission could be detected. Comparing the vertically excited S1(FC) curves in Fig. 4b and c (resp. S8 and S9‡) an interesting detail can be seen, namely the existence of an energy barrier in the case of 2 and a lack of one in 3. The former may lead to a higher extent of deactivation through the E* channel, which could be confirmed comparing the overall quantum yields (Table S1‡) of 0.011 for 2 and 0.019 for 3 in acetonitrile (resp. 0.031 vs. 0.068 in toluene). The efficiency of ESIPT (conversion from E* to K*) could be estimated in addition by using eqn (3) derived in:32
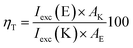 | (3) |
According to this equation, 43% of 2E* converts to 2K*, while in 3 the efficiency is 58%, confirming the general conclusions above. Experimental evidence for the additional relaxation in 2 has been reported by time dependent fluorescent spectroscopy.20
The incorporation of nitro substituent causes strengthening of the charge transfer character of the excited state proton exchange. The process involves strongly the nitro group as seen in Fig. 5. Even in the case of 3, where two nitro groups are available, the involvement of the group on 7th position is more pronounced.
Another interesting detail can be seen comparing the excited states of 1 and 2/3. As mentioned above, in the case of 1, the proton transfer is associated to larger shortening of the N–O distance comparing to ground state (Fig. S7‡). This phenomenon is not observed in 2/3, where the N–O distance shortens to the same extent as in the ground state. However, the excited state process is accompanied by a nitro group (ortho one in 3) getting perpendicular to the HBQ backbone in the region around rO–H ∼ 1.3 Å. The electron density projection over the para-NO2 in 2 and ortho-NO2 in 3 shows (Fig. 5) their involvement in the corresponding excited state keto forms.
The theoretical data about ground and excited state properties of 1–3 allow the observed spectral characteristics to be rationalized. As can be seen from Table S1‡ the addition of a second nitro group in 3 comparing to 2, does not lead to changes in the absorption and emission band positions. An inspection of Fig. 4b and c shows that although the ground and excited states are stabilized in different ways in 2 and in 3, the transition energies are approximately the same in these compounds in the same solvents,33 which leads to almost the same absorption and emission bands positions in acetonitrile. Similar conclusion can be drawn in toluene as well (Fig. S8 and S9‡). However, comparing to 1, the absorption and emission in 2 and 3 are correspondingly red and blue shifted, logically causing shorter Stokes shifts. Again an explanation could be found in Fig. 4 for acetonitrile and in Fig. S7–S9‡ for toluene: the introduction of the acceptor substituent(s) in 2 and 3 leads to stabilization of the FC state, which reduces the vertical transition energy (red absorption shift comparing to 1). In addition, the stabilization of 2K and 3K in ground state leads to blue shifts in the emission maxima. Another interesting difference between 1 and 2–3 is the lack of substantial changes in the keto emission in the former and a tendency in the latter as a function of the solvent. According to the data in Table S4‡ the dipole moments of the ground state enol and excited state keto form of 1 are relatively low, causing a corresponding state less perceptive to the solvent change. The substantially larger dipole moments of 2 and 3 (especially between ground and excited state keto forms) reasonably lead to a solvent effect.
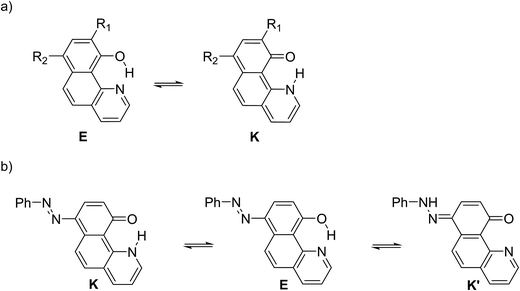
Structure 4
Compound 4 is a very interesting example for investigation, because the attachment of an azo group to the HBQ fragment, in analogy to 2, could stabilize the keto tautomer to some extent. On the other hand azo-quinonehydrazone (4E/4K′) tautomerism is possible as well. The absorption spectra in various solvents (Fig. S10‡) show an intensive band at 390 nm and a shoulder at ∼470 nm, i.e. the system behaves as a two component mixture. No measurable emission was detected, which is not surprising having in mind the photophysical behavior of azodyes with similar structure, caused by the de-activation channel to the low-lying nπ*-states of the azo nitrogen atoms and the increased flexibility around the azo group.32,34 Theoretical data are summarized in Fig. S11‡ and Scheme 3. As seen from Fig. S11,‡ a stable 4K is predicted in acetonitrile at rOH ∼ 1.5 Å. In general the situation is similar to that in 2 (Fig. 3b), but taking into account that N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N group is a moderate electron acceptor, the corresponding relative energies at rOH = 1.5 Å are higher with appr. 1 kcal mol−1. The 4K′–4E energy gap is predicted to be 21.2 kcal mol−1 in gas phase (Scheme 3), which leads to a conclusion that the quinonehydrazone tautomer is not present in solution. Consequently the absorption maximum at 470 nm is attributed to a few percent of the 4K form. It should be noted that no keto tautomer was detected in CDCl3 by NMR.23
N group is a moderate electron acceptor, the corresponding relative energies at rOH = 1.5 Å are higher with appr. 1 kcal mol−1. The 4K′–4E energy gap is predicted to be 21.2 kcal mol−1 in gas phase (Scheme 3), which leads to a conclusion that the quinonehydrazone tautomer is not present in solution. Consequently the absorption maximum at 470 nm is attributed to a few percent of the 4K form. It should be noted that no keto tautomer was detected in CDCl3 by NMR.23
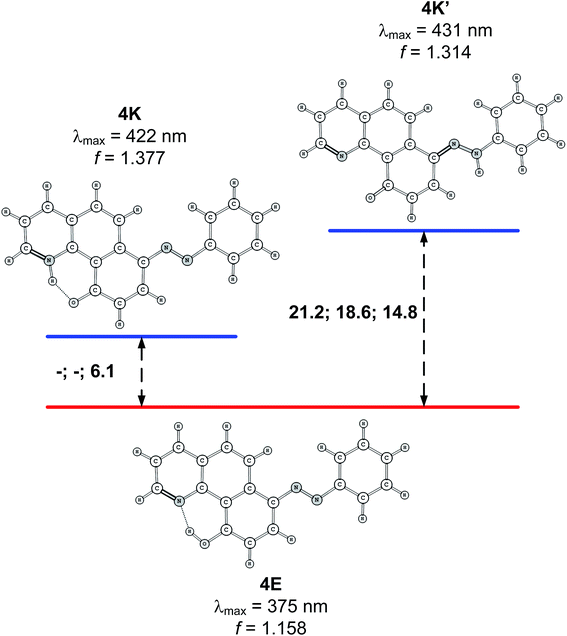 | ||
| Scheme 3 Relative stability (in kcal mol−1 units) of the tautomers of 4 in gas phase, toluene and acetonitrile. Lack of data means that the corresponding tautomer does not exist (see Fig. S11 for details‡). Predicted spectral characteristics are for acetonitrile. | ||
Having in mind that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group interacts well with metal ions and that it forms a cavity with the neighboring nitrogen atom in 4K′, attempts have been made to shift the process from 4E towards the quinonehydrazone tautomer via external stimuli. However, the addition of metal ions (Li+ and Mg2+ as perchlorates) has not caused changes in the absorption spectra in acetonitrile. Taking into account that the distance between O and N atoms in the HBQ moiety is 2.75 Å and the ionic radius of Li+ is 0.9 Å, it seems that the high relative energy of 4K′ could be a reason for preventing a complex formation. The process of protonation can be considered as a rough model of the complexation and as seen from Fig. 6, a new band at 510 nm appears, belonging to the protonated form. The protonated form (Scheme 4) has quinonehydrazone structure and could be considered as an approximation of 4K′. Actually the experimental order of the bands (4E – 390 nm, 4K – 475 nm and 4K′ – red shifted comparing to the latter) is confirmed by the order of the theoretically predicted long wavelength band positions in acetonitrile (Scheme 4).
O group interacts well with metal ions and that it forms a cavity with the neighboring nitrogen atom in 4K′, attempts have been made to shift the process from 4E towards the quinonehydrazone tautomer via external stimuli. However, the addition of metal ions (Li+ and Mg2+ as perchlorates) has not caused changes in the absorption spectra in acetonitrile. Taking into account that the distance between O and N atoms in the HBQ moiety is 2.75 Å and the ionic radius of Li+ is 0.9 Å, it seems that the high relative energy of 4K′ could be a reason for preventing a complex formation. The process of protonation can be considered as a rough model of the complexation and as seen from Fig. 6, a new band at 510 nm appears, belonging to the protonated form. The protonated form (Scheme 4) has quinonehydrazone structure and could be considered as an approximation of 4K′. Actually the experimental order of the bands (4E – 390 nm, 4K – 475 nm and 4K′ – red shifted comparing to the latter) is confirmed by the order of the theoretically predicted long wavelength band positions in acetonitrile (Scheme 4).
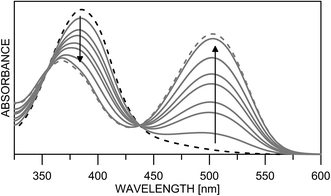 | ||
| Fig. 6 Absorption spectra of 4 in acetonitrile upon protonation from neutral (black dashes) to fully protonated (grey dashes). | ||
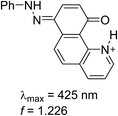 | ||
| Scheme 4 Structure and predicted long wavelength absorption band of protonated 4 according to the theoretical calculations in acetonitrile. | ||
Structure 5
Compound 5 mimics the working tautomeric switches based on 4-(phenyldiazenyl)naphthalen-1-ol and 4-((phenylimino)methyl)naphthalen-1-ol (6 and 7, Scheme 5).24 However, two differences must be underlined: there are no competitive hydrogen bonds in 6 and 7; their tautomeric backbones (i.e. without antenna) exist as tautomeric mixtures a priori and the incorporation of the antenna leads to shift of the equilibrium in one or another direction depending on the external stimuli (protonation or complexation35); the equilibrium in 1 is strongly shifted towards the enol form, where the tautomeric proton is already involved in strong intramolecular hydrogen bonding, limiting the action of the antenna in 5. The latter is supported by the data collected in Scheme 6, where it is seen that forms 5E and 5E′′ have approximately the same stability, i.e. the sidearm does not interact with the tautomeric OH group. The observed absorption and emission spectra are practically identical with those of 1 (Table S1†). The experimental data suggest that the mechanisms of ESIPT in 1 and 5 are identical, but it has to be mentioned that the availability of a flexible antenna in the latter leads in some of the solvents to lower quantum yield.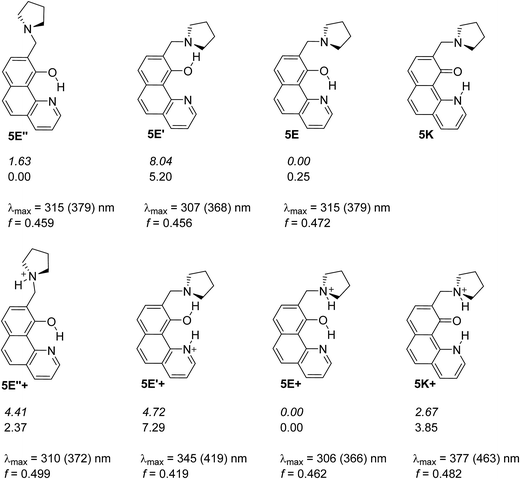 | ||
| Scheme 6 Possible structures of 5 in neutral (above) and in protonated (below) state. The relative energies in gas phase (italic) and in acetonitrile are given in kcal mol−1 units. The lack of relative energy indicates a structure which does not exist according to the theoretical calculations. Absorption characteristics are calculated for acetonitrile and then corrected (in brackets) according to the linear plot from Fig. S3a.‡ | ||
The free rotation of the antenna is confirmed by the performed NOESY experiments revealing that H-12 atoms (see Experimental part for the numbering) do not interact with H-8 (i.e. the distance through space between them is more than 3 Å). The observed interaction between H-12 and OH-group is also quite weak (see Fig. S12‡), and the existence of hydrogen bonding between OH-group and N-atom from pyrrolidine ring cannot be confirmed in diluted CDCl3 solution (ca. 0.01 M).
Being clear that the process is already switched to the enol tautomer with or without sidearm, it is interesting to know if protonation could shift the process to the keto form as it happens in 6/7. Absorption spectra of 5 upon protonation in acetonitrile are compared in Fig. 7 with those of 1. It is clearly seen that the initial protonation leads to appearance of a new, red shifted absorption maximum (∼390 nm) in the case of compound 1 (structure 1+, Scheme 7) and causes a slight hypsochromic effect in the case of 5. Obviously the addition of acid protonates the nitrogen atom from the sidearm giving structures 5E+ and to some extent 5E′′+ (see Scheme 6), which are blue shifted with respect to the neutral 5E/5E′′. In this case the chromophore system is only slightly affected, which does not lead to substantial changes in the absorption spectrum. Further addition of acid could protonate the HBQ backbone (structure 5E′′++, Scheme 7), which spectrum is red shifted and actually a new band ∼370 nm is observed in a very acidic medium. The process of protonation does not lead to a keto form 5K+, which should be observed above 450 nm (Scheme 6) like the keto tautomer of 2 and 3. As a final result no switching is achieved from 5E to 5K in acidic media, which can be attributed to the fact that the sidearm does not take part in the tautomeric process, located exclusively in the O–N moiety of the HBQ backbone, and therefore cannot influence it.
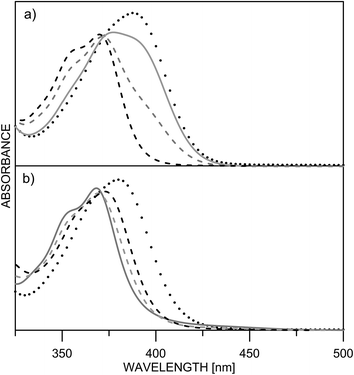 | ||
| Fig. 7 Absorption spectra of 1 (a) and 5 (b) in acetonitrile upon protonation: pH = 5.7 (black dashes) 4.3 (grey dashes) 4.0 (grey solid line) 0.3 (dots). | ||
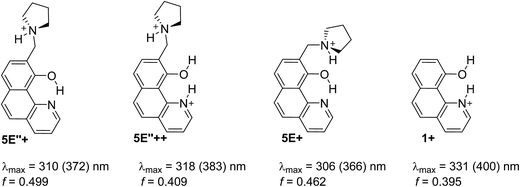 | ||
| Scheme 7 Possible structures obtained upon protonation of 1 and 5 in acetonitrile. Absorption characteristics are calculated for acetonitrile and then corrected (in brackets) according to the linear plot from Fig. S3a.‡ | ||
Conclusions
While 10-hydroxybenzo[h]quinoline (1) exists as the enol tautomer in the ground and shows typical ESIPT behavior in the excited state, incorporation of a nitro group on 7th position (2) leads to appearance of a keto tautomer in a number of solvents. Actually this structural change leads to transition from barrierless PT in the ground state to double-well energetics. Substantial changes are observed in excited state as well – the S1 state of the enol form becomes a “dark” state according to the theoretical calculations. Introduction of one more nitro group (on 9th position, compound 3) slightly increases the proportion of the keto tautomer and does not substantially change the photophysical behavior. There is a general trend to decrease the Stokes shifts upon substation which can be attributed mainly to the relative stabilization of the keto tautomer in the ground state. Attempts to achieve controlled shift in the position of the tautomeric equilibrium with incorporation of an azo group on 7th position (4) or a flexible sidearm, e.g. containing a pyrrolidine ring on 9th position (5) failed due to the fact that proton transfer occurs exclusively in the HBQ backbone.Experimental part
Synthesis
Reagents and solvents were purchased from Sigma-Aldrich, Acros and Alfa-Aesar, and used without further purification. HBQ (1) was purchased from TCI. Fluka silica gel/TLC-cards 60778 with fluorescence indicator 254 nm were used for TLC chromatography. Merck silica gel 60 (0.040–0.063 mm) and basic alumina (Brockmann activity, 0.05–0.15 mm) were used for flash chromatography purification of the products. Melting points were determined on a Gallenkamp apparatus and are uncorrected. The NMR spectra of compounds 2–4 were recorded on a Varian Inova 600 or a Varian Mercury 300 NMR spectrometer in either CDCl3 or DMF-d7, using tetramethylsilane (TMS) as an internal standard. Mass spectra of compounds 2–4 were recorded on a LCQ-Deca ion trap instrument from Thermo-Finnigan, equipped with an atmospheric pressure chemical ionization interface (APCI) running in both negative and positive mode using the infusion technique. The NMR spectra of compound 5 were recorded on a Bruker Avance II+ 600 (600.13 MHz for 1H and 150.92 MHz for 13C NMR). Chemical shifts (δ) are expressed in ppm relative to the internal standard tetramethylsilane. 13C of compound 5 was referenced to the solvent peak, and signal assignments were confirmed by applying 2D NMR techniques (COSY, HSQC, HMBC and NOESY). The mass spectra of 5 were recorded on a Thermo Scientific High Resolution Magnetic Sector MS DFS.The details about the synthesis of 7-nitro-10-hydroxybenzo[h]quinoline (2), 7,9-dinitro-10-hydroxybenzo[h]quinoline (3) and 7-(2-phenyldiazenyl)-10-hydroxybenzo[h]quinoline (4)23 are provided in the ESI.‡
9-Pyrrolidine-10-hydroxybenzo[h]quinoline (5)
The synthesis of the new compound 5 was accomplished in acidic media according to a published method.36 Briefly, a mixture 10-hydroxybenzo[h]quinolone 1 (1.0 g, 5.12 mmol), paraformaldehyde (0.169 g, 5.64 mmol) and pyrrolidine (0.47 ml, 5.64 mmol) in acetic acid was refluxed for 4 h, and then stirred for 24 h at r.t. The solvent was evaporated and the residue dissolved in dichloromethane and washed with aq. ammonia and water. The organic phase was dried over anhydrous MgSO4 and the solvent evaporated under reduced pressure, and the residue was dissolved in MTBE and filtered through 10 g basic Al2O3. The solvent was evaporated and the crude product purified by column chromatography (40 g silica gel; phase – (a) DCM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MTBE = 2
MTBE = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (b) DCM
1, (b) DCM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MTBE
MTBE![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aq. NH3 = 100
aq. NH3 = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to give a viscous yellow oil (0.38 g, 27% yield). ESI-MS m/z 280 (98, M + 1), 208 (100, M-pyrrolidine). HRMS (EI): calcd for C18H18N2O (M+) 278.14191, found 278.14110, 0.96 ppm error. 1H NMR (CDCl3, 600.13 MHz, Fig. S13‡) δ 15.37 (s, 1H, OH), 8.78 (dd, 1H, H-2, J = 4.6, 1.7 Hz), 8.22 (dd, 1H, H-4, J = 8.0, 1.7 Hz), 7.77 (d, 1H, H-5, J = 8.8 Hz), 7.73 (d, 1H, H-8, J = 8.0 Hz), 7.57 (d, 1H, 6-H, J = 8.8 Hz), 7.52 (dd, 1H, H-3, J = 8.0, 4.6 Hz), 7.39 (d, 1H, 8-H, J = 8.0 Hz), 3.98 (s, 2H, H-11), 2.67 (m, 4H, H-12), 1.81 (m, 4H, H-13). 13C NMR (CDCl3, 150.92 MHz, Fig. S14‡): δ = 157.17 (C-10), 148.42 (C-10b), 144.59 (C-2), 136.10 (C-4), 134.00 (C-6a), 131.52 (C-8), 129.10 (C-5), 126.32 (C-4a), 124.06 (C-6), 123.84 (C-9), 120.61 (C-3), 117.30 (C-7), 115.44 (C-10a), 54.33 (C-12), 54.01 (C-11), 23.49 (C-13). Anal. calcd for C18H18N2O (278.36): C, 77.67; H, 6.52; N, 10.06. Found: C, 77.73; H, 6.56; N, 10.01% (Scheme 8).
1) to give a viscous yellow oil (0.38 g, 27% yield). ESI-MS m/z 280 (98, M + 1), 208 (100, M-pyrrolidine). HRMS (EI): calcd for C18H18N2O (M+) 278.14191, found 278.14110, 0.96 ppm error. 1H NMR (CDCl3, 600.13 MHz, Fig. S13‡) δ 15.37 (s, 1H, OH), 8.78 (dd, 1H, H-2, J = 4.6, 1.7 Hz), 8.22 (dd, 1H, H-4, J = 8.0, 1.7 Hz), 7.77 (d, 1H, H-5, J = 8.8 Hz), 7.73 (d, 1H, H-8, J = 8.0 Hz), 7.57 (d, 1H, 6-H, J = 8.8 Hz), 7.52 (dd, 1H, H-3, J = 8.0, 4.6 Hz), 7.39 (d, 1H, 8-H, J = 8.0 Hz), 3.98 (s, 2H, H-11), 2.67 (m, 4H, H-12), 1.81 (m, 4H, H-13). 13C NMR (CDCl3, 150.92 MHz, Fig. S14‡): δ = 157.17 (C-10), 148.42 (C-10b), 144.59 (C-2), 136.10 (C-4), 134.00 (C-6a), 131.52 (C-8), 129.10 (C-5), 126.32 (C-4a), 124.06 (C-6), 123.84 (C-9), 120.61 (C-3), 117.30 (C-7), 115.44 (C-10a), 54.33 (C-12), 54.01 (C-11), 23.49 (C-13). Anal. calcd for C18H18N2O (278.36): C, 77.67; H, 6.52; N, 10.06. Found: C, 77.73; H, 6.56; N, 10.01% (Scheme 8).
Spectral measurements
Spectral measurements were performed on a Jasco V-570 UV-Vis-NIR spectrophotometer, equipped with a thermostatic cell holder (using Huber MPC-K6 thermostat with precision 1 °C) and Jasco FP-6600 spectrofluorimeter in spectral grade solvents at 25 °C. Protonation was made with 96% sulfuric acid. Quantum yields were calculated by comparison of a solution of quinine in 1 N H2SO4.The derivative spectra were calculated using the “step-by-step filter” as previously described.37 The absorption spectra of 2 and 3 in the used solvents were analyzed by a quantitative procedure based on resolution of overlapping bands, which yields tautomeric molar fractions in each solution and the individual spectra of the single tautomers.38,39
Quantum-chemical calculations
Quantum-chemical calculations were performed using the Gaussian 09 D.01 program suite.40 The M06-2X functional41 was used with TZVP basis set.42 This fitted hybrid meta-GGA functional with 54% HF exchange is specially developed to describe main-group thermochemistry and non-covalent interactions, showing very good results in prediction of the position of the tautomeric equilibrium in azo naphthols possessing intramolecular hydrogen bond.43 All structures were optimized in ground state without restrictions, using tight optimization criteria and ultrafine grid in the computation of two-electron integrals and their derivatives. TD-DFT method was used for excited state optimizations conditions again without restrictions using normal optimization criteria and ultrafine grid in the computation of two-electron integrals and their derivatives. The true minima were verified by performing frequency calculations in the corresponding environment. Solvent effects are described using the Polarizable Continuum Model (the integral equation formalism variant, IEFPCM, as implemented in Gaussian 09).44The proton transfer processes were modeled by gradually changing the O–H distance (rO–H) in steps of 0.1 Å and optimizing the rest of the molecule at each step. For the ground state tight optimization criteria were used, while normal optimization ones were applied in excited state.
The vertical excitation energies were calculated using the TD-DFT formalism. TD-DFT calculations were carried out at the same functional and basis set, which is in accordance with conclusions about the effect of the basis set size and the reliability of the spectral predictions.30,45 The emission spectra of the compounds were predicted following the procedure as implemented in Gaussian 09 D.01.40
Acknowledgements
The financial support from the Bulgarian National Science Fund (access to MADARA computer cluster by project RNF01/0110) and the Swiss National Science Foundation (SupraChem@Balkans.eu and SupraMedChem@Balkans.Net Institutional partnership projects under SCOPES Program) is gratefully acknowledged. S.H. is indebted to the European Social Fund (BG051PO001-3.3.07-0002 Internships for university students project) for the internship at Bulgarian Academy of Sciences. We also thank Prof. Stefan Lochbrunner (University of Rostock) for the helpful discussion concerning the ESIPT in the investigated compounds.References
- Hydrogen-Transfer Reactions, ed. R. L. Schowen, J. P. Klinman, J. T. Hynes and H. H. Limbach, Wiley-VCH, Weinheim, 2007 Search PubMed.
- Tautomerism: Methods and Theories, ed. L. Antonov, Wiley-VCH, Weinheim, 2013 Search PubMed.
- (a) J. E. Kwon and S. Y. Park, Adv. Mater., 2011, 23, 3615–3642 CrossRef CAS PubMed; (b) S. M. Ormson and R. G. Brown, Prog. React. Kinet., 1994, 19, 45–91 CAS; (c) D. le Gourrierec, S. M. Ormson and R. G. Brown, Prog. React. Kinet., 1994, 19, 211–275 CAS.
- (a) J. Jankowska, M. F. Rode, J. Sadlej and A. L. Sobolewski, ChemPhysChem, 2012, 13, 4287–4294 CrossRef CAS PubMed , 2014, 15, 1643–1652; (b) A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 1999, 1, 3065–3072 RSC; (c) M. F. Rode and A. Sobolewski, J. Phys. Chem. A, 2010, 114, 11879–11889 CrossRef CAS PubMed; (d) M. J. Paterson, M. A. Robb, L. Blancafort and A. D. DeBellis, J. Phys. Chem. A, 2005, 109, 7527–7537 CrossRef CAS PubMed; (e) M. Boggio-Pasqua, M. J. Bearpark, F. Ogliaro and M. A. Robb, J. Am. Chem. Soc., 2006, 128, 10533–10540 CrossRef CAS PubMed; (f) W.-E. Wu, J. Phys. Org. Chem., 2015, 28, 596–601 CrossRef CAS; (g) D. Jacquemin, E. Perpete, G. E. Scuseria, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2008, 4, 123–135 CrossRef CAS PubMed; (h) M. Savarese, E. Bremond, L. Antonov, I. Giofini and C. Adamo, ChemPhysChem DOI:10.1002/cphc.201500589.
- (a) C. C. Hsieh, P. T. Chou, C. W. Shih, W. T. Chuang, M. W. Chung, J. Lee and T. Joo, J. Am. Chem. Soc., 2011, 133, 2932–2943 CrossRef CAS PubMed; (b) C. C. Hsieh, C. M. Jiang and P. T. Chou, Acc. Chem. Res., 2010, 43, 1364–1374 CrossRef CAS PubMed; (c) C. C. Lin, C. L. Chen, M. W. Chung, Y. J. Chen and P. T. Chou, J. Phys. Chem. A, 2010, 114, 10412–10420 CrossRef CAS PubMed; (d) C. Tanner, C. Manca and S. Leutwyler, Science, 2003, 302, 1736–1739 CrossRef CAS PubMed; (e) M. H. V. Huynh and T. Meyer, Jpn. Chem. Rev., 2007, 107, 5004–5064 CrossRef CAS PubMed; (f) C. Fang, R. R. Frontiera, R. Tran and R. A. Mathies, Nature, 2009, 462, 200–204 CrossRef CAS PubMed.
- K. Y. Chen, C. C. Hsieh, Y. M. Cheng, C. H. Lai and P. T. Chou, Chem. Commun., 2006, 4395–4397 RSC.
- (a) D. Kuila, G. Kvakovszky, M. A. Murphy, R. Vicari, M. H. Rood, K. A. Fritch and J. R. Fritch, Chem. Mater., 1999, 11, 109–116 CrossRef CAS; (b) J. Catalan, J. C. del Valle, R. M. Clararmunt, D. Sanz and J. Dotor, J. Lumin., 1996, 68, 165–170 CrossRef CAS; (c) Yu. P. Tsentalovich, O. A. Snytnikova, M. D. E. Forbes, E. I. S. V. Chernyak and S. V. Morozov, Exp. Eye Res., 2006, 83, 1439–1445 CrossRef CAS PubMed.
- (a) M. Irie, T. Fukaminato, K. Matsuda and S. Kobataka, Chem. Rev., 2014, 114, 12174–12277 CrossRef CAS PubMed; (b) J. Wu, W. Liu, J. Ge, H. Zhang and P. Wang, Chem. Soc. Rev., 2011, 40, 3483–3495 RSC; (c) D. Nedeltcheva, Controlled tautomerism: is it possible?, in tautomerism: concepts and applications in science and technology, ed. L. Antonov, Wiley-VCH, Weinheim, 2016 Search PubMed.
- (a) S. Kim, J. Seo, H. K. Jung, J. J. Kim and S. Y. Park, Adv. Mater., 2005, 17, 2077–2082 CrossRef CAS; (b) S. H. Kim, S. Park, J. E. Kwon and S. Y. Park, Adv. Funct. Mater., 2011, 21, 644–651 CrossRef CAS; (c) S. Park, J. E. Kwon, S. H. Kim, J. Seo, K. Chung, S. Y. Park, D. J. Jang, B. M. Medina, J. Gierschner and S. Y. Park, J. Am. Chem. Soc., 2009, 131, 14043–14049 CrossRef CAS PubMed; (d) W. H. Sun, S. Li, R. Hu, Y. Qian, S. Wang and G. Yang, J. Phys. Chem. A, 2009, 113, 5888–5895 CrossRef CAS PubMed; (e) H. C. Peng, C. C. Kang, M. R. Liang, C. Y. Chen, A. Demchenko, C. T. Chen and P. T. Chou, ACS Appl. Mater. Interfaces, 2011, 3, 1713–1720 CrossRef CAS PubMed.
- (a) J. Lee and T. Joo, Bull. Korean Chem. Soc., 2014, 35, 881–885 CrossRef CAS; (b) P. T. Chou, Y. C. Chen, W. S. Yu, Y. H. Chou, C. Y. Wei and Y. M. Cheng, J. Phys. Chem. A, 2001, 105, 1731–1740 CrossRef CAS.
- J. Piechowska and D. T. Gryko, J. Org. Chem., 2011, 76, 10220–10228 CrossRef CAS PubMed.
- (a) M. L. Martinez, W. C. Cooper and P. T. Chou, Chem. Phys. Lett., 1992, 193, 151–154 CrossRef CAS; (b) M. Higashi and S. Saito, J. Phys. Chem. Lett., 2011, 2, 2366–2371 CrossRef CAS.
- C. Schriever, M. Barbatti, K. Stock, A. J. A. Aquino, D. Tunega, S. Lochbrunner, E. Riedle, R. de Vivie-Riedle and H. Lischka, Chem. Phys., 2008, 347, 446–461 CrossRef CAS.
- (a) E. L. Roberts, P. T. Chou, T. A. Alexander, R. A. Agbaria and I. M. Warner, J. Phys. Chem., 1995, 99, 5431–5437 CrossRef CAS; (b) P. T. Chou, G. R. Wu, Y. I. Liu, W. S. Yu and C. S. Chiou, J. Phys. Chem. A, 2002, 106, 5967–5971 CrossRef CAS; (c) J. C. del Valle and J. Catalan, Chem. Phys., 2001, 270, 1–12 CrossRef.
- (a) T. Mutai, H. Sawatani, T. Shida, H. Shono and K. Araki, J. Org. Chem., 2013, 78, 2842–2850 CrossRef PubMed; (b) P. G. Yi and Y. H. Liang, Chem. Phys., 2006, 322, 382–385 CrossRef CAS; (c) M. W. Chung, T. Y. Lin, C. C. Hsieh, K. C. Tang, H. Fu, P. T. Chou, S. H. Yang and Y. Chi, J. Phys. Chem. A, 2010, 114, 7886–7891 CrossRef CAS PubMed.
- (a) M. Ghedini, M. La Deda, I. Aiello and A. Grisolia, Synth. Met., 2003, 138, 189–192 CrossRef CAS; (b) V. Kumar, V. K. Rai, R. Srivastava and M. N. Kamalasanan, Synth. Met., 2009, 159, 177–185 CrossRef; (c) H. P. Shi, L. Xu, X. F. Zhang, L. Q. Jiao, Y. Cheng, J. Y. He, J. X. Yao, L. Fang and C. Dong, J. Mol. Struct.: THEOCHEM, 2010, 950, 53–58 CrossRef CAS.
- K. Y. Chen, T. Hsing-Yang, L. Wei-Chi, C. Hou-Hsein, W. Yu-Ching and C. Chih-Chieh, J. Lumin., 2014, 154, 168–175 CrossRef CAS.
- B. K. Paul and N. Guchhait, J. Lumin., 2011, 131, 1918–1926 CrossRef CAS.
- I. Deperasinska, D. T. Gryko, E. Karpiuk, B. Kozankiewicz, A. Makarewicz and J. Piechowska, J. Phys. Chem. A, 2012, 116, 12049–12055 CrossRef CAS PubMed.
- J. Piechowska, K. Huttenen, Z. Wrobel, H. Lemmetyinen, N. V. Tkachenko and D. T. Gryko, J. Phys. Chem. A, 2012, 116, 9614–9620 CrossRef CAS PubMed.
- A. J. Stasyuk, M. K. Cyrański, D. T. Gryko and M. Solà, J. Chem. Theory Comput., 2015, 11, 1046–1054 CrossRef CAS PubMed.
- G. A. Parada, T. F. Marke, S. D. Glover, L. Hammarstrom, S. Ott and B. Zietz, Chem.–Eur. J., 2015, 21, 6362–6366 CrossRef CAS PubMed.
- P. E. Hansen, F. S. Kamounah and D. T. Gryko, Molecules, 2013, 18, 4544–4560 CrossRef CAS PubMed.
- (a) L. Antonov, V. Deneva, S. Simeonov, V. Kurteva, D. Nedeltcheva and J. Wirz, Angew. Chem., Int. Ed., 2009, 48, 7875–7878 CrossRef CAS PubMed; (b) V. Deneva, Y. Manolova, L. Lubenov, V. Kurteva, F. S. Kamounah, R. Nikolova, B. Shivachev and L. Antonov, J. Mol. Struct., 2013, 1036, 267–273 CrossRef CAS.
- K. Y. Chen, C. C. Hsieh, Y. M. Cheng, C. H. Lai and P. T. Chou, Chem. Commun., 2006, 42, 4395–4397 RSC.
- The same deprotonation is observed in the other solvents listed in Table 1, but in decreasing extent going from acetonitrile to toluene.
- Although there are data for substitution with CHO group on 7th position in HBQ, no interpretation is available in respect of the ground state tautomerism: K. Y. Chen, T. Hsing-Yang, L. Wei-Chi, C. Hou-Hsein, W. Yu-Ching and C. Chih-Chieh, J. Lumin., 2014, 154, 168–175 CrossRef CAS.
- Tautomerism: Methods and Theories, ed. L. Antonov, Wiley-WCH, Weinheim, 2013, ch. 11 Search PubMed.
- (a) M. J. Kamlet, J. M. L. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877–2887 CrossRef CAS; (b) M. H. Abraham, P. L. Grellier, J. L. M. Abboud, R. M. Doherty and R. W. Taft, Can. J. Chem., 1988, 66, 2673–2686 CrossRef CAS.
- (a) A. D. Laurent, C. Adamo and D. Jacquemin, Phys. Chem. Chem. Phys., 2014, 16, 14334–14356 RSC; (b) D. Jacquemin, E. A. Perpete, I. Ciofini, C. Adamo, R. Valero, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2071–2085 CrossRef CAS PubMed; (c) L. Antonov, V. Deneva, S. Simeonov, V. Kurteva, A. Crochet, K. M. Fromm, B. Shivachev, R. Nikolova, M. Savarese and C. Adamo, ChemPhysChem, 2015, 16, 649–657 CrossRef CAS PubMed; (d) S. Kawauchi, L. Antonov and Y. Okuno, Bulg. Chem. Commun., 2014, 46A, 228–237 Search PubMed.
- J. Lee, C. H. Kim and T. Joo, J. Phys. Chem. A, 2013, 117, 1400–1405 CrossRef CAS PubMed.
- H. Joshi, C. Gooijer, G. van der Zwan and L. Antonov, J. Photochem. Photobiol., A, 2002, 152, 83–191 CrossRef.
- As can be seen from Fig. 4, the relative energies of both 2 and 3 are in the range 87 and 88 kcal mol−1 for the S0–S1(FC) transition of the enol form and 78 and 79 kcal mol−1 for the keto form, and 67–73 kcal mol−1 for the S1–S0 transition of the K* form in acetonitrile.
- R. M. Christie, Fluorescent Dyes, in Handbook of Textile and Industrial Dyeing, vol. 1, ed. M. Clark, Woodhead Publishing, Cambridge, 2011, ch. 17 Search PubMed.
- L. Antonov, V. Kurteva, S. Simeonov, V. Deneva, A. Crochet and K. M. Fromm, Tetrahedron, 2010, 66, 4292–4297 CrossRef CAS.
- N. A. Negm, S. M. I. Morsy and M. M. Said, Bioorg. Med. Chem., 2005, 13, 5921–5926 CrossRef CAS PubMed.
- (a) L. Antonov, Trends Anal. Chem., 1997, 16, 536–543 CrossRef CAS; (b) V. Petrov, L. Antonov, H. Ehara and N. Harada, Comput. Chem., 2000, 24, 561–569 CrossRef CAS PubMed.
- Tautomerism: Methods and Theories, ed. L. Antonov, Wiley-WCH, Weinheim, 2013, ch. 2 Search PubMed.
- (a) L. Antonov and D. Nedeltcheva, Chem. Soc. Rev., 2000, 29, 217–227 RSC; (b) L. Antonov and V. Pertov, Anal. Bioanal. Chem., 2002, 374, 1312–1317 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- (a) Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS; (b) Y. Zhao and D. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Kawauchi and L. Antonov, J. Phys. Org. Chem., 2013, 26, 643–652 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- (a) C. Adamo and D. Jacquemin, Chem. Soc. Rev., 2013, 42, 845–856 RSC; (b) R. Improta in Computational Strategies for Spectroscopy, ed. V. Barone, Wiley-VCH, Weinheim, 2012 Search PubMed; (c) D. Jacquemin, B. Mennucci and C. Adamo, Phys. Chem. Chem. Phys., 2011, 13, 16987–16998 RSC.
Footnotes |
| † This paper is dedicated to Prof. Nikolai Tyutyulkov (1927–2015), founder of quantum chemistry in Bulgaria, memorable teacher and a good person. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra20057a |
| This journal is © The Royal Society of Chemistry 2015 |