View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C5RA19970K (Paper) RSC Adv., 2015, 5, 106141-106150

Probing the structural and electronic properties of doped gallium oxide and sulfide, M(GaX2)2 where M = alkali or coinage metal; X = O, S†

N. Seeburruna, I. A. Alswaidanb, H.-K. Funbc, E. F. Archibongd and P. Ramasami*a
aComputational Chemistry Group, Department of Chemistry, Faculty of Science, University of Mauritius, Réduit ​80837, Mauritius. E-mail: p.ramasami@uom.ac.mu; Fax: +230 4656928; Tel: +230 4657507
bDepartment of Pharmaceutical Chemistry, College of Pharmacy, King Saud University, P.O. Box 2457, Riyadh 11451, Saudi Arabia
cX-ray Crystallography Unit, School of Physics, Universiti Sains Malaysia, 11800, Penang, Malaysia
dDepartment of Chemistry and Biochemsistry, University of Namibia, Namibia

Received 27th September 2015 , Accepted 2nd December 2015

First published on 3rd December 2015

Abstract

A theoretical study on the equilibrium geometries, vibrational frequencies and electronic features of a series of doped gallium oxide and sulfide clusters, M(GaX2)2 (M = alkali or coinage metal; X = O or S), was conducted. The ground and low-lying excited states of these clusters were studied using DFT, MP2 and single point CCSD(T) levels of theory, in conjunction with 6-311+G(2df) and Stuttgart quasi-relativistic pseudo-potential (SDD) basis sets. In most cases, the substitution of an alkali or coinage metal atom in the gallium oxide and sulfide clusters does not drastically affect the structural characteristics. The vertical electron detachment energies (VEDEs) of gallium oxide and sulfide doped with alkali metals range from 2.88 [CCSD(T)//B3LYP] to 4.51 (B3P86) eV while with the coinage metals, the values vary from 3.36 [CCSD(T)//MP2] to 6.92 (MP2) eV. The VEDEs of coinage-gallium sulfide clusters namely Cu(GaS2)2, Ag(GaS2)2 and Au(GaS2)2 are higher than that of GaS2. This feature is observed as the extra electron of the anion is localized mainly around the GaS2 moiety. Furthermore, anions with high VEDEs interacted with a positive counter ion to form salts. The fragmentation energies indicate that the studied clusters are stable.

1. Introduction

Superhalogens have received substantial attention owing to their high electron affinities. Gutsev and Boldyrev proposed the general formula of a conventional superhalogen as MX(n+1)/m where M is a main group or transition metal atom with valency n and X is an electronegative atom with valency m.1,2 Such species have electron affinities1 above that of chlorine (3.62 eV) atom.3 Superhalogens have immense potential in the field of synthesis of unusual organic compounds (e.g. Xe+[PtF6]−).4 Willis et al.5 showed that hierarchical structures called “hyperhalogens” can be made by replacing halogen atoms in a traditional superhalogen with other superhalogens. Interestingly, the hyperhalogens should have electron affinities that even surpass their constituent superhalogen building blocks5 and therefore can serve as ingredients in the synthesis of a new species known as ‘hypersalt’.6

Extensive efforts have been devoted over the past few years to the superhalogens.1,2,4,7–10 Initially, a superhalogen consisted of a core metal atom surrounded by halogen atoms1,2 but, it was found that clusters with no halogens or metal atoms or both could exhibit superhalogen properties.7–12 For example, boron dioxide (BO2) is a superhalogen even though it has a non-metal center surrounded by oxygen atoms.7 Aluminium and gallium dioxide (AlO2 and GaO2) are superhalogens as their electron affinities exceed that of chlorine atom.8,9 Turning to the sulfur congener, BS210 and GaS2[thin space (1/6-em)]11 can act as superhalogens. The dimers M2O4 (M = B, Al and Ga)8,9 can also be classified as superhalogens owing to their high electron affinities while B2S4 does not qualify to be a superhalogen.10 Recently, Kandalam and co-workers12 illustrated the ability of (BO2)2 and subsequent higher oligomers (BO2)n (n = 3, 4) to retain their superhalogen characteristics. The interaction between Au atoms and BO2 moieties13 has been a driving force for the search of new hyperhalogens. The electron affinity of Au(BO2)2 is higher than that of BO2 superhalogen and it is termed as a hyperhalogen.13 A series of hyperhalogen species were studied experimentally and theoretically on simple metals (Zn14 and Al15) and transition metal atoms containing boron oxide (Au,13,16,17 Cu,18 Ag,19,20 Mn and Fe21). Subsequent experiments were extended to Al(BH4)n, Al(BF4)n (n = 1–4),22 Na[Na(BF4)2]2, Li[Li(BF4)2]2[thin space (1/6-em)]23 and MAu4 (M = Al and Ga) complexes24 in order to confirm the hyperhalogen concept. Akin to BO2,7 BS210 is a potential hyperhalogen because the electron affinities of Au(BS2)2, Li(BS2)2 and K(BS2)2 surpass that of their building blocks BS2.

In view of the above, the substitution of an atom by another can induce electronic properties. Fueled by these interesting results and an urge to see if significant differences in the properties are noted on going from boron to gallium and oxygen to sulfur, the objectives of this investigation were: (i) to study the equilibrium structures of dimeric GaO2 and GaS2 doped with alkali (Li, Na and K) and coinage (Cu, Ag and Au) metals (ii) to provide a reliable theoretical prediction of the relative stabilities, harmonic vibrational frequencies and energetic features (iii) to compare the ground state geometries with analogous boron and aluminium structures and finally (iv) to determine whether the studied clusters possess electron affinities higher than those of the building blocks.

2. Computational details

Electronic structure computations of neutral and negatively charged M(GaX2)2 [M is an alkali metal (Li, Na and K) or a coinage metal (Cu, Ag and Au) and X is O or S] were performed using Gaussian 09[thin space (1/6-em)]25 program package by means of the resources provided by GridChem Science Gateway.26–28 Initial configurations considered for geometry optimizations were taken from previous investigations on valence isoelectronic boron oxide7 and sulfide.10 New initial structures with superhalogen moieties bound to the metal atom were also considered to determine the ground state geometries. The tight convergence criterion was applied for all the computations. The 6-311+G(2df) one-particle basis set was employed for Li, Na, K, Ga, O and S9,11 atoms and the Stuttgart quasi-relativistic pseudo-potential (SDD) basis set was used for Cu, Ag and Au atoms.29–31 The density functional theory (DFT) with the B3P86, B3PW91 and B3LYP functionals32–37 and the MP2 38,39 method were employed. To calculate the electronic properties of the ground state geometries, single point computations at the CCSD(T) level40 were performed by using B3LYP and MP2 optimized structures. The adiabatic electron affinity (AEA), adiabatic electron detachment energy (AEDE) and vertical electron detachment energy (VEDE) were calculated as follows:

AEA = E (optimized neutral at ground state) − E (optimized anion at ground state);

AEDE = E (optimized corresponding neutral) − E (optimized anion);

VEDE = E (neutral at optimized anion geometry) − E (optimized anion).

Furthermore, the harmonic vibrational frequencies of the optimized geometries were also analyzed to verify the nature of the stationary points. Natural bond orbital (NBO) analysis41,42 was performed theoretically to provide an insight into the bonding nature of the studied species. The HOMO–LUMO gaps of the studied clusters were calculated with the B3LYP functional.

3. Results and discussion

Optimized geometrical configurations of the lowest-lying energy states of the studied clusters are shown in Fig. 1–4 while the low-lying structures are presented in Fig. S1 and S2.† The relative energies (ΔE) of the ground state geometries and first low-lying isomers are listed in Tables 1 and 2. The internal coordinates of the ground state geometries and harmonic vibrational computations are available in the Supporting Information section (Tables S1–S6†). The AEAs, AEDEs and VEDEs of the studied clusters using different levels of theory are presented in Table 3.
Table 1 Energy shifts (eV) of the first low-lying isomers with respect to ground state geometries of M(GaX2)2 clusters where M = alkali metal; X = O, S
Cluster B3P86 B3PW91 B3LYP MP2
Li(GaO2)2 0.08 0.08 0.07 0.11
Li(GaO2)2− 0.94 0.86 0.66 0.99
Na(GaO2)2 0.18 0.17 0.18 0.19
Na(GaO2)2− 0.90 0.88 0.88 0.89
K(GaO2)2 0.09 0.08 0.08 0.14
K(GaO2)2− 0.71 0.69 0.69 1.07
Li(GaS2)2 0.003 0.003 0.003 0.0006
Li(GaS2)2− 0.78 0.73 0.46 0.98
Na(GaS2)2 0.53 0.53 0.53 0.54
Na(GaS2)2− 0.72 0.66 0.41 1.07
K(GaS2)2 0.40 0.39 0.39 0.44
K(GaS2)2− 0.78 0.71 0.47 1.72

Table 2 Energy shifts (eV) of the first low-lying isomers with respect to ground state geometries of M(GaX2)2 clusters where M = coinage metal; X = O, S
Cluster B3P86 B3PW91 B3LYP MP2
Cu(GaO2)2 0.04 0.08 0.11 0.16
Cu(GaO2)2− 0.0009 0.001 −0.0001 0.03
Ag(GaO2)2 0.22 0.21 0.20 0.16
Ag(GaO2)2− 0.61 0.56 0.42 0.80
Au(GaO2)2 0.40 0.60 0.62 0.36
Au(GaO2)2− 0.02 0.02 0.02 0.05
Cu(GaS2)2 0.20 0.18 0.26 0.29
Cu(GaS2)2− 0.005 0.005 0.003 0.03
Ag(GaS2)2 −0.02 0.02 0.02 0.42
Ag(GaS2)2− 0.07 0.07 0.06 0.08
Au(GaS2)2 0.37 0.32 0.25 0.53
Au(GaS2)2− 0.11 0.11 0.08 0.18

Table 3 Adiabatic electron affinities (AEAs), adiabatic electron detachment energies (AEDEs) and vertical electron detachment energies (VEDEs) of the studied clusters using different levels of theory
Methods B3P86 B3PW91 B3LYP MP2
AEA AEDE VEDE AEA AEDE VEDE AEA AEDE VEDE AEA AEDE VEDE
Li(GaO2)2 3.98 3.98 4.33 3.37 3.37 3.73 3.46 3.46 3.81 3.82 3.82 4.19
Na(GaO2)2 3.71 3.71 4.02 3.01 3.01 3.42 3.20 3.20 3.50 3.54 3.54 3.91
K(GaO2)2 3.56 3.56 3.87 2.95 2.95 3.26 3.03 3.03 3.33 3.44 3.44 4.02
Cu(GaO2)2 3.92 5.15 4.83 3.31 4.55 5.42 3.53 4.58 4.86 4.05 4.02 6.07
Ag(GaO2)2 3.97 3.99 4.29 3.33 3.37 3.68 3.39 3.39 3.75 3.76 3.74 5.70
Au(GaO2)2 3.89 5.65 5.84 3.28 5.06 5.24 3.43 5.07 5.25 3.86 5.37 6.10
Li(GaS2)2 4.24 4.24 4.51 3.67 3.67 3.94 3.69 3.69 3.96 3.72 3.72 4.02
Na(GaS2)2 4.02 4.02 4.25 3.45 3.48 3.69 3.48 3.48 3.71 3.49 3.49 3.78
K(GaS2)2 3.85 3.85 4.07 3.27 3.27 3.50 3.29 3.29 3.50 3.47 3.47 3.60
Cu(GaS2)2 4.32 5.31 5.36 3.76 5.31 4.80 4.02 4.71 4.77 3.37 6.53 6.92
Ag(GaS2)2 4.25 5.41 5.42 3.67 5.41 4.86 3.84 4.94 4.83 3.27 5.60 5.64
Au(GaS2)2 4.25 5.35 5.36 3.71 5.35 4.80 3.87 4.76 4.78 3.46 4.07 5.27

3.1. Structural and geometrical properties

The ground state geometry of neutral and anionic Li(GaO2)2 is composed of a dimerized GaO2 bound to a Li atom, which is of Cs symmetry (Fig. 1). Similar lowest-energy configuration was observed for doped sodium aluminium oxide congener.8 The substitution of a Li atom by Na and K atoms does not alter the structural properties of alkali-gallium oxide clusters. Akin to Li(GaO2)2, neutral and anionic Na(GaO2)2 and K(GaO2)2 consist of a dimerized GaO2 bound to their corresponding alkali metals (Fig. 1). Analogous with neutral Li(BS2)2,10 Li(GaS2)2 consists of a dimerized GaS2 in which the Li atom is attached to one sulfur atom (C1 symmetry) (Fig. 2). Anionic Li(GaS2)2 adopts the same ground state geometry as the oxygen analogue. Neutral Li(GaO2)2 and Li(GaS2)2 maintain the geometries of their corresponding dimers.9,11 Neutral and anionic Na(GaS2)2 adopt same ground state geometries as neutral and anionic Li(GaS2)2. On the other hand, neutral and anionic K(GaS2)2 possess similar ground state geometries as the oxygen congener. The terminal Ga–X bond remains fairly constant while the Ga–X–M (M = Li, Na and K; X = O and S) bond angle increases from lithium to potassium series in the neutral and anionic doped gallium oxide and sulfide clusters. The increase in bond angle can be explained by the increase in size from lithium to potassium atom. A decrease in the terminal bond length and Ga–X–M (M = Li, Na and K; X = O and S) bond angle is observed from the neutral to its corresponding anion. The low-lying isomer of neutral Li(GaO2)2 is formed by the rupture of one Li–O bond, thus leading to a structure which is composed of a Li atom attached linearly to the planar ‘D2h’ geometry of Ga2O4 while that of its anion is linear. The low-lying configuration of Li(GaS2)2 resembles the ground state geometry but is of Cs symmetry. The isomer is, 0.003 eV (Table 1) above the ground state geometry with the three DFT functionals. Akin to neutral Li(GaO2)2, the low-lying configuration of neutral and anionic M(GaO2)2 (M = Na and K) and neutral M(GaS2)2 (M = Na and K) is composed of the alkali metal atom attached linearly to the planar ‘D2h’ geometry of Ga2O4/Ga2S4. A planar chair-like structure (C2h symmetry) is obtained as the low-lying isomer for anionic M(GaS2)2 (M = Li, Na and K) (Fig. S1†).
image file: c5ra19970k-f1.tif
Fig. 1 Geometrical features of gallium oxide clusters containing alkali metals. Bond lengths are in Å and bond angles in °. aB3P86, bB3PW91, cB3LYP and dMP2.

image file: c5ra19970k-f2.tif
Fig. 2 Geometrical features of gallium sulfide clusters containing alkali metals.

Turning to the coinage metals, neutral Cu(GaO2)2 is composed of a Cu atom attached diagonally to one terminal oxygen atom of the planar ‘D2h’ geometry of Ga2O4 (Cs symmetry) (Fig. 3). The anion adopts a twisted chair-like structure (C2h symmetry) with each GaO2 unit attached to the Cu atom unlike analogous Cu(BO2)2 which is planar.19 Neutral Ag(GaO2)2 and Au(GaO2)2 possess the same ground state geometry as Cu(GaO2)2. The lowest-energy configuration of anionic Ag(GaO2)2 adopts a structure similar to anionic M(GaO2)2 (M = Li, Na and K) while that of anionic Au(GaO2)2 resembles the copper congener and Au(BO2)2.19 The M–O–Ga (M = Cu, Ag and Au) bond angle increases in the order Cu(GaO2)2 > Ag(GaO2)2 > Au(GaO2)2. However, the terminal Ga–O bond length increases in the order Ag(GaO2)2 > Au(GaO2)2 > Au(GaO2)2. A similar geometric trend was reported with the coinage-boron oxide clusters.19 Neutral Cu(GaS2)2 is composed of a pentagon to which a sulfur atom is bound to one gallium atom and the other gallium atom forms a cyclic moiety with the copper and sulfur atoms (Fig. 4). Anionic Cu(GaS2)2 adopts a distorted chair-like configuration. Akin to the oxide analogue, Ag(GaS2)2 comprises of a Ag atom attached diagonally to one terminal sulfur atom of the planar ‘D2h’ geometry of Ga2S4. Neutral Au(GaS2)2 adopts the same structure as Cu(GaS2)2. Anionic Ag(GaS2)2 and Au(GaS2)2 adopt planar chair-like structures. It is noteworthy that Ag(BO2)2− and Au(BO2)2−19 possess similar but non-planar geometries. The geometry of GaS2− is almost unchanged in the case of anionic M(GaS2)2 (M = Cu, Ag and Au), indicating its integrity in bonding with the central metal atoms. Similarly, the Ga–S bond length of the GaS2 moiety remains fairly constant but the M–S–Ga bond angle of Ag(GaS2)2 is largest followed by Cu(GaS2)2. The low-lying isomer of neutral Cu(GaO2)2 is similar to the ground state geometry of M(GaO2)2 (M = Li, Na and K) and that of Cu(GaS2)2 resembles its ground state geometry but with the cyclic moiety arranged in a distorted manner (Fig. S2†). In the case of Ag(GaO2)2, the low-lying isomer is composed of a silver metal atom attached linearly to the planar ‘D2h’ geometry of Ga2O4 while for Au(GaO2)2 and Au(GaS2)2, the gold atom is attached diagonally. The low-lying configuration of Ag(GaS2)2 is above the ground state geometry with energies of 0.02 (B3PW91 and B3LYP) and 0.42 eV (MP2) (Table 2), respectively. Anionic Cu(GaO2)2, Au(GaO2)2 and Cu(GaS2)2 prefer planar chair-like configurations and anionic Ag(GaO2)2, Ag(GaS2)2 and Au(GaS2)2 adopt W-shaped geometries as first low-lying isomers.


image file: c5ra19970k-f3.tif
Fig. 3 Geometrical features of gallium oxide clusters containing coinage metals.

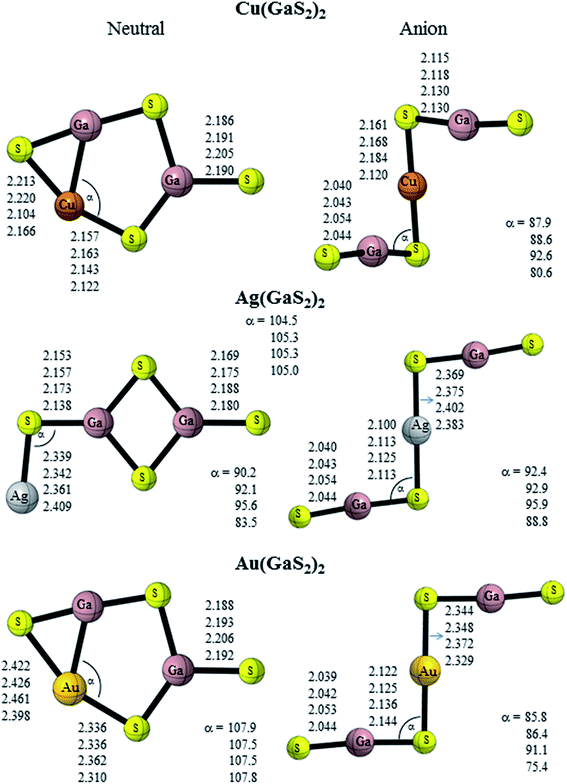image file: c5ra19970k-f4.tif
Fig. 4 Geometrical features of gallium sulfide clusters containing coinage metals.

3.2. Vibrational properties

The harmonic vibrational frequencies of the lowest-energy states of the clusters are presented in Tables S1–S6 (ESI†). All the ground state geometries of the studied doped gallium oxide and sulfide clusters do not have imaginary vibrational frequencies with the B3LYP functional and MP2 method. An analysis of the modes of vibration of M(GaX2)2 (M = Li, Na and K; X = O and S) indicates that the highest frequency mode corresponds to the asymmetrical Ga–X stretch which is bound to the rhombic Ga2X2 and alkali metal. In the case of anionic M(GaX2)2, with the exception of anionic Li(GaS2)2, the highest frequency mode is attributed to the stretching of the terminal Ga–X bond. The most active mode of Cu(GaO2)2, Ag(GaO2)2 and Au(GaO2)2 is the stretching of the Ga–O bond attached to the corresponding coinage metal while that of Ag(GaS2)2 refers to the symmetrical stretching of the Ga2S2 ring. The highest frequencies of Cu(GaS2)2 and Au(GaS2)2 correspond to the stretching of the Ga–S bond in the cyclic moiety. For anionic Cu(GaO2)2, Au(GaO2)2, Cu(GaS2)2, Ag(GaS2)2 and Au(GaS2)2, the stretching along the linear GaO2/GaS2 moiety has the highest frequency value while that of anionic Ag(GaS2)2 corresponds to the terminal Ga–S stretch.

3.3. Electronic properties

I. AEAs, AEDEs and VEDEs. As the ground state structures of neutral and anionic M(GaO2)2 (M = Li, Na and K) and K(GaS2)2 are identical, the AEDEs of the anionic clusters correspond to the AEAs of the neutral clusters (Table 3). The AEAs of the studied clusters at the CCSD(T)//B3LYP and CCSD(T)//MP2 levels are collected in Table S7.† The AEAs of Li(GaO2)2 are 3.98 (B3P86), 3.37 (B3PW91), 3.46 (B3LYP), 3.82 (MP2) and 3.40 eV with the single point CCSD(T) computations. The AEA of Li(GaO2)2 is less than that of the GaO2 superhalogen at the DFT, MP2, CCSD(T)//B3LYP and CCSD(T)//MP2 levels and is even smaller when compared to dimeric GaO2 superhalogen.9 The AEAs of Li(GaS2)2 are 4.24 (B3P86), 3.67 (B3PW91), 3.69 (B3LYP), 3.72 (MP2), 3.51 [CCSD(T)//B3LYP] and 3.59 [CCSD(T)//MP2] eV. The AEA value of Li(GaS2)2 surpass that of GaS2 with the B3P86 functional only. The question that arises is: can Li(GaS2)2 be classified as a hyperhalogen when its AEA is higher than that of GaS2? To solve this ambiguity, the VEDEs of the anions were calculated (Table 3). The VEDEs of Li(GaS2)2 are higher in comparison to that of GaS2 at the B3P86, B3LYP and MP2 levels. Consequently, the possibility of Li(GaS2)2 behaving as a hyperhalogen is negated. Turning to the sodium and potassium series, Na(GaO2)2 and K(GaO2)2 and their respective sulfur analogues possess smaller AEA values than GaO2 and GaS2 at different levels of theory employed. Again, these clusters cannot be classified as hyperhalogens.

The AEAs of coinage-gallium oxide (M = Cu, Ag and Au) clusters are lower than the GaO2 superhalogen at all the levels of theory employed and therefore cannot be classified as hyperhalogens. However, they have substantially high VEDE values. For instance, Au(GaO2)2 has the highest VEDE among the oxide series. Akin to the boron congener,19 Ag(GaO2)2 has higher VEDE values than Au(GaO2)2. Cu(GaS2)2, Ag(GaS2)2 and Au(GaS2)2 display high VEDE values at different levels of theory employed, with CuGa2S4 having a VEDE of 6.92 eV (MP2). However, the AEAs of Cu(GaS2)2, Ag(GaS2)2 and Au(GaS2)2 are higher than that of GaS2 with the B3P86 functional only. Therefore, the possibility of such clusters to exist as ‘hyperhalogen’ is negated.

II. NBO charges. In order to analyze the distribution of the extra charge in the anionic species, the NBO41,42 charges on the alkali and coinage metals of each cluster are summarized in Table 4 and the contribution of the atoms to the selected orbitals are given in Tables S8–11.† The charges on alkali and coinage metal atoms are positive. The excess electron in the anionic gallium oxide doped with alkali metals is mainly localized on the oxygen atom of the terminal Ga–O bond from the charge density plots (Fig. S3†). This is further confirmed by natural population analysis (NPA). The bonding orbital on the Ga–O terminal bond has more contribution from the oxygen atoms (Table S8†). Akin to the oxygen analogue, the excess electron in the anionic gallium sulfide doped with alkali metals is localized on the sulfur atom of the terminal Ga–S bond (Fig. S3†). Turning to the coinage metal, the excess electron is delocalised over the OCuO moiety for Cu(GaO2)2−, terminal Ga–O bond for Ag(GaO2)2− and over the whole system for Au(GaO2)2−. The excess electron in the anionic gallium sulfide doped with coinage metals is localized on the sulfur atoms (Fig. 4).
Table 4 NBO charges on alkali and coinage metals in neutral and anionic clusters with the B3LYP functionala
Clusters NBO charges on alkali metals Clusters NBO charges on coinage metals
Neutral Anion Neutral Anion
a All values are in e.
Li(GaO2)2 0.45 0.87 Cu(GaO2)2 0.40 0.67
Na(GaO2)2 0.48 0.94 Ag(GaO2)2 0.41 0.77
K(GaO2)2 0.48 0.93 Au(GaO2)2 0.31 0.49
Li(GaS2)2 0.39 0.70 Cu(GaS2)2 0.28 0.38
Na(GaS2)2 0.44 0.83 Ag(GaS2)2 0.31 0.45
K(GaS2)2 0.46 0.86 Au(GaS2)2 0.15 0.25

III. HOMO–LUMO gaps. The HOMO–LUMO gaps of the neutral clusters are presented in Table 5. A large value of the HOMO–LUMO energy gap enhances the chemical stability of the cluster.43 The HOMO–LUMO gaps of the lowest-energy configurations are large, varying from 3.33 [Ag(GaS2)2] to 5.04 eV [Li(GaO2)2] with the B3LYP functional. A decrease in the HOMO–LUMO gaps is observed from Li(GaO2)2 to K(GaO2)2 and from Li(GaS2)2 to K(GaS2)2. This feature can be rationalized by the size of atom. Similar decrease in the HOMO–LUMO gaps is seen from Cu(GaO2)2 to Au(GaO2)2 but an irregular trend is noted for the sulfur counterpart.
Table 5 HOMO–LUMO gaps of the studied clusters with the B3LYP functional
Clusters HOMO–LUMO gaps Clusters HOMO–LUMO gaps
Li(GaO2)2 5.04 Li(GaS2)2 4.74
Na(GaO2)2 4.79 Na(GaS2)2 4.37
K(GaO2)2 4.69 K(GaS2)2 4.36
Cu(GaO2)2 3.81 Cu(GaS2)2 3.99
Ag(GaO2)2 3.54 Ag(GaS2)2 3.33
Au(GaO2)2 3.41 Au(GaS2)2 4.10

IV. Thermodynamic stability. The thermodynamic stabilities of the lowest-energy isomers for neutral clusters were examined against fragmentation into selected channels (Table 6). The dissociation energy (De) is obtained as the difference in total energies of the initial state and the sum of total energies of the decay fragments. The ground state geometries of neutral MGaX2 (M = alkali or coinage metal; X = O or S) was explored in order to determine the dissociation energies of M(GaX2)2. The dissociation energies are all positive, indicating these clusters are stable against any fragmentation. The M(GaX2)2 → M(GaX2) + GaX2 (M = Li, Na and K; X = O, S) fragmentation pathway requires lower energies than the M(GaX2)2 → M + (GaX2)2 process. Similar feature is observed for gallium sulfide doped with copper and silver metals. However, the most preferred channel of the oxide series is M(GaO2)2 → M + (GaO2)2 (M = Cu, Ag and Au). No significant trend is observed on the dissociation energy values upon substitution of the alkali or coinage metal atom to the gallium oxide and sulfide clusters.
Table 6 Dissociation energies (De, eV) of the studied clusters through different channels
Channels B3P86 B3PW91 B3LYP MP2
Li(GaO2)2 → Li(GaO2) + GaO2 3.99 3.92 3.71 4.64
Li(GaO2)2 → Li + (GaO2)2 5.09 4.88 4.98 5.48
Na(GaO2)2 → Na(GaO2) + GaO2 4.06 3.98 3.79 4.69
Na(GaO2)2 → Na + (GaO2)2 4.26 4.07 4.09 4.74
K(GaO2)2 → K(GaO2) + GaO2 3.96 3.87 3.68 3.74
K(GaO2)2 → K + (GaO2)2 4.46 4.27 4.25 3.85
Cu(GaO2)2 → Cu + (GaO2)2 3.30 3.18 3.16 2.20
Cu(GaO2)2 → Cu(GaO2) + GaO2 3.99 3.91 3.71 4.45
Ag(GaO2)2 → Ag + (GaO2)2 2.60 2.47 2.44 2.15
Ag(GaO2)2 → Ag(GaO2) + GaO2 3.98 3.90 3.69 4.61
Au(GaO2)2 → Au + (GaO2)2 2.60 2.11 2.07 2.99
Au(GaO2)2 → Au(GaO2) + GaO2 4.40 4.32 4.08 4.80
Li(GaS2)2 → Li(GaS2) + GaS2 2.65 2.60 2.32 3.31
Li(GaS2)2 → Li + (GaS2)2 4.12 3.98 3.97 4.25
Na(GaS2)2 → Na(GaS2) + GaS2 2.47 2.41 2.23 3.08
Na(GaS2)2 → Na + (GaS2)2 3.55 3.41 3.34 3.74
K(GaS2)2 → K(GaS2) + GaS2 2.72 2.65 2.37 3.65
K(GaS2)2 → K + (GaS2)2 3.77 3.63 3.54 4.34
Cu(GaS2)2 → Cu(GaS2) + GaS2 2.86 2.76 2.48 2.19
Cu(GaS2)2 → Cu + (GaS2)2 3.49 3.34 3.21 3.60
Ag(GaS2)2 → Ag(GaS2) + GaS2 2.46 2.40 2.11 1.65
Ag(GaS2)2 → Ag + (GaS2)2 2.55 2.45 2.32 3.11
Au(GaS2)2 → Au + (GaS2)2 2.89 2.75 2.54 3.52
Au(GaS2)2 → Au(GaS2) + GaS2 4.14 4.03 3.66 4.88

V. Interaction with electropositive potassium counter ion. Although Cu(GaS2)2, Ag(GaS2)2 and Au(GaS2)2 cannot be classified as hyperhalogens, these clusters were interacted with a countercation. This was done by adding a positive ion such as K+ to the anionic ground state geometries. Fig. 5 shows the ground state structures of these salt moieties. The stability of these salts was determined by considering the energetics of the following fragmentation pathways:6
ΔE1 = −[KMGa2X4 − K+ − MGa2X4−]

ΔE2 = −[KMGa2X4 − K − MGa2X4]

ΔE3 = −[KMGa2X4 − KGaX2 − MGaX2]
image file: c5ra19970k-f5.tif
Fig. 5 Geometrical features of some proposed salts. aB3P86, bB3PW91 and cB3LYP.

These energies, given in Table 7, are positive, indicating that the salts' clusters are stable with respect to fragmentation.

Table 7 Fragmentation energies (eV) with the DFT functionals
Functionals B3P86 B3PW91 B3LYP
KCuGa2S4
ΔE1 4.27 4.51 4.42
ΔE2 3.54 3.97 3.82
ΔE3 3.21 3.60 3.47
[thin space (1/6-em)]
KAgGa2S4
ΔE1 4.07 4.31 4.25
ΔE2 3.41 3.71 3.55
ΔE3 2.70 3.12 3.02
[thin space (1/6-em)]
KAuGa2S4
ΔE1 4.13 4.35 4.26
ΔE2 3.51 3.75 3.61
ΔE3 4.36 4.84 4.70

4. Conclusions

Using DFT, MP2 and single point CCSD(T) based computations, a systematic theoretical study of the structures and stabilities of neutral and anionic M(GaX2)2 (M = alkali or coinage metal; X = O or S) was carried out. The substitution of a Li atom by Na and K in the studied gallium oxide and sulfide clusters does not alter the structural properties. The AEAs and VEDEs of M(GaX2)2 (M = alkali metal; X = O or S) are lower than that of GaO2 and GaS2, respectively. On the other hand, the VEDEs of gallium oxide and sulfide containing coinage metals are substantially higher but with AEAs lower than the ones for GaO2 and GaS2. On this basis, none of the studied clusters can be termed as hyperhalogens. Because experimental data are limited, these results open more ventures on future experimental and theoretical studies regarding doped gallium oxide and sulfide clusters.

Acknowledgements

N.S. acknowledges support from the Mauritius Tertiary Education Commission (TEC) for the grant of MPhil/PhD scholarship. The authors also acknowledge facilities from the University of Mauritius and University of Namibia. The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for the research group Project No. RGP VPP-207. The authors would like to thank reviewers for their useful comments to improve the manuscript.

References

  1. G. L. Gutsev and A. I. Boldyrev, Chem. Phys., 1981, 56, 277 CrossRef.
  2. G. L. Gutsev and A. I. Boldyrev, Adv. Chem. Phys., 1985, 61, 169 CrossRef CAS.
  3. H. Hotop and W. C. Lineberger, J. Phys. Chem. Ref. Data, 1985, 14, 731 CrossRef CAS.
  4. N. Bartlett, Proc. Chem. Soc., London, 1962, 6, 218 Search PubMed.
  5. M. Willis, M. Götz, A. K. Kandalam, G. F. Ganteför and P. Jena, Angew. Chem., 2010, 122, 9150 CrossRef.
  6. S. Behera, D. Samanta and P. Jena, J. Phys. Chem. A, 2013, 117, 5428 CrossRef CAS PubMed.
  7. H. Zhai, L. Wang, S. Li and L. Wang, J. Phys. Chem. A, 2007, 111, 1030 CrossRef CAS PubMed.
  8. K. Pradhan and P. Jena, J. Chem. Phys., 2011, 135, 144305 CrossRef PubMed.
  9. N. Seeburrun, H. H. Abdallah and P. Ramasami, J. Phys. Chem. A, 2012, 116, 3215 CrossRef CAS PubMed.
  10. L.-P. Ding, X.-Y. Kuang, S. Shao, M.-M. Zhong and Y.-R. Zhao, RSC Adv., 2013, 3, 15449 RSC.
  11. N. Seeburrun, H. H. Abdallah, E. F. Archibong and P. Ramasami, Struct. Chem., 2014, 25, 755 CrossRef CAS.
  12. A. K. Kandalam, K. Boggavarappu, P. Jena, S. Pietsch and G. Ganteför, Phys. Chem. Chem. Phys., 2015, 17, 26589 RSC.
  13. M. Willis, M. Götz, A. K. Kandalam, G. F. Ganteför and P. Jena, Angew. Chem., Int. Ed., 2010, 49, 8966 CrossRef CAS.
  14. D. Samanta, M. M. Wu and P. Jena, J. Am. Chem. Soc., 2012, 134, 8400 CrossRef CAS.
  15. G. L. Gutsev, C. A. Weatherford, L. E. Johnson and P. Jena, J. Comput. Chem., 2012, 33, 416 CrossRef CAS PubMed.
  16. M. Götz, M. Willis, A. K. Kandalam, G. F. Ganteför and P. Jena, Chem. Phys. Chem., 2010, 11, 853 CrossRef PubMed.
  17. W.-J. Tian, H.-G. Xu, X.-Y. Kong, Q. Chen, W.-J. Zheng, H.-J. Zhai and S.-D. Li, Phys. Chem. Chem. Phys., 2014, 16, 5129 RSC.
  18. Y. Feng, H.-G. Xu, W. J. Zheng, H. M. Zhao, A. K. Kandalam and P. Jena, J. Chem. Phys., 2011, 134, 094309 CrossRef PubMed.
  19. H. Chen, X.-Y. Kong, W. Zheng, J. Yao, A. K. Kandalam and P. Jena, Chem. Phys. Chem., 2013, 14, 3303 CrossRef CAS.
  20. X.-Y. Kong, H.-G. Xu, P. Koirala, W.-J. Zheng, A. K. Kandalam and P. Jena, Phys. Chem. Chem. Phys., 2014, 16, 26067 RSC.
  21. P. Koirala, K. Pradhan, A. K. Kandalam and P. Jena, J. Phys. Chem. A, 2013, 117, 1310 CrossRef CAS PubMed.
  22. C. Paduani, M. M. Wu, M. Willis and P. Jena, J. Phys. Chem. A, 2011, 115, 10237 CrossRef CAS PubMed.
  23. C. Paduani and P. Jena, J. Phys. Chem. A, 2012, 116, 1469 CrossRef CAS PubMed.
  24. T. Zhao, Y. Li, Q. Wang and P. Jena, Chem. Phys. Chem., 2013, 14, 3227 CrossRef CAS.
  25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, R. D.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
  26. R. Dooley, K. Milfeld, C. Guiang, S. Pamidighantam and G. J. Allen, J. Grid Comput., 2006, 4, 195 CrossRef.
  27. K. Milfeld, C. Guiang, S. Pamidighantam and J. Giuliani, Proceedings of the 2005 Linux Clusters: The HPC Revolution Linux Clusters Institute, 2005 Search PubMed.
  28. R. Dooley, G. Allen and S. Pamidighantam, Proceedings of the 13th Annual Mardi Gras Conference Louisana State University, Baton Rouge, LA, 2005 Search PubMed.
  29. P. Schwerdtfeger, M. Dolg, W. H. E. Schwarz, G. A. Bowmaker and P. D. W. Boyd, J. Chem. Phys., 1989, 91, 1762 CrossRef CAS.
  30. M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866 CrossRef CAS.
  31. P. Koirala, M. Willis, K. Boggavarapu, A. K. Kandalam and P. Jena, J. Phys. Chem. C, 2010, 114, 16018 CAS.
  32. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef.
  33. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406 CrossRef.
  34. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef.
  35. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS.
  36. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
  37. A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
  38. R. J. Bartlett, Annu. Rev. Phys. Chem., 1981, 32, 359 CrossRef CAS.
  39. W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986 Search PubMed.
  40. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
  41. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899 CrossRef CAS.
  42. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735 CrossRef CAS.
  43. M. M. Zhong, X. Y. Kuang, Z. H. Wang, P. Shao and L. P. Ding, J. Mol. Model., 2013, 19, 263 CrossRef CAS PubMed.

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra19970k
This journal is © The Royal Society of Chemistry 2015
Click here to see how this site uses Cookies. View our privacy policy here.