Computational insights into inhibitory mechanism of azole compounds against human aromatase

Abstract

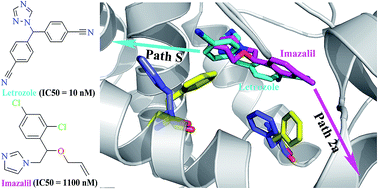
Human aromatase, also known as cytochrome P450 19A1, specifically catalyzes the conversion of androgens to estrogens, and therefore represents an important drug target for the treatment of breast cancer. Recently, azole compounds previously used as agricultural fungicides and antimycotic drugs were reported to exhibit potent inhibitory activity against aromatase. However, the molecular mechanism of these azole compounds against aromatase remains unclear. In this study, a combination of molecular docking and several types of molecular dynamics (MD) simulations including conventional MD, random acceleration MD and steered MD, was employed to investigate the interactions of aromatase with letrozole and imazalil, two azole compounds with distinct inhibitory activities against aromatase. The binding modes of these two inhibitors were obtained by molecular docking and refined by MD simulation. The binding free energies were calculated based on the MD snapshots by using the MM-GBSA method and were found to be in agreement with the relative potency of the experimental binding affinities. Our results further demonstrated that these inhibitors had different favorable unbinding pathways in aromatase, and the unbinding manners differed in their favorable dissociation routes. Several residues lining the pathways were found important for the inhibitor egress. These findings would be helpful not only for understanding the inhibitory mechanism of azole compounds against aromatase, but also for designing new aromatase inhibitors.