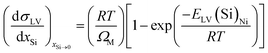DOI:
10.1039/C5RA16597K
(Communication)
RSC Adv., 2015,
5, 90866-90870
Reactive wetting of Ni–Si alloys on graphite substrates: effects of Si and Ni
Received
17th August 2015
, Accepted 15th October 2015
First published on 15th October 2015
Abstract
In recent years, the reactive wetting of Ni–Si on graphite has attracted increasing attention. However, most attention has been focused on the effect of Si on the wetting behavior of Ni–Si/C systems. In this work, the wetting process of Ni–Si alloys with different Si content (20, 28, 35, 45 and 55 wt%) on graphite substrates has been investigated at 1523 K in a high vacuum using a modified sessile drop method. The threshold activity of Si in liquid to form SiC at 1523 K can be calculated to be 0.0173, corresponding to a Si content of 33 at% (19 wt%). In addition, a minimum equilibrium contact angle of 20° can be observed in the Ni–45 wt% Si/C system. The adsorption energies of Si at the interface and at the surface of the Ni metal are 5.36 kJ mol−1 and −20.9 kJ mol−1, respectively; whereas, the adsorption energies of Ni at the interface and at the surface of the Si metal are −5.38 kJ mol−1 and 68.9 kJ mol−1, respectively. Moreover, the effects of Si and Ni on the change in the equilibrium contact angle have been evaluated in terms of the solid–liquid interfacial energy and the surface energy of the liquid alloy.
1. Introduction
The field of surface wetting has attracted increasing attention in recent years.1–6 In particular, the wetting behavior of metal matrix composites on ceramic substrates, such as the Me–Si/graphite system (Me = Cu, Al, Fe),7–11 is of great interest, which includes the reaction infiltration of liquid Si into graphite, and results in the formation of “reaction bond carbide” or SiC composites.12,13 It is well established that the surface active element Si plays an important role in the reactive wetting process in the Ni–Si/C system. Si can react with graphite to form wettable SiC, which leads to the decrease in solid–liquid interfacial energy, and thus promotes the spreading of the liquid alloy.14–18 In addition, Si can reduce the surface energy of the liquid alloy (i.e., Ni, Cu, Au, Fe).19–21
On the other hand, Ni is also critical in the wetting behavior of many alloys. U. Gangopadhyay et al.22 reported that the equilibrium contact angle of Au/C can be decreased by 7.8° with the addition of 15 at% Ni, due to the adsorbed Ni layer at the interface. This was also verified by the crater-edge profiling experiment. In addition, P. Wynblatt et al.23 found that the contact angles of the Pb/C system decreased with increasing Ni content. The adsorption content of Ni at the interface, measured using the CEP technique, also increased with increasing Ni content. However, most attention has been focused on the effect of Si on the reactive wetting of Ni–Si/C systems. In this work, the wetting processes of five Ni–Si alloys, with different Si content (20, 28, 35, 45 and 55 wt%), on porous graphite substrates have been investigated at 1523 K in a high vacuum, using a modified sessile drop method. Particular attention has been focused on the effects of Si and Ni on the wetting process of Ni–Si/C to provide comprehensive information on the fundamentals of this important wetting system.
2. Experimental procedure
High purity graphite plates (99.99 wt%, Toyo Carbon, Japan) with a density of 1.82 g cm−3 were used as substrates with an ash content less than 20 ppm. Before the wetting experiments, the surfaces of the substrates were mechanically polished using diamond paste to obtain an average roughness of 19 nm. The Ni–Si alloys with 20, 28, 35, 45 and 55 wt% Si content in nominal compositions were prepared by arc-melting of high-purity Ni (99.999 wt%, Alfa Aesar China, Tianjin, China) and Si (99.999 wt%, Alfa Aesar China, Tianjin, China) plates in argon (99.999% purity). The specimens were referred to as Ni–20 wt% Si, Ni–28 wt% Si, Ni–35 wt% Si, Ni–45 wt% Si and Ni–55 wt% Si. The raw materials were melted and solidified in a water-cooled copper crucible four times with the assistance of electromagnetic stirring to ensure the chemical homogeneity of the resulting alloys. Then the alloys were cut into cubes for the wetting experiments. Both the graphite plates and the Ni–Si cubes were ultrasonically cleaned in alcohol.
The wetting behaviors of the Ni–Si alloys were investigated using a modified sessile drop method in an average vacuum of 10−4 Pa. A detailed description of the experimental procedure is given elsewhere.24,25 In brief, the alloys and substrates were separated before the experiment to avoid pre-interaction upon heating. Once the desired temperature was reached, the alloy was dropped onto the graphite substrate through an Al2O3 tube. The wetting process was recorded using a charge-coupled device camera (1504 × 1000 pixels), as shown in Fig. 1.
 |
| | Fig. 1 Wetting process of Ni–35 wt% Si alloy on graphite at 1523 K obtained in vacuum using a modified sessile drop method. | |
Some wetting couples were cross-sectioned using a diamond saw and polished for microstructure observation using scanning electron microscopy (Supra-55, Zeiss, Jena, Germany) coupled with energy-dispersive X-ray spectroscopy (X-Max, OXFORD instruments, Oxford, England) analysis.
3. Results and discussion
Fig. 2 shows the cross-section of the Ni–Si/C systems after being held at 1523 K in a vacuum for 90 min. It is clear that a continuous layer of SiC (∼3 μm) can be observed at the interface between the alloy and the graphite substrate (in Fig. 2a–c). In addition, some faceted SiC crystals are present above the reaction layer in the Ni–45 wt% Si/C system (in Fig. 2d). Similar results have also been reported in Ni–Si/C systems15,16 and Cu–Si/C systems.16 Moreover, the morphology of the NiSi2 phase (dark regions) changes from dendrites (in Fig. 2a) to spheres (in Fig. 2c) when the Si content increases from 35 to 55 wt%. B. A. Julies also reported that a high content of Si promotes the growth of the NiSi2 phase in Ni–Si alloys due to the reaction between excess Si and the matrix.26
 |
| | Fig. 2 SEM micrographs of the cross-section of the Ni–Si/C systems after being held at 1523 K in a vacuum for 90 min, for (a) the Ni–35 wt% Si/C system, (b) the Ni–45 wt% Si/C system, and (c) the Ni–55 wt% Si/C system. (d) is the magnified image of the interface between alloy and graphite in (b). | |
The activity of a compound in a given system can be written as:
| | |
aZ = exp[(uZ − μθZ)/RT]
| (1) |
where
uZ is the chemical potential of component Z,
μθZ is the molar Gibbs energy of pure Z and
R is the gas constant.
Fig. 3 shows the activities of Si and Ni in the Ni–Si binary alloys at 1523 K. It is clear that the activities of Si and Ni increase significantly at the Si/Ni fraction (molar) of about 0.3 and 0.6, respectively.
 |
| | Fig. 3 The activities of Si and Ni for the Ni–Si binary system at 1523 K, calculated using Thermo-Calc codes. | |
By assuming that the formation of SiC only depends on the Si content rather than that of C, the threshold activity of Si in liquid to form SiC, aSi (SiC), can be calculated using the following equations:14,27,28
| |
 | (2) |
| | |
ΔG0f(T) = −113482 + 37.4872T
| (3) |
where
aNic is the activity of C in liquid Ni–C with the supersaturated dissolution of graphite, and Δ
G0f(
T) the Gibbs energy of formation of SiC from pure molten Si and solid C. The threshold activity of Si in liquid to form SiC at 1523 K can be calculated to be 0.0173. Correspondingly, the threshold content of Si in the liquid Ni–Si alloy at 1523 K is about 33 at% (19 wt%), in good agreement with previous work in the literature.
15
Fig. 4 shows the change in contact angle in the Ni–Si/C system at 1523 K as a function of time. It is clear that the contact angle of all specimens decreases with increasing time. In addition, a minimum equilibrium contact angle of 20° can be observed in the Ni–45 wt% Si/C system. Similar results have been found in other alloy systems, including Au–Si/SiC,29,30 Cu–Ti/SiC,31 Ag–Zr/AlN,32 and Sn–Al/Al2O3, which could be attributed to the change in the energy of adsorption by varying the compositions.33 It is also known that the equilibrium contact angle in a reactive wetting system corresponds to the contact angle of the alloy on the reaction product.15,16 The equilibrium contact angle in the present work can thus be associated with the contact angle of Ni–Si on SiC.
 |
| | Fig. 4 Contact angle versus time for the Ni–Si alloys on graphite, measured at 1523 K in a vacuum using the modified sessile drop method. | |
To explain the change in the equilibrium contact angle for the different compositions used in this work, the chemical adsorption of Ni and Si on SiC has been evaluated using the Gibbs adsorption equation34 as follows:
where
σ is the solid–liquid interfacial energy,
ΓA/B is the relative adsorption of element A with respect to element B, and
μA is the chemical potential of component A. For the Ni–Si/C system,
eqn (4) can be written as follows:
| |
 | (5) |
where
aNi is the activity of Ni in the liquid alloy and
aSi is the activity of Si in the alloy. In addition, the relative adsorption of Ni with respect to Si can be calculated using the following equation:
34,35| |
 | (6) |
where
ΩM is the molar interfacial area of the liquid alloy (40
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
500 m
2 mol
−1 for the Ni–Si system
36),
ySi is the molar fraction of Si at the last layer of liquid in contact with SiC, and
xSi is the molar fraction of Si in bulk liquid. Furthermore, the work of immersion
Wi can be calculated as follows:
| |
Wi = σSL − σSV = −σLV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ
| (7) |
where
σSL is the solid–liquid interfacial energy,
σSV is the surface energy of the solid,
σLV is the surface energy of the liquid alloy,
15,19 and
θ is the equilibrium contact angle.
Based on eqn (7), the value of (σSL − σSV) can be associated with the activity of Si or Ni in liquid (aSi or aNi), as shown in Fig. 5. Based on the slopes of Fig. 5, the relative adsorptions of Ni and Si at the interface, ΓNi/Si and ΓSi/Ni can be calculated to be 8.51 × 10−6 and −1.26 × 10−5, respectively. Based on eqn (6), ySi/xSi and yNi/xNi can be calculated to be 0.655 and 1.53, respectively. C. Rado et al. reported that yNi/xNi ranges from 1.43 to 1.91 when the Ni content in the Ni–Si system increases from 15 to 60 (in mol%).34 This further confirms the adsorption of Ni on SiC in the present work.
 |
| | Fig. 5 Variation of (σSL − σSV) for Ni–Si alloys as a function of ln(aNi) and ln(aSi) at 1523 K, calculated based on Fig. 3 and 4. | |
Additionally, the adsorption energy of Si at the interface (ESL(Si)Ni) and at the surface of the Ni metal (ELV(Si)Ni) can be described by the following equations.33–35
| |
 | (8) |
| | |
ELV(Si)Ni = (σSiLV − σNiLV)Ω − mλ
| (9) |
where
σSiLV and
σNiLV are the surface energies of pure Ni and Si (
σNiLV = 1.83 ± 0.09 J m
−2,
σSiLV = 0.72 ± 0.04 J m
−2),
19,34 λ is the exchange energy of the alloy (−96 kJ mol
−1)
34,37 and
m is a structural parameter (0.25).
34 Based on
eqn (8) and
(9), one can calculate that
ESL (Si)
Ni and
ELV(Si)
Ni are 5.36 kJ mol
−1 and −20.9 kJ mol
−1, respectively. Similarly,
ESL(Ni)
Si and
ELV(Ni)
Si are −5.38 kJ mol
−1 and 68.9 kJ mol
−1, respectively.
Given ESL(Si)Ni and ELV(Si)Ni, the solid–liquid interfacial energy and the surface energy of the liquid alloy, σSL and σLV, can be expressed as a function of the Si content by the following equations:
| |
 | (10) |
| |
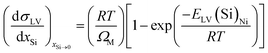 | (11) |
It is clear that the slope of (dσSL/dxSi)xSi→0 or (dσLV/dxSi)xSi−0 is negative when ESL(Si)Ni or ELV(Si)Ni is negative; whereas, the slope of (dσSL/dxSi)xSi→0 or (dσLV/dxSi)xSi→0 is positive, but very small, if ESL(Si)Ni or ELV(Si)Ni is positive.35 As for the case of infinitely dilute Si in Ni (xSi→0), increasing the Si content reduces the surface energy of the liquid, and thus results in the decrease in the equilibrium contact angle. As for the case of infinitely dilute Ni in Si (xNi→0), the smaller equilibrium contact angle can be mainly attributed to the decrease in interfacial energy with the addition of Ni. Therefore, the equilibrium contact angle does pass through a minimum value, consistent with the experimental results in Fig. 4.
Therefore, the Ni/Si ratio (in wt%) plays an important role in the activity of Ni and Si in liquid, the equilibrium contact angle of the Ni–Si/C system, and the surface energy of the liquid as well as the solid–liquid interfacial energy. Firstly, the activity of Ni increases with an increasing Ni/Si ratio (in Fig. 3). Secondly, the equilibrium contact angle decreases with a decreasing Ni/Si ratio in the range from 1.2 to 4.0 and increases with a decreasing Ni/Si ratio in the range from 0.82 to 1.2 (in Fig. 4). As for the case of infinitely dilute Si in Ni, a decreasing Ni/Si ratio reduces the surface energy of the liquid, and thus results in the decrease in the equilibrium contact angle. As for the case of infinitely dilute Ni in Si, the smaller equilibrium contact angle can be mainly attributed to the decrease in interfacial energy with the increasing Ni/Si ratio (in Fig. 5).
4. Conclusions
In present work, the reactive wetting of Ni–Si alloys on graphite substrates has been investigated at 1523 K in a high vacuum using a modified sessile drop method. A minimum equilibrium contact angle of 20° has been observed in the Ni–45 wt% Si/C system. In addition, the threshold activity of Si in liquid to form SiC at 1523 K is determined to be 0.0173, corresponding to a Si content of 33 at% (19 wt%). Moreover, the effects of Si and Ni on the change in the equilibrium contact angle have been analyzed in terms of the adsorption energy, the solid–liquid interfacial energy and the surface energy of the liquid alloy. The findings on the effects of Si and Ni on the reactive wetting of Ni–Si alloys on graphite substrates will shed light onto a better understanding of the nature of reactive wetting systems.
Acknowledgements
This work was supported by the program of the National Natural Science Foundation of China (50471007, 51102045). The authors are thankful to the Key Laboratory of Automobile Materials in Jilin University for their kind help in high temperature experiments.
References
- W. Barthlott and C. Neinhuis, Planta, 1997, 202, 1–8 CrossRef CAS.
- T. Zhang, J. Wang, L. Chen, J. Zhai, Y. Song and L. Jang, Angew. Chem., Int. Ed., 2011, 50, 5311–5314 CrossRef CAS PubMed.
- R. P. Evershed, R. Berstan, F. Grew, M. S. Copley, A. J. H. Charmant, E. Barham, H. R. Mottram and G. Brown, Nature, 2004, 432 Search PubMed.
- Q. Cheng, M. Li, Y. Zheng, B. Su, S. Wang and L. Jiang, Soft Matter, 2011, 7, 5948–5951 RSC.
- Q. Cheng, M. Li, F. Yang, M. Liu, L. Li, S. Wang and L. Jiang, Soft Matter, 2012, 8, 6740–6743 RSC.
- Q. Cheng, L. Jiang and Z. Tang, Acc. Chem. Res., 2014, 47, 1256–1266 CrossRef CAS PubMed.
- M. Brochu, M. Pugh and R. A. L. Drew, Intermetallics, 2004, 12, 289–294 CrossRef CAS PubMed.
- A. Gauffier, E. Saiz, A. P. Tomsia and P. Y. Hou, J. Mater. Sci., 2007, 42, 9524–9528 CrossRef CAS.
- J. Xu, X. Liu, M. A. Bright, J. G. Hemrick, V. Sikka and E. Barbero, Metall. Mater. Trans. A, 2008, 39, 1382–1391 CrossRef.
- G. F. Ma, N. Liu, H. F. Zhang, H. Li and Z. Q. Hu, J. Alloys Compd., 2008, 456, 379–383 CrossRef CAS PubMed.
- R. P. J. Yunes, L. Hong, N. Saha-Chaudhury, R. Bush and V. Sahajwalla, ISIJ Int., 2006, 46, 1570–1576 CrossRef.
- T. J. Whalen and A. T. Anderson, J. Am. Ceram. Soc., 1975, 58, 396–399 CrossRef CAS PubMed.
- G. W. Liu, F. Valenza, M. L. Muolo, G. J. Qiao and A. Passerone, J. Mater. Sci., 2009, 44, 5990–5997 CrossRef CAS.
- O. Dezellus, F. Hodaj and N. Eustathopoulos, J. Eur. Ceram. Soc., 2003, 23, 2797–2803 CrossRef CAS.
- V. Bougiouri, R. Voytovych, O. Dezellus and N. Eustathopoulos, J. Mater. Sci., 2007, 42, 2016–2023 CrossRef CAS.
- O. Dezellus and N. Eustathopoulos, J. Mater. Sci., 2010, 45, 4256–4264 CrossRef CAS.
- A. Ciftja, T. A. Engh and M. Tangstad, Metall. Mater. Trans. A, 2010, 41, 3183–3195 CrossRef CAS.
- B. Drevet and N. Eustathopoulos, J. Mater. Sci., 2012, 47, 8247–8260 CrossRef CAS.
- J. B. Keene, Surf. Interface Anal., 1987, 10, 367–383 CrossRef PubMed.
- Y. M. Wang and W. Cai, Mater. Sci. Forum, 2015, 817, 772–777 CrossRef.
- G. P. Khilya and Y. N. Ivashchenko, Dokl. Akad. Nauk SSSR, 1973, 69–72 CAS.
- U. Gangopadhyay and P. Wynblatt, J. Mater. Sci., 1995, 30, 94–100 CrossRef CAS.
- P. Wynblatt, Acta Mater., 2000, 48, 4439–4447 CrossRef CAS.
- L. Yang, P. Shen, Q. Lin, F. Qiu and Q. Jiang, Appl. Surf. Sci., 2011, 257, 6276–6281 CrossRef CAS PubMed.
- L. Yang, P. Shen, Q. Lin, F. Qiu and Q. Jiang, Mater. Chem. Phys., 2010, 124, 499–503 CrossRef CAS PubMed.
- B. A. Julies, D. Knoesen, R. Pretorius and D. Adams, Thin Solid Films, 1999, 347, 201–207 CrossRef CAS.
- Q. Lin and R. Sui, J. Alloys Compd., 2013, 274–279 CrossRef CAS PubMed.
- M. Singleton and P. Nash, J. Phase Equilib. Diffus., 1989, 10, 121–126 CAS.
- B. Vet, S. Kalogeropoulou and N. Eustathopoulos, Acta Metall. Mater., 1993, 41, 3119–3126 CrossRef.
- Y. V. Naidich, V. Zhuravlev and N. Krasovskaya, Mater. Sci. Eng., A, 1998, 245, 293–299 CrossRef.
- S. J. Li, X. M. Zang and H. P. Duan, Key Eng. Mater., 2002, 224–226, 749–754 CrossRef CAS.
- A. Koltsov, F. Hodaj, N. Eustathopoulos, A. Dezellus and P. Plaindoux, Scr. Mater., 2003, 48, 351–357 CrossRef CAS.
- J. G. Li, Compos. Interfaces, 1993, 1, 37–53 CrossRef CAS PubMed.
- C. Rado, S. Kalogeropoulou and N. Eustathopoulos, Acta Mater., 1999, 47, 461–473 CrossRef CAS.
- J. G. Li, L. Coudurier and N. Eustathopoulos, J. Mater. Sci., 1989, 24, 1109–1116 CrossRef CAS.
- D. Chatain, I. Rivollet and N. Eustathopoulos, J. Chim. Phys. Phys.-Chim. Biol., 1986, 83, 561–567 CAS.
- M. Lindholm and S. Bo, Metall. Mater. Trans. A, 1996, 27, 2897–2903 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. 





![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 m2 mol−1 for the Ni–Si system36), ySi is the molar fraction of Si at the last layer of liquid in contact with SiC, and xSi is the molar fraction of Si in bulk liquid. Furthermore, the work of immersion Wi can be calculated as follows:
500 m2 mol−1 for the Ni–Si system36), ySi is the molar fraction of Si at the last layer of liquid in contact with SiC, and xSi is the molar fraction of Si in bulk liquid. Furthermore, the work of immersion Wi can be calculated as follows:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ