Structural, vibrational study and UV photoluminescence properties of the system Bi_(2−x)Lu_(x)WO₆ (0.1 ≤ x ≤ 1)

Abstract

The bismuth lutetium tungstate series Bi_(2−x)Lu_(x)WO₆ with 0.1 ≤ x ≤ 1 were synthesized by solid state reaction of oxide precursors at 1000 °C for 3 h. The as-prepared polycrystalline compounds were characterized by X-ray diffraction (XRD), scanning electron microscopy (SEM), Raman spectroscopy and photoluminescence (PL) analyses. Biphasic samples were obtained in the composition range of 0.1 ≤ x ≤ 0.3. Solid solutions were obtained in the composition range of 0.4 ≤ x ≤ 1, and their monoclinic crystal structure was refined using the Rietveld method. SEM micrographs showed that solid solutions presented homogeneous morphologies. Attributions of Raman vibrational modes were proposed. A shift in the vibrational wavenumber depending on the lutetium composition was observed. The specific broadening of the spectral bands was interpreted in terms of long range Bi/Lu disorder and local WO₆ octahedron distortions in the structure. The PL experiments were performed under UV-laser light irradiation. Each PL band was decomposed into three Gaussian components with energies close to 1.25, 1.80 and 2.1 eV. Their integrated intensities increased with the value of x. The presence of the near infrared band at 1.25 eV is discussed.

---

I. Introduction

In the general framework of the development of multifunctional materials for various applications, we focus our attention on the correlations between the structure and luminescence properties of tungstate-based materials. In general, it is well established that extrinsic and intrinsic point defects can play a prominent role in photoluminescence properties.

Tungstate materials have been extensively studied and investigated because of their potential applications in numerous fields as functional materials in high-performance luminescent materials,^1–4 catalysts,^5,6 scintillators,⁷ laser hosts,⁸ as well as microwave applications^9,10 and humidity sensors.¹¹ Metal tungstates with the general formula AWO₄ can be divided into two groups depending on the tungsten environment: (i) scheelite-type structures with WO₄²⁻ tetrahedral groups and (ii) wolframite-type structures with WO₆⁶⁻ octahedral groups.¹² Depending on the radius of the A²⁺ cation, CaWO₄,^13,14 PbWO₄ (ref. 15 and 16) and AREWO₄ (with A = alkali metal, RE = rare earth element)^17–20 crystallize in the scheelite-type structures, whereas CdWO₄,²¹ ZnWO₄,²² MgWO₄ (ref. 23) and BaWO₄ (ref. 24) crystallize in the wolframite-type structures. Due to charge transfer linked to the tetrahedral or octahedral groups, tungstates can present interesting photoluminescence properties. Tungstates with the general formula RE₂WO₆ (RE = Y, La, Lu, Gd) belong to the second group with distorted WO₆ units and have attracted great attention in the field of luminescence.²⁵

Recently, lutetium-based compounds, such as Lu₂SiO₅,²⁶ Lu₃Al₅O₁₂,²⁷ LuAlO₃,²⁸ LuBO₃,²⁹ Lu₂O₃ (ref. 30 and 31) and undoped and doped Lu₂WO₆,^32–34 have attracted increasing interest for their potential applications due to their excellent luminescence properties.

In our recent study,³⁵ we synthesized the new monoclinic compound bismuth lutetium tungstate, BiLuWO₆, with a structure similar to that of the BiREWO₆ (RE = rare earth: Gd, Nd, Y) series. Its structure was characterized by disorder due to the Bi/Lu bonding competition. In a previous study,³⁶ we determined the local structure and the electrical properties of layered phase Bi₂WO₆. In preliminary studies, we observed that for compositions lower than x = 0.1, a solid solution could be obtained with the orthorhombic structure of Bi₂WO₆. In the intermediate composition range, we observed a biphasic system with two structures similar to those of Bi₂WO₆ (orthorhombic) and BiLuWO₆ (monoclinic). Finally, for compositions with x > 0.35, we observed a unique monoclinic phase, similar to that of BiLuWO₆.

In the present study, we investigate the Bi₂WO₆–BiLuWO₆ system represented by the general formula Bi_2−xLu_xWO₆ with 0.1 ≤ x ≤ 1. We use the Rietveld method to refine the crystal structure of solid solutions with compositions of 0.4 ≤ x ≤ 1 and present the first vibrational analyses from Raman spectroscopy. Finally, we perform the first photoluminescence analyses under UV excitation as a function of the value of x for lutetium.

II. Experimental section

II.1. Synthesis of the material

Bismuth lutetium tungstate compounds were prepared using a solid state reaction process. To prepare the Bi_(2−x)Lu_(x)WO₆ compounds, appropriate amounts of lutetium oxide Lu₂O₃ (Alfa Aesar Aldrich >99%), bismuth oxide Bi₂O₃ (Fluka Chemika >99%) and tungsten oxide WO₃ (Fluka Chemika >99%) were mixed and milled in an agate mortar, as reported in our earlier paper.³⁵ The mixture was then heated at 1000 °C for 15 hours.

II.2. X-ray diffraction

The X-ray diffraction (XRD) patterns were collected using an EMPYREAN PANALYTICAL diffractometer operating at 45 kV/35 mA, using CuKα radiation with a Ni filter in continuous mode with a step size of 0.013°. Data suitable for Rietveld refinement were collected over the 2θ range of 5–90°.

II.3. Microstructural characterization

Scanning electron microscopy (SEM) analysis was used to observe the morphology and the local composition of the polycrystalline material. Determination of the chemical compositions was performed using Energy Dispersive Spectroscopy (EDS) in surface scanning mode. Preliminary images were obtained with a SUPRA 40 VP COLONNE GEMINI ZEISS instrument using a maximum voltage of 20 kV.

II.4. Raman spectroscopy

Raman spectra (RS) were obtained on a VERTEX 70 Raman spectrometer using a power of 30 mW and the wavelength of Ar green laser λ = 514.5 nm. The frequency bands ν ranged from 50 to 1100 cm⁻¹.

II.5. UV photoluminescence

The equipment used to perform the photoluminescence (PL) measurements under UV excitation was a Horiba Jobin-Yvon HR800 LabRam spectrometer. The entrance slit, positioned behind the filter, is a diaphragm whose diameter can range from 50 to 500 μm. The irradiated zone was limited to 1 μm in diameter for all samples. The polycrystalline samples were in the form of compacted pellets obtained under a fixed pressure of 5 kbar. The spherical mirror, characterized by an 800 mm focal length, allows reflecting the scattered radiation from the input to the dispersive grating to obtain a spectra slot. The 364.5 nm (3.40 eV) line of an Ar-ion laser was used as the excitation source. The power applied to the samples was fixed to 0.005 mW with the acquisition time set to 100 ms.

III. Results and discussion

III.1. X-ray diffraction analyses

Fig. 1 illustrates the XRD patterns of the synthesized compounds with compositions from x = 0.1 to x = 1. A biphasic system is observed in the composition range of 0.1 ≤ x ≤ 0.3. Characteristic peaks of orthorhombic bismuth tungstate Bi₂WO₆ were detected in addition to the peaks of the monoclinic BiREWO₆ (RE = Lu) phase. It should be recalled that all the as-prepared ceramics were thermally treated at 1000 °C and were highly crystallized. The substituted compounds ranging from 0.4 ≤ x ≤ 1 present a monoclinic structure and constitute a solid solution. This structural modification (orthorhombic/monoclinic) can be explained from the two electronic configurations of Bi³⁺ and Lu³⁺; in the case of the Bi³⁺ cations (electron configuration 6s² 6p⁰), the lone pair (6s²) could play a spatial role in the structure organization, which is not the case for the Lu³⁺ cations. In addition, the ionic size of the Lu³⁺ cations, which is smaller than that of the Bi³⁺ cations, favors the formation of a solid solution having the structure of the limiting phase, BiLuWO₆.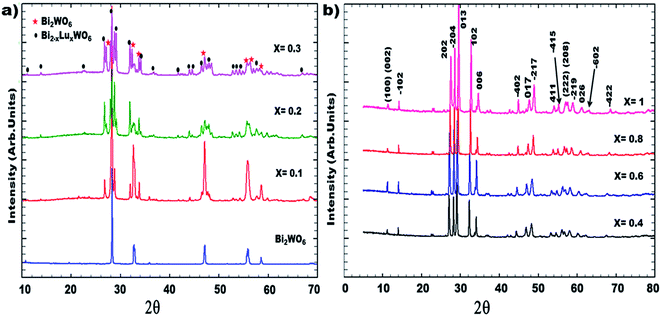

Fig. 1 XRD pattern of Bi_(2−x)Lu_(x)WO₆ obtained at room conditions: (a) biphasic system up to x = 0.3; (b) monoclinic solid solution up to x = 1.

The identification of these compounds was firstly obtained from the standard JCPDS files (Joint Committee standards for Powder Diffraction)³⁷ in which the standard phases BiYWO₆, BiNdWO₆, BiGdWO₆ and H–Bi₂WO₆ were referenced. Fig. 2 shows that the diffraction peaks of the monoclinic solid solution are shifted to higher angles as x increases.

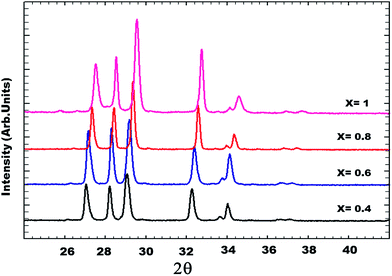Fig. 2 XRD patterns as a function of lutetium composition (x) of the solid solution for 0.4 ≤ x ≤ 1.

The structural parameters of the solid solutions with ‘x’ ranging from 0.4 ≤ x ≤ 1 were refined using FullProf suite software,³⁸ which allows refinement of atomic coordinates, site occupancies and atomic displacement parameters as well as profile parameters (instrument parameters, background parameters, lattice constants and peak shape). The disordered model based on the work of Berdonosov and co-workers^39,40 for the series Bi_2−xLn_xWO₆ (Ln = lanthanide) was used in our Rietveld calculations. In this model, Lu atoms are assumed to be distributed on the two bismuth sites of the H–Bi₂WO₆ monoclinic structure characterized by a centrosymmetric A2/m space group. Such a substitution should involve specific disordered distortions of the octahedral WO₆ groups due to alternation of the short Lu–O and long Bi–O bonds.

We refined the atom coordinates of the heavy atoms (Bi/Lu) and W, including their individual Debye factors, while keeping the oxygen coordinates fixed by using the monoclinic A2/m space group. The occupancy factors of all atoms were fixed in agreement with the global composition x. We obtained a significant goodness of fit and the factors R_p, R_exp, R_wp and R_B are quite reliable. Table 1 reports the final calculated cell parameters for the solid solution samples. Table 2 summarizes the atom coordinates used for the refinement calculations. In the calculations, each (Bi,Lu) site is assumed to be occupied by Bi and Lu atoms in proportions corresponding to the composition x. The occupancy factors used in the Rietveld procedure are in an arbitrary scale.

Table 1 Cell parameters and Debye–Waller factors for the solid solution compounds

	a (Å)	b (Å)	c (Å)	B (°)	Biso (Bi/Lu)	Biso (W)
Bi1.6Lu0.4WO6	8.1683(2)	3.7797(1)	16.1564(3)	102.184(1)	0.28(3)	0.33(4)
Bi1.4Lu0.6WO6	8.1403(2)	3.7619(3)	16.0923(3)	102.209(1)	0.57(4)	0.35(2)
Bi1.2Lu0.8WO6	8.1134(1)	3.7405(3)	16.0202(2)	102.382(1)	1.11(3)	0.32(3)
BiLuWO6 [ref. 34]	8.0830(1)	3.7238(1)	15.9493(2)	102.634(2)	0.72(3)	0.31(2)

---

Table 2 Atom coordinates (x, y, z, N) of (Bi,Lu) W and O atoms

Compositions	Atom coordinates (x, y, z) and occupancy factors N (arbitrary scale)
		x	y	z	N(Bi)/N(Lu) N(W) or N(O)
a Note on the reliability factors: Rp = 100. {∑|yi^obs − yi^calc|/∑|yi^obs|}, Rexp = 100. {[(N − P + C)/∑wi|yi^obs|^2]^1/2}, RB = 100. {∑|Ik^obs − Ik^calc|/∑|Ik^obs|}, RF = 100. {∑|Fk^obs − Fk^calc|/∑|Fk^obs|} where N, P and C are the number of observations, parameters and constraints, respectively.
x = 1	Bi/Lu(1)	0.9224(2)	0.000	0.000(2)	0.125/0.125
	Bi/Lu(2)	0.3960(2)	0.000	0.3170(2)	0.125/0.125
	W(1)	0.2951(3)	0.4792(3)	0.4925(3)	0.250
Reliability factors	Rp = 7%; Rexp = 3%; RB = 4.99%; RF = 4.74%
x = 0.8	Bi/Lu(1)	0.9233(3)	0.000	0.3321(2)	0.150/0.100
	Bi/Lu(2)	0.3943(4)	0.000	0.3176(3)	0.100/0.150
	W(1)	0.2960(2)	0.4450(2)	0.4970(3)	0.250
Reliability factors^a	Rp = 8.35%; Rexp = 7.73%; RB = 6.20%; RF = 4.72%
x = 0.6	Bi/Lu(1)	0.9266(3)	0.000	0.3327(2)	0.175/0.075
	Bi/Lu(2)	0.3929(2)	0.000	0.3189(2)	0.075/0.175
	W(1)	0.3020(2)	0.4485(3)	0.4994(2)	0.250
Reliability factors^a	Rp = 9.21%; Rexp = 6.79%; RB = 7.43%; RF = 5.48%
x = 0.4	Bi/Lu(1)	0.9277(2)	0.000	0.3331(3)	0.200/0.050
	Bi/Lu(2)	0.3950(3)	0.000	0.3183(2)	0.05/0.200
	W(1)	0.2985(3)	0.4560(3)	0.4990(4)	0.250
Reliability factors^a	Rp = 9%; Rexp = 7.87%; RB = 5.46%; RF = 5.24%
Fixed oxygen atoms	O(1)	0.1188	0.000	0.2489	0.250
	O(2)	0.3640	0.500	0.2338	0.250
	O(3)	0.3224	0.000	0.5284	0.125
	O(4)	0.5068	0.438	0.5745	0.250
	O(5)	0.1709	0.414	0.5669	0.250
	O(6)	0.1664	0.609	0.3992	0.250
	O(3a)	0.2978	0.000	0.4628	0.125

---

Fig. 3 shows the calculated and observed diffraction profiles Y_obs and Y_calc of the Bi_(1.2)Lu_(0.8)WO₆ compound. Fig. 4 shows the evolution and the influence of substitution of bismuth by lutetium on the cell parameters. The cell parameters a, b and c varied quasi-linearly with the composition x according to the respective equations:

a (Å) = −0.1414x + 8.2252 (R² = 0.999),

b (Å) = −0.0945x + 3.8177 (R² = 0.997),

and

c (Å) = −0.3467x + 16.297 (R² = 0.999).

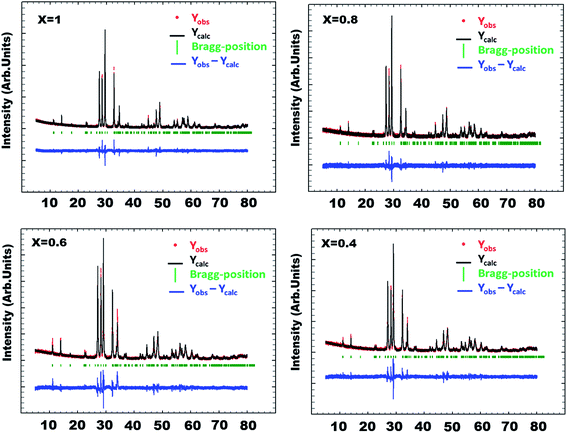Fig. 3 Rietveld refinement of Bi_2−xLu_xWO₆ (x = 0.4, 0.6, 0.8 and 1) using disordered structure and space group A2/m.

Fig. 4 Evolution of cell parameters as a function of lutetium fraction x.

The Debye–Waller factor B of the (Bi,Lu) site increases as x increases, with an apparent maximum value at x = 0.8 (Fig. 5). With regard to the standard deviations (close to 10%) of these B values, this increase can be ascribed to the existence of increasing local distortions involving disorder on the (Bi/Lu) site. The disorder can be illustrated by the alternation of different chemical bonds Bi–O and Lu–O, as discussed in ref. 35, 39 and 41.

Fig. 5 Evolution of Debye–Waller factor B of (Bi,Lu) site as a function of x.

The monoclinic structure of bismuth lutetium tungstates can be considered as being close to a wolframite-type structure. Fig. 6 shows the alternating (Bi,Lu)₂O₂ layers and the WO₆ edge sharing octahedra. Crystallographic data obtained from our Rietveld calculations showed that the WO₆ octahedral complexes have irregular shapes with short, medium and long bonds ranging from 1.65 Å to 2.13 Å.

Fig. 6 Crystal structure of monoclinic Bi_2−xLu_xWO₆ compounds in the (010) plane.

III.2. Scanning electron microscopy

The SEM micrographs reported in Fig. 7 show the morphology of the synthesized Bi_(2−x)Lu_(x)WO₆:

Fig. 7 SEM micrographs of the as-synthesized samples. Biphasic samples: (a) x = 0.1, (b) x = 0.2, (c) x = 0.3. Solid solutions (with inset showing regular rounded shapes): (d) x = 0.4, (e) x = 0.6, (f) x = 0.8, (g) x = 1.

• In the range of 0.1 ≤ x ≤ 0.3, the samples present two types of grain morphologies with small grains similar to those observed in the pure Bi₂WO₆ samples and micrometric grains similar to those observed in the monoclinic samples (0.4 ≤ x ≤ 1): these two aspects are compatible with the XRD analyses that show the presence of two phases.

• In the solid solution range 0.4 ≤ x ≤ 1, the morphology is quite uniform and consists of rounded grains having dimensions of 1 to 2 μm, as shown in the inset micrographs.

The EDS microanalysis is congruent with the nominal chemical composition of the heavy atoms in Bi_(2−x)Lu_(x)WO₆ and no significant variation in the composition can be observed on the local scale. Table 3 reports the theoretical and the experimental composition of the as-synthesized samples (O atoms were excluded during the EDS analysis). Each EDS experimental fraction is determined with a standard deviation of about 2%.

Table 3 Theoretical and experimental composition from EDS analysis

Compound	Theoretical compositions in at%	EDS analyses in^a at%
a Note: statistical deviations (in %) of Bi, Lu and W compositions are about: Bi (2–4%)/Lu (4–15%)/W (4%). Determination from series of surface analyses.
x = 0.1	Bi (63.33), Lu (3.33), W (33.33)	Bi (64), Lu (3), W (33)
x = 0.2	Bi (60.00), Lu (6.66), W (33.33)	Bi (59), Lu (8), W (33)
x = 0.3	Bi (56.66), Lu (10.00), W (33.33)	Bi (57), Lu (10), W (33)
x = 0.4	Bi (53.33), Lu (13.33), W (33.33)	Bi (53), Lu (14), W (33)
x = 0.6	Bi (46.66), Lu (20.00), W (33.33)	Bi (46), Lu (20), W (34)
x = 0.8	Bi (40.00), Lu (29.33), W (33.33)	Bi (40), Lu (27), W (33)
x = 1	Bi (33.33), Lu (33.33), W (33.33)	Bi (33), Lu (33), W (34)

---

III.3. Raman spectroscopy analyses

In the case of the Bi_2−xRE_xWO₆ structures, detailed assignments of the vibrational modes were previously proposed by Rocha et al.⁴² for the bismuth rare earth monoclinic compounds (RE = Y, Nd, Gd). The irreducible representation for these structures is as follows:

Γ = 24A_g + 18A_u + 18B_g + 24B_u (44 active Raman modes)

In general, these Raman modes (i.e., A_g and B_g) can be classified into four categories: (i) symmetric and asymmetric stretching vibrations of the WO₆ octahedrons, (ii) bending vibrations of WO₆, (iii) stretching and bending vibrations of the (Bi₂O₂)²⁺ layers, and (iv) vibrations involving translational motions of Bi³⁺/Lu³⁺ and W⁶⁺ ions.

Fig. 8 presents the vibrational bands of the compounds belonging to the composition range (0.4 ≤ x ≤ 1): all the compounds exhibit the same vibrational band profiles with a shift to higher wavenumber as the composition of lutetium ‘x’ increases. Table 4 reports the assignments of the Raman bands of the solid solution and the Full Width at Half Maximum (FWHM) of each composition. As the lutetium composition ‘x’ increases, we observe increasing wavenumber and broadening (FWHM) of all vibrational bands. This can be ascribed to the increasing population of Lu–O bonds having stronger force constants with increasing distortions due to the disordered distributions of Lu–O and Bi–O bonds.

Fig. 8 Raman spectra (λ = 514.5 nm) of the solid solution Bi_(2−x)Lu_(x)WO₆ (0.4 ≤ x ≤ 1).

Table 4 Raman spectroscopy data and assignments of vibration bands for the solid solution (0.4 ≤ x ≤ 1). Wavenumber (ν) and full width at half maximum (FWHM) in cm⁻¹

Wavenumber (FWHM)				Assignments [ref. 42]
x = 0.4	x = 0.6	x = 0.8	x = 1 [ref. 35]
891 (20)	897 (25)	905 (30)	912 (40)	Asymmetric stretching of WO6 (apical O)
750 (30)	762 (27)	770 (20)	785 (30)	Symmetric stretching of WO6 (apical O)
—	708 (—)	729 (3)	731 (5)
667 (20)	664 (18)	665 (20)	670 (22)	Asymmetric stretching of WO6 (equatorial O)
—	—	647 (—)	649 (22)
544 (12)	550 (10)	554 (19)	558 (20)	Bending of WO6 and stretching + bending of (Bi,Lu)O6 polyhedra
500 (22)	504 (30)	509 (27)	511 (20)
440 (—)	451 (9)	459 (10)	465 (15)
413 (—)	417 (10)	428 (10)	430 (16)
347 (18)	353 (15)	359 (17)	364 (15)	Remaining bending of the octahedral oxygen and Bi2O3 layers
286 (21)	289 (19)	299 (20)	303 (12)
251 (21)	251 (22)	249 (20)	249 (20)
—	—	—	214 (—)
189 (11)	189 (10)	189 (8)	191 (10)
154 (16)	158 (18)	160 (17)	162 (15)	Translation of Bi^3+/Lu^3+ and W^6+ ions lattice modes
77 (21)	77 (25)	83 (27)	89 (35)

---

The vibrational motions of the WO₆ octahedra and (Bi/Lu)₂O₂ layers are directly perturbed by the disorder of the Bi–O and Lu–O bonds induced by the increasing content of lutetium, involving increasing disorder in the oxygen positions of the WO₆ octahedra. This should be a major argument in support of the disorder model used in the Rietveld refinements to interpret our XRD data. As already reported for the BiLuWO₆ sample, the Raman bands can be highlighted as follows:

• The Raman peaks at 904 and 760 cm⁻¹ can be ascribed to the symmetric and antisymmetric stretching modes of WO₆ octahedra, which involve the apical motion of oxygen atoms perpendicular to the layers.

• The peaks in the region of 720–640 cm⁻¹ may be associated with the asymmetric stretching of octahedra, involving equatorial motions of oxygen atoms within layers.^43–47

• The bands in the mid-region 370–589 cm⁻¹ represent the bending modes of WO₆ and stretching-bending modes of (Bi, Lu)O_n.

• Some bands are well defined in the spectral range of 180–370 cm⁻¹ and are related to bending modes of the oxygen in the Bi–O polyhedra of the Bi₂O₂ layers.

• The bands below 180 cm⁻¹ can be ascribed to the translation of Bi³⁺/Lu³⁺ and W⁶⁺ ions.^43,48,49

III.4. Photoluminescence properties

In prior studies, the luminescence of scheelite tungstates was interpreted in terms of electronic charge transfer in the WO₄²⁻ complex oxyanions or in WO₃ defect centers.⁵⁰ Using a molecular orbital model for the octahedral WO₆⁶⁻ oxyanion, von Oosterhout et al.⁵¹ showed that the excited state consisted of an electron initially on an oxygen 2p orbital (O2p) and occupying the tungsten 5d orbitals (W5d) with t_2g symmetry. Following this model, the emission spectra suggest transitions starting from the double triplet ³T_1u levels to the ground ¹A_g1 level. Other authors^52–55 proposed similar interpretations some of them described the basic emissions through transitions from two triplet states ³T₁ and ³T₂ to the ¹A₁ ground state in the case of scheelite structures (charge transfer in WO₄²⁻ oxyanions) or from two triplet states ³T_1u and ³T_2u to the ¹A_1g ground state in the case of wolframite structures (charge transfer in WO₆⁶⁻ oxyanions). In the case of octahedral WO₆⁶⁻ oxyanions, two additional transitions corresponding to weaker energies were also envisaged. Recently, in our study on Ca_1−xCd_xWO₄ solid solutions,⁵⁶ we observed photoluminescence bands under UV excitation, localized in the approximate energy range from 2.1 to 2.7 eV.

In the case of bismuth-based compounds, the photoluminescence signals under UV excitation were previously ascribed to internal bismuth transitions:⁵⁷ the authors used theoretical calculations to justify emissions with wavelengths ranging between the UV-visible range 300 and 600 nm and the near infrared (NIR) emissions with wavelengths observed in the approximate range from 800 nm to 1500 nm (and above). NIR emissions were frequently observed in various bismuth-doped materials, including glasses.^58,59 These NIR emissions depended on the excitation energies and on the host material itself. The origins of these emissions are unclear to date. According to these authors, these emissions could be generated by bismuth species, such as Bi²⁺, Bi⁺ or BiO molecules, as probable defect centers (the list of possible defect centers was not clearly defined by the authors).

The photoluminescence bands obtained under UV excitation (energy of 3.40 eV) are presented in Fig. 9. The emission bands present energies ranging between 1.1 and 2.8 eV. The PL bands were decomposed into three Gaussian components (G1, G2, and G3). The resulting fit is quite satisfactory. The multi-Gaussian decomposition analyses are shown in Fig. 9. Table 5 gives the characteristics of the fitted Gaussian functions: energies of maximum, integrated intensities, and FWHM.

Fig. 9 Luminescence spectra of the polycrystalline Bi_(2−x)Lu_(x)WO₆ phosphors with 0.1 ≤ x ≤ 1, three Gaussian components are shown in each figure.

Table 5 Characteristics of the fitted Gaussian functions: energies of maximum, integrated intensities and FWHM

		Energies of maximum (eV)	Integrated intensity (a.u.)	FWHM (eV)
X = 0.1	G1	1.279	26.8	0.08
	G2	1.791	192.3	0.22
	G3	2.160	70.1	0.34
X = 0.2	G1	1.295	53.7	0.07
	G2	1.779	475.8	0.20
	G3	2.101	161.2	0.37
X = 0.3	G1	1.322	69.6	0.08
	G2	1.778	770.2	0.21
	G3	2.022	460.0	0.29
X = 0.4	G1	1.321	125.4	0.09
	G2	1.781	1117.6	0.20
	G3	1.967	546.9	0.31
X = 0.6	G1	1.359	127.3	0.08
	G2	1.770	1128.7	0.21
	G3	1.971	527.3	0.29
X = 0.8	G1	1.272	669.1	0.02
	G2	1.739	1250.4	0.19
	G3	1.941	684.3	0.29
X = 1	G1	1.272	924.5	0.02
	G2	1.762	901.7	0.19
	G3	1.927	627.7	0.36

---

In Fig. 10, each Gaussian function is characterized by its intensity and its energy as a function of the composition x. The energies of the G1 (close to 1.27 eV) and G2 (close to 1.78 eV) components are quasi-independent of the composition x. As x increases, G3 shows a shift to lower energies moving from 2.16 eV to 1.92 eV.

Fig. 10 Integrated intensities and centroid energies of the three Gaussians as a function of lutetium composition.

The G1 component appears to be a narrow band for high lutetium content and is strongly related to the increasing lutetium composition. The origin of the G1 component seems to be unclear. As it has a low energy, Wang et al.⁶⁰ in their study on ZnWO₄ interpreted the broad emission band close to 990 nm (with wavelengths ranging between 850 and 1100 nm) as being related to the presence of defect centers due to oxygen vacancies. In other terms, their broad NIR signal would be related to defect centers on the WO₆⁶⁻ groups. However, in our case, the emission band G1, observed at 991 nm or 1.27 eV, is a narrow band. As the intensity of our G1 emission band is strongly conditioned by the lutetium composition, a different interpretation might be proposed. This narrow band could result from a transition due to specific bismuth species acting as defect centers as previously suggested.^57,58 In the case of increasing lutetium composition, these bismuth species should appear as more isolated defects giving rise to high sensitization under UV excitation. For a low concentration of lutetium, the low intensity of this G1 component might result from a quenching effect. For high lutetium fractions, i.e., lower fraction of bismuth, this quenching effect might decrease.

The high energetic component G2, which has a maximum at x = 0.8, is attributed to the allowed transition ¹T_1u → ¹A_1g of the tungstate groups. Although the G3 component presents the same behavior as the G2 component, the former increases with x till a maximum at x = 0.8, this component could be linked to the ³T_1u → ¹A_g transitions.

The integrated intensities of the experimental data are shown in Fig. 11. It should be noted that the intensities of all components increase strongly in the composition range of 0.1 ≤ x ≤ 0.4, corresponding to the biphasic system. The total intensity (G1 + G2 + G3) is quasi-constant for compositions of x > 0.4 corresponding to the solid solutions, despite the fact that the intensity of the small G1 component increases slowly as x increases. In the biphasic system, this may be due to the progressive formation of the second (Bi–Lu) phase coexisting with the inactive Bi₂WO₆ phase, while in the (Bi–Lu) monoclinic solid solution, activation of the luminescence (G1, G2 and G3 components) should occur. As the G2 and G3 intensities remain quasi-constant, this luminescence could be ascribed to charge transfer (or defect centers) linked to the WO₆ groups of the monoclinic structure.

Fig. 11 Experimental integrated intensities as function of composition x.

VI. Conclusion

In this study, we investigated the complex tungstate system (1 − x)Bi₂WO₆– xBiLuWO₆ or Bi_2−xLu_xWO₆ and observed the existence of a mixed system for x < 0.4 and a solid solution for 0.4 ≤ x ≤ 1. Rietveld refinements of the monoclinic structures of the solid solution system showed that the Lu³⁺ cations are distributed on the Bi sites. X-ray diffraction analyses coupled with Raman spectroscopy results showed the existence of disordered distributions of Lu and Bi atoms, associated with local distortions.

The photoluminescence (PL) under monochromatic UV excitation seems to be strongly related to the formation of the monoclinic structure induced by the substitution of bismuth by lutetium. The PL spectra were decomposed into two types of emissions: the classical emission of tungstate groups WO₆⁶⁻ with two components due to charge transfer “W5d → O2p” in the case of octahedral coordination and a specific emission (narrow band at 1.25 eV) strongly related to the presence of lutetium. The exact origin of this NIR emission is not clearly established. If we refer to literature results on tungstates, this NIR emission might be due to defect centers due to oxygen vacancies or defect centers due to bismuth species with different valences or different molecular clustering.

Acknowledgements

A part of this study was financially supported by the CNRS-CNRST project N° 0749/14, Materials and Environment Laboratory (Agadir-Morocco), the Regional Council of Provence-Alpes-Côte d'Azur and the General Council of Var and the Toulon Provence Mediterranean.

References

1. H. Y. Li, H. K. Yang, B. K. Moon, B. C. Choi, J. H. Jeong, K. Jang, H. S. Lee and S. S. Yi, J. Alloys Compd., 2011, 509, 8788–8793.
2. H. Y. Li, H. K. Yang, B. K. Moon, B. C. Choi, J. H. Jeong, K. Jang, H. S. Lee and S. S. Yi, Inorg. Chem., 2011, 50, 12522–12530.
3. V. S. Marques, L. S. Cavalcante, J. C. Sczancoski, A. F. P. Alcantara, M. O. Orlandi, E. Moraes, E. Longo, J. A. Varela, M. S. Li and M. R. M. C. Santos, Cryst. Growth Des., 2010, 10, 4752–4768.
4. W. Zhang, J. Long, A. Fan and J. Li, Mater. Res. Bull., 2012, 47, 3479–3483.
5. A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278.
6. K. Kamata, T. Kimura, H. Sunaba and N. Mizuno, Catal. Today, 2014, 226, 160–166.
7. L. Huo and Y. Chu, Mater. Lett., 2006, 60, 2675–2681.
8. H. Zhao, J. Wang, J. Li, H. Zhang, J. Zhang, Z. Ling, H. Xia and R. I. Boughton, Mater. Lett., 2007, 61, 2499–2501.
9. J. C. Sczancoski, L. S. Cavalcante, M. R. Joya, J. A. Varela, P. S. Pizani and E. Longo, J. Chem. Eng. Data, 2008, 140, 632–637.
10. J. Liu, J. Ma, B. Lin, Y. Ren, X. Jiang, J. Tao and X. Zhu, Ceram. Int., 2008, 34, 1557–1560.
11. T. Thongtem, A. Phuruangrat and S. Thongtem, J. Ceram. Process. Res., 2008, 9, 258–261.
12. J. Ungelenk, M. Speldrich, R. Dronskowski and C. Feldmann, Solid State Sci., 2014, 31, 62–69.
13. V. B. Mikhailik, H. Kraus, G. Miller, M. S. Mykhaylyk and D. Wahl, J. Appl. Phys., 2005, 97, 083523.
14. Y. G. Su, L. P. Li and G. S. Li, Chem. Mater., 2008, 20, 6060–6067.
15. J. Yang, C. Lu, H. Su, J. Ma, H. Cheng and L. Qi, Nanotechnology, 2008, 19, 035608.
16. X. L. Hu and Y. J. Zhu, Langmuir, 2004, 20, 1521–1523.
17. F. Lei, B. Yan, H. H. Chen and J. T. Zhao, Inorg. Chem., 2009, 48, 7576–7584.
18. W. Bolanos, J. J. Carvajal, M. C. Pujol, X. Mateos, G. Lifante, M. Aguilo and F. Diaz, Cryst. Growth Des., 2009, 9, 3525–3531.
19. F. Esteban-Betegon, C. Zaldo and C. Cascales, Chem. Mater., 2010, 22, 2315–2324.
20. F. Wang, X. P. Fan, D. B. Pi, Z. Y. Wang and M. Q. Wang, J. Solid State Chem., 2005, 178, 825–830.
21. Y. Abraham, N. A. W. Holzwarth and R. T. Williams, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 1733–1741.
22. H. Ait ahsaine, A. Taoufyq, M. Ezahri, A. Benlhachemi, B. Bakiz, S. Villain, M. Arab, F. Guinneton and J.-R. gavarri, J. Mater. Environ. Sci., 2014, 5, 2449–2454.
23. S. Wannapop, T. Thongtem and S. Thongtem, Appl. Surf. Sci., 2012, 258, 4971–4976.
24. W. M. Chance, M. D. Smith and H. C. zur Loye, J. Chem. Crystallogr., 2014, 44, 20–24.
25. X.-Y. Chen, Z.-J. Zhang, A. Feng, M. Xu, J.-T. Zhao and F.-F. Xu, Mater. Res. Bull., 2015, 70, 26–31.
26. M. Zhuravleva, S. Friedrich and C. L. Melcher, Appl. Phys. Lett., 2012, 101, 101902.
27. Y. Zorenko, V. Gorbenko, I. Konstankevych, A. Voloshinovskii, G. Stryganyuk, V. Mikhallin, V. Kolobanov and D. Spassky, J. Lumin., 2005, 114, 85–94.
28. D. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 214115.
29. B. I. Zadneprovski, V. V. Sosnovtsev, D. G. Permenov, A. A. Meotishvili and G. I. Voronova, Tech. Phys. Lett., 2009, 35, 815–818.
30. N. Kalyvas, P. Liaparinos, C. Michail, S. David, G. Fountos, M. Wójtowicz, E. Zych and I. Kandarakis, Appl. Phys. A, 2011, 106, 131–136.
31. H. Ait ahsaine, L. Atourki, M. Ezahri, K. Bouabid, A. Ihlal, S. Villain and A. Benlhachemi, Mater. Lett., 2015, 160, 415–418.
32. A. Madej, M. E. Witkowski, A. J. Wojtowicz and E. Zych, J. Lumin., 2015, 160, 50–56.
33. X.-Y. Chen, Z.-J. Zhang, L.-L. Zhu, M. Xu, H. Wang, A.-G. Li and J.-T. Zhaoc, Appl. Surf. Sci., 2014, 317, 730–736.
34. Z. Zhang, H. Zhang, C. Duan, J. Yuan, X. Wang, D. Xiong, H. Chen and J. Zhao, J. Alloys Compd., 2008, 466, 258.
35. H. Ait ahsaine, A. Taoufyq, L. Patout, M. Ezahri, A. Benlhachemi, B. Bakiz, S. Villain, F. Guinneton and J.-R. Gavarri, J. Solid State Chem., 2014, 218, 124–130.
36. A. Taoufyq, H. Ait ahsaine, L. Patout, A. Benlhachemi, M. Ezahri, F. Guinneton, A. Lyoussi, G. Nolibe and J.-R. Gavarri, J. Solid State Chem., 2013, 203, 8–18.
37. Powder Diffraction File PDF data base sets. JCPDS, International Center for Diffraction Data. Swathmore, P.A, U.S.A. (1994).
38. J. Rodriguez-Carvajal, Commission on Powder Diffraction (IUCr) Newsletter, 2001, vol. 26, pp. 12–19.
39. P. S. Berdonosov, D. O. Charkin, K. S. Knight, K. E. Johnston, R. J. Goff, V. A. Dolgikh and P. Lightfoot, J. Solid State Chem., 2006, 179, 3437–3444.
40. P. S. Berdonosov, D. O. Charkin, V. A. Dolgikh, S. Yu Stefanovich, R. I. Smith and P. Lightfoot, J. Solid State Chem., 2004, 177, 2632–2634.
41. A. Watanabe, Y. Sekikawa and F. Izumi, J. Solid State Chem., 1982, 41, 138.
42. G. N. Rocha, L. F. L. Melo, M. C. Castro Jr, A. P. Ayala, A. S. de Menezes and P. B. A. Fechine, J. Phys. Chem., 2010, 71, 579–582.
43. M. Maczka, L. Macalik, K. Hermanowicz, L. Kepinski and P. Tomaszewski, J. Raman Spectrosc., 2010, 41, 1059–1066.
44. M. Maczka, L. Macalik and S. Kojima, J. Phys.: Condens. Matter, 2011, 23, 405902.
45. H. C. Gupta, Archana and V. Luthra, J. Mol. Struct., 2011, 1005, 53–58.
46. M. Maczka, L. Macalik and J. Hanuza, J. Raman Spectrosc., 2009, 40, 2099–2103.
47. M. Maczka, J. Hanuza, W. Paraguassu, A. G. Souza Filho, P. T. C. Freire and J. Mendes Filho, Appl. Phys. Lett., 2008, 92, 112911.
48. H. Huang, H. Chen, Y. Xia, X. Tao, Y. Gan, X. Weng and W. Zhang, J. Colloid Interface Sci., 2012, 370, 132–138.
49. L. W. Zhang, Y. J. Wang, H. Y. Cheng, W. Q. Yao and Y. F. Zhu, J. Adv. Mater., 2009, 21, 1286–1290.
50. V. Nagirnyi, E. Feldbach, L. Jönsson, M. Kirm, A. Lushchik, C. Lushchik, L. L. Nagornaya, V. D. Ryzhikov, F. Savikhin, G. Svenson and I. A. Tupitsina, Radiat. Meas., 1998, 29, 247–250.
51. A. B. J. von Oosterhout, Chem. Phys., 1977, 67, 2412–2418.
52. V. B. Mikhailik, H. Kraus, G. Miller, M. S. Mykhaylyk and D. Wahl, J. Appl. Phys., 2005, 97, 083523.
53. V. Nagirnyi, E. Feldbach, L. Jonsson, M. Kirm, A. Kotlov, A. Lushchik, V. A. Nefedov and B. I. Zadneprovski, Nucl. Instrum. Methods Phys. Res., Sect. A, 2002, 486(1), 395–398.
54. A. E. Ovechkin, V. D. Ryzhikov, G. Tamulaitis and A. Žukauskas, Phys. Status Solidi A, 1987, 103(1), 285–290.
55. R. Grasser, E. Pitt, A. Scharmann and G. Zimmerer, Phys. Status Solidi B, 1975, 69, 359–368.
56. A. Taoufyq, F. Guinneton, J.-C. Valmalette, M. Arab, A. Benlhachemi, B. Bakiz, S. Villain, A. Lyoussi, G. Nolibe and J.-R. Gavarri, J. Solid State Chem., 2014, 219, 127–137.
57. V. O. Sokolov, V. G. Plotnichenko and E. M. Dian, Opt. Lett., 2013, 33, 1488–1490.
58. R. Cao, M. Peng, J. Zheng, J. Qiu and Q. Zhang, J. Opt. Soc. Am., 2012, 16, 18505.
59. B. Xu, D. Tan, S. Zhou, Z. Hong, K. N. Sharafudeen and J. Qiu, J. Opt. Soc. Am., 2012, 20(27), 29105.
60. H. Wang, F. Medina, M. S. Antonious, C. Parkanyi, J. E. Haky, D. M. Baird and Y. D. Zhou, Chem. Phys. Lett., 1993, 205, 497–501.

---