Ultrathin graphene-based solar cells

Abstract

Ultrathin solar cells (USC) have the potential to provide ubiquitous, cheap, and efficient sources of energy. Practical issues, however, prevent the formation of solar cells below 100 nm. Cracks, voids, and inhomogeneities result in leakage pathways that render ultrathin solar cells unusable. We here demonstrate the use of graphene as the top electrode for ultrathin solar cells. Graphene was shown to suspend over pinholes in the active layer and enable current leakage–current-free carrier transport even for ultrathin semiconductor films. This advantage enabled the fabrication of solid-state dye-sensitized solar cells with TiO₂ thicknesses between 5 nm and 100 nm, which represents some of the thinnest solar cells produced to date. The produced ultrathin USCs exhibit a unique dye-loading characteristic that was attributed to the quasi two-dimensional nature of the TiO₂ film. Carrier recombination was found to be significantly enhanced in these thin films which limits the performance for increasing TiO₂ thicknesses. Finally, charge compensation of the photoexcited dye poses limitations on the minimum thickness of the TiO₂ which was found to be 10 nm. This work highlights the limits of USC scaling and opens up a new route to producing ultrathin solar cells for transparent and flexible applications.

---

Introduction

Ultrathin solar cells (USCs) have significant advantages over their bulk counterparts. Due to their lower volume, USCs require less material which decreases their cost.¹ Furthermore, their low thickness results in high transparency and mechanical flexibility that opens up new applications in energy harvesting windows and wearable generators.² Finally, short carrier transport lengths result in enhanced efficiencies.³

Despite the positive effect of decreasing their thickness, current USCs exhibit thicknesses in excess of 200 nm.^4–7 This relatively large thickness results in absorption coefficients of >15% which results in visible tints and prevents them from application as transparent generators.

The observed limit of scaling is caused by practical issues with the USCs' contacts. Voids in the deposited thin films cause leakage that short-circuit the solar cells and limit their efficiency.

We here demonstrate that the application of graphene electrodes can overcome these issues and enable the fabrication of USCs with less than 20 nm thickness. Graphene is a two-dimensional carbon allotrope which combines several unique properties that make it ideally suited for solar cell applications.⁸ Firstly, graphene is highly transparent with absorption of ∼2.3% per layer over the whole visible spectrum.⁹ The most important features of graphene for the present application are its high mechanical stability and flexibility: graphene has shown the ability to be suspended over large distances without breaking or touching the substrate.¹⁰ This property allows it to cover pinholes or pores that would cause leakage currents. Furthermore, graphene's high flexibility enables it to conform to rough surfaces¹¹ thus increasing its contact area with the underlying material. Finally, dry transfer techniques have been developed that enable soft landing deposition in inert environments and make graphene USC electrodes suitable for many different fabrication schemes.^12,13

In the present work, we apply graphene-based electrodes to solid state dye-sensitized solar cells. Because of their high absorption and internal quantum efficiency, dyes are a promising system for USCs. Solid-state DSSCs furthermore exhibit no complex boundaries as found at the electrolyte–electrode interface of traditional DSSCs. Thus, USCs can serve as a model system for the optimization of graphene-based DSSCs which represent an important application of graphene.^14–17

We here investigate the thickness dependence of solar-cell properties in order to understand the limits of scaling the thickness of USCs. It is demonstrated that thin films of 10 nm thickness exhibit the highest performance due to the competition between interface effects and recombination losses.

Experimental

TiO₂ thin films were deposited on a transparent electrode (FTO (Hartford Glass TEC A7)) by sputtering. The films were then immersed in Z907 dye (Everlight Chemical Industrial Co.) for 24 hours. Graphene was synthesized at large scale using chemical vapor deposition (CVD) following previous reports.¹⁸ Briefly, a copper catalyst (Cu-foil, Alfa 13382) was pretreated by electropolishing and then annealed for 30 minutes at high temperature (1000 °C) and low pressure (10⁻³ Torr) in a hydrogen atmosphere to improve the surface smoothness and remove surface contamination. Then, methane was introduced as a carbon precursor that is catalytically decomposed and assembled into graphene. After 3 hours growth, the sample was cooled to room temperature in a hydrogen atmosphere. The resulting graphene has a sheet resistance of ∼700 Ω □⁻¹ and has been demonstrated to be high quality and single layer.¹⁹

The graphene was deposited onto the dye by a dry-transfer technique. Thermal release tape (TRT, SUNUP High Tech CO., LTD. (TR-120-40/N-D)) was laminated onto the graphene/copper sample at ∼0.2 MPa pressure and room temperature. Then, the copper substrate was destructively removed by wet etching in FeCl₃ (0.76 M, 40 min). After drying the graphene/TRT it was positioned onto the TiO₂/dye thin film and heated to 140 °C. At this temperature the adhesion between the TRT and graphene is minimized and the graphene will stick to the TiO₂ thin film instead. Contact to the device was made by silver adhesive (TED PELLA, INC. Product No.: 16035). The resulting device structure is shown in Fig. 1. Cross sectional SEM characterization confirms the nanoscale dimension of the produced structure (ESI Fig. S1†).

Fig. 1 Structure and fabrication steps of the graphene-based USC.

The current–voltage diagram were measured under dark conditions and under white-light illumination (35 mW cm⁻²). Electrical measurements were carried out on a Keithley B2912A source measurement unit.

Results and discussion

Atomic force microscope (AFM) images were obtained after transferring graphene onto the dye/TiO₂/FTO structure (Fig. 2(a)). Occurring wrinkles after transfer suggest that graphene was suspended on bigger particles. Fig. 2(b) shows histograms of the height distributions for dye/TiO₂/FTO samples with and without a graphene top electrode. The smaller FWHM of the roughness distribution demonstrates that the graphene-covered sample results in a smoother surface. This change is suggesting that graphene is being suspended on the surface of TiO₂ and covers cracks and voids in the underlying film.

Fig. 2 (a) AFM image of graphene on 10 nm TiO₂/Z907, (b) height histogram before and after deposition of graphene on 10 nm TiO₂/Z907, (inset) depiction of origin of different roughness, (c) comparison of leakage currents for graphene on 10 nm and 100 nm TiO₂ and Pt on 100 nm TiO₂.

To identify the effect of this smoothening on carrier transport, the current between top and bottom electrode were characterized under dark conditions. Fig. 2(c) shows the comparison of traditionally deposited Pt electrodes and graphene electrodes on 100 nm TiO₂ films. A decrease in leakage current by 6 orders of magnitude is observed that demonstrates the potential of suspended graphene electrodes for USCs.

These promising results prompted us to decrease the TiO₂ thickness to 10 nm (Fig. 2c) and the extracted low-bias resistances are very similar for 10 nm and 100 nm devices (321 MΩ and 382 MΩ, respectively).

Fig. 3(a) shows the transmittance spectrum of a 10 nm thick device and its individual components. Due to the low thickness, the device exhibits an average absorption across the visible spectrum of less than 10% which makes it suitable for energy harvesting windows.²

Fig. 3 (a) Transmittance spectra of the device and its constituents (left inset): Z907 solution spectrum, (inset, right) photo of the resulting transparent solar cell, (b) dye transmittance vs. immersion time.

The constant and small light absorption of graphene allows the direct characterization of the dye even at low concentrations. The Z907 dye exhibits an absorption peak at 526 nm (inset of Fig. 3(a)) in agreement with previous findings.²⁰ The analysis of this feature allows characterization of the time evolution of the dye adsorption process on the TiO₂ film. It can be seen from Fig. 3(b) that the absorption is quickly approaching a maximum value A₀ following eqn (1).

A = A₀ exp(−t/τ) (1)

The fitted result from Fig. 3(b) shows that the time constant τ is only 16 minutes. This is in strong contrast to previous results on the dye loading kinetics where several hours of immersion were needed.²¹

The observed surface-limited adsorption results in a dye concentration that is independent of TiO₂ thickness, TiO₂ and dye absorption coefficients of 3% were measured for all TiO₂ thicknesses. This behavior gives us the opportunity to investigate the effect of TiO₂ thickness on cell performance without having to consider the impact of different amount of dye loading that is commonly occurring for porous films.

In the limit of film thicknesses approaching zero, graphene's mechanical strength is not sufficient to avoid leakage. Below 10 nm thickness the TiO₂ was found to not produce continuous films but individual particles and graphene is contacting the bottom electrode directly. In order to avoid leakage and access this thickness regime, we modified the device design and used an 50 nm aluminum film as bottom electrode. The film was exposed to air before deposition of TiO₂ which results in the formation of a native oxide layer. This oxide layer was found to result in a consistently low leakage current by producing a contact resistance of ∼100 MΩ.

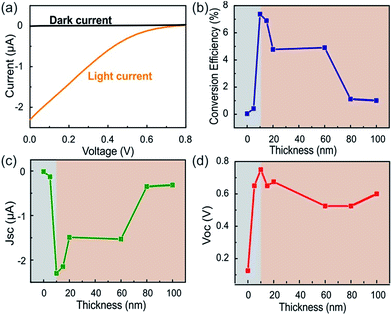
One issue arising from the modification is the decrease in current due to the large series resistance resulting in reduction of overall device efficiencies to 1% of state-of-the-art devices.²² Fig. 4(a), however, demonstrates clear distinction between the dark and bright I–V curve of our USC with a TiO₂ thickness of 10 nm.

Fig. 4 (a) Current–voltage diagram for 10 nm thick device under light and dark condition, (b–d) effect of TiO₂ thickness on (b) conversion efficiency, (c) short circuit current, (d) open circuit voltage.

Fig. 4(b) shows the conversion efficiency, defined as the ratio of measured efficiency and theoretical internal quantum efficiency for Z907,²³ for devices with varying TiO₂ film thicknesses between 10 nm and 100 nm. It can be seen that an optimum thickness exists at which the conversion efficiency is maximized. Both the behavior and the low critical thickness are surprising and warrant further investigation.

Fig. 4(c) shows the evolution of the short-circuit current density (J_SC) with TiO₂ thickness. We find that under identical conditions increasing the film thickness beyond an optimal point will result in decreasing J_SC. The decaying trend for thicknesses larger than 20 nm is attributed to an enhanced carrier recombination.

To describe this effect, the current density for TiO₂ thicknesses (d) between 20 nm and 80 nm was fitted to the diffusive carrier concentration profile in eqn (2).

C = C₀erfc(d/L), (2)

where C₀ is the injection concentration and L is the diffusion length of the photoexcited electron.

The extracted diffusion length is 100 nm which is several orders of magnitude smaller than observed in porous films.²⁴

The observation can be explained by the difference in TiO₂ film structure. Commonly, DSSCs are composed of TiO₂ in anatase configuration.²⁵ In this structure, TiO₂ has an indirect band gap with low effective mass.²⁶ This situation will result in large diffusion coefficients and long electron lifetimes. X-ray photoelectron spectroscopy of the here employed sputter deposited TiO₂, however shows the absence of anatase (ESI Fig. S4†). Instead rutile or brookite phases may coexist with amorphous regions²⁷ which exhibit direct and smaller band gaps and a larger electron mass.²⁸ Consequently, a lower diffusion coefficient and shorter lifetime are expected. These results suggest that vacuum deposition of TiO₂, which is normally associated with higher quality, is inferior to film formation from crystalline particles.

The fast electron decay consequently necessitates minimization of the film thickness. On the other hand a rapid increase in J_SC for TiO₂ thicknesses between 0 and 20 nm indicates that another mechanism exists that limits the minimum film thickness.

To understand this effect, we investigate the open circuit voltage (V_OC) dependence on film thickness (Fig. 4(d)). We find a similar increasing behavior for low film thicknesses (d < 20 nm) as seen for J_SC. This behavior suggests that a minimum film thickness exists for which the described DSSC mechanism applies. Previously, electroabsorption techniques suggested the formation of an enhanced dipole moment at the dye/TiO₂ interface.²⁹ This result was explained by DFT calculations showing a substantial delocalization of the photoexcited state in the TiO₂.³⁰ In this situation, the decrease of film thickness would weaken the dipole and deteriorate electron injection from the dye into the semiconductor.

We approach this behavior with a simple electrostatic model of uncompensated charges: the electric field on the dye-side of the interface has to be balanced by charges within the TiO₂ to retain charge neutrality. Therefore, a decrease of the film thickness below the depletion width will result in a decrease of the built-in electric field. Using parameters for TiO₂ (ref. 31) we calculate a critical film thickness in the order of tens of nanometers using eqn (3).

This good agreement proves the importance of a minimum layer thickness to accommodate the charge of the photoexcited dye.

Conclusions

In conclusion, we have demonstrated the application of graphene electrodes to ultrathin solar cells (USCs). Graphene's mechanical strength was found to enable the leakage-free carrier transport by suspending over cracks and voids. Investigation of the effect of USC thickness on performance reveals two regimes. Carrier recombination was found to be more significant in vacuum deposited TiO₂ films than sintered films and this process limits the performance for high thicknesses. Charge compensation of the photoexcited dye poses limitations on the minimum thickness of the TiO₂ which was found to be ∼10 nm.

These findings highlight the potential of our approach in understanding the fundamental properties of USCs and enabling their practical applications.

Acknowledgements

YP Hsieh and M. Hofmann acknowledges financial support from Applied Materials, Inc., the Ministry of Science and Technology (Grant number 102-2112-M-194-003-MY3; 103-2218-E-006-004), and Industrial Technology Research Institute of Taiwan.

References

1. M. Kaelin, D. Rudmann and A. Tiwari, Sol. Energy, 2004, 77, 749–756.
2. T. Miyazaki, A. Akisawa and T. Kashiwagi, Renewable Energy, 2005, 30, 281–304.
3. K. H. Khoo, Y. Chen, S. Li and S. Y. Quek, Phys. Chem. Chem. Phys., 2015, 17, 77–96.
4. E. Della Gaspera, Y. Peng, Q. Hou, L. Spiccia, U. Bach, J. J. Jasieniak and Y.-B. Cheng, Nano Energy, 2015, 13, 249–257.
5. M. Kaltenbrunner, M. S. White, E. D. Głowacki, T. Sekitani, T. Someya, N. S. Sariciftci and S. Bauer, Nat. Commun., 2012, 3, 770.
6. N. R. Paudel, K. A. Wieland and A. D. Compaan, Sol. Energy Mater. Sol. Cells, 2012, 105, 109–112.
7. T. Jiao, D. Wei, J. Liu, W. Sun, S. Jia, W. Zhang, Y. Feng, H. Shi and C. Du, RSC Adv., 2015, 5, 73202–73206.
8. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
9. X. Li, Y. Zhu, W. Cai, M. Borysiak, B. Han, D. Chen, R. D. Piner, L. Colombo and R. S. Ruoff, Nano Lett., 2009, 9, 4359–4363.
10. I. Frank, D. M. Tanenbaum, A. van der Zande and P. L. McEuen, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2007, 25, 2558–2561.
11. S. P. Koenig, N. G. Boddeti, M. L. Dunn and J. S. Bunch, Nat. Nanotechnol., 2011, 6, 543–546.
12. J. Kang, S. Hwang, J. H. Kim, M. H. Kim, J. Ryu, S. J. Seo, B. H. Hong, M. K. Kim and J.-B. Choi, ACS Nano, 2012, 6, 5360–5365.
13. S. Bae, H. Kim, Y. Lee, X. Xu, J.-S. Park, Y. Zheng, J. Balakrishnan, T. Lei, H. R. Kim and Y. I. Song, Nat. Nanotechnol., 2010, 5, 574–578.
14. C.-Y. Ho and H.-W. Wang, Appl. Surf. Sci., 2015, 357(Part A), 147–154.
15. L. Qiu, H. Zhang, W. Wang, Y. Chen and R. Wang, Appl. Surf. Sci., 2014, 319, 339–343.
16. Y.-J. Jeon, J.-M. Yun, D.-Y. Kim, S.-I. Na and S.-S. Kim, Appl. Surf. Sci., 2014, 296, 140–146.
17. J. Fan, S. Liu and J. Yu, J. Mater. Chem., 2012, 22, 17027–17036.
18. X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung and E. Tutuc, Science, 2009, 324, 1312–1314.
19. Y.-P. Hsieh, M. Hofmann and J. Kong, Carbon, 2014, 67, 417–423.
20. H. An, D. Song, J. Lee, E.-M. Kang, J. Jaworski, J.-M. Kim and Y. S. Kang, J. Mater. Chem. A, 2014, 2, 2250–2255.
21. S.-W. Lee, K.-S. Ahn, K. Zhu, N. R. Neale and A. J. Frank, J. Phys. Chem. C, 2012, 116, 21285–21290.
22. X. Chen, Q. Tang, B. He and H. Chen, RSC Adv., 2015, 5, 43402–43407.
23. G. Y. Margulis, B. E. Hardin, I. K. Ding, E. T. Hoke and M. D. McGehee, Adv. Energy Mater., 2013, 3, 959–966.
24. M. Wang, P. Chen, R. Humphry-Baker, S. M. Zakeeruddin and M. Gratzel, ChemPhysChem, 2009, 10, 290–299.
25. D. Chen, F. Huang, Y.-B. Cheng and R. A. Caruso, Adv. Mater., 2009, 21, 2206–2210.
26. J. Zhang, P. Zhou, J. Liu and J. Yu, Phys. Chem. Chem. Phys., 2014, 16, 20382–20386.
27. D. A. Hanaor and C. C. Sorrell, J. Mater. Sci., 2011, 46, 855–874.
28. B. Prasai, B. Cai, M. K. Underwood, J. P. Lewis and D. Drabold, J. Mater. Sci., 2012, 47, 7515–7521.
29. V. Roiati, E. Mosconi, A. Listorti, S. Colella, G. Gigli and F. de Angelis, Nano Lett., 2014, 14, 2168–2174.
30. W. R. Duncan and O. V. Prezhdo, Annu. Rev. Phys. Chem., 2007, 58, 143–184.
31. M. C. Sellers and E. G. Seebauer, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2011, 29, 061503.

---

Footnote

† Electronic supplementary information (ESI) available: Electron micrograph and XPS characterization. See DOI: 10.1039/c5ra19393a

---