Mechanistic insight of TiCl₄ catalyzed formal [3 + 3] cyclization of 1,3-bis(silyl enol ethers) with 1,3-dielectrophiles

Abstract

The mechanism of TiCl₄ mediated formal [3 + 3] cyclization of 1,3-bis(silyl enol ethers) with 1,3-dielectrophiles is studied at the B3LYP level of density functional theory (DFT) to rationalize the experimental regioselectivity. Methyl and trifluoromethyl substituted 1,3 dielectrophiles are studied theoretically since they show different regioselectivities. Two different mechanisms involving 1,2 and 1,4 addition of 1,3-bis(silyl enol ethers) on 1,3-dielectrophiles are studied for each dienophile. The intramolecular transition metal catalyzed and non-catalyzed dynamic shift of the silyl moiety is also studied. The structure of the 1,3 dienophile and the associated Mulliken charges are the driving forces for different regioselectivities in methyl and trifluoromethyl dienophiles.

---

Introduction

Functionalized arenes are interesting class of organic molecules, and find applications in natural products,¹ polymers² and medicinal chemistry.³ The traditional approaches for the synthesis of substituted arene involve direct substitution of already existing benzene scaffolds. The widely used strategies based on this classical approach involve electrophilic⁴ and nucleophilic substitution⁵ (in the case of aryl halides) and transition metal catalyzed coupling reactions.⁶ However, these strategies suffer from some serious drawbacks such as activating/deactivating effects of electron-donating/withdrawing groups,⁷ sequences in multistep reactions, low yields and decreased availability of functionalized arenes as starting materials.^7,8

A significant alternative is the “acyclic approach” for the synthesis of highly functionalized arenes, which are based on acyclic precursors.⁸ These cyclocondensation reactions include [3 + 2 + 1] Dötz reaction,⁹ transition metal catalyzed [2 + 2 + 2] cyclisation, [4 + 2] cycloadditions,¹⁰ [4 + 2] Danheiser alkyne-cyclobutenone cyclization,¹¹ 1,6-electrocyclization reactions,¹² cyclocondensations of dielectrophiles with dinucleophiles and [5 + 1] benzannulations between alkenoyl keteneacetals and nitroalkanes.¹³ However, these annulations proceeds in harsh reaction conditions, require highly expensive catalysts, suffers from regiochemical ambiguities and lack of substrate generality.⁸

The [3 + 3] addition of 1,3-bis(silyloxy)-1,3-butadienes with 3-silyloxy-2-en-1-ones is an important TiCl₄ mediated one pot cyclization reaction based on the “acyclic approach”.¹⁴ The significance of the reaction includes its high regioselectivity,¹⁴ excellent yields, moderate reaction conditions, and commercial availability of the catalyst.^15,16 TiCl₄ is an efficient Lewis acid and shows significant affinity for oxygen containing organic compounds. The catalyst is effective in many organic transformations,¹⁷ particularly in Pinacol coupling reaction,¹⁸ pyrrolidine synthesis,¹⁹ Claisen rearrangements,²⁰ and asymmetric aldol reaction.²¹ The alkene production from molecular reductive coupling of carbonyl compounds such as aldehydes, ketones, acylsilanes, ketoesters, and oxoamides are also prominent applications of titanium in organic chemistry.¹⁷

Chan and coworkers (in 1979) reported the synthesis of arenes by formal [3 + 3] cyclization of 1,3-bis(silyl enol ethers) with 1,3-dielectrophiles, using titanium(IV) as a Lewis acid (Scheme 1).²² The reaction is widely used for synthesis of valuable functionalized arenes.⁷ For example, Lewis acid promoted reaction of 1,3-bis(silyl enol ether) 1 with 2 delivers functionalized arene 3.

Scheme 1 TiCl₄ catalyzed cyclization of 1,3 bis(silyl enol ether) with 1,1,3,3-tetramethoxypropane.

Similarly, a biphenyl derivative 6 can be generated (Scheme 2) by the reaction of 1,3-bis(silyl enol ether) 4 and 3-silyloxy-2-en-1-one 5.

Scheme 2 TiCl₄ catalysed regioselective [3 + 3] addition of 1,3-bis(silyloxy)-1,3-butadienes with 3-silyloxy-2-en-1-ones.

Despite much synthetic advancements, mechanistic details of formal [3 + 3] cyclization are very limited. A proposed mechanism by Langer and coworkers⁷ is presented in Scheme 3. TiCl₄ selectively activates one of the two electrophilic centers of the unsymmetrical 1,3-dielectrophile by forming six membered chelation ring, which leads to the formation of exclusively one isomer and results in regioselective cyclization. Nature of the Lewis acid also affects the reaction pathway because specific functional groups are activated by specific Lewis acid.

Scheme 3 Proposed mechanism of TiCl₄ catalysed 3 + 3 addition of 1,3-bis(silyloxy)-1,3-butadienes with 3-silyloxy-2-en-1-ones.

The proposed mechanism involves coordination of 7 with TiCl₄ to give intermediate Int1, which is then attacked by the terminal carbon atom of 4 to give intermediate Int2. The Int2 loses OSiMe₃ moiety to deliver Int3. Cyclization of Int3 followed by aromatization in Int4 delivers a functionalized arene 8 (Scheme 3). The above mechanism allows to rationalize the regioselectivity of a particular formal [3 + 3] reaction, however, it is relatively silent regarding the different regioselectivities starting from two structurally similar substrates (Scheme 4, vide infra). Moreover, the mechanism is based on a 1,4 addition of 1,3-bis(silyloxy)-1,3-butadienes on 1,3-dienophile. A competitive 1,2 addition is not invoked in the mechanism.

Scheme 4 Illustration of observed regioselectivities in [3 + 3] addition of 1,3-bis(silyloxy)-1,3-butadienes with 3-silyloxy-2-en-1-ones.

With the computational tools in hand, we became interested to investigate the mechanism of the formal [3 + 3] addition and the results are presented here. There appears no theoretical reports on the mechanism of the titanium catalyzed [3 + 3] addition of 1,3-bis(silyloxy)-1,3-butadienes with 3-silyloxy-2-en-1-ones.

Computational methods

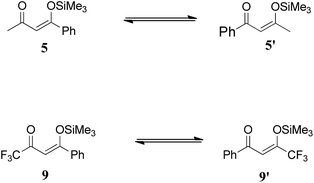
All calculations were performed with Gaussian 09. Geometries of the structures were optimized without any symmetry constraints at hybrid B3LYP method using 6-31G* basis set. The B3LYP method consists of three parameter hybrid functional of Becke in conjunction with the correlation functional of Lee, Yang, and Parr. The B3LYP method provides a nice balance between cost and accuracy, and it is known to perform reasonably well for the prediction of geometries and behaviour of neutral and charged species²³ including transition metals. The B3LYP method has been used in the theoretical simulations of properties and reactions catalysed by Titanium.²⁴ Each optimized structure was confirmed by frequency analysis at the same level (B3LYP/6-31G*) as a true minimum (no imaginary frequency) or a transition state (with one imaginary frequency). Imaginary frequencies of transition states were also evaluated to confirm that their associated eigenvector correspond to the motion along the reaction coordinates. Moreover intrinsic reaction coordinates (IRC) calculations were performed to confirm that the transition states connect to the concerned starting materials and products. IRC was performed until the stationary point was reached with RMS gradient less than 1 × 10⁻⁴. Stationary points located through IRC were then fully optimized at the above mentioned method. The reported energies for all structures are in kcal mol⁻¹ and include unscaled zero point energy corrections.

Density functional theory (DFT) calculations were performed to gain mechanistic insight for the regioselectivity observed for the [3 + 3] addition of 1,3-bis(silyloxy)-1,3-butadienes with 3-silyloxy-2-en-1-ones (Scheme 4). An ortho phenyl substituted benzoate ester 6 is the dominant product from 5 (a methyl ketone) whereas para phenyl substituted benzoate ester 10 is the major product from 9. The regioselectivity is altered when methyl ketone is replaced with a trifluoromethyl ketone, 9. A number of questions needs to be answered in order to logically investigate the mechanism; is the silyl group in dielectrophiles 5 and 9 dynamic between the two oxygen atoms (5 → 5′ and 9 → 9′)? If yes, then which isomer is more stable? What is the stability order for these two isomers when they are bound to titanium? Is it a direct addition of 4 on 5, or a 1,4 addition?

Therefore, in this study, we have attempted to address all these questions and the results are described below. However, to reduce the computational cost, SiMe₃ group is replaced with SiH₃.

Shift of the silyl group

α, β unsaturated ketones 5 and 9 can exist in isomeric species 5′ and 9′, respectively by the shift of the silyl group between two oxygen atoms (Scheme 5). The dynamic shift is studied both in the presence and absence of the transition metal (Ti) and it is observed that the shift of the silyl group both in fluorinated and non-fluorinated substrates, 9 and 5, respectively, is a kinetically favourable process even in the absence of the transition metal (titanium). A transition state for the silyl shift in 5 is located at a barrier of 2.91 kcal mol⁻¹ from 5 (titanium free conditions), and the reaction is exothermic by 0.36 kcal mol⁻¹. The low activation barrier for the silyl shift may be attributed to the close proximity of the silyl group to the keto oxygen in 5. The O1–Si bond (see Fig. 1 for numbering) in the transition state slightly increases to 1.89 Å compared to 1.73 Å in 5 (Fig. 2). The O1–Si bond in the product 5′ is 2.27 Å. On the other hand, the O2–Si bond decreases to 1.88 Å in TS1 from 2.22 Å in 5, and finally to 1.74 Å in 5′. The stronger bond of silicon with both oxygen atoms may be another reason for low activation barrier.

Scheme 5 Reversible silyl shifts between oxygens of 3-silyloxy-2-en-1-ones.

Fig. 1 Numbering scheme for discussion, and description of 1,2 and 1,4 addition.

Fig. 2 Potential energy diagram for silyl shift between 5 and 5′. All values are relative to 5 at 0.0 kcal mol⁻¹. All bond distances are in Angstroms. Unnecessary hydrogen atoms are removed for clarity.

A similar behaviour is also observed for the fluorinated substrate 9. A transition state (Fig. 3) for silyl shift is observed at a barrier of 4.06 kcal mol⁻¹, and the reaction is exothermic by 0.9 kcal mol⁻¹. A relatively higher activation barrier from 9 (compare 5 → 5′) may be attributed to the electron withdrawing effect of the CF₃ functional group which decreases the electron density on the keto oxygen. Therefore, the nucleophilic attack of the keto oxygen on the silyl group is relatively difficult. The shift of the silyl group in 5 and 9 is kinetically a favourable process even in the absence of transition metal.

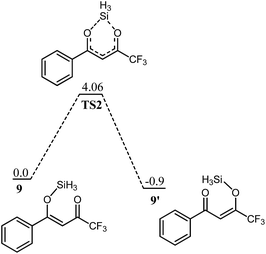Fig. 3 Potential energy diagram for silyl shift between 9 and 9′. All values are relative to 9 at 0.0 kcal mol⁻¹.

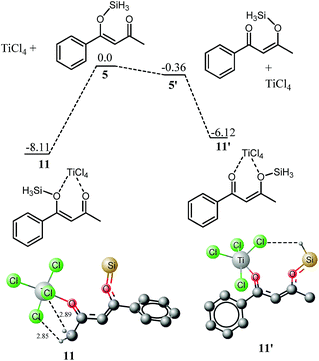
Complexation with titanium

Phenyl ketones 5′ and 9′ are more stable compared to their alkyl/trifluoroalkyl ketones 5 and 9, respectively, therefore, compounds 5′ and 9′ are anticipated as active species in the reaction. However, the situation is somewhat different after complexation with titanium. Although 5′ is more stable than 5; but, its titanium tetrachloride complex 11′ is relatively unstable by 2 kcal mol⁻¹ compared to 11, a complex from 5. The greater stability of 11 relative to 11′ can be explained on the basis of attractive interaction between the hydrogens of CH₃ with the chlorides of TiCl₄. H–Cl bond distances in 11 are 2.89 Å and 2.85 Å (Fig. 4).

Fig. 4 Potential energy diagram for complexation of 5 and 5′ with titanium to deliver 11 and 11′, respectively. All values are in kcal mol⁻¹ with respect to 5 at 0 kcal mol⁻¹. All bond lengths are in Angstroms, and unnecessary hydrogen atoms are removed for clarity.

For 9, this reversal of stability on complexation with titanium is not observed (Fig. 5). The complex of 9′ with titanium (12′) is still more stable than 12 by 0.38 kcal mol⁻¹. The higher stability of 12′ over 12 is supportive to our hypothesis above that interaction of hydrogen of CH₃ with the chlorides of TiCl₄ is the main driving force for the higher stability of 11 over 11′. The attractive interactions (CH₃⋯Cl) in 11 are replaced by repulsive interactions in 12 (CF₃ with chlorides).

Fig. 5 Potential energy diagram for complexation of 9 and 9′ with titanium to deliver 12 and 12′, respectively. All values are in kcal mol⁻¹ with respect to 9 at 0 kcal mol⁻¹.

In the next step of our mechanistic investigation we analyzed the distribution of charges in 11, 11′, 12 and 12′ (shown in Fig. 6) in order to predict the reactivity based on charge densities. In both 11 and 11′, the position of highest positive charge density is the carbon bearing the methyl group regardless of the fact whether this carbon is a keto carbon or silyloxy bearing carbon. In 11, C2 and C4 (see Fig. 1 for labelling) have 0.5 and 0.389 positive charges, respectively whereas in 11′, C2 and C4 bear 0.46 and 0.45 positive charges respectively. Since 11 is more stable and has higher positive charge on methyl ketone carbon therefore we believe that this isomer will be the active participating species in the reaction. For the fluorinated arene 12, the situation is quite opposite; a high positive charge is observed on carbon bearing the phenyl ring (C4). In 12′, carbons 2 and 4 have 0.327 and 0.439 positive charges, respectively whereas in 12, carbons 2 and 4 bear 0.394 and 0.414 positive charges, respectively. It is interesting to note that both isomers (of any system) have similar sequence of charge distribution.

Fig. 6 Mulliken charges analyses on carbon 2 and 4 in 11, 11′, 12 and 12′.

Discussion in the subsequent section has been divided into fluorinated and methyl systems, and in each section 1,4 and 1,2 addition are discussed in detail.

Fluorinated 1,3 dielectrophile

1,2 Addition

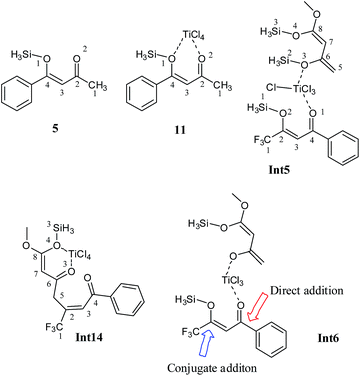
The bis silyl ether 4 contains two oxygen atoms which are available for binding with titanium therefore, it is believed that the bis silyl ether binds to 12 before the reaction takes place. The titanium is penta coordinated in 12′ and the binding of 4 with titanium of 12 would generate an octahedral complex, Int5. Coordination of oxygen with titanium is followed by loss of the silyl chloride (Scheme 4). The literature reveals that octahedral complexes of titanium are well known, and are quite stable.^25,26

Complexation of 4 with 12′ generates an intermediate octahedral complex Int5 where both oxygen atoms are in cis orientation. O1–Ti and O3–Ti bond lengths are 2.12 and 2.38 Å, respectively. The large bond distance of siloxy-Ti may be due to steric reasons (Fig. 7). The chlorides–Ti bonds trans to oxy ligands are relatively short (2.24 Å) whereas other Ti–Cl bonds are somewhat elongated (2.29 and 2.32 Å, shown in Fig. 8). The cis orientation of the oxy ligands is necessary for subsequent addition reaction. Any trans orientation of these group will not be favourable for C–C bond formation. A chloride ligand on titanium in Int5 is parallel to the silyl group at a distance of 3.29 Å.

Fig. 7 Potential energy diagram for elimination of H₃Si–Cl followed by C–C bond formation (Int5 → Int8); all energies are relative to Int5 at 0 kcal mol⁻¹. All bond lengths are in Angstroms. Unnecessary hydrogen atoms are removed for clarity. Values in parenthesis correspond to trimethylsilyl substituted derivatives.

Fig. 8 Optimized geometries of Int5, TS3 and Int6. All bond lengths are in Angstroms, and unnecessary hydrogen atoms are removed for clarity.

A transition state for the concomitant elimination of the silyl and chloride groups is located at a barrier of 19.36 kcal mol⁻¹. The transition state (TS3) has the geometry very similar to Int5 except the bond lengths change at the reaction site. The Ti–Cl bond elongates to 2.45 Å in TS3 from 2.24 Å in Int5. Cl–Si and O3–Si2 bond distances are 2.35 and 1.96 Å, respectively in the transition state. The reaction has low activation barrier, and easily accessible at room temperature. Moreover this step is also driven thermodynamically. The product of the reaction, Int6 is 6.99 kcal mol⁻¹ more stable than the starting material (Int5). The loss the silyl group generates an oxy ligands where both organic ligands are not well suited for C–C bond formation. Conformation changes are required to bring both organic fragments in proper orientation for C–C bond formation. This conformational change costs 7.66 kcal mol⁻¹. A transition state is located at a barrier of 5.2 kcal mol⁻¹ from Int6′. This low activation energy may be attributed to relatively higher positive and negative charge densities on C4 and C6 carbons, respectively. The C–C bond being formed has a bond length of 2.29 Å in the transition state. Some other bond lengths also change considerably during the C–C coupling reaction. The O3–Ti bond length increases from 1.78 Å in Int6′ to 1.90 Å in the TS4 whereas the O1–Ti bond length decreases from 2.06 to 1.94 Å.

Since we have replaced the trimethylsilyl group with SiH₃ in order to reduce the computational cost, it was of interest whether this simplification affects the activation barriers, and may change the regioselectivities. Towards this end, activation barriers for the key step (1,2 or 1,4 (vide infra)) are studied with Si(CH₃)₃ groups as well, and the activation barriers are given in the parenthesis (see Fig. 7 and 10). It is very obvious from Fig. 7 that the activation barrier is not affected considerably by replacing trimethylsilyl (4.84 kcal mol⁻¹) group with SiH₃ (5.20 kcal mol⁻¹).

Int7 is believed to undergo an interesting rearrangement of OTiCl₃ to the silyl group which subsequently delivers Int9 by elimination of TiCl₃(OSiH₃). Although transition state for this oxy-titanium shift is located for methyl system (vide infra); however, no such transition state is located for fluorinated analogue. Rather, a true minimum Int8 is observed in which oxytitanium is bound to both, silyl moiety and carbon 5. The O3–C5 and O3–Si1 bond distances are 2.66 Å and 3.04 Å, respectively. Thermodynamic cost for this shift is 16.42 kcal mol⁻¹. Int9 undergoes coordination of the 2^nd silyloxy oxygen (O4) which is followed by elimination of another Si and Cl, very similar to the one observed in Int5. The transition state for the elimination of silyl chloride (TS5) is not modelled here. The activation barrier for the elimination of silyl chloride, is believed similar to the one observed in Int5. The product of the silyl chloride elimination, Int10 undergoes nucleophilic attack on the CF₃–CO group. Kinetic barrier for the step is 26.56 kcal mol⁻¹. The reaction is also favourable thermodynamically; the product (Int11) lies 18.7 kcal mol⁻¹ lower in energy than Int10 (Fig. 9). The cyclized product is believed to undergo loss of a water molecule and finally tautomerization to deliver the product. The possibility of elimination of silyl chloride with concomitant cyclization to deliver the final product cannot be excluded safely.

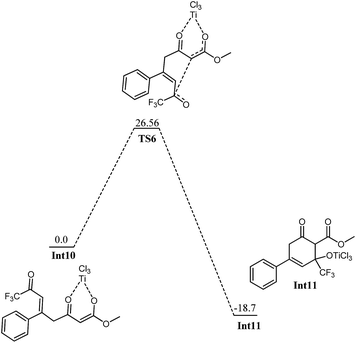Fig. 9 Potential energy diagram for cyclization in Int10 to generate Int11. All energies are in kcal mol⁻¹ relative to Int10 at 0.0 kcal mol⁻¹.

1,4 Addition

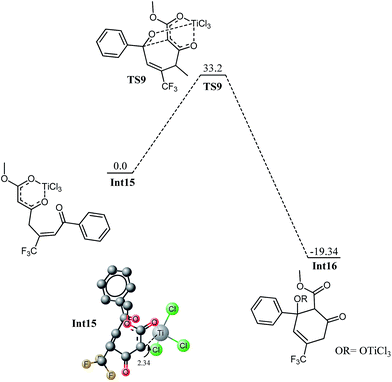
The competitive reaction for Int6′ is 1,4 addition on enone fragment instead of a 1,2 addition. The activation barrier for C–C bond formation through 1,4 addition was found higher compared to the 1,2 attack; 13.10 kcal mol⁻¹ for 1,4 addition compared with 5.2 kcal mol⁻¹ for the 1,2 attack. The higher activation barrier for Int6 → Int12 (Fig. 10) compared to Int6–Int6 → Int7 may be due to steric crowding at the carbon bearing the siloxy and CF₃ moieties, or may be due to electronic factors because of reduced charge density at keto carbon C2. The C6–C2 bond distance is 2.39 Å in the transition state (TS7), compared to 2.29 Å in the transition state for the 1,2 attack, TS4. The titanium has trigonal bipyramidal geometry in TS7 where fluorine atoms of CF₃ do not coordinate to the titanium. The reaction is thermodynamically favourable (E_R = 16.12 kcal mol⁻¹). The activation barrier for the similar reaction but involving Si(CH₃)₃ has a very similar activation barrier (12.37 kcal mol⁻¹). These findings are consistent with those in Fig. 7 that replacing a trimethylsilyl group with SiH₃ does not change the activation barrier to alter the regioselectivities.

Fig. 10 Potential energy diagram for 1,4 addition in Int6 to generated Int12, followed by change in coordination to generate Int13. Hydrogen atoms are removed for clarity. All bond lengths are in Angstroms. Values in parenthesis correspond to trimethylsilyl substituted derivatives.

Int12 undergoes elimination of O–SiH₃ (next to CF₃) and TiCl₃ moiety to generate the species for the next step, Int13. This process may be a direct one step process for the methyl ketone (vide infra) or may be a multistep process as in the case of trifluoro species. For the trifluoro species, first the silyl oxygen coordinates to titanium and a transition state TS8 has been located for this coordination. This is just an addition reaction because it does not involve elimination of any other group. The cyclic species undergoes cleavage of OSiH₃ and TiCl₃ to generate Int14 (see ESI†). In Int14, a silyl group is parallel to a chloride on titanium therefore; elimination of silyl chloride generates the enolxy species Int15. The geometry of Int15 has some interesting features; C7 is coordinating with titanium at a distance of 2.34 Å, the carboxylate oxygen (O4) along with the ortho carbon C7 behave as bidentate ligand for titanium, the titanium in Int15 has distorted octahedral geometry. Nucleophilic attack of C7 on C4 in Int15 generates the cyclic species Int16. The reaction has kinetic demand of 33.20 kcal mol⁻¹ (Fig. 11). In the transition state, C7–C4 bond distance is 2.68 Å whereas the C–Ti distance is increased to 2.75 Å. Although kinetically unfavourable, the reaction is highly favourable thermodynamically. The reaction is exothermic by 19.32 kcal mol⁻¹. Thermal energy available at room temperature is not sufficient to surpass this barrier which clearly illustrates that this is not the pathway which should be observed experimentally. The regioselectivity observed experimentally is in marked contradiction with the product obtained from 1,4 addition.

Fig. 11 Potential energy diagram for intramolecular cyclization in Int15 to generate Int16, all energy values are relative to Int15 at 0.0 kcal mol⁻¹. Hydrogen atoms are removed for clarity all bond lengths are in Angstroms.

The 1,2 addition is a favourable pathway energetically, and it explains the right regioselectivity. Although the calculations above reveal that 1,2 attack of enol on the keto oxygen delivers the product which is observed experimentally yet there is another set of similar calculations but with CF₃ ketone bound to titanium in the first step rather than a phenyl ketone. We have also considered this as a possible reaction in our study.

1,2 Attack on CF₃ ketone

Calculations have been performed on a titanium bound complex starting from CF₃ ketone, Int17. Typically the nature and the number of step are almost comparable to those for phenyl ketone regarding both 1,2 and 1,4 attack. We have repeated the same set of calculations for CF₃ ketone to explore the associated kinetics and thermodynamics. The first step is elimination of silyl chloride from Int17 for which a transition state has been located at a barrier of 19.67 kcal mol⁻¹ from starting complex. The activation barrier is very comparable to the elimination of silyl chloride in Int5 (19.36 kcal mol⁻¹). The reaction is thermodynamically favourable by 8.52 kcal mol⁻¹. A few important changes in bond distances on going to transition states are given in the table below (Table 1).

Table 1 Comparison of some important geometric parameters in Int17 and TS10

Bond	Int17	TS10
TiCl	2.24	2.45
Ti–O	2.36	2.00
O–Si	1.72	1.95
Si–Cl	3.31	2.35

---

Nucleophilic attack of enol on the C2 in Int18′ is a kinetically favourable (E_act 6.22 kcal mol⁻¹, see Fig. 12) but this activation energy is slightly higher (1 kcal mol⁻¹) compared to the activation barrier for nucleophilic attack on phenyl ketone Int6 (E_act = 5.2 kcal mol⁻¹). This difference in activation barrier may be attributed to the density of the positive charge of 12′ and 12 (vide supra). The important C6–C2 bond (being formed) has bond length of 2.37 Å in the transition state TS11 compared to 3.61 Å and 1.54 Å in Int19 and Int18, respectively. The similar reaction using Si(CH₃)₃ group instead of SiH₃ has the activation barrier of 6.63 kcal mol⁻¹ (see ESI, Fig. SI1†).

Fig. 12 Potential energy diagram of Ti catalyzed 1,2 addition of enol on CF₃ ketone, all values are in kcal mol⁻¹ relative to Int17 at 0.0 kcal mol⁻¹.

The next key step in this pathway is the cyclization of Int20 to Int21, a reaction which generates the cyclic intermediate (Int21) from enol by nucleophilic attack (Fig. 13). The calculated activation barrier for the cyclization is 20.60 kcal mol⁻¹. This activation barrier is although high but still accessible under the reaction conditions. Although energetics associated with this pathway are not very high (may proceed under reaction conditions); however, its comparison with 1,2 attack on phenyl ketone (1,2 attack starting from Int6) shows that this pathway is energetically less favourable. Moreover, the theoretical findings are consistent with the experimental regioselectivities (compare the structure of Int21 and Int11 with Int10).

Fig. 13 Potential energy diagram for cyclization in Int20. All values are in kcal mol⁻¹ relative to Int20 at 0.0 kcal mol⁻¹.

The 1,4 attack on CF₃ ketone is expected to be kinetically demanding, although it delivers the desired product. The 1,4 addition on CF₃ ketone is also modelled, and found to have high activation barriers (see Fig. SI2 and SI3†). The first 1,4 attack has an activation barrier of 15.99 kcal mol⁻¹ (much higher than any of the above three mechanisms). This high activation barrier is expected because this reaction not only involves 1,4 attack which is kinetically demanding but it involves intermediate 18′ on which attack is even more demanding kinetically. Analysis of the pathways, shown above, clearly indicates that the charge density shown in Fig. 6 is a good tool to predict the regioselectivity of the reaction. Moreover, pathways with 1,2 attack on ketone are energetically more favourable whereas conjugate addition is thermodynamically less favourable.

Methyl system

From Fig. 6, it is apparent that the methyl ketone 11 has higher Mulliken charge density on C2; therefore, this structure is only considered for mechanistic studies. The phenyl ketone 11′ is not considered for both 1,2 and 1,4 attack because higher activation barriers are expected than 11 (vide supra). Moreover, the regioselectivity expected through a 1,2 attack is in contradiction to what is observed experimentally.

1,2 Attack

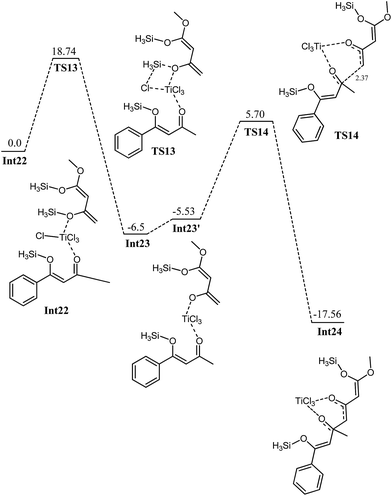
The first step is typically cleavage of a chloride and a silyl group in Int22. The titanium in Int22 has an octahedral geometry where both oxygen ligands are cis to each other. The O3–Ti–O2 bond angle is 81.77 degrees. The O3–Ti and O2–Ti bond distances are 2.40 and 2.06 Å, respectively. The Ti–Cl (trans to oxy ligands) bond lengths are in the range of 2.24–2.25 Å whereas the other chloride–titanium bond lengths are 2.30–2.31 Å. One of the chlorides is bent towards silyl group primarily because of the dipole dipole interactions (Fig. 14). A transition state for the cleavage of silyl chloride in Int22 is located at a barrier of 18.74 kcal mol⁻¹ (from Int22, see Fig. 15). In the transition state TS13, Cl–Ti bond distance increases to 2.46 Å. The alkoxide–titanium bond distance decreases to 2.01 Å in TS13. The geometry around titanium also changes. The Cl–Ti–O3 (silyl) angle drops to 159.0 degrees in TS13 from 176.18° in Int22. This activation barrier for the cleavage of a silyl and a chloride is very comparable to the one observed for the trifluoro system (vide supra). These findings clearly illustrate that the cleavage is not significantly influenced by the structure of the complex. The reaction is exothermic by 6.5 kcal mol⁻¹. The complex Int23 has trigonal bipyramidal geometry around titanium. The two chlorides and alkoxide ligands do not make a perfect trigonal planar structure. O–Ti–Cl bond angle is 114–115 degrees, whereas Cl–Ti–Cl bond angle is 127.65 degrees. Two chlorides and the alkoxide ligands are in one plane (trigonal). The third chloride and keto oxygen are in the perpendicular plane. The alkoxide–Ti and keto–titanium bond distances are 1.74 and 2.14 Å, respectively. The subsequent C–C bond formation in Int23 has kinetic demand of 11.23 kcal mol⁻¹, whereas the reaction is thermodynamically favourable by 12.03 kcal mol⁻¹. In the transition state TS14, the C2–C6 bond distance is 2.23 Å. Moreover, the O3–Ti and O3–C5 bond distances are 1.88 and 1.31 Å, respectively. The newly formed O2–Ti and C2–O2 bond distances are 1.94 and 1.30 Å, respectively. The Int23, generated as a result of C–C bond formation, undergoes an interesting cleavage/shift of titanium oxy group on the silyl group. This shift is predicted to have a kinetic demand of 19.12 kcal mol⁻¹. In the transition state, O1–C2 bond distance is 2.15 Å whereas the O2–Si1 bond distance is 3.17 Å.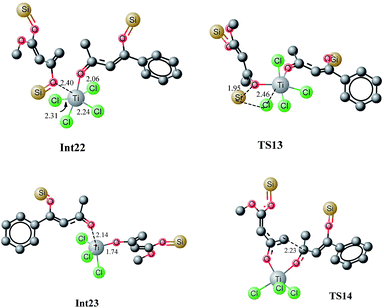

Fig. 14 Optimized geometries of Int22, TS13, Int23 and TS14. Unnecessary hydrogen atoms are removed for clarity. All bond lengths are in Angstroms.

Fig. 15 Potential energy diagram for elimination of silyl chloride followed by 1,2 addition of enol to methyl ketone to generate Int24. All values are in kcal mol⁻¹ relative to Int22 at 0.0 kcal mol⁻¹.

The titanium oxy group interacts very loosely with the silyl groups, as it is reflected with bond separation in the TS. This behaviour of the methyl system is remarkably different than what is observed for the trifluoromethyl analogue. In the case of trifluoromethyl system, this type of transition state is not observed rather an intermediate is observed in which titanium oxy species is located between carbon and silyl group (vide supra).

It is believed that the Int25 generated in the above step (Fig. 16) soon loses Cl₃Ti–OsiH₃ species and binds to TiCl₄ to generate Int26, as a precursor for the next step. Cleavage of a silyl and chloride in Int26 generates an intermediate Int27 ready for cyclization. Cyclization in Int27 is a kinetically and thermodynamically favorable process (Fig. 17). The titanium in TS16 has a trigonal bipyramidal geometry where two chlorides and an oxo ligand lie in the plane of trigon; however, the CH and chloride ligands are in the vertical axis. The CH–metal bond distance increases to 3.02 Å in the transition state from 2.22 Å in Int27. Moreover, the CH and keto carbon bond distance is 2.87 Å which indicates a very early transition state. The calculated activation barrier for the cyclization is 19.54 kcal mol⁻¹. Dehydration and tautomerization in Int28 may deliver the final aromatic product.

Fig. 16 Potential energy diagram for migration of OTiCl₃ to silyl moiety in Int24 to generate Int25. All values are in kcal mol⁻¹ relative to Int24 at 0.0 kcal mol⁻¹.

Fig. 17 Potential energy diagram for cyclization in Int27. All values are in kcal mol⁻¹ with respect to Int27 at 0.0 kcal mol⁻¹.

1,4 Addition

Int23 generated by the loss of a silyl chloride molecule can also undergo a 1,4 addition on the α, β unsaturated ketone to deliver intermediate Int29 which is thermodynamically more stable than the intermediate Int23 by 3.03 kcal mol⁻¹. The reaction has kinetic demand of 19.57 kcal mol⁻¹ which is higher than the kinetic demand for the 1,2 addition in Int23′ (11.23 kcal mol⁻¹). These observations are also consistent with the theoretical calculations for the trifluoromethyl system (vide supra) where direct attack is more favourable than the 1,4 addition. From these calculations, one can infer that 1,2-addition is a more feasible pathway compared to 1,4-addition for these formal [3 + 3] addition reactions (1,4 addition). The difference in activation barrier for 1,2 and 1,4 attack is 8.34 kcal mol⁻¹ for the methyl system whereas this difference is about 7.9 kcal mol⁻¹ for the trifluoromethyl analogue.

The subsequent cyclization has a calculated activation barrier of 19.72 kcal mol⁻¹ which is not significantly different than the one calculated for the cyclization in Int27 which clearly illustrates that the selectivity is governed at the first addition step of the formal [3 + 3] addition reaction. The 1,2 addition (1,2 addition), shown in Fig. 16 and 17, delivers the product with the experimentally observed regioselectivity. The 1,4 addition (shown in Fig. 18) does not deliver the product with the correct regioselectivity. These findings are consistent with our the calculations that 1,2 addition is a favourable process with lower activation barriers compared to the 1,4 addition.

Fig. 18 Potential energy diagram for Ti catalyzed 1,4 addition of enol to enone in Int23 All values in kcal mol⁻¹ with respect to Int23 at 0.0 kcal mol⁻¹.

In summary, we have shown that the experimentally observed different regioselectivities for CH₃ and CF₃ enones can be explained by a common mechanism where 1,2 addition of 1,3-bis(silyl enol ethers) on 1,3-dielectrophiles is a more favorable pathway than the competing 1,4 addition. The differences in regioselectivities originate from different isomeric structures of enones entering in the catalytic cycle.

Conclusions

Density functional theory calculations have been performed to gain mechanistic insight of the formal [3 + 3] addition of 1,3-bis(silyl enol ethers) and 1,3-dielectrophiles to explain the experimentally observed regioselectivities. For this purpose, reaction of 1,3-bis(silyl enol ethers) with two different 1,3-dielectrophiles (5 and 9) is studied. The silyl moieties in 1,3-dielectrophiles are dynamic even in the absence of a metal catalyst (E_act < 5 kcal mol⁻¹). The isomeric dielectrophiles (for example 5 and 5′) differ in their reactivity in formal [3 + 3] addition, and it depends on the strength of the positive charge (Mulliken charges) on the electrophilic carbon atom. Calculations reveal that a single mechanism can justify the experimentally observed different regioselectivities for 5 and 9 depending on the isomeric species entering in the catalytic cycle (11 and 12′). 1,2 and 1,4 addition mechanisms have been studied for both isomeric forms of each dielectrophile. The calculations reveal that 1,2 addition of 1,3-bis(silyl enol ethers) on 1,3-dielectrophile is a favorable process over the conjugate (1,4) addition. A typical mechanism involves coordination of 1,3-bis(silyl enol ethers) and 1,3-dielectrophiles with TiCl₄ followed by elimination of silyl chloride. The elimination of silyl chlorides has an activation barrier of about 19–20 kcal mol⁻¹. The elimination of the silyl chloride is followed by a nucleophilic attack on the dielectrophile. This nucleophilic addition governs the selectivity of the reaction. For trifluoromethyl, 1,2 addition (1,2 addition) is kinetically much favorable (E_act = 5.2 kcal mol⁻¹) than the 1,4 addition (E_act = 13.1 kcal mol⁻¹, Fig. 18). For the methyl analogue, the difference in the activation barriers for the 1,2 and 1,4 addition is even more pronounced in the favor of 1,2 addition (about 8.34 kcal mol⁻¹). The trends in the activation barrier for 1,2 and 1,4 addition for both dielectrophiles can be correlated to Mulliken charges at the electrophilic centers.

Acknowledgements

The authors acknowledge the financial support from Higher Education Commission of Pakistan (Grant No. 1899), COMSATS Institute of Information Technology, and University of Rostock. This work has been partly supported by the BMBF within the project “Light2Hydrogen” (Spitzenforschung und Innovation in den Neuen Ländern), by the European Union (European Social Funds, ESF) within the project “PS4H” and by the Ministry for Education, Science and Culture of Mecklenburg-Vorpommern.

Notes and references

1. R. J. Nijveldt, et al. , Am. J. Clin. Nutr., 2001, 74, 418–425.
2. L. Brunsveld, et al. , Chem. Rev., 2001, 101, 4071–4098.
3. Z. Rappoport, The Chemistry of Phenols, John Wiley & Sons, 2004.
4. W. Langenaeker, K. Demel and P. Geerlings, J. Mol. Struct.: THEOCHEM, 1991, 234, 329–342 , and reference herein.
5. O. N. Chupakhin, V. N. Charushin, and H. C. van der Plas, Nucleophilic aromatic substitution of hydrogen, Academic Press, 2012.
6. N. Miyaura and A. Suzuki, Chem. Rev., 1995, 95, 2457–2483.
7. G. Karapetyan, et al. , Curr. Org. Chem., 2012, 16, 557–565.
8. G. Shkoor, M.Sc. Thesis, University of Rostock, 2010.
9. K. Dötz and P. Tomuschat, Chem. Soc. Rev., 1999, 28, 187–198.
10. L. V. Bonaga, et al. , J. Am. Chem. Soc., 2005, 127, 3473–3485.
11. R. L. Danheiser, et al. , J. Am. Chem. Soc., 1990, 112, 3093–3100.
12. S. Serra, C. Fuganti and A. Moro, J. Org. Chem., 2001, 66, 7883–7888.
13. X. Bi, et al. , J. Am. Chem. Soc., 2005, 127, 4578–4579.
14. H. Feist and P. Langer, Synthesis, 2007, 3, 327–347.
15. T. Mukaiyama, Angew. Chem., Int. Ed. Engl., 1977, 16, 817–826.
16. H.-H. Zhang, et al. , Org. Lett., 2014, 16, 4896–4899.
17. P. Choudhary, et al. , Mod. Chem. Appl., 2012, 2013, 1.
18. M. Bandini, et al. , Tetrahedron Lett., 1999, 40, 1997–2000.
19. S. Ramesha, H. Bhojya Naik and H. Harish Kumar, J. Sulfur Chem., 2007, 28, 573–579.
20. K. Narasaka, E. Bald and T. Mukaiyama, Chem. Lett., 1975, 1041–1044.
21. C. Gennari, et al. , J. Am. Chem. Soc., 1985, 107, 5812–5813.
22. T.-H. Chan and P. Brownbridge, J. Chem. Soc., Chem. Commun., 1979, 578–579.
23. V. Specowius, et al. , Adv. Synth. Catal., 2012, 354, 1163–1169.
24. T. J. de Bruin, et al. , Organometallics, 2003, 22, 3404–3413.
25. R. Clark, J. Chem. Soc., 1963, 1377–1384.
26. R. Clark, et al. , J. Chem. Soc., 1963, 379–387.

---

Footnote

† Electronic supplementary information (ESI) available: Total electronic, zero-point and Gibbs free energies along with the Cartesian coordinates of the optimized geometries are shown in the ESI. See DOI: 10.1039/c5ra19238b

---