Photoluminescence enhancement from silicon quantum dots located in the vicinity of a monolayer of gold nanoparticles†
Abstract
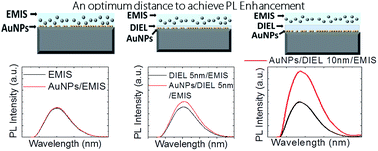
In this paper we show that it is possible to carry out a functional coupling between a thin film of silicon quantum dots embedded in a silicon nitride matrix (SiQDs) and a monolayer of gold nanoparticles by using dry and low temperature techniques, such as those used in microelectronics industry, i.e., Remote Plasma Enhanced Chemical Vapor Deposition (RPECVD) and Sputtering. The coupled structure showed 105% of photoluminescence (PL) enhancement, compared with PL observed from the SiQDs without the gold monolayer. The SiQDs used as light emitters have an average diameter of 3.1 nm, a particle density of 6.04 × 1012 particles per cm2 and a maximum PL peak at 505 ± 5 nm. Additionally, the gold nanoparticles were designed with the following characteristics: the particles are embedded in a silicon nitride matrix, show quasi-spherical shapes, an average diameter of 2.9 nm, a particle density of 2.52 × 1012 particles per cm2 and their surface plasmon resonance is located at 540 ± 3 nm. We found that there is an optimum separation distance between SiQDs and the gold monolayer to achieve the maximum photoluminescence enhancement. For our structure, such optimal distance was 10 ± 1 nm. We consider that there could be two combined physical effects responsible of the enhancement: (a) a plasmonic diffraction-limited coupling and (b) a change of the scattering mechanisms of the primary laser light.

 Please wait while we load your content...
Please wait while we load your content...