Structure–property relationship in lead-free A- and B-site co-doped Bi_0.5(Na_0.84K_0.16)_0.5TiO₃–SrTiO₃ incipient piezoceramics

Abstract

In this work, a phase diagram of A- and B-site co-substituted 0.96[{Bi_0.5 (Na_0.84K_0.16)}_1−x−yLi_xMg_y(Ti_1−zNb_z)O₃]–0.04SrTiO₃ (abbreviated as LMN-doped BNKT–ST), where x, y and z = 0.00–0.030, was schematically constructed on the basis of crystal structure and electromechanical, dielectric and piezoelectric properties. The underlying mechanism of the compositionally-induced non-ergodic (NR) to ergodic relaxor (ER) phase transition was explored, and emphasis was given on relating the chemically-induced polymorphic structural phase transition to the dynamics of polar nano-regions (PNRs) and their random fields, which strongly affect the dielectric, ferroelectric, piezoelectric and field-induced strain properties of the investigated system. X-ray diffraction patterns revealed that LMN doping resulted in a transition from coexistence of rhombohedral and tetragonal phases to a pseudocubic phase. Both the dielectric constant and the ferroelectric–relaxor transition (T_F–R ∼ 100 °C) temperature decreased with an increase in LMN content. The piezoelectric and ferroelectric responses of the BNKT–ST ceramics were significantly decreased by the addition of LMN. However, the destabilization of the piezoelectric and ferroelectric properties was accompanied by significant enhancements in the bipolar and unipolar strains. A large electric-field-induced strain (S = 0.28%) and a corresponding dynamic piezoelectric constant (S_max/E_max) of 560 pm V⁻¹ were observed under the driving field of 5 kV mm⁻¹ when 1.5 mol% LMN was substituted on respective sites. This significant strain enhancement at this composition, with LMN = 0.015, may be attributed to both the field-induced reversible structural transition and the compositionally-induced NR to ER phase transition. The composition- and temperature-dependence of the energy storage density (W) were studied to demonstrate the practicability of the LMN-doped BNKT–ST. It was found that the addition of LMN enhanced the difference between maximum polarization and remnant polarization, resulting in an improvement of the energy storage properties. For the composition with LMN = 0.020, a nearly temperature-invariant large recoverable energy density (W = 0.70 J cm⁻³) was achieved under 5.5 kV mm⁻¹ in the wide temperature range of 100–150 °C. These properties indicate that the synthesized system might be a promising lead-free candidate for actuator and energy storage capacitor applications.

---

1. Introduction

Since the discovery of the piezoelectric phenomenon in polycrystalline materials, lead-based ceramics such as Pb(Zr,Ti)O₃ (PZT) and Pb(Mg,Nb)O₃–PbTiO₃ (PMN–PT) have been widely used in the electronics industry for various applications, such as in sensors and actuators. However, due to environmental issues, considerable attention has been shifted towards non-hazardous materials to replace toxic Pb-based materials for use in device fabrication.^1–4 In the search for lead-free piezoelectric materials, Bi_0.5Na_0.5TiO₃ (BNT)-based systems have become the focus of intense interest in the past few decades on account of their environmental friendliness, excellent ferroelectric properties and their piezoelectric properties. However, poling of pure BNT ceramics is difficult due to their high conductivity and coercive field (E_c), resulting in BNT ceramics having comparatively low piezoelectric properties, which are insufficient for practical applications.⁴ Enduring efforts have been made in the last decade to improve the piezoelectric properties of BNT ceramics by modification with different ABO₃ additives, resulting in varying degrees of success.^5–8 In addition, BNT-based materials are categorized as relaxor materials, i.e. their dielectric response is frequency-dependent and is linked to local structural fluctuations (polar nano-regions (PNRs)).⁹

Analogously to PZT, improved electromechanical responses were observed in BNT-based materials at morphotropic phase boundary (MPB) compositions. In the MPB composition of the BNT–BKT binary system, a relatively high strain of 0.19% with a corresponding normalized strain (d^*₃₃ = S_max/E_max) of 240 pm V⁻¹ has been observed.⁷ Although many efforts have been devoted to further improving their electromechanical responses in order to incorporate them into devices with acceptable performance, the overall piezoelectric properties of the lead-free counterparts are still inferior to those of lead-based systems. A number of previous studies have reported that the electromechanical properties can be improved by modifying the BNT–BKT system with various A-site (such as Li⁺, Sr²⁺, Nd³⁺, La³⁺ and Er³⁺)^10–16 and B-site single elements (like Ta⁵⁺, Sn⁴⁺, Nb⁵⁺, Hf⁴⁺, Zr⁴⁺, etc.),^3,17–21 as well as with ABO₃-type perovskites.^21–30 These studies suggest that the base composition and the nature of chemical modifiers significantly affect the ferroelectric and piezoelectric properties of BNT-based ceramics. Recently, co-doping of impurities into A- and B-sites at the same time was found to be very effective in enhancing the electric-field-induced strain response.^31,32 It was found that the origin of the large electromechanical strain in lead-free BNT-based ceramics may be due to the formation of a weak relaxor phase (recently identified as an ergodic relaxor phase (ER)) by chemical modification, which transforms into a long-range ferroelectric state under the influence of an external electric field.^{15–18,23,24} However, the origin of the enhanced electric-field-induced strain is still under debate.

Even though several promising BNT-based solid solutions were recently investigated, it has become evident that one single compound will not be likely to replace lead-containing materials across the whole diverse range of piezoelectric applications. Rather, multiple tailored lead-free solutions are sought for individual applications. In search of new alternatives for lead-based materials in electronic devices, A- (Li, Mg) and B-site (Nb) co-modified BNKT–ST ceramics were synthesized by a conventional mixed oxide route, and the effects of A- and B-site (Li, Mg and Nb, referred to as LMN) simultaneous doping on the structural and electromechanical properties were studied in detail. In this work, the underlying mechanism of the compositionally-induced NR to ER phase transition was explored and a phase diagram was schematically constructed on the basis of crystal structure, dielectric, ferroelectric and piezoelectric properties and electric-field-induced strain measurements. The main emphasis was given to relating the chemically-induced polymorphic structural phase transition to the dynamics of polar nano-regions (PNRs) and their random fields, which strongly affect the dielectric, ferroelectric, piezoelectric and field-induced strain properties of the investigated system.

2. Experimental procedure

Piezoelectric ceramics with composition 0.96[{Bi_0.5(Na_0.84K_0.16)}_1−x−yLi_xMg_y(Ti_1−zNb_z)O₃]–0.04SrTiO₃ (x, y, z = 0–0.030) were synthesized by a conventional solid-state reaction technique. Commercially available reagent grade oxide and carbonate powders of Bi₂O₃, Na₂CO₃, TiO₂, K₂CO₃, SrCO₃, Li₂CO₃, MgO and Nb₂O₅ (99.9%, Sigma Aldrich Co. St. Louis, MO) were used as starting materials. The hygroscopic Na₂CO₃ powder was dried in an oven at 100 °C for 24 h. For each composition, the starting materials were weighed according to the stoichiometric formula and powder mixtures were ball milled for 24 h in ethanol with zirconia balls as milling media. The slurries were subsequently dried and calcined at 850 °C for 2 h. After calcination, the mixtures were ball milled for 24 h and dried. The dried powders were pulverized, mixed with an aqueous polyvinylalcohol (PVA) solution as a binder for granulation and passed through a 150 mesh sieve. Disk-shaped ceramic specimens with a diameter of 10 mm were then prepared by compacting the granulated powders at 98 MPa. The pressed disks were sintered at 1160 °C for 2 h in covered alumina crucibles. To minimize the evaporation of the volatile elements Bi and Na, the disks were embedded in the powder of the same composition.

Silver paste was coated on both faces of the sintered samples and fired at 650 °C for 0.5 h to form electrodes. The specimens used to measure the piezoelectric properties were poled in a silicone oil bath with a dc field of 4 kV mm⁻¹ for 15 min. All the electrical measurements were performed after aging for at least 24 h. The crystal structures were characterized using X-ray diffractometry (X’pert MPD 3040, Philips, The Netherlands). Raman spectral lines at room temperature were obtained using a dispersive Raman spectrometer (ALMEGA, Nicolet, USA). Surface morphology was checked through scanning electron microscopy (SEM, JP/JSM5200, Japan). The dielectric constants and losses of the ceramics were measured by an automatic acquisition system using an impedance analyzer (Agilent HP4292A, USA) in the temperature range of 25–500 °C at different frequencies. Polarization versus electric field (P–E) hysteresis loops were measured in silicon oil with the aid of a ferroelectric test system (Precision LC, Radian Technologies Inc., Albuquerque, NM) at 20 Hz. Field-induced strain was measured with a contact-type displacement sensor (Millitron; Model 140).

3. Results and discussion

Fig. 1(a) plots the X-ray diffraction (XRD) patterns of the LMN-modified BNKT–ST ceramics, measured between 2θ = 20–70°. The compositions with LMN ≤ 0.020 have a pure perovskite structure within the detection limit of XRD, showing a stable solid solution at the optimized sintering temperature of 1160 °C. At higher dopant levels (LMN > 0.020), traces of secondary phases were observed (which may be due to segregation of elemental phases at grain boundaries), displaying the solubility limit of LMN in the BNKT–ST matrix. To further investigate the symmetry of the perovskite phase, Fig. 1(b) shows magnified XRD patterns of the LMN-doped BNKT–ST ceramics. In agreement with previous work, the pure BNKT–ST sample (‘LMN 0.00’) exhibited coexistence of rhombohedral and tetragonal symmetry, evident from visible splitting of the (111)/(11̄1) and (002)/(200) peaks at 40° and 46°, respectively.⁷ For the sample ‘LMN 0.010’, both the (111)/(11̄1) and (002)/(200) peaks are close to each other, resulting in relatively high piezoelectric performance (see Fig. 6). However, for LMN 0.015, the (111)/(11̄1) and (002)/(200) split peaks of the rhombohedral and tetragonal phases merged into single (111) and (002) peaks at 40° and 46°, respectively, indicating a phase transition from mixed rhombohedral–tetragonal phases to a single pseudocubic phase. All LMN ≥ 0.015 compositions show the single pseudocubic symmetry.^19,32 The properties of ferroelectric (FE) materials are sensitive to structural changes at angstrom (unit cell), nanometer (nano-domains) and micrometer (FE domains) scales. The driving forces for these changes are mainly of two types: randomized driving forces (chemical pressure (dopant), thermal pressure (temperature)) and an organized driving force (electric field). Of the list, most interest is focused on the status of polar nano-domains under these driving forces, which directly affect the properties of these FE materials. Recently, the presence of two types of domains at the nanoscale, rhombohedral (R3c) and tetragonal (P4bm), was proposed and experimentally confirmed by transmission electron microscopy (TEM) and piezo force microscopy (PFM) supported by Raman spectroscopy in BNT-based ceramics, which is encouraging for the understanding of some controversial and unclear issues relating to the structure–property relationships of the relaxor FE materials.^33–35 The compositionally-driven structural phase transition and corresponding FE properties shed light on the structure–property relationships of these materials.

Fig. 1 X-ray diffraction patterns of LMN-doped BNKT–ST (LMN = 0.00–0.030) ceramics in the 2θ ranges of (a) 20–70°, (b) 39–41° and 45–47°.

Room-temperature Raman spectra of LMN-modified BNKT–ST ceramics are shown in Fig. 2. The four main regions in the Raman spectra are as follows: (1) the observed vibrational mode at around 135 cm⁻¹ is associated with the A-site cations, (2) the 260 cm⁻¹ mode is related to Ti–O vibrations, (3) the 450–700 cm⁻¹ region hosts modes ascribed to the vibration of the TiO₆ octahedra, and (4) the high-frequency region above 700 cm⁻¹ features modes related to A₁ (longitudinal optical) and E (longitudinal optical) overlapping bands.^36,37 The mode at ∼135 cm⁻¹ can be associated with vibrations of A-site cations in the perovskite structure, influenced by A-site doping. It can be found that the mode corresponding to Ti–O vibrations, centered at around 260 cm⁻¹, becomes broader and starts splitting into two bands that are shifted apart from each other; this may be due to the co-occupancy of different cations (Ti/Nb) with different sizes at the B-site, resulting in the distortion of the unit cell. The two overlapping bands associated with the vibration of the TiO₆ octahedra in the range of 450–650 cm⁻¹ separate into two distinct bands in samples with higher LMN content, which demonstrates particular phonon behavior in the structural evolution and a phase mixture.³⁷ The Raman scattering, along with XRD and electrical measurements, revealed that LMN modification significantly influenced the host BNKT–ST perovskite.

Fig. 2 Room-temperature Raman spectra of LMN-doped BNKT–ST (LMN = 0.00–0.030) ceramics.

The secondary electron SEM images of sintered LMN-doped BNKT–ST ceramics with compositions with LMN = 0.00, LMN = 0.010, LMN = 0.020 and LMN = 0.030 are shown in Fig. 3. Noticeably dense microstructures were observed for all the investigated samples. The partial substitution with LMN seems not to have exerted any significant influence on the morphology or the average grain size of the BNKT–ST ceramics.

Fig. 3 SEM micrographs of the LMN-doped BNKT–ST ceramics (LMN = 0.00, 0.010, 0.020 and 0.030) sintered at 1160 °C.

Fig. 4 shows the temperature dependences of the dielectric constant (ε_r) and dielectric loss (tan δ) of the LMN-doped BNKT–ST poled ceramics with LMN = 0.00, 0.010 and 0.030 at frequencies of 1, 10 and 100 kHz. Two dielectric anomalies were observed in ε_r at all measured frequencies, corresponding to the maximum dielectric constant temperature (T_m) and the FE–relaxor transition temperature (T_F–R), which were attributed to thermal evaluation of polar nano-regions (PNRs) of R3c and P4bm symmetry. It can be seen from Fig. 4 that T_F–R, which is determined from the inflection point in ε_r (T), is relatively frequency-independent but is composition-dependent. The single spike peak in tan δ at T_F–R (∼100 °C) in the mixed R3c/P4bm phase region (LMN = 0.00 and 0.010) has become broad and shifted to lower temperature for the single pseudocubic (for the LMN ≥ 0.015 compositions) phase. In the mixed-phase region, T_F–R and d₃₃ are inversely related to each other as a function of compositional disorder. At T_F–R, the field-induced FE-state is destabilized (depolarized) during heating, accompanied by a sudden drop in d₃₃ (T), shown in Fig. 9. This depolarization process shifted to lower temperatures with increasing compositional disorder. A high d₃₃ (210 pC N⁻¹) was observed for the sample with LMN = 0.010. It can be explained by the coexistence of two types of PNRs with 14 energetically-equivalent polarization orientations at this MPB composition, which are easily accessible under the applied electric field due to competitive free energy between the R3c/P4bm PNRs, resulting in high intrinsic strain and d₃₃. Interactions among these two types of PNRs for compositions with LMN = 0.00 and 0.010 with T < T_F–R are not dynamically random, but cooperatively quenched and strongly dependent on the random A- and B-site cationic occupancy. Such quenched random electric fields among the R3c/P4bm PNRs with intermediate-range (not short-range nor long-range) inhibit the formation of long-range order and cause a non-ergodic relaxor (NR) state. This NR state can transform irreversibly from this cooperatively frozen nano-domain state to more ordered macro-size FE domains under the external electric field (poling) at room temperature, evidenced by a high coercive field (E_c). The coalescence of these nano-domain PNRs due to the cooperative freezing of PNRs results in frequency-independent dispersionless dielectric curves in the low doping region (LMN = 0.00 and 0.010) at low temperatures. The poling of these NR compositions enhances the piezoelectric constant. On the other hand, both the randomizing external fields (i.e. the increase in dopant concentration and temperature) can induce the polymorphic phase transition (PPT) and also dilute the cooperative interaction between PNRs, changing the symmetry, size and dynamics of the PNRs with a noticeable increase in ε_r (T). Thus, for T > T_F–R, dispersive and diffusive behavior of ε_r with destabilized FE order was observed, which is a hallmark of the ER state, which transforms reversibly to the FE state under the applied electric field. This increase in the degree of ergodicity may be due to the different relaxation time responses of A- and B-site chemically-induced R3c and P4bm PNRs to the external AC fields. The diffusive and frequency-dispersive behavior around T_F–R and T_m strongly suggests that both undoped BNKT–ST and LMN-simultaneously-doped ceramics could be classified as relaxors, as reported for other BNT-based ceramics.^{15–18,23,24}

Fig. 4 Temperature dependence of dielectric constant and dielectric loss of poled LMN-doped BNKT–ST (LMN = 0.00, 0.010 and 0.030) ceramics as a function of different frequencies.

The diffuse phase transition was observed for all samples, as demonstrated by the dielectric peak broadening. To explain the dielectric behavior with the diffuse phase transition, the value of γ was calculated using the modified Curie–Weiss law:^38–41

Fig. 5 shows plots of log(1/ε_r − 1/ε_m) vs. log(T − T_m) at 1 kHz for the samples with compositions LMN = 0.00 and 0.030. The equation 1/ε_r = (T − T_m)² has been shown to be valid over a wide temperature range instead of the normal Curie–Weiss law, where T_m is the temperature at which the dielectric constant reaches its maximum, ε_m is the maximum dielectric constant, γ is the diffusivity for the phase transition (which indicates the degree of dielectric relaxation) and c₂ is the Curie constant. For γ = 1, the materials are normal ferroelectrics, while those with γ = 2 correspond to relaxor ferroelectrics. The values of both γ and c₂ depend on the composition and structure of the materials. The slope of the curve was obtained at 1 kHz after fitting the curve (Fig. 5). The γ values were found to be 1.42, 1.56, 1.79 and 1.87 for LMN = 0.00, LMN = 0.010, LMN = 0.020 and LMN 0.030, respectively, which confirmed the diffuse phase transition in the LMN-doped BNKT–ST system.

Fig. 5 Plots of log(1/ε_r − 1/ε_m) vs. log(T − T_m) at 1 kHz for the LMN-doped BNKT–ST ceramics (LMN = 0.00 and 0.030).

The P–E hysteresis loops of the LMN-doped BNKT–ST ceramics with LMN = 0.00, 0.010, 0.015, 0.020 and 0.030 measured at room temperature are shown in Fig. 6. Undoped BNKT–ST ceramics display typical well-saturated P–E hysteresis loops with relatively large remnant polarization (P_r) and coercive field (E_c). For this composition, the applied electric field, that is strong enough to overcome the random fields between PNRs, induces FE order, and the NR state is converted into a permanently-ordered FE state irreversibly for temperatures lower than T_F–R. As is evident in the hysteresis curves, LMN exerts a significant influence on the shape and polarization values of the P–E loops. Also, the profiles of the P–E hysteresis loops are in good agreement with the XRD results. For the first two compositions (LMN = 0.00 and LMN = 0.010), with the coexistence of rhombohedral (R3c PNRs) and tetragonal (P4bm PNRs) symmetry (see Fig. 1), the effect of increasing the LMN content was simply to dilute the NR phase without any structural changes up to the LMN = 0.010 composition (evident from XRD results). At the critical composition (LMN = 0.015), the crystal structure of the material changes from mixed rhombohedral–tetragonal phases into a single pseudocubic phase with mixed ER and NR symmetry. This structural change at the unit cell level may cause changes to the symmetry of the PNRs, and consequently weaken the interaction between PNRs (which favors the ER state), resulting in sharp decreases of P_r and E_c and the hysteresis curve becoming slightly pinched and slimmer. Further, for LMN > 0.015, the gradual decreases of P_r and E_c may be ascribed to the stabilization of the ER phase.^3,5,9–12 Moreover, along with E_c, the small signal piezoelectric coefficient (d₃₃) initially increased from 160 pC N⁻¹ (undoped poled BNKT–ST) to 210 pC N⁻¹ (LMN = 0.010) in the NR state, as shown in Fig. 7. The increase in d₃₃ for the sample with LMN = 0.010 can be explained by the intrinsic piezoelectric contribution to strain. The enhanced intrinsic strain at the unit cell level is a function of chemical pressure, which is supported by both a comparably small hysteresis in the linear strain response (see Fig. 11) and an increase in negative strain (see Fig. 10). The increase in E_c may be due to sluggish movement of FE domains. With further increase in LMN concentration (LMN > 0.010), the continuous decrease in d₃₃ can be linked with the increase in the degree of ergodicity of the material. The observed trend of d₃₃ was also in good agreement with dielectric and electromechanical measurements. The alignment and conversion of nano-domains to FE domains in the field-induced FE phase for the NR compositions (LMN = 0.00, 0.010) were largely preserved after the poling field was removed, and relatively high d₃₃ values were measured. In contrast, the alignment of dynamically-fluctuating PNRs in the ER (LMN > 0.010) is not preserved after the removal of a strong poling field. As a consequence, small values of d₃₃ were observed.

Fig. 6 Effects of LMN substitution on the ferroelectric properties of LMN-doped BNKT–ST (LMN = 0.00–0.030) ceramics.

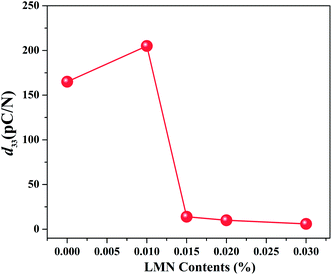Fig. 7 Variation in the room-temperature piezoelectric constant (d₃₃) of LMN-doped BNKT–ST (LMN = 0.00–0.030) ceramics as a function of different compositions.

Since the stability of the relaxor FE phase is a function of both the composition and temperature, the temperature-dependent polarization P–E loops were also investigated, as shown in Fig. 8. Similarly to the effects of chemical modification, ergodicity also increases monotonously with temperature. The NR phase becomes unstable at ∼100 °C and the relaxor is predominantly ER. The thermally-induced ergodicity results in the pinching of P–E loops, and also a sudden decrease in d₃₃ as a function of temperature at T_F–R (Fig. 9). Due to limitations of our measurement equipment, it is hard to measure d₃₃ directly at higher temperature. Instead, we measured the d₃₃ values of the poled samples at room temperature after annealing the samples for 20 min at each chosen temperature. The room temperature P–E loop is typical for a FE with clear hysteresis and saturation. As the temperature increased above T_F–R (∼100 °C), both P_r and E_c dropped sharply, corresponding to the emergence of the ER state, where the electric-field-induced polarization in short-range nano-domains reverted back to the equilibrium ER state after the removal of the electric field. For the composition with LMN = 0.020, a pure ER state was observed over the whole temperature range with slim P–E loops. Due to the comparable effects of temperature and compositional disorder, it is expected that FE properties for a relaxor, which is already an ER at room temperature, will decrease upon heating. The temperature-dependent d₃₃ values reveal a slight enhancement from room temperature up to the vicinity of T_F–R, and then a sudden decrease for T > T_F–R was observed for the composition with LMN = 0.00, due to the enhancement of the degree of ergodicity (Fig. 9).

Fig. 8 Temperature dependence of P–E loops of LMN-doped BNKT–ST (LMN = 0.00 and 0.015) ceramics as a function of LMN content.

Fig. 9 Variation in the temperature-dependent piezoelectric constant (d₃₃) of LMN-doped BNKT–ST (LMN = 0.00 and 0.020) shown in black and red respectively ceramics as a function of composition.

Fig. 10 shows the bipolar strain hysteresis loops of the LMN-modified BNKT–ST ceramics measured at 5 kV mm⁻¹. It is evident that the BNKT–ST without any addition of LMN exhibited a butterfly-shaped strain hysteresis loop with noticeable negative strain (S_neg, defined in Fig. 10 (inset): the difference between the zero-field strain and the lowest strain, which is only visible in the bipolar cycle) that is typical for FE materials. In contrast, as the LMN content was increased, the strain loops show a gradual deviation from typical FE behavior, evident from the reduction in S_neg, closely related to domain back-switching during bipolar cycles.¹⁹ Maximum strains of 0.25% were observed for the sample with LMN = 0.015. Beyond this, the maximum strain gradually decreased, while the S_neg nearly vanished. Based on previous reports on BNT-based ceramics, the FE order was significantly disrupted by A- and/or B-site doping.^{3–7,13–21} This destabilization of the FE order was accompanied by an enhancement in the unipolar strain. In the present case, the enhanced strain response may be attributed to the combined effect of the compositionally-induced structural phase transition from mixed rhombohedral–tetragonal to a single pseudocubic phase (LMN = 0.015) and the nano-scale NR to ER phase transition.

Fig. 10 The room-temperature bipolar field-induced strain curves of the LMN-doped BNKT–ST (LMN = 0.00–0.030) ceramics.

The unipolar electric-field-induced strain curves of the LMN-doped BNKT–ST ceramics with LMN = 0.00, 0.010, 0.015, 0.020 and 0.030 are shown in Fig. 11. Similarly to bipolar strain, the unipolar strain initially increased significantly with increasing LMN content up to LMN = 0.010, and then decreased beyond this critical composition. A large strain (S = 0.28%) and corresponding normalized strain (d^*₃₃ = 560 pm V⁻¹) were observed at the composition with LMN = 0.010. Initially, over the narrow compositional range with mixed rhombohedral–tetragonal states, the materials exhibit very low strain-electric field hystereses, relatively large dielectric constants and maximum piezoelectric coefficients at room temperature. For compositions with LMN ≥ 0.010, the large degree of hysteresis indicates that the high strain level is mainly derived from the extrinsic contribution and very weakly from the intrinsic piezoelectric response (d₃₃ < 20 pC N⁻¹). Similar strain behavior has been observed in various BNT-based ceramics prepared by conventional solid-state reaction.^13–21 The overall enhancement in the strain level may be due to both the strain-generating structural- and the NR-to-ER-phase transitions under the applied electric field.

Fig. 11 (a) Room-temperature unipolar strain curves and (b) corresponding S_max/E_max values of LMN-doped BNKT–ST (LMN = 0.00–0.030) ceramics.

The temperature-dependent bipolar and unipolar strain responses of BNKT–ST ceramics with LMN = 0.00 and 0.015 are shown in Fig. 12. For the sample with LMN = 0.00, the FE behavior of the NR state persisted up to ∼90 °C with an increasing degree of ergodicity, possibly due to the increase in the random fields with temperature, which may be evidenced from the gradual decrease in the S_neg and E_c. Also, the gradual increase in unipolar strain for T ≤ 90 °C, and abrupt increase for 135 °C ≤ T > 90 °C for the sample with LMN = 0.00, are consistent with a bipolar S–E loop. The abrupt increase in usable strain (S_max) with the sharp decrease in S_neg at 100 °C (near T_F–R) may indicate the thermally-induced structural phase transition and the conversion of long-range FE order to a short-range ER state. On the contrary, the chemically-induced high strain composition of LMN = 0.015 lies in the ER state with high random fields, and the external thermal field just randomized the already existent random PNRs and prohibited the establishment of FE order evident by the almost-zero S_neg, P_r, E_c and d₃₃.

Fig. 12 Temperature-dependent bipolar and unipolar strain curves of LMN-doped BNKT–ST (LMN = 0.00 and 0.015) ceramics.

The significant decrease in polarization, along with the rapid degradation of the piezoelectric coefficient d₃₃ and the noticeable change in the loop shape with both the high LMN concentration and high temperature, suggest the onset of an ER state that converts reversibly between stable relaxor and metastable FE phases during cycling of an external electric field. Thus, both the LMN dopants and the temperature induced a phase transition in the BNKT–ST lattice from a NR to an ER state, passing through an intermediate mixed stage (i.e. near LMN = 0.015) where both the NR and ER phases coexist. Furthermore, the ER phase dominated at higher LMN concentrations and temperatures, which delays the transformation from the ER phase to the FE phase.

Based on the structural analysis and the dielectric, ferroelectric, piezoelectric and electric-field-induced measurements, a schematic phase diagram for the poled LMN-modified BNKT–ST solid solutions was constructed, as shown in Fig. 13. With the introduction of LMN, the FE-to-relaxor temperature, T_F–R, can be adjusted to RT at around a critical composition, resulting in the enhancement of the electromechanical response. It is proposed that the disappearance of the piezoelectric properties, the pinched polarization hysteresis loops and the large strain response in the present study are derived from the composition- and temperature-induced relaxor-to-FE phase transition.

Fig. 13 Schematic phase diagram of the LMN-doped BNKT–ST (LMN = 0.00–0.030) ceramics.

It is well known that electrical poling treatment significantly affects the crystal symmetry, domain switching and reorientation of PNRs in BNT-based ceramic systems. Therefore, the effects of poling treatment on the crystal structure of the BNKT–ST ceramics was investigated and is shown in Fig. 14. XRD patterns of unpoled and poled samples for the FE composition with LMN = 0.00 and the ER composition with LMN = 0.015 are shown in Fig. 14(a) and (b), respectively. The (111)/(11̄1) split peaks of the rhombohedral phase at 40° for the unpoled FE (LMN = 0.00) sample (Fig. 14(a)) merged into a single (111) peak after poling, while the splitting in the (002)/(200) peaks at 46° for the unpoled ceramic was suppressed by applying poling treatment, indicating that poling treatment has a vital influence on the crystal structure of the studied material. It is suggested that initially in the undoped NR state, two types of frozen ordered nano-domains with rhombohedral and tetragonal symmetries co-exist. However, the external biased condition changes the symmetry of the crystal, and, consequently, the co-existing rhombohedral–tetragonal PNRs transform to single tetragonal PNRs with a long-range permanent FE ordering, as shown schematically in Fig. 14(c) (evident from the high d₃₃, P_r and E_c). The permanent structural change (after the poling process) can further facilitate the alignment of PNRs, while the random fields between PNRs are easily overcome by strong dc fields in the FE state.

Fig. 14 X-ray diffraction patterns of the LMN-doped BNKT–ST ceramics before and after the electric poling process, illustrating a field-induced phase transition: (a) LMN = 0.00 and (b) LMN = 0.015. (c) Schematic representation of an irreversible NR-to-FE transition. (d) Schematic representation of a reversible ER-to-FE transition.

On the other hand, for the ER composition with LMN = 0.015, no significant changes in the single (111) peak at 40° and the (200) peak at 46° were observed after poling (see Fig. 14(b)), indicating that the poling treatment has no noticeable influence on the crystal structure. It is suggested that the unpoled sample with LMN = 0.015 is already in the high-symmetry pseudocubic phase (evident from XRD, Fig. 1) and that the external bias field does not change the crystal symmetry. For this composition, the ER state has strong random fields between dynamically-fluctuating PNRs (compositional and charge disorder are increased due to the Li⁺, Mg²⁺ and Nb⁵⁺ simultaneous doping, and thus random fields are strong for the sample with LMN = 0.015), and electrical poling is not able to overcome these random fields to establish a long-range permanent FE state (evident from the small d₃₃, P_r and E_c). It is proposed that a temporary FE order (low entropy state) was induced only under biased conditions. However, after the poling process, the metastable FE order reverts back to the initial short-range disordered ER phase (high-entropy state). Recently, in situ XRD results collected under an induced electric field for La-doped BNKT–BST⁴² and Nb-doped BNKT–BST¹⁸ ceramics revealed reversible structural phase transitions between pseudocubic and mixed rhombohedral–tetragonal phases. The current observations, combined with the above mentioned previous structural investigations of Nb- and La-doped BNKT–BST ceramics, reveal that the origin of the large strain response in the LMN-modified BNKT–ST system may be due to a reversible polymorphic structural phase transition between ER and FE states under the influence of an electric field, as shown in Fig. 14(d). It is suggested that the crystal structure of the initial virgin LMN = 0.015 composition, with pseudocubic symmetry, becomes unstable under the applied electric field, and a metastable polymorphic phase transition may occur only under biased conditions. These structural changes under an electric field at the unit cell level may modify the random fields and affect the size, shape, symmetry and dynamics of PNRs, facilitating the reversible inter-conversion of FE- and nano-domains of PNRs, which can contribute to a large extrinsic strain for the given composition.

To evaluate the potential application of the ceramic LMN-doped BNKT–ST for capacitive storage systems, the energy storage density (W) was calculated from P–E loops using the formula W = ∫EdP. The W is strongly dependent on P_r, P_max and E_c. Ceramic materials with small P_r, E_c and high P_max will possess high W. The P–E loops of the LMN-doped BNKT–ST ceramics at room temperature are shown in Fig. 15(a). It can be seen that the sample with LMN = 0.020, with high P_max − P_r, gave the maximum room temperature energy storage density of ∼0.40 J cm⁻³ at a moderate field, which is much higher than the W ∼ 0.05 J cm⁻³ of the FE state (with LMN = 0.00) and comparable to previously reported values for lead-free and lead-based bulk ceramics.^43,44 The high W composition lies at the boundary between the ER and NR states.

Fig. 15 The P–E hysteresis loops of a LMN-doped BNKT–ST ceramic (LMN = 0.020) under different electric fields measured at (a) 25 °C; the inset shows the energy density of the LMN = 0.020 ceramic under different electric fields. (b) The energy density as a function of LMN content at RT. (c) The unipolar P–E hysteresis loops of the sample with LMN = 0.020 at various temperatures (25–150 °C). (d) The energy density as a function of temperature; the inset shows W at 100 °C.

The dependences of energy storage density on applied field and temperature were examined for the sample with LMN = 0.020. Fig. 15(a) and (c) show the field-dependent bipolar and temperature-dependent unipolar P–E hysteresis loops of the LMN = 0.020 composition, respectively. The energy density increased almost linearly with the increment of electric field up to 2 kV mm⁻¹ and then sharply increased, reaching the maximum value of ∼0.40 J cm⁻³ at 6 kV mm⁻¹. Fig. 15(c) and (d) show the energy density and unipolar hysteresis loop (the inset) of the sample with LMN = 0.020 at different temperatures (20–150 °C) under an electric field of 5.5 kV mm⁻¹. It is observed that the W increased with increasing temperature up to 100 °C, with an increasing degree of ergodicity, and then became almost stable until 150 °C.

4. Conclusion

Lead-free LMN-modified BNKT–ST piezoelectric ceramics were successfully synthesized by a solid-state reaction method. The results of X-ray diffractometry revealed a compositionally-induced structural phase transition, from rhombohedral–tetragonal phase coexistence to pseudocubic symmetry at the composition with LMN = 0.015. The unpoled and poled XRD results revealed that an electric-field-induced irreversible structural transformation from the coexisting rhombohedral–tetragonal phases to a single tetragonal phase occurred in the undoped BNKT–ST sample. However, the LMN = 0.015 composition showed a reversible phase transition after the poling process. Temperature-dependent dielectric properties revealed relaxor-like characteristics in all solid solutions. The FE order in the BNKT–ST ceramics was significantly disrupted by the addition of LMN, resulting in a drastic degradation in the remnant polarization, coercive field and negative strain. However, the degradation of the polarization was accompanied by a significant enhancement in the strain behavior. In particular, a large electric-field-induced strain (S = 0.28%) and a corresponding dynamic piezoelectric constant (d^*₃₃ = 560 pm V⁻¹) were obtained for the LMN = 0.015 composition. This strain enhancement can be attributed to the combined effect of the compositionally-induced phase transition from the NR to the ER state and the field-assisted reversible structural phase transition between the mixed rhombohedral–tetragonal and pseudocubic phases. A nearly temperature-invariant energy storage density of approx. 0.70 J cm⁻³ was found for the LMN = 0.020 composition in the range of 100–150 °C, which is favorable for energy storage capacitor applications. The relatively large energy storage density is ascribed to the increase in the degree of ergodicity and stabilization of the ER state. This study reveals that the compositional modification with simultaneous A- and B-site elements in the BNKT–ST system induces a polymorphic phase transition, which strongly affects the electrical properties of the material.

Acknowledgements

This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), as funded by the Ministry of Education, Science and Technology (MEST) (2011-0030058) and Ministry of Education (MOE) and National Research Foundation of Korea (NRF) through Human Resource Training Project for Regional Innovation (No. 2013H1B8A2032206). The authors are indebted to Prof. Wook Jo (Ulsan National Institute of Science and Technology, South Korea) for the temperature-dependent strain measurements.

References

1. G. H. Haertling, J. Am. Ceram. Soc., 1999, 82, 797–818.
2. J. Rödel, K. G. Webber, R. Dittmer, W. Jo, M. Kimura and D. Damjanovic, J. Eur. Ceram. Soc., 2015, 35, 1659–1681.
3. A. Zaman, Y. Iqbal, A. Hussain, M. H. Kim and R. A. Malik, J. Mater. Sci., 2014, 49, 3205–3214.
4. R. A. Malik, A. Hussain, A. Maqbool, A. Zaman, C. W. Ahn, J. U. Rahman, T. K. Song, W. J. Kim and M. H. Kim, J. Am. Ceram. Soc., 2015, 1–7,  DOI:10.1111/jace.13722.
5. T. Takenaka, K. Maruyama and K. Sakata, Jpn. J. Appl. Phys., 1991, 30, 2236–2239.
6. Y. Hiruma, Y. Imai, Y. Watanabe, H. Nagata and T. Takenaka, Appl. Phys. Lett., 2008, 92, 262904.
7. A. Sasaki, T. Chiba, Y. Mamiya and E. Otsuki, Jpn. J. Appl. Phys., 1999, 38, 5564–5567.
8. S. T. Zhang, A. B. Kounga and E. Aulbach, Appl. Phys. Lett., 2007, 91, 112906.
9. B. W. Eerd, D. Damjanovic, N. Klein, N. Setter and J. Trodahl, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 104112.
10. M. B. Quan, W. J. Feng and Z. G. Zhong, Chin. Phys. Lett., 2008, 25, 3776–3778.
11. J. Yoo, D. Oh, Y. Jeong, J. Hong and M. Jung, Mater. Lett., 2004, 58, 3831–3835.
12. Z. Yang, Y. Hou, B. Liu and L. Wei, Ceram. Interfaces, 2009, 35, 1423–1427.
13. T. H. Dinh, H. Y. Lee, C. H. Yoon, R. A. Malik, Y. M. Kong, J. S. Lee and V. D. N. Tran, J. Korean Phys. Soc., 2013, 62, 1004–1008.
14. P. Fu, Z. Xu, H. Zhang, R. Chu, W. Li and M. Zhao, Mater. Des., 2012, 40, 373–377.
15. M. Acosta, N. Liu, M. Deluca, S. Heidt, I. Ring, C. Dietz, R. W. Stark and W. Jo, J. Appl. Phys., 2015, 117, 134106.
16. B. Wang, L. Luo, F. Ni, P. Du, W. Li and H. Chen, J. Alloys Compd., 2012, 526, 79–84.
17. H. S. Han, W. Jo, J. K. Kang, C. W. Ahn, I. W. Kim, K. K. Ahn and J. S. Lee, J. Appl. Phys., 2013, 113, 154102.
18. A. Ullah, R. A. Malik, A. Ullah, D. S. Lee, S. J. Jeong, J. S. Lee, I. W. Kim and C. W. Ahn, J. Eur. Ceram. Soc., 2014, 34, 29.
19. R. A. Malik, J. K. Kang, A. Hussain, C. W. Ahn, H. S. Han and J. S. Lee, Appl. Phys. Express, 2014, 7, 061502.
20. A. Hussain, C. W. Ahn, A. Ullah, J. S. Lee and I. W. Kim, Jpn. J. Appl. Phys., 2010, 49, 041504.
21. A. Hussain, C. W. Ahn, J. S. Lee, A. Ullah and I. W. Kim, Sens. Actuators, A, 2010, 158, 84–89.
22. E. A. Patterson, D. P. Cann, J. Pokorny and I. M. Reaney, J. Appl. Phys., 2012, 111, 094105.
23. H. B. Lee, D. J. Heo, R. A. Malik, C. H. Yoon, H. S. Han and J. S. Lee, Ceram. Interfaces, 2013, 39, S705–S708.
24. K. Wang, A. Hussain, W. Jo and J. Rodel, J. Am. Ceram. Soc., 2012, 95, 2241–2247.
25. J. Hao, B. Shen, J. Zhai and H. Chen, J. Appl. Phys., 2014, 115, 034101.
26. M. Zou, H. Fan, L. Chen and W. Yang, J. Alloys Compd., 2010, 495, 280–283.
27. A. Hussain, J. U. Rahman, A. Zaman, R. A. Malik, J. S. Kim, T. K. Song, W. J. Kim and M. H. Kim, Mater. Chem. Phys., 2014, 143, 1282–1288.
28. P. Fu, Z. Xu, R. Chu, X. Wu, W. Li and M. Zhao, J. Alloys Compd., 2012, 535, 5–9.
29. P. Jaita, A. Watcharapasorn, D. P. Cann and S. Jiansirisomboon, J. Alloys Compd., 2014, 596, 98–106.
30. A. Ullah, C. W. Ahn, R. A. Malik, J. S. Lee and I. W. Kim, J. Electroceram., 2014, 33, 187–194.
31. V. Q. Nguyen, H. S. Han, K. J. Kim, D. D. Dang, K. K. Ahn and J. S. Lee, J. Alloys Compd., 2012, 511, 237–241.
32. R. A. Malik, A. Hussain, J. U. Rahman, A. Maqbool, T. K. Song, W. J. Kim, S. Y. Ryou and M. H. Kim, Mater. Lett., 2015, 143, 148–150.
33. J. Kling, W. Jo, R. Dittmer, S. Schaab and H. J. Kleebe, J. Am. Ceram. Soc., 2013, 96(10), 3312–3324.
34. C. Ma and X. Tan, J. Am. Ceram. Soc., 2011, 94(11), 4040–4044.
35. R. Dittmer, W. Jo, J. Rödel, S. Kalinin and N. Balke, Adv. Funct. Mater., 2012, 22, 4208–4215.
36. E. Aksel, J. S. Forrester, B. Kowalski, M. Deluca, D. Damjanovic and J. L. Jones, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 024121.
37. J. Hao, B. Shen, J. Zhai, C. Liu, X. Li and X. Gao, J. Appl. Phys., 2013, 113, 114106.
38. K. Uchino and S. Nomura, Ferroelectr., Lett. Sect., 1982, 44, 55–61.
39. I. A. Santos and J. A. Eiras, J. Phys.: Condens. Matter, 2001, 13, 11733.
40. T. V. D. Ngoc, H. S. Han, K. J. Kim, R. A. Malik, A. Hussain and J. S. Lee, J. Ceram. Process. Res., 2012, 13, 177–180.
41. A. Maqbool, A. Hussain, R. A. Malik, J. U. Rahman, A. Zaman, T. K. Song, W. J. Kim and M. H. Kim, Mater. Sci. Eng., B, 2015, 199, 105–112.
42. A. Ullah, A. Ullah, I. W. Kim, D. S. Lee, S. J. Jeong and C. W. Ahn, J. Am. Ceram. Soc., 2014, 97(8), 2471–2478.
43. F. Gao, X. Dong, C. Mao, W. Liu, H. Zhang, L. Yang, F. Cao and G. Wang, J. Am. Ceram. Soc., 2011, 94, 4382–4386.
44. H. Zhang, X. Chen, F. Cao, G. Wang and X. Dong, J. Am. Ceram. Soc., 2010, 93, 4015–4017.

---