Structural and electrical behaviour in Bi14YO22.5
M. Struzika,
M. Malys*a,
M. Krynskia,
M. Wojcika,
J. R. Dygasa,
W. Wrobela,
F. Kroka and
I. Abrahams*b
aFaculty of Physics, Warsaw University of Technology, ul. Koszykowa 75, 00-662 Warszawa, Poland. E-mail: mmalys@wp.pl; Tel: +48 22 234 8216
bMaterials Research Institute, Department of Chemistry and Biochemistry, School of Biological and Chemical Sciences, Queen Mary University of London, Mile End Road, London E1 4NS, UK. E-mail: i.abrahams@qmul.ac.uk; Tel: +44 207 882 3235
First published on 24th September 2015
Abstract
Structure and electrical conductivity in the oxide ion conducting compound Bi14YO22.5 have been investigated by powder X-ray and neutron diffraction, a.c. impedance spectroscopy, measurements of transference number and ab initio molecular dynamics (MD) simulations. Phase behaviour was studied using variable temperature X-ray diffraction and differential thermal analysis. The structure at room temperature is of the βIII tetragonal-type, details of which are discussed, including its relationship to both β and δ phases of Bi2O3. Bi14YO22.5 undergoes a reversible phase transition to a cubic δ-Bi2O3 type phase at high temperatures. This phase exhibits very high electrical conductivity, with transference numbers indicating that this conductivity is almost purely ionic in nature. MD simulations confirm 3-dimensional oxide ion transport in the βIII-phase.
1. Introduction
There is much current interest in fast oxide ion conducting solids for use as solid electrolytes in various electrochemical devices, such as fuel cells, oxygen pumps, sensors, etc. Much of this research is focused on developing materials suitable for intermediate temperature (ca. 500 °C to ca. 700 °C) devices. The highest known oxide ion conductivity in a solid is seen in bismuth oxide. This oxide shows complex polymorphism, with two stable polymorphs, α and δ, observed on heating and two metastable polymorphs, β and γ, obtainable depending on cooling conditions. The high temperature δ-phase possesses high oxide ion conductivity, with values in the order of 1 S cm−1 at temperatures above ca. 730 °C.1 Partial substitution of bismuth by a variety of cations can lead to stabilization of the δ-phase or closely related ordered fluorite phases at room temperature.2–7At relatively low levels of substitution of bismuth (ca. 0.05 mol%), β or γ (sillenite) phases are often observed. Above this level of substitution, a variety of fluorite based phases can be obtained, depending on the dopant and level of substitution. Recently, there has been interest in phases with a Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratio of 14
M ratio of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (6.67 mol% substitution), such as Bi14ReO24.5 (ref. 8 and 9) and Bi14MO24 (where M = W, Mo, Cr).10 Bi14ReO24.5 exhibits exceptionally high conductivity at intermediate temperatures, in the order of 10−3 S cm−1 at 300 °C.8,9
1 (6.67 mol% substitution), such as Bi14ReO24.5 (ref. 8 and 9) and Bi14MO24 (where M = W, Mo, Cr).10 Bi14ReO24.5 exhibits exceptionally high conductivity at intermediate temperatures, in the order of 10−3 S cm−1 at 300 °C.8,9
The (Bi1−xYx)2O3 system has been reviewed by Sammes et al.5 At bismuth rich compositions, around the 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Bi
1 Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y ratio, a tetragonal phase is observed, which forms part of a solid solution range extending from ca. 5.8 to ca. 8.1%.11 However, it has been argued by Watanabe12 that the observed tetragonal solid solution is in fact metastable. Using an alternative phase diagram, he argued that the lowest x-value room temperature stable phase in this system is the end member of a solid solution ranging from x = 0.215 to x = 0.24, with compositions at lower x-values possessing only mixtures of this phase and α-Bi2O3 as the stable phases.
Y ratio, a tetragonal phase is observed, which forms part of a solid solution range extending from ca. 5.8 to ca. 8.1%.11 However, it has been argued by Watanabe12 that the observed tetragonal solid solution is in fact metastable. Using an alternative phase diagram, he argued that the lowest x-value room temperature stable phase in this system is the end member of a solid solution ranging from x = 0.215 to x = 0.24, with compositions at lower x-values possessing only mixtures of this phase and α-Bi2O3 as the stable phases.
We have previously studied δ-phase compositions around x = 0.25 in the (Bi1−xYx)2O3 system, which show high levels of conductivity13,14 and revealed details of the vacancy ordering, using total neutron scattering analysis.15 Ab initio modelling of the x = 0.25 composition reveals that yttrium acts as a trap for mobile oxide ions, effectively lowering ionic conductivity compared to the parent δ-Bi2O3.16 In the present study we examine a more bismuth rich composition in the (Bi1−xYx)2O3 system at the 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Bi
1 Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y ratio (x = 0.067), which exhibits a tetragonal structure at room temperature and a cubic fluorite phase at high temperatures.12 Here details of the structure and electrical conductivity of this composition have been studied in detail using X-ray and neutron powder diffraction, in combination with a.c. impedance spectroscopy, differential thermal analysis (DTA) and measurements of transference number. These results are compared with those from ab initio molecular dynamics calculations.
Y ratio (x = 0.067), which exhibits a tetragonal structure at room temperature and a cubic fluorite phase at high temperatures.12 Here details of the structure and electrical conductivity of this composition have been studied in detail using X-ray and neutron powder diffraction, in combination with a.c. impedance spectroscopy, differential thermal analysis (DTA) and measurements of transference number. These results are compared with those from ab initio molecular dynamics calculations.
2. Experimental
2.1 Sample preparations
The title compound, Bi14YO22.5 was prepared using stoichiometric amounts of Bi2O3 (Aldrich, 99.99%) and Y2O3 (Aldrich, 99.95%). The starting mixture was ground in ethanol using a planetary ball mill for ca. 24 h. The dried mixture was heated initially at 750 °C for 24 h, then cooled, reground and pelletized. Pellets were pressed isostatically at a pressure of 400 MPa, then sintered at 800 °C for 24 h, before cooling in air to room temperature over a period of approximately 12 h.2.2 Electrical measurements
Electrical parameters were determined by a.c. impedance spectroscopy using a fully automated Solartron 1255/1286 system, in the frequency range 1 Hz to 5 × 105 Hz (18 frequencies per decade). Samples for impedance measurements were rectangular blocks (ca. 6 × 2 × 3 mm3) cut from sintered pellets using a diamond saw. Platinum electrodes were sputtered by cathodic discharge on the two smallest flat polished parallel faces of the blocks. Impedance spectra were recorded during heating and cooling ramps between ca. 300 °C and ca. 800 °C, at stabilized temperatures. Drift of impedance was monitored during measurement using an algorithm described earlier17 and controlled to be within 2%.The ionic and electronic contributions to the total conductivity were measured using a modified EMF method, with an external adjustable voltage source in the concentration cell O2 (pO2 = 1.01 × 105 Pa):Pt|oxide|Pt:O2 (pO2 = 0.2095 × 105 Pa), as described in detail elsewhere.18 Measurements were performed on cooling between ca. 780 °C and 430 °C at stabilized temperatures. Samples were prepared as sintered pellets of 14 mm diameter and ca. 2 mm thickness. The Pt electrode had a diameter of 10.7 mm.
2.3 Differential thermal analysis
Differential thermal analysis (DTA) was carried out using a TA Instruments Q600 scanning differential thermal analyser. Approximately 50 mg of powdered sample in an alumina crucible was monitored over heating and cooling cycles, between ambient temperature and 900 °C at a heating/cooling rate of 20 °C min−1 in flowing air.2.4 Diffraction
X-ray powder diffraction data were collected on a Philips X'Pert Pro X-ray diffractometer using Ni filtered Cu-Kα radiation (λ1 = 1.54056 Å and λ2 = 1.54439 Å) in flat plate θ/θ geometry with an X'Celerator detector. Calibration was carried out with an external LaB6 standard. Data were collected at selected temperatures in the range ambient to 850 °C, using an Anton-Paar HTK 1200 camera. Data at room temperature and at 800 °C were collected over the 2θ range 5–105°, in steps of 0.033°, with a scan time of 250 s per step. For intermediate temperatures, shorter scans were performed with a scan time of 25 s per step.Powder neutron diffraction data were collected on the Polaris diffractometer at the ISIS Facility, Rutherford Appleton Laboratory. Data collected on back-scattering and low-angle detectors were used in subsequent refinements, covering the respective time of flight ranges 1.0 to 20 and 0.5 to 20 ms. The sample was contained in a cylindrical 11 mm diameter vanadium can located in front of the back-scattering detectors. Data were collected at room temperature for ca. 200 μA h.
Structure refinement was carried out by Rietveld whole profile fitting using the GSAS suite of programs.19 For the room temperature analysis, a combined X-ray and neutron approach was adopted. For the high temperature phase, a simple cubic fluorite model in space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m was used for refinements, as previously described.13 For the low temperature structure, initial refinements were based on the structure of β-Bi2O3 (ref. 20 and 21) in space group P
m was used for refinements, as previously described.13 For the low temperature structure, initial refinements were based on the structure of β-Bi2O3 (ref. 20 and 21) in space group P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c (no. 114 (ref. 22)). Difference Fourier maps were used to locate interstitial oxide ion scattering density. It was found that the structure exhibited considerable positional disorder with respect to the structure of β-Bi2O3. The systematic absences for space group P
21c (no. 114 (ref. 22)). Difference Fourier maps were used to locate interstitial oxide ion scattering density. It was found that the structure exhibited considerable positional disorder with respect to the structure of β-Bi2O3. The systematic absences for space group P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c are in fact a subset of those for P42/nmc, and therefore a satisfactory refinement can be obtained in the lower symmetry space group, even when the true symmetry is higher. However, close inspection of the diffraction data reveal that the systematic absences are consistent with the higher symmetry space group, showing absence of Bragg peaks of the type hk0, when h + k = 2n + 1 (Fig. 1). We have previously reported the structure of βIII-Bi1.85Zr0.15O3.075 (ref. 23) in space group P42/nmc (no. 137, origin choice 2 (ref. 22)). This model is also consistent with that proposed for Bi7Y0.5O25,24 but exhibits greater positional disorder. Refinement of the βIII-model resulted in an excellent fit to the data for Bi14YO22.5 at room temperature and the structure presented here corresponds to this model. The extent of Y substitution in the present system is low and therefore Bi and Y atom parameters were tied to a single site. Anisotropic displacement parameters were refined for all atoms. A large U33 parameter on O(3) indicated that the site was split and in the final refinements this was placed on an 8g site. Oxide ion site occupancies were initially allowed to vary. The occupancies for O(1) and O(3) were found to be correlated with the amount of yttrium in the system and in the final refinements these were fixed according to stoichiometry. Crystal and refinement parameters for Bi14YO22.5 at room temperature are presented in Table 1.
21c are in fact a subset of those for P42/nmc, and therefore a satisfactory refinement can be obtained in the lower symmetry space group, even when the true symmetry is higher. However, close inspection of the diffraction data reveal that the systematic absences are consistent with the higher symmetry space group, showing absence of Bragg peaks of the type hk0, when h + k = 2n + 1 (Fig. 1). We have previously reported the structure of βIII-Bi1.85Zr0.15O3.075 (ref. 23) in space group P42/nmc (no. 137, origin choice 2 (ref. 22)). This model is also consistent with that proposed for Bi7Y0.5O25,24 but exhibits greater positional disorder. Refinement of the βIII-model resulted in an excellent fit to the data for Bi14YO22.5 at room temperature and the structure presented here corresponds to this model. The extent of Y substitution in the present system is low and therefore Bi and Y atom parameters were tied to a single site. Anisotropic displacement parameters were refined for all atoms. A large U33 parameter on O(3) indicated that the site was split and in the final refinements this was placed on an 8g site. Oxide ion site occupancies were initially allowed to vary. The occupancies for O(1) and O(3) were found to be correlated with the amount of yttrium in the system and in the final refinements these were fixed according to stoichiometry. Crystal and refinement parameters for Bi14YO22.5 at room temperature are presented in Table 1.
 | ||
Fig. 1 Detail of fit to neutron low-angle data in space group P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c, showing systematic absence of hk0 peaks when h + k = 2n + 1. Position of the absent 210 peak is marked by an asterisk. 21c, showing systematic absence of hk0 peaks when h + k = 2n + 1. Position of the absent 210 peak is marked by an asterisk. | ||
| a For definition of R-factors see ref. 19. | |
|---|---|
| Chemical formula | Bi14YO22.5 |
| Formula weight | 3374.62 g mol−1 |
| Crystal system | Tetragonal |
| Space group | P42/nmc |
| Unit cell dimension | a = 7.75622(3) Å, c = 5.63625(3) Å |
| Volume | 339.071(3) Å3 |
| Z | 0.533 |
| Density (calculated) | 8.814 g cm−3 |
| R-factorsa | (a) Neutron backscattering Rwp = 0.0111, Rp = 0.0230, Rex = 0.0062, RF2 = 0.0351 |
| (b) Neutron low angle Rwp = 0.0281, Rp = 0.0325, Rex = 0.0220, RF2 = 0.0840 | |
| (c) X-ray Rwp = 0.0405, Rp = 0.0251, Rex = 0.0170, RF2 = 0.2044 | |
| (d) Overall Rwp = 0.0174, Rp = 0.0252, χ2 = 3.151 | |
| Total no. of variables | 140 |
| No. of profile points used | 3949 (neutron backscattering) |
| 5139 (neutron low angle) | |
| 2842 (X-ray) | |
| No. of reflections | 1237 (neutron back-scattering) |
| 1023 (neutron low-angle) | |
| 232 (X-ray) | |
2.5 DFT calculations
Density functional theory (DFT) calculations were carried out within a 2 × 2 × 1 supercell (160 ions in total) of βIII-Bi14YO22.5 using the Vienna Ab initio Simulation Package (VASP) and a plane wave basis set.25–28 The exchange-correlation function was treated within the generalized gradient approximation of Perdew–Burke–Ernzerhof29 and the electron–ion interactions were described by the full potential projector augmented wave method,30 with 5, 6 and 11 valence electrons for Bi, O and Y respectively (including 4s and 4p electrons for the latter). Forces were calculated according to the Hellmann–Feynman theorem31,32 and the kinetic energy was controlled by means of the Nose–Hoover thermostat.33,34 The plane wave cutoff energy was 430 eV for all calculations. The sampling of the Brillouin zone was performed using the Monkhorst–Pack scheme35 at the gamma point. All calculations were performed under periodic boundary conditions. The MD simulations were performed from initially relaxed structures. The global break point for the electronic loop was set to 10−5 eV per cell. The initial structural model was based on the results from the diffraction analysis. Bismuth and yttrium atoms were distributed randomly over the cation sites in the supercell, while oxygen atoms were distributed quasi randomly over the three types of anion site according to the site occupancies in the crystallographic model. The MD simulations were carried out at 850 °C, over a total of 40 ps in steps of 5 fs. Three parallel runs were performed to yield sufficient statistical quality. To minimize the influence of initial thermodynamic relaxation of the system, the data corresponding to the first 5 ps were not taken into account for further analysis. The simulation temperature of 850 °C, although above the existence range of the βIII-phase (see Discussion), was chosen to ensure sufficient oxide ion movement within a reasonable simulation time.To capture the oxide ion jump trajectories, high frequency oscillations of the oxide ions were excluded from calculations using a low pass Chebyshev filter. The cutoff frequency for the Chebyshev filter was determined based on the Fourier analysis of the ionic trajectories. For the frequencies above 5 × 1012 Hz, only thermal vibrations are observed. Energy distribution landscapes were derived from ionic density maps assuming a Boltzmann distribution.
Structural graphics were prepared using ORTEP-3 for Windows36 and VESTA.37
3. Results and discussion
3.1 Structure of βIII-Bi14YO22.5
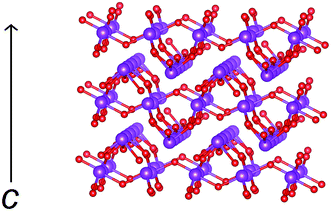
Fitted diffraction profiles from the Rietveld analysis of βIII-Bi14YO22.5 at room temperature are shown in Fig. 2, with the refined structural parameters given in Table 2 and significant contact distances in Table 3. The structure of βIII-Bi14YO22.5 is closely related to that of Pb2F2O.38 An idealised model of βIII-Bi14YO22.5 (containing no structural disorder) consists of interconnected Bi4O4 rings, with bismuth in an essentially trigonal pyramidal geometry, forming a corrugated layered structure, with layers stacked parallel to the c-axis (Fig. 3). The Bi4O4 rings in adjacent layers are aligned such that they form a channel structure, with channels running parallel to the c-axis.| Atom | Wyc. | x | y | z | Occ. |
|---|---|---|---|---|---|
| Bi/Y | 8g | 0.25 | 0.00572(5) | 0.48660(6) | 0.933/0.067 |
| O(1) | 16h | 0.5428(4) | 0.0590(4) | 0.2797(5) | 0.467 |
| O(2) | 4d | 0.25 | 0.25 | 0.6496(1) | 1 |
| O(3) | 4c | 0.25 | 0.75 | 0.3110(9) | 0.133 |
| Anisotropic thermal parameters (Å2) | ||||||
|---|---|---|---|---|---|---|
| Atom | U11 | U22 | U33 | U12 | U13 | U23 |
| Bi/Y | 0.0308(2) | 0.0102(2) | 0.0204(2) | 0 | 0 | −0.0067(1) |
| O(1) | 0.0176(5) | 0.0405(11) | 0.0157(11) | 0.0052(5) | −0.0030(6) | 0.0166(7) |
| O(2) | 0.0346(4) | 0.0124(4) | 0.0204(4) | 0 | 0 | 0 |
| O(3) | 0.043(5) | 0.076(7) | 0.016(4) | 0 | 0 | 0 |
| Bi/Y–O(1) | 2.138(4) × 2 | O(1)–Bi/Y–O(1) | 97.49(9) |
| Bi/Y–O(1)′ | 2.250(4) × 2 | O(1)–Bi/Y–O(1)′ | 90.19(3) |
| Bi/Y–O(2) | 2.1057(5) | O(1)–Bi/Y–O(2) | 86.70(7) |
| Bi/Y–O(3) | 2.217(2) | O(1)–Bi/Y–O(3) | 93.72(10) |
| Bi/Y⋯O(1)′′ | 2.842(2) × 2 | O(1)′–Bi/Y–O(1)′ | 82.33(9) |
| Bi/Y⋯O(1)′′′ | 2.586(2) × 2 | O(1)′–Bi/Y–O(2) | 80.22(7) |
| Bi/Y⋯O(2)′ | 2.6829(6) | O(1)′–Bi/Y–O(3) | 100.26(12) |
| Bi/Y⋯O(3)′ | 2.598(3) | O(2)–Bi/Y–O(3) | 179.354(1) |
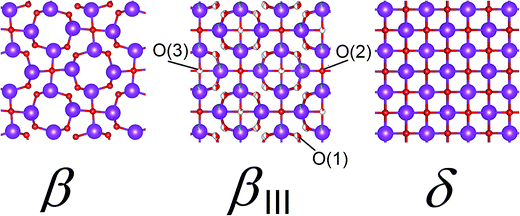
The structure of βIII-Bi14YO22.5 may be thought of as lying between those of β-Bi2O3 and δ-Bi2O3 (Fig. 4). The structure of β-Bi2O3,21 consists of a near cubic close packed array of bismuth cations, with O2− anions distributed in 3/4 of the tetrahedral cavities. The vacant tetrahedral cavities are ordered to yield channels perpendicular to the c-axis. The main difference between the structures of the β and δ phases of Bi2O3 lies in the vacancy ordering. In the latter case, vacancies are disordered over all the tetrahedral cavities on the crystallographic scale. Additionally, the cations in β-Bi2O3 are arranged in a slightly corrugated fashion above and below the x–y plane, while in the structure of δ-Bi2O3, the cations lie within the corresponding planes, as clearly evident in Fig. 3. In the case of the βIII-phase, the cation distribution shows the ideal planarity of the δ-phase, but the anion distribution more closely resembles that in the β-phase. The O(1) and O(2) sites in βIII-Bi14YO22.5 lie close to the corresponding sites in β-Bi2O3. However, the O(3) site in the βIII-phase corresponds to a site in the vacant channels of the β-phase and hence, in this respect, the anion distribution of the βIII-phase approaches that of the δ-phase. The O(1) site shows positional disorder compared to the corresponding position in β-Bi2O3. Since the shortest O(1)⋯O(1) contact distance is only 0.379 Å, a maximum occupancy of 0.5 is possible for this site. The initial refinements indicated that the occupancy of the O(1) site was significantly lower than this maximum value, with the total number of oxide ions on this site approximately equal to the amount of bismuth in the structure.
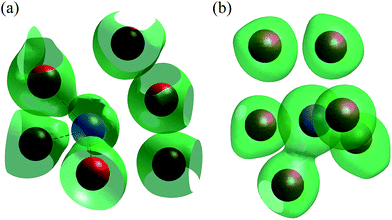
In βIII-Bi14YO22.5, the bismuth coordination is asymmetric, reflecting stereochemical activity of the Bi 6s2 lone pair of electrons, with three short Bi–O contacts of 2.11 to 2.25 Å and longer Bi–O contacts of 2.59 to 2.84 Å (the number of contacts takes into account the disorder on the O(1) site, which prevents simultaneous occupancy of neighbouring sites). These longer contacts may be considered to be non-bonding interactions, resulting in an essentially trigonal pyramidal coordination for Bi (Fig. 5a). The weighted average O–Bi–O angle within the trigonal pyramid is 85.7° for the configuration shown in Fig. 5a, which is again consistent with stereochemical activity of the Bi 6s2 lone pair of electrons. Based on geometrical considerations only, the alignment of the Bi 6s2 lone pair is such that it points towards the nominally empty channel (nominally empty, since O(3) is located in the channel), as previously described in the βIII-Bi1.85Zr0.15O3.075 system.23 The O(3) site occupancy initially refined close to double that of the yttrium occupancy of the Bi/Y 8g site and taking into account the multiplicities of these two sites this gave an approximate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio for Y
1 ratio for Y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O(3). The absence of atoms in a position corresponding to O(3) in the undoped system, β-Bi2O3 and the 1
O(3). The absence of atoms in a position corresponding to O(3) in the undoped system, β-Bi2O3 and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Y
1 Y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O(3) ratio, suggest that oxide ions on the O(3) site are exclusively associated with the Y3+ cation and allow it to adopt a more characteristic distorted octahedral coordination geometry involving O(1), O(2) and O(3) ions (Fig. 5b). The average Y–O bond length is 2.31 Å, which is slightly longer than the average value of 2.27 Å observed in Y2O3.39 Bond valence sums calculated using the parameters of Brese and O'Keeffe40 for Bi3+ and Y3+ were 3.08 and 3.03, respectively, for the proposed coordination geometries in Fig. 5.
O(3) ratio, suggest that oxide ions on the O(3) site are exclusively associated with the Y3+ cation and allow it to adopt a more characteristic distorted octahedral coordination geometry involving O(1), O(2) and O(3) ions (Fig. 5b). The average Y–O bond length is 2.31 Å, which is slightly longer than the average value of 2.27 Å observed in Y2O3.39 Bond valence sums calculated using the parameters of Brese and O'Keeffe40 for Bi3+ and Y3+ were 3.08 and 3.03, respectively, for the proposed coordination geometries in Fig. 5.
The geometrical position of the bismuth lone pairs is critical in determining the nature of the ionic conduction mechanism in this compound. In order to examine details of the nature of the interactions between bismuth and the surrounding oxygen atoms, ab initio calculations of the valence electron distribution in βIII-Bi14YO22.5 were carried out. Fig. 6a shows an iso-surface plot of valence electron density of a representative bismuth atom from these calculations. The figure clearly shows significant polarization of electron density between bismuth and the three closest oxygen atoms, indicative of a significant degree of covalency in these interactions. The next nearest oxygen atoms show no obvious polarization of electron density in the direction of the bismuth atom, consistent with these interactions being much weaker in bonding character. The three bonded atoms are arranged in a trigonal pyramidal coordination with bismuth, with the lone pair on bismuth pointing out of the pyramid apex. The results therefore agree with the proposed directionality of the bismuth lone pair based on the geometrical considerations above. Fig. 7 shows the valence electron density around a empty channel in βIII-Bi14YO22.5 and confirms that the lone pairs on bismuth point into the channel as previously proposed in the structure of βIII-Bi1.85Zr0.15O3.075.23 An iso-surface plot of valence electron density around a representative yttrium atom is shown in Fig. 6b. The figure reveals six oxygen atoms in the yttrium coordination sphere, confirming the coordination derived from the crystallographic analysis. Interestingly, only one of the oxygen atoms shows significant polarization of electron density in the direction of the yttrium atom. This suggests that the majority of yttrium–oxygen contacts are ionic in nature.
3.2 Thermal and electrical behaviour of Bi14YO22.5
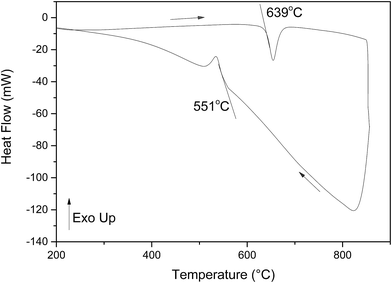
The DTA thermogram for Bi14YO22.5 is shown in Fig. 8. On heating, a single endothermic event is observed with an onset temperature of 639 °C, while on cooling the corresponding endotherm occurs at 551 °C. No melting endotherm is observed on heating in the temperature range studied. The thermal evolution of the X-ray diffraction pattern of the title compound is shown in Fig. 9. These data confirm a direct transition from the tetragonal βIII-phase to a cubic fcc phase between 600 and 650 °C on heating, with some residual tetragonal phase evident in the diffraction pattern at 650 °C. The reverse transition occurs between 600 and 550 °C on cooling. In order to analyse the structure volume expansion as a function of temperature, it is helpful to define an equivalent fluorite cell volume (Vf):
 | (1) |
 | ||
| Fig. 10 Thermal evolution of equivalent fluorite volume, Vf, in Bi14YO22.5 on heating (open symbols) and cooling (filled symbols). | ||
Fig. 11 shows the Arrhenius plot of total conductivity for the title compound on heating and cooling. Two linear regions are observed, one at low temperatures and a second of lower activation energy at high temperatures, with a significant jump in conductivity between the low and high temperature regions. There is thermal hysteresis associated with the transition, which occurs at around 650 °C on heating and ca. 550 °C on cooling, in good agreement with the results from DTA and X-ray measurements. The characteristic values of conductivity at 300 °C (σ300) and at 800 °C (σ800) are 1.06(1) × 10−5 S cm−1 and 1.83(7) S cm−1, respectively. The corresponding activation energies for the low (ΔELT) and high (ΔEHT) temperature regions are 0.96(1) eV and 0.64(4) eV, respectively. These values confirm very high conductivity for the cubic fluorite phase.
 | ||
| Fig. 11 Arrhenius plot of total electrical conductivity for Bi14YO22.5 on successive heating (open symbols) and cooling (closed symbols) runs. | ||
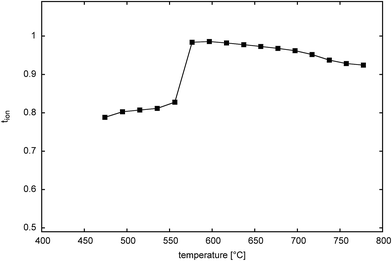
Fig. 12 shows the thermal variation of ionic transference number for Bi14YO22.5 on cooling. The plot reflects the cubic to tetragonal phase transition seen in this system, with a transition between ca. 650 and 600 °C. The transition occurs at around the same temperature as seen in heating measurements using other techniques and reflects the fact that very long equilibration times are used in the transference number measurements. Both tetragonal and cubic phases show predominantly ionic conductivity over the measured temperature range, with the tetragonal phase exhibiting a transference number of around 0.8 and the cubic phase around 0.95 for oxide ion conduction.
We have previously proposed an oxide ion transport mechanism for the βIII-phase in the bismuth zirconate system,23 involving oxide ion hopping along the c-axis channels, facilitated by the positioning of the bismuth lone electron pairs. It is possible to use the results from the DFT calculations to derive a 3-dimensional map of energy distribution, which allows for the identification of energetically favourable pathways for oxide ion migration. An energy distribution landscape was derived from the ionic density map assuming a Boltzmann distribution of ion positions:16,42
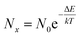 | (2) |
Energy distribution landscapes for vacant and filled channels in the structure of βIII-Bi14YO22.5 are shown in Fig. 13. The energy barriers at the saddle points for conduction along the channels are lower in the empty channels compared to those in the filled channels, with average values of 0.39 and 0.44 eV, respectively. Traces of oxide ion movements over the total simulation time (Fig. 14) show that oxide ion jumps occur not only through the c-axis channels (in the z-direction), but also between channels in the x–y plane. These results suggest that ion conduction in βIII-Bi14YO22.5 is in fact 3-dimensional in character and is similar to that in δ-Bi2O3. The level of ionic conductivity in the βIII-phase is relatively low compared to that in the δ-phase observed at high temperatures. This can be attributed to the reduced mobility of oxide ions at lower temperatures. Interestingly, at higher levels of substitution (x = 0.25) in the (Bi1−xYx)2O3 system, where the δ-phase is readily preserved to room temperature, low temperature values of ionic conductivity are quite similar (σ300 = 3.7 × 10−5 S cm−1 in Bi3YO6) to those in the present study, but a higher value of the low temperature activation energy (ΔELT = 1.19 eV)15 is observed in the δ-phase.
 | ||
| Fig. 13 Energy distribution landscapes in βIII-Bi14YO22.5, showing sections through (a) an empty channel and (b) a filled channel. Scales are given in eV. | ||
 | ||
| Fig. 14 Individual oxide ion trajectories (marked by different colours) projected onto (a) x–y and (b) x–z planes in βIII-Bi14YO22.5. | ||
4. Conclusions
Bi14YO22.5 adopts a βIII-type tetragonal structure at room temperature, which is closely related to that of β-Bi2O3. Crystal structure analysis and ab initio calculations confirm that bismuth exhibits a trigonal pyramidal bonding coordination with oxygen atoms, with stereochemical activity of the bismuth 6s2 lone pairs, which point into the nominally vacant channels running parallel to the c-axis. Yttrium atoms are proposed to exhibit a distorted octahedral coordination environment, with the majority of close Y–O interactions predominantly ionic in nature. Bi14YO22.5 shows polymorphism, with a cubic δ-Bi2O3 type phase occurring at elevated temperatures. Thermal hysteresis is evident in the tetragonal ↔ cubic phase transition, with the transition on cooling occurring at almost 100 °C lower than on heating. No evidence was seen in this study for instability of the tetragonal or cubic phases under the experimental conditions used. Cubic δ-Bi14YO22.5 exhibits very high electrical conductivity at 800 °C and is confirmed as being almost a pure ionic conductor. MD simulations confirm the conduction mechanism to be 3-dimensional in character, similar to that observed in the δ-phase.Acknowledgements
We are grateful to Dr S. Hull at the Rutherford Appleton Laboratory, for his help in neutron data collection and the STFC ISIS facility for beam time. I.A. gratefully acknowledges the Centre of Advanced Studies, Warsaw University of Technology for a visiting professorship. We gratefully acknowledge the National Science Centre Poland for project grant numbers 2012/05/E/ST3/02767 and 2013/09/N/ST3/04326.References
- T. Takahashi, H. Iwahara and Y. Nagaj, J. Appl. Electrochem., 1972, 2, 97 CrossRef CAS.
- G. Mairesse, in Fast Ion Transport in Solids, ed. B. Scrosati, A. Magistris, C. M. Mari and G. Mariotto, Kluwer Academic Publishers, Dordrecht, 1993, p. 271 Search PubMed.
- J. C. Boivin and G. Mairesse, Chem. Mater., 1998, 10, 2870 CrossRef CAS.
- P. Shuk, H. D. Wiemhöfer, U. Guth, W. Göpel and M. Greenblatt, Solid State Ionics, 1996, 89, 179 CrossRef CAS.
- N. M. Sammes, G. A. Tompsett, H. Näfe and F. Aldinger, J. Eur. Ceram. Soc., 1999, 19, 1801 CrossRef CAS.
- A. M. Azad, S. Larose and S. A. Akbar, J. Mater. Sci., 1994, 29, 4135 CrossRef CAS.
- J. B. Goodenough, A. Manthiram, M. Paranthaman and Y. S. Zhen, Mater. Sci. Eng., B, 1992, 12, 357 CrossRef.
- T. E. Crumpton, J. F. W. Mosselmans and C. Greaves, J. Mater. Chem., 2005, 15, 164 RSC.
- R. Punn, A. M. Feteira, D. C. Sinclair and C. Greaves, J. Am. Chem. Soc., 2006, 128, 15386 CrossRef CAS PubMed.
- T. E. Crumpton, M. G. Francesconi and C. Greaves, J. Solid State Chem., 2003, 175, 197 CrossRef CAS.
- R. K. Datta and J. P. Meehan, Z. Anorg. Allg. Chem., 1971, 383, 328 CrossRef CAS PubMed.
- A. Watanabe, Solid State Ionics, 1996, 86–88, 1427 CrossRef CAS.
- I. Abrahams, A. Kozanecka-Szmigiel, F. Krok, W. Wrobel, S. C. M. Chan and J. R. Dygas, Solid State Ionics, 2006, 177, 1761 CrossRef CAS PubMed.
- F. Krok, I. Abrahams, M. Holdynski, A. Kozanecka-Szmigiel, M. Malys, M. Struzik, X. Liu and J. R. Dygas, Solid State Ionics, 2008, 179, 975 CrossRef CAS PubMed.
- I. Abrahams, X. Liu, S. Hull, S. T. Norberg, F. Krok, A. Kozanecka-Szmigiel, M. S. Islam and S. J. Stokes, Chem. Mater., 2010, 22, 4435 CrossRef CAS.
- M. Krynski, W. Wrobel, C. E. Mohn, J. R. Dygas, M. Malys, F. Krok and I. Abrahams, Solid State Ionics, 2014, 264, 49 CrossRef CAS PubMed.
- J. R. Dygas, P. Kurek and M. W. Breiter, Electrochim. Acta, 1995, 40, 1545 CrossRef CAS.
- M. Malys, J. R. Dygas, M. Holdynski, A. Borowska-Centkowska, W. Wrobel and M. Marzantowicz, Solid State Ionics, 2012, 22, 493 CrossRef PubMed.
- A. C. Larson and R. B. von Dreele, Los Alamos National Laboratory Report, 1987, LAUR-86-748 Search PubMed.
- S. K. Blower and C. Greaves, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1988, 44, 587 CrossRef.
- S. Hull, S. T. Norberg, M. G. Tucker, S. G. Eriksson, C. E. Mohn and S. Stolen, Dalton Trans., 2009, 8737 Search PubMed.
- International Tables for Crystallography, Volume A Space Group Symmetry, ed. T. Hahn, International Union of Crystallography, Kluwer Academic Publishers, Dordrecht, The Netherlands, 1992 Search PubMed.
- I. Abrahams, A. J. Bush, S. C. M. Chan, F. Krok and W. Wrobel, J. Mater. Chem., 2001, 11, 1715 RSC.
- J. Ducke, M. Troemel, D. Hohlwein and D. Kizler, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1996, 52, 1329 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 47, 558 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 Search PubMed.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- G. Kresse and J. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- H. Hellmann and F. Deuticke, Einführung in die Quantenchemie, Leipzig, 1937 Search PubMed.
- R. Feynman, Phys. Rev., 1939, 56, 340 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511 CrossRef PubMed.
- W. Hoover, Phys. Rev. A, 1985, 31, 1695 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 Search PubMed.
- L. Farrugia, J. Appl. Crystallogr., 1997, 30, 565 Search PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272 Search PubMed.
- B. Aurivillius, Chem. Scr., 1976, 10, 156 Search PubMed.
- M. G. Paton and E. N. Maslen, Acta Crystallogr., 1965, 19, 307 Search PubMed.
- N. E. Brese and M. O'Keeffe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192 Search PubMed.
- M. Holdynski, M. Sintyureva, X. Liu, W. Wrobel, J. R. Dygas, M. Pisarek, R. M. Nix, F. Krok and I. Abrahams, J. Phys.: Condens. Matter, 2012, 24, 045904 Search PubMed.
- A. Kushima and B. Yildiz, J. Mater. Chem., 2010, 20, 4809 Search PubMed.
| This journal is © The Royal Society of Chemistry 2015 |