ZnO quantum dots and graphene based heterostructure for excellent photoelastic and highly sensitive ultraviolet photodetector

Abstract

Heterostructures comprised of zinc oxide quantum dots (ZnO QDs) and graphene are presented for ultraviolet photodetectors (UV PD). Graphene–ZnO QDs–graphene (G–ZnO QDs–G) based PD demonstrated an excellent UV photoresponse with outstanding photoelastic characteristics when illuminated for several cycles with a periodicity 5 s. PD demonstrated faster detection ability with the response and recovery times of 0.29 s in response to much lower UV illumination. A direct variation in photoresponse is revealed with the bias voltage as well as UV illumination intensity. A drastic reduction in the dark current is noticed due to potential barrier formation between adjacent ZnO QDs and the recombination rate reduces by directly transferring photogenerated charge carriers from ZnO QDs to graphene for enhanced the charge mobility.

---

Introduction

Graphene, a unique two dimensional structure of carbon atoms arranged in a hexagonal honeycomb lattice, has attracted research interest due to its extraordinary optical, mechanical, thermal, and electrical properties.^1–3 The propagation of electrons in graphene behaves as massless Dirac fermions, where the energy and momentum obey linear relationship⁴ that displays high transport charge carriers mobility up to 10⁵ cm V⁻¹ s⁻¹ at ambient temperature and therefore graphene is preferable in high-speed electronic and optoelectronic device applications.^4–7 Among those, graphene is highly preferable in photodetectors (PD) because of tunable energy band gap, which allows it to use for different PD applications such as broad band,^8,9 visible-blind infrared^10,11 visible-blind ultraviolet (UV),^12,13 etc. In addition, graphene based devices display thermoelectric,¹⁴ photo-thermoelectric,^15,16 photo-bolometric,^17,18 etc. mechanisms. Therefore, graphene is extremely preferable in heterostructure based PDs for improved performance.^19–21 Along with graphene, compound semiconductors with large band gap and unique optical properties are highly desirable in fabricating heterostructure based PDs.^22,23 Among these, zinc oxide (ZnO) is a direct band gap (3.37 eV) compound semiconductor with unique optical properties suitable for the UV photodetection. It has large exciton binding energy of 60 meV and exhibits an excitonic emission at room temperature.²⁴ So far, UV PDs based on various carbon nanomaterials like graphene and carbon nanotubes along with ZnO nanostructures such as nanorods, nanowires, etc. have been reported.^{19,23,25–27} However, these reports mostly demonstrated a much lower photoresponse including the low detection speed, poor reproducibility and large dark current etc. during UV photodetection. Recently, ZnO quantum dots (QDs) have presented excellence in optoelectronics due to unique optical properties, large surface-to-volume ratio and tunable optical band gap,^20,28 applicable in various optoelectronic applications. In QDs, the charge carriers are confined in all the three directions and hence induce quantum tunneling of charge carriers with abundant charge trapping states on the surface. Hence, it is important to present ZnO QDs and graphene based heterostructure that implement the excellent UV photoresponse with low dark current, excellent reproducibility with faster photodetection speed.

In this study, we have demonstrated the photoresponse of a heterostructure based on ZnO QDs and graphene for visible-blind UV detector. The graphene–ZnO QDs–graphene (G–ZnO QDs–G) PD demonstrated excellent UV illumination sensitivity, outstanding reproducibility for UV photo signal along with low dark current. As mentioned earlier, the presence of abundant charge trapping states on ZnO QDs surface largely enhances photocurrent during UV illumination. Moreover, barrier formation between adjacent ZnO QDs surfaces reduces the dark current. Graphene induces high mobility in photogenerated free charge carriers that are drifted by the generation of internal electric field as well as applied external electric field to significantly amplify the photocurrent. Also, Schottky barrier formation at graphene and ZnO QDs interface reduces detection speed during UV illumination.

Experimental section

Materials and methods

The materials used for the synthesis of both ZnO QDs and graphene are potassium hydroxide (KOH), ethanol (CH₃CH₂OH), zinc acetate dihydrate (Zn(CH₃COO)₂·H₂O), copper foil, poly(bisphenol carbonate) (PC), ferric chloride (FeCl₃), silver paste and chloroform that were procured from the Sigma Aldrich and Alfa Aesar.

The sample characterization was performed using optical microscopy (Nikon ECLIPSE LV100), Raman spectroscopy (HORIBA JOBIN YVON LabRAM HR), transmission electron microscope (TEM, FEI Tecnai F30 S-TWIN TEM), X-ray diffraction (XRD, Rigaku Smart lab), photoluminescence (Perkin Elmer Luminescence Spectrometer LS-55), UV-visible spectroscopy (Perkin Elmer Lambda 750), UV illumination source (Philips TL-D 18 W and NARVA UVK 125-2 8), Keithley source meter (2611B) and ORIEL IQE 200, respectively.

Synthesis of ZnO QDs and graphene

The synthesis of ZnO QDs was performed by initially dissolving 30 mM potassium hydroxide into ethanol followed by adding 65 mL of this solution drop by drop in 125 mL solution of 10 mM zinc acetate dihydrate dissolved in ethanol. Afterward, the solution was stirred for 2 hours vigorously at 60 °C and the milky color precipitate was collected. The product was centrifuged for several times after changing ethanol each time and finally redispersing in ethanol.²⁹

The graphene was synthesized by atmospheric chemical vapor deposition where a copper foil of 25 μm thickness and 1 cm² area was used as a substrate. Before growth of graphene, copper substrate was cleaned in acetone, isopropyl alcohol and deionized water followed by drying in nitrogen gas. The cleaned copper substrate was loaded in the heating zone of a tubular furnace kept at 960 °C in the presence of argon gas flowing at a constant rate of 1000 sccm (standard cubic centimeters per minute). The substrate was then annealed for 1 hour in presence of both hydrogen (400 sccm) and argon gases to remove the native oxide from the surface of the copper substrate. The graphene growth was conducted by introducing methane gas (20 sccm) for 3 minutes and the furnace was suddenly cooled down to room temperature in presentence of both hydrogen and argon gases.³⁰

Graphene transfer and characterizations

The graphene, grown on copper substrate was cut into desired dimension and each piece was coated with poly(bisphenol carbonate) (PC) solution (0.3 gm PC in 10 mL chloroform) on both the sides by spin coating (5000 rpm) and then dried at 90 °C for 1 hour. The PC-coated graphene on copper substrate was then dipped into ferric chloride solution (2 gm FeCl₃ in 40 mL deionized water) for 5 hours to etch the copper. The copper free PC-coated graphene was then transferred onto the silicon wafer (SiO₂ (1 μm)/Si) and then dipped into chloroform for 4 hours to separate graphene from the PC. Afterward, the sample was washed in deionized water for 5 times.

The transferred graphene on silicon wafer was first evaluated by optical microscopy, thereafter Raman spectroscopy analysis provided the information about the quality of graphene. The surface topography of ZnO QDs and elemental analysis were performed using TEM and EDS. XRD analysis was employed to study of crystal structure of ZnO QDs and the optical behavior was investigated using photoluminescence and UV-visible spectroscopy.

Device fabrication and photoresponse measurements

For the fabrication of ZnO QDs and graphene heterostructure based PD, two graphene layers of same dimensions were transferred onto the silicon wafer by maintaining a constant distance ∼200 μm between them. One micro liter (1 μL) of colloidal ZnO QDs of thickness around 20 μm was drop-casted between the gap and dried by radiation heating. Silver conductive paste was used to make the conduction channels through both the graphene electrodes and the detailed steps involved in the fabrication of G–ZnO QDs–G heterostructure PD of device size 1 cm × 1 cm are illustrated in Fig. 1(a). Fig. 1(b) demonstrates the schematic illustration of complete experimental setup for G–ZnO QDs–G UV PD. The photoresponse of fabricated G–ZnO QDs–G PD was evaluated using 365 nm wavelength of UV illumination on 150 μm × 150 μm illumination area at different illumination intensities. Keithley source-meter recorded the variation in current during the UV illumination. Cyclic as well as saturation photoresponses were measured at different bias voltages and UV illumination intensities. Furthermore, the external quantum efficiency dependence of the fabricated PD with illumination wavelength was performed using ORIEL IQE 200 technique. Moreover, specific detectivity dependence on illumination wavelength was also evaluated.

Fig. 1 Schematic illustration of (a) the steps involved in the fabrication process of G–ZnO QDs–G heterostructure and (b) illustration of the complete device upon UV exposure.

Results and discussion

The optical image of transferred graphene layers onto silicon wafer is shown in Fig. 2(a). Uniform layers of graphene can be observed on the wafer and a gap of ∼200 μm is clearly visible from the color contrast. Fig. 2(b) demonstrates an optical image after drop-casting colloidal ZnO QDs in between the gap as depicted in Fig. 1(a). The surface topography of colloidal ZnO QDs is shown in TEM image (Fig. 2(c)) demonstrating the distribution of colloidal ZnO QDs of size ∼5 nm. Another high magnification image of ZnO QDs in Fig. 2(d) demonstrates the crystalline nature of colloidal ZnO QDs with interplanar spacing of 0.27 nm representing (002) plane of ZnO QD. Moreover, Fig. 2(e) represents the EDS spectrum of colloidal ZnO QDs where only zinc and oxygen are present without any other impurity. The additional elements namely carbon and copper appear due to carbon coated copper mesh used for substrate.

Fig. 2 Optical images of (a) graphene layers on silicon wafer and (b) drop-casted ZnO QDs between the gap. TEM images of colloidal ZnO QDs (c) at low magnification and (d) high magnification. (e) An EDS spectrum of colloidal ZnO QDs.

Fig. 3(a) illustrates the Raman spectrum of transferred graphene depicting peaks around 1345 cm⁻¹, 1582 cm⁻¹, 2450 cm⁻¹, 2697 cm⁻¹ and 2950 cm⁻¹, respectively that represents D, G, G*, 2D and D + G bands of graphene. The D band represents the disorder-induced band originated from the lattice mismatch in the middle of the Brillouin zone.^30,31 This could also arise due to the thermal expansion coefficients mismatch of graphene and copper substrate during growth and defects appear during transfer process of graphene onto the wafer.^30–33 The G band associated with the first order Raman scattering process appears due to doubly-degenerate (in-plane transverse optical and longitudinal optical) phonon modes at the center of Brillouin zone and 2D band originates from second order Raman scattering process due to two-doubly degenerate phonons.^31,34 These G and 2D bands are mainly responsible for the determination of the number of graphene layers. The peak intensity ratio of 2D to G bands (∼1.37) represents the bilayer graphene.^30–35 Moreover, the low intensity additional Raman peak, known as G* at around 2450 cm⁻¹ is observed, which could be mainly attributed to the intervalley of double resonance Raman process with the combination of both in-plane transverse optical and longitudinal acoustic phonon modes of graphene.^31,36

Fig. 3 (a) Raman spectrum of transferred graphene on silicon wafer. (b) XRD pattern of ZnO QDs. Room temperature optical measurements of ZnO QDs: (c) photoluminescence and (d) absorption spectra.

The crystal structure of ZnO QDs dispersed on silicon wafer is shown in Fig. 3(b). The high intensity diffraction peaks at around 2θ = 32.9° and 69.2° appear due to the silicon wafer and represent (200) and (400) diffraction planes of silicon.^37,38 The additional diffraction peaks (inset image) appear at around 2θ = 31.71°, 34.4° and 36.30°, respectively, indicating the hexagonal wurtzite reciprocal representation of ZnO with diffraction planes (100), (002) and (101), respectively.^30,39

The photoluminescence spectrum of ZnO QDs at room temperature is shown in Fig. 3(c). The spectrum shows an emission peak at around 382 nm (3.25 eV). This emission peak attributes to the intrinsic recombination of free excitons corresponding to the UV emission. The additional blue emission peaks at around 405 nm (3.06 eV) and 435 nm (2.85 eV), respectively attribute to the zinc interstitial defects where at an interstitial site, zinc atom is surrounded by more than one oxygen atoms.^40,41

Hence, two peaks at 405 nm and 435 nm, originated from the intrinsic zinc defects and extended intrinsic zinc defects are located at around 0.22 eV and 0.5 eV, respectively that is below the conduction band of ZnO.^40–42 Therefore, when UV illumination energy is equal or larger than the band gap of ZnO QDs, the electrons excite from valance to the conduction band. These localized electrons then directly recombine with the holes in valance band results in UV emission (3.25 eV) and some of the conduction electrons transitioned into energy levels of the zinc intrinsic defects and extended zinc intrinsic defects and finally recombine with the valance band holes by illuminating the blue emissions at wavelengths around 405 nm and 435 nm. The room temperature UV-visible absorption spectrum of ZnO QDs is shown in Fig. 3(d). The optical absorption edge at wavelength of ∼365 nm apportions the intrinsic band gap absorption due to the transition of electrons from valance to the conduction band. Inset in Fig. 3(d) shows the variation of first derivative of absorption with respect to the photon energy and used for the optical band gap determination of ZnO QDs. The value of maximum derivative appears at around photon energy of 3.39 eV indicating the optical band gap of ZnO QDs lies in UV region.^43,44

The typical current–voltage (I–V) analysis of G–ZnO QDs–G PD in presence and absence of UV illumination is shown in Fig. 4(a), where voltage was swept from –2 to +2 V. The significant enhancement of photocurrent during UV illumination is observed that is mainly contributed to photogeneration of free charge carriers where the energy of illumination (∼3.39 eV) is greater than the band gap of ZnO QDs. This can be described in light of conventional ZnO nanostructures (nanowires, nanorods etc.) based UV PD, where the photodetection mechanism involves following: in dark, oxygen molecules, adsorbed on ZnO nanostructure surface form a low conductivity depletion region on the nanostructure surface by trapping free electrons from n-type ZnO nanostructure [O₂(g) + e⁻ → O₂⁻(ad)]. Under UV illumination, electron–hole pairs of energy equal or greater than the band gap of ZnO are photogenerated [hν → e⁻ + h⁺]. The photogenerated holes migrate to the nanostructure surface along with the potential slope induced by upward energy band-bending and desorb the oxygen molecules from the ZnO nanostructure surface [h⁺ + O₂⁻(ad) → O₂(g)]. This resulted in reducing the depletion region followed by free electrons contributing to the enhancement of conductivity in the form of large photocurrent.^45,46 Generally, this oxygen adsorption/desorption processes are slow which results in slower photodetection speed as was observed previously in ZnO nanowires based UV photodetectors.^47,48 However, in ZnO QDs system the surface introduces more charge trapping states due to the quantum confinement of charge carriers. In addition to oxygen desorption during UV illumination, the quantum confinement of charge drastically changes due to quantum tunneling of photo-induced charge carriers through the potential barriers between adjacent ZnO QDs interface. Also, probably there is interband transition of charge carriers during UV illumination that contributes to additional photocurrent.^40,41,49 These quantum tunneling, interband transitions and presence of surface charge trapping states induce drastic increase in the photocurrent during UV illumination, which is not only much higher as compared to nanorods, nanowires, nanoparticles etc. based PDs but also demonstrated fast carrier recombination while turning off UV illumination. An asymmetric variation of I–V is observed as shown in inset of Fig. 4(a) that clearly shows the generation of 210 nA and 75 nA absolute photocurrents at the bias voltage of 0.5 V and −0.5 V, respectively. It has been observed that an asymmetric I–V is attributed to the rectifying (Schottky) barrier formation between graphene and ZnO heterostructure system because of the difference in the work function (Φ) of graphene and the electron affinity (χ) of ZnO.^19,50 Therefore, the current (I) through the Schottky barrier which is mainly dominated by thermionic emission (TE) of majority charge carrier under forward bias can be ascribed as, I = I₀[exp(qV/ηkT) − 1]; where, I₀ = AA*T² exp(−qΦ_S/ηkT) is the reverse saturation current, q is the charge of electron, η = (q/kT)(dV/dln I) is the ideality factor, T is the absolute temperature, k is the Boltzmann constant, A is the area of the Schottky barrier, A* is the Richardson constant and Φ_S = Φ − χ is the Schottky barrier height.^19,50

Fig. 4 (a) Current–voltage analysis of G–ZnO QDs–G PD in a bias voltage range of −2 to 2 V and inset shows the low bias voltage range, −0.5 to 0.5 V at UV illumination intensity of 1.3 mW cm⁻². (b) Response current and time analysis at different bias voltage and (c) the variation of saturation response current with bias voltage at UV illumination intensity of 1.3 mW cm⁻². (d) Time-dependent cyclic photoresponse analysis for 54 cycles, where each cycle is for 5 s of UV illumination at bias voltage 1 V.

The current is demonstrated as a function of both Schottky barrier height, Φ_S as well as applied bias voltage, V which determine the variation in I–V. It is clear from the results that in G–ZnO QDs–G device, possibly there is formation of two back-to-back Schottky barriers (diodes), where one diode behaves as forward bias and other as reversed bias and vice versa.⁵⁰ On the other hand, the magnitude of dark currents observed at voltage 2 V and −2 V are 600 nA and 800 nA, respectively, whereas the photocurrents remains same as 1200 nA (Fig. 4(a)), which could be due to quantum mechanical tunneling and thermionic-field emission (TFE) of photogenerated electron through the ZnO QDs and graphene Schottky barrier at relatively large bias voltage.^51,52 Moreover, the self-heating at relatively large bias voltage help in the direct quantum tunneling of charge carriers through the Schottky barriers under both reverse as well as forward bias. These results display the linear behavior of I–V during UV illumination.⁵² Also, it has been observed that, in graphene based device the phonon scattering enhanced along with the bias voltage and display anomalous behavior of I–V.^30,53,54

The study of response current–time, where response current (I = I_UV − I_dark; I_UV and I_dark are the currents in presence and absence of UV illumination) analysis at different bias is shown in Fig. 4(b). The variation in response current shows that within 5 s of UV exposure, the response current saturates at all bias voltages. Fig. 4(c) shows the variation of saturation response current with the bias voltage. An increase is observed with the bias voltage since the drift velocity of photogenerated charge carriers is proportional to the applied electric field.^55,56 Overall, twelve times enhancement in saturation response current is observed at a bias voltage of 2 V as compared to low bias voltage of 0.25 V. Further analysis reveals that the photoresponse is a direct function of bias voltage with excellent repeatability. The time-dependent cyclic photoresponse behavior of G–ZnO QDs–G based PD is depicted in Fig. 4(d), where UV radiation was illuminated for 54 cycles and each cycle for 5 s at a bias voltage of 1 V. Fig. 4(d) shows the repeatability of UV photoresponse without any significant change in the saturation response current as compared to single cycle response. This excellent cyclic photoresponse of the PD reveals the outstanding reproducible photoresponse at UV illumination intensity of 1.3 mW cm⁻².

For more clarity, the photoresponse of PD for 15 cycles and single cycle of UV illumination is revealed in Fig. 5(a) and (b), respectively. The magnified cyclic photoresponse (Fig. 5(b)) for single cycle clearly demonstrates that within a small interval of UV illumination, the photoresponse saturates very fast and then quickly falls to the original value during OFF state of UV illumination. Furthermore, the response time (t_r) (time required for the response current to reach from 10 to 90% of its saturation value) and recovery time (t_d) (time required to fall the response current from 90 to 10% from its saturation value) determines the detection speed of PD.^55,57 Fig. 5(c) and (d) show the estimation of t_r and t_d values and both the observed values are 0.29 s. These values are smaller than previously reported most of ZnO heterostructure based UV PDs thus PD demonstrates the faster detection ability for UV signal of 1.3 mW cm⁻² intensity.^{20,27,55–57}

Fig. 5 Time-dependent cyclic photoresponse analysis for (a) 15 cycles and (b) single cycle, where each cycle of UV illumination was for 5 s at a bias voltage of 1 V. Calculation of (c) response time and (d) recovery time of G–ZnO QDs–G PD.

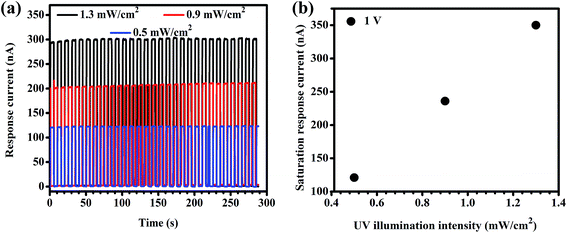
The study of UV photoresponse at different UV illumination intensity is shown in Fig. 6(a). The UV radiation was exposed for 29 cycles and each cycle for 5 s at different UV illumination intensities (0.5 mW cm⁻², 0.9 mW cm⁻² and 1.3 mW cm⁻²), respectively. The time-dependent cyclic photoresponse analysis determines the reproducible photoresponse at all UV illumination intensities. Similarly, Fig. 6(b) shows the variation of saturation response current with UV illumination intensity. It shows that the saturation response current increases with UV illumination intensity since the photogeneration efficiency is directly proportional to absorbed photon flux.⁴⁶ Hence, these studies demonstrate that the G–ZnO QDs–G PD is highly sensitive to the low UV illumination and provides reproducible photoresponse.

Fig. 6 (a) Time-dependent cyclic photoresponse analysis for 29 cycles at different UV illumination intensity and (b) variation of saturation response current with UV illumination intensity at a bias voltage of 1 V.

The charge transport mechanism in G–ZnO QDs–G based PD is revealed by the schematics in Fig. 7. In ZnO QD, the charge carriers are confined in all the three directions. Therefore, there is a potential barrier between adjacent ZnO QDs during electrical transportation. The formation of potential barrier height between adjacent ZnO QDs further increases due to the formation of low conductive depletion region on the surfaces due to adsorption of oxygen molecules in absence of UV illumination (Fig. 7(a)) as mentioned earlier. During UV illumination, the potential barrier height reduces drastically by inducing more photogenerated carries due to reduced depletion region as shown in schematic in Fig. 7(b). Hence, the enhanced electrical transportation amplifies the photocurrent. After transportation of photogenerated charge carrier from ZnO QDs to graphene, the electrical mobility further enhanced by graphene that in turn reduces the probability of charge carriers recombination.

Fig. 7 Schematic illustration of charge conduction mechanism involved in G–ZnO QDs–G based PD: (a) oxygen molecules adsorb on ZnO QDs surface (smaller and bigger solid spheres represent the O₂⁻ and ZnO QD, respectively) in dark as shown in top schematic and the bottom schematic represents the energy band diagram, where the formation of potential barrier between adjacent ZnO QDs is shown clearly. (b) Under UV illumination, desorption of oxygen molecules and hence reduction in potential barrier as shown in the schematics.

Moreover, the analysis of external quantum efficiency (EQE) defined as the number of charge carriers generated per number of incident photons on G–ZnO QDs–G PD as shown in Fig. 8(a).^4,55 The variation of EQE with illumination wavelength shows that a peak appears in UV wavelength region, where the illumination energy is equal or greater than the band gap of ZnO QDs. However, a small peak observed at wavelength around 400 nm that could be due to the intrinsic zinc related defects present in ZnO QDs (as discussed previously in Fig. 3(c)). Therefore, this analysis demonstrates that the G–ZnO QDs–G based PD is only sensitive to the UV illumination (visible-blind). Furthermore, an additional device parameter namely specific detectivity (D*) of an PD characterizes its ability to detect small photo signal and is directly related to the noise of an PD.^4,58,59 Generally, the sources of noise generated in PD is mainly due to the contributions from dark current and thermal fluctuation. The shot noise mainly occurs due to the dark current, where Johnson and flicker noises arise due to the thermal fluctuation. At a very low and a high frequency based PDs, the flicker noise and Johnson noise play significant role. So, if we consider the major contribution of noise is due to the dark current then D* can be written as, where A is effective area of UV illumination, q is the elementary charge, ν is the frequency of absorbed photon, h is Planck's constant and I_dark is the dark current.^4,58,59 Fig. 8(b) shows the dependence of D* with the illumination wavelength at bias voltage of 1 V. Similarly, the peak value of D* is also observed in the UV illumination region due to the photo-induced charge carriers and the value is of the order of 10⁹ Jones (1 Jones = 1 cm Hz^1/2 W⁻¹). Hence, a large value of D* is in agreement with the low illumination detection ability with the low noise current based PD.

Fig. 8 Dependence of (a) external quantum efficiency and (b) specific detectivity on the illumination wavelength at a bias voltage of 1 V.

Conclusion

In summary, novel ZnO QDs based heterostructure is fabricated along with graphene layers to demonstrate excellent UV photoresponse and outstanding stability for visible-blind UV PD. Presented G–ZnO QDs–G based PD shows the faster detection speed and excellent sensitivity to low UV illumination signals. The formation of both potential barrier between adjacent ZnO QDs and rectifying barrier between graphene and ZnO QDs reduce the dark current of PD. Transportation of photogenerated charge carriers to graphene enhances the mobility and amplifies the photocurrent by reducing the recombination during UV illumination. Furthermore, the additional device parameters, namely external quantum efficiency and specific detectivity of the G–ZnO QDs–G based PD reveal visible-blind, low noise and low UV signal sensitive PD. Overall, the presented G–ZnO QDs–G based PD demonstrates outstanding reproducibility, excellent stability and faster detection speed at low UV illumination signal.

References

1. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
2. F. Bonaccorso, Z. Sun, T. Hasan and A. C. Ferrari, Nat. Photonics, 2010, 4, 611.
3. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109.
4. Z. Sun and H. Chang, ACS Nano, 2014, 8, 4133.
5. F. Xia, T. Mueller, Y. Lin, A. Valdes-Garcia and P. Avouris, Nat. Nanotechnol., 2009, 4, 839.
6. L. Liao, Y.-C. Lin, M. Bao, R. Cheng, J. Bai, Y. Liu, Y. Qu, K. L. Wang, Y. Huang and X. Duan, Nature, 2010, 467, 305.
7. T. Mueller, F. Xia and P. Avouris, Nat. Photonics, 2010, 4, 297.
8. H. Qiao, J. Yuan, Z. Xu, C. Chen, S. Lin, Y. Wang, J. Song, Y. Liu, Q. Khan, H. Y. Hoh, C.-X. Pan, S. Li and Q. Bao, ACS Nano, 2015, 9, 1886.
9. Y. Zhang, T. Liu, B. Meng, X. Li, G. Liang, X. Hu and Q. J. Wang, Nat. Commun., 2013, 4, 1811.
10. Z. Sun, Z. Liu, J. Li, G. Tai, S.-P. Lau and F. Yan, Adv. Mater., 2012, 24, 5878.
11. B. Chitara, L. S. Panchakarla, S. B. Krupanidhi and C. N. R. Rao, Adv. Mater., 2011, 23, 5419.
12. Q. Zhang, J. Jie, S. Diao, Z. Shao, Q. Zhang, L. Wang, W. Deng, W. Hu, H. Xia, X. Yuan and S.-T. Lee, ACS Nano, 2015, 9, 1561.
13. V. Q. Dang, T. Q. Trung, D.-I. Kim, L. T. Duy, B.-U. Hwang, D.-W. Lee, B.-Y. Kim, L. D. Toan and N.-E. Lee, Small, 2015, 11, 3054.
14. F. Mazzamuto, V. H. Nguyen, Y. Apertet, C. Caer, C. Chassat, J. Saint-Martin and P. Dollfus, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 235426.
15. X. Xu, N. M. Gabor, J. S. Alden, A. M. V. D. Zande and P. L. McEuen, Nano Lett., 2010, 10, 562.
16. J. C. W. Song, M. S. Rudner, C. M. Marcus and L. S. Levitov, Nano Lett., 2011, 11, 4688.
17. J. Yan, M.-H. Kim, J. A. Elle, A. B. Sushkov, G. S. Jenkins, H. M. Milchberg, M. S. Fuhrer and H. D. Drew, Nat. Nanotechnol., 2012, 7, 472.
18. H. Vora, P. Kumaravadivel, B. Nielsen and X. Du, Appl. Phys. Lett., 2012, 100, 153507.
19. B. Nie, J.-G. Hu, L.-B. Luo, C. Xie, L.-H. Zeng, P. Lv, F.-Z. Li, J.-S. Jie, M. Feng, C.-Y. Wu, Y.-Q. Yu and S.-H. Yu, Small, 2013, 9, 2872.
20. D. I. Son, H. Y. Yang, T. W. Kim and W. I. Park, Appl. Phys. Lett., 2013, 102, 021105.
21. G. Konstantatos, M. Badioli, L. Gaudreau, J. Osmond, M. Bernechea, F. P. G. de Arquer, F. Gatti and F. H. L. Koppens, Nat. Nanotechnol., 2012, 7, 363.
22. K. K. Manga, J. Wang, M. Lin, J. Zhang, M. Nesladek, V. Nalla, W. Ji and K. P. Loh, Adv. Mater., 2012, 24, 1697.
23. H. Chang, Z. Sun, K. Y.-F. Ho, X. Tao, F. Yan, W.-M. Kwok and Z. Zheng, Nanoscale, 2011, 3, 258.
24. M. H. Huang, S. Mao, H. Feick, H. Yan, Y. Wu, H. Kind, E. Weber, R. Russo and P. Yang, Science, 2011, 292, 1897.
25. J. G. Ok, J. Lee, H. Baac, S. Tawfick, L. J. Guo and A. J. Hart, ACS Appl. Mater. Interfaces, 2014, 6, 874.
26. J. Tian, S. Liu, H. Li, L. Wang, Y. Zhang, Y. Luo, A. M. Asiri, A. O. Al-Youbicd and X. Sun, RSC Adv., 2012, 2, 1318.
27. L. Hu, J. Yan, M. Liao, H. Xiang, X. Gong, L. Zhang and X. Fang, Adv. Mater., 2012, 24, 2305.
28. K.-F. Lin, H.-M. Cheng, H.-C. Hsu, L.-J. Lin and W.-F. Hsieh, Chem. Phys. Lett., 2005, 409, 208.
29. W. Guo, S. Xu, Z. Wu, N. Wang, M. M. T. Loy and S. Du, Small, 2013, 9, 3031.
30. B. D. Boruah, D. B. Ferry, A. Mukherjee and A. Misra, Nanotechnology, 2015, 26, 235703.
31. L. M. Malard, M. A. Pimenta, G. Dresselhaus and M. S. Dresselhaus, Phys. Rep., 2009, 473, 51.
32. S. Amini, J. Garay, G. Liu, A. A. Balandin and R. Abbaschian, J. Appl. Phys., 2010, 108, 094321.
33. Y. Zhang, L. Zhang and C. Zhou, Acc. Chem. Res., 2013, 46, 2329.
34. A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401.
35. D. Kim, J. Y. Han, D. Lee, Y. Lee and D. Y. Jeon, J. Mater. Chem., 2012, 22, 20026.
36. R. John, A. Ashokreddy, C. Vijayan and T. Pradeep, Nanotechnology, 2011, 22, 165701.
37. K. N. Chappanda, Y. R. Smith, M. Misra and S. K. Mohanty, Nanotechnology, 2012, 23, 385601.
38. L. Tian, T. Ouyang, K. P. Loh and J. J. Vittal, J. Mater. Chem., 2006, 16, 272.
39. Y. Lv, L. Yu, H. Huang, Y. Feng, D. Chen and X. Xie, Nanotechnology, 2012, 23, 065402.
40. S. Vempati, A. Celebioglu and T. Uyar, Nanoscale, 2015, 7, 16110.
41. F. Kayaci, S. Vempati, I. Donmez, N. Biyikli and T. Uyar, Nanoscale, 2014, 6, 10224.
42. D. I. Son, B. W. Kwon, D. H. Park, W.-S. Seo, Y. Yi, B. Angadi, C.-L. Lee and W. K. Choi, Nat. Nanotechnol., 2012, 7, 465.
43. Y. Chen, D. Zeng, K. Zhang, A. Lu, L. Wang and D.-L. Peng, Nanoscale, 2014, 6, 874.
44. A. K. Zak, R. Razali, W. H. A. Majid and M. Darroudi, Int. J. Nanomed., 2011, 6, 1399.
45. H. Kind, H. Yan, B. Messer, M. Law and P. Yang, Adv. Mater., 2002, 14, 158.
46. C. Soci, A. Zhang, B. Xiang, S. A. Dayeh, D. P. R. Aplin, J. Park, X. Y. Bao, Y. H. Lo and D. Wang, Nano Lett., 2007, 7, 1003.
47. Q. H. Li, T. Gao, Y. G. Wang and T. H. Wang, Appl. Phys. Lett., 2005, 86, 123117.
48. D. Hou, A. Dev, K. Frank, A. Rosenauer and T. Voss, J. Phys. Chem. C, 2012, 116, 19604.
49. B. L. Wehrenberg, C. Wang and P. Guyot-Sionnest, J. Phys. Chem. B, 2002, 106, 10634.
50. X.-W. Fu, Z.-M. Liao, Y.-B. Zhou, H.-C. Wu, Y.-Q. Bie, J. Xu and D.-P. Yu, Appl. Phys. Lett., 2012, 100, 223114.
51. F. A. Padovani and R. Stratton, Solid-State Electron., 1966, 9, 695.
52. E. M. Mills, B. K. Min, S. K. Kim, S. J. Kim, M.-A. Kang, W. Song, S. Myung, J. Lim, K.-S. An, J. Jung and S. Kim, ACS Appl. Mater. Interfaces, 2015, 7, 18300.
53. N. Vandecasteele, A. Barreiro, M. Lazzeri, A. Bachtold and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 045416.
54. M. Popinciuc, V. E. Calado, X. L. Liu, A. R. Akhmerov, T. M. Klapwijk and L. M. K. Vandersypen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 205404.
55. B. D. Boruah, A. Mukherjee, S. Sridhar and A. Misra, ACS Appl. Mater. Interfaces, 2015, 7, 10606.
56. J. G. Ok, J. Y. Lee, H. W. Baac, S. H. Tawfick, L. J. Guo and A. J. Hart, ACS Appl. Mater. Interfaces, 2014, 6, 874.
57. W. Tian, T. Zhai, C. Zhang, S.-L. Li, X. Wang, F. Liu, D. Liu, X. Cai, K. Tsukagoshi, D. Golberg and Y. Bando, Adv. Mater., 2013, 25, 4625.
58. X. Gong, M. Tong, Y. Xia, W. Cai, J. S. Moon, Y. Cao, G. Yu, C.-L. Shieh, B. Nilsson and A. J. Heeger, Science, 2009, 325, 1665.
59. X. Wang, H. Wang, W. Huang and J. Yu, Org. Electron., 2014, 15, 3000.

---