Production of gold nanoparticles using atmospheric pressure glow microdischarge generated in contact with a flowing liquid cathode – a design of experiments study

Abstract

Direct current atmospheric pressure glow microdischarge (dc-μAPGD) generated between a miniature flow Ar plasma microjet and a small-sized flowing liquid cathode (FLC) was characterized with respect to the effects of the selected operating factors on the particle size of the synthesized Au nanoparticles (AuNPs). The factors that were investigated were the discharge current, the flow rate of the solution of the FLC, and the flow rate of the Ar plasma microjet-supporting gas. The effects of the individual factors and their inter-factor dependencies on the size and size distribution of the synthesized AuNPs were evaluated by changing the operating conditions according to the Box–Behnken design (BBD) plan and monitoring the wavelength of the maximum (λ_max) of the localized surface plasmon resonance (LSPR) absorption band. The response surface methodology (RSM) was used to fit the experimental data with an appropriate regression model and optimize the plasma-reactor system to produce spherical AuNPs having the lowest particle size and size dispersion. It was established that a high discharge current and a low flow rate of the solution of the FLC facilitated the production of spherical, uniform and the smallest in size AuNPs. The correctness of the model was validated by producing the AuNPs in optimal and non-optimal conditions and the analysis of the resultant nanofluids by UV-Vis absorption spectrophotometry, dynamic light scattering (DLS), and scanning electron microscopy (SEM).

---

Introduction

A crucial step in the synthesis of metal nanoparticles (NPs), such as gold NPs (AuNPs), is the reduction of the appropriate metal ions to their metallic forms. In currently used protocols, this step is predominately accomplished through chemical reduction facilitated by various reducing agents.¹ These chemical-based reductions are generally time-consuming and multistage processes. Additionally, these methods provide a relatively low level of control over the surface chemistry of the resulting AuNPs, and thus the AuNPs contain many undesirable surface products that must subsequently be removed.

Recent works have illustrated non-equilibrium atmospheric pressure plasmas (APPs) to be a viable alternative to the chemical reduction step in the synthesis of the AuNPs. APPs have been shown to facilitate the reduction of metal ions in solutions through the production of numerous reactive species, including radicals (H, O, OH), electrons, UV photons, and metastable excited atoms and molecules.^2–5 The most important advantages of the APPs-based synthesis of the AuNPs, extensively explored in the last few years, are the short processing time and the possibility to produce the nanostructures of Au in a single step process at room temperature and under atmospheric pressure.^2,6,7 No reducing agents, or even capping agents, are required in these conditions; hence, the resulting AuNPs contain fewer surface impurities and are more suitable for downstream applications.^6–8

Two unique groups of batch systems utilizing the APPs for the synthesis of the AuNPs have been reported in the literature. In the first group of these systems, the plasma, operated in the glow discharge (GD) regime, was sustained between two electrodes that were fully immersed in solutions of the AuNPs' precursor and supplied with a pulsed direct current-high voltage (dc-HV).^3,5,9,10 These solutions were either not pH adjusted or initially corrected to values above 6 by the addition of KOH or NaOH.^3,4,6,11,12 While water is primarily used as the solvent in these solutions, organic solvents, such as ethylene glycol¹³ or reverse micelle solutions containing dodecane,^5,14 have also been utilized. Mo wires,^4–6,9–15 Pt rods,³ and Au wires^7,8,16 have all been used as the electrodes in the discharge systems. In the latter case, Au electrodes were immersed in water and the AuNPs were synthesized due to the erosion of both electrodes and the sputtering of the cathode.^7,8,16

The second group of the plasma systems involves the synthesis of the AuNPs at the plasma–liquid interface of the APP gaseous jets in contact with aqueous HAuCl₄ solutions. Similarly to the first group of systems, the plasma was sustained in the GD regime by supplying a dc-HV to the anodes consisting of, for example, carbon rods,^17,18 a Pt rod,¹⁹ or Pt foils,^2,20–22 while the APP jets were grounded and served as the cathodes. The APP jets were generated across the gap between the surface of the solutions and the stainless steel^{2,17,18,20–25} or Cu¹⁹ capillaries, through which flows of He^{2,17,18,21,23–25} or Ar^19,20,22 were passed. In the dual plasma systems reported by Tochikubo and co-workers^23,25 and by Shirai and co-workers,²⁴ an additional plasma jet was used in place of a metallic anode. Hence the AuNPs were generated by the irradiation at the plasma–liquid interface with electrons from the negatively charged plasma jet (the plasma cathode) as well as by positive ions from the positively charged plasma jet (the plasma anode).

Very recently, our group reported the development of a unique APP-based system and its application in the synthesis of the AuNPs.²⁶ In this system, which represents the continuous-flow mode production of the NPs, a low power, direct current atmospheric pressure glow microdischarge (dc-μAPGD) was sustained between a positively charged Ar plasma microjet and a small-sized flowing liquid cathode (FLC). The resulting plasma–liquid interactions facilitated the on-line and continuous-flow production of the stable AuNPs by the positive ions' irradiation of the flowing solutions of the precursor. Ghosh and his co-workers²⁷ also lately described a APP-based system operated at the surface of a liquid microjet for the continuous synthesis of AgNPs. An interesting system, in which a stream of micro-sized liquid droplets were injected into APP, was proposed and assumed to open up possibilities to the microfluidic synthesis of nanocrystals as well.²⁸

The formation of the AuNPs through the plasma–liquid interactions has typically been performed in the presence of stabilizers and capping agents added to the solutions; i.e., hexadecyltrimethylammonium chloride (CTAC),³ polyethylene glycol (PEG),⁸ sodium dodecyl sulfate (SDS),^9,10,23–25 sodium bis(2-ethylhexyl)sulfosuccinate in dodecane,^5,14 polyvinylpyrrolidone (PVP),¹³ sodium alginate,^15,16 sodium citrate,¹⁹ or fructose.^2,20 These substances were applied to stabilize the resultant suspensions of the AuNPs and control their particle size and shape through preventing uncontrolled growth and aggregation. However, the dispersion stability of Au nanofluids was rather high as the synthesized AuNPs were negatively charged, therefore making them well-dispersed and stable in water. In these conditions, the use of capping and stabilizing agents in the synthesis of the AuNPs was not necessary.^{6,11,12,17,18,26} Interestingly, during the operation of the APPs in contact with the solutions and the synthesis of the AuNPs, it was found that different experimental conditions could influence the size and the shape of nanostructures. Hence, to have control over the processes of the nucleation, the growth, and the formation of the size distribution of the colloidal AuNPs, the effect of different parameters has been studied in reference to the position of the wavelength of the maximum (λ_max) of the localized surface plasmon resonance (LSPR) absorption band, the intensity of this band, and the full width at half maximum (Δλ_FWHM) value. In this way, the relationship between selected parameters, i.e., the concentration of HAuCl₄ in solutions,^{10,17,18,25,26} the concentration of the added surfactant,^13,14,16,19 the type of the surfactant,²⁶ the pH of solutions³ and their temperature,^4,8,12,21 the stirring mode,^19,21 the discharge/process time,^{2,8–10,14–16,19,20,22,24,25} the discharge gap,⁶ the dc duty ratio,¹¹ the discharge voltage,^9,10 the discharge current,^17,18,21 the discharge power,¹⁹ and the shape and the size of the AuNPs, in addition to the rate of their synthesis, was assessed. Unfortunately, a one-factor-at-a-time (OFAT) approach was used in all these studies to determine which of the listed parameters and selected conditions provided the production of the smallest in size, mono-dispersed, and spherical AuNPs. The use of the OFAT approach required a great number of individual experiments to be run in order to achieve the desired precision of estimated effects of studied parameters, could not examine any possible interactions between parameters, and finally missed optimal settings of APP-based systems giving the best process performance.

The main objective of the present work was to determine the optimal operating conditions of the μAPGD-based plasma-reactor system in reference to the synthesis of the AuNPs with the smallest particle size and the lowest dispersion. In order to avoid the limitations of the OFAT approach, a design of experiments (DOE) approach was used and the effect of selected, simultaneously varied parameters was studied on the wavelength of the maximum of the LSPR absorption band.

Experimental

Reagents and solutions

Re-distilled water was used throughout. All reagents were of the analytical grade or better and used as received. Solid HAuCl₄·4H₂O was purchased from Avantor Performance Materials (Gliwice, Poland) and used to prepare a 1000 mg L⁻¹ stock solution of Au. Working solutions of the precursor of AuNPs were prepared by appropriately diluting the stock solution and contained 50 mg L⁻¹ of Au. Prior to the synthesis of the AuNPs in a dc-μAPGD-based plasma-reactor system, these solutions needed to be conductive and therefore were acidified with a 1.0 mol L⁻¹ HCl (Avantor Performance Materials, Gliwice, Poland) solution to a final concentration of 0.1 mol L⁻¹. In addition, gelatine (with an average molecular weight of 80 000 g mol⁻¹ and purity of 99.9% m/m), obtained from Rousselot International (Dubuque, IA, USA), was added to these solutions as a capping and stabilizing agent of the synthesized AuNPs. The final concentration of gelatine was 0.5% m/v. Pure Ar (99.996%) was supplied by Messer (Wroclaw, Poland).

Synthesis of the AuNPs in a plasma-reactor system

A miniature plasma-reactor system, based on dc-μAPGD, was used for the synthesis of the AuNPs in a continuous-flow mode. The discharge was stably sustained in the open-to-air atmosphere between an Ar plasma microjet, acting as the anode, and a solution of the FLC, containing the precursor of the AuNPs. For normal operation of the plasma-reactor system and the synthesis of the AuNPs, miniature flows (60–180 mL min⁻¹) of Ar were passed through a stainless steel nozzle (ID 500 μm) while solutions of the FLC were continuously introduced to the system at a flow rate within 3.0–5.0 mL min⁻¹ through a graphite tube (ID 4.0 mm) mounted on the top of a quartz delivery capillary (ID 2.0 mm). The flow rate of the Ar plasma microjet-supporting gas was controlled using a Tylan General (Tylan General Inc., San Diego, CA, USA) mass flow controller, model FC-2900, combined with a Tylan General digital flow meter, model RO-28. A LabCraft (France) two-channel peristaltic pump, model Hydris 05, was applied to deliver working solutions of the precursor of the AuNPs to the plasma-reactor system. dc-μAPGD was initiated and maintained after supplying a proper dc-HV (900–1400 V) to both electrodes; i.e., a positive potential to the stainless steel nozzle of the Ar plasma microjet (the source of positive ions) and a negative potential to the FLC (the source of electrons) through a Pt wire attached to the graphite tube. The dc-HV was supplied from a dc-HV generator (Laboratory Electronic Instrumentation Production, Wroclaw, Poland). The stainless steel nozzle and the graphite/quartz tube were vertically oriented; the distance between them was 5.0 mm. By increasing the supplied dc-HV, the discharge current flowing through both electrodes, was changed from 15 to 45 mA, and stabilized by a 10 kΩ ballast resistor inserted in a circuit. A schematic diagram of the plasma-reactor system for the production of the AuNPs based on reactions and processes occurring at the interface of the gas phase of dc-μAPGD and the liquid phase are presented in Fig. 1. The synthesis of the AuNPs was carried out in a continuous-flow mode during the operation of the discharge. Following the treatment by dc-μAPGD, the working mixtures of the AuNPs precursor (HAuCl₄ along with added gelatin and HCl) overflowed the graphite tube and were collected in a small glass reservoir of the FLC compartment and instantly drained from the plasma-reactor system by another LabCraft Hydris 05 peristaltic pump. These solutions, which contained the AuNPs synthesized in the different experimental conditions, were saved for the further characterization.

Fig. 1 A schematic diagram of the reaction-plasma system with dc-μAPGD sustained between an Ar plasma microjet and a small-sized flowing liquid cathode.

Characterization of the AuNPs

The working mixtures treated by dc-μAPGD in the plasma-reactor system were analyzed in reference to the optical properties and the particle size of colloidal suspensions of the AuNPs. Accordingly, the optical absorption characteristics of Au nanostructures, caused by the LSPR, were assessed using UV-Vis absorption spectrometry and analyzing the morphology of the measured absorption spectra of the treated solutions. The solutions were measured after 24 h of the treatment by dc-μAPGD since such time was recently found to give the highest absorption values at the maximum of the LSPR absorption band.²⁶ A Thermo Scientific (Thermo Scientific Poland, Warsaw, Poland) Genesis™ 10S UV-Vis spectrophotometer, with a high-intensity xenon lamp, a dual-beam optical geometry, and an internal reference detector, was used for the measurements. All absorption spectra of the solutions were recorded in the spectral range of 400–1100 nm, using a spectral bandwidth of 1.8 nm, a wavelength scan speed of 4200 nm min⁻¹, and an interval of 0.5 nm. A quartz cuvette (ID 1.0 cm) was used. The acquired absorption spectra gave the information about the shift in the position of the λ_max of the LSPR absorption band for the AuNPs, normally located within 520–550 nm in the case of the spherical Au nanostructures.^4,13,16 This information was used to elucidate changes in the particle size of the resultant AuNPs according to the Mie scattering theory,²⁷ i.e., a decrease in their size in case of the λ_max of the LSPR band shifted toward shorter wavelengths. In addition, the shape of the LSPR absorption band, related to its Δλ_FWHM, was used to reveal the information about the particle size distribution of the synthesized AuNPs.^6,11,18

The particle size by volume of the colloidal AuNPs, referred to as the hydrodynamic diameter, was measured using dynamic light scattering (DLS) and laser diffraction. A Nicomp 380ZLS (Nicomp International Inc., Orlando, FL, USA) particle sizing system, equipped with an excitation source (a green laser) operated at 532 nm at 50 mW, was used. A frequency of the photon counting was set at 200 kHz while a scattering angle was fixed at 90°. The temperature of the measured media was in the range of 23–25 °C. Disposable polymethyl methacrylate cuvettes (ID of 1.0 cm) were applied. The calculation of the hydrodynamic diameter was based on the Stokes–Einstein equation²¹ taking into consideration water as a continuous phase; the viscosity of water taken was between 0.931 and 0.890 mPa s, and the diffusion coefficient of the measured nanoparticles was in the range of (2.14–4.81) × 10⁻⁸ cm³ s⁻¹.

Finally, the morphology of the resulting AuNPs was assessed using scanning electron microscopy (SEM). A Joel (Joel USA Inc., Peabody, MA, USA) JSM-6610LVnx instrument, equipped with an Oxford Aztec Energy energy-dispersive X-ray spectroscopy attachment (EDS), and a CCD camera, was used. The pressure in the SEM chamber was in the range of 10 to 270 Pa. Prior to the imaging of the AuNPs, they were appropriately washed with re-distilled water using a three-step centrifugation/decantation protocol recently described.²⁶ The purified AuNPs were diluted and placed on a carbon sticky tape and evaporated. An operating voltage within 24–27 kV was used. The magnification with a satisfactory sharpness and resolution was from 14 000 to 15 000.

Design of experiments and the surface response methodology

To study the effect of the selected operating factors of the dc-μAPGD plasma-reactor system on the λ_max corresponding to the production of the spherical AuNPs with the lowest particle size, a Box–Behnken experimental design (BBD) was created. The response of the system, i.e., the λ_max, was based on the UV-Vis absorption spectra of the AuNPs precursor solutions after their treatment by dc-μAPGD. The mean values of the λ_max for 3 independently repeated measurements were considered in the design matrix. Because 3 continuously changed experimental factors related to the performance of dc-μAPGD and the course of the interactions of the gas phase of the discharge with the liquid phase were selected, counting the discharge current (A), the flow rate of the solution of the FLC (B), and the flow rate of the Ar plasma microjet-supporting gas (C), the BBD was composed of 15 randomized measurements (runs) at 3 different levels, including 3 center points. The levels of the factors were set arbitrarily within the regions of a stable operation of dc-μAPGD. The results obtained for the created design matrix were analyzed by the response surface methodology (RSM) in order to model the effect of the factors on the and to identify the optimal settings of the system.

Results and discussion

Statistical analysis and the model development

Table 1 presents the BBD design matrix with the actual and coded levels of the factors along with the results of the measurements at the given experimental conditions. The analysis started with the inspection of the data by checking the variability of the response (λ_max) between measurements. It was established that the variability of the results was probably due to the presence of the active factors in the presented experimental design, as determined based on a scatter plot of the series of the repeated values of the λ_max (n = 3) at the given experimental conditions versus the randomized run order.²⁹ No correlation was observed between the range of the λ_max values at the given experimental conditions versus the mean value of the λ_max. This indicated that there was no need to stabilize the variance of the response (λ_max) through its transformation, e.g., with decimal or natural logarithm.³⁰ Finally, a scatter plot of the mean value of the λ_max versus the randomized run order indicated no trends or patterns in the acquired data; hence, it was concluded that the optimized system was probably not affected by any uncontrolled external variables.

Table 1 The Box–Behnken design with the actual and coded values of the experimental factors (A – the discharge current, B – the flow rate of the solution of the flowing liquid cathode, C – the flow rate of the Ar plasma microjet-supporting gas), the standardized and randomized orders of runs, and the results (λ_max). The experiments followed the randomized run order

Run order		Actual and (coded) levels of factors			Response (λmax, nm)
Standardized	Randomized	A, mA	B, mL min^−1	C, mL min^−1	Mean (n = 3)	Range
1	3	15 (−1)	3.0 (−1)	120 (0)	559.0	14.5
2	6	45 (+1)	3.0 (−1)	120 (0)	550.7	1.5
3	7	15 (−1)	5.0 (+1)	120 (0)	571.3	28.0
4	11	45 (+1)	5.0 (+1)	120 (0)	565.5	8.0
5	5	15 (−1)	4.0 (0)	60 (−1)	562.8	16.5
6	1	45 (+1)	4.0 (0)	60 (−1)	559.3	6.5
7	13	15 (−1)	4.0 (0)	180 (+1)	557.7	14.5
8	9	45 (+1)	4.0 (0)	180 (+1)	558.8	3.5
9	8	30 (0)	3.0 (−1)	60 (−1)	559.5	3.0
10	10	30 (0)	5.0 (+1)	60 (−1)	568.2	2.5
11	12	30 (0)	3.0 (−1)	180 (+1)	561.7	7.5
12	2	30 (0)	5.0 (+1)	180 (+1)	568.2	1.5
13	4	30 (0)	4.0 (0)	120 (0)	561.5	13.5
14	14	30 (0)	4.0 (0)	120 (0)	566.7	2.0
15	15	30 (0)	4.0 (0)	120 (0)	566.3	2.0

---

The RSM was used to find the effect of the studied factors on the λ_max and to determine the optimal values of their settings to provide the lowest (minimum) value of the λ_max. The response surface was approximated with a second-order polynomial model (a linear and square combination of the studied factors) using the least square regression method. After fitting the experimental data, the developed empirical polynomial model of the surface response over the region of the studied factors was as follows (in uncoded units): λ_max = 545.3 + 0.596A − 0.900B + 0.0700C − 0.0176A² + 0.750B² − 0.000336C² + 0.0420AB + 0.00130AC − 0.00900BC. The competence and the significance of this full model were examined by an analysis of the variance (ANOVA) and a lack-of-fit test. The results of this analysis at α = 0.1 are given in Table 2.

Table 2 The analysis of variance (ANOVA) and the lack-of-fit test for the response surface full model^a

Source of data	DF	SS	Adjusted MS	F-value^b	p-value > F
a DF – degrees of freedom. SS – sum of squares. MS – mean of squares. A – the discharge current. B – the flow rate of the solution of the liquid cathode. C – the flow rate of the Ar plasma microjet-supporting gas.b The value of the F-test for comparing the model variance with the residual (error) variance.
Model	9	333.32	37.04	3.09	0.113
Linear	3	259.58	86.52	7.22	0.029
A	1	34.03	34.03	2.84	0.153
B	1	224.01	224.01	18.70	0.008
C	1	1.53	1.53	0.13	0.735
Square	3	65.56	21.85	1.82	0.260
A^2	1	57.85	57.85	4.83	0.079
B^2	1	2.08	2.08	0.17	0.694
C^2	1	5.39	5.39	0.45	0.532
Two-way interactions	3	8.18	2.73	0.23	0.874
AB	1	1.56	1.56	0.13	0.733
AC	1	5.44	5.44	0.45	0.530
BC	1	1.17	1.17	0.10	0.767
Error	5	59.90	11.98
Lack-of-fit	3	43.17	14.39	1.72	0.388
Pure error	2	16.72	8.36
Total	14	393.22

---

As can be seen, a suitable approximation for the functional relationship between the studied factors (A, B and C) and the response (λ_max) was not found. The full model was determined not to be statistically significant on the basis of the ANOVA output (the F value of 3.09, the p-value of 0.113), although in contrast, the lack-of-fit test failed to identify a lack of-fit of the full model (the p-value of 0.388).

Although the R² of the model equation was 84.8%, meaning that the full model well fitted the experimental data and explained almost 85% of the variance of the response, the adjusted R² was much lower, 57.5%, indicating that the model was over-fitted due to too many insignificant terms. Unfortunately, the predicted R² was 0.0% and meant that the full model could not predict new data due to an over-fit. Hence, the developed full model could not be used to make any generalizations beyond the sample data.

Next, a response surface regression with a forward selection of terms, which is a stepwise procedure of adding terms to maintain a hierarchical model at each step, was used in order to select only the significant factors in the model. The regression equation found (in uncoded units) was as follows: λ_max = 531.8 + 0.909A + 5.292B − 0.01745A². The significance of this model was checked with an ANOVA. Results of this analysis are given in Table 3. As can be seen, the terms A, B and A² were include in the fitted model and their effect on the response was significant; respective p-values for these terms were 0.050 (A), 0.000 (B) and 0.016 (A²). The R² was reasonably high at 80.3%, showing that more than 80% of the variation of the λ_max could be explained by the developed regression model. A lack of fit of the model was not detected using a lack-of-fit test (p-value = 0.644).

Table 3 The analysis of variance (ANOVA) and the lack-of-fit test for the response surface model with the forward selection of terms (α = 0.1)^a

Source of data	DF	SS	Adjusted MS	F-value^b	p-value > F
a DF – degrees of freedom. SS – sum of squares. MS – mean of squares. A – the discharge current. B – the flow rate of the solution of the liquid cathode.b The value of the F-test for comparing the model variance with the residual (error) variance.
Model	3	315.58	105.19	14.90	0.000
Linear	2	258.05	129.02	18.28	0.000
A	1	34.03	34.03	4.82	0.050
B	1	224.01	224.01	31.74	0.000
Square	1	57.53	57.53	8.15	0.016
A^2	1	57.53	57.53	8.15	0.016
Error	11	77.64	7.06
Lack-of-fit	9	60.92	6.77	0.81	0.664
Pure error	2	16.72	8.36
Total	14	393.21

---

The values of the adjusted and predicted R² were satisfactory, 74.9% and 61.8%, respectively. In this case, a small difference between the R² and the adjusted R² indicated that the fitted model was not over-fitted. A relatively high value of the predicted R² demonstrated that the regression model could well predict new values and could be used for making generalization about the process.

Validation of the model

To check the quality of the proposed model and to validate its assumptions, the residuals were analyzed by plotting the residual graphs, i.e., the distribution of the standardized residuals (Fig. 2a) and the standardized residuals versus the fitted values (Fig. 2b). As can be seen, no unusual observations or deviations from the normal distribution of the residuals were observed. In the plot of the standardized residuals versus the fitted values for the proposed model, no unusual structure nor patterns were noted, pointing out that the residuals had a constant variance. This confirmed the correctness of the model and the goodness of fit of the experimental data with the surface regression. Taken together, these observations all led to the conclusion that there was no reason to reject the model.

Fig. 2 The residual plots for the λ_max: the distribution of the standardized residuals (a) and the standardized residuals versus the fitted values (b).

Considering the regression equation and a graphical interpretation of the developed model in the form of a surface plot (Fig. 3) of the λ_max versus the factors with the largest coefficients in the fitted model, the discharge current (A) and the flow rate of the solution of the FLC (B), it was evident that the optimal value of the λ_max (having the lowest value) was achieved at 45 mA (A) and 3.0 mL min⁻¹ (B). The predicted value of the λ_max in these experimental conditions was 553.3 nm with a 95% prediction interval of 546.4–560.2 nm.

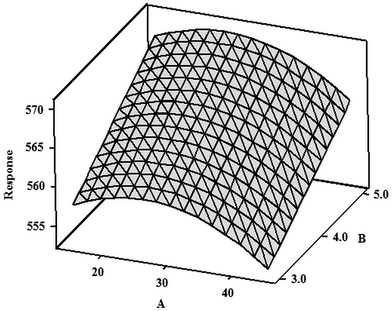Fig. 3 A surface plot for the response (λ_max in nm) versus the discharge current (A, in mA) and the flow rate of the solution of the flowing liquid cathode (B, in mL min⁻¹).

In a further validation experiment (n = 4), it was established that the independently repeated measurements carried out at the optimal settings of the discharge current (45 mA) and the flow rate of the solution of the FLC (3.0 mL min⁻¹) gave the measured value of the λ_max of 556.4 ± 3.6 nm. This result corresponded very well to the value predicted by the model; the relative error was only 0.6%.

Effects of the main factors on the λ_max

The model developed with the aid of the BBD and the response surface regression with the forward selection of terms revealed that the discharge current (A) and the flow rate of the solution of the FLC (B) had the highest contribution to the R². A graphical representation of effects of both factors is shown in Fig. 4 with labeled optimal settings corresponding to the production of the AuNPs having the lowest particle size. As can be seen, the increase of the discharge current (A) up to 26.5 mA was established to result in a decrease in the value of the λ_max, then, a further increase of this factor was accompanied by a gradual reduction of the λ_max, finally reaching the optimal value (553.3 nm) at 45 mA. According to the operating mechanism of GD generated in contact with a flowing liquid given by Cserfalvi and Mezei,³¹ such a behavior likely resulted from an intensification of the rate of bombardments of the surface of the FLC by positive ions. In these conditions, the production of reactive oxygen species in the solutions was certainly higher; hence, more active species for the reduction of the precursor of the AuNPs was available, i.e., molecules of H₂O₂. As a consequence, the production rate of AuNPs was likely faster and more AuNPs with the smaller particle size were formed. In addition, the concentration of the solvated electrons in the solution was possibly increased, and therefore, the AuNPs could be easily charged and then repel each other preventing the agglomeration and a further growth.

Fig. 4 The effect of the significant factors on the λ_max.

Similar observations were described by Wang et al.¹⁹ and Huang et al.²¹ in the case of APGDs operated between the negatively charged Ar jets and non-flowing, bulky solutions containing HAuCl₄ and acting as the anodes. In both cited papers, the effect of the discharge power was found to be critical in determining the size of the AuNPs and its distribution in the resultant nanofluids. The authors state that the size of the produced AuNPs was inversely correlated with the discharge current. However, the reason was ascribed to a higher number of electrons injected from the Ar plasma jets into the solutions per unit time.

The effect of the flow rate of the solution of the FLC on the particle growth of the AuNPs, monitored by UV-Vis absorption spectrometry and the position and shape of the LSPR absorption band, was also explained by the operating mechanism of APGD.³¹ As can be seen in Fig. 4, a decrease of the flow rate of the solution of the FLC from 5.0 to 3.0 mL min⁻¹ was associated with a linear decrease of the λ_max of the obtained AuNPs, with the minimal λ_max obtained at a flow rate of 3.0 mL min⁻¹.

This relationship is likely associated with a prolonged contact time of the discharge phase with the liquid phase. In our recent experiments with a comparable dc-μAPGD system with an Ar plasma jet,³² it was seen that a decrease of the flow rate of the solution of the FLC resulted in a noticeable increase in the overall acidification (as the concentration of H₃O⁺ ions, in mol L⁻¹, increased) and the concentration of H₂O₂ (in mg L⁻¹) in the solution of the FLC treated by the discharge. In addition, the concentration of reactive nitrogen species (RNS) like NO₃⁻ and NO₂⁻ ions also increased in these conditions. Accordingly, a 2.5-fold decrease of the flow rate of the solution of the FLC led to the enhancement of mentioned species by 54% (H₃O⁺), 44% (H₂O₂), 140% (NO₃⁻) and 100% (NO₂⁻).³² It can be reasoned that the production of the smaller sized AuNPs was favored at the lowest flow rate due to the increased concentration of HNO₃ and H₂O₂. The increased concentration of H₂O₂ likely enhanced the reduction rate of HAuCl₄, leading to a relatively high number of nucleation seeds being produced, therefore resulting in the formation of the small-sized AuNPs.¹⁷ A significant reduction of the particle size of the AuNPs could also have concurrently occurred due to their dissolution in the medium with an increasing concentration of HNO₃.¹⁰ As a result, the uniform, spherical, small-sized AuNPs were formed as a generic product of the interaction of dc-μAPGD with the solution of the FLC under optimized conditions.

Interestingly, the effect of the flow rate of the Ar plasma jet-supporting gas was not significant in the full model and the finally developed model of the surface response. A reasonable explanation for such a behavior could be related to an irrelevant effect of this factor on the overall acidification of the solution of the FLC and its concentration of H₂O₂ that was observed by Jamroz et al.³²

Confirmation of the size and the shape of the AuNPs by DLS and SEM

Finally, DLS and SEM was used to confirm the effect of the significant factors on the particle size and shape of the AuNPs produced using optimal conditions (the discharge current of 45 mA and the flow rate of the solution of the FLC of 3.0 mL min⁻¹) and the contrary, non-optimal conditions (15 mA, 5.0 mL min⁻¹). In both cases, the flow rate of the Ar plasma jet-supporting gas was set at 120 mL min⁻¹. As can be seen in Fig. 5, the blue shift (from 582 to 550 nm) of the λ_max of the LSPR absorption band was noticed when the operating settings were changed from non-optimal to optimal. This indicated a change of the particle growth of the produced AuNPs. In addition, the second absorption band with a maximum at 850 nm, referred to the longitudinal surface plasmon resonance for non-spherical AuNPs,³³ disappeared in the UV-Vis absorption spectra. The decrease in the average particle size of the nanoparticles was confirmed by DLS measurements. In accordance with the UV-Vis observations, the DLS measurements detected a decrease in the average particle size from 204 to 42 nm. In addition, the dispersion of the particle size (expressed as the standard deviation, SD, of the average diameter) was also reduced from 90 to 25 nm, indicating a much better consistency of the diameter of the AuNPs and their arrangement in the resulting nanofluids. Correspondingly, the Δλ_FWHM of the LSPR absorption band was decreased from 128 (15 mA, 5.0 mL min⁻¹) to 69 nm (45 mA, 3.0 mL min⁻¹), which shows a very good agreement with the aforementioned decrease in the SD of the average diameter determined on the basis of the DLS.

Fig. 5 UV-Vis absorption spectra (a), DLS histograms (b), and SEM images (c) of the AuNPs synthesized under different experimental conditions (optimal and non-optimal).

All of these findings also displayed very good agreement with SEM images of the AuNPs. As can be seen in Fig. 5, the AuNPs synthesized under optimal conditions were spherical, well dispersed in the medium, and did not tend to agglomerate. However, when the AuNPs were produced in a plasma-rector system working at the non-optimal conditions, they had a tendency to form agglomerates and aggregates. In addition, they had a broadened particle size distribution and were not uniform in shape since triangular, pentagonal, and hexagonal forms of the AuNPs in addition to nanorods were observed to be generated in these experimental conditions.

Conclusions

This work concerns a fully controlled and predictable synthesis of the AuNPs in a continuous-flow plasma-reactor system based on dc-μAPGD operated between a miniature flow Ar plasma jet and a small-sized FLC. By using the DOE approach followed by the RSM, it was possible to optimize the plasma-reactor system in order to fabricate the spherical, uniform and small in size AuNPs, as well as elucidate and predict the effect of the significant experimental factors responsible for the performance of dc-μAPGD and the rate of reactions and processes occurred in the plasma–liquid interface.

On the basis of the developed model of the surface response, which was the λ_max of the LSPR absorption band, it was established that the smallest in size AuNPs, with the average diameter of 42 nm evaluated using DLS, were produced at the boundary conditions of the examined experimental factors, i.e., the highest discharge current (45 mA) and the lowest flow rate of the solution of the FLC (3.0 mL min⁻¹). However, it could be certainly assumed that the production of the spherical AuNPs having even smaller diameters could be achieved by increasing the diameter of the nozzle supplying Ar to the gaseous jet and the graphite-quartz tube delivering the solutions of the FLC, as well as enhancing the contact area of the gas phase of the discharge with the liquid phase. Relevant experiments associated with this are being undertaken.

Acknowledgements

This work was financed by a statutory activity subsidy from the Polish Ministry of Science and Higher Education for the Faculty of Chemistry of Wroclaw University of Technology. The project was funded by the National Science Center. Authors are thankful to Dr Tomasz Kozlecki (Department of Chemical Engineering, Faculty of Chemistry, Wroclaw University of Technology) for DLS measurements. In addition, the support from the Wroclaw Centre of Biotechnology, program the Leading National Research Centre (KNOW) for years 2014–2018, is acknowledged.

References

1. D. Mariotii and R. M. Sankaran, J. Phys. D: Appl. Phys., 2010, 43, 323001.
2. T. Yan, X. Zhong, A. E. Rider, Y. Lu, S. A. Furman and K. Ostrikov, Chem. Commun., 2014, 50, 3144.
3. M. A. Bratescu, S.-P. Cho, O. Takai and N. Saito, J. Phys. Chem. C, 2011, 115, 24569.
4. Y. K. Heo, M. A. Bratescu, T. Ueno and N. Saito, J. Appl. Phys., 2014, 116, 024302.
5. S.-P. Cho, M. A Bratescu, N. Saito and O. Takai, Nanotechnology, 2011, 22, 455701.
6. Y. K. Heo and S. Y. Lee, Met. Mater. Int., 2011, 17, 431.
7. M. A. Bratescu, O. Takai and N. Saito, J. Alloys Compd., 2013, 562, 74.
8. X. L. Hu, O. Takai and N. Saito, J. Phys.: Conf. Ser., 2013, 417, 012030.
9. J. Hieda, N. Saito and O. Takai, J. Vac. Sci. Technol., A, 2008, 26, 854.
10. N. Saito, J. Hieda and O. Takai, Thin Solid Films, 2009, 518, 912.
11. Y. K. Heo and S. Y. Lee, Met. Mater. Int., 2011, 17, 943.
12. Y. K. Heo, M. A. Bratescu, D. Aburaya and N. Saito, Appl. Phys. Lett., 2014, 104, 111902.
13. S. M. Kim, G. S. Kim and S. Y. Lee, Mater. Lett., 2008, 62, 4354.
14. J. Hieda, N. Saito and O. Takai, Surf. Coat. Technol., 2008, 202, 5343.
15. A. Watthanaphanit, Y. K. Heo and N. Saito, J. Taiwan Inst. Chem. Eng., 2014, 45, 3099.
16. A. Watthanaphanit, G. Panomsuwam and N. Saito, RSC Adv., 2014, 4, 1622.
17. J. Patel, L. Nemcova, P. Maguire, W. G. Graham and D. Mariotti, Nanotechnology, 2013, 24, 245604.
18. D. Mariotti, J. Patel, V. Svrcek and P. Maguire, Plasma Processes Polym., 2012, 9, 1074.
19. R. Wang, S. Zuo, D. Wu, J. Zhang, W. Zhu, K. H. Becker and J. Fang, Plasma Processes Polym., 2014, 12, 380.
20. C. Richmonds and R. M. Sankaran, Appl. Phys. Lett., 2008, 93, 131501.
21. X. Huang, Y. Li and X. Zhong, Nanoscale Res. Lett., 2014, 9, 572.
22. W.-H. Chiang, C. Richmonds and R. M. Sankaran, Plasma Sources Sci. Technol., 2010, 19, 034011.
23. F. Tochikubo, N. Shirai and S. Uchida, J. Phys.: Conf. Ser., 2014, 565, 012010.
24. N. Shirai, S. Uchida and F. Tochikubo, Jpn. J. Appl. Phys., 2014, 53, 046202.
25. F. Tochikubo, Y. Shimokawa, N. Shirai and S. Uchida, Jpn. J. Appl. Phys., 2014, 53, 12601.
26. A. Dzimitrowicz, P. Jamroz, K. Greda, P. Nowak, M. Nyk and P. Pohl, J. Nanopart. Res., 2015, 17, 185.
27. S. Ghosh, B. Bishop, I. Morrison, R. Akolkar, D. Scherson and R. M. Sankaran, J. Vac. Sci. Technol., A, 2015, 33, 021312.
28. P. D. Maguirem, C. M. O. Mahony, C. P. Kelsey, A. Bingham, E. P. Montgomery, E. D. Bennet, H. E. Potts, D. Rutherford, D. A. McDowell, D. A. Diver and D. Mariotti, arXiv:1503.03532v1 [physics.plasm-ph].
29. K. K. Pochampally and S. M. Gupta, Six sigma case studies with Minitab, CRC Press, Boca Raton, 2014.
30. G. E. P Box, J. S. Hunter and W. G. Hunter, Statistics for experimenters: design, innovation and discovery, John Wiley & Sons, Oxford, 2005.
31. T. Cserfalvi and P. Mezei, Fresenius' J. Anal. Chem., 1996, 355, 813.
32. P. Jamroz, K. Greda, P. Pohl and W. Zyrnicki, Plasma Chem. Plasma Process., 2014, 34, 25.
33. H. E. Toma, V. M. Zamarion, S. H. Toma and K. Araki, J. Braz. Chem. Soc., 2010, 21, 1158.

---