Accelerated aging test of hydrogenated nitrile butadiene rubber using the time–temperature–strain superposition principle
Abstract
The effect of physical aging on the long-term performance of hydrogenated nitrile butadiene rubber (HNBR) is very important to its engineering applications. In this paper, aging tests of HNBR have been conducted systematically at different temperatures and levels of uniaxial tensile strain. Fracture strain was chosen as the index of the severity of aging. Applied strain shows an equivalent effect on aging acceleration to that of temperature; the higher the temperature and strain level are, the faster the aging is. A WLF-type time–temperature–strain superposition principle (TTSSP) is proposed to study the long-term aging performance of HNBR with short-term test data. With the constructed master curves, time and cost can be significantly reduced for the evaluation of the long-term aging behavior of the rubber materials.
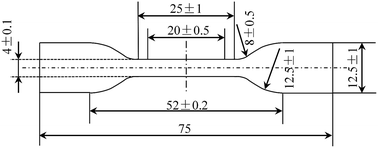

 Please wait while we load your content...
Please wait while we load your content...