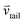Equimolar mixtures of aqueous linear and branched SDBS surfactant simulated on single walled carbon nanotubes
Manaswee Suttipong and
Alberto Striolo*
Department of Chemical Engineering, University College London, London WC1E 7JE, UK. E-mail: a.striolo@ucl.ac.uk
First published on 12th October 2015
Abstract
In our previous simulation study [J. Phys. Chem. C, 2011, 115, 17286], branched sodium dodecyl benzene-sulfonate (SDBS) surfactants showed self-assembled structures on single-walled carbon nanotubes (SWNTs) that were strongly dependent on tube diameter. Those results suggested that branched SDBS, as opposed to their linear counterparts, could specifically stabilize SWNTs of narrow diameter. Experimental data, however, show that SDBS stabilizes aqueous SWNTs of many diameters. This discrepancy between simulated and experimental results could be explained by the fact that experimental SDBS samples are isomeric mixtures. To test this possibility we report here molecular dynamics (MD) simulation results for equimolar mixtures of aqueous linear and branched SDBS on (6,6) and (20,20) SWNTs at ambient conditions. Our results suggest that there is no strong effect due to nanotube diameter on the morphology of mixed SDBS surfactant aggregates, although the adsorbed aggregate structure strongly depends on surfactant coverage. In-plane radial distribution functions suggest that linear and branched molecules distribute evenly onto the surfaces of (6,6) SWNTs, while some evidence of segregation, in which branched SDBS predominantly pack near other branched molecules, was obtained on (20,20) SWNTs at high surface coverage. These results suggest that the lack of specificity in stabilizing aqueous dispersions of carbon nanotubes using SDBS surfactants is probably due to the presence of multiple isomeric molecules in commercial surfactant samples. Perhaps more importantly, these simulations suggest that using mixtures of surfactants could affect the structure of the adsorbed aggregates, and the stability of aqueous dispersion of carbon nanotubes.
Introduction
Surfactants are extensively used in stabilizing dispersions of single-walled carbon nanotubes (SWNTs).1 As it is the case with polymers2 and lipids,3 surfactants physically adsorb on the SWNT surfaces without altering their electronic properties. This adsorption is in general due to hydrophobic forces between the surfactant tails and the SWNT surfaces, yielding self-assembled structures in which the surfactant tails adsorb on the nanotube walls and the hydrophilic heads are exposed to water.A wide variety of surfactants have been investigated for stabilizing aqueous dispersions of SWNTs, and it is now well-known that the surfactant aggregates self-assembled on SWNTs depend on surfactant type,4–7 molecular architecture,8–11 concentration,12–15 the presence of salts,16–18 nanotube diameter,19–21 temperature,22 pH,6,23 etc. For example, flavin mononucleotide (FMN) surfactants were shown to provide selectivity in stabilizing (8,6) SWNTs in water, due to the helical self-assembly of the flavin moiety on the SWNTs surface.19 Sodium dodecyl benzene-sulfonate (SDBS) and sodium deoxycholate (DOC) were found to be effective dispersants for HiPCO nanotubes.24 Sodium dodecyl sulfate (SDS) was found not as good a stabilizer as sodium cholate (SC) or SDBS for (9,4) SWNTs at 40 °C.22 Gemini surfactants with aromatic spacers were found able to disperse SWNTs at higher surfactant/SWNT weight ratios than SDS, SDBS, or cetyltrimethylammonium bromide (CTAB).25 Two co-surfactants (DOC and SDS) were used to successfully suspend and isolate individual SWNTs with diameter up to 1.7 nm.26
Understanding why some surfactants behave better than others would allow us to design novel compounds to stabilize carbon nanotubes of desired diameter, and perhaps chirality. Computer simulations, coupled with experiments, could prove useful in this objective because they can yield a detailed atomic-level picture of the aggregates formed on nanotubes. Using molecular dynamics (MD) simulations, Tummala and Striolo found disordered aggregates of SDS on SWNTs.27 Xu et al.28 computed the potential of mean force (PMF) between SWNTs covered by SDS; the results showed that the structure of adsorbed aggregates affects the PMF, with higher surfactant densities yielding more repulsive pair potentials. Lin and Blankschtein reported the structure of SC on SWNTs and calculated the SWNT–SWNT PMF.29 Suttipong et al. reported that the morphology of anionic dodecyl sulfate surfactants is affected by the counter-ions (Cs+ instead of Na+), with Cs+ ions yielding a more compact coverage of (6,6) SWNTs.30 Lin et al. examined how self-assembled SC, SDS, and CTAB aggregates pre-formed on a SWNT influence the adsorption of aryl diazonium salt.31 They found that less rigid surfactant structures facilitate the formation of ionic bonds between the nanotube and the aryl group. Shih et al. developed coarse-grained (CG) MD simulations, combined with colloidal theories, to predict the amount of SC surfactant adsorbed as a function of bulk surfactant concentration.32 At high SC concentration small-diameter SWNTs can adsorb higher SC amounts than large-diameter ones, while the opposite occurs at low SC concentrations.
We previously studied the effect of SDBS molecular structure on the morphology of adsorbed self-assembled aggregates.33 Isomerically pure linear and branched SDBS were considered in those calculations. While the simulations were analysed by quantifying the structure of the self-assembled aggregates on SWNTs of different diameter [i.e., (6,6), (12,12) and (20,20) SWNTs were compared] and at different surface coverage, combining our results with insights from PMF calculations,21 we concluded that the branched molecules could be used to selectively stabilize aqueous dispersions of narrow, i.e., (6,6), SWNTs. This appears to be at odds with experimental observations. In fact, experiments show that SDBS can stabilize carbon nanotubes of a wide range of diameters.7,19,24,34–36 The present investigation stems from the observation that commercial SDBS samples typically contain isomeric mixtures: we are interested in quantifying the structure of self-assembled aggregates formed on (6,6) and (20,20) SWNTs by equimolar mixtures of linear and branched SDBS molecules, to understand whether the lack of specificity observed experimentally in the stabilization of SWNTs using SDBS surfactants could be due to the isomeric composition of the typical commercial samples. Linear-rich and branched-rich SDBS surfactant mixtures were not simulated, as it is expected that such systems would show features more similar to isomerically pure SDBS surfactants (linear and branched, respectively). We also did not consider SDBS surfactants in which the benzene ring is tethered to carbon atoms other than the first or the middle of the alkane chain, as it is expected that these surfactants would yield results intermediate between those obtained for the surfactants considered here and in our prior work.
The remainder of the manuscript is organized as follows: first, we summarize the simulation protocol; we then present the results in terms of the morphology of the surfactant aggregates and the packing of linear and branched surfactant molecules on the SWNT surfaces, and discuss the results against those presented previously for isomerically pure SDBS surfactants; finally, we summarise our conclusions.
Computational details
Molecular dynamics (MD) simulations of aqueous mixtures containing SDBS surfactants self-assembled on (6,6) and (20,20) SWNTs were performed using the GROMACS 4.6.1 software package.37 Each simulated system was composed of one SWNT, a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of linear and branched dodecyl benzenesulfonate surfactants, a sufficient number of Na+ ions to obtain an electrically neutral system, and water molecules. In the top panel of Fig. 1 we provide the schematic chemical structures for linear and branched SDBS surfactants. One SDBS consists of the dodecane backbone, one benzene ring, and one sulfonate head. In the branched molecule, the benzene-sulfonate group is attached to the 5th carbon atom in the tail. Each portion of the surfactant (i.e., CH2 (CH for branched) and CH3 tail segments, centre of mass of benzene rings, centre of mass of the sulfonate group in the head groups, and Na+ ions) was used in quantifying the density profiles away from the SWNT surface. The vectors represented in the bottom panel of Fig. 1, one to identify the surfactant tail
50 mixture of linear and branched dodecyl benzenesulfonate surfactants, a sufficient number of Na+ ions to obtain an electrically neutral system, and water molecules. In the top panel of Fig. 1 we provide the schematic chemical structures for linear and branched SDBS surfactants. One SDBS consists of the dodecane backbone, one benzene ring, and one sulfonate head. In the branched molecule, the benzene-sulfonate group is attached to the 5th carbon atom in the tail. Each portion of the surfactant (i.e., CH2 (CH for branched) and CH3 tail segments, centre of mass of benzene rings, centre of mass of the sulfonate group in the head groups, and Na+ ions) was used in quantifying the density profiles away from the SWNT surface. The vectors represented in the bottom panel of Fig. 1, one to identify the surfactant tail  and the other to identify the benzene-sulfonate segment
and the other to identify the benzene-sulfonate segment  , were used to compute the probability distribution of the orientation angle between each SDBS molecule and the SWNT axis.
, were used to compute the probability distribution of the orientation angle between each SDBS molecule and the SWNT axis.  was defined as the vector originating from the terminal CH3 group to the primary CH2 (linear SDBS) or CH3 (branched SDBS) group.
was defined as the vector originating from the terminal CH3 group to the primary CH2 (linear SDBS) or CH3 (branched SDBS) group.  was defined as the vector originating from the carbon atom within the benzene ring [which is linked to CH2 (linear SDBS) or CH (branched SDBS) group of the tail] to the sulphur atom of the head.
was defined as the vector originating from the carbon atom within the benzene ring [which is linked to CH2 (linear SDBS) or CH (branched SDBS) group of the tail] to the sulphur atom of the head.
We considered (6,6) and (20,20) SWNTs of 7.44 nm in length. Periodic boundary conditions were applied in three dimensions. Because of periodic boundary conditions, the SWNTs were infinitely long. The SWNTs diameters were of ∼0.81 and ∼2.71 nm for (6,6) and (20,20) SWNTs, respectively. The following SDBS surface coverages were examined: 1.0 SDBS molecules per nm2 (≅1.0 nm2 per headgroup) and 2.8 SDBS molecules per nm2 (≅0.4 nm2 per headgroup), which we refer to as ‘low’ and ‘high’ surface coverage, respectively. The compositions of the simulation systems studied in this work are listed in Table 1. The number of water molecules was sufficient to obtain a molecular density comparable to that of liquid water at ambient conditions far from the SWNTs (∼33 water molecules per nm3).
| SWNT | No. of C atoms in SWNT | No. of water molecules | No. of SDBS molecules simulated | Nominal surface coverage (nm2 per headgroup) | No. of adsorbed [non-adsorbed] SDBS molecules | Effective surface coverage (nm2 per headgroup) | ||
|---|---|---|---|---|---|---|---|---|
| Linear | Branch | Linear | Branch | |||||
| (6,6) | 520 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 105 |
10 | 10 | 0.95 | 10 [0] | 10 [0] | 0.95 |
| (20,20) | 2400 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 465 465 |
32 | 32 | 0.99 | 30 [2] | 29 [3] | 1.07 |
| (6,6) | 520 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 441 441 |
27 | 27 | 0.35 | 22 [5] | 22 [5] | 0.43 |
| (20,20) | 2400 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 313 313 |
89 | 89 | 0.36 | 48 [41] | 32 [57] | 0.79 |
The carbon atoms in SWNTs were treated as rigid uncharged Lennard–Jones (LJ) sites, based on the model proposed by Cheng and Steele.38 SDBS surfactants were assumed to completely dissociate into dodecyl benzene-sulfonate ions and Na+ ions. The SDBS hydrophobic tails (dodecyl groups) were modelled as chains of united-atom LJ spheres.39–41 The benzene-sulfonate groups were described within the all-atom formalism using the DREIDING force field.42 Water molecules were modelled using the SPC/E formalism.43 The force fields were the same as those implemented in our prior work33 to provide sound comparison.
In all simulated systems, one SWNT was maintained at the centre of the simulation box of size 10 × 10 × 7.44 nm3, and kept rigid throughout the simulation. The empty space outside of the SWNT was filled with the solvent molecules (mixed linear and branched molecules, Na+ ions, and water). The number of Na+ ions was always equal to the number of surfactants. Water was placed in the simulation system by using the genbox algorithm available in GROMACS. As the nanotube is hollow, the software inserted water molecules within it. These were removed, as we are interested in the behaviour of surfactants outside of the SWNTs. The equations of motion were integrated with the leaf-frog algorithm using a time step of 2 fs.44 All simulations were conducted under the NVT ensemble using the Nose–Hoover thermostat with a relaxation time of 0.1 ps.44 The long-range electrostatic interactions were calculated with the particle mesh Ewald method with a precision of 10−4.45 All interactions were treated with cutoff set at 9 Å. The conjugate gradient algorithm was utilized to minimize the energy of the initial configurations for ∼2 ps. To ensure that the results were not affected by the initial configurations, we randomized them by performing short (1 ns) MD runs at T = 600 K. The systems were then abruptly brought to T = 300 K, at which T equilibration was followed by production. Most systems were simulated for 250 ns, and one system, comprising of the (6,6) SWNT with surfactants at high surface coverage, was simulated for 300 ns. All systems were considered equilibrated when the results did not change over 50 ns of simulation time. Only the results collected during the last 20 ns of each simulation are reported in what follows.
Results and discussion
Aggregate morphology – inspection of simulation snapshots
Representative simulation snapshots of an equimolar mixture of linear and branched SDBS surfactants adsorbed on (6,6) and (20,20) SWNTs at low and high surface coverage are shown in Fig. 2 and 3, respectively. At low coverage, SDBS molecules lie flat on the SWNT surfaces. The surfactant tails and most benzene rings are close to the nanotube surfaces, while most of the head groups are slightly protruded into water. Some head groups can be found near the substrates. On the (6,6) SWNT the linear SDBS molecules tend to align along the nanotube axis (see Fig. 2a). Similar to what reported in the case of SDS,27 isomerically pure linear SDBS,33 CTAB,46 and single-tailed lipids3 self-assembled on narrow SWNTs, this preferential orientation rises from the maximization of the contacts between the alkane chain and the SWNT surface, while minimizing the bending of the alkyl tails.47 The branched SDBS molecules are found to assemble randomly on the nanotube surface on both (6,6) and (20,20) SWNTs at low coverage. On the (20,20) SWNT, shown in Fig. 2b, linear and branched SDBS surfactants wrap around the tube. Some linear molecules preferentially lie near each other, maximizing favourable tail–tail contacts. Our simulations show evidence of a few surfactants forming a small aggregate in water, even though unoccupied SWNT surface is available for adsorption. As noted previously,29 MD atomistic simulations are not long enough to describe the equilibrium amount of surfactants adsorbed on a SWNT. The effective surface coverage observed in our simulations is reported in Table 1 for all systems considered. | ||
| Fig. 2 Front (left panels) and side (right panels) views of representative simulation snapshots for mixed linear and branched SDBS self-assembled on (a) (6,6) and (b) (20,20) SWNTs at low surface coverage. In the top panels of (a) and (b) we highlight the linear SDBS molecules (the branched isomer is transparent); in the bottom panels we highlight the branched SDBS molecules (the linear isomer is transparent). Water molecules are not shown for clarity. The colour code is the same as that used in Fig. 1. | ||
 | ||
| Fig. 3 Same as Fig. 2 but for high surface coverage. | ||
Upon increasing the surface coverage, the results in Fig. 3 show that equimolar SDBS mixtures not only pack more densely, but also remain highly disordered on both SWNTs. The results shown in Fig. 3a demonstrate that at the conditions chosen linear and branched molecules cover most of the (6,6) SWNT surface. Due to the reduction in nanotube surface area available per each surfactant molecule, most benzene rings and head groups are protruded toward the water phase. Similar behaviour is observed on the (20,20) SWNT (Fig. 3b), suggesting that the aggregate structure is due mostly to the surface density rather than to the SWNT diameter. Within the simulated system containing the (20,20) SWNT we observe one surfactant micelle adsorbed on the aggregate, and two small micelles dispersed in water, suggesting that perhaps the amount of surfactants simulated exceeds the maximum amount that could be adsorbed on this SWNT. It is possible that the amount of surfactant simulated was larger than that which can be adsorbed on the (20,20) SWNT at the thermodynamic conditions considered, although it is also possible that the initial configurations led to the desorption of some of the surfactants from the nanotubes. As mentioned above, atomistic simulations are at present not able, because of computing power limitations, to assess the equilibrium amount of surfactant adsorbed. Coarse-grained approaches such as those proposed by Lin et al.31 would allow this type of calculations. Because a few surfactants desorbed in some of the systems simulated, the effective surface coverage differed from the nominal one in some cases. Both effective and nominal surface coverage are reported in Table 1. At high surface coverage, the simulation snapshots suggest that there is no preferential orientation of the linear molecules with respect to the nanotube axis, but instead the linear molecules tend to adopt random orientations.
In all cases considered in Fig. 2 and 3, it is clear that many counterions accumulate near the head groups. This is due to the strong electrostatic interactions between the oppositely charged groups on the sulfonate heads and on the Na+ counterions. On the (20,20) SWNT at high surface coverage we observe a high concentration of Na+ ions sandwiched between the head groups belonging to the surfactants in the micelle and those adsorbed on the SWNT (see Fig. 3b). Several reports document similar counterion-condensation phenomena.27,29,30,33,48
Effective surface coverage
To quantify the effective surfactant coverage on the SWNTs we computed the time-averaged number of surfactant molecules adsorbed. One surfactant molecule was considered adsorbed if its centre of mass was found within a cutoff distance of 12 Å and 14 Å at low and high surface coverage, respectively, from the nanotube surface. The number of non-adsorbed SDBS molecules was calculated as the difference between the latter number and the total number of SDBS molecules in the simulation box. Results regarding the population analysis are shown in Table 1. At low surface coverage all surfactants (linear and branched) remain adsorbed on the (6,6) SWNT, yielding the effective surface coverage of 0.95 nm2 per SDBS head group. In the case of (20,20) SWNTs some SDBS molecules form one small aggregate in the bulk, yielding a higher effective surface coverage than that obtained on the narrow SWNT. As the number of surfactants in the simulated system increases, the number of non-adsorbed surfactants also increases, with the trend more pronounced on the (20,20) than on the (6,6) SWNT. On the (6,6) SWNT both at low and at high surface coverages, the numbers of linear and branched molecules adsorbed onto the tubes are equivalent, maintaining an equimolar surfactant mixture. This is not the case for the (20,20) SWNT, on which the adsorbed surfactants are enriched in linear molecules at both conditions considered. While these results suggest that perhaps different surfactant isomers have different propensity for adsorbing on the SWNTs, this cannot be guaranteed by the present simulations, because of the already mentioned limitations in the real time accessible with the available computing power. This however does not compromise the conclusions from the present study.Aggregates morphology – radial density profiles
We quantify the structural observations by calculating density distributions of surfactant tail, benzene ring, sulfonate head, and Na+ ion along the radial distance from the nanotube surface. These results are reported in Fig. 4. In the left and right panels we show results obtained at low and high surface coverages, respectively. At low surface coverage, our results suggest no strong effect of SWNT diameter on the adsorbed aggregate. Only the intensity of the peaks depends on the nanotube diameter. We observe a strong peak in the density profiles of the tail groups at 4.0 Å, indicating the formation of one surfactant layer near the SWNT surfaces (Fig. 4a). It should be noted that this aggregate structure on the (6,6) SWNT is different than that proposed by Matarredona et al.,49 who suggested the formation of a cylindrical micelle of SDBS molecules with SWNTs at the centre. Our results are instead consistent with a disordered surfactant aggregate on the SWNT surface, which has been discussed for many simulated surfactant-SWNT systems reported in the literature.48 The surfactant aggregate is expected to resemble that proposed by Matarredona et al.49 only when the surfactants surface density is extremely high.28 | ||
| Fig. 4 Atomic density profiles of (a and e) surfactant tails, (b and f) benzene rings, (c and g) head groups, and (d and h) Na+ ions of SDBS molecules adsorbed on (6,6) and (20,20) SWNTs (r is measured radially from the nanotube surface). On the left and right panels we report the results obtained at low and high surface coverages, respectively. The black-solid and red-dashed lines represent the results obtained on (6,6) and (20,20) SWNTs, respectively. System compositions and effective coverages are reported in Table 1. | ||
The density profiles obtained at low surfactant density show that most benzene rings are positioned close to the substrates, yielding a peak at 4.0 Å and a shoulder at 6.0 Å (Fig. 4b). Although some head groups are located near the SWNTs, as illustrated by two small peaks at 4.0 Å and 5.5 Å (Fig. 4c), one broad peak located at 7.5–10 Å from the nanotube surfaces indicates that the head groups are in large part projected towards water. On the two SWNTs, the results obtained for the counterion density profiles show that the Na+ ions strongly correlate to the head groups (Fig. 4d).
When the surface coverage increases, the peak at 4.0 Å in the tail density profiles for (6,6) and (20,20) SWNTs become stronger, suggesting that the surfactant monolayer becomes more compact via the packing of linear and branched molecules on the nanotube surfaces (Fig. 4e). The benzene rings are mainly away from the (6,6) SWNT, as demonstrated by a strong density peak at 6.5 Å (Fig. 4f), although some benzene rings remain positioned near the nanotube surface. We find that the majority of head groups on the (6,6) SWNT are projected into water, manifesting a broad peak at ∼9.0 Å (Fig. 4g), while a few remain in contact with the (20,20) SWNT surface, as suggested by the density peaks at 4.0 Å and 5.5 Å. On the (20,20) SWNT, a small peak at 14 Å in the head group density profiles is due to the formation of the micellar aggregate adsorbed on the aggregate (the snapshot discussed in Fig. 3b). As mentioned above, coarse-grained approaches are needed to clarify why some surfactants desorb from the nanotubes. The counterion density profiles show that the Na+ ions pack close to the head groups, yielding a strong peak at ∼10.0 Å (Fig. 4h). On (20,20) SWNTs, some Na+ ions are located near the substrate, where they are attracted by the presence of sulfonate heads. In summary, based on our results at low and high surface coverages, the structure of linear and branched SDBS aggregates formed on the SWNTs does not depend strongly on the nanotube diameter.
It is worth noting that the position of the head groups is expected to play an important role in the stabilization of aqueous SWNT dispersions.27–29 Prior simulations have indeed suggested that the electrostatic repulsion between like-charged head groups, as well as the steric repulsion between such groups experienced at relatively close nanotube–nanotube separations, are necessary for stabilizing aqueous SWNT dispersions.
Surfactant packing arrangement on the SWNTs surfaces
To quantify whether linear and branched surfactants segregate from each other on the SWNT surfaces we computed in-plane radial distribution functions (RDFs) between the sulphur atoms in the head groups. Only the adsorbed surfactants were considered for these calculations. We projected the position of each atom of the surfactants adsorbed on the SWNT onto a plane parallel to the nanotube axis. According to this procedure, the projected x′, y′ and z′ coordinates of an atom (originally in position x, y, and z) are obtained, as illustrated in Fig. 5, by unwrapping a circular arc of length rθ onto a linear segment [r is the distance between the atom of interest and the centre of the nanotube, θ is the angle between the reference vector (oriented from the centre of the nanotube along the Y direction, as illustrated in Fig. 5), and the vector connecting the centre of the nanotube to the atom of interest]. The x′ coordinate then equals rθ. The y′ coordinate corresponds to the radial distance of the atom from the centre of the nanotube (y′ = r). The z′ coordinate corresponds to the z coordinate of the atom.We used the unwrapped coordinates to calculate in-plane RDFs.50 The in-plane RDFs between linear-branched, linear–linear, and branched–branched SDBS molecules self-assembled on (6,6) and (20,20) SWNTs are shown in Fig. 6. On the (6,6) SWNT, at low and high surface coverage (Fig. 6a and b, respectively) the results are indicative of random packing, suggesting that linear and branched SDBS surfactants do not segregate on this substrate but instead they mix on the nanotube surface. On the (20,20) SWNT at low surface coverage (Fig. 6c) we instead observe a relatively strong peak at 6.5 Å in the RDF between linear surfactants, suggesting that the linear isomers prefer to segregate with other linear surfactants. Some evidence of preferential segregation among branched surfactants is observed at high surface coverage (Fig. 6d), but in general the results are consistent with a good degree of mixing of the two surfactant types on both SWNTs.
Discussion
In this section we analyse the preferential orientation of linear and branched SDBS molecules adsorbed on SWNT surfaces, and compare the results to those obtained for isomerically pure surfactants presented in our prior report.33 We consider the orientation vectors shown in Fig. 1, bottom panel, with respect to the SWNT axis. An angle of 0° or 180° indicates that the correspondent vector is parallel to the nanotube axis, 90° indicates that the vector is perpendicular to the nanotube axis. The results are shown in Fig. 7 and 8, obtained on (6,6) and (20,20) SWNTs, respectively, in the form of probability distributions. On the (6,6) SWNT at low surface coverage, the surfactant tails of equimolar mixtures of linear and branched SDBS surfactants tend to be parallel to the SWNT axis, as indicated by the largest peaks in the angle distribution profiles at 0° and 180° (Fig. 7a). At these conditions the benzene-sulfonate segments are preferentially perpendicular to the SWNT axis, yielding one broad peak centred at ∼90° (Fig. 7b). As the surface coverage increases the surfactant tails in equimolar SDBS mixtures are neither parallel nor perpendicular to the nanotube axis (Fig. 7c), while a significant amount of benzene-sulfonate groups remain perpendicular to the tube axis (Fig. 7d). Comparing the probability distributions just discussed against those obtained for pure linear and branched SDBS molecules, our results suggest that the surfactants from an equimolar mixture of linear and branched surfactants behave preferentially like pure branched SDBS surfactants, which orient their benzene-sulfonate groups for the most part perpendicularly to the nanotube axis. This is probably a consequence of the fact that when both linear and branched surfactants are present on the nanotube (1) the surfactant molecules wrap more tightly around the (6,6) SWNT than pure linear isomers do, and (2) linear molecules within the equimolar mixtures accommodate the presence of the branched counterparts. On (20,20) SWNT, at low and high surface coverage (Fig. 8), the results show no significant difference in orientation probability distributions for either surfactant tails or benzene-sulfonate groups among those obtained for equimolar SDBS mixtures, pure linear and branched surfactants. The surfactant tails tend to form any angle with respect to the nanotube axis (Fig. 8a and c), while the benzene-sulfonate segments mainly orient perpendicular to it, as indicated by the broad peak at 90°. | ||
| Fig. 7 Probability distribution of the (a and c) the surfactant tails and (b and d) the benzene-sulfonate segment orientation angle with respect to the (6,6) SWNT axis. In the left and right panels, the results are obtained at low and high surface coverages, respectively. The black-solid, blue-dashed, and red-dotted lines represent the results obtained on mixed linear and branched, pure linear, and pure branched molecules, respectively. The results of pure linear and branched SDBS are reproduced from our prior work.33 | ||
 | ||
| Fig. 8 Same as Fig. 7 but for surfactants adsorbed on (20,20) SWNTs. | ||
Finally, we compare the radial density profiles obtained from equimolar mixtures of linear and branched SDBS surfactants to those obtained for pure linear and branched ones.33 The results are shown in Fig. 9 and 10, obtained on (6,6) and (20,20) SWNTs, respectively. On the (6,6) SWNT at low surface coverage the peak positions of each surfactant segment (i.e., tail groups, benzene rings, head groups, and Na+ ions) in the density profiles for equimolar SDBS mixtures are found near the correspondent peaks obtained for pure linear and branched surfactants. This can, for instance, be seen clearly in the benzene ring and sulfonate group density profiles, in which some benzene rings and head groups for equilmolar SDBS mixtures remain in contact to the nanotube surface (which is consistent with results obtained for pure linear surfactants), while some other benzene rings are further from substrate (consistent with results obtained for pure branched molecules). When the surface coverage increases, the adsorbed aggregates formed by equilmolar SDBS mixtures are very similar to those obtained for the pure branched surfactants (Fig. 9e–h). In particular, our results show that most head groups from the equimolar mixtures of linear and branched SDBS surfactants are exposed to water, as was the case for pure branched surfactant. The Na+ ions accumulate near their head groups. On the (20,20) SWNT the radial density profiles obtained for the equimolar mixtures of linear and branched SDBS surfactants show that the results obtained for the surfactants near the tube surface are similar to those obtained for the pure linear surfactants, while those obtained for the surfactants whose heads are protruded into water are similar to those obtained for pure branched SDBS surfactants. This is observed both at low (Fig. 10a–d) and high (Fig. 10e–h) surface coverage.
 | ||
| Fig. 9 Radial atomic density profiles of (a and e) surfactant tails, (b and f) benzene rings, (c and g) sulfonate heads, and (d and h) Na+ ions belonging to mixed linear and branched systems (black-solid line), pure linear (blue-dashed line), and pure branched (red-dotted line) surfactants adsorbed on the (6,6) SWNT. In the left panels we report the results obtained at low surface coverage; in the right panels, we report those obtained at high surface coverage. The results of pure linear and branched SDBS are reproduced from our prior work.33 | ||
 | ||
| Fig. 10 Same as Fig. 9 but for the (20,20) SWNTs. | ||
Conclusions
We employed all-atom molecular dynamics simulations to investigate the morphology of equimolar mixtures of linear and branched SDBS surfactants on (6,6) and (20,20) SWNTs in water. Equimolar SDBS mixtures were found to yield disordered aggregates on both SWNTs, although the aggregates structure depends on surface coverage. At both surface coverages considered, the surfactant tails pack on the SWNT surfaces, while the head groups tend to extend more towards water as the surfactant coverage increases. We did not observe significant changes in the structure of the adsorbed aggregates as a function of the SWNT diameter. Comparing the self-assembled aggregates formed by equimolar SDBS mixtures against prior simulation results obtained for isomerically pure linear and branched SDBS surfactants at comparable surface densities, we found that, in general, mixtures of SDBS surfactants yield features (e.g., probability orientation distribution and radial density profiles for each surfactant portion) that are consistent with those obtained for either pure linear or pure branched SDBS surfactants. These simulation results suggest that SDBS does not show the ability of stabilizing SWNTs of selective diameters in experiments because experimental samples contain isomeric mixtures of the surfactants. While experimental validation is required to assess the reliability of our predictions, our simulations suggest that using mixtures of different surfactants could help manipulate the stability of aqueous dispersions of carbon nanotubes, which is consistent with recent advances reported in the literature (ACS Nano, 2015, 9, 5377).Acknowledgements
The authors acknowledge financial support from the Department of Chemical Engineering at University College London and from the US National Science Foundation (NSF) under Grant No. CMMI-1068705. Generous allocations of computing time were provided by the National Energy Research Scientific Computing Center (NERSC) at Lawrence Berkeley National Laboratory, Berkeley, CA, from the Oklahoma Supercomputer Center for Education and Research (OSCER), in Norman, OK, and from the Legion Supercomputer at University College London, in London, UK.Notes and references
- M. F. Islam, E. Rojas, D. M. Bergey, A. T. Johnson and A. G. Yodh, Nano Lett., 2003, 3, 269–273 CrossRef CAS.
- I. Pochorovski, H. L. Wang, J. I. Feldblyum, X. D. Zhang, A. L. Antaris and Z. N. Bao, J. Am. Chem. Soc., 2015, 137, 4328–4331 CrossRef CAS PubMed.
- J. Määttä, S. Vierros and M. Sammalkorpi, J. Phys. Chem. B, 2015, 119, 4020–4032 CrossRef PubMed.
- T. Hertel, A. Hagen, V. Talalaev, K. Arnold, F. Hennrich, M. Kappes, S. Rosenthal, J. McBride, H. Ulbricht and E. Flahaut, Nano Lett., 2005, 5, 511–514 CrossRef CAS PubMed.
- V. C. Moore, M. S. Strano, E. H. Haroz, R. H. Hauge, R. E. Smalley, J. Schmidt and Y. Talmon, Nano Lett., 2003, 3, 1379–1382 CrossRef CAS.
- E. A. Whitsitt and A. R. Barron, Nano Lett., 2003, 3, 775–778 CrossRef CAS.
- Y. Tan and D. E. Resasco, J. Phys. Chem. B, 2005, 109, 14454–14460 CrossRef CAS PubMed.
- B. Fang, G. Martyna and Y. F. Deng, Comput. Phys. Commun., 2007, 177, 362–377 CrossRef CAS PubMed.
- W. Wenseleers, I. I. Vlasov, E. Goovaerts, E. D. Obraztsova, A. S. Lobach and A. Bouwen, Adv. Funct. Mater., 2004, 14, 1105–1112 CrossRef CAS PubMed.
- F. Bonaccorso, T. Hasan, P. H. Tan, C. Sciascia, G. Privitera, G. Di Marco, P. G. Gucciardi and A. C. Ferrari, J. Phys. Chem. B, 2010, 114, 17267–17285 CAS.
- A. Di Crescenzo, S. Cambré, R. Germani, P. Di Profio and A. Fontana, Langmuir, 2014, 30, 3979–3987 CrossRef CAS PubMed.
- K. Yurekli, C. A. Mitchell and R. Krishnamoorti, J. Am. Chem. Soc., 2004, 126, 9902–9903 CrossRef CAS PubMed.
- H. Wang, W. Zhou, D. L. Ho, K. I. Winey, J. E. Fischer, C. J. Glinka and E. K. Hobbie, Nano Lett., 2004, 4, 1789–1793 CrossRef CAS.
- C. Fantini, J. Cassimiro, V. S. T. Peressinotto, F. Plentz, A. G. Souza Filho, C. A. Furtado and A. P. Santos, Chem. Phys. Lett., 2009, 473, 96–101 CrossRef CAS PubMed.
- J. G. Duque, C. G. Densmore and S. K. Doorn, J. Am. Chem. Soc., 2010, 132, 16165–16175 CrossRef CAS PubMed.
- S. Niyogi, S. Boukhalfa, S. B. Chikkannanavar, T. J. McDonald, M. J. Heben and S. K. Doorn, J. Am. Chem. Soc., 2007, 129, 1898–1899 CrossRef CAS PubMed.
- S. Niyogi, C. G. Densmore and S. K. Doorn, J. Am. Chem. Soc., 2009, 131, 1144–1153 CrossRef CAS PubMed.
- S. Ou, S. Patel and B. A. Bauer, J. Phys. Chem. B, 2012, 116, 8154–8168 CrossRef CAS PubMed.
- S.-Y. Ju, J. Doll, I. Sharma and F. Papadimitrakopoulos, Nat. Nanotechnol., 2008, 3, 356–362 CrossRef CAS PubMed.
- T. Okazaki, T. Saito, K. Matsuura, S. Ohshima, M. Yumura and S. Iijima, Nano Lett., 2005, 5, 2618–2623 CrossRef CAS PubMed.
- N. R. Tummala, B. H. Morrow, D. E. Resasco and A. Striolo, ACS Nano, 2010, 4, 7193–7204 CrossRef CAS PubMed.
- T. J. McDonald, C. Engtrakul, M. Jones, G. Rumbles and M. J. Heben, J. Phys. Chem. B, 2006, 110, 25339–25346 CrossRef CAS PubMed.
- B. White, S. Banerjee, S. O'Brien, N. J. Turro and I. P. Herman, J. Phys. Chem. C, 2007, 111, 13684–13690 CAS.
- A. J. Blanch, C. E. Lenehan and J. S. Quinton, J. Phys. Chem. B, 2010, 114, 9805–9811 CrossRef CAS PubMed.
- A. Di Crescenzo, R. Germani, E. Del Canto, S. Giordani, G. Savelli and A. Fontana, Eur. J. Org. Chem., 2011, 5641–5648 CrossRef CAS PubMed.
- J. A. Fagan, E. H. Hároz, R. Ihly, H. Gui, J. L. Blackburn, J. R. Simpson, S. Lam, A. R. Hight Walker, S. K. Doorn and M. Zheng, ACS Nano, 2015, 9, 5377–5390 CrossRef CAS PubMed.
- N. R. Tummala and A. Striolo, ACS Nano, 2009, 3, 595–602 CrossRef CAS PubMed.
- Z. Xu, X. Yang and Z. Yang, Nano Lett., 2010, 10, 985–991 CrossRef CAS PubMed.
- S. Lin and D. Blankschtein, J. Phys. Chem. B, 2010, 114, 15616–15625 CrossRef CAS PubMed.
- M. Suttipong, N. R. Tummala, A. Striolo, C. S. Batista and J. Fagan, Soft Matter, 2013, 9, 3712–3719 RSC.
- S. Lin, A. J. Hilmer, J. D. Mendenhall, M. S. Strano and D. Blankschtein, J. Am. Chem. Soc., 2012, 134, 8194–8204 CrossRef CAS PubMed.
- C.-J. Shih, S. Lin, M. S. Strano and D. Blankschtein, J. Phys. Chem. C, 2015, 119, 1047–1060 CAS.
- M. Suttipong, N. R. Tummala, B. Kitiyanan and A. Striolo, J. Phys. Chem. C, 2011, 115, 17286–17296 CAS.
- R. Haggenmueller, S. S. Rahatekar, J. A. Fagan, J. Chun, M. L. Becker, R. R. Naik, T. Krauss, L. Carlson, J. F. Kadla, P. C. Trulove, D. F. Fox, H. C. DeLong, Z. Fang, S. O. Kelley and J. W. Gilman, Langmuir, 2008, 24, 5070–5078 CrossRef CAS PubMed.
- M. D. Clark, S. Subramanian and R. Krishnamoorti, J. Colloid Interface Sci., 2011, 354, 144–151 CrossRef CAS PubMed.
- M. Bystrzejewski, A. Huczko, H. Lange, T. Gemming, B. Büchner and M. H. Rümmeli, J. Colloid Interface Sci., 2010, 345, 138–142 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS.
- A. Cheng and W. A. Steele, J. Chem. Phys., 1990, 92, 3867–3873 CrossRef CAS PubMed.
- J. I. Siepmann, S. Karaborni and B. Smit, Nature, 1993, 365, 330–332 CrossRef CAS PubMed.
- M. G. Martin and J. I. Siepmann, J. Am. Chem. Soc., 1997, 119, 8921–8924 CrossRef CAS.
- B. Smit, S. Karaborni and J. I. Siepmann, J. Chem. Phys., 1995, 102, 2126–2140 CrossRef CAS PubMed.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, Orlando, FL, 1st edn, 1996 Search PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS PubMed.
- B. Sohrabi, N. Poorgholami-Bejarpasi and N. Nayeri, J. Phys. Chem. B, 2014, 118, 3094–3103 CrossRef CAS PubMed.
- T. Yang, S. Berber, J. F. Liu, G. P. Miller and D. Tomanek, J. Chem. Phys., 2008, 128, 124709 CrossRef PubMed.
- N. R. Tummala and A. Striolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021408 CrossRef.
- O. Matarredona, H. Rhoads, Z. Li, J. H. Harwell, L. Balzano and D. E. Resasco, J. Phys. Chem. B, 2003, 107, 13357–13367 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Clarendon Press, Oxford, 1987 Search PubMed.
| This journal is © The Royal Society of Chemistry 2015 |