Ion implantation of low energy Si into graphene: insight from computational studies

Abstract

By employing both molecular dynamics (MD) simulations and ab initio calculations based on the density functional theory (DFT), we studied the efficiency of doping graphene with low energy Si ions implantation. Mainly two types of substitutional doping configurations resulting from Si ion implantation were found in graphene, namely perfect Si substitution at monovacancy (Si@MV), and Si interstitial defect at divacancy site (Si@DV). High efficiency for Si substitutions was obtained within a wide energy range varied between 30–150 eV. At the optimum energy of 70 eV, up to 59% of the incident Si ions would be incorporated in graphene by Si@MV. Moreover, the experimental doping efficiency should be higher than the above value of 59% because Si adatom on graphene surface can be eventually turned into a substitution atom via annihilating with a vacancy defect produced in the collision process. Such high doping efficiency makes ion implantation a powerful tool to dope graphene with Si and similar elements. Our results provide a theoretical clue for the property engineering of graphene by using ion irradiation technique, in particular for doping graphene with heavy ions.

---

1. Introduction

In recent years, numerous research works have been devoted to the studies of graphene intrinsic properties and its potential applications in novel nanotechnology.^1,2 Pristine graphene has many excellent physical and chemical properties, such as high electron mobility, good thermal conductivity and strong mechanical properties, which make it an ideal block material for novel nanoelectronic devices.^3,4 Graphene based systems have shown very promising applications in many fields, such as gas detection,⁵ photovoltaics,⁶ and DNA sequencing.⁷ Despite these successful applications, doping graphene with other elements is necessary to obtain good device performance, as pristine graphene has some disadvantages such as zero band gap,⁸ which makes the electronic devices have low operation controllability due to small on-off ratios, moreover, its inert chemical reactivity also makes the post-functionalization rather difficult.⁹

In the past few years, many efforts have been made to dope graphene with foreign elements. The most studied elements are N and B. It has been demonstrated that N- or B-doped graphene displays n- or p-type semiconductor behavior, resulting from the impurity levels in the N/B dopants.^10,11 It was also found that, although pristine graphene is a non-magnetic material, by doping of transition metal atoms, local magnetism could be introduced in its lattice, which is rather important for the applications in graphene based spintronics devices.^12,13 In addition, graphene doped with various foreign non-metallic atoms, such as oxygen, phosphor, sulfur, selenium, silicon, etc., has been proved to be very promising as an environmental-friendly and sustainable metal-free catalysts,¹⁴ which shows high catalytic reactivity in numerous chemical reactions, such as oxygen reduction reactions in fuel cells,¹⁵ oxidative dehydrogenation,¹⁶ reduction of nitrobenzene,¹⁷ etc.

Till now, many methods have been developed for the synthesis of doped graphene. For instance, N- or B-doped graphene sheets could be prepared by chemical vapor deposition (CVD) methods during the growth of graphene,¹⁸ by post treatments like in plasma,¹⁹ or by arc-discharge techniques with N/B containing precursors.²⁰ Currently, these doping methods have been proved to be successful in several doping elements (e.g. N, B, S, F, Cl, Br, I). However, suitable precursors containing the dopant element must be first supplied in these methods, limiting their wider applications in the doping of heavy elements which cannot be easily vaporized. Although other doping methods through the complex chemical reactions with graphene oxides²¹ to prepare doped graphene have wider choices of dopant elements, these chemical doping routes may suffer from problems like poor controllability in doping site selectivity, adsorption contamination from various chemical residuals, and secondary impurities. Therefore, developing a clean, high efficient doping method which can be applied to various dopant species is highly desirable.

Another choice in graphene doping is to use ion implantation technique, which has already been widely applied in doping semiconductors²² and metals.²³ Recently, Åhlgren et al.²⁴ predicted from MD simulations that direct doping of N and B atoms in graphene lattice could be achieved via low-energy ion implantation, which has been later realized by Bangert et al.²⁵ in experiments, in which substitutional N and B dopants in graphene resulting from ion irradiations were first visualized via high-resolution transmission electron microscopy. Since ion implantation is a highly industrialized technique used for material property modification in today's semiconductor industry, ion implantation doping in graphene can be directly compatible to IC technologies. Besides, this technique is independent of special choices for dopant precursors, as it works by directly substituting C atoms in graphene with the energetic dopant ions. Therefore, it could be used as a potential universal doping method for a wide range of dopant element species.

In previous studies,²⁶ very few reports have been found in the synthesis of Si-doped graphene, which is very important for developing high-efficiency molecule sensor devices using graphene. For examples, Chen et al.²⁷ showed that NO or NO₂ molecules have high reactivity with the Si dopants in graphene, and for various big molecules adsorbed on graphene, doping of Si could also improve the detection sensitivities by several orders due to the enhanced surface Raman spectra.²⁶

In case of doing graphene with Si, ion implantation is one suitable tool because Si ion beams are easily produced with an ion implanter. The problem is how to choose ion parameters such as ion energy, incident angle to successfully insert Si ions into the graphene sheet with high efficiency. The results obtained when implanting N or B ions into graphene²⁴ can be helpful in designing experiments to dope Si into graphene, but different behaviors may arise from the large mass difference between Si ions and N or B ions, and the strong chemical interaction of Si–C bonds.²⁸

In this work, we report the dependence of doping efficiency for Si on ion parameters by using MD simulation. In our simulations, low energy Si ions ranging from 20 eV to 200 eV were employed. We showed that up to 59% and 11% of incident Si could be directly incorporated into graphene by the substitution of one and two carbon atoms at the optimum energies of 70 eV and 100 eV, respectively. Besides classic molecular dynamics simulations, we also employed DFT method to analyze the final stable structure of ion implantation induced defect structures involving Si incorporation in graphene. Our results provide a theoretical clue for solving the problem of doping the heavy element Si into graphene, which can be used as a reference for the future experiment designs.

2. Computational details

MD simulations were performed on the Sandia National Laboratories ‘large-scale/molecular massively parallel simulator (LAMMPS)’.²⁹ The adaptive intermolecular reactive empirical bond order (AIREBO) potential function³⁰ was used to calculate the interactions between carbon atoms in graphene. To model the energetic collisions between incident Si ions with graphene, the employed Si–C Tersoff potential taken from ref. 31 was smoothly joined to Ziegler–Biersack–Littmark (ZBL) repulsive potentials³² at short interatomic separations. All these parameters have been well tested in our previous studies considering the ion irradiation defect production in graphene.^33–35

Ion irradiations were conducted on a free standing graphene sheet consisting of 2048 C atoms, with a lateral size of 68.17 × 78.72 Ų. The simulation setup is shown in Fig. 1, in which the Si ion was placed initially at 20 Å above the graphene sheet, and given incident energies within a range of 20–200 eV. Without special emphasis, irradiations were all performed in the normal direction toward graphene. During the dynamical simulations, periodic boundary conditions (PBCs) were used, and the NVE ensemble was employed to deal with the collision processes. After the irradiation, the system was allowed to relax under a temperature of 1500 K for 100 ps with the Nosé–Hoover algorithm,^36,37 in order to eliminate most metastable defect structures. For each ion energy, 500 independent simulation runs were carried out, in which all the impact points were randomly distributed in a 10 × 10 Ų square area located in the center of graphene sheet.

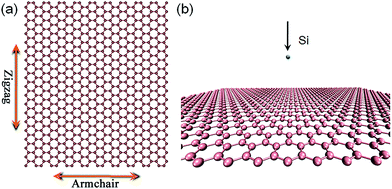Fig. 1 Schematic representation of a suspended graphene sheet (a), and the MD simulation setup (b) in this study. In the suspended graphene, the zigzag and armchair orientations are indicated.

In general, MD simulation lasts in ns scale, which is not long enough for defects formed in the irradiation process to relax to their final stable structures. Therefore, to obtain the energetic favorable defect structures, we performed DFT calculations as implemented in VIENNA AB INITIO SIMULATION PACKAGE (VASP).^38,39 The core electrons were described by projected augmented wave (PAW) potentials⁴⁰ and the Perdew–Burke–Ernzerhof (PBE) functional of the generalized gradient approximation⁴¹ was employed to express the exchange–correlation energy of interacting electrons. The plane wave cutoff energy was set to 600 eV. Γ-Centered 6 × 6 × 1 k-point sampling was used for the Brillouin-zone integration. We have chosen a 6 × 6 supercell (72 atoms) of graphene for our calculations, and a vacuum slab with thickness of 20 Å along the perpendicular direction was adopted to avoid interlayer interactions.

3. Results and discussions

3.1. Property and production probabilities of various irradiation structures involving Si incorporation in graphene

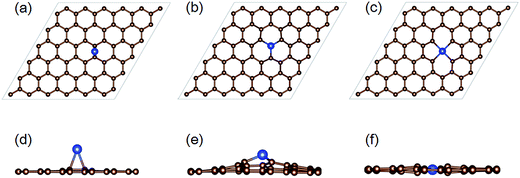
Several defect structures can be formed due to Si ion implantation. Three typical irradiation induced structures involving Si incorporation in graphene are shown in Fig. 2, namely (i) Si adatom, (ii) perfect Si substitution in a graphene monovacancy (Si@MV); (iii) Si interstitial defect at a divacancy site (Si@DV) created by the removal of a C–C pair, where the Si atom has a 4-fold coordination with neighboring atoms. All the structures shown in Fig. 2 have been fully optimized by DFT methods with the initial irradiation configurations obtained from MD simulations.

Fig. 2 Typical Si incorporation configurations in suspended graphene after the irradiations: (a) Si adatom; (b) Si substitution in a graphene monovacancy (Si@MV); (c) Si interstitial defect at a divacancy (Si@DV). (d), (e), (f) Show the corresponding side views of the above three defect configurations, respectively. All the structures have been fully optimized by DFT methods, with the initio structures obtained from MD simulations.

Since the substitution of C in graphene is a much more efficient and stable configuration for graphene doping, we firstly focus on the probability of substitutional implantation. In the following sections, the energy and incident angle dependence of Si implantation in graphene are systematically studied.

3.1.1. Si@MV. The perfect substitution (Si@MV) occurs when a C atom is knocked out from graphene lattice and replaced by the incident Si ion. In the equilibrium configuration for Si@MV, as shown in Fig. 2b, the Si dopant is finally stabilized at a height of 1.54 Å above the graphene layer, forming strong chemical bonds with its nearest three C atoms by an equal bond length of 1.75 Å. Fig. 2e is the side view of Si@MV structure in graphene, from which we see that a large geometrical distortion in graphene is induced by the incorporation of Si, where the C atoms at the Si-nearby region are displaced outward from the graphene sheet by a height of 0.88 Å. In fact, by analyzing the electron energy-loss spectroscopy for various Si defects in graphene,⁴² it is demonstrated that the threefold coordinated Si in the Si@MV structure adopts a sp³ hybridization, which explains the origin for the above Si@MV nonplanar structure.

In Fig. 3, the production probability of Si@MV under low-energy Si implantation is plotted as a function of ion energy. The maximum probability is about 59%, which lies in a range of incident ion energy between 50–70 eV. Compared to graphene implanted with N and B,²⁴ in which less than 10% of the incident N/B ions would take the substitutional positions at energies beyond 100 eV, the doping efficiency of Si is much higher.

Fig. 3 Probabilities for perfect Si substitution in graphene (Si@MV) as a function of ion energy. The lines are connected as guide for eyes.

Since Si atom is heavier than N/B atoms, it has a larger defect cross section during the collisions with carbon atoms, which results in the above higher substitution probability in our simulations. Besides, the peak in the probability is also much broader compared to that in N/B implantation, implying that high-probability Si substitution could be achieved in a wide energy range. If we take the substitution probability of 10% as the measure criterion, the energy range of Si ions could be varied from 30 eV to 150 eV, therefore one can expect that in the experiment setup for Si ion beams, the demand on the ion beam facility is easy to be satisfied.

Besides, the onset of Si substitution event shown in Fig. 3 occurred with a probability of 7.8% even at the lowest irradiation energy of 20 eV, which seems impossible since the displacement energy of C atom, which is the minimum kinetic energy for a C atom to displace from the graphene lattice, is 25 eV determined by the AIREBO potential.³⁰ This phenomenon could be interpreted by the role of chemical effect,²⁸ resulting from the bonding property of incident ions with C atoms. In our previous work considering the ion irradiation defect production in carbon nanotubes (CNTs),²⁸ the chemical interaction between carbon atoms and incident ions would greatly decrease in the threshold displacement energy for C atoms. As a consequence, the minimum kinetic energy for Si to displace a C atom in CNTs is 15 eV (for a head-on collision), which is much smaller compared to the 30 eV as predicted by the binary collision approximation.⁴³ Therefore, considering the same C–C sp² hybridization bonding property in both CNTs and graphene, one can expect that similar mechanism could also be employed in graphene. With increasing ion energy, more kinetic energy transfer from Si to C atoms leads to a higher defect production probability in graphene, and the maximum substitution probability is obtained at 70 eV. After that, more energetic recoiling Si ions, which have high probabilities to pass through the graphene sheet, are produced, and the probability of Si substitutions decreases at the high energy range.

3.1.2. Si@DV. Another typical Si substitution configuration shown in Fig. 2c is produced by the displacement of two neighboring C atoms while the Si ion itself stops at the graphene sheet. The probability for this process under Si ion implantation is presented in Fig. 4 as a function of Si ion energy, from which we can see that the highest substitution probability (11%) is found upon Si implantation at 100 eV. Compared to Si@MV, the production probability for Si@DV is much lower, while the optimum energy shifts to high energy side (100 eV) because more kinetic energy is needed to break more C–C bonds.

Fig. 4 Probabilities for Si interstitial defect in graphene (Si@DV) as a function of ion energy.

As demonstrated in ref. 24 there are two possible mechanisms for DV production in graphene under heavy ions irradiation: (i) simultaneous displacement of two carbon atoms by the impact of the incident ion in the middle of the C–C bond; (ii) successive displacement of two carbon atoms in which the first displaced C atom cause another C atom to be sputtered. In the case of graphene irradiation by low-energy N ions, due to a smaller cross section for C displacements, the maximum probability for the dopants occupying at the DV site is only ∼3%, while this value is almost 4 times higher in Si implantation. Besides, as shown in Fig. 3 and 4, the energy range for high-probability Si@MV is overlapped with that of Si@DV, therefore, one can expect that for Si doped graphene prepared by this method, the final substitution configurations in graphene are combinations of both Si@MV and Si@DV. However, the onset energy for Si@DV production is higher than that of Si@MV. In our simulations, a maximum value (64.25) of the ratio between Si@MV with Si@DV was obtained at 40 eV. Hence, if one wants to eliminate the possible mixing effects from these two structures, for example, in graphene post functionalization, irradiation at the low energy side (30–40 eV) of the probability peak is highly recommended.

In Fig. 2c and f, we show the equilibrium structure of Si@DV, from which we see that the Si impurity prefers to stay in the same plane as the graphene lattice, stabilized by the strong chemical bonds with its nearest four C atoms by an equal bond length of 1.90 Å. Such planar structure results from the sp²d hybridization bonding property,⁴² where the four Si–C bonds are formed by the mixing of the 3s, 3p, and 3d states in Si atom. In previous studies, numerous works^27,44–46 on the Si doping effect in graphene and CNTs by the form of Si@MV structure were published, but the property of Si@DV has rarely been investigated. As can be seen from the above results, the bonding property of Si–C in Si@DV brings minimal protrusions with respect to the surrounding graphene sheet than the case of Si@MV. More importantly, the different bonding configurations may bring a big difference in their chemical reactions with other adsorbed molecules in the gas sensing applications.²⁷ Since a considerable amount of Si@DV was generated during the Si ion implantation, further work should be done on the property modification of graphene chemical reactivity by Si@DV doping structures.

3.2. The effect of ion incident angle on the probability of various defect structures

Besides ion energy, ion incident angle also has a significant influence on the irradiation damage production. A big difference in Si substitution probability is observed in Fig. 5 as the ion incident angle increases from 0° to 60° (with respect to the surface normal line). Here, we take the 100 eV Si implantation as an example, to show the ion angle effect. In view of the possible influence from atomic arrangement direction on the final defect production, irradiations were performed along both armchair and zigzag orientations in graphene, respectively. The simulation results as displayed in Fig. 5 reveal that no significant difference due to different irradiation orientations was observed. For the convenience of discussion, results shown below are all referred to the irradiation in the zigzag orientation.

Fig. 5 Probabilities for (a) Si@MV, (b) Si@DV, and (c) Si@complex as a function of ion incident angles in the case of 100 eV Si ion implantation.

In Fig. 5a, at first, an enhanced probability for the perfect substitution (Si@MV) was observed with increasing ion incident angles, and reached its maximum of 53% at 40°. After that, the production probability dropt quickly at high angles. A similar tendency was also observed for Si@DV, in which the maximum probability was found to be 22% at the same optimum angle of 40°. One should notice that, the highest Si@MV probability obtained here is almost comparable to the maximum value (59%) for perpendicular irradiations, while the maximal probability for Si@DV is even two times higher.

The enhanced substitution probability under oblique irradiation is a result of the higher stopping ability on the incident ions in graphene. Due to the low dimension with only one atomic layer thickness of graphene, there is plenty of free space for the incident ions to escape, therefore, only low energy ions at a very narrow energy range could be stopped in its lattice. However, when the ion irradiates graphene with an oblique angle, the atomic density seen by the ion is much higher compared to the case of normal incidence. As a result, more kinetic energy will be transferred to graphene sample, which will result in an increased trapping probability for higher energy ions. Moreover, as Si is a much heavier element than C, it is less likely to be scattered away from the graphene surface. In our simulations, we find that, at the incident angle of 60°, most of the impinging Si were adsorbed on graphene sheet as adatoms, but were normally found far away from their original impact sites, finally stopped by a series of collisions with C atoms. In our statistics, the probability for Si adatoms can reach 44.8% and 86.6% at 50° and 60°, respectively, which causes the decrease in substitution probability at higher angles.

Besides, some complex defect structures with Si incorporations (Si@complex) were also found in graphene for oblique irradiations. From the above analysis, we see that more carbon atoms would take part in the collisions with the impinging Si at higher incident angles, which would occasionally lead to the simultaneous displacement of several C atoms, forming large vacancies in the graphene lattice. In our simulations, Si@trivacancy accounts for a large proportion of the complex incorporation structures as shown in Fig. 5c. Another normally seen defect structures at high angles is the nonhexagonal ring, which was formed during the rearrangement of displaced C atoms in the ion impact area. The highest probability for Si incorporation at these complex structures is found to be 7% at the incident angle of 40°, which is rather small compared to that of the two most important substitution structures, Si@MV and Si@DV. However, special attention should be given to the production of these complex structures, since they are more constructive to the graphene lattice due to the larger defect size.

Although here only 100 eV irradiations were investigated, one can expect that the above mechanism could also be applied to even higher incident energies. Therefore, compared to perpendicular irradiations, it seems that more Si substitutions in graphene could be achieved by irradiation with proper incident angles, which may offer as an alternative option for graphene doping by using the ion implantation scheme.

3.3. Dopant as an adatom

In general, substitutional doping is what we want most in graphene. Besides the above mentioned direct formation process, there exists another indirect way to obtain substitutional structures by the recombination of Si adatoms and vacancy defects in graphene. As shown in Fig. 6, large numbers of Si adatom could be formed for very low energy implantations, in which clearly two stages are found: (i) at ion energies below 70 eV, the production probability drops quickly with increasing incident energy; (ii) after that, a small peak appears at 130 eV, with a maximum probability of 10%. Closer inspection of the atomic structure reveals that this tendency results from two different Si adsorption schemes on graphene. First, for low energy ions, they are easily to be attached to the pristine graphene as adatoms, because they have energies enough to overcome the surface barrier but not sufficient to knock out the C atoms from graphene. However, as the incident energy increases, it is more likely for the impinging Si to create vacancies in graphene, while the low energy recoiling Si may be trapped nearby the defect sites by the strong attractive force of Si–C bonds. From our MD results, the onset for the production of the latter Si adatoms adsorbed on defective graphene occurs at 70 eV, which explains the above two stages phenomenon in Fig. 6.

Fig. 6 Probabilities for Si adatom in graphene as a function of ion energy. Obvious two stages are found, as divided by the blue dashed line located at 70 eV. The inserts show the typical Si adatom configurations appearing at corresponding stages, in which the highly unstable Si adatom structures at stage II are likely to turn into the stable substitution configurations.

DFT calculations show that the Si adatom at stage I prefers to occupy the bridge position on top of the middle of a C–C bond, and the distance between Si atom and the nearest two carbon atoms is 2.1 Å, as shown in Fig. 2a and d. A slight lattice stretching less than 3.5% is observed for the carbon atoms nearby the Si atom, while the displacement of C atoms outward graphene plane is within 2%. The adsorption energy is determined to be −1.69 eV, revealing a weak interaction between the Si adatom and graphene sheet.

In fact, the atomic configurations for Si adatoms at stage II shown in the inserts of Fig. 6 are not stable. According to DFT calculations, they can be easily transferred to substitutional Si during structure optimization, which give rise to a total system energy decrease of 8.13 eV and 7.03 eV for the adatoms to occupy the monovacancy and divacancy sites, respectively. The above phenomenon was caused by the high mobility of Si adatoms on graphene. For an estimation of migration barrier we simply calculate the energy difference between Si adsorption energies on typical adsorption sites of C–C bond bridge (B), top of carbon atoms (T), and the middle of hexagon rings (H). The minimum energy limit for Si migration between two adjacent equilibrium bridges is found to be 0.08 eV along the B–T–B path. On the other hand, Nakada et al.,⁴⁷ in their LDA calculations, found the migration barrier for Si on graphene to be 0.05 eV. Since the threshold barrier energy for atomic migration at room temperature is roughly 0.5 eV,⁴⁷ the very low migration energy indicates that Si adatoms on graphene sheets are highly mobile, and have a high rate of forming substitutional atoms via the annihilation with the vacancies created by energetic ions. In our MD simulations, we partly took into account the annealing effect to speed up the migration of Si atoms by elevating the system temperature (1500 K). However, considering the thermodynamic fluctuations, the real migration paths for Si atoms are randomly distributed. Therefore, to observe the Si adatoms annihilation with carbon vacancies, long simulation time is indeed needed, which is not suitable for MD simulations considering its high computational cost. As a consequence, limited to a finite simulation time (0.1 ns), the recombinations of Si adatoms with vacancies were only occasionally counted. However, one can expect that by using post-annealing treatment in experiments, the final number of substitutional Si in graphene could be further increased. In addition, to obtain a highly doped graphene sheet with few irradiation defects, Åhlgren et al.²⁴ also provided an optional implantation scheme for N/B substitutional doping in graphene by a two-energy irradiation scheme, namely, one at the substitution maximum and another below the single-vacancy-creation threshold. They expect that the created vacancies during ion irradiations could be finally turned into substitutional doping by recombinations with the mobile dopants. However, the high migration energy barrier for N adatom (1.1 eV) on graphene would make the implementation of this plan very inefficient. In contrast, this two-energy irradiation scheme seems to be much more suitable for Si implantation. In fact, as mentioned above, large amounts of Si adatoms are found in our MD simulations for Si ion implantation at high irradiation angles. For an example, the probability for the stage I and stage II Si adatoms shown in Fig. 6 are 18.6% and 75.2%, respectively, during 100 eV Si irradiations at 60°. From the above analysis, these adatoms have high probabilities to be finally turned into substitutional Si, implying a much higher substitution probabilities than that shown in Fig. 5a and b.

4. Conclusion

In conclusion, our results show that, by employing low-energy ion implantation technique, a high fraction of substitutional Si dopants in graphene could be achieved, which depends on the ion parameters including both ion energy and incident angles. By choosing suitable parameters, doping efficiency of Si could be as high as 59%, which is sufficient for practical applications. Besides, since various ion species could be supplied by ion implantation technique, the above doping scheme could also be applied to other elements, which may serve as a potential universal route for foreign element doping in graphene, as it is clean, controllable, and very efficient.

Acknowledgements

This work is financially supported by NSAF (Grant No. U1230111) and NSFC (Grant No. 91226202).

References

1. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
2. A. K. Geim, Science, 2009, 324, 1530–1534.
3. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
4. K. Kim, J.-Y. Choi, T. Kim, S.-H. Cho and H.-J. Chung, Nature, 2011, 479, 338–344.
5. F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652–655.
6. Z. Yin, S. Sun, T. Salim, S. Wu, X. Huang, Q. He, Y. M. Lam and H. Zhang, ACS Nano, 2010, 4, 5263–5268.
7. G. F. Schneider, S. W. Kowalczyk, V. E. Calado, G. Pandraud, H. W. Zandbergen, L. M. Vandersypen and C. Dekker, Nano Lett., 2010, 10, 3163–3167.
8. A. H. Castro Neto, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162.
9. D. W. B. A. M. I. Katsnelson, Nano Lett., 2008, 8, 4373.
10. B. Guo, Q. Liu, E. Chen, H. Zhu, L. Fang and J. R. Gong, Nano Lett., 2010, 10, 4975–4980.
11. D. J. Late, A. Ghosh, K. S. Subrahmanyam, L. S. Panchakarla, S. B. Krupanidhi and C. N. R. Rao, Solid State Commun., 2010, 150, 734–738.
12. A. V. Krasheninnikov, P. O. Lehtinen, A. S. Foster, P. Pyykkö and R. M. Nieminen, Phys. Rev. Lett., 2009, 102, 126807.
13. X. Liu, C. Z. Wang, M. Hupalo, W. C. Lu, M. C. Tringides, Y. X. Yao and K. M. Ho, Phys. Chem. Chem. Phys., 2012, 14, 9157–9166.
14. X.-K. Kong, C.-L. Chen and Q.-W. Chen, Chem. Soc. Rev., 2014, 43, 2841.
15. K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Science, 2009, 323, 760–764.
16. J. Zhang, X. Liu, R. Blume, A. Zhang, R. Schlögl and D. S. Su, Science, 2008, 322, 73–77.
17. B. Li and Z. Xu, J. Am. Chem. Soc., 2009, 131, 16380–16382.
18. T. Wu, H. Shen, L. Sun, B. Cheng, B. Liu and J. Shen, New J. Chem., 2012, 36, 1385–1391.
19. H. M. Jeong, J. W. Lee, W. H. Shin, Y. J. Choi, H. J. Shin, J. K. Kang and J. W. Choi, Nano Lett., 2011, 11, 2472–2477.
20. N. Li, Z. Wang, K. Zhao, Z. Shi, Z. Gu and S. Xu, Carbon, 2010, 48, 255–259.
21. X. Wang, G. Sun, P. Routh, D. H. Kim, W. Huang and P. Chen, Chem. Soc. Rev., 2014, 43, 7067–7098.
22. J. Williams, Mater. Sci. Eng., A, 1998, 253, 8–15.
23. J. Hirvonen, C. Carosella, R. Kant, I. Singer, R. Vardiman and B. Rath, Thin Solid Films, 1979, 63, 5–10.
24. E. Åhlgren, J. Kotakoski and A. Krasheninnikov, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115424.
25. U. Bangert, W. Pierce, D. M. Kepaptsoglou, Q. Ramasse, R. Zan, M. H. Gass, J. A. van den Berg, C. B. Boothroyd, J. Amani and H. Hofsass, Nano Lett., 2013, 13, 4902–4907.
26. R. Lv, M. C. dos Santos, C. Antonelli, S. Feng, K. Fujisawa, A. Berkdemir, R. Cruz-Silva, A. L. Elías, N. Perea-Lopez and F. López-Urías, Adv. Mater., 2014, 26, 7593–7599.
27. Y. Chen, B. Gao, J. X. Zhao, Q. H. Cai and H. G. Fu, J. Mol. Model., 2012, 18, 2043–2054.
28. S. Zhao, J. Xue, Y. Wang and S. Yan, Appl. Phys. A, 2012, 108, 313–320.
29. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
30. S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472–6486.
31. R. Devanathan, T. Diaz de la Rubia and W. J. Weber, J. Nucl. Mater., 1998, 253, 47–52.
32. J. F. Ziegler and J. P. Biersack, in Treatise on Heavy-Ion Science, Springer, US, 1985, ch. 3, pp. 93–129.
33. W. Li, X. Wang, X. Zhang, S. Zhao, H. Duan and J. Xue, Sci. Rep., 2015, 5, 9935.
34. W. Li, L. Liang, S. Zhao, S. Zhang and J. Xue, J. Appl. Phys., 2013, 114, 234304.
35. S. Zhao, J. Xue, Y. Wang and S. Yan, Nanotechnology, 2012, 23, 285703.
36. S. Nosé, Mol. Phys., 1984, 52, 255–268.
37. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695.
38. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
39. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
40. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
42. W. Zhou, M. D. Kapetanakis, M. P. Prange, S. T. Pantelides, S. J. Pennycook and J.-C. Idrobo, Phys. Rev. Lett., 2012, 109, 206803.
43. J. F. Ziegler, Nucl. Instrum. Methods Phys. Res., Sect. B, 2004, 219–220, 1027–1036.
44. J. Zhao, Y. Chen and H. Fu, Theor. Chem. Acc., 2012, 131, 206803.
45. P. A. Denis, Chem. Phys. Lett., 2010, 492, 251–257.
46. R. Bian, J. Zhao and H. Fu, J. Mol. Model., 2013, 19, 1667–1675.
47. K. Nakada and A. Ishii, Solid State Commun., 2011, 151, 13–16.

---