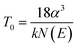Investigating spin reversal and other anomalies in magnetic, transport and specific heat measurements of NdFeO₃ and NdFe_0.5Ni_0.5O₃ ortho-perovskites

Abstract

Polycrystalline NdFeO₃ (NFO) and NdFe_0.5Ni_0.5O₃ (NFNO) compounds were synthesized by the standard solid state reaction route and were characterized to understand their structural, electrical, magnetic and thermal properties, and electronic structure. Rietveld refinements of the X-ray diffraction pattern confirm the single phase nature of both these compounds with an orthorhombic structure having the space group Pbnm. The temperature dependent resistivity follows the variable range hopping (VRH) model. From this model, the parameters such as density of states (DOS) at the Fermi level N(E_F), hopping distance R_h, hopping energy E_h etc. were calculated. Electrical, magnetic and specific heat [C_p(T)] properties of the NFO and NFNO compounds were systematically studied in the temperature range of 2 to 300 K to understand the spin reorientation transition, magnetic intersection and magnetic inversion anomalies. NFO and NFNO exhibit an interesting phenomenon of spin reversal at low temperatures. The magnetic behaviour at low temperatures and fields is explained based on the competition among magnetic moments of rare earth (Nd) and transition metal ions (Fe/Ni). At a low magnetic field (500 Oe), the zero field cooled (ZFC) and field cooled (FC) branches intersect at low temperatures T_X of 8.75 K and 17.05 K for NFO, and NFNO respectively. Below T_X, the magnetization is negative. The FC curve crosses the M = 0 axis at 4.7 K for NFO, and 5.2 K for NFNO. The spin reorientation transitions are observed in the temperature range of 100–200 K for NFO and NFNO samples with a transition of the Fe³⁺/Ni³⁺ magnetic moments from Γ₄(G_x,F_z)-type ordering (at high temperatures) to Γ₂(G_z,F_x)-type ordering (at low temperatures). The isothermal hysteresis loops show a decrease of magnetization and increase of coercivity with the temperature and complements the magnetization versus temperature data. The Schottky and crossing point anomalies and the effect of an applied magnetic field over them at low temperatures of these compounds were also investigated. In addition to the above properties and magnetic and the thermal anomalies of NFO and NFNO instigated by the spin reorientation were also discussed.

---

Sajad A. Mir

Sajad Ahmad Mir did his Bachelors degree in Science from Sri Pratap College of University of Kashmir and Master degree in Physics from University of Kashmir (J&K), India. He was awarded Kashmir University's Gold Medal and Professor Rayees Gold Medal for achieving first position in M.Sc Physics. He is currently doing PhD in Physics (Materials Science) from National Institute of Technology (N.I.T) Srinagar, India. His main research interest includes Rare-Earth Ortho-perovskites and ion irradiation studies.

1. Introduction

Perovskite-type rare-earth transition metal oxides (RTMO) with a stoichiometric chemical formula of RFeO₃ (RFO, where R is a rare-earth ion) are commonly called orthoferrites and RNiO₃ (RNO), called orthonicklates, are model compounds in solid state physics and these remain at the central focus of many research studies over few last decades. These compounds are important to understand the interplay between lattice, charge and spin degrees of freedom. Being a strongly correlated electron system, RFO exhibits unusual but interesting functional properties such as catalytic^1,2 gas sensitivity,³ dielectric,^4,5 magnetic,⁶ and magnetoelectric⁷ properties. Spin reorientation in phase transition is another important characteristics of orthoferrites, in which direction of the easy axis of magnetization changes from one crystal axis to another.^8,9 The type of reorientation transition that happens in orthoferrites is according to the sequence Γ₄(G_x,F_z) → Γ₂₄(G_xz,F_xz) → Γ₂(G_z,F_x). This characteristic of RFO renders them potential materials in modern technologies, such as laser induced, ultrafast spin reorientation.^10,11 Below Neel temperature (T_N), out of the two major subsystems of RFO, the Fe ion subsystem orders into a canted antiferromagnetic (AFM) structure with antiferromagnetic moment G along the a (=x) axis of crystal and a weak ferromagnetic (FM) moment F due to spin cantedness known as canted moment along the c (=z) axis of crystal. The other subsystem of rare-earth ion is paramagnetic but because of polarization acquires some magnetization of moment m in the molecular field of Fe ions subsystem.¹² The total magnetization of the system is M = F + m. So, the significant property of the Nd subsystem is the magnetic anisotropy of paramagnetic susceptibility to the molecular field, χ^a_Nd ≠ χ^c_Nd, insinuate as a key factor for spin-reorientation.^13–17 The reorientation is due to the continuous rotation of vector F and vector G in the (a, c) plane over the temperature range [T₂–T₁] such that T₂ < T₁ < T_N. Temperatures T₁ and T₂ indicate two second order phase transitions.

The studies of the RTMOs have revealed many interesting aspects. In particular, the substitution of homovalent transition metal ions leads to many distinctive changes in the system. In the case of LaFeO₃ and PrFeO₃, the Ni substitution leads to quite unusual properties like the insulator–metal transition, ferromagnetic to paramagnetic transition, etc. The structural, magnetic and electronic studies of Ni-doped LaFeO₃ as well as Ni-doped PrFeO₃ have shown many remarkable aspects concerning the semiconducting ferromagnetic behaviour. The Ni substitution stabilizes the magnetic structure by reducing the asymmetry in hysteresis.^3,4 These investigations on homovalent, Ni³⁺, substitutions at the Fe³⁺ site reveal the new magnetic behaviour of the ensemble and may cause spin reorientation. The Fe³⁺ and Ni³⁺ states may lead to new magnetic interactions between each other due to the interplay with the intrinsic magnetic behavior of the rare earth sublattices at low temperatures.

NdFeO₃ (NFO) and NdNiO₃ (NNO) are two end members of RTMO family conform to orthorhombically distorted perovskite structure with D¹⁶_2h–Pbnm space group possessing four formula units per elementary cell.^18,19 NFO in which Fe is in +3 valence state and prefers high spin state (3d⁵:t³_2ge²_g). It is insulator at room temperature and contains three different elemental exchange interactions. The Fe–Fe superexchange interaction is strong one that causes long range AFM ordering below T_N = 690 K.²⁰ Nd–Fe is intermediate interaction results in spin-reorientation transition (SRT)²¹ and polarization of Nd³⁺ ion moments below 25 K.¹¹ Nd–Nd interactions is the weakest of all the three, instigates long range AFM ordering of Nd³⁺ magnetic moments at 1.5 K.²² NNO in which Ni is in +3 valence state and prefers low spin state (3d⁷:t⁶_2ge¹_g)²³ in contrast to NFO is metallic at room temperature. It undergoes metal–insulator transition (T_MI) and antiferromagnetic–paramagnetic transition (T_N, called Neel temperature) at the same temperature of 200 K (T_MI = T_N = 200 K)^24,25 and exhibits metal–semiconductor transition at 130 K.²⁶ However, below T_MI NNO is considered to be band insulator with a charge ordered ground state.²⁷ The ordering of Ni moments takes place in such a way so that in quadrupled magnetic unit cell (includes 6-Ni ions) each Ni ion coupled ferromagnetically to three nearest neighbors and antiferromagnetically to the other three.^28–30 Magnetic ordering of Nd³⁺ ions take place in the NNO around 0.77 K.²⁴ Thus NFO and NNO are electrically and magnetically different species of same family. The coalescence of NFO and NNO develops a new hybrid compound with distinctive and interesting electric and magnetic regimes around spin reversal spin reorientation and other magnetic anomalies.

Nd orthoferrite possesses orthorhombically distorted type perovskite type structure with Pbnm space group. In this ferrite there are three major magnetic interactions: Fe–Fe, Nd–Fe and Nd–Nd.¹⁸ These competing exchange interactions determine their fascinating magnetic properties and lead to a numerous applications. Mossbauer studies of the RNi_0.98Fe_0.02O₃ (R = Lu, Y, Tl) where 2 percent Fe is substituted at Ni site have provided independent evidence for the presence of two different Ni sites.³¹ The spin reorientation phenomenon has been observed in various Nd–Fe-based compounds including intermetallic compounds such as Nd₂Fe₁₄B,³² NdDyFe₁₄B³³ and NFO.³⁴

Present study focuses on the electronic, electrical and magnetic structures of NFO and NdFe_0.5Ni_0.5O₃ (NFNO). Nd³⁺ ion subsystem is paramagnetic with small m and Fe³⁺ion subsystem is antiferromagnetic with small F due to spin canting with an angle of 2.8 mrad below T_N.^35,36 So one expects a spin-glass-like behavior of NFO below T_N and observe how this behavior evolves in NFNO when it is replaced half of Fe by Ni ions in the unit cell. It also focuses to explore the spin reversal, spin reorientation, magnetic intersection and other anomalies and the phenomenon arise in behavior of NFO and the effect of 50 percent Ni substitution at Fe-site over the anomalies and investigate corresponding electrical transport and thermal properties which are scarcely found in literature. In this study, we also attempt to highlight the room temperature electronic structure and the correlation between electronic structure, electric, magnetic and thermal properties of NFO and NFNO orthoferrites which may provide some new information and further understanding of underlying physical mechanism.

2. Experimental details

Polycrystalline samples of NFO and NFNO were synthesized by standard solid state reaction technique using the stoichiometric amounts of high purity (>99.99%) compounds of Nd₂O₃, Fe₂O₃ and NiO obtained from Sigma Aldrich.³⁷ All chemicals were mixed in high purity acetone and ground in an agate mortar to get a homogenous mixture. This mixture was heated at 900 °C for 12 h. Heating and cooling rates for samples in programmable furnace were maintained at 4 °C min⁻¹ during sintering at all temperatures. The mixture was again ground thoroughly and heated at 1200 °C for 12 h. After this heat treatment, disc-shaped pellets of 10 mm diameter and 2 mm thickness from the mixed powder were prepared in a cylindrical die under a pressure of 5 tons per inch² using hydraulic press. These were then finally sintered at 1300 °C for 24 h. The phase purity of sintered pellets was studied at room temperature using Bruker D8 X-ray diffractometer with Cu Kα radiation for 20 ≤ 2θ ≤ 80 degrees with a scanning step of 0.02. The Mössbauer spectra were analysed by least-squares fitting using the NORMOS/SITE program developed by Brand.³⁸ Temperature dependent resistivity was measured from 5–300 K temperature using two probe resistivity method with a Keithley 6430 Sourcemeter and LakeShore 340 temperature controller. Magnetization and specific heat measurements were carried out in the temperature range of 1.8–300 K using a physical property measurement system (Quantum design, Model-6000). The zero-field cooling (ZFC) and field cooling (FC) curves were performed under an applied field of 500 Oe and 10 kOe. Magnetic field hysteresis loops were traced at specific temperatures between 5 K and 300 K. All these magnetic and electrical measurements were done at IUC, Indore.

3. Results and discussion

3.1. Structural studies

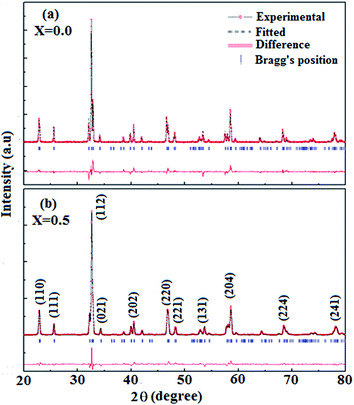
The type of crystal structure and phase formation of NFO and NFNO oxides were investigated using the X-ray diffraction studies. Analysis of XRD pattern for both these compounds was performed with Rietveld refinement using FULLPROF code. Fig. 1(a) and (b) show the fitted Rietveld refined pattern for these oxides and are in good agreement with the calculated profile with the goodness of fit χ² ≈ 1.05 and 1.10. The ‘goodness of fit’ parameter of samples represent better fitting with the reference model. It suggests that the NFNO contains no impurity phases and possesses orthorhombic structure with Pbnm space group. It also shows that there is no symmetry breaking in the perovskite structure of NFO even when a fifty percentage of Fe ions are replaced by Ni. However, a decrease in unit cell volume is found in NFNO due to Ni doping at Fe-site. Lattice parameters, unit cell volume and other structural parameters like the pattern R factor (R_p) and weighted pattern R factor (R_wp) are listed in Table 1. The decrease in unit cell volume may possibly be due to presence of Ni in +3 valence state which possess small ionic radii compared to ionic radii of Fe³⁺.³⁹ The same charge state of ions in NFO is consistent with reported ones.⁴⁰ A small shift in peaks towards higher 2θ values has been observed which depicts the contraction of lattice responsible for distortion of Fe/NiO₆ octahedra. The presence of all elements corresponding to pristine sample, NFO shows Nd, Fe and O and to Ni doped samples, NFNO shows Nd, Fe, Ni and O are confirmed from EDX pattern as shown in Fig. 2.

Fig. 1 Rietveld refined XRD pattern of (a) NFO and (b) NFNO.

Table 1 Orthorhombic structural parameters obtained from XRD analysis

System	a (Å)	b (Å)	c (Å)	V (Å)^3 unit cell volume	χ^2	Rp	Rwp
NFO	5.4438	5.5788	7.7514	235.408	1.05	8.37	8.82
NFNO	5.4303	5.5237	7.7158	231.438	1.10	8.50	9.39

---

Fig. 2 EDX of (a) NFO and (b) NFNO.

3.2. Mössbauer studies

To account for local environment of Fe ions and electronic phenomenon involved in the bulk samples the Mössbauer spectra of NFO and NFNO samples is carried out. Fig. 3 shows the room temperature Mössbauer spectra of NFO and NFNO samples, in the absence of the magnetic field. The Mössbauer spectra of ⁵⁷Fe probe reflect the structural and the chemical factors which help in characterizing both their local environment and electronic phenomena as well involved in the bulk. All these orthoferrites under Mössbauer studies yield simple Zeeman split sextet below the T_N and an unsplit line above T_N in agreement with the existence of only one type of crystallographic site of Fe.⁴¹ The Mössbauer spectrum of NFO shows a simple 6-line spectra (sextet), whereas in the spectrum of NFNO the 6-line split disappears and is fitted only with a single quadrupole doublet which reveals the paramagnetic behaviour. The values of parameters measured by the Mössbauer effect are given in the Table 2. In perovskite NFO, Fe sub lattice is almost simple cubic therefore the replacement of B-site Fe by Ni decreases the total number of Fe–O–Fe exchange channels. On 50 percent Ni substitutions at Fe-sites of NFO, isomer shift (IS) in NFNO shows almost of one-third of a decrease. Generally, IS is negatively proportional to the s-electron density ρ_s(0) at the nucleus therefore the decrease in IS in NFNO is simply suggestive of a decrease in volume with Ni substitution. The decrease in volume with Ni substitution is in agreement with results obtained from XRD analysis. Taking into consideration the +3 state of Fe, the IS values can be influenced due to chemical factor corresponding to the covalency of Fe³⁺–O bond, which depends upon the inductive effect of Ni³⁺–O bond and a geometric factor, which depends on Fe³⁺–O and Ni³⁺–O bond distances. The ρ_s(0) at the Fe nucleus can develop a significant change due to the mechanism called overlap distortion effect where the Fe inner ns-shells (n = 1–3) overlap with O-2p_σ wave functions. It is due to this overlap distortion effect where the Pauli exclusion principle forces the electrons to keep out of the overlap region to enhance ρ_s(0) value and thus reduces the IS value. In NFNO, the Fe–O distance decreases and the overlap distortion effect plays the role in the reduction of the IS value. Besides the decrease in IS value due to overlap distortion effect, an increase of Ni 3d and 4s orbitals population also influences on the IS value in the opposite direction.⁴² The quadrupole splitting (QS) value (−0.005) calculated for NFO is similar to the value calculated earlier by Eibschutz et al.⁴¹ However, QS value increases in NFNO. Breakdown of magnetically ordered state to paramagnetic state from NFO to NFNO evidences that the magnetic transition is connected with a substantial change in the electronic structures of these oxides. Based on spin cross over model, it can be inferred that the spectra in this range present the features of charge transfer, charge fluctuations and also possibly as a precursor to closure of the ligand–metal interband gap. The charge fluctuations of the type dⁿ → dⁿ⁺¹L take place, where n = 5 and L is the hole in O 2p band. So the charge fluctuations occur between the Fe-sites of low spin (LS) ferric like (d⁵) and LS ferrous like (d⁶). This valence equilibrium condition is supposed to stem from a small charge transfer (CT) gap Δ = K_BT. The CT gap lowers if there is an increase in both the O-2p and Fe-3d (Hubbard) bandwidths. So, Ni ion induced decrease of inter atomic distances of Fe–O ions due to smaller ionic radii of Ni or changes in the super exchanges angle is expected to lead to a reduction of CT gap. The higher value of QS in Ni doped NFNO are due to d⁵ electronic configuration which has one unpaired electron in the t_2g level. Therefore the factors which are responsible for transition from the magnetic to paramagnetic state include volume reduction, super-exchange angle and above all the spin crossover. This result of magnetic transition will be further put to test in magnetization variation with applied field measurements discussed in the next section of this paper.

Fig. 3 ⁵⁷Fe Mössbauer spectra of NFO and NFNO recorded at room temperature in the absence of magnetic field showing magnetic transitions.

Table 2 Parameters fitted in Mössbauer spectra of NFO and NFNO

System	Spectrum fit.	IS (mm s^−1)	QS (mm s^−1)
NFO	Sextet	0.3900	−0.00522
NFNO	Paramagnetic doublet	0.1385	−0.5014

---

3.3. Magnetic measurements

The temperature dependence of the magnetic behavior observed from ZFC and FC curves for NFO and NFNO compounds under an applied magnetic field of 10 kOe is shown in Fig. 4(a) and (b). It has been found that these compounds obey Curie–Weiss law χ = C/(T − θ), where C is Curie constant and θ is Weiss constant, below the Neel temperature (T_N), while above T_N the sample behaves like a normal paramagnet obeying the Curie law.⁴³ So the essential feature is the Curie–Weiss contribution of the paramagnetic component is due the Nd ions. At higher magnetic fields (10 kOe) the paramagnetic contribution of Nd ions becomes prominent and both ZFC and FC curves merge and are almost reversible. However, an increase in magnetization is observed at low temperatures in both the compounds, which are exhibiting weak FM behavior within AFM exchange interaction. It may be noted that there is almost no trace of bifurcation between ZFC and FC curves at high and low temperatures. However, from the insets of Fig. 4(a) and (b), these curves are slightly separated out from each other over the temperature range from 10–40 K for NFO and 20–75 K for NFNO. This bifurcation may be the representation of magnetically disordered state (MDS) or spin-glass like behavior resulted from the heterogeneous mixture of F and AF order instead of individual F or AF order. Similar interpretation was reported for Pr based orthoferrites.⁴⁴ The MDS in the NFO happens in between polarization temperature of Nd³⁺ ions and spin reorientation transition (SRT) of NFO. The disordered state stays over wide temperature range in NFNO compared to NFO and is attributed to the size disorder introduced by substitution of Ni in place of Fe ions and formation of intricate interaction between Ni³⁺ and Nd³⁺ ions. The mismatch of ionic radii of Fe/Ni ions causes distortion in Fe/NiO₆ octahedra which results in uncompensated magnetic moment at two magnetic sublattices in NFNO. The possible reason may be due a decrease in magnetic moment of NFNO. ZFC and FC cycles of NFO and NFNO under an applied magnetic field of 500 Oe are shown in Fig. 4(c) and (d). There is strong divergence of ZFC and FC branches and existence of MDS or spin-glass like behavior. The behaviour of ZFC branch observed in M-T measurement is entirely inverse to FC branch and develop mirror image and produce thermal hysteresis below 40 K and 75 K for NFO and NFNO respectively. This type of thermal hysteresis possibly signify a first-order phase transition.^45,46 At lower fields, the paramagnetic component due to Nd ions is relatively less predominant and is seen only in the ZFC curve. At low magnetic field (500 Oe), the ZFC and FC branches intersect at low temperatures and are observed at temperature (intersecting temperature, T_X) of 8.75 K and 17.05 K for NFO and NFNO respectively. Below T_X magnetization is negative. Under low magnetic field (500 Oe) at T_X ZFC and FC branches meet at a single point. It is that point where spins loss their sense to the external applied field. T_X increases in the Ni substituted sample and is related with the impact of paramagnetic Nd³⁺ ions, whose magnitude becomes more prominent at lower temperatures. FC curve crosses the M = 0 axis at temperature (crossing temperature, T₊) 4.7 K for NFO and 5.2 K for NFNO. At temperatures just above T₊, curves almost intersect with each other but do not cross. The magnetization peaks happens at 42 K in NFO and at 44 K in NFNO where one expect strong ferromagnetic response of both the compounds. Fig. 5(a–c) shows the magnetization loops at 5 K, 50 K and 300 K for NFO and NFNO. These temperatures were chosen based on their magnetic responses. At 300 K, the FM component is increased within antiferromagnetic (AFM) exchange interaction and coercive field (H_c) of NFO is maximum reaches to a value of 3004 Oe. At 50 K, these compounds exhibit MDS the H_c of NFO attains a value of 1428 Oe. At low temperature (5 K) H_c (307 Oe) of NFO decreases rapidly due to sufficiently large susceptibility of Nd (χ_Nd(T) ∼ 1/T) until magnetization becomes fully reversible in the paramagnetic state, the total moment of the material reverse its sign (spin reversal) and is in consistence with results shown in Fig. 4. For comparison purpose, the coercivity and retentivity of NFO and NFNO are given in Table 3. From M-H behavior of these materials we conclude that these involve a transition of unsaturated FM state at room temperature to paramagnetic state at lower temperature (5 K). Also, Ni substitution at Fe-site provide a means to mold the magnetic behavior with a transition of magnetic properties.

Fig. 4 Magnetization variation with temperature of (a) NFO at 10 kOe, (b) NFNO at 10 kOe, (c) NFO at 500 Oe and (d) NFNO at 500 Oe. The inset shows the temperature dependence of separated part of ZFC and FC in (a) NFO and (b) NFNO. Inverse susceptibility variation with temperature of (e) NFO at 10 kOe, (f) NFNO at 10 kOe.

Fig. 5 Magnetization variation with applied field of NFO and NFNO samples taken at (a) 300 K, (b) 50 K and (c) 5 K.

Table 3 Magnetic parameters obtained from magnetization measurements shown in Fig. 5. The Curie–Weiss constant (θ) and total effective magnetic moment (μ_eff) obtained from χ⁻¹ vs. T plots shown in Fig. 5(e) and (f)

System	5 K		50 K		300 K		θ (K)	μeff (μB)
	Coercitivity (Oe)	Retentivity (emu g^−1)	Coercitivity (Oe)	Retentivity (emu g^−1)	Coercitivity (Oe)	Retentivity (emu g^−1)
NFO	−307.367	0.719	−1428.981	0.347	−3004.624	0.381	−374	5.347
NFNO	−617.053	0.716	−1847.718	0.196	−3725.946	0.213	−301	5.050

---

Fig. 4(e) and (f) shows the inverse susceptibility as a function of temperature obtained for NFO and NFNO samples respectively. The Curie–Weiss constant θ is obtained as the intersecting point of extrapolation of high temperature region of χ⁻¹ vs. T plots. The value of θ is −374 K for NFO and −301 K for NFNO. The decrease in θ with Ni substitution represents the fall in negative molecular field with the decrease in AFM frustration. The AFM frustration gives rise to weak ferromagnetic component which arises from the canted-AFM spin arrangement of Fe³⁺ magnetic moments in the transition metal ion magnetic sub lattice.⁴⁷ The hysteresis loops shown in Fig. 5 also show that the materials are in weak ferromagnetic state and magnetization is gradually decreasing with the enhancement of Ni substitution, whereas magnetic anisotropy is reduced substantially. From these observations, one can infer that these systems show potential for spin driven devices. From the results of linear fitting of χ⁻¹ vs. T curves total effective magnetic moment (μ_eff) in NFO and NFNO are calculated to be 5.347μ_B for NFO and 5.054μ_B. The calculated values of μ_eff deduce that Fe ions are in +3 high spin state whereas Ni ions are presumed to be in +3 low spin state. This is also confirmed from the XRD studies of NFO and NFNO.

The magnetic behavior of these oxides can be understood in analogy to a classical ferrimagnetic system which contains two networks (rare-earth and transition-metal sub-lattices) coupled antiferromagnetically and possessing uncompensated magnetic moments. The only difference with these systems is that, out of two networks, one of the networks is composed of paramagnetic spins with 1/T type Curie–Weiss thermal dependence. Therefore, with varying temperature there is competition between two networks, reaching a point where the magnetic moments cross M = 0 axis and are fully compensated. This becomes negative if the magnetic moment of rare-earth is sufficiently large compared to transition-metal (TM) moments. According to this model, these systems are composed of Fe/Ni ferromagnetic sub lattice and a negatively polarized Nd sub lattice. After ZFC process, on warming, Nd based sub lattice behaves as a canted structured system. During this procedure Nd moments mostly experiences the effect of external field and obey Curie–Weiss law. During FC process, Fe/Ni moments will order ferromagnetically, escalating the local field at the Nd-sites. Based on mean-field approximation, the magnetic moment of Nd (M_Nd) is proportional to the local field developed by the moments of Fe/Ni. Under such magnetic environment the total magnetization (M_T) of the samples is sum of the magnetizations contributed by Fe/Ni sub lattice (M_Fe+Ni) and Nd sub lattice (M_Nd)

M_T = M_Nd + (M_Fe+Ni) = −Jχ_Nd(M_Fe+Ni) + (M_Fe+Ni)

M_T = (1 − δχ_Nd)(M_Fe+Ni),

where J is a negative interaction between sublattices and ä takes into account sign and magnitude of the magnetic interaction between sublattices. From this relationship, one can see that becomes sufficiently large at low temperatures and the total magnetic moment reverse its sign (magnetic inversion). Thus one may construe from the model developed above that three components are required to explain this spin reversal. Firstly, the TM sublattice should be considered as frozen ferromagnetic state below ordering temperature (above which it will produce local field over Nd moments). Secondly, R sublattice should be considered paramagnetic with 1/T type magnetization. Finally, both R and TM sublattices should be considered as negatively polarized coupled through negative exchange interaction (J < 0).

The jump in the magnetization branches at high field and intersection at low field are the two magnetic anomalies encountered in both NFO and NFNO. This seems to be dynamical phenomenon and deserve some attention as it all happens in the magnetic surrounding of magnetic inversion. At first sight, it appears to depend on the sweep rate of the magnetic field. This kind of dependence is comprehensively described for some manganite perovskite systems and intermetallic germanide in literature.^48–52 Nevertheless, both these anomalies erupt out from the subtle equilibrium between the magnetic moments of Nd³⁺, Fe³⁺, and Ni³⁺ ions. Such kind of anomalies are also present in the high magnetic field (10 kOe) data of Pr based orthoferrites published elsewhere.⁵³ Magnetization jump at low temperatures in high magnetic field (10 kOe) and reduction of difference between ZFC and FC in case of NFO and NFNO possibly be due to breakdown of AFM ordering and the system becomes paramagnetic at low temperature. At low fields (500 Oe), the maximum FC magnetic moment of NFO sample in the MDS is 0.34 emu g⁻¹ at 44 K and at high fields (10 kOe) it is 2.59 emu g⁻¹ at 10 K. In case of NFNO, the maximum of FC magnetic moment in MDS is 0.12 emu g⁻¹ occurs at 44 K at low fields and at high field it is 0.16 emu g⁻¹ at 19 K. So, when the magnetic field is increased to 10 kOe, the magnetic moment increases but the transition temperature decreases and the AFM ordering is broken and system behavior becomes paramagnetic. However, on introduction of Ni, the NFNO magnetic moment is decreased. It is expected as the spin-only magnetic moments of Ni³⁺(1.73μ_B) is less compared to Fe³⁺(5.92μ_B) and are consistent with XRD results. Secondly, to address magnetization intersection anomaly, one need to consider the isotropic, the antisymmetric, and the anisotropic–symmetric exchange interactions between different types of magnetic entities, Nd³⁺–Fe³⁺ and Fe³⁺–Fe³⁺ as outlined in above sections.

During M-T measurement in FC cycle, the negative magnetization below T₊ is possibly due to the paramagnetic effect of Nd ions whose magnetic moments are spaced in opposite direction to that of canted Fe/Ni ones. Primarily, under low applied field (500 Oe) the magnetic moments of Nd³⁺ ions are AF coupled with canted F moments of Fe³⁺/Ni³⁺ and as the temperature decreases the Nd³⁺ magnetic moments are more and more aligned in the internal field of Fe³⁺/Ni³⁺ moments till a point on temperature scale reaches where total magnetic moment of system compensates (M = 0). Above this point of temperature scale, further alignment of Nd³⁺ magnetic moments (Nd-sublattice) exceeds the canted F component of Fe³⁺/Ni³⁺ ions (Fe/Ni-sublattice) yielding a negative magnetization (spin reversal) [Fig. 2(c) and (d)]. However, during ZFC cycle measurement done in warming process, polarization of Nd³⁺ ions produce a local field over Fe³⁺/Ni³⁺ ions and is just opposite to what happened in FC measurements. Therefore ZFC branch traverse almost a mirror image to FC branch during M-T measurements along x-axis under low applied fields. Secondly, under high external field (10 kOe) the local field from Fe³⁺/Ni³⁺ sub-lattice is vanished which prevent the opposite alignment of Nd³⁺ moments with respect to the weak canted F component of Fe³⁺/Ni³⁺and therefore, no negative magnetic moment is noticed [see Fig. 4(a) and (b)]. Indeed a large increase of magnetization begins to develop with a decreasing temperature.

From the offered magnetic behavior, we conclude that the presented materials represent spin reversal and may undergo the spin reorientation that will be further discussed in the specific heat studies section of this paper.

3.4. Electrical transport measurements

The dc electrical resistivity of NFNO samples were measured as a function of temperature (2–300 K) and is shown in Fig. 6(a). Since NFO exhibited highly resistive behavior, 30% Ni doped NFO was selected, (referred as NF3NO) merely for confirmation and comparison of its resistive variations as a function of temperature with NFNO system. A metal–semiconductor transition was found in the measured temperature range. The transition temperature is 56 K for NF3NO and 40 K for NFNO [see the inset of Fig. 6(a)]. Another electrical transition is seen at 108 K in case of NF3NO and at 93 K in case of NFNO system. So the resistivity of NFNO compound is very high over the temperature range from 40–93 K and for NFNO it is from 55–108 K. One can note that the temperature range for NFNO converge with its MDS. Thus, a possible reason for high resistance over this temperature range might be a magnetic disorder. The resistivity of NF3NO is 600 mΩ cm and of NFNO is 50 mΩ cm near room temperature.

Fig. 6 Resistivity variations of NFNO and NFNO' with temperature (a) resistivity as a function of temperature (b) fitting by Arrhenius model (c) fitting by Mott's 3D VRH model. Inset in (a) shows temperature dependent resistivity.

To examine the thermal conduction of the samples, a fit of the temperature dependence of electrical resistivity (ρ) by Arrhenius equation ρ = ρ₀ exp(W/kT), where, ρ₀ is pre-exponential factor, k is Boltzmann constant, W is thermal activation energy at high temperatures and T is absolute temperature.^54,55 A charge carrier (electron/hole) moves from one localized state to another localized state due to exchange energy between the charge carrier and phonon. The electrical resistivity versus inverse of temperature of both NFNO and NF3NO are shown in Fig. 6(b). From this plot one can observe that the data does not display linear behavior at higher temperatures. Nevertheless, one can estimate the values of activation energy over the temperature range where data fits well with the above model. Above model is not suitable to explain electric transport at higher temperatures.

Since, these compounds show semiconducting behavior at higher temperatures, so one can further examine the conduction mechanism by fitting the temperature dependent electrical resistivity by Mott variable range hopping (VRH) model^54–57 as:

ρ = ρ₀ exp(T₀/T)^1/4

where, T₀ is Mott's characteristic temperature. The electrical resistivity of the samples is plotted as ln ρ versus (T)^−1/4 in Fig. 4(c). The data of NFNO fits well both at lower and higher temperatures. This suggests charge carriers (electrons and holes) can move through localized states due to tunneling processes stimulated by phonons possible even at low temperatures. The density of states (DOS) available, N(E) clearly favors the hopping conductivity as it increases the probability to hop from one to another site. However, for NFNO electrical resistivity data deviates around 66 K which possibly due to onset of some magnetic ordering. The relationship among T₀, N(E) and α (inverse of localization length) is given⁵⁸ as:

T₀ of NF3NO is nearly twice of NFNO (see Table 2) which may be due to slight variations of N(E). The mean hopping distance R_h(T) and hopping energy E_h(T) are given⁵⁹ as;

The values of R_h(T) and E_h(T) have been calculated for NFNO and NF3NO and are given in Table 4. It is also observed higher N(E) and lower R_h and E_h of NFNO at room temperature compared to NF3NO. Because conductivity is proportional to hopping distance and enhanced charge carriers concentration at Fermi level and hence improved electrical conductivity^59,60 and the values of activation energy supports the hoping conductivity in both the samples. Debye characteristic temperature (θ_D) is twice of temperature at which versus (1/T) plot just deviates from linearity. In our case θ_D (see Table 4) of NFNO is greater than NF3NO. From the same plot we have also estimated optical phonon frequency, ν_ph = kθ_D/h (h is plancks constant) and is higher for NFNO than NF3NO and similar is the case with activation energy (W). It suggests that incorporation of Ni at Fe site by 50 percent or less in NFO sample tends to delocalize the charge carriers and enhance the electrical conductivity.

Table 4 Physical parameters of NdFe_0.7Ni_0.3O₃ and NdFe_0.5Ni_0.5O₃ obtained from resistivity measurements

System	θD (K)	W (meV)	νph (Hz)	T0 (K)	N(E) (eV^−1 cm^−3)	Rh (Å)	Eh (meV)
NF3NO	328.306	115.398	6.840 × 10^12	26.649 × 10^7	8.601 × 10^18	51.806	198.404
NFNO	279.016	100.179	5.813 × 10^12	14.415 × 10^7	15.901 × 10^18	44.429	170.159

---

In Fig. 6(b), one of the important features emerges out is that the plot consists of two straight line portions, hence there are two activation energies for the two regions. The possible reason behind the change in the slope may be due to the Neel temperatures⁶¹ or to the alteration in the conductivity mechanism⁶² due to different kind of magnetic ordering. The same is reported here⁶³ for cobalt ferrialuminates. This kind of anomaly believably supports the effect of magnetic ordering upon the conduction process. So, the curves exhibit two slopes with a transition may correspond to occurrence of SRT. It occurs in NFNO and NF3NO at, respectively, 101 K and 117 K. It proposes that the Ni placement at Fe-site in NFO bring SRT to lower value on temperature scale. One of the possible reasons may be the lower magnetic moment of Ni³⁺ ion compared to Fe³⁺ ion. The Ni³⁺ placement at Fe-site in NFO will reduce the contribution of Fe³⁺ to magnetic interaction in NFNO and NFN3O samples. The magnetic exchange interaction of Fe–Nd is weaker in NFNO compared to NF3NO and similarly in NF3NO compared to NFO. Thus, it results in SRT at lower temperature in NFNO than NF3NO. Similar interpretation is lent by Y. Du. et al. for DyFeO₃ where Dy³⁺ion is replaced by zero magnetic moment La³⁺ion.⁶⁴

Fig. 6(a) (see inset) envisions the higher resistive regime of NFNO between 14.73 K and 95.17 K and of NF3NO in the temperature range of 56.51–108.73 K. It is pertinent to realize that the MDS of NFNO sample stays over the temperature range from 20–75 K which lies well within the high resistive regime of the sample. Thus, a high resistive regime might be commenced from MSD.

The dc resistivity of NdFeO₃ as a function of temperature (figure not shown) was measured using high resistance measurement set up with Keithley Electrometer (6517B). It exhibited semiconductive behavior and there was no metal–semiconductor transition.

3.5. Specific heat studies

In order to study the thermal anomalies driven by spin reversal in NFO and NFNO, zero field specific heat data C(T) for these samples in the temperature range 1.8–300 K have been carried out. The results are shown in Fig. 7(a) and (b). Near 1.8 K and at 3.4 K there is a peak of C_p called Schottky anomaly for NFO and NFNO respectively (see upper left inset of Fig. 5(a) and (b) for 0 T). It is known that Schottky anomaly in the heat capacity of rare-earth compounds is due to the anisotropy (including crystal field and molecular field generated by Fe³⁺/Ni³⁺sublattice) splitting of lowest J-term (⁴I_9/2) of Nd³⁺ (ref. 65) paramagnetic ions by internal and external magnetic fields. At low temperatures, 3.4 K, for NFNO, it is induced by antiferromagnetic ordering of Nd³⁺ moments. Above which NFNO is paramagnetic in the M-T curves. Near 12 K, there is a specific heat minimum (0.796 J mol⁻¹ K⁻¹) for NFO due to the interaction between Nd³⁺ and Fe³⁺ ions similar to one reported for Er and Tm ortho-ferrites⁶⁶ and to the paramagnetic Nd³⁺ ions. However, specific heat minimum (1.540 J mol⁻¹ K⁻¹) occurs at 13 K in case of NFNO may be due to the introduction of new weak Nd³⁺–Ni³⁺ type of interactions confirmed by Mössbauer studies. The higher value (2 fold increase) of the minimum specific heat in case of NFNO compared to NFO may possibly be due to its greater molecular weight.

Fig. 7 Specific heat versus temperature (K). Lower inset: zero-field data with the fitting result. Upper inset: specific heat versus temperature at different magnetic fields near Schottky anomaly in (a) NFO and (b) NFNO. Specific heat divided by temperature versus temperature. Inset: specific heat divided by temperature around the spin reorientation temperatures in (c) NFO and (d) NFNO.

A hysteretic magnetization is observed over entire SRT interval (see Fig. 2), which is rarely the case with other pure or doped RFeO₃ systems. The most commonly studied SRT in these systems are the type Γ₄(G_x,F_z) → Γ₂₄(G_xz,F_xz) → Γ₂(G_z,F_x) pictorially shown in the Fig. 8. The C_p(T) in zero field shows a small anomaly in the spin reversal region and is not clearly reflected. But as shown in the inset in Fig. 7(c) and (d), on comparing a zero field C_p/T against temperature, anomaly is clearly seen. It is noted that the anomalies corresponding to the spin reversal region for NFO and NFNO are characterized by a valley instead of peak possibly may be due to magnetic disorder. In case of NFO and NFNO, SRT is observed between 100 (T₁) and 200 K (T₂) [see insets of Fig. 7(c) and (d)], with the gradual transition of the Fe^3+/Ni³⁺ magnetic moment ordering from (G_x,F_z)-type of ordering at high temperatures to (G_z,F_x)-type ordering at low temperatures via (G_xz,F_xz)-type ordering at intermediate temperatures. The SRT observed in electrical transport measurements for NFNO is at 101 K which is close to T₁ and may possibly represent Γ₂(G_z,F_x) magnetic ordering.

Fig. 8 The elementary cell of an orthorhombic orthoferrite showing ideal positions of Fe or Ni ions, replaced by Fe (filled green circles), Nd ions (filled black circles), and their spin directions for T < T₁ where M_Nd > M_Fe/Ni (Γ₂), T < T₁ where M_Nd < M_Fe/Ni (Γ₂), T₁ < T < T₂ (Γ₂₄), and T < T₂ (Γ₄).

The bump in the low temperature specific heat data for NFO and NFNO is the dominant feature in the measurement. This is attributed to the Schottky anomaly due to paramagnetic behavior of Nd³⁺ ions and this needs further attention. Taking into account of both the lattice (phononic) contribution and a simple Schottky effect for a two level system, one can fit the zero field data not only to the standard phonon nature but to the equation:^67–69

where β, β₅, and β₇ are the phononic specific heat parameters using the low frequency expansion of Debye function C_p(T) = βT³ + β₅T⁵ + β₇T⁷,⁵⁶ N/R is the number of free spins with R the universal gas constant. Δ = gμ_BH is the gap value for Zeeman splitting of Nd³⁺ doublet.^54–56 H is the total effective field plus the exchange interaction field of the compound. The two level Schottky fitting for zero field C(T) is shown in the lower insets in Fig. 7(a) and (b). The fit of NFO is nearly perfect with the parameters β = 1.11 × 10⁻⁴ J mol⁻¹ K⁻⁴, β₅ = −2.32 × 10⁻⁹ J mol⁻¹ K⁻⁶, β₇ = 1.96 × 10⁻¹⁴ J mol⁻¹ K⁻⁸, N = 239.58 J mol⁻¹ K⁻¹, Δ = 13.38 meV. For NFNO the parameters β = 1.10 × 10⁻⁴ J mol⁻¹ K⁻⁴, β₅ = −2.30 × 10⁻⁹ J mol⁻¹ K⁻⁶, β₇ = 1.45 × 10⁻¹⁴ J mol⁻¹ K⁻⁸, N = 240.72 J mol⁻¹ K⁻¹, Δ = 16.36 meV. The fitting results point out that magnetic specific heat is mainly from Schottky anomaly of Nd³⁺ that does not form long-range ordered state at low temperatures. The upper left insets of Fig. 7(a) and (b) show C_p against temperature plot at different magnetic fields. From these plots one infers that with an increase in magnetic field the thermal anomaly is gradually reduces and shift towards higher temperatures. It suggests field induced states are more ordered and making entropy to higher temperatures.⁷⁰ These insets further show that specific heat at low temperatures enhances with increasing magnetic field, suggesting Nd³⁺ might undergo a magnetic transition below 1.8 K. Such a transition needs to be ratified. Using the fitting values of zero field C(T) we calculated internal exchange field (H^int) of the compounds and are 115.57 T and 141.31 T for NFO and NFNO respectively. The results (Δ_NFNO > Δ_NFO/H^int_NFNO > H^int_NFO) also evidence the introduction of Ni strongly polarizes the Nd sublattice by Nd–Ni exchange with the symmetry similar to its own magnetic order and thereby reducing the magnetic entropy. However, inelastic neutron scattering and muon-spin-relaxation experimental data is due to accomplish deep understanding of this phenomenology. From the specific heat data, a spin reorientation transition from Γ₄(G_x,F_z) through Γ₂₄(G_xz,F_xz) to Γ₂(G_z,F_x) is observed in the temperature ranges of 100–200 K for NFO and NFNO and the transition is pictorially represented in Fig. 8. On comparing the results obtained from polycrystalline NFO with the single crystal NFO existing in literature^71–74 it is observed that the results are comparable to a good extent. A SRT is observed in a wide temperature range from 100 to 170 K in case of SC NFO and in our case for polycrystalline NFO it is observed in the temperature of 100–200 K. In our case Schottky anomaly in specific heat measurement of polycrystalline NFO is observed at 1.8 K while the same is reported for single crystal NFO at 2.4 K. Near 12 K, we found there is a specific heat minimum (0.796 J mol⁻¹ K⁻¹) for PC NFO and the same is stated in case of single crystal NFO at 15 K. No data on the single crystal of NFNO is available in literature.

4. Conclusion

Rietveld analysis of polycrystalline NFO and NFNO orthoferrites show that both these compounds belong to space group Pbnm. The Ni substitution by 50 percent at Fe-site of NFO changes the ferromagnetic to paramagnetic character. The Mossbauer spectra revealed that the isomer shift show a decrease along with an increase of quadrupole splitting values with Ni substitution at Fe-site due to overlap distortion. The observed magnetization jump at low temperatures and higher fields are due to breakdown of AFM ordering. Ni substitution also leads to decrease in magnetic moment. Magnetization intersection anomaly found in both NFO and NFNO compounds is considered due to the isotropic, the antisymmetric, and the anisotropic–symmetric exchange interactions leading to different magnetic entities in these compounds. From M-H behavior of these materials, a transition of unsaturated FM state at room temperature to paramagnetic state at lower temperature (5 K) is observed. Ni substitution at Fe-site also provides a means to modify the magnetic behavior with a transition of magnetic properties. VRH model fits well at temperatures in and around SRT, magnetic inversion and intersection and suggests that charge carriers move through localized states due to tunneling processes stimulated by phonons. The DOS and activation energy in NFNO favors hopping conductivity. The low temperature specific heat anomaly gradually reduces and shifts towards higher temperatures with increasing applied magnetic field in both these oxides and taking entropy to higher temperatures. It is interesting to observe that the temperature at which anomalies (inversion, intersection and Schottky) took place shifts towards higher temperature when Ni substitution is halved Fe concentration in NFO. In brief, taking into consideration these different anomalies, the Ni substitution at Fe sites of the NFO system, showing a transition of electrical and magnetic properties with a significant modification in thermal properties. These are the essential features in the electric and magnetic devices for technological applications.

Acknowledgements

Authors (S. A. M and M. I) thank Dr Alok Banerjee, and the Director, IUC, CSR-Indore for their support in electrical and magnetic measurements. They acknowledge Dr R. J. Choudhury (IUC, CSR Indore) for research discussion and suggestions and also thank Director, IUAC, New Delhi for necessary experimental facilities and Prof. Rajat Gupta, Director NIT Srinagar for constant encouragement in this research work.

References

1. L. Ju, Z. Chen, L. Fang, W. Dong, F. Zheng and M. Shen, J. Am. Ceram. Soc., 2011, 94, 3418.
2. X. Li and Z. Q. Duan, Mater. Lett., 2012, 89, 262.
3. H. Obayashi, Y. Sakurai and T. Gejo, J. Solid State Chem., 1976, 17, 299.
4. M. Idrees, M. Nadeem, M. Atif, M. Siddique, M. Mehmood and M. M. Hassan, Acta Mater., 2011, 59, 1338.
5. B. Lal, K. K. Bamzai, P. N. Kotru and B. M. Wanklyn, Mater. Chem. Phys., 2004, 85, 353.
6. W. C. Koehler, E. O. Wollan and M. K. Wilkinson, Phys. Rev., 1960, 118, 58.
7. Y. Tokunaga, S. Iguchi, T. Arima and Y. Tokura, Phys. Rev. Lett., 2008, 101, 097205.
8. B. Berini, A. Fouchet, E. Popova, J. Scola, Y. Dumont, N. Franco, R. M. C. da Silva and N. Keller, J. Appl. Phys., 2012, 111, 053923.
9. L. T. Tsymbal, Ya. B. Bazaliy, V. N. Derkachenko, V. I. Kamenev, G. N. Kakazei, F. J. Palomares and P. E. Wigen, J. Appl. Phys., 2007, 101, 123919.
10. A. V. Kimel, A. Kirilyuk, A. Tsvetkov, R. V. Pisarev and T. Rasing, Nature, 2004, 429(6994), 850.
11. J. A. de Jong, A. V. Kimel, R. V. Pisarev, A. Kirilyuk and T. Rasing, Phy. Rev. B, 2011, 84(10), 104421.
12. L. T. Tsymbal, V. I. Kamenev, Ya. B. Bazaliy, D. A. Khara and P. E. Wigen, Phys. Rev. B, 2005, 72, 052413.
13. Ya. B. Bazaliy, L. T. Tsymbal, G. N. Kakazei and P. E. Wigen, J. Appl. Phys., 2004, 95, 6622.
14. La Chen, Tongwei Li, S. Cao, S. Yuan, F. Hong and J. Zhang, J. Appl. Phys., 2012, 111, 103905.
15. B. H. Kim and B. I. Min, Phy. Rev. B, 2008, 77, 094429.
16. L. A. Prelorendjo, C. E. Johnson, M. F. Thomas and B. M. Wanklynz, J. Phys. C: Solid State Phys., 1980, I3, 2567.
17. G. W. Durbin, C. E. Johnson and M. F. Thomas, J. Phys. C: Solid State Phys., 1975, 8, 3051.
18. J. Bartolome, E. Palacios, M. Kuzmin, F. Bartolome, I. Sosnowska, R. Sonntag and M. Lukina, Phys. Rev. B, 1997, 55, 11432.
19. J. S. Zhou and J. B. Goodenough, Phys. Rev. B, 2004, 69, 153105.
20. D. Treves, J. Appl. Phys., 1965, 36, 1033.
21. K. P. Belov, A. M. Kadomtseva, T. L. Ovchnnikowa, V. A. Timofeeva and V. V. Uksov, Phys. Solid State, 1971, 13, 518.
22. R. Prezenioslo, I. Sosnowska, P. Fischer, W. Marti, F. Bartolome, J. Bartolome, E. Palacois and R. Sonntag, J. Magn. Magn. Mater., 1996, 160, 370.
23. X. Granados, J. Fontcuberta, X. Obradors, L. Manosa and J. B. Torrance, Phys. Rev. B, 1993, 48, 11666.
24. F. Bartolome, M. D. Kuzmin, J. Bartolome, J. Blasco, J. Garcia and J. sapina, Solid State Commun., 1994, 91, 177.
25. S. R. Barman, A. Chainani and D. D. Sarma, Phys. Rev. B, 1994, 49, 8475.
26. J. K. Vassiliou, M. Hornbostel, R. P. Ziebarth and F. J. Di Salvo, J. Solid State Chem., 1989, 81, 208.
27. J. L. Garcia-Munoz, M. A. G. Aranda, J. A. Alonso and M. J. Martinez-Lope, Phys. Rev. B, 2009, 79(1-5), 134432.
28. J. L. Garcia-Munoz, J. Rodriguez-Carvajal and P. Lacorre, Europhys. Lett., 1992, 20, 241.
29. S. A. Mir, M. Ikram and K. Asokan, J. Phys.: Conf. Ser., 2014, 534, 012017.
30. T. Mizokawa and A. Fujimori, Phys. Rev. B, 1996, 54, 5368.
31. S. J. Kim, G. Demazeau, A. PresniakovI, K. V. Pokholok, A. V. Baranov, A. V. Sobolev, D. A. Pankratov and N. S. Ovanesyan, Phys. Rev. B, 2002, 66, 014427.
32. C. Abache and H. Oesterreicher, J. Appl. Phys., 1985, 57, 411.
33. W. B. Yelon, B. Foley, C. Abache and H. Oesterreicher, J. Appl. Phys., 1986, 60, 2982.
34. W. P. Wolf, J. Appl. Phys., 1969, 40, 1061.
35. S. Mathur, H. Shen, Nicolas Lecerf, Arne Kjekshus, H. Fjellvag and G. F. Goya, Adv. Mater, 2002, 14, 1405.
36. S. Yuan, Y. Wang, M. Shao, F. Chang, B. Kang, Y. Isikawa and S. Cao, J. Appl. Phys., 2011, 109, 07E141.
37. S. A. Mir, M. Ikram and K. Asokan, Optik, 2014, 125, 6903.
38. R. A. Brand, Laboratorium Fuer Angewandte Physik, ed. Lotharstr, Universitaet Duisburg, Duisburg 1, 1990, vol. 1, p. D4100.
39. R. D. Shannon, Acta Crystallogr., 1976, A32, 751.
40. Abida Bashir, M. Ikram, Ravi Kumar, P. Thakur, K. H. Chae, W. K. Choi and V. R. Reddy, J. Phys.: Condens. Matter, 2009, 21, 325501.
41. M. Eibschutz, S. Shtrikman and D. Treves, Phys. Rev., 1967, 156, 562.
42. B. G. Landa, J. M. de Teresa, M. R. Ibarra, C. Ritter, R. Drost and M. R. Lees, J. Appl. Phys., 1998, 83, 7664.
43. I. Sosnowska and P. Fischa, Amer. Phys. Inst. (API), 1982, 89, 346.
44. A. Bashir, M. Ikram, R. Kumar, P. N. LisboaFilho and P. Thakur, Mater. Sci. Eng., B, 2010, 172, 242.
45. Y. Cao, S. Cao, W. Ren, Z. Feng, S. Yuan, B. Kang, B. Lu and J. Zhang, Appl. Phys. Lett., 2014, 104, 232405.
46. S. J. Yuan, W. Ren, F. Hong, Y. B. Wang, J. C. Zhang, L. Bellaiche, S. X. Cao and G. Cao, Phys. Rev. B, 2013, 87, 184405.
47. B. Andrzej, L. Barbara, M. Jacek and P. Andrzej, J. Magn. Magn. Mater., 2003, 257, 206.
48. V. Hardy, C. Yaicle, S. Hebert, A. Maignan, C. Martin, M. Hervieu and B. Raveau, J. Appl. Phys., 2003, 94, 5316.
49. V. Hardy, A. Maignan, S. Hebert, C. Yaicle, C. Martin, M. Hervieu, M. R. Lees, G. Rowlands, D. Mc. K. Paul and B. Raveau, Phys. Rev. B, 2003, 68, 220402(R).
50. V. Hardy, S. Majumdar, M. R. Lees, D. Mc K. Paul, L. Herve, A. Maignan, S. Hebert, C. Martin, C. Yaicle, M. Hervieu and B. Raveau, Phys. Rev. B, 2004, 69, 020407(R).
51. D. S. Rana, D. G. Kuberker, M. B. Stone, P. Schiffer and S. K. Malik, J. Phys.: Condens. Matter, 2005, 17, 989.
52. E. M. Levin, K. A. Gschneidner Jr and V. K. Pecharsky, Phys. Rev.B, 2002, 65, 214427.
53. A. B. Makhdoomi, M. Ikram and R. kumar, J. Magn. Magn. Mater., 2010, 322, 2581.
54. N. F. Mott, J. Non-Cryst. Solids, 1968, 1, 1.
55. N. F. Mott, Philos. Mag., 1969, 19, 835.
56. I. G. Austin and N. F. Mott, Adv. Phys., 1969, 18, 41.
57. Y. Sun, X. Xu, W. Tong and Y. Zhang, Appl. Phys. Lett., 2000, 78, 643.
58. I. Ahmad, M. J. Akhtar, R. T. A. Khan and M. M. Hassan, J. Appl. Phys., 2013, 114, 034103.
59. M. W. Khan, R. Kumar, R. J. Choudhary, J. P. Srivastava, S. I. Patil and W. K. Choi, J. Phys. D: Appl. Phys., 2008, 41, 175409.
60. M. Viret, L. Ranno and J. M. D. Coey, J. Appl. Phys., 1997, 81, 4964.
61. A. P. Komar, Bull. Russ. Acad. Sci.: Phys., 1954, 18, 122.
62. K. R. Krishna Murthy, PhD Thesis, IIT, Madras, India, 1975.
63. N. H. Vasoya, V. K. Lakhani, P. U. Sharma, K. B. Modi, R. Kumar and H. H. Joshi, J. Phys.: Condens. Matter, 2006, 18, 8063.
64. Y. Du, Z. X. Cheng, X. L. Wang and S. X. Dou, J. Appl. Phys., 2010, 107, 09D908.
65. D. J. Jermano and R. A. Butera, Phy. Rev. B, 1981, 24, 3912.
66. K. Saito, Y. Yamamura, J. Mayer, H. Kobayashi, Y. Miyazaki, J. Ensling, P. Gutlich, B. Lesniewska and M. Sorai, J. Magn. Magn. Mater., 2001, 225, 381.
67. X. M. Wang, Z. Y. Zhao, C. Fan, X. G. Liu, Q. J. Li, F. B. Zhang, L. M. Chen, X. Zhao and X. F. Sun, Phy. Rev. B, 2012, 86(17), 174413.
68. Q. J. Li, Z. Y. Zhao, H. D. Zhou, W. P. Ke, X. M. Wang, C. Fan, X. G. Liu, L. M. Chen, X. Zhao and X. F. Sun, Phy. Rev. B, 2012, 85(17), 174438.
69. S. J. Yuan, Y. M. Cao, L. Li, T. F. Qi, S. X. Cao, J. C. Zhang, L. E. DeLong and G. Cao, J. Appl. Phys., 2013, 114, 113909.
70. A. Bhattacharjee, K. Saito and M. Sorai, J. Phys. Chem. Solids, 2002, 63(4), 569–574.
71. S. Yuan, Y. Wang, M. Shao, F. Chang, B. Kang, Y. Isikawa and S. Cao, J. Appl. Phys., 2011, 109, 07E141.
72. J. Jiang, Z. Jin, G. Song, X. Lin, G. Ma and S. Cao, Appl. Phys. Lett., 2013, 103, 062403.
73. Y. Wang, X. Yan, J. Chen, J. Deng, R. Yu and X. Xing, CrystEngComm, 2014, 16, 858.
74. G. Song, J. Jiang, B. Kang, J. Zhang, Z. Cheng, G. Ma and S. Cao, Solid State Commun., 2015, 211, 47.

---