Near-field electrospinning enhances the energy harvesting of hollow PVDF piezoelectric fibers

Abstract

In this study we used the near-field electrospinning (NFES) process with the metallic coaxial needle injector to fabricate piezoelectric poly(vinylidene fluoride) (PVDF) hollow fiber tubes. Using these tubes, we designed an energy capture device featuring parallel electrodes to harvest low-frequency energy. We examined the effects of several parameters on the properties of the piezoelectric PVDF fiber tubes (PPTs), including the core flow rate, shell flow rate, concentration of PVDF, rotating tangential speed, and electric field. The elongation of the PPTs was greater than that of solid PVDF fibers, with the tensile strength of the PPTs reaching 32.49 MPa (as determined through a micro-tensile measurement). The output voltage of the PPTs was considerably higher (71.66 mV) and, with an external load resistance of 6 MΩ, the output power was also significantly greater (856.07 pW) than the solid PVDF fiber (output voltage = 45.66 mV and the maximum output power = 347.61 pW). As a result, the power generation of the PPTs was 2.46 times higher than that of the solid fibers. Thus, the PPTs not only displayed mechanical stiffness but also produced a greater power output.

---

1. Introduction

Fiber-based piezoelectric energy generators are applied in many electrical devices and systems.^1–5 The useful piezoelectric polymer poly(vinylidene fluoride) (PVDF) has been widely used due to its good thermal properties, high flexibility, and low cost that give PVDF many potential applications for energy conversion including electro-mechanical actuators, microelectric-mechanical devices, and energy harvesters. Four crystalline phases (α, β, γ, and δ) of PVDF semicrytalline polymer have been reported⁶ and the nonpolar α-phase is the most commercially used. Fan et al. used density functional theory to verify the piezoelectric characteristic and relationship of electric field for the α-phase and β-phase of PVDF.^7–9 However, the dipole moments in the α-phase have a random orientation and result in cancelling each other out. In contrast, the β-phase of PVDF polymer possesses dipole moments pointing in the same direction and thus it is useful for piezoelectric applications.^10–13 Many studies have focused on using far-field electrospinning (FFES)¹⁴ and near-field electrospinning (NFES)¹⁵ to improve the piezoelectric properties of PVDF. Although electrospinning has been recognized as an efficient technique for fabricating polymer fibers¹⁶ and was first patented in the US in 1902, this process was largely forgotten until the 1990s.^17,18 With the rapid development of nano-fibers and their applications, electrospinning has become a pioneering technique in this field.¹⁹ Fibers featuring complex architectures, such as fiber tubes, can be produced using special electrospinning methods.^20–22 The diameters and morphologies of electrospun fibers can be controlled by adjusting the molecular weight, the solution properties (such as surface tension, conductivity, and viscosity), the flow rate, the electric potential, and the distance between the needle and the collection plate during electrospinning.^23–25 The development of coaxial electrospinning was one of the most significant breakthroughs in this area.^26–28 Most researchers have been used quite similar to that used previously for electrospinning.²⁹ A heating system is used for coaxial electrospinning to fabricate phase-changed nanofibers through a melt method.³⁰ The much simpler method only slightly different have reported from two separate syringes with differently sized capillaries, with the smaller capillary inserted from outside into a Taylor cone formed at the exit of the larger capillary.³¹ The resulting fibers have found in drug delivery and tissue engineering applications because they allow the controlled release of drugs and growth factors.^32–35

In this paper we present an NFES process using a coaxial needle device, including two precision flow syringe pumps, for the production of piezoelectric PVDF fiber tubes (PPTs). To enhance the stability of the electrospinning process, we optimized the core and shell flow rates, the concentration of PVDF, the collecting tangential speed, and the electric field. Herein, we describe the mechanical and electrical properties of the as-spun PPT.

2. Experimental section

The experimental set-up of the NFES is displayed in Scheme 1; it includes a needle clamping apparatus, two precision flow syringe pumps, a high-voltage power supply, and a fiber collector device. The collector device, with tangential speeds in the range from 942.3 to 1989.3 mm s⁻¹, was mounted on an X–Y platform (ST-9090, Tanlian). The coaxial needle device was connected to the anode of a high-voltage source; the rotation of the collector device was grounded. A high-voltage (8–16 kV) was applied to form a high electric field (from 8 × 10⁶ to 1.6 × 10⁷ V m⁻¹) between the needle and the collector device (the gap between the needle and the collector was set at 1 mm). When the PVDF solution was subjected to the high-voltage electric field, a Taylor cone was formed and then the PPT was spun out.

Scheme 1 Schematic representations of the (a) NFES equipment and (b and c) coaxial needle device used for electrospinning.

2.1 Solution

The concentrations of the ingredients used to form the different PVDF solutions are listed in Table S1.† Dimethyl sulfoxide (DMSO) solvent was used for the PVDF powder (M_w = 534 000) and fluorosurfactant (ZONYL®UR) in acetone was added to improve the evaporation rate and decrease the surface tension of the PVDF solution, respectively. The solution mixture was sealed in the sample container to prohibit any evaporation effect at room temperature.

2.2 Experimental setup

NFES and a coaxial needle were used to produce PPT and solid PVDF fibers. The coaxial needle device was assembled from two coaxial stainless-steel needles, attached to a Teflon tube through which the fluid was pumped. The inner diameter of the outer steel needle was 1.07 mm; the inner diameter of the inner steel needle was 0.63 mm. The coaxial needle device had two injection inlets separately connected to two syringe pumps (KDS-100, Kdscientific). Fig. 1 displays the outer needle filled with PVDF solution for shell formation and the inner needle filled with air for core formation. While the PVDF solution was injected into the outer needle at a flow rate of 3 mL h⁻¹, air was fed into the inner needle at 0–15 mL h⁻¹ at the same time.

Fig. 1 (a and b) Taylor cone of electrospinning. (c–f) SEM images of the cross sections of piezoelectric coaxial fiber tubes of PVDF obtained when the flow rate of the PVDF solution was 3 mL h⁻¹ and the air flow rate was (c) 6, (d) 9, (e) 12, and (f) 15 mL h⁻¹. (g) Diameters of piezoelectric coaxial fiber tubes plotted with respect to the flow rates of the inner and outer needles.

2.3 Properties of PPTs

Flexible poly(ethylene terephthalate) (PET) and copper parallel electrodes were applied to test the PPTs, as displayed in Scheme 2. Approximately 1200 fibers with a stacked area of 15 × 10 mm were placed on the parallel copper electrodes to test displacement. Schematic representations of the vibration measurement systems are provided in Schemes 2(b) and (c). The actual parallel electrode on a flexible PET substrate is displayed in Fig. 2(d). This device was characterized under periodic external strains by using a tapping device (operated at 7 Hz) to deform the flexible PET structure. The mechanical compressive and tensile stress induced the formation of free charges from the piezoelectric fibers. The mechanical strain distributed along the fibers was converted into an alternating voltage and current through the piezoelectric d₃₃ mode. An NI9234 instrument (maximum sampling frequency per channel: 51.2 kS s⁻¹; 24 bit resolution; 102 dB) was used to measure the voltage; a CHI 611D instrument (potential control range: ±10 V; current range: ±250 mA) was used to measure the current.

Scheme 2 (a) Photograph of the vibration measurement system. (b) Schematic representation of the vibration measurement system. (c) Photograph of the parallel-electrodes device. (d) Schematic representation of the parallel-electrodes device.

Fig. 2 Diameters of solid fibers and fiber tubes plotted with respect to the (a) concentration of the PVDF solution, (b) electric field, and (c) tangential velocity of collector device.

3. Results and discussion

3.1 Effect of PPT

The inner and outer needle flow rates in the metallic coaxial needle during NFES were key parameters in this study. During coaxial electrospinning, the inner needle was filled with air (for the fiber cores) and the outer needle was filled with a PVDF solution (for the fiber shells). The shell flow rate had to be controlled accurately to ensure that the core was wrapped in the PVDF fiber. An appropriate ratio of the air flow rate to the flow rate in the outer needle had to be maintained at a certain value to form a stable Taylor cone (Fig. S1†). If the shell flow rate was too low or too high, the electrospinning process would fail (Fig. S1†).

We obtained the PPTs using the following electrospinning parameters: an electric field of 1.2 × 10⁷ V m⁻¹, a concentration of 18 wt%, a rotating tangential velocity of 1570.5 mm s⁻¹, an X–Y stage motion velocity of 50 m s⁻¹, a fixed gap between the needle and collector of 1 mm, a fixed flow rate of the PVDF solution in the outer needle of 3 mL h⁻¹, and air flow rates in inner needle varying from 3 to 15 mL h⁻¹. Fig. 1 displays the cross section of a PPT obtained when the flow rate of air was 3 mL h⁻¹; the outer diameter was 13.18 μm, the inner diameter was 3.26 μm, and the tube wall thickness was 4.96 μm. When the air flow rate increased to 6, 9, 12, and 15 mL h⁻¹, the average outer diameter of the fiber tubes remained constant (ca. 13.16–13.18 μm), while the inner diameter of the fiber increased from 4.17 to 5.16 μm [Fig. 1(g)]. When the air flow rate reached 16 mL h⁻¹, however, the viscosity of the solution was unable to bear the air tension required to maintain the Taylor cone, resulting in interruption of the electrospinning process.

3.2 Parameters affecting the diameters of the fibers

The NFES parameters had a dramatic effect on the fabrication of the PPTs. We examined the effects of the electric field (from 8 × 10⁶ to 1.6 × 10⁷ V m⁻¹), the tangential velocity of the collector (523.6–2618.1 mm s⁻¹), and the concentration of the PVDF solution (15–19 wt%) on the PPT and solid fibers. Fig. 2(a) reveals that the outer diameters of the solid fibers and PPTs decreased upon increasing the concentration of the PVDF solution from 15 to 19 wt%. The concentration of the PVDF solution also influenced its viscosity. A high-concentration PVDF solution was more likely to be affected by charge accumulation, but the Taylor cone could not form when the concentration of PVDF reached 19 wt%, such that the electrospinning process was interrupted. Higher electrostatic fields caused stronger electrostatic forces and the formation of thinner fibers. Fig. 2(b) displays the diameters of the solid fibers and the outer and inner diameters of the PPTs. Upon increasing the electric field, the diameter of the solid fibers decreased from 28.88 to 13.29 μm; for the PPTs, the outer diameter decreased from 25.98 to 10.98 μm and the inner diameter decreased from 16.67 to 2.66 μm. Although these diameters decreased upon increasing the electrical field, short-circuiting occurred when the electric field was too high. Therefore, the electric field had to be controlled to a certain extent. Fig. 2(c) reveals that the diameters of the solid fibers and the outer and inner diameters of the PPTs decreased from 50.16 to 13.07 μm, from 46.22 to 10.68 μm, and from 36.57 to 3.17 μm, respectively, upon increasing the tangential velocity of the collector device from 523.6 to 2018.1 mm s⁻¹. At a greater rotational speed of the collector, the PPTs experienced a greater pull force, resulting in thinner PPTs.

3.3 Characteristics of PPTs

We used a micro tensile testing machine to examine the mechanical characteristics of the solid fibers and PPTs. We prepared test samples of the solid fibers and PPTs by setting the flow rate of the inner needle at 0, 3, 6, 9, 12, and 15 mL h⁻¹. Fig. 3(a) displays a specimen clamped in the micro tensile machine. Fig. 3(b) presents test piece length marks of approximately 15 mm. The tensile rate was set at 0.015 mm s⁻¹; a 250 N load cell was chosen. Fig. 3(c)–(h) display the stress–strain diagrams of the solid fibers and PPTs. When the core rate was 0, 3, 6, 9, 11, and 15 mL h⁻¹, the thickness of the fiber wall was 0 (solid fiber), 4.96, 4.51, 4.32, 4.16, and 4.01 μm, respectively. The ultimate tensile strength arises from the relationship among the stress, axial force, and surface area. The maximum tensile strengths for the samples prepared with core rates of 0, 3, 6, 9, 11, and 15 mL h⁻¹ were 29.06, 32.49, 32.27, 30.09, 28.26, and 17.38 MPa, respectively [Fig. 3(i)]; the Young's moduli ranged from 2.51 to 2.91 GPa. In addition, when the flow rate of the inner needle (core rate) was 3 mm h⁻¹, the ultimate stress of the PPTs was better than that of the solid fibers. When the core rate was greater than 9 mm h⁻¹, however, the ultimate stress was lower than that of the solid fibers, presumably because the walls of the fiber tubes became too thin and the porosity in the PPTs decreased their strength. PVDF has three crystalline phases: α, β, and γ. Its unpolarized phases are the α- and γ-phases; the β-phase is the most important characteristic of a piezoelectric crystal phase. Therefore, PVDF must go through a polarization step to convert its α-phase into the β-phase. Aligned dipole moments in the β-phase direction result in PVDF displaying piezoelectric properties. Therefore, the content of the β-phase represents the piezoelectric strength of PVDF. There are three main crystal orientation angles of the α-phase: 18.4, 20.1, and 26.8°; the main characteristic of the piezoelectric crystal orientation angle for the β-phase is 20.6°. We performed XRD analyses of samples prepared at flow rates of 0, 3, and 15 mL h⁻¹. Fig. S2† displays the intensity of the size of the β-phase arrangement. Our results reveal that significant piezoelectric properties and better crystallization of PVDF fibers occurred when the core and shell rates were both set at 3 mL h⁻¹.

Fig. 3 (a and b) Photographs of (a) PVDF fiber tubes clamped onto a test machine carrier for determining micro-mechanical properties and (b) tensile test samples of PVDF fiber tubes and solid fibers. (c–h) Stress–strain diagrams of PVDF fiber tubes obtained at inner-needle flow rates of (c) 0, (d) 3, (e) 6, (f) 9, (g) 12, and (h) 15 mL h⁻¹. (i) Ultimate stress plotted with respect to the core rate.

Yee et al.³⁶ reported that β-phase possesses mainly well-aligned dipoles which can induce electric potential when mechanical strain rate is applied. However, the dipoles in α-phase are distributed randomly without any alignment orientation. When external strain rate is applied, the induced potential can be cancelled each other. Therefore no obvious power can be harvested. Fig. 7 shows XRD results where the relation between β and α phases of tubular fibers can be seen clearly. It reveals tubular fibers contain stronger β signal than the solid ones. That is why tubular fibers can produce more energy. In addition, the powder-based film was also tested using XRD. No β phase can be observed, which means that this film cannot induce any voltage and energy.

3.4 Energy-harvesting test

We fabricated an energy-harvesting device, measuring 15 × 35 mm² in area, on a flexible substrate. The energy-harvesting device was characterized under periodic external strains by using a tapping rod at 7 Hz. Because the β-phase exhibited better crystallization when the inner and outer flow rates were both 3 mL h⁻¹, we measured the output voltage under different low frequencies, ranging from 4 to 7 Hz. The maximum output voltage was obtained at a frequency of 7 Hz [Fig. 4(a)]. Fig. 4(b) reveals that the output voltage of the PVDF fiber tubes ranged from 56 to 72 mV, with a higher frequency providing a higher voltage output. When the frequency reached 8 Hz, however, the output voltage decreased because the vibration frequency was greater than the response of the PET substrate.

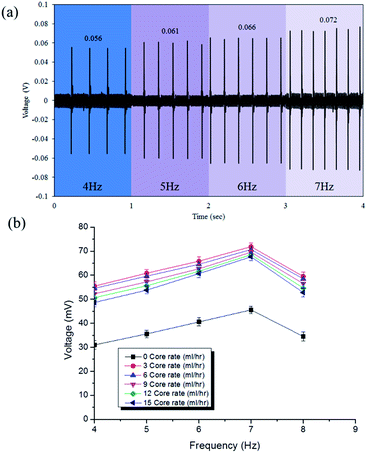Fig. 4 (a) Voltage output diagram of PVDF fiber tubes under frequencies from 4 to 7 Hz; the flow rates of the outer and inner needles were both 3 mL h⁻¹. (b) Voltages of the PVDF solid fibers and fiber tubes plotted with respect to the frequency.

To obtain a better understanding of the energy-harvesting performance of the solid fibers and PPTs, we measured the output voltage, current, and strain of their devices. The maximum peak voltage and current of the solid-fiber energy-harvesting device were 47 mV and 2.73 × 10⁻⁸ A, respectively, under a strain rate of 0.135 s⁻¹ (Fig. 5). The maximum peak voltage and current of the fiber-tube energy-harvesting device were 72 mV and 1.53 × 10⁻⁷ A, respectively, under a strain rate of 0.135 s⁻¹ (Fig. 6).

Fig. 5 (a) Voltage, (b) current, and (c) strain of PVDF solid fibers obtained at a tapping frequency of 7 Hz; the flow rate of the outer needle had been set at 3 mL h⁻¹.

Fig. 6 (a) Voltage, (b) current, and (c) strain of PVDF fiber tubes obtained at a tapping frequency of 7 Hz; the flow rates of the outer and inner needles had both been set at 3 mL h⁻¹.

Fig. 7 XRD analysis of PVDF hollow fibers, PVDF solid fibers and PVDF powder.

Thus, the energy-harvesting efficiency of the PPTs was better than that of the solid fibers. To verify the piezoelectric effect, Fig. 8 displays the effects of positive and negative connections of the electrodes on the voltage of the PVDF solid fibers and PPTs. The piezoelectricity of the PVDF fiber tubes was that of a piezoelectric field (EZ < 0) resulted in the fiber tubes during the tensile strain along the z-axis, and induced a piezopotential (V⁺). When the applied tensile strain was released rapidly, the piezopotential decreased and the local free carriers accumulated at both ends of the nanofibers flowed quickly, creating the circular flow of electron in the external circuits. When the measuring system was reverse connected, all the response signals exhibited reversed output. These results arose from the piezoelectric responses instead of artificial effects. If the signals arose from noise or other forms instead of piezoelectric responses, the shape of the response would remain the same even when the polarities of the contacts were changed.

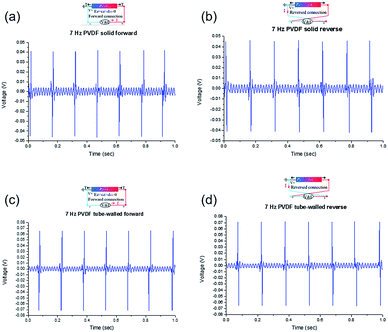Fig. 8 Voltages measured from (a and c) positive and (b and d) negative connections of electrodes to (a and b) PVDF solid fibers and (c and d) fiber tubes.

When the piezoelectric fibers were made in tubular structures, the moment of inertia (I) can be increased. To some extent, the mechanical strength can become stiffer and stronger, which means the tubular piezoelectric fibers exhibit larger Young's modulus (E). That is why the frameworks of bikes, fishing rods and truss elements are made in hollow structures to increase their own mechanical strength. Theoretically speaking, stiffer structures can induce higher vibration frequency and strain rate, compared to more flexible ones.³⁷ Therefore, the relationship between the induced electric current (i) and Young's modulus is given by eqn (1),³⁸

i = d₃₃EA[small epsi, Greek, dot above] (1)

where d₃₃ is the piezoelectric coefficient, A is cross-sectional area and [small epsi, Greek, dot above] is strain rate of the material. The higher strain rate and E cause higher harvested electric current and energy. The experimental result in Fig. 9 shows good agreement with the discussion above. The fibers with higher E can induce a larger electric voltage.

Fig. 9 Relationship of core rate, Young's modulus and induced voltage.

Finally, we investigated the relationships among the voltage, output power, and external resistance of the solid fibers and fiber tubes. The harvested power can be derived from eqn (2) and (3) (Ohm's law). Then harvest power can be re-arranged again as listed in eqn (4),

P = Vi (2)

V = iR (3)

P = V²/R (4)

where V and i are measured voltage and current with external load resistor, and R is external load resistor.

The maximum output power of the solid fibers was 347.61 pW when the external resistance was 6 MΩ and the voltage was 45.69 mV [Fig. 10(a)]. The maximum output power of the PPTs was 856.07 pW when the external resistance was 6 MΩ and the voltage was 71.66 mV [Fig. 10(b)]. Thus, the voltage of the PPTs was more than 1.5 times greater and the output power was more than 2.4 times greater that those of the solid fibers.

Fig. 10 Voltages and output powers of (a) solid fibers and (b) fiber tubes, plotted with respect to the external resistance.

4. Conclusion

We have used an NFES process with a coaxial needle device, including two precision flow syringe pumps, to produce PPTs. We examined the effects of several parameters (core and shell flow rates; concentration of PVDF; collecting tangential speed; electric field) on the mechanical and electrical properties of the as-spun PPTs. Significant piezoelectric properties and greater crystallization of PVDF fibers occurred when the core and shell rates were both set at 3 mL h⁻¹. In addition, the ultimate stresses of the PPTs were greater than those of the solid fibers. In an energy-harvesting test, the voltage of the PPTs was more than 1.5 times greater than that of the solid fibers, while the output power was more than 2.4 times greater.

Acknowledgements

This study was supported financially by the Ministry of Science and Technology, Taiwan under contracts MOST103-2221-E-110-079-MY3 and MOST102-2221-E-110-008-MY3.

References

1. P. L. Wang, Y. M. Fu, B. W. Yu, Y. Y. Zhao, L. L. Xing and X. Y. Xue, J. Mater. Chem. A, 2015, 3, 3529–3535.
2. T. Park, B. Kim, Y. Kim and E. Kim, J. Mater. Chem. A, 2014, 2, 5462–5469.
3. D. Farrar, K. Ren, D. Cheng, S. Kim, W. Moon, W. L. Wilson, J. E. West and S. M. Yu, Adv. Mater., 2011, 23, 3954–3958.
4. K. Ren, W. L. Wilson, J. E. West, Q. M. Zhang and S. M. Yu, Appl. Phys. A, 2012, 107, 639–646.
5. J. Fang, H. Niu, H. Wang, X. Wang and T. Lin, Energy Environ. Sci., 2013, 6, 2196–2202.
6. T. T. Wang, J. M. Herbert and A. M. Glass, The applications of ferroelectric polymers, Chapman & Hall, New York, 1988.
7. Z. Y. Wang, H. Q. Fan, K. H. Su and Z. Y. Wen, Polymer, 2006, 47, 7988–7996.
8. W. Wang, H. Fan and Y. Ye, Polymer, 2010, 51, 3575–3581.
9. W. Wang and H. Fan, Ferroelectrics, 2010, 409, 41–44.
10. M. Neidhofer, F. Beaume, L. Ibos, A. Bernes and C. Lacabanne, Polymer, 2004, 45, 1679–1688.
11. Y. Peng and P. Wu, Polymer, 2004, 45, 5295–5299.
12. P. Sajkiewicz, A. Wasiak and Z. Goclowski, Eur. Polym. J., 1999, 35, 423–429.
13. C. T. Pan, C. K. Yen, H. C. Wu, L. W. Lin, Y. S. Lu, J. C. C. Huang and S. W. Kuo, J. Mater. Chem. A, 2015, 3, 6835–6843.
14. G. Gong and J. Wu, Novel Polyimide Materials Produced by Electrospinning, Intech, 2012.
15. D. Sun, C. Chang, S. Li and L. W. Lin, Nano Lett., 2006, 6, 839–842.
16. Z. M. Huang, Y. Z. Zhang, M. Kotaki and S. Ramakrishna, Compos. Sci. Technol., 2003, 63, 2223–2253.
17. D. Li. and Y. N. Xia, Adv. Mater., 2004, 16, 1151–1170.
18. W. E. Teo and S. Ramakrishna, Nanotechnology, 2006, 17, 89–106.
19. R. Khajavi and M. Abbasipour, Nanotechnology, 2012, 19, 2029–2034.
20. J. T. McCann, D. Li and Y. N. Xia, J. Mater. Chem., 2005, 15, 735–738.
21. W. Sigmund, J. Yuh, H. Park, V. Maneeratana, G. Pyrgiotakis, A. Daga, J. Taylor and J. C. Nino, J. Am. Ceram. Soc., 2006, 89, 395–407.
22. R. Ramaseshan, S. Sundarrajan, R. Jose and S. Ramakrishna, J. Appl. Phys., 2007, 102, 11101–11117.
23. R. Dersch, M. Graeser, A. Greiner and J. H. Wendorff, Aust. J. Chem., 2007, 60, 719–728.
24. Z. M. Huang, Y. Z. Zhang, M. Kotaki and S. Ramakrishna, Compos. Sci. Technol., 2003, 63, 2223–2253.
25. C. T. Pan, C. K. Yen, L. W. Lin, Y. S. Lu, H. W. Li, J. C. C. Huang and S. W. Kuo, RSC Adv., 2014, 4, 21563–21570.
26. N. M. Bedford, M. B. Dickerson, L. F. Drummy, H. Koerner, K. M. Singh, M. C. Vasudev, M. F. Durstock, R. R. Naik and A. J. Steckl, Adv. Energy Mater., 2012, 2, 1136–1144.
27. Y. Dzenis, Science, 2004, 304, 1917–1919.
28. X. Y. Li, Y. C. Li, D. G. Yu, Y. Z. Liao and X. Wang, Int. J. Mol. Sci., 2013, 14, 21647–21659.
29. S. Zhang, Nat. Biotechnol., 2003, 21, 1171–1178.
30. J. T. McCann, M. Marquez and Y. Xia, Nano Lett., 2006, 6, 2868–2872.
31. M. Wang, N. Jing, C. B. Su, J. Kameoka, C. K. Chou, M. C. Huang and K. A. Chang, Appl. Phys. Lett., 2006, 88, 033106.
32. Z. M. Huang, Y. Z. Zhang and S. Ramakrishna, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 2852–2861.
33. H. L. Jiang, Y. Q. Hu, Y. Li, P. C. Zhao, K. J. Zhu and W. L. Chen, J. Controlled Release, 2005, 108, 237–243.
34. B. Sun, B. Duan and X. Y. Yuan, J. Appl. Polym. Sci., 2006, 102, 39–45.
35. R. Srikar, A. L. Yarin, C. M. Megaridis, A. V. Bazilevsky and E. Kelley, Langmuir, 2008, 24, 965–974.
36. W. A. Yee, M. Kotaki, Y. Liu and X. Lu, Polymer, 2007, 48, 512–521.
37. R. C. Hibbeler, Mechanics of materials, Pearson Education, New York, 285–287, 2011.
38. J. Sirohi and I. Chopra, J. Intell. Mater. Syst. Struct., 2000, 11, 246–257.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental detail of PVDF in solution use in this study, XRD pattern of PVDF piezoelectric fibers are available. See DOI: 10.1039/c5ra16604g

---