Open Access Article
Open Access ArticleA Raman spectroscopic investigation of speciation in La2(SO4)3(aq)†
Wolfram W.
Rudolph
*a and
Gert
Irmer
b
aMedizinische Fakultät der TU Dresden, Institut für Virologie im MTZ, Fiedlerstr. 42, 01307 Dresden, Germany. E-mail: Wolfram.Rudolph@tu-dresden.de
bTechnische Universität Bergakademie Freiberg, Institut für Theoretische Physik, Leipziger Str. 23, 09596 Freiberg, Germany
First published on 29th September 2015
Abstract
Raman spectroscopic measurements have been made of aqueous solutions of La(ClO4)3, La2(SO4)3, and Na2SO4 in water and heavy water, in the terahertz frequency region (40–1400 cm−1) and down to low concentrations (0.000263 mol L−1). Temperature dependent measurements of a 0.0098 mol L−1 La2(SO4)3 solution have been carried out from 23–98 °C. In solutions of La(ClO4)3 with water and heavy water, the [La(OH2)9]3+ and [La(OD2)9]3+ have been characterized and a weak, strongly polarized band observed at 343 cm−1 and 326 cm−1 respectively assigned to the ν1 LaO9 mode, the breathing mode of the clusters. In La2(SO4)3(aq), in addition to the ν1-SO42− mode at 980 cm−1, a pronounced band component at 991 cm−1 has been assigned to an inner-sphere complex (ISC) and a similar ν1-SO42− band contour has been observed in La2(SO4)3 solutions in D2O. Sulfate may act as a monodentate ligand. Conformation of this assignment is provided by the component at 312 cm−1 of the [La(OH2)8OSO3]+ species in addition to the band at 343 cm−1 for the fully hydrated cluster, [La(OH2)9]3+. After subtraction of the component of the ISC at 991 cm−1, the ν1-SO42− band in La2(SO4)3(aq) showed systematic differences from that in Na2SO4(aq). This is consistent with a ν1-SO42− band at 983.3 cm−1 that can be assigned to the existence of an outer-sphere complex (OSCs). The observed change of the degree of sulfato-complex formation with dilution reflects the stepwise sulfato-complex formation. A K3-value has been determined at 0.9 of the equilibrium between OSC and ISC. Temperature dependent measurements on a dilute La2(SO4)3 solution has shown that the concentration of the La3+ sulfato-complex rises with increasing temperature while at the same time the concentration of the “free” sulfate diminished. The sulfato-complex formation is an endothermic process absorbing heat with increasing temperature. The following thermodynamic parameters for the rate determining equilibrium, [La(OH2)SO4]+ ↔ [LaOSO3]+ has been determined: ΔH0 = 18.6 kJ mol−1 and ΔS0 = 62.1 J mol−1 K−1.
1. Introduction
Lanthanum sulfate enneahydrate, La2(SO4)3·9H2O, is the most common hydrate of lanthanum sulfate, La2(SO4)3·nH2O (n = 1–9)1–3 and is the only stable hydrate in contact with its solution between 0° and 100°. La2(SO4)3 is sparingly soluble at room temperature and the solubility diminishes with temperature. Lanthanum exists in aqueous solution exclusively in the trivalent state and the La3+ ion is strongly hydrated due to its high charge to radius ratio. The coordination number (CN) in the primary hydration shell for La3+ in aqueous solution has been determined at nine (data in Table 1, ref. 4). The water molecules of the nonahydrate results in a hydration structure of a tricapped trigonal prism (TTP) with D3 symmetry.5 The O-atoms of the three waters in the equatorial plane (capping position) are separated from the cation by a bond distance of 2.64 Å, while six water molecules at the vertices of the trigonal prism have a La–O bond distance of 2.515 Å.5,6 A recent Raman spectroscopic investigation revealed that in concentrated La(ClO4)3(aq) ion pairs are formed while in dilute solutions the undisturbed [La(H2O)9]3+ species exist.This study has been undertaken to characterize the species formed in aqueous La3+–sulfate solutions over a very broad concentration range and at elevated temperatures. Sulfato-complex formation has been characterized in solutions on a variety of divalent and trivalent metal sulfates7–12 and the question arises whether these complexes also occur with La3+(aq). The investigation of La2(SO4)3 solutions proved to be especially challenging because lanthanum sulfate is only sparingly soluble in water and the salt shows a retrograde solubility with temperature increase. The study on the aqueous La2(SO4)3 is the first Raman experimental investigation one this dilute system. The following aqueous systems have been measured using Raman spectroscopy at 23 °C: La(ClO4)3, La2(SO4)3 and Na2SO4. Specifically, we have been interested in the vibrational characterization of the La3+–aqua stretching band at low concentration and the possible formation of ion pairs/complexes between La3+ and sulfate. Dilute Na2SO4 solutions have been measured to characterize the sulfate modes free of sulfato-complex species. A La2(SO4)3 solution at 0.0098 mol L−1 has been measured from 23 °C to 98 °C in order to characterize the sulfato-complex formation as a function of temperature. Thermodynamic parameters such as enthalpy and entropy of the sulfato-complex formation have been determined from the measured K3 values as a function of temperature.
2. Experimental details
2.1. Preparation of solutions
Lanthanum perchlorate solutions were prepared from La2O3 (Sigma-Aldrich, 99.9%) and HClO4 in a beaker until all oxide dissolved. The lanthanum ion content was analysed by complexometric titration.13 The solution density was determined with a pycnometer at 23 °C and the molar ratios water per salt were calculated (Rw-values). A La(ClO4)3 stock solution was prepared at 2.488 mol L−1 (Rw = 15.72)4 and the solution was slightly acidic with a pH value at ∼3.5. From the stock solution, the following dilution series was prepared: 0.622 mol L−1 (Rw = 81.54), 0.498 mol L−1 (Rw = 103.43) and 0.249 mol L−1 (Rw = 213.75). The solutions were analyzed for dissolved chloride with a 5% AgNO3 solution. The absence of a white AgCl precipitate proved that the stock solution was free of Cl−. For Raman spectroscopic measurements the solutions were filtered through a fine sintered glass frit (1–1.6 μm pore size). The solutions showed no Tyndall effect and were “optically empty” (see e.g.ref. 14).Lanthanum sulfate is only sparingly soluble in water. A 0.0376 mol L−1 La2(SO4)3 stock solution (0.03784 mol kg−1) was prepared from La2(SO4)3·9H2O and was used to further prepare dilute solutions. The solution density of the stock solution and its La3+ were determined as described above. The pH of the stock solution was determined with a glass electrode equal to 5.52. Nine solutions were prepared from this stock solution: 0.0302 mol L−1, 0.0189 mol L−1, 0.0093 mol L−1, 0.00754 mol L−1, 0.00606 mol L−1, 0.00377 mol L−1, 0.00189 mol L−1, 0.00121 mol L−1, 0.00094 mol L−1 and 0.00026 mol L−1. The lanthanum ion content was analysed by complexometric titration and the solution density was determined with a 5.000 mL pycnometer at 23 °C.
2.2. Spectroscopic measurements
Raman spectra were measured in the macro chamber of the T 64000 Raman spectrometer from Jobin Yvon in a 90° scattering geometry at 23 °C. These measurements have been described elsewhere in detail.15,16 Briefly, the spectra were excited with the 514.5 nm line of an Ar+ laser at a power level of 1100 mW at the sample. After passing the spectrometer in subtractive mode, with gratings of 1800 grooves per mm, the scattered light was detected with a cooled CCD detector. IVV and IVH spectra were obtained with fixed polarisation of the laser beam by rotating the polarisator at 90° between the sample and the entrance slit to give the scattering geometries:| IVV = I(Y[ZZ]X) = 45α′2 + 4γ′2 | (1) |
| IVH = I(Y[ZY]X) = 3γ′2. | (2) |
The isotropic spectrum, Iiso is then constructed:
| Iiso = IVV − 4/3IVH. | (3) |
The depolarization ratio, ρ, of the modes were determined according to eqn (4):
| ρ = IVH/IVV = 3γ′2/(45α′2 + 4γ′2). | (4) |
The polarization analyser was calibrated with CCl4 before each measuring cycle and adjusted if necessary. The depolarisation ratio of the ν1 mode of CCl4 at 459 cm−1 was determined at 0.0036 ± 0.0005 (15 independent measurements). The depolarization ratios of the depolarized CCl4 bands at 217 cm−1 and 315 cm−1 have been determined at 0.75 ± 0.02.
In order to obtain spectra defined as I(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ) which are independent of the excitation wavenumber νL, the measured Stokes intensity should be corrected for the scattering factor (νL − (
) which are independent of the excitation wavenumber νL, the measured Stokes intensity should be corrected for the scattering factor (νL − (![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ))3. When counting methods are used, the measured count rates have to be corrected with the factor (νL − (
))3. When counting methods are used, the measured count rates have to be corrected with the factor (νL − (![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ))3. The spectra were further corrected for the Bose–Einstein temperature factor, B = [1 − exp(−h
))3. The spectra were further corrected for the Bose–Einstein temperature factor, B = [1 − exp(−h![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) c/kT)] and the frequency factor,
c/kT)] and the frequency factor, ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) , to give the so called reduced or R(
, to give the so called reduced or R(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ) spectrum. It is also possible to calculate the isotropic spectrum in R-format from the corrected RVV and RVH spectra according to eqn (5):
) spectrum. It is also possible to calculate the isotropic spectrum in R-format from the corrected RVV and RVH spectra according to eqn (5):
R(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) )iso = R( )iso = R(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) )VV − 4/3R( )VV − 4/3R(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) )VH. )VH. | (5) |
In the low wavenumber region the I(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ) and RQ(
) and RQ(![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ) spectra are significantly different and only the spectra in R-format are presented. It should be noted that one of the advantages of using isotropic R-spectra is that the baseline is almost flat in the 50–700 cm−1 wavenumber region allowing relatively unperturbed observation of the presence of any weak modes.15,16
) spectra are significantly different and only the spectra in R-format are presented. It should be noted that one of the advantages of using isotropic R-spectra is that the baseline is almost flat in the 50–700 cm−1 wavenumber region allowing relatively unperturbed observation of the presence of any weak modes.15,16
The spectra were fitted to a sum of Lorentzian–Gaussian product functions and the fitting procedure has been described elsewhere in detail.17
Temperature dependent Raman measurements were carried out in sealable fused quartz cuvettes, 10 × 10 mm, with 3.5 mL volume from Hellma (Müllheim, Germany) using a home-built oven. The oven and the setup have been described in detail in ref. 17.
2.3. Quantitative Raman measurements of the sulfato complex formation
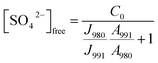
In order to be able to quantify species in solution without using an internal standard, the relative molar scattering factors (RMSF) for those bands must be determined.18 The RMSF for ν1-SO42− at 980 cm−1 for “free” SO42− in (NH4)2SO4 solutions were measured in solutions in which a known amount of NH4ClO4 had been dissolved as an internal standard (ClO4− band ν1 at 931 cm−1). From the integrated band intensities, Ai, and the concentration of the standard, the relative integrated band intensities, IR, with IR = (A980/A931)CNH4ClO4 were calculated. The quantity IR is directly proportional to the concentration of the species of interest and thus: IR = JC. From the slope of the curve, IR = JC, the so called relative molar scattering coefficient, J was obtained. For ν1 SO42− at 980 cm−1, it follows J980 = 0.788 and for bound sulfate at 991 cm−1: J991 = 0.760.The equilibrium concentrations of [SO42−]free and [SO42−]bound were obtained from the ratios of the areas of “free” SO42− mode at 980 cm−1 (this mode includes contributions from the fully hydrated sulfate, in the outer-outer-sphere and outer-sphere30–33) and the bound SO42− mode at 991 cm−1 and the relative molar scattering factors. The sum of the equilibrium concentrations [SO42−]free plus [SO42−]bound is equal to C0, the stoichiometric concentration of MnSO4 (in mol kg−1). The integrated band intensities are A980 = J980[SO42−]free and A991 = J991[SO42−]bound = J991(C0 − [SO42−]free), where J980 and J991 are the relative molar scattering factors for the bands at ∼980 and 991 cm−1. For the ratio of the integrated intensities, A980/A991 was calculated as follows:
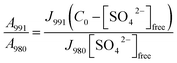 | (6) |
 | (7) |
With the equilibrium concentration of [SO42−]free determined and C0, the stoichiometric concentration of La2(SO4)3 known, the degree of bound sulfate, α, may be calculated by eqn (8):
| α = (C0 − [SO42−]free)/C0. | (8) |
3. Results and discussion
3.1. The unassociated [La(OH2)9]3+(aq)
The La3+(aq) ion is strongly hydrated in aqueous solution due to its high charge to radius ratio. A recent DFT study on a [Ln(H2O)9]3+ cluster imbedded in a polarizable dielectric continuum, taking into account the bulk water resulted in a tricapped trigonal prism (TTP) polyhedron of symmetry D3.4 The oxygen atoms of three water molecules in the equatorial plane are separated from La3+ by a bond distance of 2.64 Å, while six water molecules at the vertices of the trigonal prism are found at an average La–O bond distance at 2.515 Å.5,6 The hydration sphere of La3+(aq) is labile and a water-exchange rate constant kex at 25 °C was given at ≥2 × 108 s−1‡ (estimated from H2O–SO42− interchange rates) and a water residence time τ = ∼5 ns follows.19,20 Because of the labile coordination sphere for La3+ there is the possibility of a counterion (anion) coordination replacing water from the coordination polyhedron.21Although perchlorate is considered a non-complex forming anion, in La(ClO4)3 solutions at higher salt concentrations (1.5 mol L−1), it was shown that perchlorate forms outer sphere-ion pairs, [La(OH2)9]3+·ClO4− and at yet higher concentrations perchlorate penetrates into the first hydration sphere of the La3+.4 In La(ClO4)3(aq) at 2.488 mol L−1 the mole ratio solute to water is 15.7 and this amount of water is barely enough to completely hydrate the La3+ ion while the remaining 6.7 water molecules hydrate the three ClO4− ions. In such a concentrated solution contact ion pair formation is simply forced on La3+. Therefore, it is necessary to measure dilute La(ClO4)3 solutions but this measurement is hampered by the fact that the La–O breathing mode is very weak and its Raman scattering coefficient, 0.030, is low.
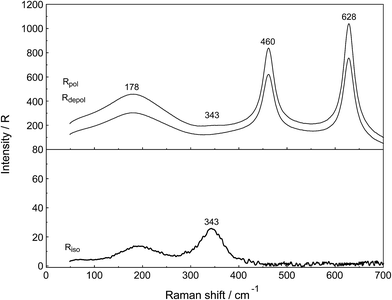
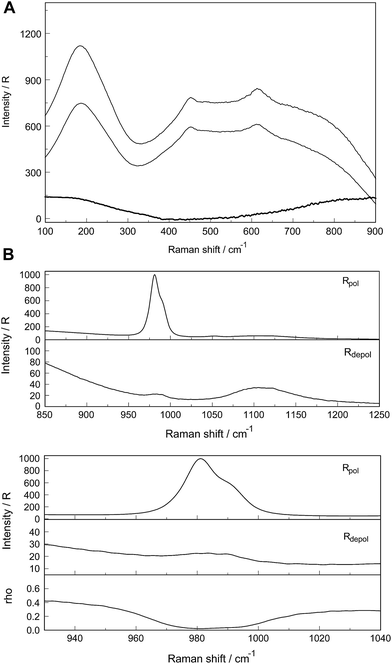
A vibrational analysis of the LaO9 skeleton modes of the [La(OH2)9]3+ species (D3h symmetry) has been carried out recently.4 Twenty four normal modes (n.m.'s) are expected for the LaO9 skeleton modes of the nonahydrate [La(OH2)9]3+. The irreducible representation of the vibrational modes is as follows: Γvib(D3h) = 3a′1(Ra) + a′2 + 5e′(Ra, i.r.) + a′′1 + 3a′′2(i.r.) + 3e′′(Ra). Two stretching modes and a bending mode are expected with character a′1 and these modes are Raman active only. Two stretching modes and three bending modes occur with character e′ and these modes are infrared and Raman active. A stretching mode and two bending modes for character a′′2 are expected and these n.m.'s are infrared active only while three modes (one stretch and two bending modes) with character e′′ are only Raman active. The modes with character a′2 and a′′1 are torsional modes and are not active. However, it was evident that only the symmetric La–O stretching mode appears in the Raman effect. The remaining LaO9 modes are too weak to be identified in Raman and this has also been observed for other metal ion–oxygen modes in aqueous solution.4 The La(ClO4)3 solution spectra reveals a Raman mode for the [La(OH2)93+] species, which is very weak, strongly polarized and broad at 343 cm−1. A 0.249 mol L−1 La(ClO4)3 solution is presented in Fig. 1. In neither NaClO4(aq) nor HClO4(aq) was this mode observed and must therefore stem from a symmetrical vibration connected to a La–O stretching band.
The perchlorate modes are well characterized so only a brief description is given.4 The ClO4− ion possesses Td symmetry and has nine modes of internal vibrations spanning the representation Γvib(Td) = a1(Ra) + e(Ra) + 2f2(Ra, i.r.). All n.m. are Raman active, but in i.r. only the f2 modes are active. The spectra of La(ClO4)3(aq) show the predicted four Raman-active bands for the tetrahedral ClO4−(aq). The ν1(a1) ClO4− band centred at 931.5 cm−1 is totally polarized (ρ = 0.005) whereas ν3(f2) ClO4− centred at 1105 cm−1 is depolarized as are the deformation modes ν4(f2) ClO4− at 631 cm−1 and ν2(e) ClO4− at 463 cm−1 (Fig. 1).
In addition to the isotropic mode, ν1 LaO9 at 343 cm−1 (fwhh = 49 ± 2 cm−1) a very weak, broad mode centered at 170 ± 10 cm−1 can be observed in aqueous La(ClO4)3 solution (isotropic Raman scattering). The mode can also be seen in pure water at ∼175 cm−1 and is moderately intense but slightly polarized. This mode has been assigned to a restricted translational mode of the H-bonded water molecules and is strongly anion and concentration dependent.4,22 A La(ClO4)3 solution in heavy water shows, in addition to the perchlorate modes, a strongly polarized band at 326 cm−1 which is due to the ν1 LaO9 at 326 cm−1 (fwhh = 47 ± 2 cm−1) of the deuterated analog of the nonahydrate, [La(OD2)9]3+(D2O).
Relative intensity measurements confirm that the scattering intensity of ν1 La–O mode is very weak and this may be the reason why the mode has been observed as an obscured shoulder in aqueous La3+ salt solutions in previous publications.23 The scattering coefficient, Sh for the ν1 La–O mode at 0.030 is small.
3.2. The unassociated SO42−(aq)
Unassociated SO42−(aq), in (NH4)2SO4(aq) for instance, has been described in detail.24 Although in Na2SO4 solutions at higher concentrations, ion pairs such as outer-outer sphere and outer-sphere ion-pairs are formed, in dilute solutions <0.1 mol L−1 the equilibrium concentrations are small relative to “free” sulfate. In a 0.101 mol L−1 Na2SO4 solution ∼13% of the total sulfate exists as ion pairs, mainly as outer-outer-sphere ion pairs while 87% are considered “free” or unassociated, SO42−(aq).25 With further dilution, the fraction of ion pairs diminishes significantly and reaches zero at infinite dilution. Therefore, dilute Na2SO4 solutions shall be briefly discussed and compared with La2(SO4)3 solutions. An overview Raman spectrum of a 0.101 mol L−1 Na2SO4(aq) from 100–1900 cm−1 is presented in Fig. 2. The spectral characteristics of the non-associated SO42−(aq) ion have been conducted.26 Here, however, a brief discussion of the results relevant to the ligated sulfate is presented.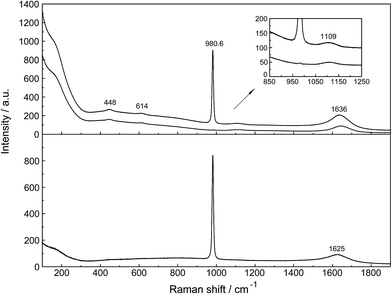 | ||
| Fig. 2 Overview Raman profiles of a 0.101 mol L−1 Na2SO4 solution. The IVV and IVH scattering orientations (upper panel) are given and in the lower panel the isotropic scattering. | ||
The non-associated SO42−(aq) ion possesses Td symmetry and thus nine modes of internal vibration, having the representation: Γvib(Td) = a1(R) + e(R) + 2f2(R, IR). All vibrational modes are Raman active, one mode with character a1 is totally polarized, and three modes with character e and f2 are depolarized but only the f2 modes are IR allowed.
In the IR spectrum only two sulfate bands are active, namely ν4(f2) and ν3(f2) located at 618 cm−1 and 1104 cm−1 respectively24 but all four modes are Raman active. Detailed Raman spectroscopic characterizations of the SO42−(aq) bands are given in ref. 24. The ν1(a1)-SO42− mode is the strongest band in the sulfate spectrum. The band for a 0.101 mol L−1 Na2SO4(aq) centred on 980.69 cm−1 (fwhh = 6.05 ± 0.05 cm−1) is almost totally polarized (ρ = 0.0035) whereas the ν3(f2)-SO42− band centred on 1109 cm−1 (fwhh = 65.0 cm−1) is depolarized. The deformation modes ν4(f2)-SO42− at 614 cm−1 (fwhh = 31 cm−1) and ν2(e)-SO42− at 448 cm−1 (fwhh = 35 cm−1) are depolarized as well.
At low frequencies, a broad and weak mode at 180 cm−1 (fwhh = 168 cm−1) was observed in the isotropic R-spectrum.24 This mode is also observable in pure water at 175 cm−1 and has been attributed to H-bonded water molecules.26,27 In Na2SO4(aq) it may be assigned to the restricted translational modes of both OH⋯O and OH⋯(OSO3)2− hydrogen-bonds thereby the contribution of the OH⋯(OSO3)2− hydrogen-bonds increases with increasing Na2SO4 concentration. In a concentrated, saturated Na2SO4 solution, 1.617 mol L−1, the restricted translational mode, ν OH⋯O was observed at 185 cm−1 with a fwhh at 130 cm−1 while in dilute solutions the restricted translational mode is determined by the OH⋯O hydrogen bonds in water and only slightly influenced by OH⋯(OSO3)2− hydrogen-bonds. The corresponding bending mode of this unit appears at ∼60 cm−1.26,27
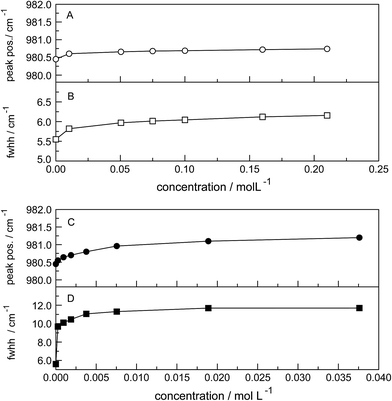
The ν1-SO42− band shape in dilute Na2SO4(aq) is symmetrical in both Raman polarization arrangements but other band parameters vary slightly with concentration (Fig. 3, panel A and B, data with open squares). For example, at 23 °C for a 1.617 mol L−1 Na2SO4 solution (Rw = 32.75), νmax for this isotropic band appears at 981.04 cm−1 with a fwhh = 6.60 cm−1, for a 0.101 mol L−1 solution (Rw = 552.2) νmax appears at 980.69 cm−1 with a fwhh = 6.05 cm−1. For an infinitely dilute solution (extrapolation to zero concentration) the ν1-SO42− band appears at 980.45 cm−1 and a fwhh = (5.55 ± 0.05) cm−1. For present purposes, it is relevant that the symmetric profile of the ν1-SO42− mode was independent of the salt concentration over the entire range studied (≤1.617 mol L−1). The ν1-SO42− band is the strongest band in the SO42−(aq) – Raman spectrum and the intensity ratio of ν1-SO42− band area to ν3-SO42− band area is 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
The band contour of the antisymmetric S–O stretching mode, ν3-SO42− is also symmetrical in both polarization arrangements but band parameters vary slightly with concentration. For example, at 23 °C for a 1.617 mol L−1 Na2SO4 solution, νmax is found at (1112 ± 2) cm−1 and shifted to slightly lower wavenumbers as the concentration was decreased, reaching (1106 ± 2) cm−1 at infinite dilution. The fwhh decreased from (76 ± 2) cm−1 for a 1.617 mol L−1 salt solution to (67 ± 2) cm−1 for a 0.100 mol L−1 solution reaching (64 ± 2) cm−1 at infinite dilution. It is important to state that the symmetric profile of the ν3-SO42− band which is completely depolarized is independent of the Na2SO4 concentration over the entire range studied (Fig. 2).
3.3. Raman spectra of La2(SO4)3(aq)
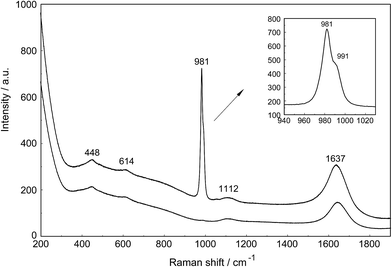
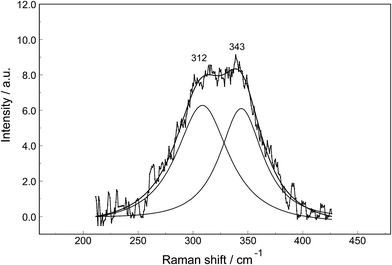
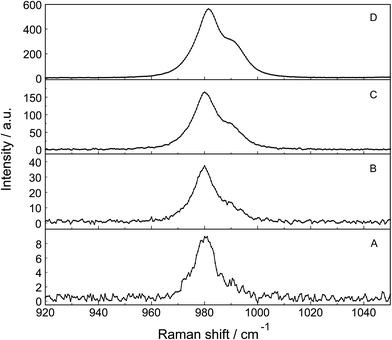
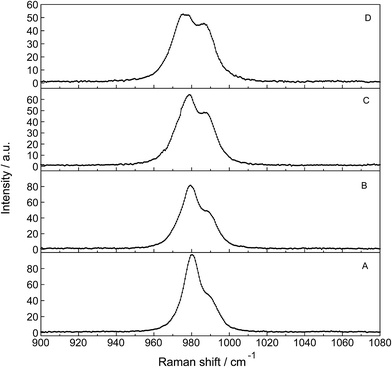
The Raman spectra of La2(SO4)3 in aqueous solution show additional features to those in the unassociated sulfate spectra and the [La(OH2)9]3+(aq) mode which have been described above. La2(SO4)3 is only sparingly soluble in water and the Raman signals are therefore of low intensity and the spectra are dominated by the solvent, water. Nevertheless these additional spectroscopic features could be observed and are now discussed in detail.An overview Raman spectrum of the 0.0376 mol L−1 La2(SO4)3 solution is presented in Fig. 4. Because of the low solute concentration, the sulfate bands appear weak and the scattering spectrum is dominated by the bands of the solute, water. The ν1(a1) SO42− stretching profile shows two band components at 981 cm−1 and at 991 cm−1. The weak anti-symmetric stretching mode, ν3 SO42− at 1112 cm−1 appears broader compared to a comparable Na2SO4 solution. Furthermore, in the terahertz frequency range, the La–O breathing mode, normally at 343 cm−1, appears in the difference spectrum of the 0.0376 mol L−1 La2(SO4)3 solution as a broad feature at ∼328 cm−1 with two separate component bands, one at 343 cm−1 assigned to the La–O breathing mode of [La(OH2)9]3+(aq) and one at 312 cm−1 assigned to hydrated La3+ where sulfate occurs in the first hydration shell, [La(OH2)8OSO3]+(aq) (Fig. 5). With further dilution of La2(SO4)3 the very small scattering coefficient of this La–O breathing mode prevents further observation of this band.
The split of the ν1(a1) SO42− stretching band into a band at 981 cm−1 and a pronounced shoulder at 991 cm−1 becomes immediately obvious in Fig. 6B. In Na2SO4(aq) the strongly polarized mode at 991 cm−1 is absent while in a variety of divalent and trivalent metal sulfate solutions sulfato-complex species could be observed.8,11,12,24 In Fig. 7, a concentration plot of ν1(a1) SO42− band profiles are given, showing the concentration dependence of four representative Raman spectra from 0.0303–0.000263 mol L−1. With dilution, the equilibrium concentration of the band at 991 cm−1 diminishes while the one of the “free” sulfate rises. The band parameters for the 980 cm−1 band and the band at 991 cm−1 is given in Table S1.† It is interesting to note that both sulfate stretching modes are strongly polarized and in the anisotropic scattering both component bands appear at 981 and 991 cm−1 (Fig. 6B) and the polarization degrees are 0.004 and 0.006 respectively. This spectroscopic observation contradicts the observation made in a similar system, MgSO4(aq), for which a dynamic exchange model was proposed to explain the occurrence of the band at 995 cm−1. (The 995 cm−1 band in MgSO4(aq), however, is the band of a sulfato-complex species.24,28) The deformation bands of sulfate, ν2 SO42− at 448 cm−1 and the band ν4 at 614 cm−1 are broadened compared to the ones in Na2SO4(aq) of comparable sulfate concentrations (Fig. 2, 3 and 6A). These two deformation bands are depolarized in the Raman scattering as shown in Fig. 2 and 6A. The anti-symmetric stretch ν3 SO42− is much broader than Na2SO4(aq) of comparable sulfate concentration and shows a band contour with peak positions at 1088 cm−1, 1127 cm−1 and 1158 cm−1 and in the broad band at 1109 cm−1 for “free” sulfate (compare band contour of Na2SO4(aq) spectra). The measured anisotropic band profile of ν3 SO42− is shown in Fig. S1† together with the sum curve of the band fit. All these spectroscopic features of the sulfate in La2(SO4)3 solutions lead to the conclusion that sulfate must have penetrated the first hydration shell of La3+(aq) forming a well-defined La3+–sulfato complex. In the terahertz frequency range of La2(SO4)3(aq) of a 0.376 mol L−1 solution, as mentioned above, the La–O band, of the LaO9 skeleton appears as a broad feature at ∼328 cm−1 while the fully hydrated, [La(OH2)9]3+ occurs at 343 cm−1. The downshift of the La3+–sulfato complex, [La(OH2)8OSO3]+ compared with the fully hydrated cation was detected in other trivalent-metal sulfate solutions. It should be pointed out that the scattering intensity of the broad La–O features is very small and the solutions are quite dilute. Only in Al2(SO4)3, Ga2(SO4)3, and In2(SO4)3 solutions which are considerably more soluble than La2(SO4)3 and therefore much easier to detect, is such a split into the aqua mode of the fully hydrated species observable without the sulfate and partially hydrated metal–sulfato complex species.8,11,12
An overview Raman spectrum of a 0.035 mol L−1 La2(SO4)3 solution in heavy water is presented in Fig. S2 (ESI†). The spectrum is dominated by the solvent D2O(l) and the deformation mode at 1204 cm−1, a broad combination band at 1554 cm−1 (ν2 + νL) and the O–D stretching profile with a band doublet at 2382 and 2477 cm−1 as well as a shoulder at 2680 cm−1. A detailed spectrum is given in Fig. S3† showing the ν1(a1) SO42− band complex with two band components at 981 cm−1 and 991.4 cm−1. This ν1(a1) SO42− band complex observed in La2(SO4)3(D2O) compares with the spectra found in solutions of light water (compare Fig. 4). This finding reinforces the assignment of sulfate band components as bands of “free” sulfate and “bound” sulfate at 981 cm−1 and 991 cm−1 respectively.
3.4. Quantitative analysis of sulfato-complex formation in La2(SO4)3(aq)
The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1 value for the hydrolysis of [La(OH2)9]3+ according to: [La(H2O)9]3+ + H2O ↔ [La(H2O)8OH]2+ + H3O+ is at −8.5 for 25 °C.29,30 Therefore, La3+(aq), in contrast to Fe3+(aq) which acts as a strong acid in solution (log
β1 value for the hydrolysis of [La(OH2)9]3+ according to: [La(H2O)9]3+ + H2O ↔ [La(H2O)8OH]2+ + H3O+ is at −8.5 for 25 °C.29,30 Therefore, La3+(aq), in contrast to Fe3+(aq) which acts as a strong acid in solution (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1 = −2.19 (ref. 31)) is not markedly hydrolyzed. A 0.01 mol L−1 La2(SO4)3 solution shows a pH value of 5.53 and therefore the formation of hydrogen sulfate, HSO4− may be neglected.
β1 = −2.19 (ref. 31)) is not markedly hydrolyzed. A 0.01 mol L−1 La2(SO4)3 solution shows a pH value of 5.53 and therefore the formation of hydrogen sulfate, HSO4− may be neglected.
The association between La3+(aq) and SO42−(aq) ions is generally thought to occur via a three step process, referred to as the Eigen mechanism,32,33 in which the strongly hydrated ions combine initially to form an outer-outer-sphere complex. The two interposing water molecules are then lost successively, forming outer-sphere and ultimately inner-sphere complexes. This process is summarized in the following reaction scheme:
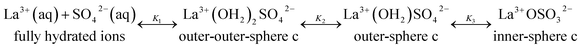 | (9) |
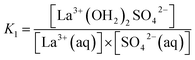 | (10) |
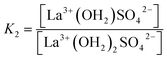 | (11) |
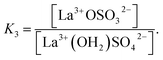 | (12) |
(The rate constants of the forward and backward reaction, the rate determining step via La3+(OH2)SO42− ↔ La3+OSO32− + H2O, may be formulated via K3 = kf/kb. The rate constants for forward (kf) and backward (kb) reactions were published from earlier ultrasound absorption measurements.19,20,34,35)
The overall association constant, KA, as measured by traditional techniques such as potentiometry or conductivity, corresponds to the equilibrium:
| La3+(aq) + SO42−(aq) ↔ LaSO4+(aq) | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry in aqueous solution (thermodynamics makes no distinction between dissolved species of identical stoichiometry but with differing levels of hydration24,28). The KA value, the overall association constant for the three step mechanism is related to the individual Ki values viaeqn (14):
1 stoichiometry in aqueous solution (thermodynamics makes no distinction between dissolved species of identical stoichiometry but with differing levels of hydration24,28). The KA value, the overall association constant for the three step mechanism is related to the individual Ki values viaeqn (14):| KA = K1 + K1K2 + K1K2K3 | (14) |
Three Ki values were obtained from ultrasound absorption (UA) experiments19,20 namely K1 = 435, K2 = 1.96 and K3 = 3.7. The reported KA value, 4200, derived from UA is too large compared with the recommended KA value at 3620 at 25 °C.36–38
The ν1-SO42− band can be fitted with three band components, a component of the ‘free’ SO42−(aq) band at ∼980 cm−1, a component at 983 cm−1 representing the SO42− in the outer-sphere-complex and the mode of the sulfato-complex at 991 cm−1 (Fig. 6B). The sulfato-complex band is quite distinct, while the band of the outer sphere complex is severely overlapped by the SO42−(aq) band at 980 cm−1. The SO42− band of the outer-outer-sphere complex is not distinguishable from the band of the free sulfate.
The degree of the sulfato-complex formation α, represents the spectroscopically-determined fraction of sulfate present as sulfato complex according to eqn (8). Fig. 8 shows the present quantitative Raman results as a function of the stoichiometric solute concentration C0. The proportion of the inner-sphere complex formed appears almost insensitive to the concentration > 0.003 mol L−1 but below this concentration vanishes more severely. This paradox can be resolved if it is assumed that the inner-sphere complex, [LaOSO3]+ is in equilibrium with the outer-sphere complex, [La(OH2)SO4]+ and not with the “free” sulfate. The Raman spectroscopically determined K3 value was determined according to eqn (12). In Table S1 (ESI†) the data of the analytical curve fitting on the ν1-SO42− band profile of the two band components at 981 cm−1 and 991.1 cm−1 are given such as integrated band intensities, A981 and A991, as well as the degree of sulfato-complex formation of the equilibrium between the outer-sphere complex and the inner-sphere-sulfato complex. From these data a K3-value was determined at 0.90 ± 0.1 at 23 °C and it appears that the Raman derived K3 value is comparable to the UA-values considering the uncertainty of the data from the UA measurements.19,20,34,35
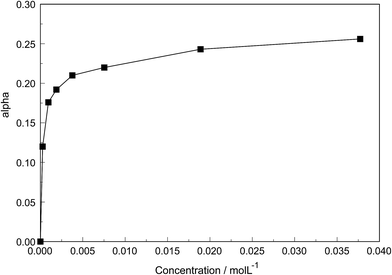 | ||
| Fig. 8 Degree of sulfato complex-formation, α, as a function of the stoichiometric La2(SO4)3 concentration at 23 °C. | ||
The increase of the La3+–sulfato complex with enhancing temperature shows that the rate determining third step of reaction (10) is an endothermic process by which heat is absorbed, making the enthalpy change positive. The change of the equilibrium constant as a function of temperature follows the equation:
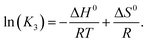 | (15) |
Plotting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K3 as a function of 1/T and assuming that the change of the heat capacity in this small temperature range is zero leads to the enthalpy and the entropy of the last step of the sulfato-complex formation, the outer-sphere, inner-sphere sulfato complex formation according to La3+(OH2)SO42− ↔ La3+OSO32−. The following quantitative results were derived from the temperature-dependence of ln(K3) as a function of the reciprocal temperature (in Kelvin): ΔH0 = 18.6 kJ mol−1 and ΔS0 = 62.1 J mol−1 K−1. The enthalpy for the rate determining step of eqn (9) compares favorably with the extrapolated value, 15 kJ mol−1, for ΔH0 taken from ref. 39.
K3 as a function of 1/T and assuming that the change of the heat capacity in this small temperature range is zero leads to the enthalpy and the entropy of the last step of the sulfato-complex formation, the outer-sphere, inner-sphere sulfato complex formation according to La3+(OH2)SO42− ↔ La3+OSO32−. The following quantitative results were derived from the temperature-dependence of ln(K3) as a function of the reciprocal temperature (in Kelvin): ΔH0 = 18.6 kJ mol−1 and ΔS0 = 62.1 J mol−1 K−1. The enthalpy for the rate determining step of eqn (9) compares favorably with the extrapolated value, 15 kJ mol−1, for ΔH0 taken from ref. 39.
Finally, it should be mentioned that Malatesta and co-workers40 showed, by comparing activity coefficient data on La2(SO4)3(aq) and La(ClO4)3(aq), that in the sulfate system of La3+ “there is evidence of short-range interactions that add to long-range interactions for lanthanum and bivalent metal sulfates, as if sulfate ions were displacing water from the hydration shells of the cations”. This is exactly what the Raman spectroscopic data show.
4. Conclusions
Raman spectroscopic measurements have been made of aqueous solutions of La(ClO4)3, La2(SO4)3, and Na2SO4 in water and heavy water, in the terahertz frequency region (40–1400 cm−1) and down to low concentrations (0.000263 mol L−1). Temperature dependent measurements have been carried out on a 0.0098 mol L−1 La2(SO4)3 solution from 23–98 °C. In solutions of La(ClO4)3 with water and heavy water, the [La(OH2)9]3+ and [La(OD2)9]3+ have been characterized and a weak, strongly polarized band observed at 343 cm−1 and 326 cm−1 respectively assigned to the ν1 LaO9 mode, the breathing mode of the clusters. The Raman spectroscopic data suggest that the [La(OH2)9]3+ ion is thermodynamically stable in dilute perchlorate. No inner-sphere complexes in these dilute solutions could be detected spectroscopically.In La2(SO4)3(aq), in addition to the ν1-SO42− mode at 980 cm−1, a pronounced band component at 991 cm−1 has been assigned to an inner-sphere complex (ISC). The sulfate is most likely bound as a monodentate ligand ([LaOSO3]+). Conformation of this assignment is provided by the component at 312 cm−1 of the [La(OH2)8OSO3]+ unit in addition to the band at 343 cm−1 for the fully hydrated cluster, [La(OH2)9]3+. A similar ν1-SO42− band contour has been observed in La2(SO4)3 solutions in heavy water. After subtraction of the component of the ISC at 991 cm−1, the ν1-SO42− band in La2(SO4)3(aq) showed systematic differences from that in (NH4)2SO4(aq) and dilute Na2SO4(aq). This is consistent with a ν1-SO42− band at 983.3 cm−1 that can be assigned to the existence of an outer-sphere complex ion (OSCs). The band profile of the weaker antisymmetric S–O stretching mode, ν3-SO42− shows asymmetry and has been fitted with four band components including the component of the “free” ν3-SO42− band reinforcing the existence of the ligated sulfate. In aqueous La2(SO4)3 solutions thermodynamically stable ISC have been detected down to very low concentrations at 0.00026 mol L−1 and in addition an OSC, [La(OH2)SO4]+ and the free non-ligated sulfate. The observed change of the equilibrium concentration of the ISC, [(LaOSO3)]+ with dilution reflects the stepwise sulfato-complex formation. A K3-value has been determined at ∼0.9 of the equilibrium between OSC and ISC.
Temperature dependent measurements (23–98 °C) on a 0.0098 mol L−1 La2(SO4)3 solution has shown that the concentration of the La3+ sulfato-complex rises with increasing temperature while at the same time the concentration of the “free” sulfate diminished. The sulfato-complex formation is an endothermic process absorbing heat with increasing temperature. The following thermodynamic parameters for the rate determining equilibrium, [La(OH2)SO4]+ ↔ [LaOSO3]+ + H2O, has been determined: ΔH0 = 18.6 kJ mol−1 and ΔS0 = 62.1 J mol−1 K−1.
References
- R. A. Vanderpool, M. A. Khan and R. Frech, J. Mol. Struct., 1991, 245, 255–273 CrossRef CAS.
- M. H. Choi, M. K. Kim, V. Jo, D. W. Lee, I. W. Shim and K. M. Ok, Bull. Korean Chem. Soc., 2010, 31, 1077–1080 CrossRef CAS.
- M. S. Wickleder, Chem. Rev., 2002, 102, 2011–2087 CrossRef CAS PubMed.
- W. W. Rudolph and G. Irmer, Dalton Trans., 2015, 44, 295–305, 10.1039/c4dt03003f.
- J. Näslund, P. Lindqvist-Reis, I. Persson and M. Sandström, Inorg. Chem., 2000, 39, 4006–4011 CrossRef.
- I. Persson, P. D'Angelo, S. de Panfilis, M. Sandström and L. Eriksson, Chem.–Eur. J., 2008, 14, 3056–3066 CrossRef CAS PubMed.
- W. W. Rudolph, D. Fischer, G. Irmer and C. C. Pye, Proceedings of the XXI International Conference on Raman Spectroscopy, ed. R. Whithnall and B. Z. Chowdhry, IM Publications, Charlton, Chichester, 2008, pp. 672–673 Search PubMed.
- W. W. Rudolph, R. Mason and C. C. Pye, Phys. Chem. Chem. Phys., 2000, 2, 5030–5040 RSC.
- W. W. Rudolph and G. Irmer, Dalton Trans., 2013, 3919–3935 RSC.
- W. W. Rudolph and G. Irmer, Dalton Trans., 2013, 14460–14472 RSC.
- W. W. Rudolph and C. C. Pye, Phys. Chem. Chem. Phys., 2002, 4, 4319–4327 RSC.
- W. W. Rudolph, D. Fischer, M. R. Tomney and C. C. Pye, Phys. Chem. Chem. Phys., 2004, 6, 5145–5155 RSC.
- A. I. Vogel, A Text-Book of Quantitative Inorganic Analysis, Longman, London, 3rd edn, 1961 Search PubMed.
- F. H. Spedding, M. J. Pikal and B. O. Ayers, J. Phys. Chem., 1966, 70, 2440–2449 CrossRef CAS ; see p. 2441.
- W. W. Rudolph and G. Irmer, Appl. Spectrosc., 2007, 61, 1312–1327 CrossRef CAS PubMed.
- W. W. Rudolph, D. Fischer and G. Irmer, Appl. Spectrosc., 2006, 60, 130 CrossRef CAS PubMed.
- W. W. Rudolph, J. Chem. Soc., Faraday Trans., 1998, 94, 489–499 RSC.
- W. W. Rudolph, Z. Phys. Chem., 1996, 194, 73–95 CrossRef CAS.
- D. P. Fay, D. Litchinsky and N. Purdie, J. Phys. Chem., 1969, 73, 544–552 CrossRef CAS.
- N. Purdie and C. A. Vincent, Trans. Faraday Soc., 1967, 63, 2745–2757 RSC.
- L. Helm and A. E. Merbach, Chem. Rev., 2005, 105, 1923–1959 CrossRef CAS PubMed.
- G. E. Walrafen, J. Chem. Phys., 1962, 36, 1035–1042 CrossRef CAS.
- H. Kanno, J. Alloys Compd., 1993, 192, 271–273 CrossRef CAS.
- W. W. Rudolph, G. Irmer and G. Hefter, Phys. Chem. Chem. Phys., 2003, 5, 5253–5261 RSC.
- R. Buchner, S. G. Capewell, G. Hefter and P. M. May, J. Phys. Chem. B, 1999, 103, 1185–1192 CrossRef CAS.
- W. W. Rudolph and G. Irmer, Appl. Spectrosc., 2007, 61, 1312–1327 CrossRef CAS PubMed.
- M. H. Brooker, G. Hancock, B. C. Rice and J. Shapter, J. Raman Spectrosc., 1989, 20, 683–694 CrossRef CAS.
- R. Buchner, W. W. Rudolph and G. Hefter, J. Chem. Phys., 2005, 123, 034508 ( J. Chem. Phys. , 2006 , 124 , 247101 ) CrossRef PubMed.
- C. F. Baes and R. E. Mesmer, The Hydrolysis of Cations, Wiley-Interscience, New York, 1976 Search PubMed.
- G. D. Klungness and R. H. Byrne, Polyhedron, 2000, 19, 99–107 CrossRef CAS.
- A. Stefasson, Environ. Sci. Technol., 2007, 41, 6117–6123 CrossRef.
- M. Eigen and K. Tamm, Z. Elektrochem., 1962, 66, 93–107 CAS.
- M. Eigen and K. Tamm, Z. Elektrochem., 1962, 66, 107–121 CAS.
- J. Reidler and H. B. Silber, J. Phys. Chem., 1973, 77, 1275–1280 CrossRef CAS.
- B. Voleišienė, G. Miglinienė and A. Voleišis, J. Acoust. Soc. Am., 1999, 105, 962 Search PubMed.
- S. A. Wood, Chem. Geol., 1990, 82, 159–186 CrossRef CAS.
- S. A. Wood, Chem. Geol., 1990, 88, 99–125 CrossRef CAS.
- J. Schijf and R. H. Byrne, Geochim. Cosmochim. Acta, 2004, 68, 2825–2837 CrossRef CAS.
- D. P. Fay and N. Purdie, J. Phys. Chem., 1970, 74, 1160–1166 CrossRef CAS.
- F. Malatesta, F. Bruni and N. Fanelli, Phys. Chem. Chem. Phys., 2002, 4, 121–126 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra16900c |
| ‡ The datum for kex at 25 °C was given incorrectly in ref. 4 page 298. |
| This journal is © The Royal Society of Chemistry 2015 |