Resorcinol–formaldehyde based nanostructured carbons for CO2 adsorption: kinetics, isotherm and thermodynamic studies†
Chitrakshi Goel ,
Haripada Bhunia and
Pramod K. Bajpai*
,
Haripada Bhunia and
Pramod K. Bajpai*
Department of Chemical Engineering, Thapar University, Patiala-147004, Punjab, India. E-mail: chitrakshigoel@yahoo.co.in; hbhunia@thapar.edu; pkbajpai@thapar.edu; Fax: +91-175-2393005; Tel: +91-175-2393438
First published on 26th October 2015
Abstract
Silica templated nanostructured carbons were developed from a resorcinol–formaldehyde polymeric precursor by varying the carbonization temperature from 400 °C to 800 °C. The prepared carbons were characterized thoroughly for their textural, surface and chemical properties followed by dynamic CO2 capture performance at various adsorption temperatures from 30 °C to 100 °C under simulated flue gas conditions. Among the prepared carbons, carbonization at 700 °C resulted in the nanostructured carbon material, as indicated by XRD and TEM results, having the best textural properties i.e. specific surface area and total pore volume around 435 m2 g−1 and 0.22 cm3 g−1, respectively. The sample obtained by carbonization at the most severe conditions (≥800 °C) exhibited textural properties comparable to that of RF-700 but showed lower CO2 adsorption capacity on account of reduction in surface basicity at higher temperatures. On the other hand, preparation of the carbon material by direct carbonization of the polymeric precursor, i.e. without using a template, resulted in a completely non-porous material with very low CO2 adsorption capacity. Moreover, both the textural properties and the surface chemistry had an effect on the CO2 adsorption performance of the prepared carbons. RF-700 exhibited the highest dynamic CO2 adsorption capacity of 0.761 mmol g−1 at 30 °C in a binary mixture of 12.5% CO2 in N2 attributed to a well-developed porous structure and high surface basicity of 1.93 meq g−1. It also demonstrated high selectivity towards CO2 over N2 and stable adsorption capacity over multiple adsorption–desorption cycles. CO2 adsorption on the prepared carbons was well described by a fractional order kinetic model. Fitting of equilibrium data of CO2 adsorption by Temkin isotherm model and variation in isosteric heat of adsorption with surface coverage indicated an energetically heterogeneous adsorbent surface. Thermodynamics of CO2 adsorption on the carbon material suggested an exothermic, random and spontaneous nature of the process. The thermal energy required for desorption of CO2 was also estimated to be around 1.9 MJ per kg CO2.
1. Introduction
Carbon dioxide concentration in the atmosphere has increased drastically in the last few decades owing to increased fossil fuel combustion to meet the world's energy requirements. Because of the greenhouse effect, increasing CO2 concentration has led to detrimental effects on the climate in terms of global warming and rising sea levels.1 Significant research efforts have been carried out in the direction of reducing atmospheric CO2 concentrations by carbon dioxide capture and sequestration (CCS).2 A variety of technologies like chemical absorption, membrane separation, cryogenic separation and adsorption have been employed for capturing CO2. State-of-the-art absorption technology by aqueous amines is most commonly used although it suffers from various disadvantages like solvent degradation, equipment corrosion, high regeneration energy requirement etc. Cryogenic distillation process also includes high energy consumption while membrane separation is applicable at low flow rates.3–6Adsorption using porous adsorbent materials presents various advantages over other methods like low operating cost and ease of application.6 Adsorbents being used for CO2 capture include porous carbons, zeolites, silica and metal–organic frameworks.7–12 Zeolite and silica adsorbents are also treated with various amine solutions in order to improve their affinity towards CO2 and hence the adsorption capacity.13,14 But the toxic and corrosive amine solutions need high regeneration temperature and degrade over various adsorption cycles.9,11,15 On the other hand, carbon based adsorbents are the versatile adsorbents being widely used in gas and liquid adsorption on account of their properties such as high specific surface area, hydrophobicity, complete regeneration over multiple adsorption cycles, high mechanical and thermal stability.16 They can be produced from a wide range of low cost materials like coal, industrial by-products, wood or biomass sources etc.17,18 by using various methods including sol–gel process, chemical vapour deposition, carbonization of carbon containing precursor and nanocasting. Among these available techniques, nanocasting technique has been used in recent times for the fabrication of carbon materials with controlled pore structure.19 A carbon precursor is generally infiltrated into the pore of a hard template and is treated thermally under a controlled atmosphere. This is followed by template removal by dissolution of template in hydrogen fluoride or sodium hydroxide solution.20 Porous carbons were obtained from nanocasting technique by using sucrose as the carbon source and nano-CaCO3 as hard template.21 Direct pyrolysis of resorcinol and formaldehyde in the presence of lysine as catalyst produced carbons having static CO2 uptake of 3.13 mmol g−1 at 25 °C under 100% CO2 flow.22 Melamine–formaldehyde and urea–formaldehyde based carbons by chemical activation with K2CO3 exhibited CO2 uptake of 1.03 mmol g−1 and 1.8 mmol g−1 at 25 °C.23 Phenolic resin and resorcinol resin based carbons were subjected to chemical activation with KOH in order to improve their textural properties.24 These materials exhibited CO2 uptake of ca. 4.36 mmol g−1 at 25 °C under static conditions.
It can be seen that most of the carbon synthesis is carried out by direct carbonization of various carbon sources and/or followed by post-synthesis treatments such as physical activation or chemical activation. But development of porous carbons by nanocasting technique helps in tailoring the pore structure of the resultant material. Also, activation is done to improve the textural properties of the obtained carbons in spite of the high energy requirement in these processes. Furthermore, these materials are evaluated for CO2 capture under pure CO2 flow at static conditions mainly at 0 °C or 30 °C and adsorption capacities evaluated under static conditions are always higher than the values obtained in dynamic systems. It is worth mentioning that for practical applications in the field of CCS, the developed adsorbents should be evaluated at high temperatures under dynamic conditions. Also, CO2 adsorption by carbon materials have been reported to strongly depend on both the textural properties and surface chemistry of the materials. Thus, it is important to develop porous carbon adsorbents with optimal textural properties in addition to highly basic character in order to achieve higher affinity towards CO2 than N2.
Present study focuses on the development of nanostructured carbons from resorcinol–formaldehyde polymeric precursor by nanocasting technique followed by thorough characterization by using various sophisticated techniques and evaluation for CO2 adsorption by fixed-bed experiments. Effect of silica template on the physico-chemical properties of the prepared carbons was also evaluated by preparing one sample by direct carbonization of RF resin and was compared with nanocasted carbons. Kinetics, isotherm and thermodynamics for CO2 adsorption on these carbons were also studied. In addition, energy duty for desorption of adsorbed CO2 was also calculated.
2. Experimental
All the reagents and solvents were purchased from M/s S. D. Fine Chemicals India Ltd. MCM-41 type mesoporous silica was used as template and was procured from M/s Tianjin Chemist Scientific Ltd., Tianjin, China. Its specific surface area and average pore diameter are 450 m2 g−1 and 3.5 nm respectively. Dry nitrogen, carbon dioxide and helium gases of grade-1 purity (99.999%) were obtained from M/s Sigma Gases and Services, India.2.1 Synthesis of porous carbons
Nanostructured carbon materials were synthesized by templating resorcinol–formaldehyde (RF) resin as polymeric precursor in the pores of mesoporous silica template by using nanocasting technique. About 100 g of resorcinol was added to 50 ml of water and was mixed for 20 minutes. To this mixture, 50 ml of 37% w/v formaldehyde solution was added and stirred for 30 minutes. Then 0.2 ml of 5 N NaOH solution was added under continued mixing for another 20 minutes to achieve the pH in the range of 4.4–5.4. Digestion was carried out, by increasing the temperature to 70–75 °C, for next 3 h to achieve refractive index in the range of 1.48 ± 0.1. Atmospheric distillation was carried out at 100 °C to remove water till the Norton flow followed by cooling to room temperature. RF resin thus obtained was dissolved in ca. 200 ml of acetone and 15 g of silica template was added to it under continuous stirring at room temperature. Excess acetone was removed from templated resin by evaporating it in oven at 60 °C. Fig. 1 presents the block diagram for the synthesis of templated RF resin.A series of adsorbents were prepared by carbonizing the templated resin samples at varying carbonization temperatures ranging from 400 °C to 800 °C for 1 h in N2 flow with a heating rate of 10 °C min−1. Silica template from the obtained materials was removed by dissolution in NaOH solution for at least 24 h followed by washing with deionized water and drying at 100 °C for 2 h. Synthesized carbon materials were marked as RF-x, where x stands for temperature of carbonization (400–800 °C). One more carbon sample was synthesized by direct carbonization of RF resin at 700 °C (based on optimized conditions for RF based carbons) in order to investigate the effect of silica template on the physico-chemical properties of the prepared carbons and this sample was denoted as ‘RF-C’.
2.2 Characterization of porous carbons
The nitrogen sorption isotherms of the synthesized carbon materials were determined at −196 °C using Micromeritics ASAP 2010 volumetric analyzer. Prior to the measurements, the samples were degassed in vacuum at 220 °C for 6 h. Surface area was obtained from Brunauer–Emmett–Teller (BET) equation and the total pore volume was estimated from the adsorbed amount at a relative pressure P/Po of 0.99. Mesopore volume and the pore size distribution were determined by the Barrett–Joyner–Halenda (BJH) method using the adsorption branch of the isotherm. Micropore volume (Vmicro) was calculated from the difference between the total pore volume and mesopore volume obtained from BJH method.The X-ray diffraction (XRD) patterns of the synthesized materials were acquired on a PANalytical X'Pert Pro diffractometer operating at 45 kV and 40 mA with Cu-Kα radiation in the scanning range (2θ) of 10 to 80°. Transmission electron microscopy (TEM) images were obtained with a Philips CM200 transmission electron microscope operating at an accelerating voltage of 200 kV. Scanning electron microscopy (SEM) images were recorded on a JEOL JSM-6510 LV scanning electron microscope with an accelerating voltage of 10.0 kV. The samples were coated with a gold film of 50 μm thickness in an automatic sputter coater (Polaron) in order to avoid charging under electron beam.
Thermogravimetric analysis of the samples was carried out using a TA Q500 (TA Instrument, USA) thermogravimetric analyzer in nitrogen at a flow rate of 50 ml min−1. The samples were heated at a heating rate of 10 °C min−1 from 30 °C to 900 °C.
Fourier transform infrared (FTIR) spectra of carbon samples were obtained using a PerkinElmer Spectrum 100 FTIR spectrometer (PerkinElmer, USA). The spectra were recorded from 4000 to 625 cm−1 at a resolution of 4 cm−1. Elemental analysis was carried out using a Thermo Finnigan Flash EA 1112 Series elemental analyzer. X-ray photoelectron spectroscopy (XPS) analysis of porous carbons was performed on a SPECS system operating at 15 kV and 10 mA. The pressure in the analysis chamber was less than 2 × 10−9 torr. The data processing was carried out with XPS peak 4.1 software and the core level spectra were fitted with mixed Gaussian–Lorentzian convoluted function (80/20) and Shirley function was used for background subtraction.
Boehm titration method25 was employed to quantify the surface functional groups of the prepared carbons. About 200 mg of the samples was immersed in 20 ml of 0.1 M solution of NaOH and HCl and stirred for 24 h. The suspension was filtered and the excess base and acid were titrated with HCl and NaOH respectively. Amount of acid and base that reacted with the carbon sample gives the number of basic and acidic sites respectively.
2.3 CO2 capture performance
Performance evaluation of the synthesized materials to separate CO2 from binary mixture of CO2 and N2 was investigated using a fixed-bed adsorption setup. The details of the experimental setup have been reported earlier.26 About 2 g of dry adsorbent, mixed with inert glass beads, was packed into the adsorption column. Prior to any adsorption study, the adsorbent was pretreated by passing pure N2 gas at 200 °C for 2 h. After this, the temperature of the adsorbent bed was reduced to the desired adsorption temperature under N2 atmosphere. Once the adsorption temperature was attained, the gas flow was switched to binary mixture of CO2 and N2 at a total flow rate of 80 ml min−1. Effect of temperature and concentration on the performance evaluation of the adsorbent was studied by varying the temperature from 30 °C to 100 °C and CO2 concentration from 5% to 12.5% by volume. Concentration of CO2 and N2 at the end of the column was monitored continuously as a function of time until saturation was reached. Desorption study was carried by raising the bed temperature to 200 °C and switching to N2 purge gas. The adsorbent bed was subjected to four consecutive adsorption–desorption cycles to evaluate their reusability. Dynamic CO2 adsorption capacity of the adsorbent was evaluated using the following equation:
 | (1) |
Carbon dioxide temperature programmed desorption (CO2-TPD) study of RF-700 was carried out on a Micromeritics AutoChem II 2920 chemisorption analyzer equipped with a thermal conductivity detector. Around 100 mg of the carbon sample was placed in a quartz reactor and pretreated under flow of pure helium gas at 200 °C. Hereafter the temperature was decreased to 30 °C and CO2 adsorption was carried out by switching to pure CO2 gas for 30 minutes. Desorption experiment was performed by switching back to He gas at a flow rate of 20 ml min−1 and increasing the temperature from 45 °C to 250 °C at a heating rate of 10 °C min−1.
2.4 Kinetic study
CO2 adsorption kinetics on the prepared carbons was investigated by employing three kinetic models namely, pseudo-first order, pseudo-second order and fractional order kinetic models. The Lagergren's pseudo-first order kinetic model is expressed as:27
 | (2) |
| qt = qe(1 − e−k1t) | (3) |
The pseudo-second order model can be written as:28
 | (4) |
 | (5) |
The fractional order kinetic model assumes adsorption rate to be affected by nth power of driving force and mth power of the adsorption time29,30 and is expressed as:
 | (6) |
 | (7) |
Based on normal standard deviation, an error function is calculated to ascertain the sufficiency of each model.
 | (8) |
2.5 Isotherm study
CO2 adsorption equilibrium for synthesized carbon adsorbents are described using various isotherm models namely Langmuir, Freundlich and Temkin models. One of the most widely used adsorption isotherm model is Langmuir isotherm. It is based on the assumption of monolayer adsorption taking place at a finite number of sites with no interaction among the adsorbed molecules. These adsorption sites are assumed to be energetically equivalent.31 The Langmuir isotherm equation can be represented as:
 | (9) |
Freundlich isotherm explains the non-ideal and reversible adsorption on energetically heterogeneous surface with non-uniform distribution of adsorption heat and affinities over the surface and is not restricted to monolayer adsorption.32 It can be written as:
| qe = KFP1/n | (10) |
Temkin isotherm describes the adsorption on heterogeneous surfaces with the assumption that adsorption heat of the molecules in the layer decreases linearly rather than logarithmically with coverage because of adsorbent–adsorbate interactions. Its derivation is characterized by a uniform distribution of binding energy.33 It can be written as:
qe = B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(KTP) ln(KTP)
| (11) |
Parameters of the above adsorption kinetic and isotherm models were obtained by nonlinear regression of the experimental data with the aid of OriginPro 8 software.
2.6 Thermodynamic study
Dependence of kinetic rate constants (k) with adsorption temperature can be explained by Arrhenius equation:| k = Ae−(Ea/RT) | (12) |
The Gibbs free energy change for the adsorption process can be obtained from the adsorption equilibrium constant by using the following equation:
ΔG° = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Keq) ln(Keq)
| (13) |
The classical van't Hoff equation relates the equilibrium constant with temperature according to the following equation:
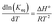 | (14) |
 | (15) |
| ΔG° = ΔH° − TΔS° | (16) |
From eqn (13) and (16), following relation is derived with the assumption that both ΔH° and ΔS° change slightly with temperature:34
 | (17) |
The thermal energy input (Q) required to regenerate the adsorbent is the sum of heat of desorption (Qst) and the sensible heat required to heat the adsorbent from the adsorption temperature up to temperature for desorption.
| Q = Qst + sensible heat | (18) |
Sensible heat requirement is a function of adsorbent's heat capacity, difference between adsorption and desorption temperatures and the adsorption capacity of the adsorbent material.35,36
 | (19) |
Heat of desorption is assumed to be equal to heat of adsorption.37 The isosteric heat of adsorption can be calculated from CO2 adsorption isotherms obtained at different temperatures by using Clausius–Clapeyron equation:38
 | (20) |
3. Results and discussion
3.1 Characterization of porous carbons
Textural properties of synthesized carbon materials were evaluated by N2 adsorption–desorption isotherms at liquid N2 temperature (−196 °C). N2 sorption isotherms of all the samples can be classified as a combination of type I and type IV isotherm, indicating the presence of both micropores and mesopores, with a hysteresis loop of type H4 (Fig. 2). Pore size distributions (PSDs) of the prepared carbons were obtained from BJH method using the adsorption branch of the isotherm and the results are presented in Fig. S1.† Carbonization at 400 °C and 500 °C resulted in carbons showing very small amount of N2 adsorption attributing to less developed porous structure while carbonization at or above 600 °C produced carbons with well-developed porosity. Small adsorption by RF-400 and RF-500 at low relative pressure P/Po of 0.05 indicated less microporosity in these samples. On the other hand, carbons obtained at carbonization temperature ≥600 °C exhibited significant adsorption at low relative pressure P/Po of 0.05 indicating presence of large number of micropores, in addition to mesopores as suggested by the hysteresis loop. | ||
| Fig. 2 N2 adsorption (closed symbols) and desorption (open symbols) isotherms at −196 °C of nanostructured carbons. | ||
As seen in Table 1, BET surface area, total pore volume, micropore volume and mesopore volume tend to increase with increase in carbonization temperature from 400 °C to 700 °C but further increase in carbonization temperature to 800 °C lead to decrease in the textural properties. Micropores contributed largely towards the total pore volume for samples obtained at carbonization temperature ≥600 °C. BET surface area and total pore volume of RF-700 were found to be 435 m2 g−1 and 0.22 cm3 g−1 with ca. 67% contribution from micropores (Vmicro = 0.148 cm3 g−1) respectively. RF-800 sample demonstrated a very small hysteresis loop indicating mainly the presence of micropores in this material and the same can be inferred from very small amount of mesopore volume as compared to micropore volume. RF-400 and RF-500 consisted mainly of mesopores having majority of the pore volume in pores of diameter above 10 nm while rest of the samples showed a well-developed PSD (<10 nm). On the other hand, for the carbon derived from RF resin without nanocasting technique, almost no adsorption of N2 was observed at liquid N2 temperature indicating this carbon to be completely non-porous material. This signifies that the carbons obtained from the same starting material under same conditions can range from completely non-porous material to highly porous material depending on the method employed for their synthesis.
| Sample | Textural parameters | Structural parameters | Elemental composition | Surface properties | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SBET (m2 g−1) | VP (cm3 g−1) | Vmicro (cm3 g−1) | Vmeso (cm3 g−1) | 2θ | d002 (nm) | C (%) | H (%) | O (%) | Acidity (meq g−1) | Basicity (meq g−1) | |
| a SBET: BET surface area; VP: total pore volume obtained at a relative pressure of 0.99; Vmicro: micropore volume obtained from difference between total pore volume and mesopore volume; Vmeso: mesopore volume obtained from BJH method using adsorption branch; 2θ: diffraction angle; d002: interlayer d-spacing of (002) diffraction plane. | |||||||||||
| RF-400 | 27 | 0.031 | 0.012 | 0.019 | 23.04 | 0.385 | 68.28 | 3.57 | 28.13 | 1.67 | 0.54 |
| RF-500 | 58 | 0.085 | 0.020 | 0.065 | 22.55 | 0.394 | 65.11 | 3.01 | 31.87 | 1.48 | 0.81 |
| RF-600 | 369 | 0.180 | 0.128 | 0.052 | 22.77 | 0.390 | 62.02 | 2.11 | 35.87 | 1.24 | 1.75 |
| RF-700 | 435 | 0.222 | 0.148 | 0.074 | 23.03 | 0.386 | 66.25 | 1.49 | 32.23 | 0.78 | 1.93 |
| RF-800 | 407 | 0.176 | 0.146 | 0.030 | 23.70 | 0.375 | 70.02 | 0.97 | 28.99 | 1.09 | 0.78 |
| RF-C | — | — | — | — | 24.12 | 0.368 | 83.66 | 1.49 | 14.83 | 0.85 | 0.88 |
Fig. 3 represents the powder XRD patterns of the synthesized carbon materials. All the samples show similar diffraction patterns with two broad peaks at ca. 23° and 43° corresponding to (002) and (100) diffraction planes respectively of graphitic carbon. Table 1 presents the 2θ values for (002) diffraction plane along with interlayer spacing (d002) values. Observed interlayer d-spacing values are larger than value for ideal graphite (d002 = 0.335 nm)39 indicating the presence of turbostratic structures in the carbon i.e. formation of fully disordered structures.40 Increase in d-spacing values leads to shifting of XRD peaks to lower angles. Carbonization up to 500 °C resulted in decrease in 2θ value and an increase in the d-spacing while further increase in carbonization temperature reduced the d002 values suggesting the formation of short ordered structures and more graphitic character at higher temperatures. The irregularity of the layer structures also increased as indicated by a decrease in the intensity of (002) diffraction plane. RF-C carbon sample exhibited very broad diffraction peak suggesting this carbon to be an amorphous material.
The synthesized carbons are nano-materials as suggested by the broadened diffraction peaks, which is due to very small crystallite size. Moreover, broadened peaks suggest the formation of amorphous carbon materials and these results are in good agreement with TEM results.
Transmission electron micrographs of prepared carbons can be seen in Fig. 4. Development of nanostructures can be clearly observed from the TEM images along with amorphous porous structure. But there is no such development of nanostructures in the carbon sample prepared without nanocasting technique thereby signifying the role of silica template in the development process of carbon materials.
SEM micrographs (Fig. S2†) of obtained carbons show the development of irregular pores on the surface that assist the adsorbate diffusion from bulk phase to the surface. Fine needle like structures are observed for carbons obtained from carbonization at or above 700 °C. However, RF-C sample is found to have very compact surface with very less porous structure.
All the prepared carbon samples show a weight loss of ca. 6–8% (Fig. S3†) up to temperature of 100 °C due to desorption of moisture and other adsorbed gases. There is an increase in the thermal stability of the materials with increase in the carbonization temperature with maximum stability being exhibited by RF-800 (up to 500 °C). On the other hand, among the prepared carbons RF-400 and RF-500 are the least thermally stable materials and show a maximum weight loss of ca. 50%. RF-700 and RF-800 exhibit maximum weight loss of 25% and 15% respectively even up to temperature of 900 °C. Carbon material obtained by direct carbonization of RF resin showed ca. 2 wt% loss up to 100 °C but exhibited similar thermal stability as that of RF-700 carbon.
Fig. S4† depicts the FTIR spectra of the porous carbons derived from RF resin at various carbonization temperatures. Small peak at 1056 cm−1 can be assigned to stretching vibration of alkoxy C–O bond while a peak at 1250 cm−1 corresponds to acyl or phenyl C–O bond. A band around 1540 cm−1 is observed attributing to stretching vibrations of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond of aromatic rings of quinone group. Peaks at 1770 cm−1 and 3000 cm−1 correspond to C
C bond of aromatic rings of quinone group. Peaks at 1770 cm−1 and 3000 cm−1 correspond to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration in carboxylic groups, anhydrides, lactones, etc. and C–H stretching vibration respectively. With increase in carbonization temperature, there is a decrease in the intensity of the band around 1540 cm−1 suggesting loss of C
O stretching vibration in carboxylic groups, anhydrides, lactones, etc. and C–H stretching vibration respectively. With increase in carbonization temperature, there is a decrease in the intensity of the band around 1540 cm−1 suggesting loss of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds present in the samples. This may be due to a decrease in the carbon content of the prepared carbons with increase in carbonization temperature. Similar results are obtained from elemental analysis of the carbons as shown in Table 1. There is a decrease in carbon content and an increase in oxygen content of the prepared carbons with increase in temperature of carbonization up to 600 °C. This could be due to cleavage of more carbon–carbon bonds than oxygen functionalities. On the other hand, further increase in carbonization temperature resulted in the opposite trend which is attributed to decomposition of oxygen containing groups at high temperatures of pyrolysis. In case of RF-C carbon, peaks for C–O and C
C bonds present in the samples. This may be due to a decrease in the carbon content of the prepared carbons with increase in carbonization temperature. Similar results are obtained from elemental analysis of the carbons as shown in Table 1. There is a decrease in carbon content and an increase in oxygen content of the prepared carbons with increase in temperature of carbonization up to 600 °C. This could be due to cleavage of more carbon–carbon bonds than oxygen functionalities. On the other hand, further increase in carbonization temperature resulted in the opposite trend which is attributed to decomposition of oxygen containing groups at high temperatures of pyrolysis. In case of RF-C carbon, peaks for C–O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond are very small as compared to other samples, demonstrating lesser oxygen functionalities which is in good accord with the elemental analysis. Majorly a broad band ca. 1540 cm−1 for stretching vibrations of C
O bond are very small as compared to other samples, demonstrating lesser oxygen functionalities which is in good accord with the elemental analysis. Majorly a broad band ca. 1540 cm−1 for stretching vibrations of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond is observed. This sample had very high carbon content and low oxygen content as compared to that of RF-700 indicating that presence of silica template effected the chemical composition of the obtained materials.
C bond is observed. This sample had very high carbon content and low oxygen content as compared to that of RF-700 indicating that presence of silica template effected the chemical composition of the obtained materials.
X-ray photoelectron spectroscopy (XPS) analysis was carried out for all the synthesized carbons to study the evolution of oxygen functional groups during carbonization process. Two typical peaks for carbon (C1s) and oxygen (O1s) are observed, around 285 and 532 eV respectively, in the survey spectra of the synthesized carbons (Fig. 5a). The absence of peak for Si suggests removal of silica via dissolution in NaOH solution.
 | ||
| Fig. 5 (a) Survey scan spectra of prepared carbons, and deconvoluted C1s spectra of (b) RF-400, (c) RF-500, (d) RF-600, (e) RF-700, (f) RF-800, and (g) RF-C. | ||
Fig. 5b–g show the C1s XPS spectra of nanostructured carbons and RF-C carbon. The C1s spectra of all the samples were deconvoluted into four well resolved peaks and their corresponding binding energy (B.E.), full width at half maximum (FWHM) and relative area contribution (A%) are reported in Table S1.† Peaks C1 and C2 are assigned for graphitic carbon and carbon in alcohol, phenol or ether groups respectively. Peak C3 corresponds to carbonyl or quinone groups and C4 corresponds to carboxyl, ester and/or lactone linkages.41 With increase in carbonization temperature from 400 °C to 500 °C, there is a drastic decrease in the relative area percentage of peak C1 from ca. 60% to 35.7% indicating decreased graphitic character, which has also been indicated by XRD results. Further increase in carbonization temperature resulted in increase in the relative area percentage of C1 peak and hence improvement in the graphitic character of the porous carbons. For RF-800, C1 peak has small area percentage of ca. 17.7% with the development of a new peak at ca. 283.4 eV for carbidic carbon. After C1 peak, relative area percentage is the maximum for peak C2 for all the prepared carbons suggesting that most of the carbon is linked to one oxygen atom by single bond. For carbons obtained at carbonization temperature ≥700 °C, no peak is observed at ca. 286.3 eV indicating the absence of carbonyl and/or quinone groups in these samples. In case of RF-C carbon, C1 and C2 peaks have similar relative percentage area as that of RF-700. But it contained carbon double bonded to oxygen in form of both carbonyl/quinone (ca. 15.3%) and carboxyl/ester (ca. 7.13%) unlike from RF-700. A considerable change is observed in C1s core level spectra of synthesized samples with carbonization temperature which indicates that condensation and cyclization of the aromatic ring structures take place during the carbonization process leading to the development of carbidic and graphitic carbon structures.
High resolution XPS spectra of O1s region of the carbon adsorbents are shown in Fig. 6. The O1s spectra were deconvoluted into three different peaks and their corresponding binding energy (B.E.), full width at half maximum (FWHM) and relative area contribution (A%) are listed in Table S2.† Peak O1 corresponds to carbonyl, ketone or lactone groups, peak O2 corresponds to oxygen of ether, phenol, alcohol and/or carboxyl oxygen of esters and/or anhydrides and peak O3 is attributed to oxygen in carboxyl groups.41 As seen in Fig. 6, there is an appreciable change in the nature of oxygen functionalities present on the carbon surface with increase in carbonization temperature. Increase in carbonization temperature from 400 °C to 500 °C lead to decrease in carboxylic content of the carbons as suggested by decrease in relative area percentage of O3 peak from ca. 28% to 16.9%. But further increase in temperature of carbonization up to 700 °C lead to increase in carboxylic content. No peak for carboxylic is observed for RF-800 sample indicating the conversion of carboxylic groups to lactone groups as indicated by large increase in relative area percentage of O1 peak. Peak O1 for RF-800 is only due to lactone group because other functional groups (i.e. carbonyl and quinone) attributing to O1 peak are already found to be absent for this carbon sample. As compared to RF-700 carbon, RF-C contained higher carbonyl or lactonic content and lower carboxylic content. Difference in these oxygen functionalities will affect the surface basicity of these carbons. Increase in lactone groups in RF-800 results in increase in surface acidity of this carbon sample as seen in Table 1. Surface acidity is found to decrease from 1.67 to 0.78 milli equivalents per gram (meq g−1) with increase in carbonization temperature from 400 °C to 700 °C. But further increase in temperature to 800 °C resulted in increase in surface acidity to 1.09 meq g−1. Carboxyl, lactone or lactols and phenol groups are responsible for surface acidity of carbon materials while functional groups like carbonyls, ethers, pyrones and chromenes contribute towards the surface basicity. Surface basicity of the prepared carbons tends to increase from 0.54 to 1.93 meq g−1 with increase in carbonization temperature from 400 °C to 700 °C and finally decreases to 0.78 meq g−1 for carbonization at 800 °C. In contrast, carbon obtained from direct carbonization of RF resin exhibited similar surface acidity as that of RF-700 but exhibited very low surface basicity of 0.88 meq g−1. For RF-700 and RF-600, amount of basic functional groups is higher than amount of acidic functional groups thereby indicating primarily basic nature of the carbon materials whereas rest of the samples have mainly acidic character.
 | ||
| Fig. 6 Deconvoluted O1s spectra of (a) RF-400, (b) RF-500, (c) RF-600, (d) RF-700, (e) RF-800, and (f) RF-C. | ||
3.2 CO2 capture performance
Dynamic CO2 adsorption capacity of the synthesized nanostructured carbon adsorbents was investigated by fixed-bed adsorption experiments at 30 °C under 10% (by volume) CO2 inlet concentration. Fig. 7a depicts the CO2 breakthrough curves of the prepared carbons. With increase in carbonization temperature from 400 °C to 700 °C, the breakthrough curves shift towards the higher times indicating an increase in adsorption capacity whereas it shifts to lower time with further increase in carbonization temperature to 800 °C, demonstrating decrease in CO2 adsorption capacity of RF-800. The breakthrough time (tb), time at which outlet concentration reaches 10% of the inlet adsorbate concentration, follows the order of RF-700 > RF-600 > RF-800 > RF-500 > RF-400 > RF-C. Equilibrium CO2 adsorption capacity (qe) of the prepared carbons, at 30 °C under 10% CO2, increased from 0.217 to 0.704 mmol g−1 with increase in carbonization temperature from 400 °C to 700 °C and then it decreased to 0.606 mmol g−1 for sample carbonized at 800 °C (Fig. 7b). RF-400 and RF-500 showed small adsorption capacities owing to their poor textural properties and high surface acidity. Alternatively, RF-600 and RF-700 samples exhibited improved textural properties and high surface basicity thereby resulting in improved CO2 capacities. Increasing the carbonization temperature to 800 °C leads to some deterioration in the textural properties with large decrease in basic functional groups thus reducing its affinity for acidic CO2 gas and hence showing a drop in adsorption capacity. Therefore, CO2 adsorption capacity of the prepared materials depends on their textural properties as well as their surface chemistry. Moreover under similar experimental conditions, RF-C carbon exhibited very low dynamic CO2 adsorption capacity of 0.152 mmol g−1. This could be attributed to almost non-porous carbon sample and this small uptake could be due to some macropores, mainly voids between the particles, present on the surface. | ||
| Fig. 7 (a) CO2 breakthrough profiles, and (b) CO2 adsorption capacity of synthesized carbons at 30 °C and 10% CO2 feed concentration. | ||
CO2 adsorption breakthrough curves for RF-700 as a function of adsorption temperature for varying CO2 feed concentrations (5–12.5% by volume) are presented in Fig. 8 and S5.† Longer breakthrough time appears at lower temperatures for a fixed feed concentration indicating drop in adsorption capacity with temperature. With increase in adsorption temperature from 30 °C to 100 °C, tb decreased from 2.12 minutes to 0.22 minutes for 5% feed concentration and for 12.5% feed concentration, tb decreased from 1.67 minutes to 0.21 minutes. Moreover, increase in feed concentration also lead to decrease in breakthrough time at a fixed temperature. It decreased from 2.12 minutes to 1.67 minutes with increase in feed concentration from 5% to 12.5%. But this decrease in tb is almost negligible at higher adsorption temperatures like at 100 °C the value is ca. 0.22 minutes at all inlet concentrations.
 | ||
| Fig. 8 Breakthrough profiles for RF-700 at 5% feed CO2 concentration at different adsorption temperatures. | ||
Dynamic adsorption capacity of RF-700 is also calculated from the breakthrough curves at all adsorption temperatures and inlet CO2 concentrations. It is observed that qe tends to increase with increase in feed CO2 concentration but decreases with increase in adsorption temperature (Fig. 9). Value of qe increased from 0.405 mmol g−1 to 0.761 mmol g−1 with increase in CO2 concentration from 5% to 12.5% at 30 °C adsorption temperature. This is attributed to increase in the driving force for the adsorption process i.e. the concentration gradient therefore leading to increased CO2 mass transfer rate across the boundary layer and within the adsorbent pores. On the other hand, decrease in qe with temperature at a fixed inlet concentration is due to exothermic nature of the adsorption process and it is favored at lower temperatures. Also with increase in adsorption temperature, both surface energy and CO2 diffusion rate increases thus decreasing the stability of CO2 on adsorbent surface and hence causing CO2 desorption. For 12.5% feed concentration, value of qe decreased from 0.761 mmol g−1 to 0.281 mmol g−1 on increasing temperature from 30 °C to 100 °C.
 | ||
| Fig. 9 CO2 adsorption capacity of RF-700 at different adsorption temperatures as a function of inlet CO2 concentration. | ||
Activated carbons obtained from fly ash demonstrated CO2 adsorption capacity of 0.93 mmol g−1 and 0.42 mmol g−1 at 30 °C and 75 °C respectively.42 RF-700 showed comparable adsorption capacity of 0.405 mmol g−1 at 75 °C and 12.5% feed concentration. This value was ∼1.8 times higher than adsorption capacity of commercial activated carbon (0.225 mmol g−1) at 75 °C under pure CO2 flow.23 For CO2 capture application from flue gas, dynamic capacities of the adsorbent materials are more pertinent at higher temperatures. Dynamic adsorption capacity of RF-700 at all temperatures is higher than dynamic capacities of synthetic carbon obtained from carbonization and steam activation of coal tar pitch and furfural.43 This synthetic carbon exhibited dynamic CO2 adsorption capacity of 0.61 mmol g−1 at 30 °C and 0.30 mmol g−1 50 °C under 15% CO2 concentration. Dynamic capacities of RF-700 are in good accord with literature reported values for carbon adsorbents evaluated under similar conditions.44
Also CO2 uptake of RF-700 at 75 °C under 12.5% CO2 concentration (0.405 mmol g−1) is comparable with dynamic adsorption capacity of isopropanol amine modified zeolite 13× (0.52 mmol g−1) and monoethanol amine modified zeolite 13× (0.45 mmol g−1) under 15% CO2 balance in He flow.9 However, monoethanol amine modified β-zeolite exhibited static CO2 uptake of 0.80 mmol g−1 at 30 °C and 1 bar.13 Amine impregnated silica adsorbents are found to exhibit higher CO2 adsorption capacity than the prepared carbons. For instance, polyethyleneimine (PEI) modified SBA-15 silica exhibited CO2 adsorption capacity of ∼2 mmol g−1 at 45 °C and 1 bar under static conditions.45 PEI impregnated monolith silica showed CO2 uptake of 3.75 mmol g−1, determined gravimetrically, at 75 °C and 5% CO2 concentration while tetraethylenepenta amine (TEPA) modified silica was evaluated for CO2 adsorption only under pure CO2 flow. There was a steady decrease in CO2 adsorption capacity during a 5 run adsorption–desorption cycle.46 In another work, TEPA modified MCM-41 silica also suffered from decrease in its CO2 uptake just after 6 adsorption cycles.47 Although amine modified silica materials have been reported to show very high CO2 uptakes as compared to other adsorbents, they suffer from the stability issue with respect to adsorption capacity over repeated cycles. However, carbon adsorbents prepared in the present work have been found to exhibit practically constant CO2 adsorption capacity over repeated cycles (as discussed in the next section).
For an efficient adsorption process, selectivity of CO2 over N2 is another significant factor besides adsorption capacity. Fig. 10a displays breakthrough curves of N2 and CO2 on RF-700 for adsorption at 30 °C and 50 °C under 12.5% feed CO2 concentration. N2 appeared instantly in the exit gas stream after the onset of adsorption process. This indicates very low N2 adsorption capacity of the adsorbent material. In contrast for adsorption at 30 °C, concentration of CO2 in exit gas stream was zero for ca. 2 minutes and increased gradually with time indicating adsorbent's affinity towards CO2. Moreover, concentration of N2 in the exit gas stream surpassed the N2 feed gas concentration. This is due to replacement of adsorbed N2 in the adsorbent by CO2 gas molecules.
It is important for an adsorbent material to maintain CO2 adsorption capacities in multiple adsorption–desorption cycles from practical application point of view. Fig. 10b demonstrates the CO2 adsorption capacity of RF-700 during multiple adsorption–desorption cycles at different adsorption temperatures and 10% feed concentration. Desorption was carried out at 200 °C under pure N2 gas. CO2 adsorption performance of RF-700 is almost unaltered for four cycles suggesting completely reversible adsorption process thereby indicating the reusability of these carbons in long-term operations.
Fig. S7† presents the CO2-TPD plot of RF-700 sample. Desorption peak in the temperature range of 75–175 °C is observed indicating chemisorption of CO2 on carbon materials48 which is attributed to covalent bond formation between the surface basic functionalities of carbon and CO2 gas molecules. Desorption peak is centred around 120 °C suggesting maximum CO2 desorption occurring at this temperature. XPS and Boehm titration results also confirm the presence of basic functional groups on the carbon surface.
3.3 Kinetic study
Kinetics of CO2 adsorption on RF-700 has been investigated by using three kinetic models. Fig. 11 presents the experimental CO2 adsorption capacity with time at 30 °C and different feed concentrations along with fitted curves obtained from all the three kinetic models while Fig. S6†presents the data for rest of the adsorption temperatures. The values of kinetic model parameters, correlation coefficients (R2) and associated errors (error %) are listed in Table S3.† Results indicate that fractional order kinetic model presents the best explanation for adsorption of CO2 on nanostructured carbons in fixed-bed system. As seen in Fig. 11 and S6,† for adsorption temperature of 30 °C and 50 °C pseudo-first order kinetic model overestimated the uptake of CO2 up to 5–6 minutes of adsorption process but it underestimated the CO2 uptake at 75 °C and 100 °C in the initial phase of adsorption process. During the final stage of adsorption, pseudo-first order kinetic model closely followed the experimental data at all adsorption temperatures and the equilibrium CO2 adsorption capacities were in close agreement with the experimental values. On the other hand, pseudo-second order kinetic model always overestimated the CO2 uptake on RF-700 and predicted very high equilibrium capacities as compared to the experimental values. Higher values of error % of both pseudo-first order and pseudo-second order kinetic models indicate that these models were not able to describe the adsorption process of CO2 on nanostructured carbons. | ||
| Fig. 11 Comparison of kinetic models for CO2 uptake on RF-700 at 30 °C as a function of feed concentration. | ||
For fractional order kinetic model, small value of error % and high R2 values indicated good conformity between experimental data and model predicted values. For all CO2 concentrations, adsorption rate constant kn was found to decrease with increase in adsorption temperature because of exothermic nature of adsorption process. At higher temperatures, adsorption rate may become faster but CO2 adsorbed is lesser due to faster desorption of CO2 from carbon surface. On the other hand, kn tends to increase with increase in CO2 concentration due to enhanced concentration gradient leading to faster diffusion of CO2 molecules into the adsorbent surface. Kinetic model parameters n and m demonstrate the effect of driving force and diffusion resistance respectively.49 Parameter n decreased with increase in adsorption temperature and was maximum at 30 °C suggesting maximum driving force at this temperature while it increased with increase in CO2 concentration. This could be attributed to increase in concentration gradient at high CO2 concentrations thereby leading to faster diffusion of CO2. Value of m indicates the fastness of adsorption process. With increase in CO2 concentrations, m tends to increase suggesting the faster adsorption of CO2 on RF-700 at high CO2 concentrations. Equilibrium CO2 adsorption capacities as predicted by fractional order model were also in good accord with the experimental values.
3.4 Isotherm study
The equilibrium adsorption data have been analyzed according to the nonlinear form of the isotherm models. The experimental adsorption data and model predicted data at different adsorption temperatures are shown in Fig. 12a and the calculated model parameters are reported in Table 2. Based on coefficient of determination (R2) for the studied isotherm models, Temkin isotherm has shown the best fit with the experimental data demonstrating energetically heterogeneous adsorbent surface. Temkin model constant b reflects bonding energy which further indicates type of adsorbate–adsorbent interaction and bonding energy up to 20 kJ mol−1 signifies physical adsorption process. Langmuir parameters qm (maximum monolayer adsorption capacity of adsorbents) and KL decreased with increase in temperature showing adsorption process to be exothermic in nature. This is also indicative of inverse relation between temperature and affinity between CO2 molecules and carbon. Freundlich parameter KF also decreased with increase in temperature suggesting favorable adsorption at lower temperatures. Value of n (Freundlich parameter) being higher than 1 implies the favorable adsorption process at all temperatures. | ||
| Fig. 12 (a) CO2 adsorption isotherm on RF-700 at different adsorption temperatures, and (b) isosteric heat of adsorption of CO2 on RF-700. | ||
| Model | Parameters | Temperature ( °C) | |||
|---|---|---|---|---|---|
| 30 | 50 | 75 | 100 | ||
| Langmuir | qm (mmol g−1) | 1.79 | 1.49 | 1.47 | 1.11 |
| KL (atm−1) | 6.12 | 5.00 | 3.13 | 2.82 | |
| R2 | 0.978 | 0.981 | 0.982 | 0.953 | |
| Freundlich | KF (mmol g−1 atm−1/n) | 3.13 | 2.51 | 2.19 | 1.61 |
| n | 1.50 | 1.41 | 1.25 | 1.22 | |
| R2 | 0.961 | 0.974 | 0.972 | 0.940 | |
| Temkin | KT (atm−1) | 55.84 | 52.13 | 43.89 | 41.63 |
| b (kJ mol−1) | 6.32 | 8.85 | 12.05 | 17.74 | |
| R2 | 0.989 | 0.986 | 0.997 | 0.985 | |
3.5 Thermodynamic study
Fig. S8† presents the Arrhenius plot for kinetic rate constants for CO2 adsorption obtained from fractional order kinetic model at all CO2 feed concentrations. The values of Arrhenius pre-exponential factor and activation energy are reported in Table 3. For adsorption at all CO2 concentrations, negative values of Ea are obtained because of the decreasing rate constant values with adsorption temperature and this trend is in agreement with literature.50,51| CO2 concentration (volume %) | A | Ea (kJ mol−1) | R2 |
|---|---|---|---|
| 5 | 0.0933 | −0.7 | 0.990 |
| 7.5 | 0.0545 | −2.6 | 0.996 |
| 10 | 0.0483 | −3.0 | 0.988 |
| 12.5 | 0.0463 | −3.5 | 0.960 |
Table 4 presents the thermodynamic parameters for CO2 adsorption on RF-700 as obtained from eqn (13) and (17). Standard enthalpy change and standard entropy change for the adsorption process were determined to be −4.2 kJ mol−1 and 0.02 kJ mol−1 K−1. The negative values of Gibbs free energy change at each adsorption temperature indicate the feasibility and spontaneity of the adsorption process. The value of ΔH° was also negative indicating the exothermic nature of the adsorption process. The positive value of ΔS° demonstrated the increase in randomness at the adsorbent–adsorbate interface and also adsorbent's affinity towards CO2.52 Small value of ΔS° indicated that there was no significant change in entropy.
| Temperature (°C) | ΔG° (kJ mol−1) | ΔH° (kJ mol−1) | ΔS° (kJ mol−1 K−1) |
|---|---|---|---|
| 30 | −10.1 | −4.2 | 0.02 |
| 50 | −10.6 | ||
| 75 | −10.9 | ||
| 100 | −11.6 |
Energy duty for CO2 desorption was calculated for RF-700 sample as it showed the best results for CO2 capture, by using eqn (18). The specific heat capacity of RF-700 was found to be 1.215 J g−1 K−1. Adsorption was carried out at 30 °C under 12.5% CO2 in N2 while desorption was carried out at 200 °C under pure N2 flow. Adsorption capacity of RF-700 under these conditions was found to be 0.76 mmol CO2 g−1. Hence the sensible heat energy required to heat the adsorbent for desorption was calculated to be 271.8 kJ per mol of CO2 captured. It is assumed that around 75% of the sensible heat required for heating the adsorbent can be recovered by direct or indirect heat exchanger.35 Therefore, the net sensible heat required for the system was estimated to be 67.9 kJ per mol of CO2 captured.
To calculate isosteric heat of adsorption, value of P is determined at multiple temperatures from isotherm for CO2 adsorption on RF-700 for a given qe and the slope is determined from the plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P against 1/T. The isosteric heat of adsorption for RF-700 is in the range of 15.1–16.8 kJ mol−1 with an average value of 15.74 kJ mol−1, demonstrating strong interaction between the carbon surface and CO2 gas molecules (Fig. 12b). With increase in surface coverage, there is small decrease in isosteric heat of adsorption which indicates energetically heterogeneous adsorbent surface. But at higher surface coverage, an increase in isosteric heat of adsorption is observed which is due to intermolecular interaction between the adsorbed CO2 molecules. Value of Qst for carbon materials have been reported to be in the range of 11–30 kJ mol−1.12,53–55
P against 1/T. The isosteric heat of adsorption for RF-700 is in the range of 15.1–16.8 kJ mol−1 with an average value of 15.74 kJ mol−1, demonstrating strong interaction between the carbon surface and CO2 gas molecules (Fig. 12b). With increase in surface coverage, there is small decrease in isosteric heat of adsorption which indicates energetically heterogeneous adsorbent surface. But at higher surface coverage, an increase in isosteric heat of adsorption is observed which is due to intermolecular interaction between the adsorbed CO2 molecules. Value of Qst for carbon materials have been reported to be in the range of 11–30 kJ mol−1.12,53–55
Thermal energy requirement for desorption is equal to 83.9 kJ per mol of CO2 captured or 1.9 MJ per kg of CO2 captured i.e. for desorption of 1 kg of CO2, energy equal to 1.9 MJ has to be supplied which is generated from the combustion of fossil fuels. As CO2 adsorption capacity at 30 °C was 0.76 mmol per g adsorbent = 0.03344 kg CO2 per kg adsorbent, energy required to desorb this much quantity of CO2 = 0.064 MJ. Assuming that bituminous coal is used as fossil fuel for energy production amount of CO2 generated is 0.0884 kg per MJ of energy.56 Hence CO2 generated to produce 0.064 MJ of energy for desorption is 0.0056 kg CO2. It can be concluded (on 1 kg adsorbent basis) that energy duty for desorption of 0.03344 kg CO2 requires 0.064 MJ of energy which leads to generation of 0.0056 kg CO2 from combustion of fossil fuel (bituminous coal) (detailed calculations are given in the ESI†).
4. Conclusions
Nanostructured carbon adsorbents were prepared from resorcinol–formaldehyde resin and silica template by nanocasting technique and were characterized for their textural, surface and chemical properties. XRD and TEM analysis confirmed the development of nanostructured carbon adsorbents having amorphous character whereas the presence of various oxygen functional groups on the carbon surface was proved by XPS analysis, FTIR analysis and surface functionality by Boehm titration. Maximum BET surface area and total pore volume were 435 m2 g−1 and 0.22 cm3 g−1 respectively for RF-700 carbon. Dynamic CO2 capture experiments were carried out under simulated flue gas composition at varying temperatures and carbon obtained by carbonization at 700 °C exhibited a dynamic CO2 adsorption capacity of 0.761 mmol g−1 at 30 °C and 0.405 mmol g−1 at 75 °C under 12.5% CO2 concentration. CO2 adsorption capacities of RF-700 decreased with increase in temperature due to exothermic nature of adsorption process while it increased with increase in CO2 feed concentrations because of increased driving force. Fast adsorption kinetics with complete and easy regeneration was observed for the prepared carbons making them potential candidates for CO2 capture from flue gas. Different adsorption kinetic models were fitted to experimental data of CO2 adsorption and fractional order kinetic model was found to describe the CO2 adsorption on prepared carbons over the entire adsorption region. Temkin isotherm model explained the adsorption of CO2 on RF-700 indicating the energetically heterogeneous adsorbent surface. Negative values of standard enthalpy change and standard Gibbs free energy change suggested the exothermic nature and feasibility of adsorption process respectively. Energy duty for CO2 desorption, estimated from the sensible heat requirement and isosteric heat of adsorption, was found to be 1.9 MJ per kg CO2.Acknowledgements
The authors gratefully acknowledge Department of Science and Technology (DST), New Delhi for financial support. Chitrakshi Goel acknowledges the financial support from DST-INSPIRE under its Assured Opportunity for Research Careers (AORC) scheme. Authors also thank Dr Samir Maity, Scientist, CSIR-Indian Institute of Petroleum, Dehradun for helpful discussions.References
- Q. Wang, J. Luo, Z. Zhong and A. Borgna, Energy Environ. Sci., 2011, 4, 42 CAS.
- J. D. Figueroa, T. Fout, S. Plasynski, H. McIlvried and R. D. Srivastava, Int. J. Greenhouse Gas Control, 2008, 2, 9 CrossRef CAS.
- J. C. Fisher, J. Tanthana and S. S. C. Chuang, Environ. Prog. Sustainable Energy, 2009, 28, 589 CrossRef CAS.
- D. Aaron and C. Tsouris, Sep. Sci. Technol., 2005, 40, 321 CrossRef CAS.
- V. Presser, J. McDonough, S.-H. Yeon and Y. Gogotsi, Energy Environ. Sci., 2011, 4, 3059 CAS.
- S. Sengupta, V. Amte, R. Dongara, A. K. Das, H. Bhunia and P. K. Bajpai, Energy Fuels, 2015, 29, 287 CrossRef CAS.
- S. Choi, J. H. Drese and C. W. Jones, ChemSusChem, 2009, 2, 796 CrossRef CAS.
- M. Sevilla, P. Valle-Vigón and A. B. Fuertes, Adv. Funct. Mater., 2011, 21, 2781 CrossRef CAS.
- R. Chatti, A. K. Bansiwal, J. A. Thote, V. Kumar, P. Jadhav, S. K. Lokhande, R. B. Biniwale, N. K. Labhsetwar and S. S. Rayalu, Microporous Mesoporous Mater., 2009, 121, 84 CrossRef CAS.
- J. R. Li, J. Sculley and H. C. Zhou, Chem. Rev., 2012, 112, 869 CrossRef CAS.
- M. B. Yue, Y. Chun, Y. Cao, X. Dong and J. H. Zhu, Adv. Funct. Mater., 2006, 16, 1717 CrossRef CAS.
- A. Wahby, J. Silvestre-Albero, A. Sepúlveda-Escribano and F. Rodríguez-Reinoso, Microporous Mesoporous Mater., 2012, 164, 280 CrossRef CAS.
- X. Xu, X. Zhao, L. Sun and X. Liu, J. Nat. Gas Chem., 2009, 18, 167 CrossRef CAS.
- R. Serna-Guerrero, Y. Belmabkhout and A. Sayari, Adsorption, 2010, 16, 567 CrossRef CAS.
- X. Xu, C. Song, J. M. Andrésen, B. G. Miller and A. W. Scaroni, Microporous Mesoporous Mater., 2003, 62, 29 CrossRef CAS.
- M. D. Hornbostel, J. Bao, G. Krishnan, A. Nagar, I. Jayaweera, T. Kobayashi, A. Sanjurjo, J. Sweeney, D. Carruthers, M. A. Petruska and L. Dubois, Carbon, 2013, 56, 77 CrossRef CAS.
- P. Davini, Carbon, 2002, 40, 1973 CrossRef CAS.
- M. G. Plaza, C. Pevida, C. F. Martín, J. Fermoso, J. J. Pis and F. Rubiera, Sep. Purif. Technol., 2010, 71, 102 CrossRef CAS.
- J. Lee, S. Han and T. Hyeon, J. Mater. Chem., 2004, 14, 478 RSC.
- T. Valdés-Solís and A. B. Fuertes, Mater. Res. Bull., 2006, 41, 2187 CrossRef.
- B. Xu, L. Peng, G. Wang, G. Cao and F. Wu, Carbon, 2010, 48, 2377 CrossRef CAS.
- G.-P. Hao, W.-C. Li, D. Qian and A.-H. Lu, Adv. Mater., 2010, 22, 853 CrossRef CAS.
- T. C. Drage, A. Arenillas, K. M. Smith, C. Pevida, S. Piippo and C. E. Snape, Fuel, 2007, 86, 22 CrossRef CAS.
- L. K. C. de Souza, N. P. Wickramaratne, A. S. Ello, M. J. F. Costa, C. E. F. da Costa and M. Jaroniec, Carbon, 2013, 65, 334 CrossRef CAS.
- M. V. Lopez-Ramon, F. Stoeckli, C. Moreno-Castilla and F. Carrasco-Marin, Carbon, 1999, 37, 1215 CrossRef CAS.
- C. Goel, H. Bhunia and P. K. Bajpai, J. Environ. Sci., 2015, 32, 238 CrossRef.
- S. Lagergren, K. Sven. Vetenskapsakad. Handl., 1898, 24, 1 Search PubMed.
- Y. S. Ho and G. McKay, Process Biochem., 1999, 34, 451 CrossRef CAS.
- A. Zhao, A. Samanta, P. Sarkar and R. Gupta, Ind. Eng. Chem. Res., 2013, 52, 6480 CrossRef CAS.
- A. Heydari-Gorji and A. Sayari, Chem. Eng. J., 2011, 173, 72 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1916, 38, 2221 CrossRef CAS.
- H. M. F. Freundlich, J. Phys. Chem., 1906, 57, 385 CAS.
- M. I. Temkin and V. Pyzhev, Acta Physicochim. URSS, 1940, 12, 327 CAS.
- S. Salvestrini, V. Leone, P. Iovino, S. Canzano and S. Capasso, J. Chem. Thermodyn., 2014, 68, 310 CrossRef CAS.
- R. Veneman, H. Kamphuis and D. Brilman, Energy Procedia, 2013, 37, 2100 CrossRef CAS.
- S. Sjostrom and H. Krutka, Fuel, 2010, 89, 1298 CrossRef CAS.
- M. Clausse, J. Merel and F. Meunier, Int. J. Greenhouse Gas Control, 2011, 5, 1206 CrossRef CAS.
- D. J. Fauth, M. L. Gray, H. W. Pennline, H. M. Krutka, S. Sjostrom and A. M. Ault, Energy Fuels, 2012, 26, 2483 CrossRef CAS.
- Y. Xia and R. Mokaya, Chem. Mater., 2005, 17, 1553 CrossRef CAS.
- B. Sakintuna and Y. Yürüm, Microporous Mesoporous Mater., 2006, 93, 304 CrossRef CAS.
- K. László, E. Tombácz and K. Josepovits, Carbon, 2001, 39, 1217 CrossRef.
- M. M. Maroto-Valer, Z. Lu, Y. Zhang and Z. Tang, Waste Manag., 2008, 28, 2320 CrossRef.
- M. Balsamo, T. Budinova, A. Erto, A. Lancia, B. Petrova, N. Petrov and B. Tsyntsarski, Sep. Purif. Technol., 2013, 116, 214 CrossRef CAS.
- A. Sayari, Y. Belmabkhout and R. Serna-Guerrero, Chem. Eng. J., 2011, 171, 760 CrossRef CAS.
- R. Sanz, G. Calleja, A. Arencibia and E. S. Sanz-Pérez, Appl. Surf. Sci., 2010, 256, 5323 CrossRef CAS.
- C. Chen, S. T. Yang, W. S. Ahn and R. Ryoo, Chem. Commun., 2009, 3627 RSC.
- M. B. Yue, L. B. Sun, Y. Cao, Y. Wang, Z. J. Wang and J. H. Zhu, Chem.–Eur. J., 2008, 14, 3442 CrossRef CAS.
- H. Chen, F. Sun, J. Wang, W. Li, W. Qiao, L. Ling and D. Long, J. Phys. Chem. C, 2013, 117, 8318 CAS.
- C. Goel, H. Bhunia and P. K. Bajpai, RSC Adv., 2015, 5, 46568 RSC.
- Q. Liu, J. Shi, S. Zheng, M. Tao, Y. He and Y. Shi, Ind. Eng. Chem. Res., 2014, 53, 11677 CrossRef CAS.
- E. R. Monazam, L. J. Shadle, D. C. Miller, H. W. Pennline, D. J. Fauth, J. S. Hoffman and M. L. Gray, AIChE J., 2013, 59, 923 CrossRef CAS.
- S. Suresh, V. C. Srivastava and I. M. Mishra, J. Chem. Eng. Data, 2011, 56, 811 CrossRef CAS.
- I. A. A. C. Esteves, M. S. S. Lopes, P. M. C. Nunes and J. P. B. Mota, Sep. Purif. Technol., 2008, 62, 281 CrossRef CAS.
- B. Guo, L. Chang and K. Xie, J. Nat. Gas Chem., 2006, 15, 223 CrossRef CAS.
- S.-C. Hsu, C. Lu, F. Su, W. Zeng and W. Chen, Chem. Eng. Sci., 2010, 65, 1354 CrossRef CAS.
- B. D. Hong and E. R. Slatick, Carbon Dioxide Emission Factors for Coal, Washington, DC, 1994 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra16255f |
| This journal is © The Royal Society of Chemistry 2015 |




