Mechanism of the Paal–Knorr reaction: the importance of water mediated hemialcohol pathway

Abstract

The Paal–Knorr synthesis of furan, pyrrole and thiophene rings is one of the most important methods of generating these very important heterocycles, but the mechanism of this reaction is not well understood. Though several mechanistic paths are suggested, the exact energy requirements of this reaction, the structural features of transition states associated with the cyclization step, have not been established, especially for furan and thiophene synthesis. In this work, we explore the mechanism of the Paal–Knorr method and establish the energy requirements, using quantum chemical methods. The Paal–Knorr reaction to give furans is endergonic by 3.7 kcal mol⁻¹ whereas the same reaction is exergonic for pyrrole and thiophene generation by 16.4 and 15.9 kcal mol⁻¹, using G2MP2 method. The cyclization step is associated with high energy barrier, however, explicit water participation reduces the barrier significantly. For example, under the neutral condition two water mediated pathways – (i) monoenol and (ii) hemiketal, are possible on the reaction leading to furan. The cyclization step in these two pathways require 28.9 and 27.1 kcal mol⁻¹, respectively. The ring formation step becomes highly favorable in the presence of H₃O⁺ with a barrier of only 11.5 kcal mol⁻¹ (solvent phase) from the monoenol to dihydrofuran derivative and 5.5 kcal mol⁻¹ (solvent phase) from hemiketal to dihydroxy dihydrofuran derivative. Similarly, a water mediated pathway involving the intermediacy of hemialcohols has been found to be energetically preferred mechanism for pyrrole and thiophene also.

---

Introduction

Organic compounds containing five membered heterocyclic rings are extremely important in chemistry.^1–3 Especially systems with furan, pyrrole and thiophene ring containing species have found extensive applications in generating pharmacologically important species using bioisosteric replacement. The pharmacophoric as well as the toxicophoric features originating from these rings were extensively explored in drug design and drug metabolism.⁴ Establishing synthetic procedures to generate polyfunctional furan, pyrrole and thiophene derivatives is an active research endeavour for organic and medicinal chemists. One common reaction to generate these three derivatives is the Paal–Knorr method^5,6 (Schemes 1–3), even though many alternative methods are reported in recent years,^7–9 the importance of this method in the synthesis of polysubstituted heterocycles continues to be high.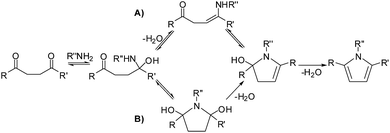

Scheme 1 Reported pathway for the Paal–Knorr synthesis of furans.

Scheme 2 Reported pathways for the Paal–Knorr synthesis of pyrroles – (A) the enamine pathway and (B) the hemiaminal pathway.

Scheme 3 Reported pathway for the Paal–Knorr synthesis of thiophenes.

The Paal–Knorr synthesis of furan was first reported in the year 1884 ^5,6 later it was modified for the synthesis of pyrrole and thiophene and its importance has been established over a period of time. Some of the recent applications of the Paal–Knorr synthesis include (i) synthesis of tri and tetrasubstituted furans by Stauffer and Neier¹⁰ (ii) synthesis of 1,2,3,5-tetrasubstituted pyrroles by Braun et al.¹¹ (iii) carrying out the reaction under deep eutectic solvents by Handy and Lavender¹² (iv) utilizing sulfamic acid as a catalyst by Luo et al.¹³ (v) utilizing MgI₂ etherate under solvent-free conditions as a catalyst to perform unique chemoselective Paal–Knorr reaction by Zhang et al.¹⁴ (vi) synthesis of conjugated C3 symmetric aryl tripyrroles and aryl bipyrroles by Saroukou et al.¹⁵ (vii) synthesis of substituted furans by successively recycled waste as a catalyst by Chen et al.¹⁶ (viii) synthesis of fully substituted symmetrical thiophenes via chemoselective Paal–Knorr approach by Ramulu et al.¹⁷ etc. Microwave assisted five membered heterocyclic ring synthesis using the Paal–Knorr reagents is also being reported.^18,19 Ionic liquids are also being adopted for the Paal–Knorr synthesis under green conditions.^20–22 Many articles are appearing where transition metal catalysts are being employed in reactions involving the Paal–Knorr method for five membered ring generation.^23–30 Use of nano catalysts^31–33 and organo-catalysts^34,35 is also being practised for the Paal–Knorr synthesis. Green chemistry methods employing nanomagnetically modified sulfuric acid³⁶ and water³⁷ catalysts for the Paal–Knorr pyrrole synthesis were also reported. Very recently, catalyst and solvent-free conditions have been employed to synthesize underivatized and N-substituted pyrroles by Cho et al.³⁸ The importance of this synthetic reaction is highlighted in the synthesis of the drugs Atorvastatin (anti-triglyceride),^39–41 Aloracetam (anti-Alzheimer's),⁴² Prodigiosin (anti-bacterial, anti-fungal and anti-malarial)^43,44 and Roseophilin (anti-tumour) (Fig. 1).^43,45–47 For example, innovative strategies are being developed for the economically viable, eco-friendly and easy bulk production of Atorvastatin using second generation synthetic procedures, which also involve the Paal–Knorr method.^48,49

Fig. 1 Drugs synthesized using the Paal–Knorr method.

Though the importance of the Paal–Knorr synthetic procedure was clear, very few studies were carried out to explore the mechanism of this reaction. A commonly accepted mechanism for the Paal–Knorr furan synthesis involved the ring closure of monoenol^50,51 followed by water elimination. Amarnath and Amarnath challenged this mechanism on the basis of the differences in the reaction rates of diastereomers and proposed a pathway involving protonation of one of the carbonyls followed by the electrophilic attack at the protonated carbonyl by the enol at the carbonyl center (Scheme 1).⁵² In the case of pyrrole synthesis the reaction between 1,4-diketone and amine is expected to yield an initial hemiaminal which may (a) get cyclised directly or (b) after the formation of an enamine (Scheme 2).^53,54 Quantum chemical studies on this reaction supported the hemiaminal path on a relative scale.⁵⁵ On the thiophene generation path, no studies on the mechanism have been reported, but the generally suggested path (Scheme 3) is quite similar to that of furan synthesis. Clearly, no common theme is being considered for the three reactions. In the synthetic pathways leading to the pyrrole and the thiophene rings, a heteroatom external to 1,4-diketone is involved. In the case of furan ring synthesis also it may be expected that none of the original oxygen atoms of the 1,4-diketone may be a part of the furanic oxygen. However, all the mechanistic paths proposed till now suggested pathways involving one of the oxygens of 1,4-dicarbonyls as a part of final product furan, this leads to many intriguing questions.

Initial quantum chemical free energy studies at G2MP2 level indicated that the Paal–Knorr furan synthesis is an endergonic process by about ∼3.7 kcal mol⁻¹, whereas the pyrrole and thiophene synthetic processes are exergonic by about ∼16.4 and ∼15.9 kcal mol⁻¹, respectively. What are the barriers of these reactions on the respective potential energy surfaces? Is there any common mechanism? What are the structures and the relative energies of the reactive intermediates? What is the role of protonated environment and what is the role of water in the reaction? These factors were not explored. In this article, we report the energy profiles of these reversible reactions and establish the mechanism using density functional methods.

Results and discussion

Initially, the overall free energy change in three reactions under gas phase and under implicit solvent phase conditions were estimated using three levels of quantum chemical analysis. It is clear from Table 1 that the furan ring formation is an endergonic process, whereas the pyrrole and thiophene ring forming reactions are exergonic processes. Also, the data indicates that spontaneity of these reactions are in the order furan < pyrrole ≈ thiophene. The M06 data is only marginally different for all the reactions with reference to the G2MP2 data, and hence, the results from M06 method will be used in the manuscript. The overall free energy values of the reactions do not differ much under implicit solvent and under the gas phase conditions.

Table 1 The free energy change (ΔG) values of the Paal–Knorr reactions (under gas phase and implicit water conditions) leading to the formation of furan, pyrrole and thiophene, estimated using various levels of quantum chemical analysis

S. No.	Method	ΔGfuran^b (kcal mol^−1)		ΔGpyrrole^b (kcal mol^−1)		ΔGthiophene^b (kcal mol^−1)
		Gas	Solvent	Gas	Solvent	Gas	Solvent
a The 6-311+G(2df,3pd) basis set is employed at all levels.b The overall free energy changes reported are for (i) furan w.r.t. 1,4-diketone; (ii) pyrrole w.r.t. ketone–imine and (iii) thiophene w.r.t. 1-keto-4-thioketone. See ESI for the ΔG value for pyrrole w.r.t. 1,4-diketone + amine.
1	B3LYP^a	0.4	1.3	−18.5	−18.8	−17.7	−17.6
2	M06^a	4.4	4.6	−15.1	−15.7	−12.4	−13.0
3	G2MP2	3.5	3.7	−15.2	−16.4	−15.1	−15.9

---

Mechanism of furan generation from 1,4-diketones

To analyse the electronic structure and reactivity of 1,4-diketones, 2,5-dimethyl-1,4-diketone (1) has been taken as a model system. The 3D structure of the most stable conformer of compound 1 is given in Fig. 2. Compound 1 is characterised by two weak intramolecular electrostatic interactions (∼3.0 Å and ∼3.2 Å) between the oxygen atom at one carbonyl center and the carbon atom at the other carbonyl center. These weak interactions are originating from the electron deficient p orbital of the carbon centers and the electron rich oxygen atoms. As can be expected, the 2,5-dimethylfuran (2) is a flat molecule with 6 π electron delocalisation.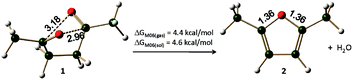

Fig. 2 The Paal–Knorr reaction for the synthesis of 2,5-dimethylfuran. The distances are given in Å (refer Table 1 for energies).

The free energy required for the formation of furan 2 from diketone 1 after the release of a water molecule is about 4.4 kcal mol⁻¹ (under gas phase) and 4.6 (under solvent phase) at M06 level of theory. Thus this reaction is endergonic reaction, surprisingly, no report till now established the endergonic character of this synthetic pathway. Considering that this reaction is being frequently reported, the endergonic character is not generally expected, this fact leads to several queries regarding the driving force for this reaction. Based on physical organic chemistry analysis a few proposed pathways are available in literature,⁵² which need to be elaborated to obtain atomic level details of the reaction mechanism. Six different pathways can be envisaged for the ring closure of 1,4-diketones to yield the furan ring – three pathways based on the initial monoenol formation (Scheme 4) and three more based on the initial hemiketal formation (Scheme 5) – (i) conversion of one of the keto groups to enol followed by cyclization, (ii) water assisted ring closure of the monoenol isomer, (iii) ring closure in proton catalysis conditions, (iv) ring closure after the initial formation of hemiketal derivative (v) water mediated hemiketal pathway and (vi) ring closure after the initial formation of hemiketal derivative in proton catalysis conditions. The potential energy surfaces of these pathways were explored in detail, the results are discussed in the following sections.

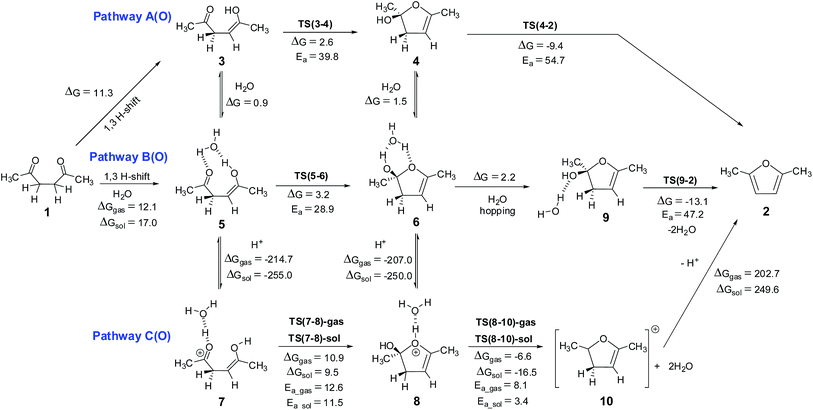Scheme 4 Monoenol pathways for the Paal–Knorr synthesis of furan – pathway A(O) without explicit water, pathway B(O) with explicit water and pathway C(O) under proton catalysis condition. The energy values (kcal mol⁻¹) are obtained using M06 method. The corresponding values obtained using B3LYP method are given in ESI.† The 3D structures of the transition states are given in Fig. 3.

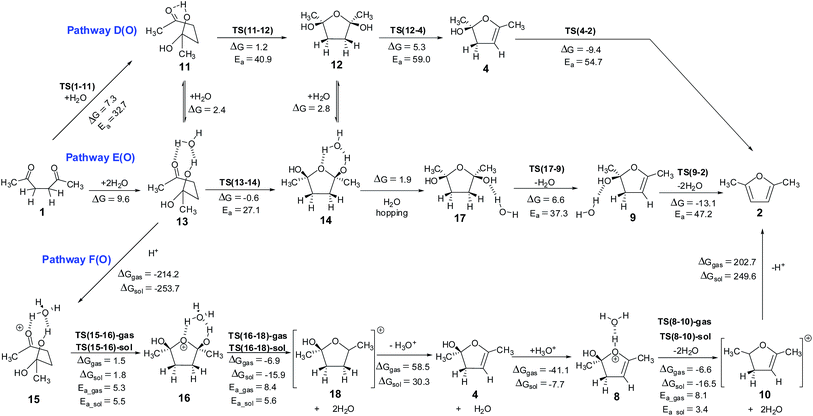Scheme 5 Hemiketal pathways for the Paal–Knorr furan synthesis – (i) pathway D(O) without explicit water, (ii) pathway E(O) with explicit water and (iii) pathway F(O) under proton catalysis conditions. The energy values (kcal mol⁻¹) are obtained using M06 method. The corresponding values obtained using B3LYP method are given in ESI.† The 3D structures of the transition states are given in Fig. 4. Structures 12, 14, 16 and 17 with cis arrangement of –OH groups are employed in this scheme. The corresponding reaction pathways for the trans arrangement are given in ESI.†

Monoenol pathway. Ketones are known to exist in keto–enol equilibrium. The monoenol tautomer 3 of compound 1 is characterized by intramolecular hydrogen bond interaction with a bond length of 1.87 Å (Fig. S1, ESI†). The energy difference between acetaldehyde and vinylalcohol is reported to be of the order of 16 kcal mol⁻¹,⁵⁶ it is generally considered that any keto–enol pair whose energy difference is less than 16 kcal mol⁻¹ is a feasible tautomerisation process.^57–59 In compound 1, the keto–enol energy difference (i.e. ΔG between 1 and 3) is estimated to be 11.3 kcal mol⁻¹, thus indicating that keto–enol tautomerism is an accessible process in 1,4-diketones.

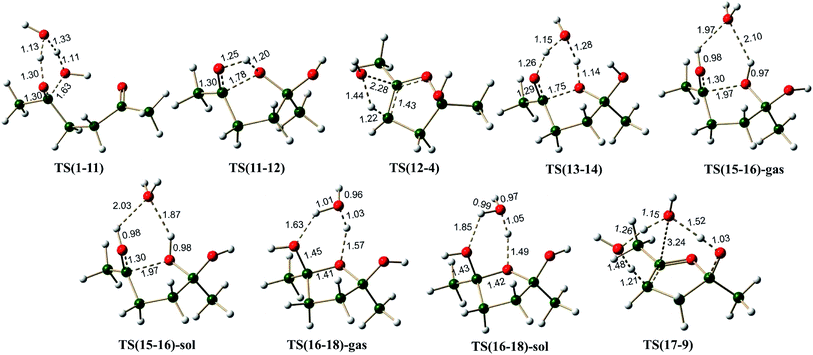
The monoenol 3 can give the cyclized intermediate 4 through a transition state TS(3-4), which involves (i) transfer of proton from the enolic oxygen to the carbonyl oxygen and (ii) the attack of enolic oxygen at the carbonyl carbon. The energy barrier for this cyclization reaction (pathway A(O), Scheme 4) is about ∼40.0 kcal mol⁻¹. The C⋯O bond length is 1.97 Å and the O⋯H(O) bond length is 1.30 Å in TS(3-4) (Fig. 3). The simultaneous hydrogen transfer and oxygen attack from the enolic OH group is a highly strained process, hence, it can be envisaged that such a process can be assisted by the participation of a water molecule. Calculations along pathway B(O) (Scheme 4) indicated that the proton transfer through a water molecule reduces the barrier to ∼29.0 kcal mol⁻¹ via the transition state TS(5-6) (Fig. 3). TS(5-6) is characterized by a C⋯O bond length of 1.97 Å, elongated H–O bonds of water and a network of hydrogen bonds through water molecule, which clearly facilitates the proton transfer as well as the oxygen attack. Thus it can be concluded that the participation of a water molecule is essential for the reaction.

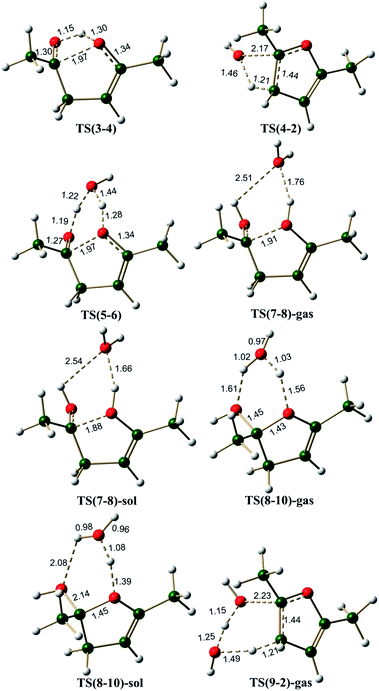Fig. 3 The 3D structures of the transition states on the potential energy surface of the monoenol pathways for the Paal–Knorr synthesis of furan. The distances are given in Å.

The Paal–Knorr synthesis is known to take place in mild acidic conditions.^1–3,60 The mechanisms considered by Amarnath and Amarnath were all in the protonated enolic state. Hence, the quantum chemical calculations were repeated under the H⁺ and H₃O⁺ conditions (pathway C(O), Scheme 4). The pathway C(O) involves proton catalysis, hence, it was explored under both gas phase and under implicit solvent (water, ε = 80.4) conditions. Compound 4 with H⁺ on furan ring oxygen does not lead to any stable structure under gas phase conditions (presumably owing to a very shallow potential well associated with this intermediate). Under the H₃O⁺ conditions, however, the cationic species (8) is stable, and hence, the barrier for its formation from 7 could be estimated through the transition state TS(7-8)-gas (under gas phase conditions) and TS(7-8)-sol (under solvent phase conditions). On the pathway C(O), under gas phase conditions, the cyclization step is an endergonic process involving 10.9 kcal mol⁻¹, with a barrier of 12.6 kcal mol⁻¹ via transition state TS(7-8)-gas. The same cyclization step under implicit water phase conditions was also observed to be an endergonic process by 9.5 kcal mol⁻¹, with an energy barrier of 11.5 kcal mol⁻¹ via transition state TS(7-8)-sol. During the cyclization, it is observed that the water molecule migrates from the carbonyl OH⁺ center to the enolic OH center. In the transition states TS(7-8)-gas and TS(7-8)-sol, the water molecule bridges the two OH groups (Fig. 3). Clearly the cyclization step along pathway C(O) under solvent phase conditions is more favorable than in gas phase conditions, also it requires very small barrier (11.5 kcal mol⁻¹), much less than the other two neutral monoenol pathways (39.8 and 28.9 kcal mol⁻¹ along pathways A(O) and B(O), respectively). The 3D structures of TS(5-6) and TS(7-8) (Fig. 3), clearly demonstrate that the role of water molecule is to stabilize a conformation for the cyclization process. The 3D structures of 5 and 7 further support this particular observation. The above mentioned observations clearly establish the importance of explicit water as well as the importance of protonated environment under solvent phase conditions in the Paal–Knorr synthesis of furan.

The neutral paths, pathway A(O) and B(O), lead to intermediates 4 and 9 respectively, which need to undergo water elimination. Intermediate 4 can undergo cis water elimination via TS(4-2) with a very high energy barrier of 54.7 kcal mol⁻¹. A water assisted cis water elimination from the intermediate 9 was found to require an energy barrier of 47.2 kcal mol⁻¹ (TS(9-2)), comparatively lower to the direct water elimination step. Alternatively, dehydration process can take place with proton catalysis (pathway C(O)), as it has been reported that the Paal–Knorr furan synthesis is normally carried out under aqueous acidic conditions with protic acids such as aqueous sulfuric or hydrochloric acid, or anhydrous conditions with a Lewis acid or dehydrating agent.^1–3,60,61 The cyclized protonated intermediate 8 can undergo water assisted dehydration to give an intermediate 10. This step is exergonic under both gas phase and implicit solvent phase conditions, involving the energy barriers of 8.1 (TS(8-10)-gas) and 3.4 (TS(8-10)-sol) kcal mol⁻¹, respectively. The overall reaction free energy from 7 to 10 is endergonic by 4.3 kcal mol⁻¹ under gas phase conditions, but it is exergonic (highly favorable) by 7.0 kcal mol⁻¹ under implicit solvent conditions. This clearly establishes that the polar environment (low dielectric constant medium) facilitates the cyclization and the water elimination steps and this stabilizing force could be the driving force for the furan ring formation, though the overall reaction is endergonic. The intermediate 10 can further loose a proton to give furan 2. This step is endergonic by 202.7 kcal mol⁻¹ under gas phase condition (249.6 kcal mol⁻¹ under implicit solvent phase condition). Initially, during H⁺ addition (5 → 7 reaction step), the system gains 214.7 kcal mol⁻¹ under gas phase condition (255.0 kcal mol⁻¹ under implicit solvent phase condition) and towards the end the system loses 202.7 kcal mol⁻¹. Hence, there is a balancing act. Overall the reaction is endergonic by only 4.4 kcal mol⁻¹ (4.6 kcal mol⁻¹ under solvent phase conditions).

Hemiketal pathway. Considering that the pyrrole and the thiophene synthetic procedures using the Paal–Knorr method involve the participation of external substrates, it may be considered that external water molecule probably is participating in the case of furan also (surprisingly such a mechanism was not considered till now). This can happen through the formation of a hemiketal intermediate, Scheme 5 shows the possible reaction pathways from 1. Addition of a water molecule to 1,4-diketone leads to the formation of a hemiketal 11 with an endergonic value of 7.3 kcal mol⁻¹ and energy barrier of 32.7 kcal mol⁻¹ via TS(1-11) (Fig. 4). Hemiketal 11 can have an orientation of –CH₃ and –OH groups such that after cyclization it can lead to tetrahydrofuran 12 having cis or trans orientation w.r.t. –OH groups. Keeping this stereochemistry aspect in mind all the calculations were carried out maintaining the cis orientation (both the –OH groups on the same side of the plane, stabilizing the molecule via an intramolecular H-bond). The results of the corresponding trans orientation are given in ESI.† Cyclization of 11 leads to the 2,5-dihydroxy derivative of tetrahydrofuran 12, with an endergonic value of 1.2 kcal mol⁻¹ and with a barrier of 40.9 kcal mol⁻¹ (through the transition state TS(11-12), Fig. 4). Alternatively, this path also may be facilitated by the direct participation of one water molecule (pathway E(O)). On this pathway, formation of the hemiketal is an endergonic process (by 9.6 kcal mol⁻¹), the cyclization is an exergonic process (−0.6 kcal mol⁻¹) and the activation energy of the cyclization is 27.1 kcal mol⁻¹ (through the transition state TS(13-14)), leading to an intermediate 14. This data clearly indicates that the water participation facilitates the cyclization in hemiketal pathway also. Hemiketal pathway involving proton catalysis (pathway F(O)) under gas phase conditions and solvent conditions was also explored. Under proton catalysis conditions the cationic species 15 (with H₃O⁺) can cyclise to give 16. The energy barrier for the cyclization process was calculated to be 5.3 kcal mol⁻¹ under gas phase conditions and 5.5 kcal mol⁻¹ under solvent phase conditions. Clearly cyclization step is quite feasible under proton catalysis conditions in comparison to the corresponding neutral conditions.

Fig. 4 The 3D structures of the transition states on the potential energy surface of the hemiketal pathways for the Paal–Knorr synthesis of furan. The distances are given in Å.

The neutral hemiketal pathway D(O) lead to an intermediate 4, after cis water elimination from 12. This step requires a high energy barrier of 59.0 kcal mol⁻¹ via TS(12-4). Pathway E(O) involves water mediated cis water elimination from 17 leading to an intermediate 9, having an energy barrier of 37.3 kcal mol⁻¹. The water mediation significantly reduced the energy barrier for the dehydration step. Intermediates 4 and 9 can further undergo water elimination very similar to in monoenol pathway. On the proton catalysis pathway F(O), the cyclized protonated intermediate 16 can undergo water assisted dehydration to give an intermediate 18. This step is exergonic under both gas phase and implicit solvent phase conditions, involving the energy barriers of 8.4 (TS(16-18)-gas) and 5.6 (TS(16-18)-sol) kcal mol⁻¹, respectively. This intermediate 18 can further loose a proton in the form of H₃O⁺ to give 4. Species 4 can further lead to 8 under H₃O⁺ conditions. The cyclized protonated intermediate 8 can undergo water assisted dehydration to give an intermediate 10 which can further loose a proton to give furan 2. Hence, pathway F(O) is the most energetically favorable path for the formation of furan from 1,4-diketones.

From the above analysis of six different pathways for the Paal–Knorr synthesis of furan, it can be concluded that the ring cyclization step is quite favorable under proton catalysis conditions, pathway C(O) and pathway F(O). The proton catalysed hemiketal path under solvent conditions, pathway F(O) requires an energy barrier of only 5.5 kcal mol⁻¹ for the ring cyclization step. Whereas, the energy barrier for the cyclization step in the proton catalysed monoenol pathway under solvent phase conditions (pathway C(O)) was calculated to be 11.5 kcal mol⁻¹. This suggests that pathway involving hemiketal formation needs to be considered extensively in all future studies. It is worth experimentally exploring the possibility of external water molecule supplying the oxygen atom of the furan molecule on the Paal–Knorr furan synthetic process.

Mechanism of pyrrole generation from 1,4-diketones

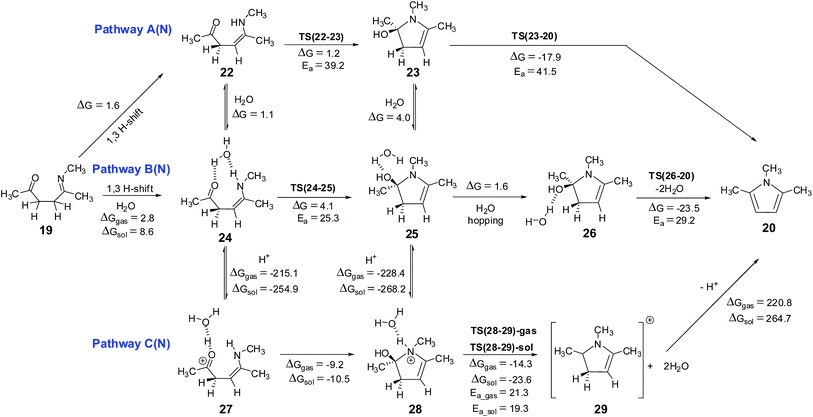
The reaction between 1,4-diketones and amines lead to the formation of imine (19), the overall energy of the reaction for the formation of pyrrole 20 from imine 19 is found to be exergonic by 15.1 kcal mol⁻¹ (under gas phase conditions) and 15.7 kcal mol⁻¹ (under implicit solvent phase conditions) at M06 level (Table 1, Fig. 5). The overall energy of the reaction between 1,4-diketones (1) and methylamine to give pyrrole 20 was also found to be highly exergonic (Table S1, ESI†). Experimental and theoretical studies (with no explicit water mediation) on the reaction supported a mechanism involving hemiaminal formation.^53–55 Six different pathways can be envisaged for the Paal–Knorr synthesis of pyrroles (pathways A(N), B(N), C(N), D(N), E(N) and F(N)).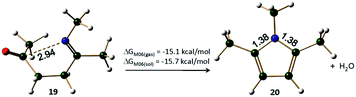

Fig. 5 The Paal–Knorr reaction for the synthesis of 1,3,5-trimethylpyrrole. The distances are given in Å (refer Table 1 for energies).

The role of water in the cyclization step of the reaction was not explored in the previous studies, thus the cyclization barriers reported were quite high for a highly spontaneous reaction exergonic by 15.7 kcal mol⁻¹. Encouraged by a significant decrease in the barrier for the furan generation in the presence of water, detailed studies on the water participation in pyrrole generation have been taken up. The Paal–Knorr reaction to give pyrrole is not reported under proton catalysis conditions. Such a possibility was recently suggested by Akbaşlar and coworkers, though they did not employ explicit acidic medium in the reaction.³⁷ Considering the basic nature of the imine and enamine intermediates, this pathway is a challenging process, which is supported by the difficulties encountered during the computational analysis. The six distinct processes of cyclization studied are (i) cyclization of an enamine intermediate directly (pathway A(N)) (ii) cyclization of an enamine intermediate with the help of water (pathway B(N)), (iii) cyclization of an enamine intermediate with proton catalysis (pathway C(N)), (iv) direct hemiaminal cyclization (pathway D(N)), (v) water assisted cyclization of hemiaminal (pathway E(N)) and (vi) cyclization of hemiaminal derivative in proton catalysis conditions (pathway F(N)).

Enamine pathway. The reaction between ketone and amine is known to give imine, in the case of 1,4-diketone, single water elimination can lead to the formation of an imine 19 (formation of 19 may be happening through an initial formation of hemiaminal, 21). Imine 19 is 6.5 kcal mol⁻¹ less stable than the two starting materials 1 and methylamine. Scheme 6 shows the possible mechanism along the pathways A(N), B(N) and C(N), starting from imine 19. Imine–enamine tautomerism in imine 19 to give enamine 22 is marginally endergonic by about 1.6 kcal mol⁻¹. For comparison, the imine–enamine tautomer energy difference in methylamine is ∼3.9 kcal mol⁻¹ in favor of imine.^57,62 In the enamine 22, the intramolecular hydrogen bond (∼2.1 Å) stabilizes the tautomer. The enamine 22 can cyclize directly (pathway A(N)) to give 23, which is about 1.2 kcal mol⁻¹ less stable. The energy barrier for the cyclization is estimated to be about 39.2 kcal mol⁻¹ via TS(22-23) (Fig. 6), the transition state involves an attack of lone pair of electrons from the –NHR center at the carbonyl carbon of the enamine 22. This pathway is also associated with a transfer of hydrogen from the –NHR center to the oxygen atom of the carbonyl group. This barrier is very high because of the two simultaneous processes, leading through a strained four membered cyclic transition state. Structure 22 is not readily suitable for cyclization. Water can assist this process and release strain significantly. As shown in pathway B(N), the cyclization step demands only 25.3 kcal mol⁻¹ barrier in the presence of water, thus facilitating the formation of the C–N bond, leading to a less stable (by 4.1 kcal mol⁻¹) intermediate 25.

Scheme 6 Enamine cyclization pathways for the Paal–Knorr pyrrole synthesis – pathway A(N) without explicit water, pathway B(N) with explicit water and pathway C(N) under proton catalysis conditions. The energy values (kcal mol⁻¹) are obtained using M06 method. The 3D structures of transition states are given in Fig. 6. The corresponding values obtained using B3LYP method are given in the ESI.†

Fig. 6 The 3D structures of the transition states on the potential energy surface of the enamine pathways for the Paal–Knorr synthesis of pyrrole. The distances are given in Å.

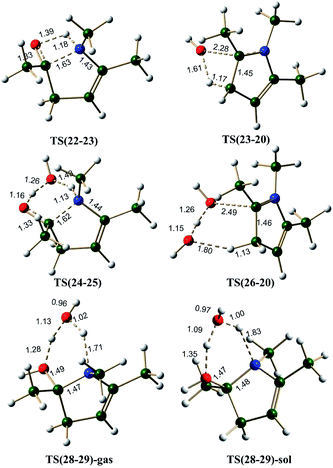
On the pathway A(N), the cyclized intermediate 23 can undergo cis water elimination via TS(23-20), to give pyrrole 20. This step involves a high energy barrier of 41.5 kcal mol⁻¹. The intermediate 25 on the pathway B(N), leads to 26 which can lose water (cis elimination, with the help of an external water molecule) to give the pyrrole with an energy barrier of 29.2 kcal mol⁻¹. Water assistance significantly reduces the energy barrier for the dehydration step very similar to furan pathways.

The Paal–Knorr pyrrole formation pathway was also considered under proton catalysis conditions (pathway C(N)). The cationic specie (27) under H₃O⁺ condition can cyclize to form 28. On the pathway C(N), the cyclization step is an exergonic process (contrary to pathway C(O) for furan formation) by 9.2 and 10.5 kcal mol⁻¹, under gas phase and implicit solvent phase conditions, respectively. All attempts to identify transition state for the cyclization step (on the potential energy surface) under proton catalysis condition failed, leading to the intermediate 28. Due to the highly exergonic nature of the cyclization step under proton catalysis conditions, this process can be considered to be spontaneous. The cyclized protonated intermediate 28 can undergo water assisted dehydration to give an intermediate 29. This step is exergonic under both gas phase and implicit solvent phase conditions, involving the energy barriers of 21.3 (TS(28-29)-gas)and 19.3 (TS(28-29)-sol) kcal mol⁻¹, respectively (Fig. 6). The activation barrier for this step is reasonably high as compared to TS(8-10) (furan synthetic pathway C(O)) under both gas phase and implicit solvent phase conditions. The reason for this can be attributed to over-pyramidalization in case of TS(28-29) (pyrrole synthesis) as compared to TS(8-10) (furan synthesis) (Fig. S3, ESI†). The overall reaction free energy from 27 to 29 is exergonic by 23.5 and 34.1 kcal mol⁻¹ under gas phase and implicit solvent conditions, respectively. The intermediate 29 can further loose a proton to give pyrrole 20.

Hemiaminal pathway. The hemiaminal (21) may be generated in a reaction between 1,4-diketone and methylamine directly (involving a free energy barrier of 26.4 kcal mol⁻¹ via TS(1-21), Scheme 7, Fig. 7), rather than the hydrolysis of the imine (involving a barrier of 29.5 kcal mol⁻¹, Scheme S4, ESI†). Mothana and Boyd supported a mechanism involving the direct cyclization of hemiaminal for the Paal–Knorr pyrrole synthesis.⁵⁵ Using quantum chemical analysis, they reported a barrier of 35.0 kcal mol⁻¹ (enthalpy, using B3LYP method) for the cyclization reaction of hemiaminal 21. The barrier estimated for this process in the current work is 34.2 kcal mol⁻¹ (Scheme 7), very close to the value reported earlier. The cyclization is triggered by the intramolecular nucleophilic attack of the lone pair of electrons on nitrogen atom at the electron deficient carbon center of the carbonyl group in 21.

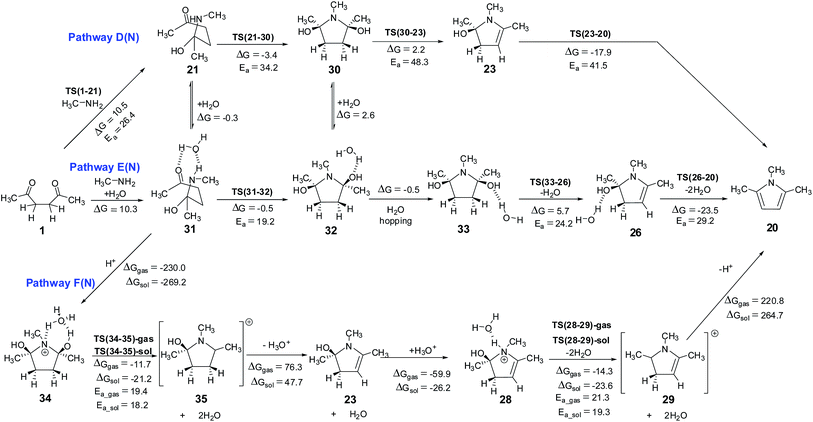Scheme 7 Hemiaminal pathways for the Paal–Knorr pyrrole synthesis – pathway D(N) without explicit water, pathway E(N) with explicit water and pathway F(N) under proton catalysis conditions. The energy values (kcal mol⁻¹) are obtained using M06 method. The corresponding values obtained using B3LYP method are given in the ESI.† The 3D structures of transition states are given in Fig. 7. The cis tautomer with reference to –OH group of structures 30, 32, 33 and 34 are used to study the reaction pathway. The corresponding reaction pathways for the trans arrangement are given in ESI.†

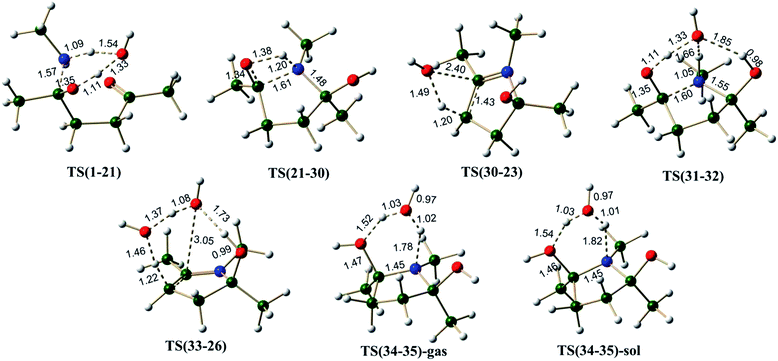Fig. 7 The 3D structures of the transition states on the potential energy surface of the hemiaminal pathways for the Paal–Knorr synthesis of pyrrole. The distances are given in Å.

The transition state TS(21-30) is associated with a strained four membered ring. Water greatly reduces the strain in TS(31-32) (through a six membered ring), thus facilitating the cyclization process. The free energy barrier for the C–N bond formation leading to cyclization (via TS(31-32)) is 19.2 kcal mol⁻¹ much less than that via TS(21-30) (∼34.2 kcal mol⁻¹). A comparison between pathway B(N) (overall barrier for cyclization – 34.6 kcal mol⁻¹ (6.5 + 2.8 + 25.3 kcal mol⁻¹)) and pathway E(N) (overall barrier for cyclization – 29.5 kcal mol⁻¹ (10.3 + 19.2 kcal mol⁻¹)), indicates that the hemiaminal pathway under explicit water conditions is relatively more favorable. On the hemiaminal pathway D(N) the cyclized intermediate 30 can undergo direct cis water elimination (via TS(30-23), Fig. 7) to form 23, involving an energy barrier of 48.3 kcal mol⁻¹. The cyclized intermediate 32, on the pathway E(N) lead to an intermediate 33 which can undergo water assisted cis water elimination (via TS(33-26), Fig. 7) to give 26. This step involves comparatively low energy barrier of 24.2 kcal mol⁻¹. Intermediates 23 and 26 can further lose a water molecule very similar to enamine pathways.

On pathway F(N), compound 31 under H₃O⁺ conditions does not lead to a stable structure (presumably owing to a very shallow potential well associated with this intermediate), instead it directly gets converted to the cyclized intermediate 34 during optimization process (pathway F(N), Scheme 7). On this pathway, the cyclized protonated intermediate 34 can undergo water assisted dehydration to give an intermediate 35. This step is exergonic under both gas phase and implicit solvent phase conditions, involving the energy barriers of 19.4 (TS(34-35)-gas) and 18.2 (TS(34-35)-sol) kcal mol⁻¹, respectively. This intermediate 35 can further loose a proton in the form of H₃O⁺ to give 23. Species 23 can further lead to 28 under H₃O⁺ conditions. The cyclized protonated intermediate 28 can undergo water assisted dehydration to give an intermediate 29 which can further loose a proton to give pyrrole 20. Hence, pyrrole formation pathways (pathway C(N) and pathway F(N)) under proton catalysis conditions are the energetically favorable paths for the formation of pyrrole from 1,4-diketones.

Mechanism of thiophene generation from 1,4-diketones

The Paal–Knorr synthesis of thiophene from 1,4-diketones is expected to take place after the initial formation of 1-keto-4-thioketo (36) derivative from the reaction of 1,4-diketone and P₄S₁₀/Lawesson's reagent.^1,2,63 The cyclization of 1-keto-4-thioketone (36) to give 2,5-dimethylthiophene is an exergonic reaction by 12.4 kcal mol⁻¹ (gas phase) and by 13.0 kcal mol⁻¹ (solvent phase) at M06 level (Table 1) (Fig. 8).

Fig. 8 The Paal–Knorr reaction for the synthesis of 2,5-dimethyl thiophene. The distances are given in Å (refer Table 1 for energies).

The mechanism for this reaction is expected to follow a pathway similar to that of the cyclization of 1,4-diketone to give furan. The initial tautomerisation of 36 to give 38 is a favorable process (ΔG = 3.9 kcal mol⁻¹ in favor of thione). Schemes 8 and 9 show the possible mechanistic pathways (A(S), B(S), C(S),D(S), E(S) and F(S)) along with the necessary energies on the pathways. The direct cyclization in thiol pathways via TS(38-39) requires 33.0 kcal mol⁻¹, but water participation reduces the barrier to 23.7 kcal mol⁻¹ (via TS(40-41)) (Scheme 8, Fig. 9). The alternative hemithioketal path also is benefitted by the participation of water in the reaction as it shows a decrease of ∼6.1 kcal mol⁻¹ (∼30.8 kcal mol⁻¹ for reaction via TS(46-47) vs. ∼24.7 kcal mol⁻¹ for reaction via TS(48-49)) (Scheme 9, Fig. 10). In this case also the participation of proton in the reaction is suggested,^63,64 hence the thiol and hemithioketal pathways with proton catalysis were also studied. The energy barrier for the cyclization with proton catalysis in pathway C(S) was found to be 10.0 kcal mol⁻¹ and 10.4 kcal mol⁻¹ under gas phase and solvent phase conditions, respectively (Scheme 8, Fig. 9). The energy barrier for cyclization step was significantly reduced in hemithioketal pathway under proton catalysis conditions. The reaction barrier for this step in pathway F(S) was found to be 0.5 kcal mol⁻¹ under solvent phase conditions (Scheme 9, Fig. 10). On the pathway F(S)-gas phase, location of transition state became tricky, presumably due to the flat potential energy surface.

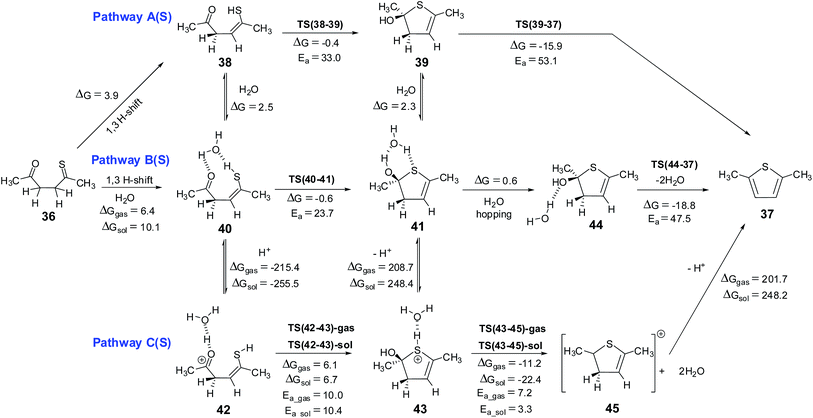Scheme 8 Thiol pathways for the Paal–Knorr synthesis of thiophene – pathway A(S) without explicit water, pathway B(S) with explicit water and pathway C(S) under proton catalysis. The energy values (kcal mol⁻¹) are obtained using M06 method. The corresponding values obtained using B3LYP method are given in ESI.† The 3D structures of the transition states are given in Fig. 9. The distances are given in Å.

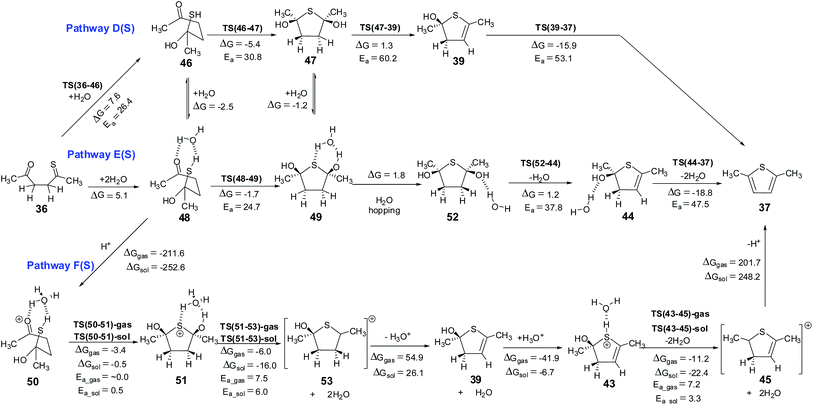Scheme 9 Hemithioketal pathways for the Paal–Knorr thiophene synthesis – pathway D(S) without explicit water, pathway E(S) with explicit water and pathway F(S) under proton catalysis. The energy values (kcal mol⁻¹) are obtained using M06 method. The corresponding values obtained using B3LYP method are given in ESI.† The 3D structures of the transition states are given in Fig. 10. Structures 47, 49, 51 and 52 with cis arrangement of –OH groups are employed in this scheme. The corresponding reaction pathways for the trans arrangement are given in ESI.†

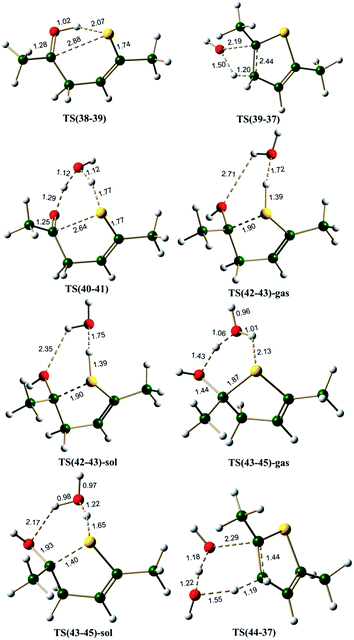Fig. 9 The 3D structures of the transition states on the potential energy surface of the thiol pathways for the Paal–Knorr synthesis of thiophene. The distances are given in Å.

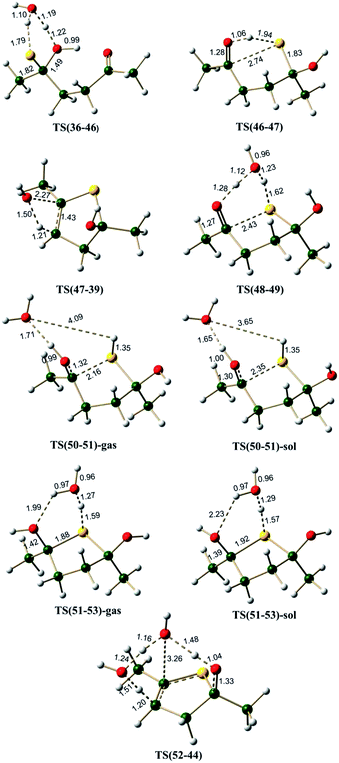Fig. 10 The 3D structures of the transition states on the potential energy surface of the hemithioketal pathways for the Paal–Knorr synthesis of thiophene.

Comparison between the possible mechanisms on the three important Paal–Knorr synthetic reactions

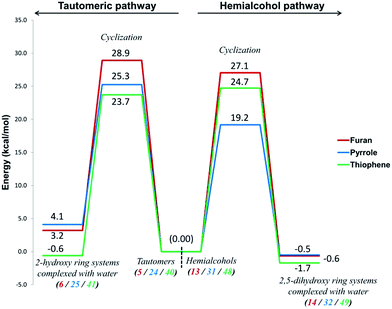
The most important step along the Paal–Knorr synthetic procedure is the cyclization step. The reactions leading to the preparation of the reagents for cyclization (hemialcohol generation/tautomersim) as well as the dehydration reactions after cyclization are the associated reaction steps. Fig. 11 shows a comparative diagram (under neutral conditions) of the energy barriers for the water mediated cyclization along the tautomeric pathways (pathways B(O), B(N) and B(S)) and the water mediated cyclization of the hemialcohols (pathways E(O), E(N) and E(S)).

Fig. 11 A correlation diagram showing the comparative potential energy surfaces for the cyclization step along the pathways B(O), B(N) and B(S) (water mediated cyclization of tautomers) and pathways E(O), E(N) and E(S) (water mediated cyclization of hemialcohols) for the Paal–Knorr synthesis of furan, pyrrole and thiophene respectively. Energy values are given in kcal mol⁻¹.

It can be noticed that these cyclization reactions are marginally favorable (exergonic) on the hemialcohol pathways, but they are marginally unfavorable (endergonic, except in thiophene case) on the tautomeric pathway. Even the energy barriers are lower for the hemialcohol pathways (except for thiophene). In the case of pyrrole both the ΔG values (4.1 vs. −0.5 kcal mol⁻¹) and the E_a values (25.3 vs. 19.2 kcal mol⁻¹) clearly favor the hemiaminal pathway. In case of furan both the pathways are comparable for the cyclization step, marginally favoring the hemiketal path. In case of thiophene, there is breakeven comparison among the two pathways. Water participation has a marginal influence in stabilizing the intermediates (stabilizing in a few cases but destabilizing in few cases). More significantly, water molecules cause positive conformational changes preparing reactive centers in the intermediates towards cyclization.

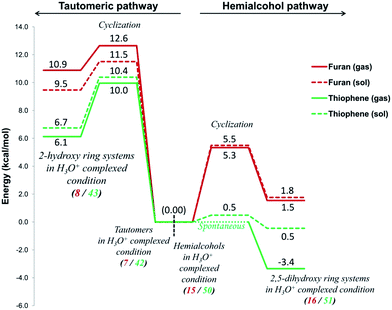
Under the proton catalysis conditions, a common mechanism can be considered for the Paal–Knorr synthesis of furan and thiophene (pathways C(O), C(S), F(O) and F(S)), both involve the participation of H₃O⁺ in a catalytic role. Fig. 12 clearly establishes that the hemialcohol pathways (under both gas and solvent phase conditions) are the favourites both in terms of kinetic and thermodynamic controls. For the pyrrole formation the proton catalysis conditions were not generally used. The transition states and the intermediates on this pathway could not be clearly established on the corresponding potential energy surface. Though, according to free energy estimates this process appears to be highly exergonic.

Fig. 12 A comparison of the proton catalyzed cyclization step on the potential energy surfaces along the tautomeric pathways C(O) and C(S) and hemialcohol pathways F(O) and F(S) for the Paal–Knorr synthesis of furan and thiophene. Energy values are given in kcal mol⁻¹.

The water elimination steps in all the pathways are also important steps. Water elimination requires significant barriers under neutral conditions (24 to 60 kcal mol⁻¹). On a relative scale, the barrier for water elimination is low for pyrrole generation as compared to furan and thiophene synthetic pathways. Under proton catalytic conditions the barriers for water elimination step for furan and thiophene generation are in the range of 7.0 to 8.5 kcal mol⁻¹ (under gas phase conditions) and 3.0 to 6.0 kcal mol⁻¹ (under implicit solvent (water) conditions). These values are marginally high to the barriers for cyclization along the hemialcohol pathways, but, they are marginally small along the tautomeric pathways.

Conclusions

Quantum chemical studies have been carried out to establish the reaction mechanism for the Paal–Knorr reaction in the generation of furans, pyrroles and thiophenes. Initially three levels of quantum chemical methods (G2MP2, M06 and B3LYP) were employed to calculate overall free energies for the Paal–Knorr synthesis of furan, pyrrole and thiophene. The free energy change along the furan synthetic path is endergonic (by ∼3.7 kcal mol⁻¹), whereas, the same for the pyrrole and thiophene synthetic paths is exergonic by ∼−16.4 and ∼−15.9 kcal mol⁻¹, respectively. Hemiketal pathway under proton catalysis conditions requiring an overall barrier of ∼5.5 kcal mol⁻¹ for the cyclization step is the most preferred pathway for the Paal–Knorr furan synthesis. Similarly, hemiaminal and hemithioketal pathways are favorable for the synthesis of pyrrole and thiophene, respectively. Water participation is quite significant in terms of reducing the energy barriers. The explicit water also specifically participates in dictating the orientation of the reactive centers towards each other by enforcing some specific conformational changes in the intermediates which facilitate the cyclization process. After the crucial cyclization step, water elimination step turned out to be highly energy demanding, explicit water participation is found to be critical at this step also.

This work establishes that a common reaction pathway (hemialcohol pathway) is the preferred mechanistic procedure for the formation of all the three products. All previous studies ignored the role of hemiketal intermediates in the Paal–Knorr furan formation. The current study highlights the importance of this pathway. This needs further experimental exploration, especially due to the fact that Paal–Knorr furan synthesis is an endergonic process on the potential energy surface.

Methods of calculations

Density functional (DFT)⁶⁵ analysis was carried out to explore the mechanism of the Paal–Knorr synthesis of furan, pyrrole and thiophene rings. The GAUSSIAN09 suite of programs⁶⁶ was used to carry out the geometry optimization of all the structures on the possible mechanistic paths of the Paal–Knorr synthesis and to estimate the absolute energies. Complete optimizations without any symmetry constraints were performed using M06 method (to incorporate the influence of the dispersion factors into the reaction profile estimation)⁶⁷ and Becke–Lee–Yang–Parr (B3LYP),^68–70 with the 6-311+G(2df,3pd) basis set. Frequencies were computed analytically with the same basis set for all optimized species to characterize stationary points to minima and transition states to first-order saddle points with one imaginary frequency vibrational mode and also to estimate the zero point vibrational energies. Each transition state is a first-order saddle point with only one imaginary vibrational mode on the potential energy surface. The NBO analysis^71,72 using the B3LYP/6-311+G(2df,3pd) and B3LYP/6-311+G(2df,3pd) levels of theory was performed to estimate partial atomic charges. The free energies of overall reactions were also explored using high accuracy G2MP2 ⁷³ level.

Acknowledgements

The authors thank Dr S. V. Rama Sastry Sripada, IISER, Mohali, Punjab, India for thorough discussions. S. A. acknowledges the financial support received from University Grants Commission (UGC), Government of India, New Delhi.

References

1. T. Eicher, S. Hauptmann and A. Speicher, The Chemistry of Heterocycles: Structures, Reactions, Synthesis, and Applications 3rd, Wiley-VCH Verlag & Co. KGaA, Weinheim, Germany, 2013.
2. J. A. Joule and K. Mills, Heterocyclic Chemistry, Blackwell, Oxford, 4th edn, 2000.
3. A. R. Katritzky, C. A. Ramsden, J. Joule and V. V. Zhdankin, Handbook of Heterocyclic Chemistry, Elsevier, Amsterdam, Netherlands, 3rd edn, 2010.
4. D. K. Dalvie, A. S. Kalgutkar, S. C. Khojasteh-Bakht, R. S. Obach and J. P. O'Donnell, Chem. Res. Toxicol., 2002, 15, 269–299.
5. L. Knorr, Ber. Dtsch. Chem. Ges., 1884, 17, 2863–2870.
6. C. Paal, Ber. Dtsch. Chem. Ges., 1884, 17, 2756–2767.
7. R. C. D. Brown, Angew. Chem., Int. Ed., 2005, 44, 850–852.
8. S. F. Kirsch, Org. Biomol. Chem., 2006, 4, 2076–2080.
9. R. A. Kretchmer and R. A. Laitar, J. Org. Chem., 1978, 43, 4596–4598.
10. F. Stauffer and R. Neier, Org. Lett., 2000, 2, 3535–3537.
11. R. U. Braun, K. Zeitler and T. J. Müller, Org. Lett., 2001, 3, 3297–3300.
12. S. Handy and K. Lavender, Tetrahedron Lett., 2013, 54, 4377–4379.
13. H. Luo, Y. Kang, Q. Li and L. Yang, Heteroat. Chem., 2008, 19, 144–148.
14. X. Zhang, G. Weng, Y. Zhang and P. Li, Tetrahedron, 2015, 71, 2595–2602.
15. M. S. Saroukou, T. Skalski, W. G. Skene and W. D. Lubell, Tetrahedron, 2013, 70, 450–458.
16. L. Chen, Y. Du, X. P. Zeng, T. D. Shi, F. Zhou and J. Zhou, Org. Lett., 2015, 17, 1557–1560.
17. B. J. Ramulu, A. Nagaraju, S. Chowdhury, S. Koley and M. S. Singh, Adv. Synth. Catal., 2015, 357, 530–538.
18. G. Minetto, L. F. Raveglia, A. Sega and M. Taddei, Eur. J. Org. Chem., 2005, 2005, 5277–5288.
19. H. S. P. Rao and S. Jothilingam, J. Org. Chem., 2003, 68, 5392–5394.
20. H. M. Meshram, B. R. V. Prasad and D. Aravind Kumar, Tetrahedron Lett., 2010, 51, 3477–3480.
21. B. Wang, Y. Gu, C. Luo, T. Yang, L. Yang and J. Suo, Tetrahedron Lett., 2004, 45, 3417–3419.
22. J. S. Yadav, B. V. S. Reddy, B. Eeshwaraiah and M. K. Gupta, Tetrahedron Lett., 2004, 45, 5873–5876.
23. K. Aghapoor, L. Ebadi-Nia, F. Mohsenzadeh, M. Mohebi Morad, Y. Balavar and H. R. Darabi, J. Organomet. Chem., 2012, 708, 25–30.
24. B. K. Banik, I. Banik, M. Renteria and S. K. Dasgupta, Tetrahedron Lett., 2005, 46, 2643–2645.
25. J. Chen, H. Wu, Z. Zheng, C. Jin, X. Zhang and W. Su, Tetrahedron Lett., 2006, 47, 5383–5387.
26. S. K. De, Synth. Commun., 2008, 38, 2768–2774.
27. N. T. S. Phan, T. T. Nguyen, Q. H. Luu and L. T. L. Nguyen, J. Mol. Catal. A: Chem., 2012, 363, 178–185.
28. S. J. Pridmore, P. A. Slatford and J. M. J. Williams, Tetrahedron Lett., 2007, 48, 5111–5114.
29. G. Yin, Z. Wang, A. Chen, M. Gao, A. Wu and Y. Pan, J. Org. Chem., 2008, 73, 3377–3383.
30. S. X. Yu and P. W. le Quesne, Tetrahedron Lett., 1995, 36, 6205–6208.
31. S. K. Pasha, V. S. V. Satyanarayana, A. Sivakumar, K. Chidambaram and L. J. Kennedy, Chin. Chem. Lett., 2011, 22, 891–894.
32. V. Polshettiwar and R. S. Varma, Tetrahedron, 2010, 66, 1091–1097.
33. G. Song, B. Wang, G. Wang, Y. Kang, T. Yang and L. Yang, Synth. Commun., 2005, 35, 1051–1057.
34. A. R. Bharadwaj and K. A. Scheidt, Org. Lett., 2004, 6, 2465–2468.
35. X. Jing, X. Pan, Z. Li, X. Bi, C. Yan and H. Zhu, Synth. Commun., 2009, 39, 3833–3844.
36. S. Cheraghi, D. Saberi and A. Heydari, Catal. Lett., 2014, 144, 1339–1343.
37. D. Akbaşlar, O. Demirkol and S. Giray, Synth. Commun., 2014, 44, 1323–1332.
38. H. Cho, R. Madden, B. Nisanci and B. Török, Green Chem., 2015, 17, 1088–1099.
39. K. L. Baumann, D. E. Butler, C. F. Deering, K. E. Mennen, A. Millar, T. N. Nanninga, C. W. Palmer and B. D. Roth, Tetrahedron Lett., 1992, 33, 2283–2284.
40. J. J. Li, D. S. Johnson, D. R. Sliskovic and B. D. Roth, Contemporary Drug Synthesis, John Wiley & Sons, Hoboken, New Jersey, 2004.
41. B. D. Roth, Prog. Med. Chem., 2002, 40, 1–22.
42. W. J. Humenny, Master of Science, The University of Western Ontario, 2012.
43. A. Furstner, Angew. Chem., Int. Ed., 2003, 42, 3582–3603.
44. B. Jolicoeur and W. D. Lubell, Can. J. Chem., 2008, 86, 213–218.
45. J. Robertson, R. J. D. Hatley and D. J. Watkin, J. Chem. Soc., Perkin Trans. 1, 2000, 3389–3396.
46. S. G. Salamone and G. B. Dudley, Org. Lett., 2005, 7, 4443–4445.
47. S. Thirumalairajan, B. M. Pearce and A. Thompson, Chem. Commun., 2010, 46, 1797–1812.
48. Z. Casar, Curr. Org. Chem., 2010, 14, 816–845.
49. Y. Kawato, S. Chaudhary, N. Kumagai and M. Shibasaki, Chem.–Eur. J., 2013, 19, 3802–3806.
50. Comprehensive Heterocyclic Chemistry II, ed. A. R. Katritzky, C. W. Rees and E. F. V. Scriven, Pergamon, Oxford, 1996.
51. J. A. Joule and G. F. Smith, Heterocyclic Chemistry, Van Nostrand Reinhold Co., London, 2nd edn, 1978.
52. V. Amarnath and K. Amarnath, J. Org. Chem., 1995, 60, 301–307.
53. V. Amarnath, K. Amarnath, W. M. Valentine, M. A. Eng and D. G. Graham, Chem. Res. Toxicol., 1995, 8, 234–238.
54. V. Amarnath, D. C. Anthony, K. Amarnath, W. M. Valentine, L. A. Wetterau and D. G. Graham, J. Org. Chem., 1991, 56, 6924–6931.
55. B. Mothana and R. J. Boyd, J. Mol. Struct.: THEOCHEM, 2007, 811, 97–107.
56. B. J. Smith, N. M. Tho, W. J. Bouma and L. Radom, J. Am. Chem. Soc., 1991, 113, 6452–6458.
57. K. Lammertsma and P. V. Bharatam, J. Org. Chem., 2000, 65, 4662–4670.
58. P. V. Bharatam, D. S. Patel and P. Iqbal, J. Med. Chem., 2005, 48, 7615–7622.
59. P. V. Bharatam and S. Khanna, J. Phys. Chem. A, 2004, 108, 3784–3788.
60. J. Li, in Name Reactions: A Collection of Detailed Mechanisms and Synthetic Applications, Springer, Switzerland, 2014, pp. 452–453.
61. L. Kurti and B. Czako, Strategic Applications of Named Reactions in Organic Synthesis, Elsevier Academic Press, San Diego, USA, 2005.
62. K. Lammertsma and B. V. Prasad, J. Am. Chem. Soc., 1994, 116, 642–650.
63. R. Mishra, K. K. Jha, S. Kumar and I. Tomer, Der Pharma chem., 2011, 3, 38–54.
64. E. Campaigne and W. O. Foye, J. Org. Chem., 1952, 17, 1405–1412.
65. R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford university press, New York, 1989.
66. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, in Gaussian, Inc., Wallingford, CT, 2009.
67. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
68. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
69. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
70. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
71. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
72. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
73. L. A. Curtiss, K. Raghavachari and J. A. Pople, J. Chem. Phys., 1993, 98, 1293–1298.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra16246g

---