DOI:
10.1039/C5RA16168A
(Paper)
RSC Adv., 2015,
5, 91751-91759
Comparative analysis of the electronic structures of mono- and bi-atomic chains of IV, III–V and II–VI group elements calculated using the DFT LCAO and LACW methods
Received
11th August 2015
, Accepted 3rd October 2015
First published on 6th October 2015
Abstract
Using the first principle non-relativistic linear combination of atomic orbitals (LCAO) and relativistic linearized augmented cylindrical wave (LACW) methods, the band structure of the covalent and partially ionic ANB8−N single atom width chain is calculated. Both the LCAO and LACW methods show that the chains of C, Si, Ge, Sn, and Pb are metallic. However, there is a great difference between the relativistic and non-relativistic band structures. The π bands crossing the Fermi level are orbitally doubly degenerate in the non-relativistic model. The relativistic LACW calculations demonstrate that the spin and orbital motion of electrons are coupled, thereby splitting the π bands. The spin–orbit gaps are equal to 1.5 meV, 28 meV, 0.22 eV, 0.45 eV, and 4 eV for the C, Si, Ge, Sn, and Pb chains, respectively. The mass–velocity corrections result in a lowering of all the valence band levels. In the carbon and silicon chains, the corrections are possibly negligible (2–5 and 10–30 meV, respectively), while in the Ge, Sn, and Pb chains the low-energy shifts are equal to 0.6, 2.2, and 3.7 eV, respectively, due to these effects. The Darwin corrections are several times smaller in comparison to the mass–velocity contributions. The transition from the covalent chains to the partially ionic ones is accompanied by a drastic change in the band structure. The C chain with all bond lengths equal has a metal type electronic structure while the BN chain is an insulator with an energy gap equal to 6–8 eV. The differences between the covalent and partially ionic chains are explained by the presence of the antisymmetric components of the electron potential in the latter case. The transition from the BN chain to the AlP, GaAs, and InSb ones is accompanied by a gradual decrease in the gaps; for example, the AlP chain is a semiconductor. According to the LCAO calculations, the GaAs chain is a semiconductor, but it is a metal according to the relativistic LACW method. The InSb chain possesses a metal type band structure, but the spin–orbit interaction splits the π states, forming the two π+ and π− sub-bands, and noticeably complicates the band structure and density of states in the vicinity of the Fermi level. In the case of compounds from the same horizontal row in the periodic table, the transition from the AIIIBV chains to the AIIBVI ones is accompanied by a sharp increase in the band gap. The calculations indicate the metallic nature of the InSe chain, but the CdTe one is an insulator. Among the atomic ANB8−N chains, there are compounds with different electrical properties: from metals to semiconductors and insulators.
1. Introduction
Within the current trends of miniaturization of electronic devices, the problems of interconnects between nanodevices attract growing interest in the stability, band structure, and conductivity of the nanowires. The thinnest possible nanowire is a single-atom width chain.1–11 The structures and properties of atomic wires are completely different from those of large dimension wires, and they are the ideal subjects for investigating quantum effects. It still remains a challenge to fabricate stable atomic chains; however, there is great progress in this field now. First, gold chains generated inside a transmission electron microscope have been reported,1–3,11–14 and stable gold wires of single-atom width up to ten-atom length were formed upon the tensile deformation of the nanometer-sized Au contacts. The structures of the Au chains were determined, and the stress–strain curves and electrical properties, including ballistic transport, were experimentally measured at the atomic scale.14 Platinum wires of single-atom width exhibiting straight shapes were produced by the retraction of a Pt nanotip from contact with a Pt plate at room temperature inside a transmission electron microscope, and a relationship between the atomic chain length and conductance was demonstrated.14–16 Binary atomic chains were generated via Au1−xAgx alloy nanorod thinning during mechanical stretching.17 Ligand-supported linear chains of transition metal atoms with well-defined organic ends are known too.18 A linear chain with 44 C atoms in compound (Tr–C44–Tr with bulky terminal groups Tr = tris(3,5-di-t-butylphenyl)methyl),19 as well as similar short chains connecting two graphene species have been detected.20,21 Carbon nanotubes can be utilized as sheaths to stabilize monoatomic chains, which are unstable alone, and can be applied in many fields. For example, entrapped La atoms arrange linearly with a typical chain length equal to 10 nm inside a nanotube of a suitable diameter.22 The incorporation of molten iodine into single-walled carbon nanotubes with a diameter of 1 nm generates iodine chains longer than 10 nm.23 A carbon chain with a length of 20 nm containing more than 100 atoms enclosed in a shell of multi-walled carbon nanotubes was found as well.24 Inorganic structures are also known to self-assemble into one-dimensional structures on a bare Si(001) surface. This includes elemental adsorbates such as indium,25–28 lead,29 bismuth,30 and rare earth metals31 that form nanowires.
Monoatomic chains are well-known as text-book examples studied using the simple tight-binding or free electron models. Now, there are many first-principles calculations of the electronic structure of such systems. The band structures and magnetic properties of all 3d transition metal infinite periodic linear and dimerized linear chains were calculated using the ab initio pseudopotential plane-wave method (PPW) taking spin–orbit coupling into account.9 Employing the linearized augmented plane-wave method considering non-perturbative spin–orbit coupling, virtually the same properties of all 4d transition metal chains were studied.10 The application of the projector augmented-wave method to the problems of transition metal chains3 show that both Pt and Au stand out as the most likely transition elements to form chains.11,14,15,32 In the case of some transition metal atoms, a variation of the total energy as a function of the lattice constant for the different magnetic states shows that the energy of infinite linear structures has a minimum for ferromagnetic and antiferromagnetic freestanding chain structures, opening new perspectives in controlling the spin-dependent ballistic conductance.9–11,33,34
In contrast to carbon and transition metal monoatomic wires,4–8,28–31 which have been thoroughly investigated, not much is known about atomic chains made from group IV (Si, Ge, Sn), group III–V (BN, AlP, GaAs, InSb, etc.), and group II–VI (ZnSe, CdTe, etc.) elements, which form well-known bulk semiconductor crystals. To the best of our knowledge, there is only one study about the structure and electron properties of these linear chains,35,36 where it was shown, using first-principles PPW calculations, that all chains are stable, the binding energies of which being close to bulk cohesive energies. The band structure calculations of a dozen ANB8−N monoatomic chains have also been performed earlier,35,36 but only in terms of a non-relativistic approach. However, because of the rotational symmetry of the linear atomic ANB8−N chains, relativistic corrections to the band structure are expected to be of great importance.30,37 Recently, the quantum conductance of short linear monatomic Si and Ge chains was calculated,38–40 and an all-silicon linear chain NMR quantum computer was suggested.
In this study, using the standard linear combination of localized orbitals (LCAO) method, we have calculated the bond lengths, formation energies, and band structures of covalent and partially ionic ANB8−N chains. As relativistic calculations are not yet implemented into the LCAO based program, we are currently calculating the band structures taking into account the spin–orbit, Darwin, and mass–velocity corrections using the original linearized augmented cylindrical wave (LACW) method.41–45 The LACW method is just a reformulation of the linearized augmented plane wave (LAPW) formalism for cylindrical multiatomic systems. The relativistic version of the LACW method can be readily obtained based on the relativistic APW techniques.46
2. Linear combination of atomic orbitals
First principles LCAO calculations of chains have been performed using the formalism of atom-centered Gaussian-type functions (GTFs). According to the LCAO approach, the crystalline orbitals φki(r) of an N-electron system are expanded as linear combinations of a set of m Bloch functions built from the local atom-centered GTFs χgj(r − Rj):| |  | (1) |
| |  | (2) |
where k is the wave vector of the irreducible representation of the group of crystal translations {g}, Rj denotes the coordinates of the nuclei in the zero cell, in which the atomic orbital χgj(r) is centered; and G, cμ, and αμ are the normalized GTFs, their coefficients and exponents, respectively, forming the basis set (BS) of an individual atom.
The DFT-LCAO method realized for various Hamiltonians, as implemented in the CRYSTAL-14 code47 and used in our calculations, differs when using the exchange-correlation functionals applied in Kohn–Sham equations:
| |  | (3) |
where
Exc is the energy functional while
ρ(
r) is the electron density function expressed
via crystalline orbitals
φki(
r). Our calculations on atomic chains were performed using the hybrid Hartree–Fock/Kohn–Sham (HF/KS) exchange–correlation functional HSE by Heyd–Scuseria–Ernzerhof
48,49 combining an exact HF non-local exchange and KS exchange operator within the generalized gradient approximation as implemented in the CRYSTAL-14 code.
47 The advantage of the hybrid HSE-LCAO calculation scheme is that it makes the results of the band structure calculations more plausible. An all-valence TZVP (Triple-Zeta Valence with Polarization) basis set
47,50 was used for all atoms in the current study. The threshold parameters of the CRYSTAL code for the evaluation of different types of bielectronic integrals (overlap and penetration tolerances for Coulomb integrals, ITOL1 and ITOL2, overlap tolerance for exchange integrals ITOL3, and pseudo-overlap tolerances for exchange integral series, ITOL4 and ITOL5) have been set to 8, 8, 8, 8, and 16, respectively. They provide truncation of the corresponding integrals when the overlap between the arbitrary atomic orbitals does not exceed 10
−ITOLn.
To achieve balanced summation over the direct and reciprocal lattices, reciprocal space integration was performed by sampling the Brillouin zone with the 10 × 1 × 1 Pack–Monkhorst k-mesh51 which results in six evenly distributed k-points within the irreducible segment of the Brillouin zone. Calculations of atomic chains with a fixed geometry are considered to be converged only when the total energy differs by less than 10−7 a.u. in two successive cycles of the self-consistency procedure. The next step of the computational procedure realized using CRYSTAL is total geometry optimization which includes the optimization of the electronic structure for each intermediate and final atomic configurations.47 Further increase in both the threshold parameters and k-meshes results in more expensive calculations yielding only a negligible gain in the total energy (∼10−7 a.u.) which can be ignored for qualitative conclusions. Table 1 shows the equilibrium bond lengths d and formation energies Eform for nanofilaments of single-atom width calculated using this method. The LCAO band structures are presented in Sec. 4 together with similar data obtained using the LACW technique.
Table 1 Equilibrium bond lengths d and formation energies Eform of linear chains as calculated by means of the LCAO-DFT approach. Negative formation energy corresponds to an energy gain
| Type of chain |
d, Å |
E
form, eV |
| C |
1.27 |
−6.74 |
| Si |
2.18 |
−2.77 |
| Ge |
2.35 |
−2.03 |
| Sn |
2.52 |
−2.89 |
| Pb |
2.75 |
−1.97 |
| BN |
1.30 |
−7.88 |
| AlP |
2.05 |
−4.70 |
| GaAs |
2.16 |
−2.21 |
| InSb |
2.70 |
−0.98 |
| ZnSe |
2.18 |
−3.10 |
| CdTe |
2.61 |
−3.13 |
3. Linearized augmented cylindrical wave method
Relativistic LACW band structure calculations were performed for the geometries optimized using the LCAO method. We started from the two-component Hamiltonian written in terms of Rydberg atomic units:46,52–54| |  | (4) |
Here, c is the speed of light, p is the momentum operator, and σ is the Pauli matrix. The first two terms correspond to the non-relativistic Hamiltonian operator H0 = −Δ + V. Methods for solving the non-relativistic Schrödinger equation, using the basis of the linear augmented cylindrical waves ΨkPMN(r), are described in previous work.41–43 The results of this calculation are the non-relativistic energies E0n(k) of different bands n at different points k in the Brillouin zone and the spin independent wave functions Ψ0n,k(r) represented as the linear combination of the basis functions:| |  | (5) |
In eqn (4), the third term is the operator of the spin–orbit interaction HS–O, which may split degenerated levels and cause the mixing of levels, thus altering the band picture in comparison with non-relativistic results. The fourth and fifth terms (the Darwin HDar and mass–velocity Hm–v corrections, respectively) are invariant under the operations of the single group and therefore do not split levels, but these terms may mix levels of the same single-group symmetry and shift non-relativistic levels appreciably.
As the non-relativistic part of the Hamiltonian makes the major contribution to the energy, it is possible to use the following procedure.46 First, we find the eigenfunctions Ψ0n,k(r) and eigenvalues E0n(k) of the non-relativistic Hamiltonian.8,41–45 Then, we double the basis to include the spin Ψ0n,k(r, χ) = Ψ0n,k(r)χ where χ = α or β are the pure spin functions. The calculation of the elements of the HS–O, HDar, and Hm–v matrices using the spinor basis Ψ0n,k(r)χ (see Appendix section)
| | 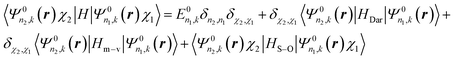 | (6) |
and diagonalization of this matrix remain to be done.
In the LACW method, we use the muffin-tin (MT) potentials and local density functional approximations for electronic potentials constructed to be spherically symmetrical in the regions of the MT spheres and constant in the inter-spherical area. The atoms of the nanofilaments are surrounded by an impenetrable cylinder-shaped potential barrier, because there is a vacuum region outside the wires. The radius a of the barrier is chosen so that the region confined within the barrier accommodates a significant portion of the electron density of the system. Here, based on previous LACW calculations on nanotubes and carbynes,8,41–47 for the fourth group chains, the barrier radii a(AIV) were set equal to the arithmetic mean value of the atomic covalent and van der Waals radii. For the partially ionic chains, the corresponding radii a(ANB8−N) were taken as being the same as for the covalent analogs: a(ANB8−N) = a(AIV).
A good convergence of the relativistic band structures is obtained using 45–50 basis functions for the monoatomic group IV chains and using 70–80 functions in the case of chains with two atoms per unit cell.
4. Results of the calculations
Fig. 1 shows the band structures of the group IV covalent chains calculated using the non-relativistic LCAO and relativistic LACW methods. The points k = 0 and k = π/d correspond to the Brillouin zone Γ center and K boundary, respectively. The generic band structures of these atomic wires are composed of the σ(s) bonding, σ*(pz) antibonding, and one π band which is bonding at k < π/(2d) and antibonding between k = π/(2d) and k = π/(d). Similar to the non-relativistic PPW method,35,36 both the LCAO and LACW techniques predict that the chains of C, Si, Ge, Sn, and Pb are metallic (Table 2). However, there is a great difference between the relativistic and non-relativistic band structures. Because of the cylindrical symmetry of the chains, the π bands crossing the Fermi level are predicted to be orbitally doubly degenerate in the non-relativistic model; the twofold orbitally degenerate π bands correspond to the semi-classical clockwise and anticlockwise rotational motion of electrons around the symmetry axis. In the absence of spin–orbit interaction with the two possible directions of the spin, the π bands would be fourfold degenerate. The LACW calculations demonstrate that the spin and orbital motion of the electrons are strongly coupled in the atomic chains, thereby splitting the fourfold degeneracy seen in Fig. 1 in the case of the relativistic LACW results. However, each π+ and π− sub-band of the relativistic model still has twofold degeneracy; the Kramers theorem on time-reversal symmetry alongside the inversion symmetry of chains preserves the spin degeneracy, the spin polarization direction between two degenerate bands being opposite to each other. The spin–orbit splitting energy ΔS–O varies between about 1.5 meV and 0.45 eV for the C and Sn chains, respectively. In the case of the chain of the heaviest element Pb, ΔS–O is already equal to 4 eV. There is no spin–orbit splitting of the orbitally nondegenerate σ bands.
 |
| | Fig. 1 Band structures of the linear group IV chains calculated using the non-relativistic LCAO and relativistic LACW methods. The zero of energy is set at the Fermi level. | |
Table 2 Electronic characteristics of the linear chains in the Fermi energy region calculated using the non-relativistic PPW and LCAO and relativistic LACW methods. The energy gaps between the valence and conduction bands (Eg) and spin–orbit gaps (ΔSO) are given in eV. The symmetries π, π+, π−, and σ of the dispersion curves crossing the Fermi level of the metallic wires or corresponding to the top of the valence and bottom of the conduction bands are shown too
| |
C |
Si |
Ge |
Sn |
Pb |
| PPW35,36 |
E
g = 0; π |
E
g = 0; π, σ* |
E
g = 0; π, σ* |
E
g = 0; π, σ* |
|
| LCAO |
E
g = 0; π |
E
g = 0; π |
E
g = 0; π, σ* |
E
g = 0; π, σ* |
E
g = 0; π, σ* |
| LACW |
E
g = 0, π; ΔSO = 0.0015 |
E
g = 0; π+, π−, σ*; ΔSO = 0.028 |
E
g = 0; π+, π−, σ*; ΔSO = 0.22 |
E
g = 0; π+, π−, σ*; ΔSO = 0.45 |
E
g = 0; π+, π−, σ*; ΔSO = 4.1 |
| |
BN |
AlP |
GaAs |
InSb |
| PPW35,36 |
E
g = 4; πK → π*K |
E
g = 1.1, 1.6; πK → σ*Γ |
E
g =0; π, σ* |
E
g = 0; π, σ* |
| LCAO |
E
g = 6; πK → π*K |
E
g = 3.5; πK → π*K |
E
g = 0.5; πK → σ*Γ |
E
g = 0; π, σ* |
| LACW |
E
g = 8; πK → π*K; ΔSO = 0.0015 |
E
g = 2.2; πK → σ*Γ; ΔSO = 0.35 |
E
g = 0; π+, σ*; ΔSO = 0.26 |
E
g = 0; π+, σ*; ΔSO = 0.51 |
| |
ZnSe |
CdTe |
| PPW35,36 |
E
g = 0.7, 0,8; πK → σ*Γ |
E
g ≈ 0; πK → σ*Γ |
| LCAO |
E
g = 3.5; πK → σ*Γ |
E
g = 2; πK → σ*Γ |
| LACW |
E
g = 6.5; πK+ → σ*Γ; ΔSO = 0.3 |
E
g = 0.8; πK → σ*Γ; ΔSO = 0.6 |
The LACW data show that the mass–velocity corrections result in the lowering of all the valence band levels. In the C and Si chains, the shifts are equal to 2–5 and 10–30 meV for different k points and are possibly negligible, but the mass–velocity shifts increase up to 0.6, 2.2, and 3.7 eV in the cases of the Ge, Sn, and Pb atomic wires. The Darwin corrections are several times smaller in comparison to the mass–velocity contributions, and can somewhat shift the energy levels to the high or low-energy region.
In the Fermi energy region, there are important differences between the band structures of the carbon and other group IV chains; the result was also observed with the non-relativistic PPW method.35,36 In the case of the C chain, the π bands cross the Fermi level at k = π/2d giving rise to Peierls’ distortion, whereas the Si, Ge, Sn, and Pb chains behave differently; in addition to the π bands, the σ* band dips below the Fermi level near the zone edge preventing Peierls’ dimerization. The LCAO optimization of the atomic positions reveals that bond length alternation is possible only in the case of the C chain, resulting in the formation of the so called polyynic carbyne semiconducting chain (–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–)∞, with the calculated C
C–)∞, with the calculated C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C and C–C bonds being equal to 1.23 and 1.32 Å, respectively. Fig. 2 shows the LCAO and LACW band structures for this semiconducting phase.
C and C–C bonds being equal to 1.23 and 1.32 Å, respectively. Fig. 2 shows the LCAO and LACW band structures for this semiconducting phase.
 |
| | Fig. 2 Non-relativistic LCAO and relativistic LACW band structures of polyynic carbyne. | |
Fig. 3 and Table 2 show that the transition from the covalent chains to the partially ionic ones is accompanied by a sharp change in the band structure. For example, the carbon chain with all bond lengths equal to 1.27 Å has a metal type electronic structure with a zero gap located at the point k = π/2d, but the boron nitride chain with almost the same bond lengths of 1.30 Å is an insulator with an optical gap corresponding to the transition between the occupied π and vacant π* states at the edge of the Brillouin zone and equal to 4, 6, and 8 eV in the PPW, LCAO, and LACW calculations, respectively. Qualitatively, the differences between the electronic bands of the covalent and partially ionic chains are explained by the presence of the antisymmetric components of the electron potential in the transition from the carbon chain to the boron nitride one. This is also the reason for a similar splitting of the σ bands in the BN chain. The transition from the atomic BN chain to the AlP, GaAs, and InSb chains is accompanied by a decrease in the ionic character of the chemical bond leading to a gradual decrease in the π–π* gap and shift of the σ*1 bands in the region of lower energies. These effects lead to the fact that the AlP chain is a semiconductor with an indirect band gap equal to 1.1–1.6 (PPW), 2.2 eV (LACW) or 3.5 eV (LCAO).
 |
| | Fig. 3 Non-relativistic LCAO and relativistic LACW band structures of the AIIIBV chains. | |
According to the LCAO calculations, the chain GaAs is a semiconductor with a band gap equal to 0.5 eV; the gap is due to a transition between the π state on the edge of the Brillouin zone and the σ state in the center. It is a metal according to both the PPW and relativistic LACW methods; the Fermi level crosses the π+ zone, a formation which is associated with spin–orbit splitting. All methods predict that the InSb chain has a metal type band structure due to the intersection of the π and σ* bands; the spin–orbit interaction splits the π states, forms the two π+ and π− bands, and noticeably complicates the band structure and density of states in the Fermi level region. The chemical bonding in the compounds AIIBVI is much more ionic than in AIIIBV; therefore, the antisymmetric component of the electron potential in the AIIIBV chains is stronger, and, in the case of compounds from the same horizontal row in the periodic table, the transition from the AIIIBV chains to the AIIBVI ones is accompanied by a sharp increase in the band gap. For example, Fig. 3 and 4 show that, in the GaAs chain, the gap is absent or equal to about 0.5 eV, based on different data, but it is large in the ZnSe chain. All calculations indicate the metal type of the band structure of the InSe chain, but CdTe is an insulator with a band gap equal to 2 and 0.8 eV in the non-relativistic LCAO calculations and in the LACW calculations with due account of relativistic corrections, respectively.
 |
| | Fig. 4 Non-relativistic LCAO and relativistic LACW band structures of AIIBVI chains. | |
It is interesting to underscore that the presence of the ionic component of the electronic potential dramatically changes the band structure in the transition from the covalent to partially ionic chains, although the ionicity almost does not affect the energy of spin–orbit splitting, which is equal to about 2 meV in the chains of the elements of the second period, of about 30 meV in the chains of the elements of the third period, of 0.3 eV in the chains of the elements of the fourth period, and 0.5 eV in the chains of the elements of the fifth period. The spin–orbit splitting of the non-degenerated σ orbital bands is absent in all the chains.
5. Concluding remarks
Using first principle non-relativistic and relativistic methods, the band structures of the covalent and partially ionic ANB8−N single-atom-width-chains are calculated. There is a great difference between the relativistic and non-relativistic band structures. The relativistic calculations demonstrate that the spin and orbital motions of electrons are coupled, thereby splitting the π bands. The mass–velocity corrections result in the lowering of all of the valence band levels. The Darwin corrections are several times smaller in comparison to the mass–velocity contributions. The transition from the covalent chains to the partially ionic ones is accompanied by a drastic change in the band structure, due to the presence of the antisymmetric components of the electron potential in the last case. The spin–orbit interaction complicates the band structure and density of states in the Fermi level region. The transition from the AIIIBV chains to AIIBVI ones is accompanied by a sharp increase in the band gap. The calculations indicate the metal type of the InSe atomic chain while the CdTe one is an insulator. The calculation results indicate that in the atomic ANB8−N wires, there are compounds with different electrical properties, from metals to semiconductors and insulators. In the covalent and partially ionic atomic ANB8−N wires, it is possible to control the electron spin transfer using an external electric field or optical radiation.
6. Appendix: matrix elements of the relativistic terms
The Hm–v and HDir parts of eqn (6) are completely determined by the matrix elements between the eigenfunctions of the non-relativistic Hamiltonian. Following the description given in ref. 46, note that the Hermitian character of the operator p4 requires that| |  | (A1) |
Because of the approximate potential V(r) = 0 in the region outside the MT-spheres, taking eqn (5) into account, we have
| |  | (A2) |
where,
| |  | (A3) |
Finally, taking the analytical form of function  given elsewhere into account,8,41–43 we obtain:
given elsewhere into account,8,41–43 we obtain:
| |  | (A4) |
Here,
| |  | (A5) |
| |  | (A6) |
| | 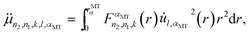 | (A7) |
The Darwin term may be rewritten in a more convenient form by using the following relations46
| | 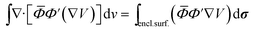 | (A8) |
| | ∇·[![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) Φ′(∇V)] = Φ′(∇V)] = ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) Φ′(∇2V) + (∇V) × (∇ Φ′(∇2V) + (∇V) × (∇![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) )Φ′ + (∇V) × (∇Φ′) )Φ′ + (∇V) × (∇Φ′)![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) | (A9) |
where the integrals are taken over the volume defined by the periodic boundary conditions. Combining these equations leads to the result, with
 and
and  :
:
| |  | (A10) |
Taking the analytical form of function  into account, we have
into account, we have
| |  | (A11) |
Here,
| | 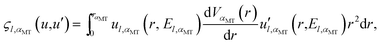 | (A12) |
| |  | (A13) |
| |  | (A14) |
| |  | (A15) |
We will not explain the meaning of the other symbols used in eqn (A3)–(A7) and (A11–A15) since they are the same as those described in ref. 8 and 41–43.
The only part of the relativistic matrix element that must be directly calculated between the spinor functions is that arising from HS–O. For this particular case of a linear atomic chain, the matrix elements 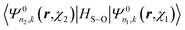 have been given in our previous publication8 and are not repeated here.
have been given in our previous publication8 and are not repeated here.
Conflict of interest
The authors declare no competing financial interest.
Acknowledgements
The research was partially supported by the EC’s 7th Framework Program CACOMEL under Grant Agreement Nr. 247007. P. D. and V. Z. are also grateful to the Russian Basic Research Foundation (Grant 14-03-00493) for the financial support.
References
- K. Tsukagoshi, B. W. Alphenaar and H. Ago, Coherent transport of electron spin in a ferromagnetically contacted carbon nanotube, Nature, 1999, 401, 572–574 CrossRef CAS.
- H. Ohnishi, Y. Kondo and K. Takayanagi, Quantized conductance through individual rows of suspended gold atoms, Nature, 1998, 395, 780–783 CrossRef CAS.
- A. I. Yanson, G. R. Bollinger, H. E. van den Brom, N. Agrait and J. M. van Ruitenbeek, Formation and manipulation of a metallic wire of single gold atoms, Nature, 1998, 395, 783–785 CrossRef CAS.
- Y. H. Hu, Bending Effect of sp-Hybridized Carbon (Carbyne) Chains on Their Structures and Properties, J. Phys. Chem. C, 2011, 115, 1843–1850 CAS.
- M. Qiu, Zh. Zhang, Zh. Fan, X. Deng and J. Pan, Transport Properties of a Squeezed Carbon Monatomic Ring: A Route to a Negative Differential Resistance Device, J. Phys. Chem. C, 2011, 115, 11734–11737 CAS.
- F. Tavazza, S. Barzilai, D. T. Smith and L. E. Levine, The increase in conductance of a gold single atom chain during elastic elongation, J. Appl. Phys., 2013, 113, 054316 CrossRef PubMed.
- P. N. D’yachkov, V. A. Zaluev, E. Yu. Kocherga and N. R. Sadykov, Tight Binding Model of Quantum Conductance of Cumulenic and Polyynic Carbynes, J. Phys. Chem. C, 2013, 117, 16306–16315 Search PubMed.
- P. N. D’yachkov and V. A. Zaluev, Spin–Orbit Gaps in Carbynes, J. Phys. Chem. C, 2014, 118, 2799–2803 Search PubMed.
- C. Ataca, S. Cahangirov, E. Durgun, Y.-R. Jang and S. Ciraci, Structural, electronic, and magnetic properties of 3d transition metal monatomic chains: First-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 214413 CrossRef.
- Y. Mokrousov, G. Bihlmayer, S. Heinze and S. Blügel, Giant Magnetocrystalline Anisotropies of 4d Transition-Metal Monowires, Phys. Rev. Lett., 2006, 96, 147201 CrossRef CAS.
- E. Y. Zarechnaya, N. V. Skorodumova, S. I. Simak, B. Johansson and E. I. Isaev, Theoretical study of linear monoatomic nanowires, dimer and bulk of Cu, Ag, Au, Ni, Pd and Pt, Comput. Mater. Sci., 2008, 43, 522–530 CrossRef CAS PubMed.
- P. Gambardella, A. Dallmeyer, K. Maiti, M. C. Malagoli, W. Eberhardt, K. Kern and C. Carbone, Nature, 2002, 416, 301 CrossRef CAS PubMed.
- L. Krusin-Elbaum, D. M. Newns, H. Zeng, V. Derycke, J. Sun and R. Sandstrom, Nature, 2004, 431, 672 CrossRef CAS PubMed.
- T. Kizuka, Atomic configuration and mechanical and electrical properties of stable gold wires of single-atom width, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 155401 CrossRef.
- T. Kizuka and K. Monna, Atomic configuration, conductance, and tensile force of platinum wires of single-atom width, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205406 CrossRef.
- T. Shiota, A. I. Mares, A. M. C. Valkering, T. H. Oosterkamp and J. M. van Ruitenbeek, Mechanical properties of Pt monatomic chains, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125411 CrossRef.
- J. Bettini, F. Sato, P. Z. Coura, S. O. Dantas, D. S. Galvao and D. Ugarte, Experimental realization of suspended atomic chains composed of different atomic species, Nat. Nanotechnol., 2006, 1, 182–185 CrossRef CAS PubMed.
- I.-W. P. Chen, M.-D. Fu, W.-H. Tseng, J.-Y. Yu, S.-H. Wu, C.-J. Ku, C.-H. Chen and S.-M. Peng, Conductance and Stochastic Switching of Ligand-Supported Linear Chains of Metal Atoms, Angew. Chem., Int. Ed., 2006, 45, 5814–5818 CrossRef CAS PubMed.
- W. Chalifoux and R. Tykwinski, Synthesis of Polyynes to Model the sp-Carbon Allotrope Carbyne, Nat. Chem., 2010, 2, 967–971 CrossRef CAS PubMed.
- C. H. Jin, H. P. Lan, L. M. Peng, K. Suenaga and S. Iijima, Deriving Carbon Atomic Chains from Graphene, Phys. Rev. Lett., 2009, 102, 205501 CrossRef.
- O. Cretu, A. R. Botello Mendez, I. M. Janowska, C. Pham-Huu, J.-C. Charlier and F. Banhart, Electrical Transport Measured in Atomic Carbon Chains, Nano Lett., 2013, 13, 3487–3493 CrossRef CAS PubMed.
- L. Guan, K. Suenaga, S. Okubo, T. Okazaki and S. Iijima, Metallic Wires of Lanthanum Atoms Inside Carbon Nanotubes, J. Am. Chem. Soc., 2008, 130, 2162–2163 CrossRef CAS PubMed.
- V. Rodrigues, J. Bettini, P. C. Silva and D. Ugarte, Evidence for Spontaneous Spin-Polarized Transport in Magnetic Nanowires, Phys. Rev. Lett., 2003, 91, 096801 CrossRef.
- X. Zhao, Y. Ando, Y. Liu, M. Jinno and T. Suzuki, Carbon Nanowire Made of a Long Linear Carbon Chain Inserted Inside a Multiwalled Carbon Nanotube, Phys. Rev. Lett., 2003, 90, 187401 CrossRef.
- D. R. Belcher, M. W. Radny, S. R. Schofield, P. V. Smith and O. Warschkow, Guided Self-Assembly of Metal Atoms on Silicon Using Organic-Molecule Templating, J. Am. Chem. Soc., 2012, 134, 15312–15317 CrossRef CAS PubMed.
- J. Javorský, M. Setvín, I. Ošťádal, P. Sobotík and M. Kotrla, Heterogeneous nucleation and adatom detachment at one-dimensional growth of In on Si(100) − 2 × 1, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165424 CrossRef.
- P. Kocán, L. Jurczyszyn, P. Sobotík and I. Ošádal, Defects on the Si(100) − (2 × 1) surface: Anchoring sites of the surface polymerization reaction of In atoms, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 113301 CrossRef.
- M. W. Radny, P. V. Smith and L. Jurczyszyn, Adsorption-enhanced reactivity of the In/Si(001) system, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085424 CrossRef.
- H. S. Yoon, M.-A. Ryu and I.-W. Lyo, Initial growth of Pb on Si(001) at room temperature and low temperature, Surf. Sci., 2003, 547, 210–218 CrossRef CAS PubMed.
- K. Miki, D. R. Bowler, J. H. G. Owen, G. A. D. Briggs and K. Sakamoto, Atomically perfect bismuth lines on Si(001), Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 14868–14871 CrossRef CAS.
- Y. Zhu, W. Zhou, S. Wang, T. Ji, X. Hou and Q. Cai, From nanowires to nanoislands: Morphological evolutions of erbium silicide nanostructures formed on the vicinal Si(001) surface, J. Appl. Phys., 2006, 100, 114312 CrossRef PubMed.
- A. Roy, T. Pandey and N. Ravishankar, Singh. A. K. Single crystalline ultrathin gold nanowires: Promising nanoscale interconnects, AIP Adv., 2013, 3, 032131 CrossRef PubMed.
- K. Critchley, B. P. Khanal, M. Grzny, L. Vigderman, S. D. Evans, E. R. Zubarev and N. A. Kotov, Adv. Mater., 2010, 22, 2338–2342 CrossRef CAS PubMed.
- A. Delin, E. Tosatti and R. A. Weht, Magnetism in Atomic-Sized Palladium Contacts and Nanowires, Phys. Rev. Lett., 2004, 92, 057201 CrossRef CAS.
- S. Tongay, E. Durgun and S. Ciraci, Atomic Strings of Group IV, III–V, and II–VI Elements, Appl. Phys. Lett., 2004, 85, 6179–6181 CrossRef CAS PubMed.
- R. T. Senger, S. Tongay, E. Durgun and S. Ciraci, Atomic chains of group-IV elements and III-V and II-VI binary compounds studied by a first-principles pseudopotential method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075419 CrossRef.
- F. Kuemmeth, S. Ilani, D. C. Ralph and P. L. McEuen, Coupling of spin and orbital motion of electrons in carbon nanotubes, Nature, 2008, 452, 448–452 CrossRef CAS PubMed.
- F.-T. Liua, Y. Cheng, F.-B. Yang and X.-R. Chen, Quantum conductance oscillation in linear monatomic silicon chains, Phys. E, 2014, 56, 96–101 CrossRef PubMed.
- K. M. Itoh, An all-silicon linear chain NMR quantum computer isotopic effects in semiconductors, Solid State Commun., 2005, 133, 747–752 CrossRef CAS PubMed.
- Y. Matsuura, Tunnel current across linear homocatenated germanium chains, J. Appl. Phys., 2014, 115, 043701 CrossRef PubMed.
- P. N. D’yachkov, O. M. Kepp and A. V. Nikolaev, Linearized Augmented-Cylindrical-Wave Method in the Electronic Structure Theory of Nanowires, Dokl. Chem., 1999, 365, 67–72 Search PubMed.
- P. N. D’yachkov, Linear Augmented Cylindrical Wave Method for Nanotubes Electronic Structure, Int. J. Quantum Chem., 2015 DOI:10.1002/qua.25000.
- P. N. D’yachkov and D. V. Makaev, Account of Helical and Rotational Symmetries in the Linear Augmented Cylindrical Wave Method for Calculating the Electronic Structure of Nanotubes: Towards the ab initio Determination of the Band Structure of a (100, 99) Tubule, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 195411 CrossRef.
- P. N. D’yachkov, D. Z. Kutlubaev and D. V. Makaev, Linear Augmented Cylindrical Wave Green’s Function Method for Electronic Structure of Nanotubes with Substitutional Impurities, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 035426 CrossRef.
- P. N. D’yachkov and D. Kutlubaev, Spin-Orbit Gaps in Armchair Nanotubes Calculated using the Linear Augmented Cylindrical Wave Method, IOP Conf. Ser.: Mater. Sci. Eng., 2012, 38, 012003 CrossRef.
- J. B. Conklin, L. E. Johnson and G. W. Pratt, Energy Bands in PbTe, Phys. Rev., 1965, 137, A1282–A1294 CrossRef.
-
R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D’Arco, M. Llunell, M. Causà and Y. Noël, CRYSTAL14 User’s Manual, University of Torino, Torino, 2014 Search PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid Functionals Based on a Screened Coulomb Potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS PubMed.
- J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, Screened Hybrid Density Functionals Applied to Solids, J. Chem. Phys., 2006, 124, 154709 CrossRef CAS PubMed.
- M. F. Peintinger, D. Vilela Oliveira and T. Bredow, Consistent Gaussian Basis Sets of Triple-Zeta Valence with Polarization Quality for Solid-State Calculations, J. Comput. Chem., 2012, 34, 451–459 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
-
A. S. Davydov, Quantum Mechanics, Pergamon Press, Oxford, New York, 2nd edn, 1965 Search PubMed.
-
L. I. Schiff, Quantum Mechanics, McGraw-Hill, New York, 1949 Search PubMed.
-
V. Galitski, B. Karnakov, V. Kogan and V. Galitski Jr, Exploring Quantum Mechanics: A Collection of 700+ Solved Problems for Students, Lecturers, and Researchers, Oxford University Press, Oxford, UK, 2013 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. 




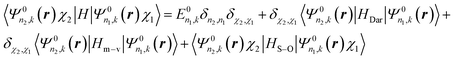

![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–)∞, with the calculated C
C–)∞, with the calculated C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C and C–C bonds being equal to 1.23 and 1.32 Å, respectively. Fig. 2 shows the LCAO and LACW band structures for this semiconducting phase.
C and C–C bonds being equal to 1.23 and 1.32 Å, respectively. Fig. 2 shows the LCAO and LACW band structures for this semiconducting phase.


 given elsewhere into account,8,41–43 we obtain:
given elsewhere into account,8,41–43 we obtain:


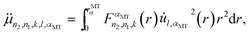
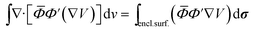
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) Φ′(∇V)] =
Φ′(∇V)] = ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) Φ′(∇2V) + (∇V) × (∇
Φ′(∇2V) + (∇V) × (∇![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) )Φ′ + (∇V) × (∇Φ′)
)Φ′ + (∇V) × (∇Φ′)![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif)

 into account, we have
into account, we have
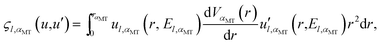



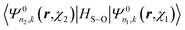 have been given in our previous publication8 and are not repeated here.
have been given in our previous publication8 and are not repeated here.




