Kinetics and mechanism for OH-initiated gas-phase chemistry of α-terpineol†
Yan Zhaoa,
Haitao Sunb,
Mei Qinb,
Renjun Wanga and
Laixiang Xu*a
aSchool of Life Sciences, Qufu Normal University, Qufu, 273165, P. R. China. E-mail: xlx150723@163.com; Fax: +86-537-4456887
bSchool of Chemistry and Chemical Engineering, Qufu Normal University, Qufu, 273165, P. R. China
First published on 26th October 2015
Abstract
α-terpineol, mainly released from widely used cleaning products, is an important indoor air pollutant. In this paper, the OH-initiated degradation mechanism of α-terpineol was studied by employing Density Functional Theory (DFT) method. A reaction scheme is proposed for the initial steps. Two barrierless addition processes and the H7-abstraction from the ring are found to be the main reaction pathways. The products, such as 6-hydroxy-hept-5-en-2-one, 4-oxopentanal, acetone, and 4-methyl-3-cyclohexen-1-one, have been detected experimentally, which are confirmed by this theoretical investigation. The suggested formation mechanism of 4-methyl-3-cyclohexen-1-one in the experimental study is not energetically feasible; instead, here an energetically favorable pathway is reported for the first time. The overall rate constant of the title reaction is evaluated to be 1.29 × 10−10 cm3 per molecule per s. The gas-phase residential time of α-terpineol with respect to OH is about 3.1 hours.
1. Introduction
Volatile organic compounds (VOCs) with a high vapor pressure, can be easily released into indoor air from various VOC emission sources, acting as the main air pollutants in the indoor environment.1 Previous experimental results have showed that VOC concentrations indoors are 10 times higher than in outdoor environments.2–5 Therefore, the influence of long-term exposure to indoor air contaminants on the health of human beings has attracted more and more attention. It has already been accepted that extensive exposure to VOCs can cause various acute and chronic health effects, such as acute and chronic respiratory effects, neurological toxicity (e.g., fatigue, headaches, etc.), eye and throat irritation, and even lung cancer.5–11 Hence, the fate of VOCs in indoor environments is worth studying.Terpenoids as common additives to numerous consumer products (perfumes, soaps, shampoos, deodorants, etc.) and also a prevalent VOC indoors, have received increasing attention.12–16 Most of the terpenoids are reported to be present at significant indoor concentrations.17,18 Among them, 1-methyl-4-isopropyl-1-cyclohexen-8-ol (α-terpineol, Scheme 1) is the main component of indoor cleaner emissions and pine oil,17 as well as an emission from some molds existing in the indoor environment.19–21
Once emitted into the indoor air, α-terpineol tends to undergo complex chemical transformations by O3, OH radicals, and NO3 radicals existed in air,22 generating various more irritating secondary pollutants (such as alcohols, aldehydes, ketones, dicarbonyls, carboxylic acids, and organic nitrates).3 Based on the above, we can conclude that the gas-phase oxidation of α-terpineol has great influences on the indoor air quality, which should be systematically investigated. Unfortunately, little is known about the gas-phase chemistry of α-terpineol. Jones and Ham have investigated the indoor reaction mechanism and the products formed during the reaction between α-terpineol and NO3 radicals. The rate constant of the NO3 radical with α-terpineol was measured by a relative rate method.23 Wells, et al. have studied the gas-phase oxidation of α-terpineol by OH radicals and O3 in the presence of NOx using smog chamber GC/MS techniques.24 The rate constants were determined to be (1.9 ± 0.5) × 10−10 and (3.0 ± 0.2) × 10−16 cm3 per molecule per s, respectively. Several reaction products were analyzed using the mass spectrometry. Nevertheless, the actual reaction pathways for the observed products have been still unclear due to the lack of geometric parameters for intermediate radical species. Direct experimental detection of the intermediate species is extremely difficult because of their short lifetimes. Quantum chemical calculations have been proven to be a promising way to determine the geometrical structures of the reactants, intermediates, transition states and products created in the detailed reaction mechanism and to investigate the kinetics property of the corresponding reaction system.25–28
Considering that there are currently no experimental or theoretical kinetic data on the OH-initiated reactions, here we performed a theoretical study on the OH-initiated gas-phase oxidation reaction of α-terpineol in the indoor environment using density function theory (DFT).29 The rate constants were evaluated by employing the multichannel Rice–Ramsperger–Kassel–Marcus (RRKM) theory to find out the rate controlling steps of the distinct reaction pathways.
2. Computational methods
The quantum chemical calculations were performed using the Gaussian 09 program suite.30 The MPWB1K function was employed to optimize the geometries of the reactants, intermediates, transition states and products at the MPWB1K/6-31+G(d,p) level in this paper.31 It is well known that MPWB1K and BB1K methods give good results for barrier height and reaction energy calculations with the mean unsigned errors of about 1 kcal mol−1.31–33 The selection of the MPWB1K method for this work is detailed in the ESI.† The harmonic vibrational frequency calculations at the same level of theory were used to identify that whether the optimized structures are the true minima or the transition state. For each transition state, the intrinsic reaction coordinate (IRC) was calculated to determine the connections between the reactants, the transition states, and the products.34 To accurately obtain total electronic energies, additional single-point high-level ab initio calculations were carried out at the MPWB1K/6-311+G(3df,2p) level of computation upon MPWB1K/6-31+G(d,p) optimized structures. The potential energy surface profile was conducted at the MPWB1K/6-311+G(3df,2p)//MPWB1K/6-31+G(d) level including zero-point vibration energy (ZPVE) correction.The kinetic calculations including tunneling corrections were carried out using Rice–Ramsperger–Kassel–Marcus (RRKM) theory with the open source MESMER program.35,36 The reliability of the tunneling corrections is detailed in the ESI.† This method has been successfully applied to several theoretical studies.37,38
The microcanonical rate constants were computed using the RRKM equation:
 | (1) |
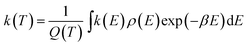 | (2) |
3. Results and discussion
The reliability of the calculated results in this study was validated first. The experimental information on the thermochemical parameters for α-terpineol is not available and the direct comparison between the theoretical calculations and the experimental data becomes impossible. Hence, we performed the geometry optimization and frequency calculation of cyclohexene and ethanol. The results at the MPWB1K/6-31+G(d,p) level agree fairly well with the corresponding experimental values. The largest deviation remains within 1.8% for geometrical parameters and 7.0% for vibrational frequencies.39,40 Consequently, we believe that the MPWB1K-DFT/6-31+G(d,p) method is a general and reliable method for the calculations involved in the OH-initiated oxidation of α-terpineol.3.1. Reaction mechanism
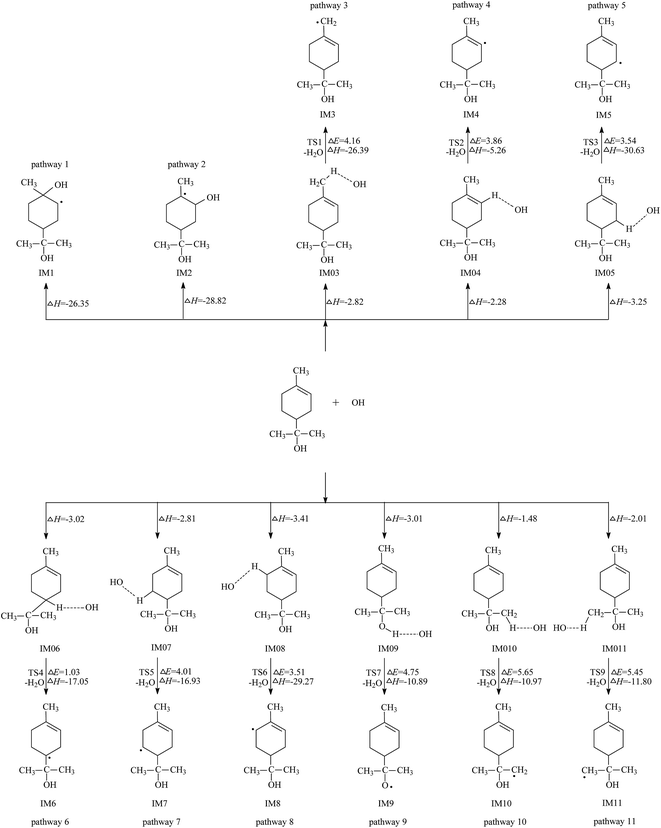
Pathways 1 and 2 represent the OH addition to C2 and C3 sites in carbon–carbon double bond, respectively. IM1 (secondary radical) and IM2 (tertiary radical) are the corresponding adducts. Calculation shows that both addition processes are barrierless. The electronic energies of IM1 and IM2 are 26.35 and 28.82 kcal mol−1 lower than the total energy of the separate reactants (α-terpineol and OH), respectively. Thus, pathway 1 and 2 can occur readily under the general gas-phase conditions due to their large exoergicity. This provides a theoretical verification for the prior study result.43 As energy-rich radical intermediates, IM1 and IM2 will further react with the oxidizing species, such as O2 and NO, which are abundant in indoor air environment.
As illustrated in Fig. 1, pathways 3, 10 and 11 are three kinds of H abstraction from different –CH3 moieties; pathways 4, 5, 6, 7 and 8 represent four possible hydrogen abstractions from the ring; pathway 9 is H abstraction from the –OH group attached to the C8 atom. Comparisons of the nine H abstraction processes show that the abstraction in C5–H7 bond, i.e. pathway 6, is the most energetically favorable process. This reaction process can be completed through two elementary steps. The first step is the approaching of OH to the atom H7, which leads to the formation of the pre-complex IM06 with a stabilization energy of −3.02 kcal mol−1. Then, the H7 atom is abstracted by OH radical to form IM6 and H2O via the transition state TS4. The bond lengths of the C5–H7 and O2–H7 in TS4 are 1.166 Å and 1.432 Å, respectively. This process has a very low energy barrier of 1.03 kcal mol−1. The energy of IM6 lies 20.07 kcal mol−1 below reactants. The same as IM1 and IM2, further reaction of IM6 in indoor air is also ineluctable due to its high reactivity.
3.2. Subsequent reactions
According to the above discussion, both addition and H7 abstraction processes are the dominant pathways for the gas-phase degradation of α-terpineol initiated by OH radicals. Therefore, two additional processes similar to the analogous OH–α-pinene reactions are dominant confirmed in previous experimental and theoretical study.44,45 In this Section, further reactions of the major primary products, IM1, IM2, and IM6, will be discussed in detail. | ||
| Fig. 2 Subsequent reaction paths of IM1 at the MPWB1K/6-31+G(d,p) level of theory. Unit: kcal mol−1. ΔE: the reaction potential barrier; ΔH: the reaction heat. | ||
For IM14, three possible reaction modes are found and described in Fig. 2. The first one includes three elementary steps: ring-opening reaction, O2 addition, and HO2 elimination. The ring-opening reaction occurs via the cleavage of C2–C3 bond to yield IM15. The energy barrier and endothermic heat are 8.55 and 3.57 kcal mol−1, respectively. Then, O2 attacks to C2 to generate a peroxide radical (IM16). This process is strongly exothermic by 35.56 kcal mol−1. IM16 is likely to undergo a direct decomposition to form the products 3-(2-hydroxypropan-2-yl)-6-oxoheptanal (P2) and HO2. A five-member ring transition state, TS13, is identified with the barrier of 12.17 kcal mol−1. However, the reaction heat and Gibbs free energy change are 11.81 and 5.53 kcal mol−1, respectively, which indicates that this process is unlikely to occur spontaneously at room temperature. This is in good agreement with the previously reported experimental results.24 The second channel is initiated from the C3–C4 bond rupture via the transition state TS14. The formation of IM17 is an exoergic process, with the emitting heat of 7.70 kcal mol−1 and energy potential barrier of 13.45 kcal mol−1. Similar to IM12, the subsequent reactions of IM17 with O2/NO also occur via two free-barrier steps to produce IM19. IM19 is not a stable product and will immediately decompose into the oxyl radical IM20 and NO2, which needs to surmount the barrier height of 19.19 kcal mol−1. The following reaction is the direct H abstraction by O2 molecule via the transition state TS16 with an energy barrier of 17.91 kcal mol−1. The production of 2-hydroxy-5-(2-hydroxypropan-2-yl)-2-methylhexanedial (P3) and HO2 accompanies the exothermic heat of 29.24 kcal mol−1. The third pathway is the reaction of IM14 with O2, similar to the intermediate IM20 mentioned above, to produce 2-hydroxy-5-(2-hydroxypropan-2-yl)-2-methylcyclohexan-1-one (P4) and HO2. This reaction process has an apparent barrier of 17.30 kcal mol−1. Through the above analysis, P3 and P4 are the possible products from further reaction of IM14.
 | ||
| Fig. 3 Subsequent reaction paths of IM2 at the MPWB1K/6-31+G(d,p) level of theory. Unit: kcal mol−1. ΔE: the reaction potential barrier; ΔH: the reaction heat. | ||
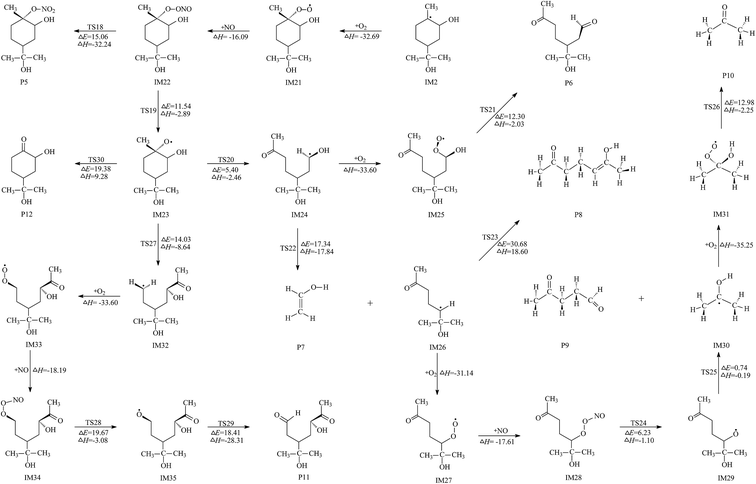
The first one is carried out by the fission of C2–C3 bond in IM23 via the transition state TS20 to generate IM24. This reaction has a low potential barrier of 5.40 kcal mol−1 and is exothermic by 2.46 kcal mol−1. IM24 is an open-shell radical and could subsequently react via the reaction with O2 or the self-decomposition reaction. First, the active site C3 in IM24 is attacked by the oxygen molecule, which is a free-barrier exothermic reaction, to result in IM25. Then, HO2 is dissociated to form the product 3-(2-hydroxypropan-2-yl)-6-oxoheptanal (P6) via TS21 with the energy barrier of 12.30 kcal mol−1. This decomposition reaction is found to be endothermic with the energy of 12.03 kcal mol−1. Moreover, the Gibbs free energy change is 4.03 kcal mol−1. As a consequence, this decomposition process is difficult to occur spontaneously under normal conditions. Second, the self-decomposition is the breakage of C4–C5 bond to form ethenol (P7) and IM26 via the transition state TS22. In TS22 structure, the length of C4–C5 bond is 2.256 Å, which is elongated by 46.40% with respect to IM24. This process has a potential barrier of 17.34 kcal mol−1 and is exothermic by 17.34 kcal mol−1. Two reaction pathways are open for IM26. The first channel is the breaking of C5–C8 bond to form 6-hydroxy-hept-5-en-2-one (P8) and methyl (CH3). TS23 is the corresponding transition state with the potential barrier of 30.68 kcal mol−1, which means this decomposition reaction is energetically favorable under general condition. The structure of TS23 is shown in Fig. S2.† The second route is the reaction with O2/NO through two barrierless associations, to produce IM28. The intermediate IM28 is one energy-rich radical which can react via two serial decomposition processes, resulting in the production of 4-oxopentanal (P9) and IM30 radical. Calculations show that these two elementary reactions can easily occur because of low potential barriers and exothermic property. IM30 is an open-shell radical and will react with O2 to generate a peroxide intermediate IM31 with 35.25 kcal mol−1 exothermicity. Subsequently, H12 migration and C8–O2 bond cleavage occur simultaneously, leading to the final product acetone (P10) and HO2 radical. This process has an energy barrier of 12.98 kcal mol−1 and is believed to proceed easily indoors. According to the description above, P7, P8, and P9 are the preferred products for this removal pathway of IM23.
The second channel of IM23 includes four elementary reactions: two barrierless processes (O2 addition and NO addition) and two elementary processes with apparent potential barriers (cleavage of O4–O5 bond and direct H11 abstraction by O2). TS28 and TS29 are the corresponding transition states and their geometric parameters are given in Fig. S2.† The calculated results manifest that these elementary steps are energetically favorable under normal conditions, which means that the product of 5-hydroxy-3-(2-hydroxypropan-2-yl)-6-oxoheptanal (P11) should exist in smog chamber. Unfortunately, P11 was not detected in the study of Wells.24 Further experimental observation would be anticipated to confirm the formation of P11.
The third channel is the direct decomposition of IM23 via the rupture of C1–C2 bond to produce 2-hydroxy-4-(2-hydroxypropan-2-yl)cyclohexan-1-one (P12) and CH3. The calculated profiles of the potential energy surface show that this channel is energetically unfavorable due to the high barrier and strong endothermicity. In other worlds, P12 is not the final product of the OH-initiated gas-phase reaction of α-terpineol.
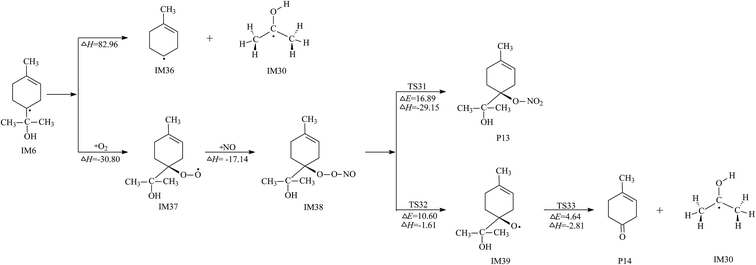
Another possible removal pathway of IM6 was revealed in this study. The detailed reaction scheme for this reaction pathway of IM6 is shown in Fig. 4. IM6 may react easily with O2 and NO, in turn, via two exothermic processes to generate IM38. The structure of IM38 is shown in Fig. S3,† which is similar to IM13 and IM22. Also, two possible reaction routes are considered. One route is the formation of P13 via the isomerization of IM38, which has a potential barrier of 16.89 kcal mol−1 and is highly exothermic by 29.15 kcal mol−1. The other route is the formation of P14 that involves two self-decomposition reactions. Calculations show that both decomposition processes are energetically favorable due to low potential barriers. Unluckily, this formation pathway of P14 was not considered in Jones' study.23 This energetically favorable formation pathway of P14 is reported for the first time and its confirmation needs further more experimental investigations.
3.3. Rate constants calculations
According to the data calculated by Gaussian 09, the kinetic calculations are performed using the RRKM method. The rate constants of the elementary reactions involved in this reaction system were calculated at 298 K and 1 atm. The computational results are presented in Table 1, and after the errors were considered, the rate constants at 298 K are listed in Table S1.† The overall rate constant of α-terpineol + OH (Table 1) is 1.29 × 10−10 cm3 per molecule per s, which is in keeping with the experimental value of 1.9 × 10−10 cm3 per molecule per s at 298 K and 1 atm total pressure. It could be deduced that our RRKM results listed in Table 1 are reasonable. With the comparison of individual rate coefficients, OH addition to C2 and C3 atoms and H abstraction from C5 atom, i.e. the formation of IM1, IM2 and IM6, are the dominant pathways. This conclusion accords well with the thermodynamic data in Section 3.1. The kinetical data mentioned above would be conductive to the construction of dynamic model predicting the transport and fate of α-terpineol and OH radical in indoor air.| Reactions | Rate constants | Reactions | Rate constants |
|---|---|---|---|
| R + OH → IM1 | 5.95 × 10−11 | IM21 + NO → IM22 | 4.36 × 10−12 |
| R + OH → IM2 | 6.37 × 10−11 | IM22 → P5 | 4.78 × 10 |
| R + OH → IM3 + H2O | 2.10 × 10−13 | IM22 → IM23 + NO2 | 5.17 × 104 |
| R + OH → IM4 + H2O | 1.31 × 10−14 | IM23 → IM24 | 2.66 × 107 |
| R + OH → IM5 + H2O | 7.04 × 10−13 | IM24 + O2 → IM25 | 5.40 × 10−12 |
| R + OH → IM6 + H2O | 3.64 × 10−12 | IM25 → P6 + HO2 | 1.41 × 104 |
| R + OH → IM7 + H2O | 1.96 × 10−14 | IM24 → IM26 | 2.85 × 10−8 |
| R + OH → IM8 + H2O | 7.19 × 10−13 | IM26 → P8 + CH3 | 4.52 × 10−10 |
| R + OH → IM9 + H2O | 1.73 × 10−15 | IM26 + O2 → IM27 | 5.90 × 10−12 |
| R + OH → IM10 + H2O | 1.27 × 10−15 | IM27 + NO → IM28 | 6.21 × 10−12 |
| R + OH → IM11 + H2O | 1.37 × 10−13 | IM28 → IM29 + NO2 | 2.96 × 107 |
| R + OH | (k)1.29 × 10−10 | IM29 → IM30 + P9 | 2.43 × 109 |
| IM1 + O2 → IM12 | 5.78 × 10−12 | IM30 + O2 → IM31 | 6.01 × 10−12 |
| IM12 + NO → IM13 | 7.11 × 10−12 | IM31 → P10 + HO2 | 2.31 × 103 |
| IM13 → P1 | 1.06 | IM23 → IM32 | 4.32 × 10 |
| IM13 → IM14 + NO2 | 2.22 × 103 | IM32 + O2 → IM33 | 5.35 × 10−12 |
| IM14 → IM15 | 3.46 × 106 | IM33 + NO → IM34 | 6.45 × 10−12 |
| IM15 + O2 → IM16 | 5.43 × 10−12 | IM34 → IM35 + NO2 | 0.12 |
| IM16 → P2 + HO2 | 9.80 × 103 | IM35 + O2 → P11 + HO2 | 5.71 × 10−53 |
| IM14 → IM17 | 1.52 × 103 | IM23 → P12 + CH3 | 1.09 × 10−2 |
| IM17 + O2 → IM18 | 5.28 × 10−12 | IM6 + O2 → IM37 | 5.96 × 10−12 |
| IM18 + NO → IM19 | 5.83 × 1012 | IM37 + NO → IM38 | 6.10 × 10−12 |
| IM19 → IM20 + NO2 | 0.10 | IM38 → P13 | 1.08 |
| IM20 + O2 → P3 + HO2 | 7.20 × 10−53 | IM38 → IM39 + NO2 | 7.18 × 104 |
| IM14 + O2 → P4 + HO2 | 4.50 × 10−27 | IM39 → IM30 + P14 | 1.68 × 108 |
| IM2 + O2 → IM21 | 5.78 × 10−12 |
The residence time of α-terpineol in indoor air can be calculated by the formula 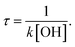 Here, k is the total rate constant of the title reaction and [OH] is the average indoor OH concentration with the value about 7 × 105 molecule per cm3.46 The gas phase retention time of α-terpineol determined by OH radicals is approximately 3.1 hours at 298 K and 1 atm total pressure.
Here, k is the total rate constant of the title reaction and [OH] is the average indoor OH concentration with the value about 7 × 105 molecule per cm3.46 The gas phase retention time of α-terpineol determined by OH radicals is approximately 3.1 hours at 298 K and 1 atm total pressure.
4. Conclusions
In this paper, the gas-phase oxidation mechanism of α-terpineol initiated by OH radical was investigated by using a high-accuracy quantum chemical method. All of the rate constants were calculated using the MESMER program. The following conclusions can be obtained based on the theoretical calculations:(1) There are two possible reaction mechanisms (OH additions and H abstractions) during the reaction between α-terpineol and OH radical. According to different chemical environments, two sites for OH addition and nine distinct sites for hydrogen abstraction are identified. Among the primary reactions, two free-barrier addition processes and the H7-abstraction from the ring are the main reaction pathways.
(2) Based on our calculation results, 2-hydroxy-5-(2-hydroxypropan-2-yl)-2-methylhexane-dial (P3), 2-hydroxy-5-(2-hydroxypropan-2-yl)-2-methylcyclohexan-1-one (P4), 6-hydroxy-hept-5-en-2-one (P8), 4-oxopentanal (P9), and acetone (P10) are the energetically feasible products from the pathways of OH addition to the >C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C< bond. 4-Methyl-3-cyclohexen-1-one (P14) is the possible product of the most favorable H-abstraction pathway. The suggested formation mechanism of P14 in the study of Jones is unreasonable. An energetically favorable formation pathway for P14 is reported for the first time.
C< bond. 4-Methyl-3-cyclohexen-1-one (P14) is the possible product of the most favorable H-abstraction pathway. The suggested formation mechanism of P14 in the study of Jones is unreasonable. An energetically favorable formation pathway for P14 is reported for the first time.
(3) The rate constant calculations show that OH radicals are preferred to react with α-terpineol through addition reaction at 298 K and 1 atm. The total rate constant of the title reaction is 1.29 × 10−10 cm3 per molecule per s, which matches well with the available experimental values. The gas-phase residential time of α-terpineol with respect to OH is about 3.1 hours.
Acknowledgements
This work is supported by National Natural Science Foundation of China (No. 21207078, 31270417, and 31200400), China Postdoctoral Science Foundation (No. 2012M511513), Shandong Province Postdoctoral Special Fund Innovative Projects (No. 201203035), Qufu Normal University Research Fund (No. XJ201206) and Fundamental Research Funds of Shandong University (No. 2015JC020).References
- H. Guo, S. C. Lee, L. Y. Chan and W. M. Li, Environ. Res., 2004, 94, 57–66 CrossRef CAS PubMed.
- C. J. Weschler, Sci. World J., 2001, 1, 443–457 CrossRef CAS PubMed.
- C. J. Weschler and H. C. Shields, Atmos. Environ., 1997a, 31, 3487–3495 Search PubMed.
- Indoor air quality-a comprehensive reference book, ed. M. Maroni, B. Seifert and T. Lindvall, Elsevier Publishers, Amsterdam, 1995 Search PubMed.
- D. Otto, H. Hudnell, D. House, L. Molhave and W. Counts, Arch. Environ. Health, 1992, 47, 23–30 CrossRef CAS PubMed.
- B. T. Burton, Volatile organic compounds, Dekker, New York, 1997 Search PubMed.
- M. J. Hodgson, J. Frohlinger, E. Permar, C. Tidwell, N. D. Traven, S. A. Olenchock and M. Karpf, J. Occup. Med., 1991, 33, 527–533 CAS.
- L. Molhave, Indoor Air, 1991, 1, 357–376 Search PubMed.
- L. Molhave, G. Clausen, B. Berglund, J. D. Ceaurriz, A. Kettrup, T. Lindvall, M. Maroni, A. C. Pickering, U. Risse, H. Rothweiler, B. Seifert and M. Younes, Indoor Air, 1997, 7, 225–240 CAS.
- L. Molhave, J. G. Jensen and S. Larsen, Atmos. Environ., Part A, 1991, 25, 1283–1293 CrossRef.
- E. Ota and E. Mulberg, Exposure to formaldehyde from indoor air, Technical Report ARB/RD-90–01, California Air Resources Board, 1990 Search PubMed.
- J. C. Harrison and J. E. Ham, Int. J. Chem. Kinet., 2010, 42, 669–675 CrossRef CAS.
- A. Lapczynski, C. S. Letizia and A. M. Api, Food Chem. Toxicol., 2008, 46, S126–S127 CrossRef CAS PubMed.
- A. Lapczynski, C. S. Letizia and A. M. Api, Food Chem. Toxicol., 2008, 46, S114–S116 CrossRef CAS PubMed.
- V. T. Politano, E. M. Lewis, A. M. Hoberman, M. S. Christian, R. M. Diener and A. M. Api, Int. J. Toxicol., 2009, 28, 80–87 CrossRef CAS PubMed.
- W. W. Nazaroff and C. J. Weschler, Atmos. Environ., 2004, 38, 2841–2865 CrossRef CAS.
- J. M. Logue, T. E. Mckone, M. H. Sherman and B. C. Singer, Indoor Air, 2011, 21, 92–109 CrossRef CAS PubMed.
- B. C. Singer, H. Destaillats, A. T. Hodgson and W. W. Nazaroff, Indoor Air, 2006, 16, 179–191 CrossRef CAS PubMed.
- B. Wessen and K. O. Schoeps, Analyst, 1996, 121, 1203–1205 RSC.
- P. Gao and J. Martin, Appl. Occup. Environ. Hyg., 2002a, 17, 430–436 Search PubMed.
- P. Gao, F. Korley, J. Martin and B. T. Chen, J.–Am. Ind. Hyg. Assoc., 2002, 63, 135–140 CrossRef CAS.
- M. S. Waring and J. R. Wells, Atmos. Environ., 2015, 106, 382–391 CrossRef CAS.
- B. T. Jones and J. E. Ham, Atmos. Environ., 2008, 42, 6689–6698 CrossRef CAS.
- J. R. Wells, Environ. Sci. Technol., 2005, 39, 6937–6943 CrossRef CAS PubMed.
- Q. Zhang, X. Qu, H. Wang, F. Xu, X. Shi and W. Wang, Environ. Sci. Technol., 2009, 43, 4105–4112 CrossRef CAS PubMed.
- L. Tadeu, B. Leonardo, C. S. Edilson and A. Graciela, J. Phys. Chem. A, 2011, 115, 7709–7721 Search PubMed.
- X. Sun, C. Zhang, Y. Zhao, J. Bai, Q. Zhang and W. Wang, Environ. Sci. Technol., 2012, 46, 8148–8155 CrossRef CAS PubMed.
- X. Sun, J. Bai, Y. Zhao, C. Zhang, Y. Wang and J. Hu, Atmos. Environ., 2011, 45, 6197–6203 CrossRef CAS.
- M. S. Waring and J. R. Wells, Atmos. Environ., 2015, 106, 382–391 CrossRef CAS.
- M. Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, revision A. 02, Gaussian. Inc., Wallingford, CT, 2009, 270, 271 Search PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 6908–6918 CrossRef CAS.
- Y. Zhao, B. J. Lynch and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 2715–2719 CrossRef CAS.
- J. J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 808–821 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS.
- P. J. Robinson and K. A. Holbrook, Unimolecular Reactions, Wiley, New York, 1972 Search PubMed.
- S. H. Robertson, D. R. Glowacki, C. H. Liang, C. Morley and M. J. Pilling, MESMER (Master Equation Solver for Multi-Energy Well Reactions), an object oriented C++ program for carrying out ME calculations and eigenvalue-eigenvector analysis on arbitrary multiple well systems, available from: http://sourceforge.net/projects/mesmer, 2008.
- J. Zhou, J. W. Chen, C. H. Liang, Q. Xie, Y. N. Wang, S. Y. Zhang, X. L. Qiao and X. H. Li, Environ. Sci. Technol., 2011, 45, 4839–4845 CrossRef CAS PubMed.
- D. R. Glowacki, C. H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560 CrossRef CAS PubMed.
- S. Coussan, Y. Bouteiller and J. P. Perchard, J. Phys. Chem. A, 1998, 102, 5789–5793 CrossRef CAS.
- CCCBDB (Computational Chemistry Comparison and Benchmark Database), available from: http://cccbdb.nist.gov/, 2015.
- R. Atkinson, J. Phys. Chem. Ref. Data, Monogr., 1989, Monograph 1 Search PubMed.
- R. Atkinson, J. Phys. Chem. Ref. Data, Monogr., 1994, Monograph 2 Search PubMed.
- R. S. Boethling and D. Mackay, Handbook of property estimation methods for chemicals: environmental and health sciences, Lewis Publishers, New York, 2000 Search PubMed.
- M. E. Davis and P. S. Stevens, Atmos. Environ., 2005, 39, 1765–1774 CrossRef CAS.
- L. Vereecken and J. Peeters, J. Phys. Chem. A, 2000, 104, 11140–11146 CrossRef CAS.
- G. Sarwar, R. Corsi, Y. Kimura, D. Allen and C. J. Weschler, Atmos. Environ., 2002, 36, 3973–3988 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra14781f |
| This journal is © The Royal Society of Chemistry 2015 |