Memory effect in weakly-interacting Fe3O4 nanoparticles†
Abstract
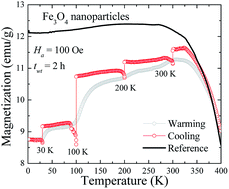
This study addresses the issue of whether the magnetite Fe3O4 nanoparticle shows a true spin-glass like behavior or if this is an artifact of interparticle interaction. Transmission electron microscopy and X-ray diffraction pattern analysis confirms the formation of pseudospherical Fe3O4 nanoparticles with a grain size of 8(1) nm. The magnetic moment relaxation M(t) follows a stretched exponential and power law function, confirming the presence of multiple-magnetic anisotropic barriers (β = 0.51(1)) and weak-interparticle interaction (n = 0.60(4)). The observed field cooling (FC) memory effect occurs because of the presence of magnetic anisotropy arising from a broad size distribution and weak-interparticle interactions. The absence of the zero-field-cooled (ZFC) memory effect signals that the Fe3O4 nanoparticle system is not a true spin-glass system, and the observed decreasing behavior of magnetization in FC measurement is an artifact of the weak-interparticle interaction.

 Please wait while we load your content...
Please wait while we load your content...