Interaction between dislocation mechanics on diffusion induced stress and electrochemical reaction in a spherical lithium ion battery electrode
Zhijun Liua,
Jianqiu Zhou*ab,
Bingbing Chena and
Jianwei Zhua
aDepartment of Mechanical and Power Engineering, Nanjing Tech University, Nanjing, Jiangsu Province 210009, China. E-mail: zhouj@njut.edu.cn; liuzhijun@njut.edu.cn.com; Fax: +86-25-83374190; Tel: +86-25-83588706
bDepartment of Mechanical Engineering, Wuhan Institute of Technology, Wuhan, Hubei Province 430070, China
First published on 24th August 2015
Abstract
The effect of coupling dislocation induced stress with electrochemical reaction in a spherical battery electrode is investigated. A new coupled model among diffusion, dislocation, reversible electrochemical reaction is established by combining diffusion induced stress (DIS), dislocation induced stress and forward reaction induced stress in the spherical electrode. The results of our model show that the interaction between dislocation induced stress and the forward reaction induced stress plays a significant role in decreasing the tensile stress and even the tensile state can be turned into the compressive stress, which may become a factor in resistance to fracture and decrepitation due to DIS. However, the electrochemical reaction results in the surface tangential stresses sharply increasing with a larger relative rate of reaction and diffusion. Therefore, we provide a new theoretical method to explain the volume change and understand the stress evolution in the electrode.
1. Introduction
Lithium ion batteries (LIBs) have been considered as the most promising alternative and green options for energy storage applied in portable electronic devices, hybrid electric vehicles (HEVs), plug-in hybrid electric vehicles (PHEVs) and other electric utilities, because of their low weight, non-toxicity, high capacity storage and high energy density compared to conventional batteries.1,2 Recent research on anodes for LIBs has been mainly focused on electrode materials and material structure design in terms of their morphologies. Significantly, there have been some successes in addressing material stability issues by designing nanostructured silicon materials including nanowires, nanotubes, nanoporous films and silicon nanoparticle carbon composites.3 This nanostructuring strategy has greatly increased the cycle life of anodes to up to a few hundred cycles with 80% capacity retention.3 However, there are still many challenges needing to be addressed for materials undergoing large volume changes. Silicon has a large charge storage capacity, low voltage plateau and low cost and this makes it an attractive anode material.4,5 However, Si suffers from large volume variation (+270%)5 during lithiation, which causes particle pulverization and amorphization, loss of electrical contact, and early cycling capacity fading.6 Owing to volume variation during Li insertion into or extraction from the active material of electrode in LIBs, there are different stresses such as diffusion induced stress (DIS), reaction stress and dislocation induced stress, which may cause fracture, and possibly cause irreversible capacity loss of the electrode.6–8 It is urgent to study the stresses in the electrode in attempts to increase the mechanical durability.Kalnaus et al. analyzed the cracking of silicon particles during Li intercalation by using the theory of DIS.9 Verbrugge and co-workers suggested that the tendency for fracture and decrepitation could be reduced or avoided by reducing the material size to the nanometer range.10–12 Chen et al. analyzed fracture damage of nanowire lithium-ion battery electrodes affected by DIS.13 Wei et al. took into account dislocation mechanics on the DIS within a spherical particle.14 Cheng et al. provided a detailed description of the effect of operating conditions, electrode particle size, particle shape and phase transformation on DISs in electrodes.10 Yang et al. studied the coupled problem of interactions of stress and diffusion.15 McMeeking et al. analyzed the role of solid mechanics in electrochemical energy systems within lithium-ion batteries.16 Verbrugge et al. studied battery cycle life prediction with coupled chemical degradation and fatigue mechanics.17 Cui et al. developed a mathematical framework to investigate the interaction between bulk diffusion and interfacial chemical reaction in binary systems.18 Chakraborty et al. studied the mechanical and chemical effects in the deformation and failure of a cylindrical electrode particles in a Li-ion battery.19 Zhang et al. analyzed the effect of reversible electrochemical reaction on Li diffusion and stresses in cylindrical Li-ion battery electrodes.7 Larché and Cahn considered the effect of stresses on local diffusion in a solid, where the coupling between diffusion and chemical stresses was addressed.20 Lee et al. studied DIS in a hollow cylinder.21 Hao et al. studied that DIS of core–shell nanotube electrodes in lithium-ion batteries.22 Bucci et al. analyzed two separate electrochemical reactions at the Si/electrolyte interface to characterize the mechanical and electrochemical response of thin film amorphous Si electrodes during cyclic lithiation.23 Wu et al. presented a coupled thermal–electrochemical modeling of uneven heat generation in lithium-ion battery packs.24 Yang et al. studied the insertion-induced expansion of a thin film on a rigid substrate.25 Li et al. provided an analytical modeling of dislocation effect on DIS in a cylindrical lithium ion battery electrode.26 Chen et al.27,28 analyzed the distribution of dislocation in a nanostructured thin film electrode and the effect of misfit dislocation on Li-ion diffusion and stress in a spherical electrode. Cheng et al. used a thermal stress analysis approach to investigate DIS evolution at the two-phase boundary during the lithiation process.29 Tavassol et al. studied the electrochemical surface stress changes during Li deposition in a model system for Li-ion battery anodes.30
Most of above mentioned analyses and studies have studied the effect of DIS affected by various influencing factors based on dislocation mechanics, solid mechanics, electrochemical theory and establishment of theoretical models. However, few works have considered the importance of the coupling between dislocation mechanics and electrochemical reaction in Li-ion battery electrodes.
In this paper, the influence of DIS and the reaction induced stress in a spherical Li-ion battery electrode is studied by studying dislocation mechanics and the reversible electrochemical reaction. Some new relations between electrochemical stresses and DIS are formulated, from which an analytical dislocation mechanics and electrochemical reaction are obtained. In this paper, we aim to study the following three aspects.
(i) Calculating and studying the DIS, dislocation-induced stress and electrochemical reaction induced stress on potentiostatic charging operation.
(ii) Providing a coupled model for explaining stresses in Li-ion battery spherical electrodes by studying the interactional effects of dislocation mechanics and electrochemical reaction.
(iii) Providing a new theoretical model to understand the volume changes and stress evolution in the electrode.
2. Analysis and methods
2.1 Diffusion-induced stresses in the spherical electrode
In this paper, consider spherical silicon negative electrode particles (storage particles) in the range of 0 < r < R, where R is the radius of the spherical electrode. Fig. 1 is a schematic of a lithium-ion battery showing the two electrodes (positive and negative), the separator and current collectors. The electrodes consist of active storage particles and Li-ions flow through the separator from the positive electrode to the negative electrode during charging and vice versa during the discharging process. Fig. 2a shows a schematic illustration of the storage particles inserting Li-ion, which is subjected to diffusion stresses, chemical stresses and dislocation-induced stress. During charging, Li-ion migrates along radial direction through the surface of electrode simultaneously and inward to the center of electrode. The process of inserting Li-ion into the storage particles causes a change in volume which leads to diffusion, stress and dislocation. During the diffusion process, reversible reaction occurs on the electrode/electrolyte interfaces. The DIS arising from the lithium ion insertion or extraction from the electrode is similar to the thermal stresses arising from heat transfer, whereas the thermal diffusivity mimics the lithium-ion diffusivity, and the temperature gradient represents the lithium-ion concentration gradient.24 So we introduce DIS by analogy to thermal stress.31,32 We assume that the electrode is an isotropic, linearly elastic solid. Therefore, the constitutive equations associated with lithium ion concentration in the solid spherical coordinate can be given by:
 | (1) |
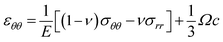 | (2) |
Because of the symmetry of sphere, the radial and tangential strains in the infinitesimal formulation of deformation can be expressed as functions of radial displacement, u, as:
 | (3) |
Considering that lithium ion diffusion in electrode material is much slower than elastic deformation and the mechanical equilibrium is much faster than the diffusion equilibrium,33 we can treat the mechanical equilibrium as a static equilibrium problem. Therefore, the force equilibrium in the axis-symmetric case is:
 | (4) |
The stress boundary conditions for the spherical model can be expressed as follows:
| σrr/r=R = 0, σrr/r=0 = finite | (5) |
Regardless of the dislocation mechanism, based on eqn (1)–(5), the expressions of radial and tangential stresses can be written as:
 | (6) |
 | (7) |
2.2 Dislocation model in the spherical electrode
According to the work of Prussin,34 an arbitrary radial infinitesimal element surface layer with the thickness of dr is shown in Fig. 2b. The solute concentration at the bottom of the diffused layer is assumed as c(r, t) in radii r position. Then the concentration on the upper surface r + Δr becomes . By exerting the solute concentration gradient, the expression of dislocation density is written as:14
. By exerting the solute concentration gradient, the expression of dislocation density is written as:14
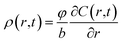 | (8) |
Wei et al. studied dislocation density in terms of the solute concentration gradient.14 Prussin34 found that when this surface stress exceeds the stress, σg, necessary to generate dislocation, the generated dislocations lie in the surface and their Burgers vectors have a positive edge component in the surface. However, they did not further study the relation between the stress and dislocation. So we assumed that dominating effect on the interaction between dislocations and diffusing solutes is the contribution to the long-range term. The relation between the stress and dislocation density can be achieved from the work of Estrin:35
 | (9) |
2.3 Electrochemical reaction induced stresses in spherical electrode
It is known that Li-ion inserted into or extracted from the electrode can cause a volume change. The electrochemical reaction can also create a volume change due to the atomic volume of reactants being different from that of the reaction product. The insertion of Li-ion into the electrode is a complicated process, which involves diffusion of Li-ion in electrolyte, migration of Li-ion through the solid electrolyte interphase (SEI), charge transfer at the SEI–electrode interface, and diffusion/reaction in the electrode.36 So the following reversible reactions occur during the insertion of Li-ion in the electrode:| Li+ + e− ⇌ Li (at the electrolyte/electrode interface) | (10a) |
| Li + xSi ⇌ LiSix (in the electrode) | (10b) |
The forward reaction can make the electrode expand and the backward reaction will make it shrink, so they can create the pressure and tension, respectively. The volumetric strain εdiffusion created by Li diffusion is:34,37
| εdiffusion = cΩ | (11) |
The volumetric strain εreaction created by formation of the reaction products is:
| εreaction = ψ(w1 − w2) | (12) |
In this paper, we will neglect the presence of a sharp interface between lithiated and unlithiated domains in the electrode for Li insertion. According to “The Law of Mass Action” of Devereux8 and the work of Yang,38 we considered a reversible electrochemical reaction of first order in the electrode. So w1 and w2 can be written as:38
 | (13) |
 | (14) |
Considering the isotropic deformation due to Li diffusion and electrochemical reaction, we can obtain the resultant volumetric strain created by the Li diffusion and electrochemical reaction by using eqn (11)–(14) as follows:
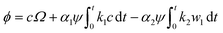 | (15) |
Under the generalized plane strain condition and following the linear theory of thermoelasticity in deriving the Duhamel–Neumann equations,39 the diffusion–reaction-induced stress in a spherical electrode can be obtained:
 | (16) |
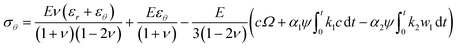 | (17) |
The items related to concentration c represents the stress induced by Li diffusion and those connected to α1, α2 represent the stress induced by the forward reaction and the backward reaction, respectively. If we ignore the effect of electrochemical reaction, i.e., α1 = α2 = 0, eqn (16) and (17) reduce to the constitutive relations for DIS. Besides, the forward reaction can make the electrode expand and the backward reaction will make it shrink, so they can create pressure and tension, respectively. The compressive stress induced by forward reaction σ1 and tension stress induced by backward reaction σ2 can be obtained:
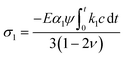 | (18) |
 | (19) |
It is obvious that dislocation-induced stress σζ and the forward reaction induced stress σ1 can act as a resistance to the process of diffusion during lithium-ion insertion and extraction and the backward reaction σ2 enhances the process of diffusion. Here, a coupled model considering dislocation-induced stress, electrochemical reaction stress and diffusion-induced stress will be firstly proposed. It has been found that the backward reaction can be ignored for both galvanostatic and potentiostatic charging.7 So the diffusion–reaction–dislocation-induced stresses in a spherical electrode at any location and time can be expressed as:
 | (20) |
 | (21) |
Therefore, DIS at any time and location of the spherical electrode, with the resistance of dislocation and the forward reaction, can be obtained if the composition profile is known. For illustration these purposes, we choose corresponding parameters in recent literatures for a Li-ion battery electrode material which are listed in Table 1.
| Parameter | Symbol | Value |
|---|---|---|
| Young’s modulus of lithiated Si | E | 30–80 Gpa |
| Poisson’s ratio | ν | 0.22 |
| Burgers vector | b | 2.532 Å |
| Maximum stoichiometric Li concentration | cs max | 2 × 10−5 m3 s−1 |
| Diffusion coefficient | D | 2 × 10 m3 mol−1 |
| Partial molar volume of solute | Ω | 2.0152 × 104 mol m−3 |
| Taylor orientation factor | M | 1.732–3.06 |
| Empirical constant | χ | 0.33 |
| Lattice constant of Si | a | 5.431 Å |
| The relative rate of reaction and diffusion | ϖ | 0–1 |
In a spherical electrode, consider the transport of the solute from outer surfaces into the interior along the radial direction of the electrode. We assume the diffusion of Si is a single-phase process and the deformation of electrode, as a linear elastically isotropic solid, is a quasi-static process. The diffusion equation can be written as:40
 | (22) |
In the paper, we merely study the interaction between dislocation effect on DIS and electrochemical reaction stress to explain the volume change and stress evolution in the electrode. As the electrochemical reaction is reversible, the respective roles between forward and backward reaction should be identified. Under potentiostatic operation, the boundary conditions and the initial solute concentration for the spherical electrode are given by:
| c|r=0 = finite | (23) |
| c|r=R = cR | (24) |
| c|0≤r≤R = c0 | (25) |
With the consideration of the diffusion equation and the boundary conditions in eqn (5) and (6), the solute concentration during insertion for potentiostatic operation can be expressed as:40
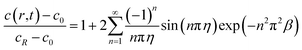 | (26) |
The solute concentration is correspondingly varying with change of time and location. Fig. 3a shows the solute concentration increases with time, and reduces continuously from the surface to the center of the spherical electrode during the charging process for potentiostatic control.
Regardless of dislocation and electrochemical reaction effect, substituting eqn (26) into eqn (6) and (7), the associated radial and tangential stresses are:
 | (27) |
 | (28) |
3. Results and discussion
Fig. 3b shows the radial stresses as a function of time and position during potentiostatic charging. The radial stresses are tensile in the spherical electrode and the surface radial stress is zero. The tensile radial stress decreases monotonically from the center of the electrode to the surface and the highest stress occurs in the center. Then the radial stress at the center reduces continuously with increasing concentration. The tangential stress is compressive at the surface and tensile at the center of the sphere electrode as is shown in Fig. 3c. The maximum tangential stress occurs at the surface at time zero. The tangential stress varies from compressive at the surface to tensile in the center consequent of the expansion of outer region being restrained by the inner region.Taking account of dislocation effects, we take eqn (8) and (26) into eqn (9) to obtain the solution for dislocation induced stress:
 | (29) |
Fig. 3d illustrates the dislocation induced stress generated by solute diffusion during potentiostatic charging under different times and location. The dislocation induced stresses are tensile in the spherical electrode and the dislocation induced stress in the center is zero. The maximum dislocation induced stress is at the surface of sphere, which has the peak value at the beginning of charging as a result of the maximum solute concentration gradient, and reduces as charging proceeds.
With the consideration of electrochemical reaction effects, we define a parameter τ = α1ψk1 as the forward reaction factor. Here the relative rate of forward reaction and diffusion ϖ = τ/Ω vary from 0 to 1.7 We can substitute eqn (26) into (18) to obtain the solution for the forward reaction induced stress:
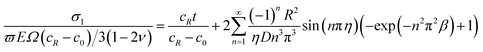 | (30) |
Fig. 4 shows the forward reaction induced stress in the spherical electrode during potentiostatic charging under different relative rates of reaction and diffusion ϖ. The relative rates of reaction and diffusion play an important role in determining the electrochemical reaction. Comparing Fig. 4a with b, the reaction induced stress with ϖ = 0.5 is about five times than that with ϖ = 0.1, indicating that reaction induced stress is much larger than DIS. The forward reaction induced stress begins to increase as the process of charging proceeds while Li-ion enters the electrode from the outer region. The forward reaction induced stress is compressive in the spherical electrode. The forward reaction induced stress gradually increases from the center to the surface of the electrode and the maximum reaction induced stress occurs at the surface. It can be found that the electrochemical reaction mechanism has a significant effect on the distribution of all kinds of stresses. Meanwhile, the forward reaction will enhance the compressive stress and decrease DIS to some extent. The tangential stress increases significantly while the electrochemical reaction is very rapid compared with the diffusion, which will accelerate structural cracking or capacity loss of the electrode. Therefore, the reaction induced stress can be regarded as a “double-edge sword”, and when properly used it is beneficial.
The radial stress and tangential stress as a function of dislocation during potentiostatic charging are illustrated in Fig. 5a and b. The dashed lines in Fig. 5 denote the DIS with the influence of dislocation while the solid lines show the reverse effect. By comparing the dashed lines with the solid lines, it can be seen that the radial stresses and tangential stresses are decreased significantly with the influence of dislocation. It is interesting to note that the tensile stresses are converted to compressive stresses under the charging process, which will decrease the propagation of cracks induced by tensile stress in the electrode. By comparing Fig. 4 with Fig. 5, we find that the influence of electrochemical reaction is stronger than that of dislocation.
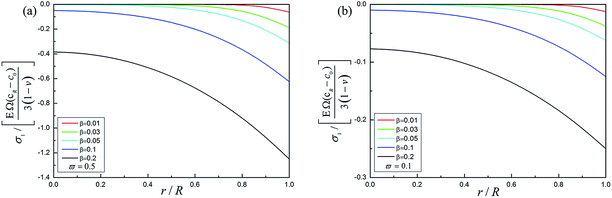
The corresponding radial, tangential stresses for ϖ = 0.5 and radial, tangential stresses for ϖ = 0.1 are shown in Fig. 6 with the influence of the forward reaction without the dislocation effect during potentiostatic charge under different radial position and different dimensionless time. The dashed lines in Fig. 6 denote the DIS with the influence of electrochemical reaction while the solid lines show the reverse effect. It can be found that the radial stresses and tangential stresses in the outer region are decreased significantly and radial stresses are even converted to compressive stresses. Comparing Fig. 6b with Fig. 6d, DIS is decreased more with a larger relative rate of reaction and diffusion.
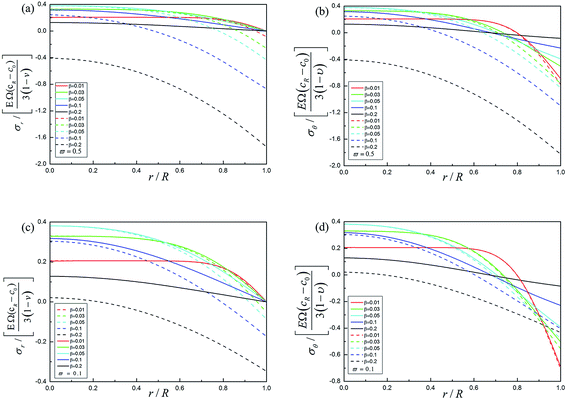
Fig. 7 shows the radial, tangential stresses in ϖ = 0.5 and radial, tangential stresses in ϖ = 0.1 combining the forward reaction and the dislocation during potentiostatic charging at different positions and time. Coupling the forward reaction with the dislocation, DIS will be decreased at some extent, which is helpful in prolonging the cycle life of the spherical electrode and decreasing the propagation of cracks induced by tensile stress in the electrode. However, under the condition of larger relative reaction and diffusion, the electrochemical reaction will play a dominant role in impacting the mechanical properties of the spherical electrode and even in turn make the electrode more prone to cracking. These numerical results account for electrochemical reaction and dislocation interaction. It is found that the coupled effect plays a significant role in determining the process of stress evolution. Furthermore, we found that, for a lower ϖ, the forward electrochemical reaction is helpful to relax the tensile stress and inhibit bulk diffusion, which is consistent to the results found by Cui.18
4. Summary and conclusions
In this paper, the interaction between dislocation effect on DIS and electrochemical reaction mechanism has been investigated by providing a coupled model considering the influence of coupling the dislocation induced stress with the forward reaction induced stresses in a spherical electrode during potentiostatic charging. Following the model used in diffusion equations and the theory of linear elasticity, it has been found that electrochemical reaction and dislocation mechanism have a more significant effect on DIS. With the coupled effect, the radial and tangential tensile stresses are decreased sharply and radial stresses are even converted to compressive stresses, and crack generation and propagation caused by tensile stresses will be decreased by some extent. However, the electrochemical reaction will result in the surface tangential stresses increasing sharply with a larger relative rate of reaction and diffusion. It is noteworthy that the outer region in the electrode tends to have a larger relative density of fractures, which makes it easier to crack. From these mechanical theories, the spherical electrode materials with lower relative rate of reaction and diffusion ϖ and high dislocation density are expected to be able to inhibit DIS and optimize their stability and cycling capacity. Our theoretical model based on the coupled effect in a spherical electrode, show that the lithiation process and stress evolution are impacted by interaction between dislocation mechanics on DIS and electrochemical reaction. Our numerical results suggest a strategy to relax tensile stress quickly by increasing the electrochemical reaction and dislocation density, which are similar with recent real experimental observations2,41–45 and mathematical frameworks.14,18 By building this new relationship of dislocation and electrochemical reaction in spherical electrodes, this paper presents a new theoretical method to optimize the mechanical properties of electrode materials, and will lead to environmental and economic benefits.Acknowledgements
This work was supported by Key Project of Chinese Ministry of Education (211061), National Natural Science Foundation of China (10502025, 10872087, 11272143), Program for Chinese New Century Excellent Talents in university (NCET-12-0712). PhD programs Foundation of Ministry of Education of China (20133221110008).References
- X. Su, Q. Wu, X. Zhan, J. Wu, S. Wei and Z. Guo, J. Mater. Sci., 2012, 47, 2519 CrossRef CAS.
- X. H. Liu and J. Y. Huang, Energy Environ. Sci., 2011, 4, 3844 CAS.
- H. Wu, G. Chan, J. W. Choi, I. Ryu, Y. Yao, M. T. McDowell, S. W. Lee, A. Jackson, Y. Yang, L. Hu and Y. Cui, Nat. Nanotechnol., 2012, 7, 310 CrossRef CAS PubMed.
- N. Liu, Z. Lu, J. Zhao, M. T. McDowell, H. W. Lee, W. Zhao and Y. Cui, Nat. Nanotechnol., 2014, 9, 187 CrossRef CAS PubMed.
- C. Pereira-Nabais, J. Światowska, A. Chagnes, A. Gohier, S. Zanna, A. Seyeux, P. Tran-Van, C.-S. Cojocaru, M. Cassir and P. Marcus, J. Phys. Chem. C, 2014, 118, 2919 CAS.
- X. Xiao, P. Liu, M. W. Verbrugge, H. Haftbaradaran and H. Gao, J. Power Sources, 2011, 196, 1409 CrossRef CAS PubMed.
- T. Zhang, Z. Guo, Y. Wang and J. Zhu, J. Appl. Phys., 2014, 115, 083504 CrossRef PubMed.
- F. D. O., Topics in Metallurgical Thermodynamics, Wiley, New York, 1983 Search PubMed.
- S. Kalnaus, K. Rhodes and C. Daniel, J. Power Sources, 2011, 196, 8116 CrossRef CAS PubMed.
- R. Deshpande, Y.-T. Cheng and M. W. Verbrugge, J. Power Sources, 2010, 195, 5081 CrossRef CAS PubMed.
- Y.-T. Cheng and M. W. Verbrugge, J. Appl. Phys., 2008, 104, 083521 CrossRef PubMed.
- M. W. Verbrugge and Y.-T. Cheng, J. Electrochem. Soc., 2009, 156, A927 CrossRef CAS PubMed.
- B. Chen, J. Zhou, X. Pang, P. Wei, Y. Wu and K. Deng, RSC Adv., 2014, 4, 21072 RSC.
- P. Wei, J. Zhou, X. Pang, H. Liu, K. Deng, G. Wang, Y. Wu and B. Chen, J. Mater. Chem. A, 2014, 2, 1128 CAS.
- F. Yang, Mater. Sci. Eng., A, 2005, 409, 153 CrossRef.
- R. M. McMeeking and R. Purkayastha, Proc. I.U.T.A.M. Symp. Opt. Methods Mech. Solids, 2014, 10, 294 Search PubMed.
- R. Deshpande, M. Verbrugge, Y.-T. Cheng, J. Wang and P. Liu, J. Electrochem. Soc., 2012, 159, A1730 CrossRef CAS PubMed.
- Z. Cui, F. Gao and J. Qu, J. Mech. Phys. Solids, 2013, 61, 293 CrossRef CAS PubMed.
- J. Chakraborty, C. P. Please, A. Goriely and S. J. Chapman, Int. J. Solids Struct., 2015, 54, 66 CrossRef CAS PubMed.
- F. C. Larché and J. W. Cahn, Acta Metall. Mater., 1992, 40, 947 CrossRef.
- S. Lee, W. L. Wang and J. R. Chen, Mater. Sci. Eng., A, 2000, 285, 186 CrossRef.
- F. Hao and D. Fang, J. Appl. Phys., 2013, 113, 013507 CrossRef PubMed.
- G. Bucci, S. P. V. Nadimpalli, V. A. Sethuraman, A. F. Bower and P. R. Guduru, J. Mech. Phys. Solids, 2014, 62, 276 CrossRef CAS PubMed.
- B. Wu, V. Yufit, M. Marinescu, G. J. Offer, R. F. Martinez-Botas and N. P. Brandon, J. Power Sources, 2013, 243, 544 CrossRef CAS.
- F. Yang, J. Power Sources, 2013, 241, 146 CrossRef CAS PubMed.
- J. Li, Q. Fang, F. Liu and Y. Liu, J. Power Sources, 2014, 272, 121 CrossRef CAS PubMed.
- B. Chen, J. Zhou, J. Zhu and Z. Liu, RSC Adv., 2014, 4, 64216 RSC.
- B. Chen, J. Zhou, J. Zhu, T. Liu and Z. Liu, J. Electrochem. Soc., 2015, 162, H493 CrossRef CAS PubMed.
- C.-K. ChiuHuang and H.-Y. Shadow Huang, J. Electrochem. Soc., 2013, 160, A2184 CrossRef CAS PubMed.
- H. Tavassol, M. K. Y. Chan, M. G. Catarello, J. Greeley, D. G. Cahill and A. A. Gewirth, J. Electrochem. Soc., 2013, 160, A888 CrossRef CAS PubMed.
- S. P. Timoshenko and J. N. Goodier, Theory of Elasticity, McGraw-Hill, New York, 1970 Search PubMed.
- J. C. J. H. S. Carslaw, Conduction of Heat in Solids, Clarendon, Oxford, 1959 Search PubMed.
- Y.-T. Cheng and M. W. Verbrugge, J. Power Sources, 2009, 190, 453 CrossRef CAS PubMed.
- S. Prussin, J. Appl. Phys., 1961, 32, 1876 CrossRef CAS PubMed.
- Y. Estrin, J. Mater. Process. Technol., 1998, 80–81, 33 CrossRef.
- M. M. Kamisah, H. Siti Munirah and M. S. Mansor, Ionics, 2007, 13, 223 CrossRef CAS.
- J. C.-M. Li, Metall. Trans. A, 1978, 9, 1353 CrossRef.
- F. Yang, J. Appl. Phys., 2010, 107, 103516 CrossRef PubMed.
- B. A. Boley and J. H. Weiner, Theory of Thermal Stress, Dover Publications, Mineola, New York, 1997 Search PubMed.
- J. Crank, The Mathematics of Diffusion, Oxford University, UK, 1998 Search PubMed.
- S. W. Lee, M. T. McDowell, J. W. Choi and Y. Cui, Nano Lett., 2011, 11, 3034 CrossRef CAS PubMed.
- M. J. Chon, V. A. Sethuraman, A. McCormick, V. Srinivasan and P. R. Guduru, Phys. Rev. Lett., 2011, 107, 045503 CrossRef CAS.
- L.-F. Cui, R. Ruffo, C. K. Chan, H. Peng and Y. Cui, Nano Lett., 2009, 9, 491 CrossRef CAS PubMed.
- C. K. Chan, H. Peng, G. Liu, K. McIlwrath, X. F. Zhang, R. A. Huggins and Y. Cui, Nat. Nanotechnol., 2008, 3, 31 CrossRef CAS PubMed.
- S. W. Lee, M. T. McDowell, L. A. Berla, W. D. Nix and Y. Cui, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4080 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |